The $AA$-iterative algorithm in hyperbolic spaces with applications to integral equations on time scales

1.   Introduction

Fixed point (fp) theorems have extensive applications in multiple disciplines. In economics, Arrow ^[1] applied these theorems to demonstrate the impossibility of a perfect voting system, a cornerstone of social choice theory. The Turing fp theorem ^[2] in computer science established the undecidability of the halting problem, a fundamental concept in the field. In physics, the fp theory is instrumental in comprehending quantum system behaviors (see ^[3]). Image processing leverages fp algorithms for image registration, aligning images for purposes such as medical imaging (see ^[4]). In game theory, Nash ^[5] employed fp theorems to prove the existence of Nash equilibria in non-cooperative games. In finance, fp methods are crucial for deriving the Black-Scholes equation ^[6], a pivotal model in financial mathematics. Social sciences utilize fp theory to study network architecture, social dynamics, and system stability (see ^[6]). Optimization techniques, like the Gauss-Seidel method for solving linear equations, frequently use fp iterations (see ^[7]). The original approach of Hutchinson ^[8] to fractals considers the defining equation as an fp problem. Barnsley and Vince ^[9] used fp theorems to demonstrate that the 'chaos game' technique almost always produces the attractor of an iterated function system. In short, the fp theory is an effective method for solving equations in many fields. The first fp theorem was given by Brouwer ^[10] in 1912. However, this theorem is not valid in infinite dimensional spaces. The first fp theorem for infinite dimensional Banach spaces was provided by Schauder ^[11] in 1930. The Schauder fp theorem guarantees the existence of fps for continuous maps defined on a compact, convex subset of a Banach space. Despite the extensive attention researchers have dedicated to analytical solutions, their scarcity in numerous scenarios remains a challenging yet accepted reality.

Given these circumstances, researchers have used iterative algorithms to seek approximate solutions. One prominent approach is the Picard iterative algorithm ^[12], which is used for contraction maps in the Banach fp theorem ^[13]. However, the Picard iterative algorithm may not always converge to an fp in the class of nonexpansive maps. Alternatively, there are several iterative schemes in the literature having various steps, for example, Mann iteration ^[14] (one-step), Ishikawa iteration ^[15] (two-step), and Noor iteration ^[16] (three-step) for approximating fps of nonexpansive maps in Banach spaces. In 2007, Agarwal et al. ^[17] introduced a two-step iteration independent of the Mann and Ishikawa iterative algorithms. This iterative algorithm is more applicable than the Picard, Mann, and Ishikawa iterative algorithms because it converges faster than these iterative algorithms for contraction maps and works for nonexpansive maps. In 2014, Abbas and Nazir ^[18] introduced a three-step iterative algorithm, which converges faster than Agarwal et al. iterative algorithm. In 2016, Thakur et al. ^[19] proposed a new three-step iterative algorithm to approximate the fps of nonexpansive maps, proving that it converges faster than existing algorithms for contraction maps. In 2018, Ullah and Arshad ^[20] proposed a new three-step iterative algorithm, called the $M$-iterative algorithm, to approximate the fps of Suzuki generalized nonexpansive maps in Banach spaces. In 2020, Ali and Ali ^[21] introduced the three-step $F$-iterative algorithm, which slightly modifies the $M$-iterative algorithm and is independent of all iterative schemes in the existing literature. They proved that this iterative algorithm converges faster than other iterative algorithms.

Abbas et al. ^[22] introduced a new four-step iterative algorithm, termed the $AA$-iterative algorithm, in Banach spaces as follows:

Using this iterative algorithm, they established a stability outcome for enriched contraction maps and convergence outcomes for enriched nonexpansive maps in Banach spaces with an application to a delay fractional differential equation. Also, they proved that the $AA$-iterative algorithm converges faster than all the previously mentioned iterative algorithms for enriched contraction maps. Moreover, Beg et al. ^[23] presented the strong and weak convergence outcomes of the $AA$-iterative algorithm (1.1) for generalized $\alpha$-nonexpansive maps in Banach spaces with an application to a delay composite functional differential equation. Later, Asghar et al. ^[24] approximated the fps of generalized $\alpha_m$-nonexpansive maps employing the $AA$-iterative algorithm in the structure of modular spaces and proved the stability theorem of this iterative algorithm for $m$-contraction maps in the modular space. In the same year, Suanoom et al. ^[25] proved the strong and weak convergence results using the $AA$-iterative algorithm for the generalized $AK$-$\alpha$-nonexpansive maps in Banach spaces. Asghar et al. ^[26] proposed an efficient inertial viscosity algorithm hybrid with the $AA$-iteration for approximating the common solution of more generalized nonlinear problems. Abbas et al. ^[27] also used the $AA$-iterative algorithm to approximate solutions for boundary value problems involving Caputo fractional differential equations and proved the stability theorem of this iterative algorithm in Banach spaces. All these studies have highlighted the widely adopted $AA$-iterative algorithm, which continues to advance computational techniques in finding fps and addressing other nonlinear problems.

Given the prevalence of nonlinear phenomena in nature, mathematicians and scientists continuously strive to devise techniques for addressing real-world nonlinear problems. Consequently, translating linear problems into their nonlinear counterparts holds significant relevance. Therefore, once the approximation of an fp is established in a Banach space, then the extension of such findings on a nonlinear domain, especially the hyperbolic space (HS) defined by Kohlenbach ^[28], is always desirable. The reason behind this fact is that the scope of many problems naturally falls within the HS setting.

Motivated by the above works, we investigate the $AA$-iterative algorithm's applicability in the HS. Our focus is developing the HS adaptation of the $AA$-iterative algorithm and establishing the weak $w^2$-stability theorem of this iterative algorithm for contraction maps. We also aim to obtain the strong and $\Delta$-convergence theorems of this iterative algorithm for generalized $(\alpha, \beta)$-nonexpansive $(G\alpha \beta N)$ maps in HSs. Furthermore, we furnish an illustrative example of $G\alpha \beta N$ maps and conduct a comparative analysis of convergence rates between the $AA$-iterative and other iterative algorithms for this class of maps. We employ our major findings to demonstrate practical applicability in solving linear Fredholm integral equations (FIEs) and nonlinear Fredholm-Hammerstein integral equations (FHIEs) on time scales, supported by a numerical example. Our study is more general and unifies the comparable results in the existing literature, such as those presented in ^[22,23,27].

2.   Preliminaries

2.1.   Essentials on metric and hyperbolic spaces

In this section, we provide essential definitions and theorems necessary for establishing our primary outcomes.

Consider a nonempty subset $L$ of a metric space $\mathbb{(M}, \varrho)$ and a map $\varphi:L \rightarrow L.$ The map $\varphi$ is called a contraction if there exists a constant $\theta \in \lbrack 0, 1)$ such that $\varrho(\varphi (u), \varphi (v))\leq \theta \varrho(u, v)$ for all $u, v\in L$. In the contraction map, if $\theta = 1$, that is, $\varrho(\varphi (u), \varphi (v))\leq \varrho(u, v)$, it is described as nonexpansive. Nonexpansive maps are a natural generalization of contraction maps. If $\varrho(\varphi (u), u^{\ast })\leq \varrho(u, u^{\ast })$ for all $u\in L$ and each $u^{\ast }\in F_\varphi,$ where $F_\varphi$ is the set of all fps of $\varphi$, it is called quasi-nonexpansive. All nonexpansive mappings with an fp are quasi-nonexpansive.

The class of nonexpansive maps has been extensively studied because of their diverse applications. Various authors have extensively studied different generalizations of nonexpansive maps (see, e.g., ^{[29,30,31,32,33,34]}). Below, we outline some of these maps.

Definition 1. Let $\varphi$ be a self-map on a nonempty subset $L$ of a metric space $\mathbb{(M}, \varrho)$. Then, the map $\varphi$ is said to be

(i) (see ^[29]) Suzuki generalized nonexpansive if for all $u, v\in L$,

(ii) (see ^[30]) generalized $\alpha$-nonexpansive if, for all $u, v\in L$, there exists $\alpha \in \lbrack 0, 1)$ such that

(iii) (see ^[31]) $\beta$-Reich-Suzuki-type nonexpansive if, for all $u, v\in L$, there exists $\beta \in \lbrack 0, 1)$ such that

It is clear that every nonexpansive map is Suzuki generalized nonexpansive, and the reverse is not always valid. See, for instance, the following example.

Example 1. [29, Example 1] Let $L = [0, 3]$ and set $\varphi :L\rightarrow L$ by

Here, the map $\varphi$ is a Suzuki generalized nonexpansive but not a nonexpansive.

When $\alpha = 0$ and $\beta = 0$ in Definition 1(ⅱ) and (ⅲ), respectively, the generalized $\alpha$-nonexpansive and $\beta$-Reich-Suzuki type nonexpansive maps are reduced to a Suzuki generalized nonexpansive map. The following example shows that the reverse implication does not generally hold.

Example 2. Let $\mathbb{M = \Re }$ be a space endowed with the usual metric $\varrho(u, v) = \vert u-v\vert$.

(i) (see [35, Example 4.6]) Let $L = [0, \infty)$ be a subset of $\mathbb{ \Re }$ and $\varphi :L\rightarrow L$ be defined as

Then, the map $\varphi$ is generalized $\frac{1}{3}$-nonexpansive but not a Suzuki generalized nonexpansive.

(ii) (see [31, Example 3.4]) Let $L = [-2, 2]$ be a subset of $\mathbb{\Re}$. Define $\varphi :L\rightarrow L$ by

Then, the map $\varphi$ is $\frac{1}{2}$-Reich-Suzuki type nonexpansive but not a Suzuki generalized nonexpansive.

In 2020, Ullah et al. ^[36] proposed a novel category of generalized nonexpansive maps that surpasses the scope of previously established classes, such as Suzuki generalized nonexpansive, generalized $\alpha$-nonexpansive, and $\beta$-Reich-Suzuki type nonexpansive maps. They also outlined the fundamental characteristics of this expanded class of maps.

Definition 2. A self map $\varphi$ on a nonempty subset L of a metric space $(\mathbb{M}, \varrho)$ is said to be $G\alpha \beta N$ if there exist $\alpha, \beta \in \Re ^{+}$ satisfying $\alpha +\beta < 1$ such that $\frac{1}{2}\cdot\varrho(u, \varphi (u))\leq \varrho(u, v)$ implies

for all $u, v\in L$.

Remark 1. The validity of the following statements is readily apparent.

(i) If $\varphi$ is identified as Suzuki generalized nonexpansive, it automatically qualifies as generalized $(0, 0)$-nonexpansive.

(ii) Whenever $\varphi$ is deemed generalized $\alpha$-nonexpansive, it implies its classification as generalized $(\alpha, 0)$-nonexpansive.

(iii) Given that $\varphi$ is characterized as $\beta$-Reich-Suzuki-type nonexpansive, it follows that $\varphi$ meets the criteria for being generalized $(0, \beta)$-nonexpansive.

Proposition 1. ^[36] Let $\varphi$ be a $G\alpha \beta N$ map. Then, the following statements are valid.

(i) If $F_\varphi\ne\emptyset$, then $\varphi$ is quasi-nonexpansive.

(ii) The set $F_\varphi$ is closed.

(iii) For all $u, v\in L,$

In 1990, Reich and Shafrir ^[37] introduced the concept of HS and investigated an iterative algorithm tailored for nonexpansive maps within these spaces. In 2004, Kohlenbach ^[28] expanded on this concept by providing a more comprehensive definition of HS.

Definition 3. ^[28] Let $(\mathbb{M}, \varrho)$ be a metric space. Then $(\mathbb{M}, \varrho, \mathcal{Q})$ will be the HS if the function $\mathcal{Q}:\mathbb{M}\times \mathbb{M}\times \lbrack 0, 1]\rightarrow \mathbb{M}$ satisfies the following properties

(i) $\varrho(z, \mathcal{Q}(u, v, \alpha))\leq \left(1-\alpha \right)\cdot\varrho(z, u)+\alpha\cdot\varrho(z, v),$

(ii) $\varrho(\mathcal{Q}(u, v, \alpha), \mathcal{Q}(u, v, \beta)) = \left\vert \alpha -\beta \right\vert\cdot\varrho(u, v),$

(iii) $\mathcal{Q}(u, v, \alpha) = \mathcal{Q}(v, u, 1-\alpha),$

(iv) $\varrho(\mathcal{Q}(u, z, \alpha), \mathcal{Q}(v, w, \alpha))\leq(1-\alpha)\cdot\varrho(u, v)+\alpha\cdot\varrho(z, w),$

for all $u, v, z, w\in \mathbb{M}$ and $\alpha, \beta \in \lbrack 0, 1].$

If $\mathbb{M}$ satisfies only condition (ⅰ), then the structure $(\mathbb{M}, \varrho, \mathcal{Q})$ coincides with the convex metric space described by Takahashi ^[38]. For the broader context of convex metric spaces, the subsequent equalities are valid: for all $u, v\in \mathbb{M}$, and $\alpha \in \lbrack 0, 1],$

It follows that

A linear instance of an HS is a Banach space, and nonlinear instances are Hadamard manifolds, the Hilbert open unit ball endowed with the hyperbolic metric, and CAT(0) spaces as defined by Gromov ^[39].

Here, we present an example of an HS which is not linear. Therefore, it is a non-trivial example of an HS.

Example 3. [31, Example 3.5] Let $\mathbb{M} = \{(u_{1}, u_{2})\in \Re ^{2}:u_{1}, u_{2} > 0\}$. Define $\varrho:\mathbb{M}\times \mathbb{M}\rightarrow [0, \infty)$ by

for all $u = (u_{1}, u_{2})$ and $v = (v_{1}, v_{2})$ in $\mathbb{M}$. Then, $(\mathbb{M}, \varrho)$ is a metric space. Now, for $\alpha \in \lbrack 0, 1]$, define a function $\mathcal{Q}:\mathbb{M}\times \mathbb{M}\times \lbrack 0, 1]\rightarrow \mathbb{M}$ by

Then, $(\mathbb{M}, \varrho, \mathcal{Q})$ is an HS but not a normed linear space.

In a given HS $(\mathbb{M}, \varrho, \mathcal{Q})$, a subset $L$ is termed convex if, for any scalar $\alpha\in[0, 1]$, the point $\mathcal{Q}(u, v, \alpha)$ lies within $L$ for all pairs of elements $u, v \in L$.

An HS $(\mathbb{M}, \varrho, \mathcal{Q})$ is uniformly convex if, for any $r > 0$ and $\epsilon \in (0, 2]$, there exists a constant $\delta \in (0, 1]$ such that

for all $u, v, \omega \in \mathbb{M}$ with $\varrho(u, \omega)\leq r$, $\varrho(v, \omega)\leq r$ and $\varrho(u, v)\geq r\cdot\epsilon.$

A map $\xi :(0, \infty)\times (0, 2]\rightarrow (0, 1]$ is called the modulus of uniform convexity if $\gamma = \xi (r, \epsilon)$ for any $r > 0$ and $\epsilon \in (0, 2]$. Additionally, the function $\gamma$ is termed monotone if it decreases with respect to $r$ for a fixed $\epsilon.$

Lemma 1. ^[40] Let $(\mathbb{M}, \varrho, \mathcal{Q})$ be a uniformly convex HS with the monotone modulus of convexity $\xi.$ Assume that $u\in \mathbb{M}$ and $\{\tau _{n}\}$ is a sequence in $[p, r]$ for some $p, r\in (0, 1).$ If $\{u_{n}\}$ and $\{v_{n}\}$ are sequences in $\mathbb{M}$ such that

for some $\varsigma\geq 0,$ then

Let $L$ be a nonempty subset of an HS $(\mathbb{M}, \varrho, \mathcal{Q})$, and $\{u_{n}\}$ be a bounded sequence in $\mathbb{M}$. For each $u\in \mathbb{M}$, define:

(ⅰ) asymptotic radius of $\left\{ u_{n}\right\}$ at $u$ by $A_r(u, \left\{ u_{n}\right\}): = \underset{n\rightarrow \infty }{\lim \sup } \text{ }\varrho(u, u_{n})$;

(ⅱ) asymptotic radius of $\left\{ u_{n}\right\}$ concerning $L$ by $A_r(L, \{u_{n}\}) = \inf \text{ }\{A_r(u, \{u_{n}\}):u\in L\}$;

(ⅲ) asymptotic center of $\left\{ u_{n}\right\}$ concerning $L$ by $A_{c}(L, \{u_{n}\}) = \{u\in L:A_{r}(u, \{u_{n}\}) = A_{r}(L, \{u_{n}\})\}.$

Lemma 2. ^[41] A bounded sequence $\{u_{n}\}$ in a complete uniformly convex HS $\mathbb{M}$ with the monotone modulus of uniform convexity $\xi$ has a unique asymptotic center concerning every nonempty closed convex subset L of $\mathbb{M}.$

In 1976, Lim ^[42] introduced the notion of $\Delta$-convergence, akin to weak convergence but applicable to metric spaces, employing the idea of the asymptotic center.

Definition 4. ^[42] In a metric space $(\mathbb{M}, \varrho)$, a sequence $\{u_n\}$ is $\Delta$-convergent to a point $u \in \mathbb{M}$ if $u$ serves as the unique asymptotic center for every subsequence $\{k_{n}\}$ of $\{u_n\}$.

Definition 5. ^[43] Two sequences $\{u_{n}\}$ and $\{p_{n}\}$ are said to be equivalent if

Timiş ^[44] defined the following concept of weak $w^2$-stability using equivalent sequences.

Definition 6. [44, Definition 2.4] Let $\mathbb{(M}, \varrho)$ be a metric space, $\varphi$ be a self-map on $\mathbb{M}$, and for arbitrary $u_{1}\in \mathbb{M}$, $\{u_n\}\subset\mathbb{M}$ be the iterative algorithm defined by

Suppose that $\{u_{n}\}$ converges strongly to $u^*\in F_\varphi$. If for any equivalent sequence $\{p_{n}\}\subset\mathbb{M}$ of $\{u_{n}\}$,

then the iterative sequence $\{u_n\}$ is said to be weak $w^2$-stable with respect to $\varphi$.

Remark 2. ^[44] Any stable iteration will be also weakly stable, but the reverse is generally not true.

2.2.   Fundamental information about time scales

In this section, we provide a concise overview of fundamental concepts in time scales. Time scale theory, which has garnered considerable interest recently, was pioneered by Hilger ^[45] in his Ph.D. thesis to bridge continuous and discrete analysis.

In this study, we denote a time scale by the symbol $\Gamma$, which signifies any arbitrary nonempty closed subset of the real numbers $\Re$. Well-known examples of time scales include $\Re$, $\mathbb{Z}$, $\mathbb{N}$, $[0, 1]$, and the Cantor set. However, $\mathbb{C}$, $\mathbb{Q}$, $\Re - \mathbb{Q}$, and $(0, 1)$ do not qualify as time scales.

The forward and backward jump operators $\sigma, \rho:\Gamma\rightarrow \Gamma$ are respectively defined by $\sigma (t) = \inf \{s\in \Gamma:s > t\}$ and $\rho (t) = \sup \{s\in \Gamma:s < t\},$ where we put $\inf \emptyset = \sup \Gamma$ and $\inf \Gamma = \sup \emptyset$. A point $t\in \Gamma$ is said to be right-dense if $\sigma (t) = t,$ right-scattered if $\sigma (t) > t,$ left-dense if $\rho (t) = t,$ left-scattered if $\rho (t) < t,$ isolated if $\rho (t) < t < \sigma (t),$ and dense if $\rho (t) = t = \sigma (t)$. The graininess function $\mu :\Gamma\rightarrow \lbrack 0, +\infty)$ is defined by $\mu (t) = \sigma (t)-t.$ If $\Gamma$ has a left-scattered maximum, then we define $\Gamma^{\kappa } = \Gamma-\max \Gamma$; otherwise, $\Gamma^{\kappa } = \Gamma.$

Definition 7. [46, Definition 1.10] Assume that $h:\Gamma\rightarrow$ $\Re$ is a function and fix $t\in \Gamma^{\kappa }$. The $\Delta$-derivative $h^{\Delta }(t)$ exists if, for every $\epsilon > 0$, there exists a neighbourhood $U = (t-\delta, t+\delta)\cap \Gamma$ for some $\delta > 0$ such that

Here, we illustrate an example of time scales.

Example 4. Let $\Gamma = \{\frac{n}{3}, \ n\in \mathbb{N} _{0} = \mathbb{N} \cup \{0\}\}$. For all $t\in\Gamma$, $\sigma (t) = t+\frac{1}{3}$ and $\mu (t) = \frac{1}{3}$. Then, all points of this time scale are right-scattered. Consider the continuous functions $h(t) = \frac{ t^{2}}{2}-\frac{t}{6}$ and $g(t) = \frac{t^{3}}{3}-\frac{t^{2}}{6}+\frac{t}{54}$ for $t\in \Gamma.$ By Theorem 1.16 in ^[46], we get

and

Definition 8. [46, Definition 1.1] A function $h:\Gamma\rightarrow$ $\Re$ is called rd-continuous, provided it is continuous at all right-dense points in $\Gamma$ and its left-sided limits exist (finite) at all left-dense points in $\Gamma.$

If $h$ is rd-continuous, then there exists a function $\mathcal{H}$ such that $\mathcal{H}^{\Delta }(t) = h(t)$ (see [46, Theorem 1.74]). In this case, the Cauchy $\Delta$-integral is defined by

Remark 3. [47, Theorem 2.14] Assume $c, d\in\Gamma$ and $c < d$. If $\Gamma =$ $\mathbb{R}$, then a bounded function $h$ on $[c, d)$ is $\Delta$-integrable from $c$ to $d$ if and only if $h$ is Riemann integrable on $[c, d)$ in the classical sense; in this case

where the integral on the right is the usual Riemann integral.

Theorem 1. ^[47] Let $c, d\in\Gamma$. Suppose $h$ and $g$ are $\Delta$-integrable on $[c, d)$.

(i) $h+g$ is $\Delta$-integrable and $\int\limits_{c}^{d}[h(t)+g(t)]\, \Delta t = \int\limits_{c}^{d}h(t)\, \Delta t + \int\limits_{c}^{d}g(t)\, \Delta t$.

(ii) If $h(t)\leq g(t)$ for all $t\in \lbrack c, d),$ then $\int\limits_{c}^{d}h(t)\, \Delta t\leq \int\limits_{c}^{d}g(t)\, \Delta t.$

(iii) Then $\left\vert \int\limits_{c}^{d}h(t)\cdot g(t)\, \Delta t\right\vert \leq \int\limits_{c}^{d}\left\vert h(t)\cdot g(t)\right\vert \, \Delta t\leq (\sup_{t\in \lbrack c, d)}\left\vert h(t)\right\vert)\cdot\int\limits_{c}^{d}\left\vert g(t)\right\vert \, \Delta t$.

Adomian ^[48] established a decomposition method in 1988, recently attracting much attention in applied mathematics and infinite series solutions. It is an effective method for solving a large class of differential and integral equations. The Adomian decomposition method defines the solution $u(t)$ by the series

or equivalently,

where the components $u_{n}(t),$ $n\in \mathbb{N} _{0}$, are to be determined recurrently. To establish the recursive relation, we substitute (2.3) into the following linear Fredholm integral equation (FIE) of the second kind on a time scale

where the kernel function $K(t, s)$ and the function $h(t)$ are given, the unknown function $u(t)$ must be determined, and $\lambda$ is a real parameter. Then, we obtain

By Theorem 1(ⅰ), we set

and so on for the other components, or equivalently,

Given (2.5), the components $u_{0}(t), u_{1}(t), u_{2}(t), ...$ are completely determined. The solution $u(t)$ of (2.4) in a series form is obtained using the series (2.3). In other words, the Adomian decomposition method converts the FIE into a determination of computable components. Note that the obtained series converges to the solution if an exact solution exists for (2.4).

3.   The weak $w^2$-stability result

Initially, we extend the $AA$-iterative algorithm (1.1) into HSs in the following manner:

where $\{\sigma _{n}\}, \{\rho _{n}\}$ and $\{\eta _{n}\}$ are real sequences in $[0, 1]$.

We prove the following strong convergence theorem, which will play a significant role in establishing our weak $w^2$-stability result.

Theorem 2. Let L be a nonempty, closed, and convex subset of an HS $\mathbb{M}$, $\varphi:L\rightarrow L$ be a contraction map with the constant $\theta \in \lbrack 0, 1)$ such that $F_\varphi \neq \emptyset$, and $\{u_{n}\}$ be an iterative sequence generated by (3.1). Then $\lim_{n\rightarrow \infty }u_{n} = u^{\ast},$ where $u^{\ast }\in F_\varphi$.

Proof. Let $u^{\ast }\in F_\varphi$. Using (3.1), we have

Since $\theta\in \lbrack 0, 1)$ and $0\leq\sigma _{n}\leq 1,$ then we know that $1-\sigma _{n}(1-\theta)\leq1.$ Thus, (3.2) becomes

We also obtain

Again, since $\theta\in \lbrack 0, 1)$ and $0\leq\rho _{n}\leq1,$ then we know that $1-\rho _{n}(1-\theta)\leq1.$ Thus, by (3.3), the inequality (3.4) becomes

From (3.1) and (3.5), we have

Since $\theta\in \lbrack 0, 1)$, by (3.3) and (3.6), we get

Finally, using (3.7) and the fact $\theta\in \lbrack 0, 1)$, we obtain

If we put $\varrho(u_{n}, u^{\ast }) = A_{n}$, then (3.8) takes the form

Hence, $\{A_{n}\}$ is a monotone decreasing sequence of real numbers. Furthermore, it is bounded below, so we have

Therefore, we get

□

Remark 4. The strong convergence theorem of the iterative algorithm (1.1) can be obtained as a corollary from Theorem 2.

Now, we prove that the modified iteration algorithm defined by (3.1) is weak $w^2$-stable.

Theorem 3. Suppose that all conditions of Theorem 2 hold. Then, the iterative algorithm (3.1) is weak $w^2$-stable with respect to $\varphi$.

Proof. We assume that the sequence $\{p_{n}\}\subset L$ is equivalent to the sequence $\{u_{n}\}$ defined by (3.1) and let the sequence $\{\epsilon_{n}\}\subset {\Re^+}$ be defined by

where $\{\sigma _{n}\}, \{\rho _{n}\}$ and $\{\eta _{n}\}$ are real sequences in $[0, 1]$. Suppose $\lim_{n\rightarrow \infty }\epsilon_{n} = 0$ and $u^{\ast }\in F_\varphi.$ Recalling that $\theta\in \lbrack 0, 1)$ and $0\leq\sigma _{n}, \eta_{n}, \rho_{n} \leq1,$ then it follows that $1-\sigma _{n}(1-\theta)\leq1, 1-\rho_{n}(1-\theta)\leq1$ and $1-\eta_{n}(1-\theta)\leq1$. So, we have

From (3.10), we obtain

Using (3.10) and (3.11), we have

By (3.1), (3.9), and (3.12), we get

As established in Theorem 2, $\lim_{n\rightarrow \infty }\varrho(u_{n}, u^{\ast }) = 0$. Therefore, we have $\lim_{n\rightarrow \infty }\varrho(u_{n+1}, u^{\ast }) = 0$. Because $\{u_{n}\}$ and $\{p_{n}\}$ are equivalent sequences, we have $\lim_{n\rightarrow \infty }\varrho(u_{n}, p_{n}) = 0$. Now, taking the limit of both sides of (3.13) and then using the assumption $\lim_{n\rightarrow \infty }\epsilon_{n} = 0$, it yields to $\lim_{n\rightarrow \infty }\varrho(p_{n+1}, u^{\ast}) = 0$. Thus, the iterative sequence $\{u_{n}\}$ is weak $w^2$-stable with respect to $\varphi$. □

Remark 5. Since the concept of weak $w^2$-stability is more general than the concept of stability, then Theorem 3 improves the stability results proved in ^[22,27].

4.   Convergence outcomes

For simplicity, we use $\mathbb{M}$ to represent a complete uniformly convex HS with the monotone modulus of uniform convexity $\xi$ for the rest of the paper.

We present the $\Delta$-convergence outcome of the modified iterative algorithm (3.1).

Theorem 4. Let L be a nonempty, closed, and convex subset of $\mathbb{M}$, $\varphi :L\rightarrow L$ be a $G\alpha \beta N$ map with $F_\varphi \neq \emptyset$, and $\{u_{n}\}$ be an iterative sequence generated by (3.1) with the real sequence $\{\sigma_{n}\}$ in $[p, r]$ for some $p, r\in (0, 1)$. Then, $\{u_{n}\}$ is $\Delta$-convergent to an fp of $\varphi.$

Proof. The proof is split into three parts.

Part 1. For any $u^{\ast }\in F_\varphi$, we prove that

Since $u^{\ast }\in F_\varphi$, by Proposition 1(ⅰ), $\varphi$ is a quasi-nonexpansive map, i.e.,

Now, using (3.1), we have

From (4.2), we obtain

By combining (4.2) and (4.3), we have

Finally, using (3.1) and (4.4), we get

Then, by (4.5), $\{\varrho(u_{n}, u^{\ast })\}$ is a non-increasing sequence of real numbers that is bounded below. Hence, it implies the desired outcome (4.1).

Part 2. Next, we prove that

From (4.1), we have $\lim_{n\rightarrow \infty }\varrho(u_{n}, u^{\ast })$ exists for each fp $u^{\ast }$ of $\varphi$. Thus, we can put

By (4.2) and (4.7), we obtain

Since $\varphi$ is quasi-nonexpansive, we get

On the other hand, by (3.1), we have

which implies that

Therefore

By (4.8) and (4.10), we obtain

From (4.11), we have

Finally, from (4.7), (4.9), and (4.12), and applying Lemma 1, we obtain the required result (4.6).

Part 3. We are ready to establish the $\Delta$-convergence of $\{u_{n}\}$. Because we have seen that the sequence $\{u_{n}\}$ is bounded, it essentially has a unique asymptotic center $A_{c}(L, \{u_{n}\}) = \{u^{\ast }\}$ by Lemma 2. Let $\{k_{n}\}$ be any subsequence of $\{u_{n}\}$ such that $A_{c}(L, \{k_{n}\}) = \{k\}.$ Then, by (4.6), we get

We want to show that $k$ is an fp of $\varphi.$ By Proposition 1(ⅲ), we have

This implies that $\varphi (k)\in A_{c}(L, \{k_{n}\}).$ Now, the uniqueness of the asymptotic center suggests $\varphi (k) = k$, that is, $k\in F_\varphi.$ Subsequently, we assert that the fp $k$ stands as the unique asymptotic center for any subsequence $\{k_{n}\}$ derived from $\{u_{n}\}$. Conversely, let us suppose that $u^{\ast }\neq k.$ By (4.1), we deduce that $\lim_{n\rightarrow \infty }\varrho(u_{n}, k)$ exists. Now, keeping the uniqueness of the asymptotic center in mind, we can see that

However, this is a contradiction. Thus, $u^{\ast}\in F_\varphi$ is the unique asymptotic center for each subsequence $\{k_{n}\}$ of $\{u_{n}\}.$ This proves that $\{u_{n}\}$ is $\Delta$-convergent to an fp of $\varphi.$ □

Now, we present the necessary and sufficient conditions for the strong convergence of the iterative algorithm (3.1).

Theorem 5. Let $L, \varphi$, and $\{u_{n}\}$ be the same as in Theorem 4. Then $\{u_{n}\}$ converges strongly to an fp of $\varphi$ if and only if

where $\varrho(u, F_\varphi) = \inf \{\varrho(u, u^{\ast }):u^{\ast }\in F_\varphi \}.$

Proof. If $\{u_{n}\}$ converges strongly to a point $u^{\ast }\in F_\varphi,$ then $\lim_{n\rightarrow \infty }\varrho(u_{n}, u^{\ast }) = 0.$ Because $0\leq \varrho(u_{n}, F_\varphi)\leq \varrho(u_{n}, u^{\ast })$, we have

For the converse part, assume that $\lim \inf_{n\rightarrow \infty }\text{ } \varrho(u_{n}, F_\varphi) = 0$. By Proposition 1(ⅱ), the set $F_\varphi$ is closed in $L.$ The rest of the proof can be continued similarly to the proof of Theorem 7 in ^[49] and hence is omitted. □

In 1974, Senter and Dotson ^[50] presented a map that fulfills condition (I), as articulated below.

Definition 9. ^[50] A map $\varphi: L \rightarrow L$ satisfies condition (I) if there exists a non-decreasing function $f: [0, \infty) \rightarrow [0, \infty)$ with $f(0) = 0$, $f(r) > 0$ for all $r \in (0, \infty)$ such that $\varrho(u, \varphi(u)) \geq f(\varrho(u, F_\varphi))$ for each $u \in L$.

Based on condition (Ⅰ), we present the following outcome.

Theorem 6. Given the assumptions outlined in Theorem 4, if $\varphi$ satisfies condition (I), then $\{u_{n}\}$ converges strongly to an fp of $\varphi.$

Proof. By (4.6), we have $\lim_{n\rightarrow \infty }\varrho(u_{n}, \varphi (u_{n})) = 0.$ By condition (Ⅰ), we get

that is, $\lim_{n\rightarrow \infty }f(\varrho(u_{n}, F_\varphi)) = 0.$ It follows from the properties of $f$ that

Since all the requirements of Theorem 5 are now available, $\{u_{n}\}$ has a strong limit in $F_\varphi.$ □

The following outcome is based on the compactness of the domain.

Theorem 7. Let L be a nonempty, compact, and convex subset of $\mathbb{M}$, $\varphi :L\rightarrow L$ be a $G\alpha \beta N$ map with $F_\varphi \neq \emptyset$, and $\{u_{n}\}$ be an iterative sequence generated by (3.1) with the real sequence $\{\sigma_{n}\}$ in $[p, r]$ for some $p, r\in (0, 1)$. Then, the sequence $\{u_{n}\}$ converges strongly to an fp of $\varphi$.

Proof. Consider an element $u^{\ast }\in L$. Given that $L$ is compact, we can conclude that there exists a subsequence $\{k_{n}\}$ of $\{u_{n}\}$ such that $\lim_{n\rightarrow \infty }\varrho(k_{n}, u^{\ast }) = 0.$ From (4.6), we have $\lim_{n\rightarrow \infty }\varrho(k_{n}, \varphi(k_{n})) = 0.$ By Proposition 1(iii), we get

Hence, we obtain $\varphi (u^{\ast }) = u^{\ast }$, that is, $u^{\ast }\in F_\varphi.$ Also, $\lim_{n\rightarrow \infty }\varrho(u_{n}, u^{\ast })$ exists by (4.1). Thus, $u^{\ast }$ is the strong limit of $\{u_{n}\}$. □

Remark 6. Theorems 4–7 extend the corresponding findings of Beg et al. ^[23] in two ways: (i) from the class of generalized $\alpha$-nonexpansive maps to the class of $G\alpha \beta N$ maps, (ii) from uniformly convex Banach spaces to complete uniformly convex HSs.

From Remark 1(ⅱ) and (ⅲ), we obtain the following new result in the literature.

Corollary 1. Consider the set $L$ and the sequence $\{u_n\}$ as defined in Theorem 4. If $\varphi :L\rightarrow L$ is a generalized $\alpha$-nonexpansive (or $\beta$-Reich-Suzuki-type nonexpansive) map such that $F_\varphi \neq \emptyset$, then the following holds:

(i) $\{u_{n}\}$ is $\Delta$-convergent to an fp of $\varphi$.

(ii) $\{u_{n}\}$ converges strongly to an fp of $\varphi$ if and only if $\underset{n\rightarrow \infty }{\lim \inf \text{ }}\varrho(u_{n}, F_\varphi) = 0 { \ or }\ \underset{n\rightarrow \infty }{\lim \sup \text{ }} \varrho(u_{n}, F_\varphi) = 0$.

(iii) If $\varphi$ satisfies condition (I) or $L$ is compact, then $\{u_{n}\}$ converges strongly to an fp of $\varphi.$

Remark 7. Corollary 1 generalizes Theorems 2–5 in ^[23] from a uniformly convex Banach space to a complete uniformly convex HS.

5.   An illustrative example

Next, we will illustrate a map that satisfies the $G\alpha \beta N$ condition but does not meet the conditions of being Suzuki generalized nonexpansive, generalized $\alpha$-nonexpansive, and $\beta$-Reich Suzuki type.

Example 5. Let $\mathbb{M = \Re }$ be a space endowed with the metric $\varrho(u, v) = \vert u-v\vert$, and $\mathcal{Q}$ be a map defined by $\mathcal{Q}(u, v, \alpha) = (1-\alpha)\cdot u+\alpha\cdot v$ for $u, v\in \mathbb{M}$ and $\alpha \in \lbrack 0, 1].$ It has been clearly seen that $(\mathbb{M}, \varrho, \mathcal{Q})$ is an HS. Assume that $L = [0, \infty).$ Consider a self-map $\varphi :L\rightarrow L$ defined by

Clearly, $u^{\ast } = 0$ is the unique fp of $\varphi$.

Now, taking $\alpha = \frac{1}{4}$ and $\beta = \frac{1}{4}$, consider the following cases.

Case 1. If $u, v\in \lbrack 0, \frac{1}{8}],$ then we obtain $\varphi (u) = \varphi (v) = 0.$ Thus,

Case 2. If $u, v > \frac{1}{8},$ then it follows $\varphi (u) = \frac{19u }{40}$ and $\varphi (v) = \frac{19v}{40}.$ Thus,

Case 3.If $u\in \lbrack 0, \frac{1}{8}]$ and $v > \frac{1}{8},$ then one has $\varphi (u) = 0$ and $\varphi (v) = \frac{19v}{40}.$ Thus,

Consequently, $\varphi$ is a $G\alpha\beta N$ map with $\alpha = \beta = \frac{1}{4}$.

Let $u = \frac{1}{8}$ and $v = \frac{23}{120}$. Then, we have that $\frac{1}{2} \cdot \varrho(u, \varphi (u)) = \frac{1}{16} < \frac{1}{15} = \varrho(u, v)$, while

(i) $\varrho(\varphi (u), \varphi (v)) = \frac{437}{4800} > \frac{1}{ 15} = \varrho(u, v),$

(ii) $\varrho(\varphi (u), \varphi (v)) = \frac{437}{4800} > \frac{ 1723}{19200} = \frac{1}{4}\cdot\varrho(u, \varphi (v))+\frac{1}{4}\cdot \varrho(v, \varphi (u)) +(1-2\cdot(\frac{1}{4}))\cdot\varrho(u, v),$

(iii) $\varrho(\varphi (u), \varphi (v)) = \left\vert \varphi (u)-\varphi (v)\right\vert = \frac{437}{4800} > \frac{ 1723}{19200} = \frac{1}{4}\cdot\varrho(u, \varphi (u)) +\frac{1}{4}\cdot \varrho(v, \varphi (v))+(1-2\cdot(\frac{1}{4}))\cdot \varrho(u, v).$

Therefore, $\varphi$ does not satisfy the conditions of being Suzuki generalized nonexpansive, generalized $\alpha$-nonexpansive, and $\beta$-Reich Suzuki type.

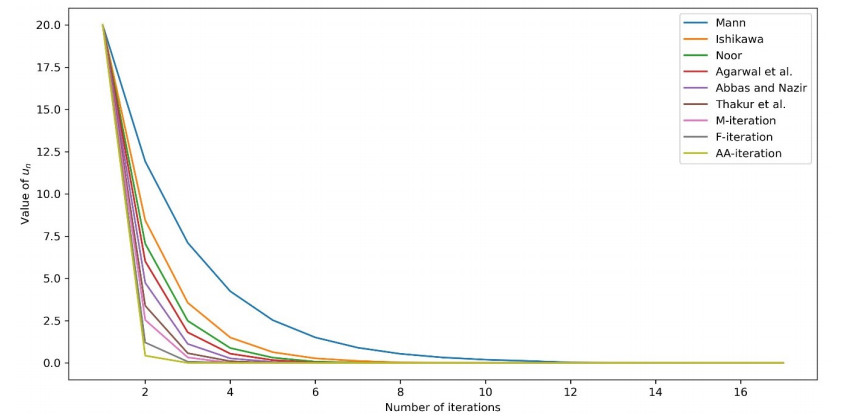
Table 1 and Figure 1 illustrate that the $AA$-iterative algorithm convergences faster than other algorithms for the map $\varphi$ with the specified parameters $\sigma _{n} = \frac{10}{13}, \rho _{n} = \frac{10}{12}$ and $\eta _{n} = \frac{10}{11}$ for all $n\in \mathbb{N}$ and the initial point $u_1 = 20$.

In Table 2, we examine the influence of initial points for various iterative algorithms using $\sigma _{n} = \frac{10}{13}$, $\rho _{n} = \frac{10}{12}$ and $\eta _{n} = \frac{10}{11}$ for all $n\in \mathbb{N}$.

Also, we obtain the influence of the parameters for various iterative algorithms with the initial point $u_1 = 20$ in Table 3.

Remark 8. In Tables 2 and 3, the items in bold show that the $AA$-iterative algorithm (3.1) has a better convergence rate than other iterative methods for the class of $G\alpha \beta N$ maps.

6.   Applications to some special integral equations on time scales

Many problems in mathematical physics, engineering, and mechanics can be formulated as Hammerstein integral equations; see ^[51,52,53]. Kalkan et al. ^[54] showed that the homogeneous FHIE of the second kind on a time scale has a unique solution. In this section, we use the $AA$-iterative algorithm to approximate the solutions of linear FIEs and nonlinear FHIEs, two particular kinds of integral equations on time scales.

We now define the nonlinear FHIE of the second kind on a time scale as follows.

Definition 10. Let $\Gamma$ be a time scale with the $\Delta$-derivative and $c, d\in \Gamma$. A nonlinear FHIE of the second kind on the time scale $\Gamma$ is defined by

where $h:[c, d]_{\Gamma}\rightarrow \Re$ is a function, $\lambda \in \Re$ is a non-zero constant, and the kernel function $K: [c, d]_{\Gamma}\times [c, d]_{\Gamma}\rightarrow \Re$ and the nonlinear function $\psi:[c, d]_{\Gamma}\times \Re \rightarrow \Re$ are $\Delta$-integrable.

Let $\mathbb{M = }C\left([c, d]_{\Gamma}\right)$ be the space of all continuous functions $u:[c, d]_{\Gamma}\rightarrow \Re$ endowed with the norm $\|u-v\| = \sup_{t\in \lbrack c, d]_{\Gamma }}\vert u(t)-v(t)\vert$. Clearly, $(\mathbb{M}, \|\cdot \|)$ is a Banach space and, therefore, a linear HS.

Next, we prove that the $AA$-iterative sequence convergences strongly to the solution of the FHIE (6.1).

Theorem 8. Let $L$ be a nonempty, compact, and convex subset of $\mathbb{M}$, and $\varphi :L{\rightarrow L}$ be defined by

Suppose the following conditions are satisfied:

(i) $h, K$, and $\psi$ are continuous functions.

(ii) There exists a constant $k\geq 0$ such that

(iii) There exists a constant $\phi \geq 0$ such that

(iv) $\left\vert \lambda \right\vert \leq \left(\phi\cdot k\right) ^{-1}.$

Then, the FHIE (6.1) has a solution in $L$, and the iterative sequence $\{u_{n}\}$ produced by (3.1) converges strongly to the solution.

Proof. Observe that, by the conditions (ⅱ), (ⅲ), and Theorem 1, we get

Thus, we have

Since $\left\vert \lambda \right\vert \cdot k \cdot \phi \leq 1,$ we obtain

Hence, $\varphi$ is a nonexpansive map and, therefore, continuous. By the Schauder fp theorem, the map $\varphi$ defined by (6.2) has an fp in $L$; that is, the FHIE (6.1) has a solution. Since $\varphi$ is a nonexpansive map, it is a Suzuki generalized nonexpansive, and so is a generalized $(0, 0)$-nonexpansive map. Consequently, all assumptions of Theorem 7 have been satisfied, and the iterative sequence $\{u_{n}\}$ produced by (3.1) converges strongly to the solution of the FHIE (6.1). □

The following example illustrates the result of Theorem 8.

Example 6. Consider the time scale $\Gamma = \Re$ and the following nonlinear FHIE

where $h(t) = \sqrt{t}-\frac{28}{9}$ is chosen so that the exact solution is $u(t) = \sqrt{t}$. Also, here $K(t, s) = 1$, $\lambda = \frac{1}{12}$ and $\psi(t, u(t)) = \sqrt{[u(t)]^2+4}$. Using the mean value theorem, we get

Hence, the inequality (6.3) holds with $k = 1$. By Remark 3, we have

that is, $\phi = 12 > 0.$ Also, we obtain $\lambda = \frac{1}{12} =$ $\frac{1}{\phi\cdot k}.$ As an outcome, all assumptions of Theorem 8 are met. Then, the iterative sequence $\{u_{n}\}$ produced by (3.1) converges strongly to the fp of the map given by

and hence to the solution of the FHIE (6.4).

If we take $u(t)$ instead of $\psi(t, u(t))$ in Theorem 8, then we can similarly obtain the following result, which is new in the literature. Hence, we omit its proof.

Theorem 9. Let $L$ be a nonempty, compact, and convex subset of $\mathbb{M}$, and $\varphi :L{\rightarrow L}$ be defined by

Suppose the following conditions are satisfied:

(i) $h$ and $K$ are continuous functions.

(ii) There exists a constant $\phi \geq 0$ such that

(iii) $\left\vert \lambda \right\vert \leq \left(\phi\right) ^{-1}.$

Then, the linear FIE (2.4) has a solution in $L$, and the iterative sequence $\{u_{n}\}$ produced by (3.1) converges strongly to the solution.

The following example illustrates the result of Theorem 9.

Example 7. Consider the time scale in Example 4 and the following linear FIE

Here, $h(t) = t+1,$ $K(t, s) = t\cdot s$ and $\lambda = 1.$ From (2.1), we get for $t\in \lbrack 0, 1]_{\Gamma}$

that is, here $\phi = \frac{1}{3} > 0.$ Also, we have $\lambda = 1 < 3 =$ $\frac{1}{\phi}.$ As an outcome, all assumptions of Theorem 9 are met. Then, the iterative sequence $\{u_{n}\}$ produced by (3.1) converges strongly to the fp of the map given by

and hence to the solution of the FIE (6.6).

The solution to the FIE (6.6) can be found using the Adomian decomposition method (2.3). If we apply this method using (2.1) and (2.2), we get

Then, the solution in a series form is given by

The solution of the FIE (6.6) is $u(t) = \frac{18}{11} \cdot t +1$, where $t\in \lbrack 0, 1]_{\Gamma}.$

7.   Conclusions

We present several novel contributions:

(ⅰ) We adapted the $AA$-iterative algorithm, as shown in (1.1), to the HS and established the stability outcome for contraction maps and convergence outcomes for $G\alpha \beta N$ maps in HSs using this modified iterative algorithm.

(ⅱ) We presented a numerical illustration of $G\alpha \beta N$ maps and employed Python software to generate tabular and graphical representations for the given example.

(ⅲ) To demonstrate the practical applicability of our results, we applied our findings to certain solutions of linear FIEs and nonlinear FHIEs on time scales.

(ⅳ) Our results hold in both Banach and CAT(0) spaces, generalizing the stability results of ^[22,27] and the convergence results of ^[23].

In forthcoming research, numerical examples of $G\alpha \beta N$ maps in HSs that do not comply with the property of Banach space and applications of our theoretical results to solve the linear and nonlinear Volterra integral equations on time scales may be offered. Furthermore, it is anticipated that convergence results for enriched $G\alpha \beta N$ maps in HSs will be investigated.

Author contributions

Aynur Şahin: conceptualization, methodology, software, supervision, writing-review and editing; Zeynep Kalkan: methodology, writing-original draft, writing-review and editing. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools to create this article.

Acknowledgments

We would like to express our sincere gratitude to the anonymous referees for their helpful comments, which contributed to improving the quality of the paper.

Conflict of interest

The authors declare that they have no conflicts of interest.