The global climate has undergone great changes in recent decades, which has a significant impact on the vegetation system, especially in arid and semi-arid areas. Based on a dynamic model, this paper studied the response of vegetation pattern to climate change in Qinghai Lake, a typical semi-arid region. The conditions for Turing instability of the equilibrium were obtained by mathematical analysis. The numerical experiments showed the influence of different climitic factors (carbon dioxide concentrations [CO2], temperature and precipitation) on vegetation pattern. The results showed that the robustness of the vegetation system was enhanced as precipitation or [CO2] increased. Furthermore, we presented evolution of vegetation system under different climate scenarios to forecast the future growth of vegetation. We compared the various climate scenarios with representative concentration pathways (RCP2.6, RCP4.5, RCP8.5). The results revealed that RCP2.6 scenario was a desired climate scenario for Qinghai Lake. Our study also highlighted the measures to avoid desertification by the method of optimal control. We expect that this study will provide theoretical basis for vegetation protection.
Citation: Juan Liang, Huilian Ma, Huanqing Yang, Zunguang Guo. Response of vegetation pattern to climate change based on dynamical model: Case of Qinghai Lake, China[J]. AIMS Mathematics, 2024, 9(1): 2500-2517. doi: 10.3934/math.2024123
| [1] | Shuo Xu, Chunrui Zhang . Spatiotemporal patterns induced by cross-diffusion on vegetation model. AIMS Mathematics, 2022, 7(8): 14076-14098. doi: 10.3934/math.2022776 |
| [2] | Yadigar Sekerci . Adaptation of species as response to climate change: Predator-prey mathematical model. AIMS Mathematics, 2020, 5(4): 3875-3898. doi: 10.3934/math.2020251 |
| [3] | Teekam Singh, Ramu Dubey, Vishnu Narayan Mishra . Spatial dynamics of predator-prey system with hunting cooperation in predators and type I functional response. AIMS Mathematics, 2020, 5(1): 673-684. doi: 10.3934/math.2020045 |
| [4] | Yanting Xu, Tinghui Li . Measurement and spatiotemporal patterns of China's digital economy efficiency. AIMS Mathematics, 2023, 8(12): 29307-29331. doi: 10.3934/math.20231500 |
| [5] | Jianping Lv, Chunguang Li, Jianqiang Dong . A high accuracy compact difference scheme and numerical simulation for a type of diffusive plant-water model in an arid flat environment. AIMS Mathematics, 2024, 9(2): 3836-3849. doi: 10.3934/math.2024189 |
| [6] | Wei Li, Guangying Lv . A fully-decoupled energy stable scheme for the phase-field model of non-Newtonian two-phase flows. AIMS Mathematics, 2024, 9(7): 19385-19396. doi: 10.3934/math.2024944 |
| [7] | Xiao-Long Gao, Hao-Lu Zhang, Xiao-Yu Li . Research on pattern dynamics of a class of predator-prey model with interval biological coefficients for capture. AIMS Mathematics, 2024, 9(7): 18506-18527. doi: 10.3934/math.2024901 |
| [8] | Yasir Nawaz, Muhammad Shoaib Arif, Kamaleldin Abodayeh, Mairaj Bibi . Finite difference schemes for time-dependent convection q-diffusion problem. AIMS Mathematics, 2022, 7(9): 16407-16421. doi: 10.3934/math.2022897 |
| [9] | Zhaoxia Li, Lihua Deng, Haifeng Shang . Global well-posedness and large time decay for the d-dimensional tropical climate model. AIMS Mathematics, 2021, 6(6): 5581-5595. doi: 10.3934/math.2021330 |
| [10] | Ufuk Sevim, Leyla Goren-Sumer . Consensus of double integrator multiagent systems under nonuniform sampling and changing topology. AIMS Mathematics, 2023, 8(7): 16175-16190. doi: 10.3934/math.2023827 |
The global climate has undergone great changes in recent decades, which has a significant impact on the vegetation system, especially in arid and semi-arid areas. Based on a dynamic model, this paper studied the response of vegetation pattern to climate change in Qinghai Lake, a typical semi-arid region. The conditions for Turing instability of the equilibrium were obtained by mathematical analysis. The numerical experiments showed the influence of different climitic factors (carbon dioxide concentrations [CO2], temperature and precipitation) on vegetation pattern. The results showed that the robustness of the vegetation system was enhanced as precipitation or [CO2] increased. Furthermore, we presented evolution of vegetation system under different climate scenarios to forecast the future growth of vegetation. We compared the various climate scenarios with representative concentration pathways (RCP2.6, RCP4.5, RCP8.5). The results revealed that RCP2.6 scenario was a desired climate scenario for Qinghai Lake. Our study also highlighted the measures to avoid desertification by the method of optimal control. We expect that this study will provide theoretical basis for vegetation protection.
Modern climate change is a world problem that is paid general attention to by all of mankind. Global climatic variability not only affects the living environment of human beings, but also affects the world economic development and social progress. Over the past 100 years, the global climate has been facing a dramatic change distinguished by temperature increasing [1,2,3,4], which was related to both natural factors and human activities. The global surface temperature between 2011 and 2020 was 1.1(∘C) greater than that between 1850 and 1900. From 1975 to 2014, CO2 concentrations [CO2] increased from 280 ppm to 387ppm [5]. Observational data from China indicates that the increase rate of the annual average temperature in China was much faster than the world during the last 50 years, especially the Tibetan Plateau [6,7].
The Qinghai-Tibetan Plateau (QTP) has become one of the most typical areas affected by climate change [8]. That is because the QTP is the highest altitude region in the middle latitudes of the world, and the high latitudes and high elevations are more susceptible to global warming. In recent decades, the QTP has undergone rapid warming, and the warming rate is almost twice that of the world [9]. The precipitation has increased over the decades, which contributes to the rising of water levels and lakes expanding [10]. The climate change of the QTP has a great impact on the adjacent areas and serves as an indicator of global climate change [11]. The researches on climate change in the (QTP) have achieved abundant results [12,13,14,15].
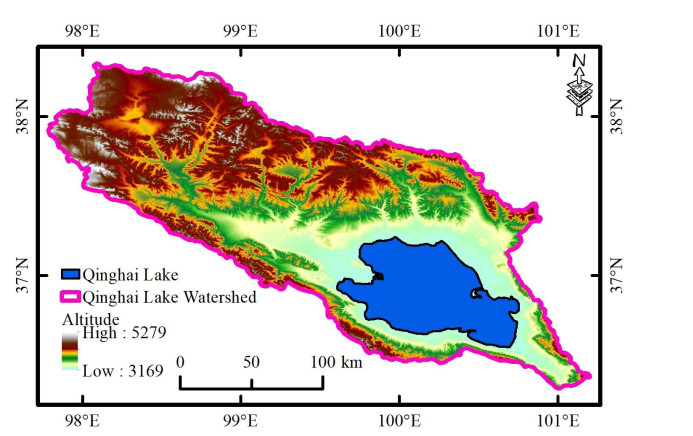
Qinghai Lake, which is the biggest salt lake in China, is located in the northeast edge of the QTP at an altitude of about 3, 200m, with longitude from 99∘36′E to 100∘47′E and latitude from 36∘32′N to 37∘15′N [16], as shown in Figure 1. Qinghai Lake is a natural barrier for controlling the eastward spread of desertification in the western region, while it lies in a monsoon transitional zone, and it is a famous tourism resort in China [17]. The average depth of the lake is 21 meters and the maximum depth exceeds 29 meters [18]. In the past 50 years, the average temperature in Qinghai Lake area increased by 0.319(∘C) every 10 years [19]. It is a typical semi-arid region, Its heterogeneous environments are vulnerable to global climate variability and the ecosystem is fragile [20].
In recent decades, Qinghai Lake has attracted increased attention [21,22,23,24,25,26]. Additionally, there have been some studies on the vegetation of Qinghai Lake. Zhang et al. studied vegetation change in the Qinghai Lake watershed by conducting pollen-based vegetation reconstruction at an archaeological site [27]. Wang et al. studied the relationship between grassland vegetation and climatic parameters in Qinghai Lake. The result showed that the main reason for the improvement of vegetation cover in the Qinghai Lake basin was the increase of precipitation [28]. The plant community characteristics of different sand-forming communities in the largest desert area on the East Coast of Qinghai Lake were studied and the results showed that species diversity of plant community and herb coverage were positively correlated with dune stability [29]. Cai et al. studied the effects of human activities and climate change on vegetation in Qinghai Lake basin [30]. We can see that most of the current researches on vegetation of the Qinghai Lake are based on observation data and statistical methods, paying little attention to spatial distribution and the growth of vegetation based on pattern dynamics. The evolution law of vegetation pattern can be qualitatively analyzed based on dynamic equation [31,32,33,34,35]. Therefore, in this paper, we present a reaction-diffusion equation and apply the pattern dynamics theory to reveal characteristics of temporal and spatial distribution of vegetation.
The study aims to address the question as follows: (1) How to establish a suitable vegetation-cilimitic dynamics model? (2) How do different climitic factors affect the growth of vegetation? (3) How will the vegetation pattern transform under different climate scenarios? (4) What are the measures to prevent desertification? In this study, the conditions of steady-state bifurcation are obtained via theoretical analysis. Moreover optimal control theory provides a framework for avoiding desertification of the ecosystem. Finally, we employ numerical simulations to verify the response of the vegetation system to climate change that aim to try to avoid desertification and enhance the robustness of the ecosystem.
Water is an essential condition for maintaining the normal physiological function of vegetation. Water resource for vegetation growth mainly comes from precipitation. When rain falls to the ground, some water seeps into the soil and is absorbed by vegetation, then some forms surface runoff. Taken together, Klausmeier established a vegetation-water model in 1999 [36]:
| {∂N∂t=RJWN2−MN+DNΔN,∂W∂t=A−LW−RWN2+V∂W∂X, | (2.1) |
where N and W represent the biomass of vegetation and water, respectively. A is the precipitation, the evaporation rate of water is L, vegetation takes up water at rate RWN2, J is the rate of conversion of biomass per unit of water consumption, the natural mortality rate of vegetation is M, DN is the diffusion coefficient of vegetation and water flows downhill at speed V.
It is worth mentioning that the shading effect of vegetation can reduce the evaporation rate of water. Here, we mainly consider the growth of vegetation on flat ground. At the same time, the carbon gain generated by photosynthesis promotes plant growth and the carbon loss generated by respiration consumes vegetation biomass. Most of the water absorbed by vegetation is lost to the atmosphere in the form of water vapor through transpiration. The major factors affecting these three physiological processes are [CO2] and temperature. Therefore, based on model (2.1) and the above facts, the dynamic model of vegetation and water is established as follows:
| {∂N∂t=Cg−RespN+DNΔN,∂W∂t=A−(1−ρN)W−Er+DWΔW, | (2.2) |
where ρ is the reduced evaporation rate of vegetation due to shading. DW is the diffusion coefficient of water. The amount of vegetation growth Cg due to photosynthesis can be given by the following expression [37]:
| Cg=Ca(1−CiCa)C1Rgco2WN2, |
where Ca is environmental CO2 concentration, C1 is the photosynthetic conversion coefficient of plant biomass and Ci is the available CO2 concentration between canopy cells. The rate of vegetation loss due to respiration Resp can be approximated by a Michaelis M10 function [37]:
| Resp=BRMT−101010, |
where BR describes the basic respiration per unit biomass.
Er stands for transpiration of vegetation, which can describe the difference between saturation specific humidity, and actual specific humidity and the expression for Er is as follows [37]:
| Er≈gcanopy(q∗−qa), | (2.3) |
where gcanopy is for canopy water transfer, which is related to water absorbed by vegetation, and q is the dimensionless specific humidity. Based on the above analysis, let
| gcanopy=gH2ORWN2=γgCO2RWN2, |
where gH2O is the maximum conductivity to H2O and CO2, respectively and γ is the conversion coefficient of diffusivity difference between CO2 and H2O.
In (2.3), specific humidity is defined as follows: q=ρvρd, where ρv(kgm−3) and ρd(kgm−3) represent the density of water vapor and dry air, respectively. According to Dalton's law, there are
| ρd=P−sRdTa,ρv=0.622sRdTa, |
where P is atmospheric pressure, s is the pressure of steam, Rd is a constant and Ta is the absolute temperature. We assume that p is large enough and has q∗=0.622s∗P. According to the above analysis, Er can be obtained:
| Er=Rγgco2WN20.622Ps∗(1−ss∗). |
According to the Clausius-Clapeyron function, the saturated vapor pressure is determined:
| s∗(T)=0.611exp(17.502TT+240.97). |
Let relative humidity be Rh=ss∗ and one has
| Er=Rγgco2WN20.622Ps∗(1−Rh)). |
Based on the above analysis, we obtained a bivariate dynamics model to study the vegetation growth in Qinghai Lake:
| {∂N∂t=JRgco2WN2−RespN+DNΔN in U=Ω×(0,T),∂W∂t=A−(1−ρN)W−Rγgco2qWN2+DWΔW in U, | (2.4) |
with J=Ca(1−CiCa)C1 and q=0.622Pe∗(1−Rh)). See appendix A for explanations of parameters in the model (2.4).
In this subsection, we shall demonstrate the occurrence of the Turing pattern by stability analysis for system (2.4). The steady states of (2.4) are
| E0=(0,A), |
| E1=(ARgco2J+Respρ+√Φ2γqRespRgco2,ARJgco2+Respρ−√Φ2gco2RJL), |
| E2=(ARgco2J+Respρ−√Φ2γqRespRgco2,ARJgco2+Respρ+√Φ2gco2RJL), |
where Φ=(ARJgco2+ρResp)2−4Rγgco2qR2esp, E1 and E2 only exist if Φ>0. E0 is the bare ground equilibrium.
In what follows, the stability of the steady states will be discussed. We assume the condition Φ>0 holds so that E1 and E2 are biologically meaningful.
Let
| F(N,W)=JRgco2WN2−RespN,G(N,W)=A−LW−Rγqgco2WN2. |
The linearization of (2.4) at E∗ is
| (∂N∂t∂W∂t)=DΔ(NW)+M(NW) | (2.5) |
with
| DΔ=(DNΔ00DWΔ),M=(a11a12a21a22), |
where
| a11=2gco2JRN∗W∗−Resp, a12=gco2JRN∗2, |
| a21=−2gco2γqRN∗W∗, a22=−gco2γqRN∗2−L. |
Consider the spatially heterogeneous perturbations [38,39]:
| (NW)=(N∗W∗)+(c1c2)eλt+iκx+c.c+O(ε2), |
where κ is a wave-number and λ reprsents a growth rate of perturbation in t. Substituting the above formula into (2.5), the characteristic equation is given:
| detM=|a11−DNκ2−λa12a21a22−DWκ2−λ|=0. | (2.6) |
It follows from (2.6) that the characteristic equation of (2.5) is:
| λ2+β1(κ)λ+β2(κ)=0, |
where
| β1(κ)=a11+a22−(DN+DW)κ2, |
| β2(κ)=DNDWκ4−(a11DW+a22DN)κ2+a11a22−a12a21. |
In accordance with the above derivation, our result reads as follows.
Theorem 2.1. Suppose that Φ>0, then the bare-soli steady state E0 is always stable and the positive steady state E2 is unstable.
Proof. The characteristic equation corresponding to the bare-soli steady state E0 is
| λ2+β1(κ)λ+β2(κ)=0, |
where
| β1(κ)=(DN+DW)κ2+Resp+1, |
| β2(κ)=(DNκ2+Resp)(DWκ2+1). |
It is easy to see that β1(κ)>0 and β2(κ)>0 (κ=0,1,2...). Therefore, E0 is always stable. Analogously, the characteristic equation is as follows for E2:
| λ2+β1(κ)λ+β2(κ)=0, |
where
| β1(κ)=(DN+DW)κ2+A2J2RgCO2−2R3espqγ+AJRespρ−AJ√Φ2R2espqγ, |
| β2(κ)=DNDWκ4+(A2J2RDNgCO2−2R3espDWqγ+AJRespDNρ−AJDN√Φ)κ22R2espqγ+12RespRgCO2qγ(Φ−AJRespgCO2√Φ−Respρ√Φ). |
It is easily seen that β2(κ)<0 when κ=0, then the positive steady state E2 is unstable.
In what follows we shall analyze the dynamic behavior of E1. First, the characteristic equation is given:
| λ2+β1(κ)λ+β2(κ)=0, |
where
| β1(κ)=(DN+DW)κ2+A2J2RgCO2−2R3espqγ+AJRespρ+AJ√Φ2R2espqγ, |
| β2(κ)=DNDWκ4+(A2J2RDNgCO2−2R3espDWqγ+AJRespDNρ+AJDN√Φ)κ22R2espqγ+12RespRgCO2qγ(Φ+AJRespgCO2√Φ+Respρ√Φ). |
It is easy to check that β2(0)>0 when κ=0. Based on the above discussion, the result reads as follows.
Theorem 2.2. Suppose that Φ>0 holds. If DN=DW=0, then E2 is stable for β1(0)>0 and unstable for β1(0)<0.
On the basis of the Turing theory, we can conclude that system (2.4) induces Turing pattern under the two conditions: First, E2 is stable without diffusion; Second, E2 is unstable in the presence of diffusion. As a result, Turing instability occurs only provided that β1(0)>0 and β1(κ)<0 for some κ∈N+.
Based on the condition for Turing instability deduced in part two, the vegetation patterns with different structures can be presented by numerical experiments. With the increase of precipitation A, vegetation patterns change from spot structure to stripe structure (shown in Figure 2), which implies that the robustness of the ecological system is enhanced. Therefore, we can prevent the degradation of the vegetation ecosystem by controlling pattern formations. Here, we aim to get the stripe structure under the case of low precipitation. The optimal control problem provides a powerful tool to realize the aim. We regard the artificial planting rate r(x,t) as a control parameter and rewrite system (2.4) as follows:
| {∂N∂t=JRgco2WN2−RespN+rN+DNΔN in U,∂W∂t=A−(1−ρN)W−Rγgco2qWN2+DWΔW in U. | (3.1) |
The set of admissible controls for r(x,t) is [40]:
| Λad={r∈L∞(U)|r1<r(x,t)<r2 a.e. in U}. |
The objective functional expresses a trade-off between the desired precision and a cost of achieving such precision. Specifically, optimal control aims to lower costs (artificial planting amount) while making the uncontrolled pattern (N(x,T),W(x,T)) approach the target pattern (NT(x),WT(x)). Consider the following optimal control problem:
| minr∈ΛadJ[N,W]=b12∫Ω[N(x,T)−NT(x)]2dx+b22∫Ω[W(x,T)−WT(x)]2dx+c2∫T0∫Ωr2(x,t)dxdt, | (3.2) |
subject to
| {∂N∂t=DNΔN+f1(n,w,r) in U,∂W∂t=DWΔW+f2(n,w,r) in U,∂N∂n=0,∂W∂n=0 on U=∂Ω×(0,T),N(x,0)=N0(x),W(x,0)=W0(x) in U, | (3.3) |
where
| f1(n,w,r)=JRgco2WN2−RespN+r, |
| f2(n,w,r)=A−LW−Rγgco2qWN2. |
J is the objective functional, NT(x) and WT(x) are the objective patterns and N(x,t) and W(x,t) are state variables. r(x.t) is the control variable and b1,b2,c are the constant.
Next, we discuss the expression of an optimal solution.
Constructing Lagrange functional [41,42,43,44,45]:
| L[N,W,r,v1,v2]=J[N,W,r]+∫T0∫Ω[−∂N∂t+DN△N+f1(N,W,r)]v1dxdt+∫T0∫Ω[−∂W∂t+DW△W+f2(N,W,r)]v2dxdt+∫T0∫∂Ω(−DN∂N∂n)v1dsdt+∫T0∫∂Ω(−DW∂W∂n)v2dsdt=J[N,W]+∫T0∫Ω∂v1∂tNdxdt+∫Ω[N(x,0)v1(x,0)−N(x,T)v1(x,T)]dx+∫T0∫ΩDN△v1Ndxdt−∫T0∫∂Ω∂v1∂nNdsdt+∫T0∫Ωf1(N,W,r)v1dxdt+∫T0∫Ω∂v2∂tWdxdt+∫Ω[W(x,0)v2(x,0)−W(x,T)v2(x,T)]dx+∫T0∫ΩDW△v2Wdxdt−∫T0∫∂Ω∂v2∂nWdsdt+∫T0∫Ωf2(N,W,r)v2dxdt. |
Here, the local optimal solution of the optimal control problem is (N∗,W∗,r∗), for any small enough and smooth function N(x,t) with N(x,t)=0. By calculation, one has the directional derivative of the Lagrange functional at (N∗,W∗,r∗,v1,v2), which satisfies the following equation:
| 0=LN[N∗,W∗,r∗,v1,v2]=b1∫Ω[N∗(x,T)−NT(x)]N(x,T)dx+∫T0∫Ω∂v1∂tNdxdt−∫Ωv1(x,T)N(x,T)dx+∫T0∫ΩDNΔv1Ndxdt−∫T0∫Ω∂v1∂nNdsdt+∫T0∫Ωf1,N(N∗,W∗,r∗)v1Ndxdt+∫T0∫Ωf2,N(N∗,W∗,r∗)v2Ndxdt. |
It follows from the arbitrariness of N(x,t) that v1 satisfies
| {−∂v1∂t=DNΔv1+f1,N(N∗,W∗,r∗)v1+f2,N(N∗,W∗,r∗)v2,∂v1∂n=0,v1(x,T)=b1[N∗(x,T)−NT(x)]. | (3.4) |
Analogously, one has
| 0=LW[N∗,W∗,r∗,v1,v2]=b2∫Ω[W∗(x,T)−WT(x)]W(x,T)dx+∫T0∫Ω∂v2∂tWdxdt−∫Ωv2(x,T)W(x,T)dx+∫T0∫ΩDWΔv2Wdxdt−∫T0∫Ω∂v2∂nWdsdt+∫T0∫Ωf1,W(N∗,W∗,r∗)v1Wdxdt+∫T0∫Ωf2,W(N∗,W∗,r∗)v2Wdxdt, |
and
| {−∂v2∂t=DWΔv2+f1,W(N∗,W∗,r∗)v1+f2,W(N∗,W∗,r∗)v2,∂v2∂n=0,v2(x,T)=b2[W∗(x,T)−WT(x)]. | (3.5) |
Substituting f1,N,f1,W,f2,N and f2,W into Eqs (3.4) and (3.5), the adjoint equation of (v1,v2) is:
| {−∂v1∂t=DNΔv1+2W∗N∗Rgco2(Jv1−rv2)−Respv1,−∂v2∂t=DWΔv2+N∗2Rgco2(Jv1−rv2)−Lv2,∂v1∂n=0,∂v2∂n=0,v1(x,T)=b1[N∗(x,T)−NT(x)],v2(x,T)=b2[W∗(x,T)−WT(x)]. | (3.6) |
Note that the allowed control set is a closed convex set. It is clear that the directional derivative of the Lagrange functional at (N∗,W∗,r∗,v1,v2) along r−r∗ satisfies:
| 0≤Lr[N∗,W∗,r∗,v1,v2]=c∫T0∫Ωr∗(r−r∗)dxdt+∫T0∫Ωf1,r(N∗,W∗,r∗)(r−r∗)v1dxdt+∫T0∫Ωf2,r(N∗,W∗,r∗)(r−r∗)v2dxdt. |
Since r is arbitrary, we substitute f1,r and f2,r into the above inequality, then the following variational inequality can be obtained:
| ∫T0∫Ω(cr∗+N∗v1)(r−r∗)dxdt≥0. | (3.7) |
By the variational inequality (3.7), it follows that
| r∗=P[r1,r2][−1cN∗v1], |
where we define the projection P as
| P[r1,r2](r)=max[r1,min[r,r2]]. |
In this section, we apply the biologically realistic parameters to perform the numerical simulations and research the response of vegetation pattern to climate change, which is based on the climatic data from 1969–2019 of Qinghai Lake. The average values of the climatic factors (precipitation, temperature and [CO2]) are obtained and they are 1.05(mm/d), 0.9879(∘C) and 396(ppm), respectively. The other parameters are fixed: BR=1,Rh=0.4,gco2=10∗10−3,M10=1.6,R=2.6∗10−2,γ=2.5∗103,C1=12,CiCa=0.6,ρ=0.24,DN=0.1,DW=100.
Figures 2 and 3, respectively, show the effects of precipitation and [CO2] on vegetation pattern. We can observe that the vegetation patterns change from spot structure to stripe structure as increase of precipitation or [CO2]. The highest density decreases gradually, the lowest density increases gradually and the distribution of vegetation is more uniform. Figure 4 illustrates the variation of vegetation patterns in regard to temperature. With increase of temperature, the transition of vegetation pattern experiences stripe and spot. In contrast with the first two meteorological factors, the highest density increases and the lowest density decreases and the distribution is more uneven, which is not conducive to the robustness of ecosystem. The three climatic factors have different effects on the mean density of vegetation. More precisely, the mean vegetation density is positively associated with rainfall and [CO2], which is in contrast to temperature. This is visualized in Figure 5.
In this section, we devote to forecast the future vegetation growth in Qinghai Lake area under three different climate scenarios. The three climate scenarios are simulated data selected from the Coupled Model Intercomparison Project Phase 5 (CMIP5) which has three representative concentration paths (RCP2.6, RCP4.5 and RCP8.5)[46,47,48]; see Table 1 for an introduction of CMIP5.
| Scenario | Interpretation | [CO2] in 2100yr |
| RCP2.6 | low radiative forcing scenario | 440 |
| RCP4.5 | middle radiative forcing scenario | 610 |
| RCP8.5 | high scenario with radiative forcing | 1170 |
We adopt linear regression analysis to statistical temperature, [CO2] and rainfall data under three different scenarios to obtain climate change trends. The results are visualized in Table 2. Temperature and [CO2] increase under the three climate scenarios, and rainfall increases in RCP4.5 and RCP8.5. To predict the future evolution of vegetation pattern in regard to different climate scenarios, Figure 6 shows the variation of vegetation pattern. We can observe that vegetation pattern transitions with the increase of time in RCP2.6: Stripes → gap → uniform, which indicates that the robustness of the vegetation system is increasing. This is reasonable to infer that the increased robustness of the vegetation system is due to the increase of precipitation and [CO2]. Compared with RCP2.6, the spatial distribution structure changes from stripe to spot in RCP4.5 and RCP8.5, which implies that the ecosystem may undergo degradation, which can finally lead to desertification.
| Scenario | A(mm/d) | T(∘C) | [CO2](ppm) |
| RCP2.6 | 0.002 | 0.0089 | 0.42 |
| RCP4.5 | -0.170 | 0.0273 | 2.10 |
| RCP8.5 | -0.471 | 0.0576 | 7.70 |
In order to increase the resilience of degraded ecosystem and avoid the occurrence of desertification, we offer the optimal conservation strategy−human activity (e.g. artificial planting). As illustrated in Figure 2, the transformation from stripe pattern to spot pattern occurs with decreasing precipitation, and spot structure can serve as an early warning signal of the catastrophic shift [49]. Moreover, the precipitation has a significant impact on the spatial distribution structure of vegetation. Choose a pattern structure corresponding to A=1.3 as the target pattern, which represents a robust ecological structure. In Figure 7, the snapshots of the optimal control r(x,t) and the associated state variable N(x,t) at rainfall A=0.8 and 1.15 are presented, respectively. Consequently, artificial planting is an effective way to transform the vegetation pattern into an ideal state.
For the last few decades, global climate has been facing a great change. The vegetation system exhibits a sensitive response to climate change, especially in arid and semi-arid regions. In this paper, we chose Qinghai Lake as the study area, which is a typical semi-arid area, and studied the response of vegetaion pattern to climate change. We developed a vegetation-water system (2.4) with climatic factors by the zero-flux Neumann conditions and investigated the dynamical behavior. First, we showd the stability of the constant equilibria for (2.4) without diffusion. Moreover, we analyzed the spatiotemporal dynamics at the constant equilibria with diffusion. The conditions for Turing instability of the positive constant equilibrium were obtained in the framework of Turing principle.
Our findings in numerical results revealed that the variation of data for climatic factors had a major impact on vegetation pattern. As precipitation or [CO2] increased, the robustness of the vegetation system was enhanced and the mean density increased. Unlike the first two climatic factors, rising temperatures not only lead to the emergence of spot pattern, but also reduced the mean density of vegetation and accelerated the degradation of the vegetation system. Furthermore, in order to forecast the future vegetation growth in Qinghai Lake, we presented evolution of the vegetation system under different climate scenarios. The results showed that the vegetation system collapses to desertification state in the future in RCP4.5 and RCP8.5 scenarios. This results from the synergy of precipitation, temperature and [CO2]. Compared to RCP4.5 and RCP8.5, due to the dual effects of the increase of precipitation and [CO2], RCP2.6 is a desired climate scenario for Qinghai Lake.
A direction for further study is how to timely avoid desertification. Owing to the method of optimal control, we can induce phase transitions between different vegetation pattern through human activities, such as artificial planting. More precisely, any presented pattern structure (e.g. spot pattern, strip pattern, and gap pattern) can be transformed into a desired pattern (see the Figure 7). As a result, artificial planting contributes to guarding against desertification of vegetation systems, even in low-rainfall regions. The result certifies the effectiveness of the optimal-control method in respect of prevention and control desertification.
This study highlighted the response of vegetation to climate change (precipitation, temperature and [CO2] from modeling point of view. It is necessary to take other climatic factors into account, for instance, light, evaporation and humidity. Based on the seasonality of climate change, another aspect for future work would be to consider the nonautonomous systems; that is, all climatic factors considered in the model are coupled as a function of time. Furthermore, previous work has revealed that spot structure can provide early warning signal for catastrophic shift [49], which is from a qualitative point of view. From the quantitative perspectives, we expect to propose a quantifiable indicator for desertification evaluation, and this is also one of the key points for future research.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Fundamental Research Program of Shanxi Province (Grant Nos. 202203021212327 and 202203021211213), Program for the (Reserved) Discipline Leaders of Taiyuan Institute of Technology, Taiyuan Institute of Technology Scientific Research Initial Funding.
The authors declare no conflict of interest.
| Parameter | Interpretation | Unit |
| gco2 | Maximal leaf conductance to CO2 | mod m−2d−1 |
| γ | Conversion coefficient from maximal leaf | mm m−2mol−1 |
| conductance to water vapor to maximal | ||
| leaf conductance CO2 | ||
| Ca | Ambient CO2 concentration | mol mol−1 |
| Ci | Intercellular CO2 concentration | mol mol−1 |
| C1 | Coefficient of conversion of photosynthesis (mol) into biomass (g) | g mol−1 |
| BR | Respiration per unit of biomass | d−1 |
| s∗(T) | Saturated vapor pressure | kPa |
| s(T) | Vapor pressure at T | kPa |
| Rh | Relative humidity e(T)e∗(T) | - |
| R | The water uptake by roots | mm/d |
| P | The ground pressure | kPa |
| ρ | Reduced evaporation rate of vegetation due to shading | - |
| T | Temperature | ∘C |
| A | Rainfall | (mmd)−1 |
| t | time | d |
| [1] |
Z. Wu, N. E. Huang, J. M. Wallace, B. V. Smoliak, X. Chen, On the time-varying trend in global-mean surface temperature, Clim. Dynam., 37 (2011), 759–773. https://doi.org/10.1007/s00382-011-1128-8 doi: 10.1007/s00382-011-1128-8

|
| [2] |
J. Huang, X. Guan, F. Ji, Enhanced cold-season warming in semi-arid regions, Atmos. Chem. Phys., 12 (2012), 5391–5398. https://doi.org/10.5194/acp-12-5391-2012 doi: 10.5194/acp-12-5391-2012

|
| [3] |
A. Dai, Drought under global warming: A review, WIREs. Clim. Change, 2 (2011), 45–65. https://doi.org/10.1002/wcc.81 doi: 10.1002/wcc.81

|
| [4] | J. Hansen, R. Ruedy, M. Sato, K. Lo, Global surface temperature change, Rev. Geophys., 48 (2010). https://doi.org/10.1029/2010RG000345 |
| [5] |
Z. Li, J. Gao, L. Wen, C. Zou, C. Feng, D. Li, et al., Dynamics of soil respiration in alpine wetland meadows exposed to different levels of degradation in the Qinghai-Tibet Plateau, China, Sci. Rep., 9 (2019), 7469. https://doi.org/10.1038/s41598-019-43904-1 doi: 10.1038/s41598-019-43904-1

|
| [6] |
J. Gao, H. Ouyang, G. Lei, X. Xu, M. Zhang, Effects of temperature, soil moisture, soil type and their interactions on soil carbon mineralization in Zoigo alpine wetland, Qinghai-Tibet Plateau, Chinese Geogr. Sci., 21 (2011), 27–35. https://doi.org/10.1007/s11769-011-0439-3 doi: 10.1007/s11769-011-0439-3

|
| [7] |
C. Mu, T. Zhang, Q. Zhao, H. Su, S. Wang, B. Cao, et al., Permafrost affects carbon exchange and its response to experimental warming on the northern Qinghai-Tibetan Plateau, Agr. Forest Meteorol., 247 (2017), 252–259. https://doi.org/10.1016/j.agrformet.2017.08.009 doi: 10.1016/j.agrformet.2017.08.009

|
| [8] |
F. Peng, Q. G. You, M. H. Xu, X. H. Zhou, T. Wang, G. Guo, et al., Effects of experimental warming on soil respiration and its components in an alpine meadow in the permafrost region of the Qinghai-Tibet Plateau, Eur. J. Soil Sci., 66 (2015), 145–154. https://doi.org/10.1111/ejss.12187 doi: 10.1111/ejss.12187

|
| [9] |
Z. X. Xu, T. L. Gong, J. Y. Li, Decadal trend of climate in the Tibetan Plateaui-regional temperature and precipitation, Hydrol. Process., 22 (2008), 3056–3065. https://doi.org/10.1002/hyp.6892 doi: 10.1002/hyp.6892

|
| [10] |
G. Zhang, T. Yao, H. Xie, K. Yang, L. Zhu, C. K. Shum, et al., Response of Tibetan Plateau lakes to climate change: Trends, patterns, and mechanisms, Earth Sci. Rev., 208 (2020), 103269. https://doi.org/10.1016/j.earscirev.2020.103269 doi: 10.1016/j.earscirev.2020.103269

|
| [11] |
J. Wang, Q. Wu, Impact of experimental warming on soil temperature and moisture of the shallow active layer of wet meadows on the Qinghai-Tibet Plateau, Cold Reg. Sci. Technol., 90-91 (2013), 1–8. https://doi.org/10.1016/j.coldregions.2013.03.005 doi: 10.1016/j.coldregions.2013.03.005

|
| [12] |
W. Wan, L. Zhao, H. Xie, B. Liu, H. Li, Y. Cui, et al., Lake surface water temperature change over the Tibetan plateau from 2001 to 2015: A sensitive indicator of the warming climate, Geophys. Res. Lett., 45 (2018), 11177–11186. https://doi.org/10.1029/2018GL078601 doi: 10.1029/2018GL078601

|
| [13] |
G. Wang, Y. Li, Q. Wu, Y. Wang, Impacts of permafrost changes on alpine ecosystem in Qinghai-Tibet Plateau, Sci. China Ser. D, 49 (2006), 1156–1169. https://doi.org/10.1007/s11430-006-1156-0 doi: 10.1007/s11430-006-1156-0

|
| [14] |
X. Wu, L. Zhao, M. Chen, H. Fang, G. Yue, J. Chen, et al., Soil organic carbon and its relationship to vegetation communities and soil properties in permafrost areas of the Central Western Qinghai-Tibet Plateau, China, Permafrost Periglac. Process., 23 (2012), 162–169. https://doi.org/10.1002/ppp.1740 doi: 10.1002/ppp.1740

|
| [15] |
X. Wu, H. Fang, Y. Zhao, J. M. Smoak, W. Li, W. Shi, et al., A conceptual model of the controlling factors of soil organic carbon and nitrogen densities in a permafrost-affected region on the eastern Qinghai-Tibetan Plateau, J. Geophys. Rese. Biogeo., 122 (2017), 1705–1717. https://doi.org/10.1002/2016JG003641 doi: 10.1002/2016JG003641

|
| [16] | S. Cao, G. Cao, Q. Feng, G. Han, Y. Lin, J. Yuan, et al., Alpine wetland ecosystem carbon sink and its controls at the Qinghai Lake, Environ. Earth Sci. 76 (2017), 210. https://doi.org/10.1007/s12665-017-6529-5 |
| [17] |
X. Li, W. Liu, L. Xu, Carbon isotopes in surface-sediment carbonates of modern Lake Qinghai (Qinghai-Tibet Plateau): Implications for lake evolution in arid areas, Chem. Geol., 300 (2012), 88–96. https://doi.org/10.1016/j.chemgeo.2012.01.010 doi: 10.1016/j.chemgeo.2012.01.010

|
| [18] |
H. Ao, C. Wu, X. Xiong, L. Jing, X. Huang, K. Zhang, et al., Water and sediment quality in Qinghai Lake, China: A revisit after half a century, Environ. Monit. Assess., 186 (2014), 2121–2133. https://doi.org/10.1007/s10661-013-3522-7 doi: 10.1007/s10661-013-3522-7

|
| [19] |
L. Tang, X. Duan, F. Kong, F. Zhang, Y. Zheng, Z. Li, et al., Influences of climate change on area variation of Qinghai Lake on Qinghai-Tibetan Plateau since 1980s, Sci. Rep., 8 (2018), 7331. https://doi.org/10.1038/s41598-018-25683-3 doi: 10.1038/s41598-018-25683-3

|
| [20] |
B. Chang, K. N. He, R. J. Li, Z. P. Sheng, H. Wang, Linkage of climatic factors and human activities with water level fluctuations in Qinghai Lake in the northeastern Tibetan Plateau, China, Water, 9 (2017), 552. https://doi.org/10.3390/w9070552 doi: 10.3390/w9070552

|
| [21] |
C. Fan, C. Song, W. Li, K. Liu, J. Cheng, C. Fu, et al., What drives the rapid water-level recovery of the largest lake (Qinghai Lake) of China over the past half century?, J. Hydrol., 593 (2021), 125921. https://doi.org/10.1016/j.jhydrol.2020.125921 doi: 10.1016/j.jhydrol.2020.125921

|
| [22] | H. Dong, Y. Song, M. Zhang, Hydrological trend of Qinghai Lake over the last 60 years: Driven by climate variations or human activities? J. Water Climate Change, 10 (2019), 524–534. https://doi.org/10.2166/wcc.2018.033 |
| [23] |
W. Zhang, S. Wang, B. Zhang, F. Zhang, Q. Shen, Y. Wu, et al., Analysis of the water color transitional change in Qinghai Lake during the past 35 years observed from Landsat and MODIS, J. Hydrol. Reg. Stud., 42 (2022), 101154. https://doi.org/10.1016/j.ejrh.2022.101154 doi: 10.1016/j.ejrh.2022.101154

|
| [24] |
T. Che, X. Li, R. Jin, Monitoring the frozen duration of Qinghai Lake using satellite passive microwave remote sensing low frequency data, Chin. Sci. Bull., 54 (2009), 2294–2299. https://doi.org/10.1007/s11434-009-0044-3 doi: 10.1007/s11434-009-0044-3

|
| [25] |
L. Feng, J. Liu, T. A. Ali, J. S. Li, J. Li, S. Kuang, Impacts of the decreased freeze-up period on primary production in Qinghai Lake, Int. J. Appl. Earth Obs., 83 (2019), 101915. https://doi.org/10.1016/j.jag.2019.101915 doi: 10.1016/j.jag.2019.101915

|
| [26] |
Z. Jin, C. F. You, Y. Wang, Y. Shi, Hydrological and solute budgets of Lake Qinghai, the largest lake on the Tibetan Plateau, Quatern. Int., 218 (2010), 151–156. https://doi.org/10.1016/j.quaint.2009.11.024 doi: 10.1016/j.quaint.2009.11.024

|
| [27] |
N. Zhang, X. Cao, Q. Xu, X. Huang, U. Herzschuh, Z. Shen, et al., Vegetation change and human-environment interactions in the Qinghai Lake Basin, northeastern Tibetan Plateau, since the last deglaciation, CATENA, 210 (2022), 105892. https://doi.org/10.1016/j.catena.2021.105892 doi: 10.1016/j.catena.2021.105892

|
| [28] |
X. Wang, T. Liang, H Xie, X. Huang, H. Lin, Climate-driven changes in grassland vegetation, snow cover, and lake water of the Qinghai Lake basin, J. Appl. Remote Sens., 10 (2016), 036017. https://doi.org/10.1117/1.JRS.10.036017 doi: 10.1117/1.JRS.10.036017

|
| [29] |
H. Zhang, L. Tian, E. Hasi, D. Zhang, W. Wu, Vegetation-soil dynamics in an alpine desert ecosystem of the Qinghai Lake watershed, northeastern Qinghai-Tibet Plateau, Front. Environ. Sci., 11 (2023), 1119605. https://doi.org/10.3389/fenvs.2023.1119605 doi: 10.3389/fenvs.2023.1119605

|
| [30] |
Y. Cai, J. Zhang, N. Yang, C. Zhang, C. Zhao, H. Long, Human impacts on vegetation exceeded the hydroclimate control 2 ka ago in the Qinghai Lake basin revealed by n-alkanes of loess, Palaeogeogr. Palaeocl., 607 (2022), 111269. https://doi.org/10.1016/j.palaeo.2022.111269 doi: 10.1016/j.palaeo.2022.111269

|
| [31] |
Z. Chen, J. Liu, L. Li, Y. P. Wu, G. Feng, Z. Qian, et al., Effects of climate change on vegetation patterns in Hulun Buir Grassland, Phys. A, 597 (2022), 127275. https://doi.org/10.1016/j.physa.2022.127275 doi: 10.1016/j.physa.2022.127275

|
| [32] |
G. Q. Sun, C. H. Wang, L. L. Chang, Y. P. Wu, L. Li, Z. Jin, Effects of feedback regulation on vegetation patterns in semi-arid environments, Appl. Math. Model., 61 (2018), 200–215. https://doi.org/10.1016/j.apm.2018.04.010 doi: 10.1016/j.apm.2018.04.010

|
| [33] |
J. Liang, C. liu, G. Q. Sun, L. li, L. Zhang, M. Hou, et al., Nonlocal interactions between vegetation induce spatial patterning, Appl. Math. Comput., 428 (2022), 127061. https://doi.org/10.1016/j.amc.2022.127061 doi: 10.1016/j.amc.2022.127061

|
| [34] |
Q. Xue, G. Q. Sun, C. Liu, Z. G. Guo, Z. Jin, Y. P. Wu, et al., Spatiotemporal dynamics of a vegetation model with nonlocal delay in semi-arid environment, Nonlinear Dyn., 99 (2020), 3407–3420. https://doi.org/10.1007/s11071-020-05486-w doi: 10.1007/s11071-020-05486-w

|
| [35] |
M. R. Aguiar, O. E. Sala, M. R. Aguiar, O. E. Sala, Patch structure, dynamics and implications for the functioning of arid ecosystems, Trends Ecol. Evol., 14 (1999), 273–277. https://doi.org/10.1016/S0169-5347(99)01612-2 doi: 10.1016/S0169-5347(99)01612-2

|
| [36] |
C. A. Klausmeier, Regular and irregular patterns in semiarid vegetation, Science, 284 (1999), 1826–1828. https://doi.org/10.1126/science.284.5421.1826 doi: 10.1126/science.284.5421.1826

|
| [37] |
S. Keˊfi, M. Rietkerk, G. G. Katul, Vegetation pattern shift as a result of rising atmospheric CO_2 in arid ecosystems, Theor. Popul. Biol., 74 (2008), 332–344. https://doi.org/10.1016/j.tpb.2008.09.004 doi: 10.1016/j.tpb.2008.09.004

|
| [38] |
X. Tang, Y. Song, T. Zhang, Turing-Hopf bifurcation analysis of a predator-prey model with herd behavior and cross-diffusion, Nonlinear Dyn., 86 (2016), 73–89. https://doi.org/10.1007/s11071-016-2873-3 doi: 10.1007/s11071-016-2873-3

|
| [39] |
W. Zuo, Y. Song, Stability and bifurcation analysis of a reaction-diffusion equation with distributed delay, Nonlinear Dyn., 79 (2015), 437–454. https://doi.org/10.1007/s11071-014-1677-6 doi: 10.1007/s11071-014-1677-6

|
| [40] |
M. R. Garvie, C. Trenchea, Optimal control of a nutrient-phytoplankton-zooplankton-fish system, SIAM J. Control Optim., 46 (2007), 775–791. https://doi.org/10.1137/050645415 doi: 10.1137/050645415

|
| [41] |
S. Lee, G. Chowell, Exploring optimal control strategies in seasonally varying flu-like epidemics, J. Theor. Biol., 412 (2017), 36–47. https://doi.org/10.1016/j.jtbi.2016.09.023 doi: 10.1016/j.jtbi.2016.09.023

|
| [42] |
L. Chang, S. Gao, Z. Wang, Optimal control of pattern formations for an SIR reaction-diffusion epidemic model, J. Theor. Biol., 536 (2022), 111003. https://doi.org/10.1016/j.jtbi.2022.111003 doi: 10.1016/j.jtbi.2022.111003

|
| [43] |
L. Chang, W. Gong, Z. Jin, G. Q. Sun, Sparse optimal control of pattern formations for an SIR reaction-diffusion epidemic model, SIAM J. Appl. Math., 82 (2022), 1764–1790. https://doi.org/10.1137/22M1472127 doi: 10.1137/22M1472127

|
| [44] |
W. Choi, E. Shim, Optimal strategies for social distancing and testing to control COVID-19, J. Theor. Biol., 512 (2021), 110568. https://doi.org/10.1016/j.jtbi.2020.110568 doi: 10.1016/j.jtbi.2020.110568

|
| [45] |
S. Kim, J. Lee, E. Jung, Mathematical model of transmission dynamics and optimal control strategies for 2009 A/H1N1 influenza in the Republic of Korea, J. Theor. Biol., 412 (2017), 74–85. https://doi.org/10.1016/j.jtbi.2016.09.025 doi: 10.1016/j.jtbi.2016.09.025

|
| [46] |
K. E. Taylor, R. J. Stouffer, G. A. Meehl, An overview of CMIP5 and the experiment design, Bull. Amer. Meteorol. Soc., 93 (2012), 485–498. https://doi.org/10.1175/BAMS-D-11-00094.1 doi: 10.1175/BAMS-D-11-00094.1

|
| [47] |
K. Calvin, B. Bond-Lamberty, L. Clarke, J. Edmonds, J. Eom, C. Hartin, et al., The SSP4: A world of deepening inequality, Global Environ. Chang, 42 (2017), 284–296. https://doi.org/10.1016/j.gloenvcha.2016.06.010 doi: 10.1016/j.gloenvcha.2016.06.010

|
| [48] |
T. Zhao, L. Chen, Z. Ma, Simulation of historical and projected climate change in arid and semiarid areas by CMIP5 models, Chin. Sci. Bull., 59 (2014), 412–429. https://doi.org/10.1007/s11434-013-0003-x doi: 10.1007/s11434-013-0003-x

|
| [49] |
J. von Hardenberg, E. Meron, M. Shachak, Y. Zarmi, Diversity of vegetation patterns and desertification, Phys. Rev. Lett., 87 (2001), 198101. https://doi.org/10.1103/PhysRevLett.87.198101 doi: 10.1103/PhysRevLett.87.198101

|
| 1. | Xinru Li, Shanlong Lu, Chun Fang, Harrison Odion Ikhumhen, Xinya Kuang, Yuan Guo, Xiaofeng Guo, Na Han, Meng Yang, Haihong Long, Jifang Ma, Yongshun Li, Yiqun Liu, Water volume changes and influencing factors in a typical lake on the Qinghai-Tibet Plateau: a case study of the basin of Lake Xiao Qaidam, 2025, 18, 1753-8947, 10.1080/17538947.2025.2488944 |
| Scenario | Interpretation | [ CO_2 ] in 2100yr |
| RCP2.6 | low radiative forcing scenario | 440 |
| RCP4.5 | middle radiative forcing scenario | 610 |
| RCP8.5 | high scenario with radiative forcing | 1170 |
| Scenario | A(mm/d) | T( ^\circ C) | [ CO_2 ](ppm) |
| RCP2.6 | 0.002 | 0.0089 | 0.42 |
| RCP4.5 | -0.170 | 0.0273 | 2.10 |
| RCP8.5 | -0.471 | 0.0576 | 7.70 |