Qualitative analytical results of complex order nonlinear fractional differential equations with robust control scheme

1.   Introduction

Fractional calculus, an expansion of classical calculus, investigates derivatives and integrals of any order, advancing a robust method for recognizing complex physical phenomena such as anomalous diffusion, wave propagation, and dynamical systems. Unlike traditional calculus, which is limited to positive integers, fractional calculus extends the opportunity to include non-integer orders, aiding the analysis of nonlocal events and memory effects ^[1,2,3].

Fractional differential equations (FDEs) are an important branch of mathematics used to study various natural processes. They are composed by considering derivatives of non-integer order and are used to describe a range of phenomena, including anomalous diffusion, viscoelasticity, and more. Existence and uniqueness of the solution for FDEs is a crucial topic that has been studied extensively in recent years. Indeed, establishing the existence and uniqueness of the solution can be a challenging task due to the properties of fractional derivatives. The most common approach to such problems is to analyze the properties of the equations, check if the equations satisfy certain conditions in order to determine the solvability of the equations, and then use the appropriate methods to find their solutions. Differential and integral equations have been extensively studied in the past and many methods have been developed to deal with them ^[4,5,6]. These methods have been classified into two portions including analytical techniques and numerical methods. Analytical methods are based on algebraic, functional analysis and calculus tools and can produce exact solutions in certain cases. For the details, readers can see the recent development in the works ^[7,8,9]. Therefore, existence and uniqueness (EU) are the essential factors in solving FDEs, which have been extensively studied by different researchers using a variety of approaches. Classical fixed point (FP) theory has been used to establish the existence and uniqueness of solutions for nonlinear FDEs ^[10,11,12].

The research focuses on controlling a nonlinear leukemia model to prevent leukemia cell spread. Sliding mode control (SMC) is used for this purpose. SMC is a nonlinear control method that can maintain stability even in model uncertainties. It has a simple structure that remains consistent across different parameters and is resistant to noise and disturbances ^[13,14]. Although chattering is a common issue with SMCs, it can be significantly reduced using higher-order SMCs, saturation approach, and continuous control methods ^{[15,16,17,18]}. These approaches ensure rapid stabilization and convergence of the system. Furthermore, SMC has been employed to improve the performance of the Euler-Lagrange system, control brain tumors with chemotherapy, regulate artificial pancreases in individuals with diabetes, and other applications ^{[19,20,21,22]}. Finite-time SMC has been designed to obtain convergence within a finite settling time. However, the finite-time system's convergence is so sensitive to the beginning values of the nonlinear system that a higher initial condition for the nonlinear system would cause the system to converge more slowly ^[23,24,25]. This limitation has led to the exploration of alternative methods, and one such novel approach is fixed-time stability. This unique concept can be used to find the convergence time regardless of the initial conditions ^[26,27].

A class of disorders known as cancer is brought on by leukemic cells that grow uncontrollably and infect nearby normal cells. Leukemia, sometimes known as "cancer of the bone marrow", is a kind of cancer. Blood cells are formed by bone marrow ^[28]. White blood cells are vital for fighting infection and sickness, red blood cells transport oxygen, and platelets perform blood clotting ^[29]. The abnormal multiplication of leukocytes, or white blood cells, is known as leukemia. Rapid production of leukocytes displaces normal cells before they reach the circulation ^[31]. It is possible to distinguish between acute and chronic leukemia subtypes by looking at the cancer's growth. Normal cell counts are drastically reduced if leukemic cells continue without being eliminated ^[32].

By applying these results, one can establish safe, compact estates (initial value problems (IVPs) and boundary value problems (BVPs)) and narrow down their study to a few initial and boundary value concerns. To get around this limitation and modify the techniques for IVPs and BVPs in a wider sense, authors have been looking for a nonlinear analytic tool. One of the most significant and useful methods, topological degree theory, operates under weak, compact circumstances as opposed to strong ones. For a wide range of problems, the suggested approach offers incredibly basic prerequisites for the presence of results. To get results, several authors have looked at a variety of challenges, including linear and nonlinear fractional-order differential equations (FODEs) and differential equations (DEs). To learn more about the degree theory of topological topology, see ^{[30,33,34,35]}.

Benchohra et al. ^[11] addressed the existence of the nonlinear implicit FDE with initial value condition and performed an Ulam stability analysis on it:

where $\mathscr{D}_{0^{+}}^a$ is the Riemann-Liouville fractional derivative (RL-FD), $\mathcal{K}:(0, T] \times \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}$ is a continuous function, and $\wp\in(0, 1)$.

Using the degree theory, Mawhin ^[36] developed relevant conclusions for the above BVPs in order to deduce EU results:

and

Krasnoselskii's fixed point theorems (FPT) was utilized by Sun et al.'s ^[37] discussion about the positive solution to the FDEs

where $L(\mathscr{D}) = \mathscr{D}^{\varsigma_n}-a_{n-1} \mathscr{D}^{\varsigma_{n-1}}-\cdots-a_1 \mathscr{D}^{\varsigma_1}, 0 < \varsigma_1 < \varsigma_2 < \cdots < \varsigma_n < 1, a_j > 0 \; (j = 1, 2, \cdots, n-1)$, $\mathscr{D}^{\varsigma_j}\; (j = 1, 2, \cdots, n)$ are RL-FDs.

Xie et al. ^[38] discussed the stability and existence of solution for multi-order FDEs on infinite interval $[0, +\infty)$.

where $L(\mathscr{D}) = { }^R \mathscr{D}_{0^{+}}^{\varsigma_n}-a_{n-1}{ }^R \mathscr{D}_{0^*}^{\varsigma_n-1}-\cdots-a_1{ }^R \mathscr{D}_{0^{+}}^{\varsigma_1}, 0 < \varsigma_1 < \varsigma_2 < \cdots < \varsigma_n < 1, n \in \mathbb{N}^{+}, a_j \in \mathbb{R}$, ${ }^R \mathscr{D}_{0^{+}}^{\varsigma_n}, { }^R \mathscr{D}_{0^{+}}{ }^{\varsigma_j}{ }^R \mathscr{D}_{0^{+}}^{\varsigma_{a_n}}\; (j = 1, 2, \cdots, n-1)$ are RL-fractional derivatives, with $\wp_n < \varsigma_j$ and $\varsigma_j+\wp_n < \varsigma_n \; (j = 1, 2, \cdots, n-1)$.

The previously mentioned study served as inspiration for the current work, which aims to analyze the solutions of an FDE using the $\mathrm{T}$-RL fractional operator. We propose a new method for condensing maps, based on the degree theory of FDEs of the form, to extract sufficient criteria for the EU of solutions to various kinds of value requirements posed by random FDEs.

with the initial condition

or the boundary conditions given by

where $L(\mathscr{D}) = { }^{RL} \mathscr{D}^{\varsigma_{n}}-a_{n-1}{ }^{RL} \mathscr{D}^{\varsigma_{n-1}}-\cdots-a_{1}^{RL} \mathscr{D}^{\varsigma_{1}}$, $0 < \varsigma_{1} < \varsigma_{2} < \cdots < \varsigma_n < 1$, $n \in \mathbb{N}^{+}, a_{j} \in \mathbb{R}$, ${ }^{RL} \mathscr{D}^{\varsigma_{n}, \mathrm{T}}, { }^{RL} \mathscr{D}^{\varsigma_{j}, \mathrm{T}}, (j = 1, 2, \cdots, n-1)$ are $\mathrm{T}$–RL fractional derivatives based on $\mathrm{T}$ which is an increasing function; $\mathrm{T}^{\prime}(\mathscr{Z}) \neq0$ for all $\mathscr{Z} \in \mathbf{I_{a}^{b}}$, $\wp, \nu, \lambda\in \mathbb{R}$, and $\mathrm{u}\in\Pi$; $\mathcal{K}:\mathbf{I_{a}^{b}}\times\mathbb{R}\times\Pi\to\mathbb{R}$ is a continuous function; and $\zeta:\mathbf{I_{a}^{b}}\to\mathbb{R}$ is continuous on $\mathbf{I_{a}^{b}}$, in the measurable space $(\Pi, \mathfrak A)$.

As far as we have discovered, no published works on FDEs having the operator $L(\mathscr{D})$-multi order FD of one function with another function have been published. Our objective in this article is to use the criteria (1.2) and (1.3), respectively, to determine the sufficient conditions for the EU of solutions for FDE (1.1). This will enable us to respond to the query regarding the existence of solutions for FDE (1.1). After (1.1) is transformed into integral equations with conditions (1.2) and (1.3), accordingly, we use the Banach and topological degree theory to study the EU of solutions. For our purposes, we convert (1.1) into integral equations using the conditions (1.2) and (1.3), respectively. We design a sliding mode control to deliver faster error convergence and improved tracking trajectory results at a fixed time. We then use the Lyapunov theorem to demonstrate the stability of a closed-loop system. We provide computational work with examples to validate our investigation's main conclusions. The primary findings of ^[38] are expanded upon by the findings presented here.

2.   Background material

Complete normed vector spaces are known as Banach spaces, after the Polish mathematician Stefan Banach. They offer a foundation for functional analysis, which makes it easier to analyze infinite-dimensional mathematical phenomena. Modern scientific and engineering achievements are based on applications across a wide range of domains, including quantum physics, signal processing, optimization, partial differential equations, and more.

Here, we will begin by presenting some essential definitions and fundamental results that are crucial for subsequent progress.

Let $\mathcal{X}: = C(\mathbf{I_{a}^{b}}, \mathbb{R})$ be a Banach space of continuous real-valued functions on $\mathbf{I_{a}^{b}} = [a, b]\subset \mathbb{R}.$ $\zeta :\mathbf{I_{a}^{b}}\rightarrow \mathbb{R}$, in which the topological norm is given by:

Assume a weighted space $\mathbb{C}^{\wp }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ of functions $\zeta$ on $\mathbf{I_{a}^{b}}$ by

Clearly, $\mathbb{C}^{\wp }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ is a Banach space with norm

Here, we will explain the fractional calculus (FC) based on another function. Let $\mathrm{T}, \zeta \in \mathcal{C}^{n}$ such that $\mathrm{T}$ is increasing and $\mathrm{T} ^{\prime }(\mathscr{Z})\neq 0$, for all $\mathscr{Z} \in \mathbf{I_{a}^{b}}$.

Definition 2.1. The $\mathrm{T}$-RL FD of a function $\mathscr{U}$ of order $\wp \in (n-1, n]$ is

where $n = [\varrho ]+1,$ $n\in \mathbb{N}$, and $\mathscr{D}_{\mathrm{T} }^{n} = \left(\frac{1}{\mathrm{T} ^{\prime }\left(\mathscr{Z} \right) }\frac{d}{d\mathscr{Z} } \right) ^{n}.$ The Eq (2.2) can be expressed as

and ${}^{RL}\mathscr{D}_{a+}^{\wp; \mathrm{T} }(\cdot)$ are called the $\mathrm{T}$-RL fractional integral and derivative defined by (see ^[2])

and

respectively. Also, the $\mathrm{T}$-Caputo FD is given by (see ^[39])

Remark 2.2. For $\mathrm{T} \left(\mathscr{Z} \right) = \mathscr{Z}$, the relations (2.2), (2.5), and (2.6) get the classical fractional operators in ^[2,39].

Lemma 2.3. ^[39] Let $\nu > 0$, $\wp > 0$, then

(1) $I_{a^{+}}^{\wp, \mathrm{T}}(\mathrm{T}(\varsigma)-\mathrm{T}(a))^{\nu-1}(\mathscr{Z}) = \frac{\Gamma(\nu)}{\Gamma(\nu+\wp)}(\mathrm{T}(\mathscr{Z})-\mathrm{T}(a))^{\nu+\wp-1},$

(2 $\mathscr{D}_{a^{+}}^{\wp, \mathrm{T}}(\mathrm{T}(\varsigma)-\mathrm{T}(a))^{\nu-1}(\mathscr{Z}) = \frac{\Gamma(\nu)}{\Gamma(\nu-\wp)}(\mathrm{T}(\mathscr{Z})-\mathrm{T}(a))^{\nu-\wp-1}.$

Lemma 2.4. ^[39] Let $\zeta \in C^n([a, b])$, $n-1 < \wp < n$, then

(1) $\mathscr{D}_{a^{+}}^{\wp, \mathrm{T}} I_{a^{+}}^{\wp, \mathrm{T}} \zeta(\mathscr{Z}) = \zeta(\mathscr{Z})$,

(2) $I_{a^{+}}^{\wp, \mathrm{T}} \mathscr{D}_{a^{+}}^{\wp, \mathrm{T}} \zeta(\mathscr{Z}) = \zeta(\mathscr{Z})-\sum_{k = 1}^n \frac{\zeta^{[k-1]}\left(a^{+}\right)}{\Gamma(k-\wp)}(\mathrm{T}(\mathscr{Z})-\mathrm{T}(a))^{k-\wp}$,

where $\zeta^{[k]}(\mathscr{Z}): = \left(\frac{1}{\mathrm{T}^{\prime}(\mathscr{Z})} \frac{d}{d \mathscr{Z}}\right)^k \zeta(\mathscr{Z})$ on $[a, b]$. In particular, given $\wp \in(0, 1)$, one has

where $c$ is a constant.

Definition 2.5 (^[40]). The Gamma function for $z \in \mathbb{C}$ in Stirling's asymptotic formulation is the following:

and

Let $\mathcal{O}_{\mathbb{R}}$ be the $\sigma$-algebra of Borel subsets of $\mathbb{R}$, and $\eta: \Pi \rightarrow \mathbb{R}$ is said to be measurable if, for any $\mathfrak{B} \in \mathcal{O}_{\mathbb{R}}$,

It is important to establish a jointly measurable map in order to achieve the goal of defining integrals of sample routes of random processes.

$\mathcal{S}: \Pi \times \mathbb{R} \rightarrow \mathbb{R}$ is a random operator (RO) if $\mathcal{S}(\mathrm{u}, \zeta)$ is measurable in $\mathrm{u}$ for all $\zeta \in \mathbb{R}$, and $\mathcal{S}(\mathrm{u}) \zeta = \mathcal{S}(\mathrm{u}, \zeta)$ and $\mathcal{S}(\mathrm{u})$ is an RO on $\mathbb{R}$. An RO $\mathcal{S}(\mathrm{u})$ on $E$ is continuous (totally bounded, compact, or completely continuous) if $\mathcal{S}(\mathrm{u}, \zeta)$ is continuous (totally bounded, compact, or completely continuous) in $\zeta$ for all $\mathrm{u} \in \Pi$. The paper ^[41] provides information on totally continuous ROs in Banach spaces as well as the features of these operators.

Definition 2.6 (^[42]). Let $\mathcal{P}(\mathbb{X})$ be a class of nonempty subsets of $\mathbb{X}$ and $\mathbb{Y}$ be a mapping from $\Pi$ into $\mathcal{P}(\mathbb{X})$. A mapping $\mathcal{S}:\{(\mathrm{u}, \mathscr{Z}): \mathrm{u} \in \Pi, \mathscr{Z} \in \mathbb{Y}(\mathrm{u})\} \rightarrow \mathbb{X}$ is called an RO with stochastic domain $\mathbb{Y}$ if $\mathbb{Y}$ is measurable (i.e., for all closed $A \subset \mathbb{X}, \{\mathrm{u} \in \Pi, \mathbb{Y}(\mathrm{u}) \cap A \neq \emptyset\}$ is measurable), and for all open $\mathfrak{B} \subset \mathbb{X}$ and all $\mathscr{Z} \in \mathbb{X}, \{\mathrm{u} \in \Pi: \mathscr{Z} \in \mathbb{Y}(\mathrm{u}), \mathcal{S}(\mathrm{u}, y) \in \mathfrak{B}\}$ is measurable.

Lemma 2.7 (^[14]). The system needs to ensure stable fixed-time convergence: $\dot {\cal Y}(x) = f(x, {\cal Y}), \, \, \, {\cal Y}(0) = {{\cal Y}_0}$, and the Lyapunov functional candidate $V({\cal Y})$ that satisfies

i. $V({\cal Y}) = 0\, \, \Leftrightarrow \, \, {\cal Y} = 0$,

ii. $\dot V({\cal Y}) \le -{l_1}V{({\cal Y})^{{k_1}}} - {l_2}V{({\cal Y})^{{k_2}}}$,

where $l_1, l_2 > 0$, $0 < k_1 < 1$, and $k_2 > 1$. Therefore, the fixed-time ${\cal T}$ is computed as

Here, we will talk about certain definitions and criteria for the measure of non-compactness, along with the topological degree theory.

Definition 2.8 (^[43]). The mapping $\mathrm{h} : \mathbb M_{\mathcal X} \rightarrow [0, \infty)$ for the Kuratowski-measure of non-compactness (KMN) is given by:

$\mathbb M_{\mathcal X}$ denoted the ball of all bounded mappings in $\mathcal X$.

Properties 2.9 (^[43]). The KMN satisfies the following:

$(1)$ $\mathrm{h}(\mathbb{P}) = 0$ $\Leftrightarrow$ $\mathbb{P}$ is relatively compact,

$(2)$ $\mathbb{P} \subset \mathbb{O} \Rightarrow \mathrm{h}(\mathbb{P}) \leq \mathrm{h}(\mathbb{O})$,

$(3)$ $\mathrm{h}(\mathbb{P}) = \mathrm{h}(\overline{\mathbb{P}}) = \mathrm{h}(conv(\mathbb{P}))$, where $\mathrm {conv} (\mathbb{P})$ and $\overline{\mathbb{P}}$ symbolize the convex hull and the closure of $\mathbb{P}$, respectively,

$(4)$ $\mathrm{h}(\mathbb{P} + \mathbb{O}) \leq \mathrm{h}(\mathbb{P}) +\mathrm{h}(\mathbb{O}),$

$(5)$ $\mathrm{h}(\lambda \mathbb{P}) = |\lambda|\mathrm{h}(\mathbb{P}), \lambda \in \mathbb R.$

For $\mathcal{M} \subset C(\mathbf{I_{a}^{b}}, X)$, we define

where $\mathcal{M}(\varsigma) = \{\zeta(\varsigma) \in \mathcal X: \zeta \in \mathcal{M}\}$.

Proposition 2.10 (^[43,44]). If $\mathcal{M} \subset C(\mathbf{I_{a}^{b}}, \mathcal X)$ is equi-continuous and bounded, so $\mathscr{Z} \rightarrow$ $\mathrm{h}(\mathcal{M}(\mathscr{Z}))$ is continuous on $\mathbf{I_{a}^{b}}$, and

Proposition 2.11 (^[43,44]). $\mathcal{M} \subset C(\mathbf{I_{a}^{b}}, \mathcal X)$ is relatively compact if, and only if, $\mathcal{M}$ is equi-continuous and, for each $\mathscr{Z} \in \mathbf{I_{a}^{b}}, \mathcal{M}(\mathscr{Z})$ is a relatively compact set in $\mathcal{X}$.

Proposition 2.12 (^[44]). Let $\left\{\zeta_n\right\}_{n \geq 1}$ be a sequence of Bochner integrable functions from $\mathbf{I_{a}^{b}}$ into $\mathcal X$ with $\left\|\zeta_n(\mathscr{Z})\right\| \leq m(\mathscr{Z})$ for almost all $\mathscr{Z} \in \mathbf{I_{a}^{b}}$ and each $n \geq 1$, where $m \in L^1\left(\mathbf{I_{a}^{b}}, \mathbb{R}_{+}\right)$, then the function $\phi(\mathscr{Z}) = \mathrm{h}\left(\left\{\zeta_n(\mathscr{Z}): n \geq 1\right\}\right)$ belongs to $L^1\left(\mathbf{I_{a}^{b}}, \mathbb{R}_{+}\right)$ and satisfies:

Definition 2.13 (^[45,46]). Let $\mathscr{V} : \mathbb{P}\longrightarrow \mathcal X$ be a continuous bounded map and $\mathbb{P} \subset \mathcal X$. The operator $\mathscr{V}$ is said to be $\mathrm{h}$-Lipschitz if we find a constant $\kappa \geq 0$ fulfilling the condition,

Moreover, $\mathscr{V}$ is called a strict $\mathrm{h}$-contraction if $\kappa < 1$.

Definition 2.14 (^[45,46]). The function $\mathscr{V}$ is called $\mathrm{h}$-condensing if

for each non-pre-compact and bounded subset $\mathbb{O}$ of $\mathbb{P}$.

In other words,

Further, we have $\mathscr{V} : \mathbb{P}\longrightarrow \mathcal X$ is Lipschitz if we find $\kappa > 0$, such that

If $\kappa < 1$, $\mathscr{V}$ is called a strict contraction.

For the next outcomes, we can refer to ^[3,36].

Proposition 2.15. If $\mathscr{V}, \mathscr{U} : \mathbb{P} \longrightarrow \mathcal X$ are $\mathrm{h}$-Lipschitz mappings with constants $\kappa_1$ and $\kappa_2$ respectively, then $\mathscr{V}+\mathscr{U} : \mathbb{P} \longrightarrow \mathcal X$ are $\mathrm{h}$-Lipschitz with $\kappa_1 + \kappa_2$.

Proposition 2.16. A compact function $\mathscr{V} : \mathbb{P} \longrightarrow \mathcal X$ is $\mathrm{h}$-Lipschitz with constant $\kappa = 0$.

Proposition 2.17. If $\mathscr{V} : \mathbb{P} \longrightarrow \mathcal X$ is Lipschitz with $\kappa$, then $\mathscr{V}$ is $\mathrm{h}$-Lipschitz also with the identical constant $\kappa$.

Theorem 2.18. Let $\mathcal{W} : \mathbb{P} \longrightarrow \mathcal X$ be $\mathrm{h}$-condensing and

If $\Xi$ is a $\mathbb{P}$ bounded set in $\mathcal X$, so there exists $r > 0$ such that $\Xi \subset {O}_r(0)$, then the degree

Consequently, $\mathcal{W}$ possesses at least one FP and the set of the FPs of $\mathcal{W}$ lies in ${O}_r(0)$.

3.   Findings of the article

We make some following assumptions for the main results of the article:

${\bf (A1)}$ There exists constant $L > 0$ with

${\bf (A2)}$ For $\mathcal{K}$, we have $M_{1}, N_{1} > 0, p\in (0, 1)$, such that

${\bf (A3)}$ For $\zeta \in \mathcal X$, there exist $M_{2}, N_{2} > 0, q \in(0, 1)$ such that

${\bf (A4)}$ For $r > 0$, there is a $\nu_r > 0$ such that

where $\mathscr{Z} \in \mathbf{I_{a}^{b}}, \mathcal{M} \subset \mathfrak{B}_r: = \left\{\|\zeta\|_{\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }} \leq r: \zeta \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}}, \mathbb{R})\right\}$ and

For simplicity, we define the following:

As a starting point in this subsection, we will define the solutions to the problem (1.1)-(1.2). For more details, see Benchohra et al. ^[11] and Xie et al. ^[38].

Definition 3.1. A function $\zeta\in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ is a solution of the FDE (1.1) if $\zeta$ satisfies $L(\mathscr{D}) \zeta(\mathscr{Z}, \mathrm{u}) = \mathcal{K}\Big(\mathscr{Z}, \mathrm{u}, \zeta(\mathscr{Z}, \mathrm{u})\Big)$ for a.e. $\mathscr{Z}\in \mathbf{I_{a}^{b}}$ and the initial data $\left(\mathrm{T}(\mathscr{Z})-\mathrm{T}(a)\right)^{1-\varsigma_{n}} \zeta(\mathscr{Z}, \mathrm{u})\Big|_{\mathscr{Z} = a} = 0$.

The next lemma has an essential position in our results.

Lemma 3.2. For every $h \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$, the solution $\zeta$ of (1.1) with conditions (1.2) is given by

Alternatively, $\zeta$ can be expressed by

By the virture of Lemma 3.2, we denote operators $\mathscr{V}, \mathscr{U} : \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}}) \longrightarrow \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ by:

and

Thus, (3.2) in Lemma 3.2 can be written as

Since $\mathcal{K}$ is continuous, $\mathcal{W}$ is well-define and its FPs are solutions of (3.2) in Lemma 3.2.

Lemma 3.3. $\mathscr{V}$ is Lipschitz with $\Lambda_\mathcal{K} = \sum_{j = 1}^{n-1} |a_{j}|\frac{(\mathrm{T}(b)-\mathrm{T}(a))^{\varsigma_{n}-\varsigma_{j}}}{\Gamma\left(\varsigma_{n}-\varsigma_{j}+1\right)}L$. Also, $\mathscr{V}$ fulfills that

for every $\mathscr{U} \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}}).$

Proof. Next, we show $\mathscr{V}$ is Lipschitz with constant $\Lambda_\mathcal{K}$. Let $\zeta, \overline{\zeta} \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$, then we get

Then,

This implies, $\mathscr{V} : \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})\longrightarrow \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ is a Lipschitzian on $\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ with the constant

By Proposition 2.17, $\mathscr{V}$ is $\mathrm{h}$-Lipschitz with constant $\Lambda_\mathcal{K}$. Also, for the growth condition, we get

This further implies that

□

Lemma 3.4. The $\mathscr{U}$ is continuous and fulfills the growth condition given as below,

Proof. To demonstrate that $\mathscr{U}$ is continuous. Let $\{\zeta_n\}, \zeta \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ with $\lim_{n\to+\infty}\|\zeta_n - \zeta \| \to 0$. Evidently, we show that $\{\zeta_n\}$ is a bounded subset of $\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$. Consequently, there is an $r > 0$ with $\|\zeta_n\|_{\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }} \leq r$ for any $n \geq 1$. Taking limit, we see $\|\zeta\|_{\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }} \leq r$. It is simple to see that $\mathcal{K}(\varsigma, \mathrm{u}, \zeta_n(\varsigma))\to \mathcal{K}(\varsigma, \mathrm{u}, \zeta(\varsigma)), \; \text{as}\; n\to+\infty$, because of the continuity of $\mathcal{K}$. On the other hand, considering (A2), we get the next inequality:

We remark that in the function $\varsigma\mapsto 2(\mathrm{T}(\mathscr{Z})-\mathrm{T}(a))^{1-\varsigma_n}\mathcal{Q}_{\mathrm{T}}^{\varsigma_n}(\mathscr{Z}, \varsigma)(M_{1}r^p+N_{1})$ is Lebesgue integrable over $[a, \mathscr{Z}]$. This fact in conjunction with the Lebesgue-dominated convergence theorem implies that

It follows that $\|\mathscr{U} \zeta_n-\mathscr{U}\zeta\| \to 0 \; \; \text{as}\; \; n\to+\infty$. Thus, the operator $\mathscr{U}$ is continuous.

Under the growth condition, utilizing the hypothesis (A2) we obtain

Therefore, we have

□

Lemma 3.5. The operator $\mathscr{U} : \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}}) \longrightarrow \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ is compact. Thus, $\mathscr{U}$ is $\mathrm{h}$-Lipschitz with 0 constant.

Proof. In order to prove the compactness of $\mathscr{U}$, with a bounded set $\Pi \subset B_r$, we need to prove that ${U}(\Pi)$ is relatively compact in $\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$. For each $\zeta \in \Pi \subset B_r$, based on the estimates (3.4), we can find

which implies ${U}(\Pi)$ is uniformly bounded. Further, for $\zeta \in\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ and $\mathscr{Z} \in \mathbf{I_{a}^{b}}$, from the definition of $\mathscr{U}$ and ${\bf (A2)}$, the operator derivative can be estimated as follows:

where we used the fact

Thus, for $\mathscr{Z}_{1}, \mathscr{Z}_{2}\in \mathbf{I_{a}^{b}}$ with $a < \mathscr{Z}_{1} < \mathscr{Z}_{2} < b$ and for $\zeta\in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$, we get

We have $(\mathscr{Z}_{2}-\mathscr{Z}_{1})\to 0$ independent of $\mathscr{U}$. So, $\mathscr{U}$ is equi-continuous.

Let

Then, by Proposition 2.11, we show that $\mathscr{Z} \rightarrow \mathrm{h}(\mathcal{M}(\mathscr{Z}))$ is continuous on $\mathbf{I_{a}^{b}}$. Also,

for all $\varsigma \in[a, \mathscr{Z}], \mathscr{Z} \in \mathbf{I_{a}^{b}}$. Utilizing (A4) and Proposition 2.12, we get

Thus,

due to

Then, we have $\mathrm{h}(\mathcal{M}) = 0$, which implies, $\mathscr{U}(\mathcal{M})$ is a relatively compact subset of $\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$. Then, there is a subsequence $\overline{\zeta}_n$ which converges uniformly on $\mathbf{I_{a}^{b}}$ to some $\overline{\zeta}_* \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ with the Arzela-Ascoli theorem, and we derive that $\mathscr{U}$ is compact. By Proposition 2.16, $\mathscr{U}$ is $\mathrm{h}$-Lipschitz with zero constant. □

Theorem 3.6. Let (A1) and (A2) be satisfied, then the IVP (1.1)-(1.2) possesses a solution $\zeta\in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ based on $\Lambda_\mathcal{K} < 1$ and the set containing solutions of the proposed problem is bounded in $\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$.

Proof. The operators $\mathscr{V}, \mathscr{U}, \mathcal{W}$ that are presented at the start of this subsection will be used. They are both continuous and bounded. Furthermore, $\mathscr{V}$ is $\mathrm{h}$-Lipschitz with $\Lambda_\mathcal{K}$, as suggested by Lemma 3.3, and $\mathscr{U}$ is $\mathrm{h}$-Lipschitz with constant $0$, according to Lemma 3.5. This further suggests that $\Lambda_\mathcal{K}$ and $\mathcal{W}$ are $\mathrm{h}$-Lipschitz. Because $\Lambda_\mathcal{K}$ is a strict $\mathrm{h}$-contraction, $\mathcal{W}$ follows likewise. Since it is $\mathrm{h}$-condensing, it is $\mathcal{W}$ since $\Lambda_\mathcal{K} < 1$. Now, examine the following collection of

We will show that the set $\Xi$ is bounded. For $\zeta \in \Xi$, we have $\zeta = \varrho \mathcal{W}\zeta = \varrho(\mathscr{U}(\zeta) + \mathscr{V} (\zeta))$, which implies that

By Eq (3.5), we have that $\Xi$ is bounded in $\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$. If it is not, then, dividing it by $\delta: = \|\zeta\|_{\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }}$ and considering $\delta \to \infty$, we get

which is a contradiction. Therefore, $\Xi$ is bounded and $\mathcal{W}$ possesses an FP. Ultimately, we have a solution of IVP (1.1). □

Remark 3.7. ${\bf (I)}$ For $p = 1$, (A2) implies that Theorem 3.6 is true if the following is found

${\bf (II)}$ For $q = 1$, (A3) implies that Theorem 3.6 is valid provided that

${\bf (III)}$ If the hypotheses (A2) and (A3) are developed for $p = 1$ and $q = 1$, then Theorem 3.6 stays valid supplemented to

Here, results for the existence and uniqueness of solution (EUS) are established.

Theorem 3.8. Under the assumption (A1), the IVP (1.1)-(1.2) possesses one, and only one, solution if

Proof. Consider that $\zeta, \overline{\zeta} \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ and $\mathscr{Z}\in \mathbf{I_{a}^{b}}$, then we can obtain

In view of the given condition $\left[\frac{(\mathrm{T}(b)-\mathrm{T}(a))^{\varsigma_{n}}}{\Gamma\left(\varsigma_{n}+1\right)}L+\sum_{j = 1}^{n-1} |a_{j}|\frac{(\mathrm{T}(b)-\mathrm{T}(a))^{\varsigma_{n}-\varsigma_{j}}}{\Gamma\left(\varsigma_{n}-\varsigma_{j}+1\right)}\right] < 1$, $\mathcal{W}$ is a contraction. Ultimately, Banach FPT ensures the uniqueness of FP of the $\mathcal{W}$. □

For EUS of solutions for (1.1) and (1.3), we need the next lemma taken from Harikrishnan et al. ^[7].

Definition 3.9. A function $\zeta\in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ is a solution of (1.1)–(1.3), if it satisfies $L(\mathscr{D}) \zeta(\mathscr{Z}, \mathrm{u}) = \mathcal{K}\Big(\mathscr{Z}, \mathrm{u}, \zeta(\mathscr{Z}, \mathrm{u})\Big)$ for a.e. $\mathscr{Z}\in \mathbf{I_{a}^{b}}$, with

Lemma 3.10. For any $h \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$, the solution function $\zeta$ of the FDE (1.1) with (1.3) is given by

By Lemma 3.10, we consider $\mathcal E, \mathcal F, \mathcal G : \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}}) \longrightarrow \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ as follows:

and

with

and

It is clear that $\mathcal H$ is well-defined. Thus, (3.8) in Lemma 3.10 can be written as

Since $\mathcal{K}$ is continuous, $\mathcal{H}$ is well-define and the FPs are the solutions of (3.8) in Lemma 3.10. From $\mathscr{V}, \mathscr{U}$ and repeating the same lines and processes of Lemmas 3.3–3.5 to deal with $\mathcal{E}, \mathcal{K}, \mathcal{G}$, one can prove the results.

Now, we move forward to the main results of the problem (1.1)–(1.3).

Lemma 3.11. The operator $\mathcal{G}: \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}}) \rightarrow \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ is Lipschitz with 0 constant. Also, $\mathcal{G}$ is $\mathrm{h}$-Lipschitz with zero constant. Furthermore, $F_1$ satisfies that:

for every $\zeta\in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$.

Lemma 3.12. The operators $\mathcal E, \mathcal F: \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}}) \rightarrow \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ are continuous. Consequently $\mathcal E+\mathcal F$ are continuous. Moreover, $\mathcal E+\mathcal F$ satisfies:

for every $\zeta\in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$.

Lemma 3.13. The operators $\mathcal E, \mathcal F: \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}}) \rightarrow \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ are compact. Conclusively, $\mathcal E+\mathcal F$ are $\mathrm{h}$-Lipschitz with 0 constant. Further, $\mathcal E+\mathcal F$ is $\mathrm{h}$-Lipschitz with 0 constant.

Theorem 3.14. Let the conditions (A1) and (A2) hold true. Then, (1.1)–(1.3) have a solution $\zeta \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ and the set containing all the solutions of the BVP (1.1)–(1.3) is bounded in $\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$.

Proof. Consider that the operators defined above are $\mathcal{E}, \mathcal{K}, \mathcal{G}, \mathcal{H}$, and are bounded and continuous. $\mathcal{G}$ is $\mathrm{h}$-Lipschitz with $0$ according to Lemma 3.11, and $\mathcal{E}+\mathcal{K}$ is $\mathrm{h}$-Lipschitz with constant $0$ according to Lemma 3.13. Consequently, $\mathcal{H}$ is $\mathrm{h}$-Lipschitz with constant $0$, according to Proposition 2.15. Thus, the operator $\mathcal{H}$ with constant $0$ is a strict $\mathrm{h}$-contraction. Thus, $\mathrm{h}$-condensing is $\mathcal{H}$.

By considering the set:

We prove that $\Xi$ is bounded. For $\zeta \in \Xi$, we obtain $\zeta = \varrho \mathcal Hu = \varrho(\mathscr{V}(\zeta) + \varsigma (\zeta))$, which shows that

Ultimately, $\Xi$ is bounded in $\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$. If it is not, then

which is a contradiction. Therefore, $\Xi$ is bounded and $\mathcal{H}$ possesses an FP, which is the solution of the FDE (1.1)–(1.3). □

Remark 3.15. ${\bf (I)}$ If we consider (A2) for $p = 1$, then Theorem 3.14 is valid if

${\bf (II)}$ For (A3) at $q = 1$, the Theorem 3.14 is valid if

${\bf (III)}$ If (A2) and (A3) are formulated for $p = 1$ and $q = 1$, then Theorem 3.14 is satisfied if we have

Next, the uniqueness of the solution is stated and proved.

Theorem 3.16. With the use of condition (A1), (1.1)–(1.3) possess a unique solution if

Proof. Let $\zeta, \overline{\zeta} \in \mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$ and $\mathscr{Z}\in \mathbf{I_{a}^{b}}$, then we obtain

By $\left(1+|\nu|\wp_{*}^{\mathrm{T}}(b)\right)\left[\frac{(\mathrm{T}(b)-\mathrm{T}(a))^{\varsigma_{n}}}{\Gamma\left(\varsigma_{n}+1\right)}L+\sum_{j = 1}^{n-1} |a_{j}|\frac{(\mathrm{T}(b)-\mathrm{T}(a))^{\varsigma_{n}-\varsigma_{j}}}{\Gamma\left(\varsigma_{n}-\varsigma_{j}+1\right)}\right] < 1$, we get that $\mathcal{H}$ is a contraction, and by Banach FPT, $\mathcal{H}$ possesses one, and only one, FP, which is a unique solution of FDE (1.1)–(1.3). □

4.   A mathematical problem for illustration of the results

Two examples are provided for the illustration of the results of the work.

Example 4.1. In the operator $L$ of (1.1), (1.2), presuming that $a_1 = a_2 = \ldots = a_n = 0$, and

we get the following example:

with initial condition:

For the verification of the Theorem 3.6, we start with

From the $\mathcal{K}\Big(\mathscr{Z}, \mathrm{u}, \zeta(\mathscr{Z}, \mathrm{u})\Big)$, we have $L = M_1 = M_2 = \frac{1}{100}$, $N_1 = N_2 = \frac{1}{50}$, $v_{r, \wp} = \frac{1}{100}$, $\mathrm{T}(t) = t$. This implies that $(A_1)$ is satisfied. Furthermore, we have

with $M_1 = \frac{1}{100}$ and $N_1 = \frac{1}{50}$. Thus, $(A_2)$ is satisfied. Also, $\Lambda_k < 1$. Hence, all the requirements of the Theorem 3.6 are fulfilled and, therefore, the presumed FDE has a solution and it is bounded in $\mathbb{C}^{\varsigma_{n} }_{\mathrm{T} }(\mathbf{I_{a}^{b}})$.

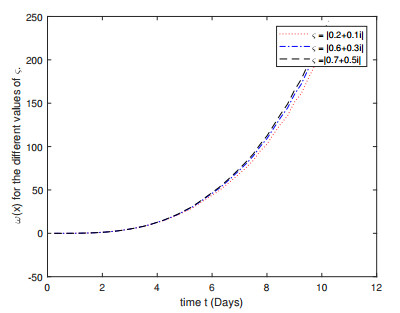
In the Figure 1, we have the numerical solution for the complex order FDE (4.1) for different orders.

Example 4.2. In the operator $L$ of (1.1), (1.3), presuming that $a_1 = a_2 = \ldots = a_n = 0$, and

we get the following example:

with boundary condition:

Consider that

Our presumed $\mathcal{K}\Big(\mathscr{Z}, \mathrm{u}, \zeta(\mathscr{Z}, \mathrm{u})\Big)$ implies that $L = M_1 = M_2 = \frac{1}{100}$, $N_1 = N_2 = \frac{1}{50}$, $v_{r, \wp} = \frac{1}{100}$, $\mathrm{T}(t) = t$. This implies that $(A_1)$ is satisfied. For the verification of the Theorem 3.8, we have, from (3.7),

In the Figure 2, we have the numerical solution for the complex order FDE (4.5) for different orders.

5.   Control design

This study employs a control scheme to analyze the dynamics of leukemia using a mathematical model. The aim is to understand better how chemotherapy affects the growth of both healthy and malignant cells. The dynamics are represented as follows ^[47]:

where

The tracking error expression is provided as $e = {\cal X} - {{\cal X}_d}$, $\dot e = \dot {\cal X} - {{\dot {\cal X}}_d}$,

Notation: The power of vectors is given as

where ${\cal Y}$ is variable and $\rho$ is constant.

The proposed sliding mode control aims to ensure strong system control along a fixed-time manifold. This involves combining nonlinear sliding surfaces with fixed-time convergence at high speeds. This study introduces a fixed-time TSMC and defines a sliding surface as follows:

where $L_1, L_2$, and $L_3$ positive are diagonal matrices, $m_2 > 1$, and $0 < m_1 < 1$.

The $\dot S$ can be computed as

By substituting (5.2) into (5.4), one can get

For controlling nonlinear systems and achieving fast response, chatter-free control, and good tracking performance, the robust fixed-time TSMC method is designed as

where $J_1 > 0$ and $J_2 > 0$ are constant, $0 < n_1 < 1$, and $n_2 > 1$.

Theorem 5.1. The expression (5.3) indicates that the states converge in a fixed time.

Proof. The Lyapunov function is chosen as

$\dot S$ can be given as

When $S = \dot S = 0$, one can have the expression from (5.3) as

where $\, \, {{\tilde L}_2} = {L_2}/{L_1}, \, \, {{\tilde L}_3} = {L_3}/{L_1}$.

By putting (5.9) into (5.8), one can have

By simplifying (5.10), one can obtain

According to Eq (2.7), the fixed convergence time can be calculated as

Hence, the state trajectories $e$ will converge to zero in a fixed time. □

Theorem 5.2. Considering the error dynamics (5.2) and the nonlinear system (5.1), with the intended control method (5.6), the trajectories will converge toward the sliding surface (5.3) in a fixed amount of time.

Proof. The Lyapunov function is selected as follows

The $\dot V_S$ is given as

By substituting (5.5) in (5.15), one can get

By substituting control input (5.6) in (5.16), one can have

With simplification of (5.17), one gets

This can be simplified as

Using Eq (2.7), one can calculate the reaching time as

As a result, the sliding surface will reach in fixed time $T_2$. This completes the proof. □

6.   Numerical simulations of control method

This section includes a case study that aims to validate the findings of the theoretical study and offer a graphical representation of the validation of the recommended methodology. The recommended controller is simulated using the widely used Matlab/Simulink, and the system parameters are listed in Table 1.

The following are the parameters of the suggested control method ^[48]:

The reference inputs are given as:

Clearly, the normal cells follow the recommended method and meet the desired inputs, as shown in Figure 3, indicating that the proposed scheme achieves the desired outcome. Figure 4 illustrates the patterns of leukemic cells using the proposed method. The suggested controller effectively tracks the leukemic cells along the intended path. The total amount of medication used by the recommended approach is depicted in Figure 5, showing the calculated and total quantities. The simulation results demonstrate that the suggested method achieves the desired outcome without impacting the therapeutic process. Additionally, Figure 6 displays the control inputs for the recommended approach.

The proposed controller effectively tracked the desired reference, resulting in lower steady-state error and faster convergence. The therapy did not harm healthy cells. The suggested method is beneficial as it requires fewer therapeutic medicines and leads to faster elimination of leukemic cells.

7.   Conclusions

In the present study, we proved the existence and uniqueness of solutions for a class of multi-complex order nonlinear FDEs. Our approach relies on a new operator suitable for non-singular FDEs with $\mathrm{T}$-RL fractional derivatives, and the use of topological degree theory. The primary findings are demonstrated within a multi-complex order fractional operator of one function with another function. It is explicitly stated and demonstrated that solutions exist and are unique. We provided two complex-order FDEs with initial and boundary values and tested them for the presence of solutions in order to validate the results. The numerical solutions for various complex orders are explained. The primary question posed is addressed by the arguments made in this paper.

The proposed control method is also utilized to regulate the dosage of chemotherapy administered to patients with acute leukemia, aiming to eradicate as few cancerous cells as possible while safeguarding healthy ones. As a result, the fixed-time TSMC control strategy for acute leukemia was developed. This approach yields strong simulation results and demonstrates exceptional tracking and error convergence to the desired references. In future research, additional related control factors should be investigated to assess their effectiveness, as this method alone may not be sufficient for disease management.

The same approach can be further considered for the systems of hybrid structure involving different initial and boundary value conditions. Moreover, multi-complex order nonlinear FDEs could be of other interest.

Author contributions

All authors contributed equally and significantly to this paper. All authors have read and approved the final version of the manuscript.

Acknowledgments

J. Alzabut, H. Khan, S. Ahmed and A.T. Azar express their sincere thanks to Prince Sultan University and OSTİM Technical University for supporting this research. The authors would like to thank Prince Sultan University, Riyadh, Saudi Arabia, for supporting the article processing charges (APC) of this publication. The authors especially acknowledge the Automated Systems and Soft Computing Lab (ASSCL) at Prince Sultan University, Riyadh, Saudi Arabia. The authors wish to acknowledge the editor and reviewers for their insightful comments, which have improved the quality of this publication.

Conflicts of interest

All the authors declared that they have no conflict of interest.