Family of ruled surfaces generated by equiform Bishop spherical image in Minkowski 3-space

1.   Introduction

Deep neural networks have shown strong performance in many fields such as computer vision, speech recognition, and natural language processing. However, the end-to-end learning mode makes the logical relationship of hidden layers and the specific decision-making process of the deep neural network model opaque, that is, the black-box model. And most existing deep neural networks have complex structures and a large number of parameters. To ensure the sustainable development of the deep neural network in fields of low-power platforms and high-risk decision-making, the interpretability and lightweight research of deep neural networks is essential.

Existing interpretable methods for machine learning models can be divided into post-hoc explainable methods and ante-hoc interpretable methods ^[1], based on whether the model interprets decisions after training or directly trains to generate interpretable models. Post-hoc explainable methods increase the number of parameters to a certain extent with the help of additional auxiliary model information, they cannot interpret the reasoning process of the actual decision-making of the model. Ante-hoc interpretable methods can be used to obtain the reasoning and decision-making processes of the model. The self-interpretability of the model reduces the number of parameters that use additional information to interpret the network model. In this paper, we adopted the prototype sample ante-hoc interpretation method of instance-based and designed an interpretable module. In the process of model training, model self-interpretability was realized by measuring the similarity between test and prototype samples. On the premise that FAPI-Net realizes self-interpretation without additional auxiliary information, compared with the latest state-of-the art models MobileNetV2_G2 ^[2] and LRPRNet ^[3], FLOPs are reduced by approximately 21 and 18% respectively. The accuracy of FAPI-Net is equivalent to that of LRPRNet, which is more accurate than MobileNetV2_G2 increased by 9.68 percentage points.

The existing lightweight deep neural network design methods are mainly divided into three directions: lightweight deep network models designed artificially ^{[4,5,6,7,8,9,10]}, deep network model compression, and designed automated lightweight neural networks based on neural architecture search ^[6,11,12]. Most of the current compression methods for deep network models need to be based on well-designed CNN models, which limit the freedom to change the configuration. The search time cost based on neural architecture search is high, and it cannot break through the performance limitations of existing network structures. The artificially designed lightweight deep network model can reduce network parameters and improve network speed without losing deep network performance. In this paper, FAPI-Net is designed artificially by changing the spatial scale and spatial structure of convolution kernels. Compared with MnasNet-A1 ^[11] and EfficientNet-B0 ^[12] design by neural architecture search, FLOPs are reduced by approximately 44 and 55% respectively, with similar accuracy.

A deep neural network model with excellent performance should be as lightweight as possible while being interpretable. The existing research on interpretable and lightweight deep neural networks are two independent directions. There is little work to ensure that the deep models can be interpreted while realizing network lightweight. This paper combined these two independent directions and designed a lightweight interpretable deep network model FAPI-Net by building lightweight FA basic evolution blocks and a PDI module with reference to the MobileNetV3 network structure. In 2019, Zhao et al. ^[13] proposed an interpretable compact convolutional neural networks model, RSNet. However, RSNet only realizes the visualization of the feature map of the pre-trained models. The visualization process and model training are two independent processes, which belong to post-hoc explainable analysis, and the explanation results are not faithful to the original network. The PDI module in this paper participates in model training. The FAPI-Net enhances the interpretability of the model and is faithful to the original network by visualizing the typical image patches that affect the model decision. In addition, the FA module in this paper is designed by multi-scale convolution fusion that expands the receptive field of feature extraction to ensure the performance of the model and reduce the complexity of the model. The main work of this paper includes the following three aspects:

1) By combining multi-scale depthwise convolution and pointwise convolution to replace conventional convolution, we designed a lightweight feature-map augmentation (FA) module. Depthwise convolution kernels of different sizes expand the receptive field of feature extraction and simultaneously help obtain more features. Compared with conventional convolution, the number of parameters was greatly reduced. Using the residual connection between FA modules, we designed the basic convolution blocks of FAPI-Net convolutional layers.

2) Preprocessing of the ILSVRC2012 dataset, prototype samples, and criticism samples were learned by measuring the maximum mean discrepancy (MMD) distance between the data and prototype data distributions. To minimize the distance between the two distributions, we filtered representative prototype samples, used them as model training sets, and filtered out criticism samples that did not represent the original class well. This improved the quality of the model training samples and helped the prototype learn the interpretable module.

3) Based on the prototype sample interpretation method, we designed the prototype dictionary interpretability (PDI) module of the FAPI-Net. In the process of model training, the prototype representation of each class of image patches in the preprocessed ILSVRC2012 training set was learned, that is, the representative parts of each class of images. By comparing the similarity between the test image and the learned prototype representation of each class, the model makes a decision and visualizes the reasoning process of the model prediction.

2.   Related works

In the era of deep learning, deep neural network models are widely used in computer vision tasks such as image classification and object detection. In recent years, many excellent deep learning models have emerged ^[14,15,16]. For these high-performance deep learning models, it is often costly and low rate to deploy them to mobile devices. Therefore, in practical applications, it is necessary to optimize high-performance deep network models. The lightweight of the deep neural network model is a key direction of optimization, the lightweight work of the deep neural network model has also made many progresses. In addition, as the performance of deep neural network models is improving further, the requirements for its transparency and security are gradually increasing. More and more researchers are committed to the interpretability of the deep neural network model. The following is a brief overview of the work related to the interpretability and lightweight of the deep network model.

2.1.   Related work on interpretability of deep network models

According to the interpretable method, the target of interpretation is the entire dataset or a single data point, which can be divided into global and local interpretations. The global interpretation is interpreting the model's way of learning, the information the model learns from the training data, and the basis for the model's decision making. Representative works include TCAV ^[17], which uses visual concepts for global interpretation and proposes to evaluate the importance of visual concepts through "concept activation vectors". To alleviate the problem of manual collection of visual concepts by TCAV, ACE ^[18] was proposed to automatically extract visual concepts. Ge et al. ^[19] proposed VRX to interpret the reasoning logic of neural networks with the structural and spatial relationships between visual concepts and visual concepts. Local interpretation is the interpretation of the decision-making process or decision-making basis of a specific sample, the contribution of the local features of the sample to the decision-making of the deep network model, etc. They can usually be divided into three categories ^[20,21,22]: visualization interpretations based on 1) back propagation, 2) perturbation, and 3) class activation mapping (CAM). Simonyan et al. ^[23] proposed a back-propagation interpretable method (Grad), which backpropagated the important information of the model decision from the output layer to the input layer and calculated the gradient change of the output compared to the input. Qi et al. ^[24] proposed the I-GOS, which uses integrated gradients to replace conventional gradients to optimize the heatmap and visualize the deep network. Zhou et al. ^[25] proposed CAM, which replaces the fully connected layer with a global average pooling layer, locates the local features in the input samples that have an impact on the decision-making of the deep network model, and visualizes them as a heat map. Ramprasaath et al. ^[26] proposed Grad-CAM by combining a back-propagation interpretable method and CAM. Grad-CAM does not require modification of the network model and avoids the loss of model accuracy caused by the addition of interpretability. The improved CAM methods include Grad-CAM++ ^[27], Score-CAM ^[28], and Relevance-CAM ^[29].

All the above mentioned interpretable methods use additional information to interpret the decision results of the model and cannot interpret the reasoning process of model decision-making, that is, post-hoc explainable methods. Ante-hoc interpretable methods can interpret the decision-making basis and process of the model without the support of additional information. However, models with complex structures are not self-interpretable. To this end, researchers have achieved the self-interpretability of models by adding interpretable modules to complex deep network models or directly modeling interpretable models. For example, Bahdanau et al. ^[30] added an attention mechanism to a decoder and visualized the attention weights to achieve interpretability. Shen et al. ^[31] modeled semantics, enabling CNNs to automatically model symbolic feature representations during end-to-end training. Wang et al. ^[32] used the Shapley value as an inter-layer feature of a neural network to alleviate the problem of the huge computational complexity of the Shapley value. Stammer et al. ^[33] proposed that iCSNs learn concept-based representations through weak supervision and prototypal representations, demonstrating the advantages of prototypal representations in understanding and modifying the latent space of neural concept learners.

Based on the ante-hoc prototype sample interpretation method, this paper designed the PDI module, added it to the deep network model, updated the prototype dictionary through network training, and visualized the prototype results corresponding to the test images in the form of heat maps. While ensuring the self-interpretability of the deep network model and providing accurate and undistorted visualization results, the performance loss of the deep network model was reduced.

2.2.   Related work on lightweight of deep network models

The research on lightweight model structures designed artificially has developed rapidly, and many representative model structures have appeared in the past few years. The typical work includes: Landola et al. proposed SqueezeNet ^[10], the core structure Squeeze layer + Expand layer. ShuffleNetV1 ^[7] and ShuffleNetV2 ^[8] were designed by setting feature map channels. Howard et al. proposed MobileNetV1 ^[4], which uses depthwise separable convolution instead of conventional convolution to reduce the number of network parameters and improve the speed of network operation. The Google team subsequently proposed MobileNetV2 ^[5]. Andrew et al. proposed MobileNetV3 ^[6], which added a squeeze-and-excitation (SE) module based on MobileNetV2 to automatically obtain the importance of each feature channel. Use of AutoML technology to find the optimal neural network architecture for a specific problem further improves the accuracy rate and reduces the network delay. In recent research, Yang et al. ^[34] analyzed the convolution structure in the MobileNet model and found that the pointwise convolution in the inverted residual structure occupied most of the model's parameters and computation. The MobileNet model was optimized by changing the computation of the pointwise convolution of the two parts in the inverted residual structure. Huawei has proposed a lightweight GhostNet model ^[35]. There are many similarities between the feature maps output by the same convolution layer. Therefore, GhostNet used a small number of standard filters to generate one part of the feature maps and then performs depthwise convolution to generate the other part of the feature maps. Finally, the two parts of the feature maps are connected in the channel dimension as the final output. Tan et al. proposed the MixNet with mixed depthwise convolutional kernels ^[36]. Sun et al. proposed the LRPRNet ^[3] using low rank pointwise residual (LRPR) evolution, which applies LRPR to MixNet. Zhong et al. proposed MobileNetV2_ G2 ^[2], which uses the group convolution technique, applying 3 × 3 and 1 × 1 dual convolution kernels on MobileNetV2.

Unlike the above work, which only changes the computation of pointwise convolution, or group convolution techniques that use pointwise convolution and depthwise convolution in separate steps. This paper combined pointwise convolution and multi-scale convolution to design an FA module, which can replace the conventional convolution anywhere in the network. The depthwise convolution kernels with different sizes expand the receptive field of feature extraction. Compared with conventional convolutions, they reduce the network parameters and ensure the model accuracy.

3.   Methods

3.1.   Design of lightweight feature-map augmentation module

In deep learning tasks related to image classification, to fully obtain the information contained in the input image, the deep network model generates a large number of redundant feature maps when extracting features, as shown in Figure 1. These redundant feature maps, generated using conventional 3 × 3 convolutions, which consume a lot of unnecessary network parameters, are either repeated or have a limited impact on the model's decision making. In this paper, a convolution operation with less parameters was used to simply transform the effective feature map, and the generated feature map was equivalent to the feature map of the redundant part generated by the conventional convolution operation, which can reduce the number of network parameters and ensure network performance. In this paper, a lightweight FA module was designed by combining pointwise convolution and multi-scale depthwise convolution to ensure sufficient richness of the feature extraction and feasible reduction in the model parameters.

The sizes of the input and output feature maps were assumed to be h*w*${C}_{in}$ and ${h}^{'}$*${w}^{'}$*${C}_{out}$, respectively, where h and w are the height and width of the input feature map, ${h}^{'}$ and ${w}^{'}$ are the height and width of the output feature map, ${C}_{in}$ and ${C}_{out}$ are the number of input channels and output channels, respectively. Other formulas in this paper are also applicable. The size of the convolution kernel was assumed to be $k*k$. The unified calculation formula of the number of convolution parameters is:

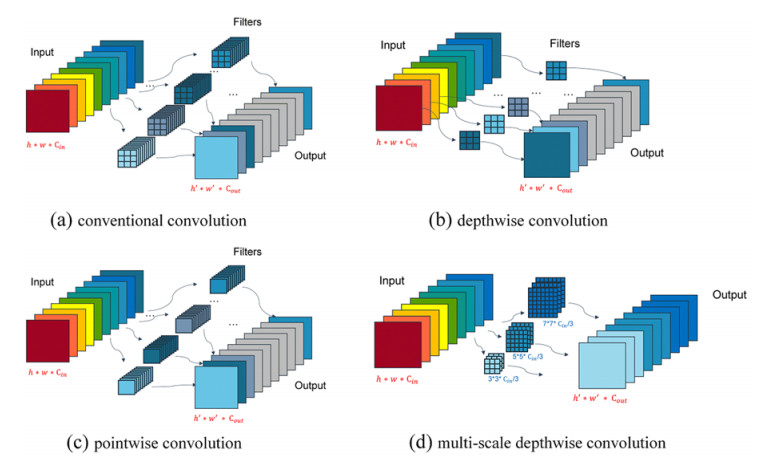
The conventional convolution operation is shown in Figure 2(a), where the size of the convolution kernel is 3 × 3, the number of parameters of the conventional convolution is $9{C}_{in}{C}_{out}$. The depthwise convolution is also known as channel-by-channel convolution, that is, a depthwise convolution kernel is responsible for one channel, as shown in Figure 2(b). The size of the depthwise convolution kernel in Figure 2(b) is also set to 3 × 3, the number of parameters of the depthwise convolution is $9{C}_{out}$. Because each depthwise convolution operation in depthwise convolution is independent, the information does not circulate between different channels in the same spatial location. In MobileNetV1, Howard et al. used pointwise convolution to combine the feature maps after depthwise convolution operations to generate new feature maps, that is, depthwise separable convolution operations. The pointwise convolution operation is shown in Figure 2(c), where the size of the convolution kernel is 1 × 1 and the number of parameters of the pointwise convolution is ${C}_{in}{C}_{out}$. The number of parameters of the depthwise separable convolution is the sum of the number of parameters of the depthwise and pointwise convolutions, namely $9{C}_{out}+{C}_{in}{C}_{out}$. It can be seen that depthwise separable convolution significantly reduced the number of network parameters.

However, since the size of the depthwise convolution kernel of the depthwise separable convolution is fixed and limited to 3 × 3, that is, the receptive field of the depthwise convolution is limited, and more information cannot be extracted. Reduction in the number of network parameters to a certain extent while ensuring network performance is a win-win situation. In this paper, a multi-scale convolution kernel was introduced into the depthwise convolution. According to the evenly divided channel method verified by MixNet ^[36], the input channels were evenly divided into three groups, where each group used depthwise convolution kernels of different scales, and a multi-scale depthwise convolution operation was designed, as shown in Figure 2(d). By grouping and using depthwise convolution kernels of different sizes, the receptive fields of different resolutions were obtained, which solved the limitation of the depthwise convolution fixed convolution kernel.

To ensure complete extraction of the features of the input image, conventional convolution often generates rich or even redundant feature maps, as shown in Figure 1. The input image is generated through the conventional convolution operation of the VGG-16 network. The feature map of the redundant part can be obtained through a simple transformation of the effective feature map. In this paper, multi-scale depthwise convolution was used to replace conventional convolution, and the effective feature map was simply transformed to generate the feature map of the redundant part, which reduced the number of network parameters while ensuring network performance.

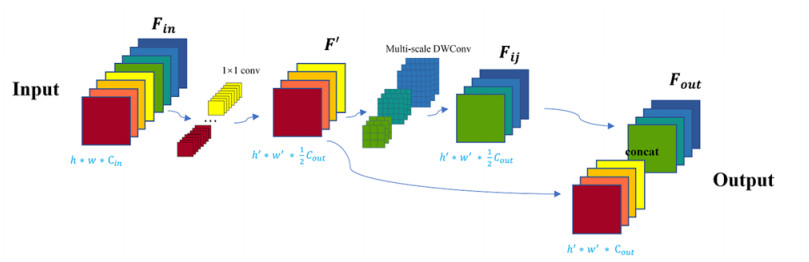
FA module. We designed a FA module by combining pointwise convolution and multi-scale depthwise convolution, which pointwise convolution is used to generate effective feature maps with rich features, and multi-scale depthwise convolution was used to perform simple transformation on effective feature maps to generate redundant feature maps. The FA module is an important part of the basic convolution block of FAPI-Net, and each FA module contains three different scales of depthwise convolution. MixNet simply replaces the ordinary depthwise convolution in MobileNet, using a small-size convolution kernel in the early stage and a large-size convolution kernel in the later stage.

Figure 3 shows the operational process of the FA module. First, the input was subjected to pointwise convolution and the number of convolution kernels was set to $\frac{1}{2}{C}_{out}$; the generated effective feature map ${F}^{'}$ can be represented by Eq (2).

where ${F}_{in}\in {R}^{h\times w\times {C}_{in}}$ is the input feature map, $f\in {R}^{{C}_{in}\times 1\times 1\times \frac{1}{2}{C}_{out}}$ is the convolution kernel of size 1 × 1, ${F}^{'}\in {R}^{{h}^{'}\times {w}^{'}\times \frac{1}{2}{C}_{out}}$, $*$ is the convolution operation. Let n be the number of feature maps required by the FA module to generate, $n = {C}_{out}$. Through this step, an effective feature map of n/2 was obtained.

Then it was divided into two branches, one of which performed a multi-scale depthwise convolution operation on the feature map ${F}^{'}$ to generate another n/2 redundant partial feature map, and its mathematical expression is shown in Eq (3).

where ${f}_{i}^{'}$ is the ith original feature map in ${F}^{'}$. ${M}_{i, j}$ is the jth multi-scale depthwise convolution operation, which is used to generate the jth feature map ${F}_{ij}$. The input feature map of the multi-scale depthwise convolution was divided into g equal groups and denoted as tensors $\left\langle{{X}^{(h, w, {C}_{1})}, \cdots, {X}^{(h, w, {C}_{g})}}\right\rangle$, and the convolution kernels of different scales in the g group were denoted as tensors $\left\langle{{W}^{({k}_{1}, {k}_{1}, {C}_{1})}, \cdots, {W}^{({k}_{g}, {k}_{g}, {C}_{g})}}\right\rangle$. The output of the tth group was represented by tensor ${Y}^{({h}^{'}, {w}^{'}, {C}_{t})} = {X}^{(h, w, {C}_{t})}*{W}^{({k}_{t}, {k}_{t}, {C}_{t})}$. The output of the final multi-scale depthwise convolution was a concatenation of the outputs of each group, and its mathematical expression is shown in Eq (4).

where $Concat$ represents the tensor concatenate operation, that is, $Concat(A, B)$ represents the matrices of two feature map A and B are concatenated according to a certain dimension. $Concat$ requires that the connected dimensions can be different, but other dimensions must be equal. In the experiments in this paper, the input feature maps of the multi-scale depthwise convolution were divided into three equal groups, namely $g = 3$ and the number of channels ${C}_{1} = {C}_{2} = {C}_{3}$. The size of the multi-scale depthwise convolution kernel was set as ${k}_{1} = 3$, ${k}_{2} = 5$, and ${k}_{3} = 7$.

Another branch concatenated the input feature map ${F}^{'}\in {R}^{{h}^{'}\times {w}^{'}\times \frac{1}{2}{C}_{out}}$ and output feature map ${F}_{ij}\in {R}^{{h}^{'}\times {w}^{'}\times \frac{1}{2}{C}_{out}}$ to generate the final output feature map ${F}_{out}\in {R}^{{h}^{'}\times {w}^{'}\times {C}_{out}}$.

3.2.   Design of prototype dictionary interpretability module

The gradual improvement in the performance of the deep network model is also accompanied by an increase in the network depth, and the network presents the characteristics of highly complex nonlinearity. In addition to realizing a lightweight deep network model, the decision-making basis and process of the deep network model cannot be ignored. The performance and application of deep network models that lack interpretability are controversial, especially when they are applied to security-sensitive industries. In image-classification-related tasks, commonly used interpretable methods include activation maximization ^[23], saliency visualization ^[37], and CAM ^[25]. These interpretable methods achieve explainability by interpreting the input part that affects the decision-making results of the network but cannot interpret the decision-making basis and reasoning process of the network.

PDI module. In this paper, an interpretability PDI module was designed by learning a prototype dictionary D during the network training process, and the prototype dictionary was updated during the model training process to realize a self-interpretable lightweight deep neural network model. Prototype refers to representative sample data in a sample space. Each column vector ${d}_{k}$ (where k is the number of classes in the original training set) in the prototype dictionary was composed of m image patches, typically representing a class of samples. For example, in the dog class image, the learned prototype representation in the dictionary may have prototype samples, such as the head, hair, and tail parts, and prototype samples were extracted from some images in the training sample. The model decision results were obtained based on the similarity scores of each column in the prototype dictionary by comparing the pixel features of the test image with those of the prototype samples in each column of the dictionary. For each test image, the decision-making basis of the classification result was the representation of each prototype of the corresponding class with the highest similarity score. Visualizing the prototypes and expressing the similarity scores of each prototype in the form of an activation map, that is, realising the decision-making process visualisation of the classification results of the test images.

In general, the similarity between two data points $({x}_{1}, {y}_{1})$ and $({x}_{2}, {y}_{2})$ in the feature space can be measured using the distance between them. Commonly used methods for calculating the distance between two data points in space are the Manhattan distance $dist = \sum _{i = 1}^{n}\left|{x}_{i}-{y}_{i}\right|$ and Euclidean distance $dist\left(X, Y\right) = \sqrt{\sum _{i = 1}^{n}{({x}_{i}-{y}_{i})}^{2}}$. For sample sets with large amounts of data, the Euclidean norm was more sensitive to outliers in the sample space. Therefore, this paper used the Euclidean distance to calculate the distance between the input and prototype features to learn the prototype dictionary. To update the prototype dictionary, the specific process is as follows.

First, m high-activation image patches cropped from the original image for each class in the original training set are randomly selected as the initial prototype samples of the prototype dictionary, that is, the initial prototype dictionary D is obtained with m rows and k columns consisting of $m\times k$ image patches.

Referring to the update method of the prototype template by Chen et al. ^[38], during the network training process, the prototype dictionary is updated by minimizing the Euclidean distance between the input feature maps and prototype samples. Let $Z = {\left\{({x}_{i}, {y}_{i})\right\}}_{i = 1}^{n}$ be the original training set, and two optimization problems need to be solved for each column prototype sample $P = {\left\{{p}_{j}\right\}}_{j = 1}^{m}$. The specific mathematical expression is shown in Eq (5).

where C is the clustering loss, and minimising C brings the potential patches in each training image close to at least one prototype sample of the correct class. S is the separation loss, and minimising S keeps the latent image patches in each training image away from the prototype samples that do not belong to their correct class. X is the input feature map and $\tilde {x}$ is the latent image patch of the input feature map. For the prototype sample ${p}_{j}\in {P}_{k}$ of class k, update, as shown in Eq (6).

According to the column ${d}_{k}\in \left\{{d}_{1}, \cdots, {d}_{k}\right\}$ of the dictionary, the prototype dictionary is updated column by column through network training, and each column element represents the prototype of a class of samples.

3.3.   Pre-filtering of the ILSVRC2012 dataset

To improve the quality of the prototypes learned by the PDI module during model training, this paper adopted the MMD-critic ^[39] criteria to preprocess the ILSVRC2012 dataset. By minimizing the MMD distance between the prototype distribution and the data distribution, a representative prototype sample was filtered for the model input. Filtering out the samples that cannot well represent each class of images improves the quality of the input samples for model learning and prediction performance of the model.

MMD is a kernel-learning method. By mapping the data points in the two distributions to the reproducing kernel hilbert space (RKHS), the distance between each data point was calculated and summed. The specific mathematical expression is shown in Eq (7):

Among them, ${X}^{s} = \left[{x}_{1}^{s}, \cdots, {x}_{n}^{s}\right]$ and ${X}^{t} = \left[{x}_{1}^{t}, \cdots, {x}_{m}^{t}\right]$ represent the existence of two distributions in the RKHS, and $\phi \left(\cdot \right):X\to H$ represents the mapping from the original space X to Hilbert space H.

The MMD-critic criteria defines a loss function ${J}_{b}\left(S\right)$ using a kernel function $k(\cdot , \cdot )$ and MMD distance, as shown in Eq (8):

where $X = \{{x}_{i}, i\in \left[n\right]\}$ represents n samples belonging to the same class, and ${X}_{s} = \{{x}_{i}, \forall i\in S\}$ is a subset of X, namely $S\subseteq \left[n\right]$. The prototype samples were learned by maximising the ${J}_{b}\left(S\right)$.

In this paper, the loss function ${J}_{b}\left(S\right)$ was used on the ILSVRC2012 dataset to filter representative prototype samples from the original training set to a certain proportion and to filter out the criticism samples that the prototype cannot represent well, to help the PDI module to learn the prototype.

3.4.   Design of lightweight interpretable convolutional neural network

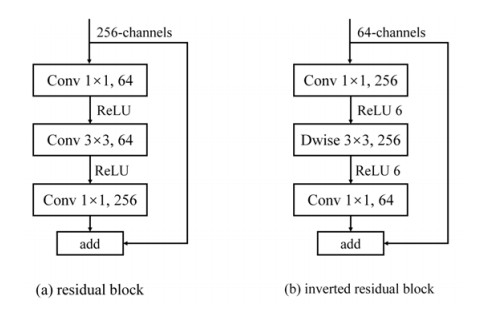
When designing a convolutional neural network, as the number of network layers increases, the performance of the model gradually improves; however, when the number of network layers increases to a certain number, the problem of gradient dissipation occurs owing to a large number of network layers, degrading the network model. The residual block of ResNet, as shown in Figure 4(a), can effectively solve the degradation problem of the deep network. The residual module includes direct mapping and residual connections, which can smoothen the network information flow. Figure 4(b) shows the inverted residual block of the MobileNetV2. First, a 1 × 1 convolution was used to expand the number of channels, and a 3 × 3 depthwise convolution was used in the middle, and the calculation number was much smaller than that of traditional convolution. Finally, a 1 × 1 convolution was used to compress the number of channels.

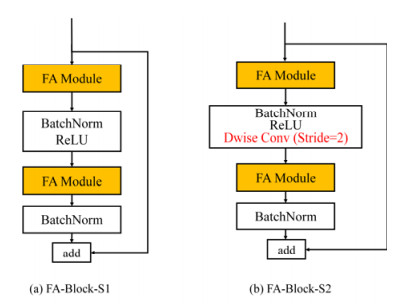
Basic convolution block. Combined with residual connection and FA module, this paper designed two basic convolution blocks, FA-Block-S1 and FA-Block-S2, whose structures are shown in Figure 5(a), (b), respectively. FA-Block-S1 refers to the inverted residual structure of MobileNetV2, which is mainly composed of two FA modules. The input feature map passes through the first FA module for channel expansion, and then through the BN and ReLU nonlinear activation layers to ensure the same distribution of the inputs of each layer; then passes through the second FA module for channel compression, later only uses the BN layer; finally uses the residual connection to add the input and output. The first FA module is equivalent to the first 1 × 1 convolution of the MobileNetV2 inverted residual module, and the second FA module is equivalent to the second 1 × 1 convolution of the inverted residual module. Because FA-Block-S1 does not support downsampling operations, we further designed FA-Block-S2. Considering the number of parameters of the model, FA-Block-S2 added a depthwise convolution with stride 2 instead of multi-scale depthwise convolution on the basis of FA-Block-S1 for downsampling. Compared with pooling operation for downsampling, using depthwise convolution can well avoid information loss.

FAPI-Net can guarantee good performance while maintaining lightweight models because of the effective combination of linear bottleneck module, FA basic convolution blocks and squeeze excitation module (that can automatically obtain the importance of feature channels). An important difference between FAPI-Net and other network architectures is that FAPI-Net has lightweight layers with fewer filters. Relatively few multi-scale filters are sufficient to obtain advanced results on the test dataset. This can reduce the network computation and increase the receptive field of feature extraction. We found that the FLOP of FAPI-Net is significantly lower than that of networks using single scale convolution, such as MobileNetV2 and MobileNetV3.

Architectural details. The FAPI-Net used in our experiments has three main components, namely, the basic convolution blocks FA-Block-S1 and FA-Block-S2, and a PDI module. The first layer of the FAPI-Net is a 3 × 3 conventional convolution layer in which output channels are 16 and stride size is 2. MobileNetV3 sets the last bneck stride to 2 for input feature maps of the same size. Refer to the position where MobileNetV3 bneck step is set to 2, FAPI-Net divides the convolutional layer into four stages according to the size of the input feature map, except that the last convolutional layer of each stage uses FA-Block-S2 and the others use FA-Block-S1. After the final 1 × 1 convolution operation, the PDI module was added after the feature extraction was complete, and the prototype dictionary was updated. The extracted features and m similarity scores of each class of prototypes in the dictionary were converted into scalars using global max pooling, and the final classification was achieved using a fully connected layer and Softmax weighted summation. The network configuration of the FAPI-Net is shown in Table 1, where SE is 1, which means that a squeeze excitation module was used.

The model complexity of FAPI-Net is mainly reflected in the FA module. In our experiments, the input feature maps of multi-scale depthwise convolution are divided into three groups. The size of each group of convolution kernels is set as ${k}_{1} = 3$, ${k}_{2} = 5$, and ${k}_{3} = 7$ respectively, so the number of parameters of the FA module is $1*1*{C}_{in}*\frac{1}{2}{C}_{out}+\frac{1}{2}{C}_{out}*\frac{1}{3}*\left(3*3+5*5+7*7\right)*\frac{1}{6}{C}_{out} = \frac{83}{36}{{C}_{out}}^{2}+\frac{1}{2}{C}_{out}*{C}_{in}$. Compared with the number of parameters $9{C}_{in}*{C}_{out}$ of the 3×3 conventional convolution, as long as $3.7{C}_{in}\ge {C}_{out}$, the number of parameters of the FA module is less than that of conventional convolution.

4.   Experiments

To verify the effectiveness of the FA module proposed in this paper, the FA module was added to the classical convolutional neural network to replace the conventional convolutional module, and the CIFAR-10 dataset ^[40] was used for experimental verification. Then, an image classification comparison experiment of FAPI-Net was performed on the ILSVRC2012 dataset ^[41] to verify the performance of FAPI-Net. Then, the MMD-critic criterion mentioned in Section 3.3 was used to pre-filter the ILSVRC2012 training set, and the filtering ratio was set to 9:1; that is, one criticism image that cannot be well represented by the prototype was filtered out of 10 training images, and the remaining images were used as the training set. The labeled validation set was used as the test set. FAPI-Net trained and learned to update the prototype dictionary and realized the visualization of the test image classification decision-making process to verify the self-interpretability of FAPI-Net, that is, the effectiveness of the PDI module.

4.1.   Experimental configuration and evaluation criteria

All experiments in this paper were implemented in the Ubuntu 18.04 environment, the CPU was Intel Xeon E5-2630L v3, the actual memory was 62 G, the GPU was NVIDIA GeForce RTX 3090, and the video memory was 24 G. The deep learning framework adopted PyTorch, which is open-source on Facebook. All experiments used the widely used random initialization method to initialize the parameters, and all the models were trained from scratch. For the CIFAR-10 dataset, the unified input size was 32 × 32 and the network was optimized using a stochastic gradient descent algorithm with a momentum of 0.9. The batch size, epoch, and learning rate were set to 64,300, and 0.1, respectively. For the ILSVRC2012 dataset, the unified input size was 224 × 224 and the network was optimized using a stochastic gradient descent algorithm with a momentum of 0.9. The batch size, epoch, and learning rate were set to 16,200, and 0.1, respectively.

For all training and test images, the widely used image augmentation techniques were used for processing, and the specific operations are shown in Table 2.

For image classification tasks, the following four indicators are used for evaluation.

where P (positive) is the number of positive examples in the sample, and N (negative) is the number of negative examples. TP (true positive) is the number of samples of positive class predicted to be positive class, TN (true negative) is the number of samples of negative class predicted to be negative class, FP (false positive) is the number of samples of negative class predicted to be positive class, FN (false negative) is the number of samples of positive class predicted to be negative class. Accuracy is the most common metric. In general, the higher the accuracy, the better the classifier. In the image classification experiment on ILSVRC2012 dataset, we use Top-1 error. Suppose the model predicts the class of an object, the model outputs one prediction result. The probability that the result can be judged correctly is the Top-1 accuracy. The probability of error judgment is Top-1 error.

For the evaluation of lightweight network models, the main indicators are the parameters and the floating-point operations (FLOPs) of the model. For convolutional layers, we have:

where k is the size of the convolution kernel, ${C}_{in}$ is the number of input channels, ${C}_{out}$ is the number of output channels. H and W are the height and width of the output image. For fully connected layers, we have:

where I and O are the input dimensionality and the output dimensionality. The number of parameters is an important indicator to measure the memory space consumed by the network. The FLOPs is an important indicator to measure the complexity of the network.

4.2.   Verification ablation experiment of FA module

In this part, we performed a FA module ablation experiment. The FA module proposed in this paper is added to the typical classification networks ResNet-101 and VGG-16 respectively, we trained four models on the CIFAR-10 dataset: ResNet-101 and VGG-16 with no FA module, FA-ResNet-101 and FA-VGG-16 with the FA module. In addition, we trained FA-Net without the PDI module and advanced lightweight networks GoogleNet, ShuffleNetV2 and MobileNetV2 on the ILSVRC2012 dataset. Through these experiments, we verify the effectiveness of our FA module. The experimental results of comparing their parameters, FLOPs, accuracy, precision, recall and F-measure, are listed in Tables 3 and 4.

It can be seen from the experimental results in Table 3 that adding FA module can significantly reduce the parameters and computation while ensuring the classification accuracy to almost equal to that of baseline network. The number of parameters of the network was reduced by approximately 40%, and the number of FLOPs was reduced by approximately 30%. The results exhibited certain differences for networks with different structures.

From the experimental results in Table 4, compared to GoogleNet, the number of parameters and FLOPs of the FA-Net was reduced by approximately 23 and 89% respectively, the accuracy of the FA-Net was increased by approximately 16%. Compared to MobileNetV2, the number of FLOPs of the FA-Net was reduced by approximately 45%, and the accuracy is raised. Compared to ShuffleNetV2, the accuracy of the FA-Net has been increased by 4.8 percentage points, the number of parameters and FLOPs raised slightly.

In addition, the Accuracy, Precision, Recall and F-measure of each model are very close in Tables 3 and 4, which proves that these models can extract stable features. Therefore, it can be concluded that the FA module proposed in Section 3.1 can effectively reduce network complexity without losing network accuracy.

4.3.   FAPI-Net image classification experiment

This section describes the lightweight interpretable deep network FAPI-Net designed in Section 3.4, trained on the ILSVRC2012 dataset that has not been filtered by the MMD-critic criteria, and the adoption of the standard cross-entropy loss by the loss function. We compared classical convolutional neural network models such as MobileNetV3 for image classification experiments and compared their parameters, FLOPs, and Top-1 error. The experimental results are listed in Table 5.

In Table 5, we show the benchmark results of comparing the baseline model with some existing models and the FAPI-Net of this paper on the ILSVRC2012 dataset. Compared with the high-accuracy lightweight network InceptionV3, MobileNetV3 has reduced parameters and FLOPs by 79 and 84% respectively. Compared with MobileNetV1, MobileNetV2 and SqueezeNet, MobileNetV3 reduces the FLOPs by 60, 27 and 47% respectively, and the accuracy increases by 4.55, 5.98 and 17.1 percentage points respectively. The FLOPs of MobileNetV3 are also lower than those of MnasNet and EfficientNet based on neural architecture search. It can be seen that compared with existing models, MobileNetV3 has lower FLOPs and higher accuracy. Compared with the baseline model MobileNetV3, FAPI-Net added PDI trainable module, which lost a bit of accuracy, but achieved model self-interpretation and reduced network parameters and FLOPs.

In addition, we show the benchmark results of comparing FAPI-Net with other state-of-the-art models on the ILSVRC2012 dataset in Table 5. Compared to the lightweight networks MobileNetV1 and MobileNetV2, FAPI-Net has a lower Top-1 error rate (3.48 and 4.91 percentage points lower, respectively), and FLOPs are greatly reduced (approximately 69 and 42% lower, respectively). Compared with the high-performance convolutional neural network model DenseNet121, the parameters of FAPI-Net were reduced by approximately 34%, and the Top-1 error rate basically remained the same. Compared with the MnasNet and the EfficientNet based on neural architecture search, the number of FLOPs was reduced by approximately 44 and 55% respectively. The Top-1 error rate of MnasNet basically remained the same, but the Top-1 error rate of EfficientNet increased. Compared with the latest state-of-the-art models MobileNetV2_G2 and LRPRNet_MixNet, FAPI-Net has lower Flops (reduced by approximately 21 and 18% respectively), and its accuracy is 9.68 percentage points higher than MobileNetV2_G2. However, except for MobileNetV3, the number of parameters of FAPI-Net is slightly higher than other lightweight networks in Table 5. In general, lightweight convolutional neural network models lost their classification accuracy while achieving light weight. In addition, there was a conflict between the model's accuracy and interpretability. It can be seen from the above results that for the FAPI-Net, on the premise of including an interpretable PDI training module, while realising a lightweight network, the network accuracy was basically not lost.

On the whole, FAPI-Net has great advantages in network computation (FLOPs), classification accuracy is almost the same as that of the advanced models, and the performance of network parameters is poor. Because the size of the 2/3 convolution kernels in the multi-scale convolution of FAPI-Net constructed in this paper is larger than that of the 3 × 3 conventional convolution kernel, the network parameters increase. It can be improved by changing the grouping strategy of the number of convolution filters at different scales or adjusting the proportion of FA modules added.

4.4.   Prototype samples pre-filtering results of ILSVRC2012 dataset

The MMD-critic criteria proposed in Section 3.3 was used to preprocess the original training set of ILSVRC2012, and the representative prototype samples were filtered as the training set for the visualisation experiment of model classification and reasoning in Section 4.5. This section considers the two types of data of goldfish and great_white_shark as examples and provides some criticism samples by filtering out the MMD-critic criteria, as shown in Figure 6, respectively.

From the images shown in Figure 6, it can be seen that the criticism samples removed by the MMD-critic were partial images with incomplete targets, blurred images, and easy confusion. These images were not helpful for the classification decision of the model, and the prototype could not be well represented. Therefore, filtering out such criticism data improved not only the quality of the prototype sample set, but also the prediction performance of the model.

Figures 7 and 8 show the comparison of some prototype samples of two types of data, goldfish and great_white_shark, learned from the prototype dictionary before and after the original training set of ILSVRC2012 was filtered by MMD-critic criteria.

From the results in Figures 7 and 8, it can be observed that the prototype samples learned from the original training set after filtering better reflected the important information of the class, such as head and body parts. Therefore, it can be concluded that after the original training set was filtered by the MMD-critic standard to remove criticism samples that cannot be well represented by the prototype, it was helpful for the PDI module to learn more representative prototype samples.

4.5.   FAPI-Net decision reasoning visualization

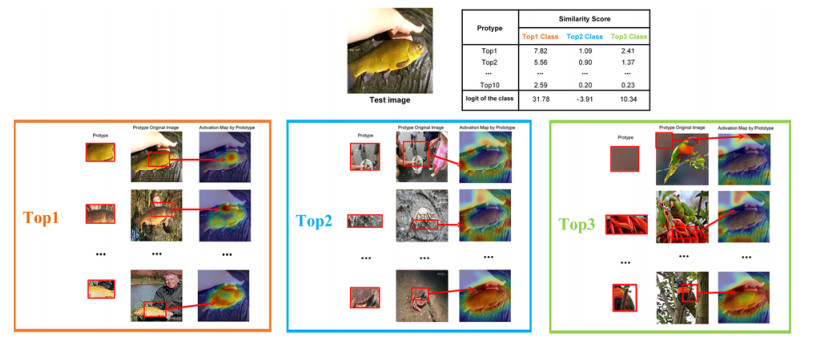
This section presents the visualization results of the classification decision-making process for specified test images, and verifies the PDI module proposed in Section 3.2. For a test image, the top 10 prototype images in each class were the most similar to the test image. The highest similarity means the largest similarity score of the Euclidean distance transformation between the test image and prototype images. The similarity scores of the ten most similar prototype images in each class were weighted and summed to obtain the similarity scores of each category with the test images, and the classes with similarity scores in the top 10 were visualized.

This section presents test images of the three classes of tench, toucan, and Scotch_terrier as examples. The first tench-class test image provided the visualization results of the top three classes of similarity scores, as shown in Figure 9. The second toucan-class and third Scotch_terrier-class test images provided visualization results of the classes with the highest similarity scores that influenced the model's decision, as shown in Figures 10 and 11. In addition, the prototypes were visualized, and the initial images of the prototypes and activation maps for similarity score transitions between prototypes and test image patches upsampled to test images were also visualized.

From the visualisation results in Figure 9, it can be observed that the test images with a real class of 0 were compared with the prototype images in each class, and according to the similarity score of the test image and each prototype, the score of the test image belonging to the class was obtained by weighting. Top1_class, Top2_class, and Top3_class had scores of 31.78, -3.91, and -4.4, respectively. The model determined that the class of the test image was 0 according to the class with the highest similarity score.

5.   Conclusions

This paper introduces FAPI-Net: a lightweight interpretable deep network model based on feature augmentation convolution blocks and a PDI module, which reduces network complexity and makes the model reasoning process transparent through multi-scale convolution fusion and ante-hoc prototype sample interpretable methods. The ablation experiment results on the cifar10 dataset confirm that the FA module can effectively reduce the number of network parameters and computation. An image classification experiment was carried out on the ILSVRC2012 dataset, and the visualization of the model classification and reasoning process was realized. The experimental results show that FAPI-Net has the self-interpreting ability, and outperformed its underlying network MobilenetV3, MobilenetV2 and other advanced convolutional neural networks such as MobilenetV2_G2 and DenseNet121 in terms of computation (FLOPs) at the same accuracy level. FAPI-Net is inferior to the most advanced baseline model in terms of network parameters. We anticipate further research in FAPI-Net to change the grouping strategy of the number of convolution filters at different scales or adjust the proportion of FA modules in networks, to design more lightweight Convolutional Neural Network models. In addition, we hope that our work will draw more attention toward a broader view of the research of interpretable lightweight deep neural network models.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 61976217), the Opening Foundation of Key Laboratory of Opto-technology and Intelligent Control, Ministry of Education (KFKT2020-3), the Fundamental Research Funds of Central Universities (No. 2019XKQ YMS87), Science and Technology Planning Project of Xuzhou (No. KC21193).

Conflict of interest

The authors declare there is no conflict of interest.