Abbreviations
PCA = Principal component analysis
WT = Wavelet transform
RBF = Radial basis function
IMF = Intrinsic mode function
EMD = Empirical mode decomposition
ANN = Artificial neural networks
DWT = Discrete wavelet transform
GPR = Gaussian process regression
BP-NN = Artificial neural networks base backpropagation screening
BP = Backpropagation screening
MAE = Average absolute error
MAPE = Relative errors
PSO = Particle swarm optimization
RMSE = Deviation
STDn = Standard deviation
Csi = Flame stability
MLP = Multi-layer perceptron
ave = Mean value of correlation function
Sh = Information entropy based on gray histogram
S = Flame area
th = Segmentation threshold
var = Gray variance
gl = Gray scale
Asm = Image energy of flame area
Nomenclature
k = number of nodes in hidden layer
m = length of y
n = length of x
s = number of times in sifting process
SDps = termination criterion
t = time parameter
rn(t) = the nth residue
x = input vector
y = output vector
ˆy(n) = estimation of time series
y(n) = original time series
mk = center vector of the kth node in hidden layer
Greeks
||x−ck|| = Euclidean norm between x and ck
σk = bandwidth vector of the kth node in hidden layer
λ(||x−ck||) = kernel function of the kth center in hidden layer
wik= connecting weight vector between the kth center in hidden layer and yi
ck = parameter vector
1.
Introduction
Biodiesel, an important renewable energy, possesses high calorific value and low pollution characteristics and is increasingly utilized as a substitute for traditional fossil fuels in various industries [1,2]. In this study, the flame stability characteristics of waste cooking oil biodiesel combustion in industrial furnaces are investigated. Previous studies, such as those by Hashimoto et al. [3] and Chong et al. [4], investigated the combustion characteristics of alternative fuels for gas turbines and the spray flames of jet A-1 and palm biodiesel under continuous and stable swirl conditions, respectively. Jhalani et al. [5] examined the characteristics of various ether fractions used as oxidation fuel additives in cottonseed oil biodiesel-diesel mixed fuel in a diesel engine. Shen et al. [6] assessed the combustion characteristics of biodiesel, including flame speed and total signal intensity of hydrogen and oxygen using hydrogen and oxygen PLIF (planar laser-induced fluorescence technology).
Flame stability during the combustion process has consistently been a research focus. Junga et al. [7] explored the influence of liquid fuel additives on combustion temperature and emissions of pulverized coal combustion in a boiler. Yu et al. [8] analyzed the flame structure and oscillation characteristics of oxy-fuel combustion in heavy oil boilers to evaluate burner performance in boilers, discovering that an increase in oxygen concentration reduces oscillation generation. Zhang et al. [9] employed a large eddy simulation and partially stirred reactor to study wet/steam dilution combustion in a premixed swirl burner, utilizing a proposed method to quantify the wet flame behavior in stable and low emission operation.
As research progresses, the nonlinear characteristics of flame during the combustion process have garnered significant attention. Gao et al. [10,11] investigated the oxygen-enriched combustion process of biodiesel in industrial furnaces, concluding that the combustion process is a nonlinear dynamic process significantly influenced by initial variables. Additional studies, such as those by Ding et al. [12] and Gu et al. [13], examined the nonlinear dynamic characteristics of natural gas combustion instability in an in-cylinder injection engine and the combustion stability of diesel engines through quantitative analysis of cyclic fluctuation rates of combustion parameters. Consequently, it is evident that the combustion process exhibits nonlinear dynamic characteristics, which may adversely impact the sustainability and stability of combustion and diminish combustion efficiency.
Empirical mode decomposition (EMD) represents an analytical method proposed by scholars that is highly adaptive to generalized linear time-frequency, thereby accurately describing time-varying signals in the time-frequency plane. This method is particularly effective for analyzing component signals resulting from multifactorial superposition [14,15]. EMD facilitates the smoothing of non-stationary data, followed by the execution of a Hilbert transform to obtain the time spectrum, thereby determining frequencies with physical significance, independent of Fourier transform theory. Invented by Bi et al., a novel method for extracting knock characteristics by vibration signal was used to decrease thermal efficiency and limit the performance enhancement of the gasoline engine [16]. Lu et al. employed empirical mode decomposition in conjunction with the least squares method to study trend extraction and identification of flame temperature in cement combustion zones [17]. A low-complexity empirical mode decomposition method, proposed by Mishra et al., was trained via a kernel-based algorithm and used to predict wind power in Californian wind farms across different time ranges (i.e., 10 minutes to 5 hours) [18]. Mi et al. developed a novel multi-step wind speed prediction model based on singular spectrum analysis, empirical mode decomposition, and convolution support vector machine [19]. Aghbashlo et al. found that, in comparison to traditional genetic programming methods and artificial neural network methods, the empirical mode decomposition method can enhance the working performance of direct injection diesel engines [20]. Wang et al. [21] use the EMD to predict the annual CO2 emissions under data decomposition mode. Thus, it is evident that the EMD analysis method offers considerable advantages in accurate data optimization and control. However, the use of this method remains infrequent in applications related to biodiesel combustion stability.
In recent years, the proliferation of artificial intelligence has led to increased interest in using sophisticated intelligent algorithms for controlling and predicting combustion processes. Piloto-Rodríguez et al. [22] devised a model for estimating the cetane number of biodiesel from fatty acid methyl ester using multiple linear regression and an artificial neural network. Gurgen et al. [23] employed the artificial neural network method to model the cycle variability of diesel engines using diesel and butanol-diesel blends. Dubey et al. [24] introduced a flame shape descriptor based on coordinates of the flame edge to predict flame image edges. Adewole et al. [25] constructed an artificial neural network model to predict the flame temperature and pollutant emission of liquefied petroleum gas burned by a swirl burner. Taghavi et al. [26] developed an accurate prediction model based on intake air mixing characteristics, using three popular architectures: nonlinear autoregressive network, multi-layer perceptron (MLP), and radial basis function (RBF), to control the start of the combustion (SOC). Wen et al. [27] proposed a robust fusion algorithm based on the Takagi-Sugino fuzzy model to address issues of data loss, data distortion, or signal saturation during multi-sensor infrared flame detection. Gajewski et al. [28] improved the service efficiency of the diesel engine with different physical parameters by using MPL and RBF to predict the combustion state of the diesel engine.
The radial basis function (RBF) neural network, compared to other neural networks, possesses potent nonlinear fitting capabilities, which enables it to map any complex nonlinear relationships. Additionally, it exhibits strong memory capacity, robustness, and self-learning abilities. The integration of empirical mode decomposition (EMD) with RBF can enhance prediction data accuracy, demonstrating particular suitability for nonlinear data prediction. Yang et al. [29] identified flow patterns in a narrow channel via feature extraction of conductivity measurements with a support vector machine. Li et al. [30] developed a novel forecasting method for the settlement price prediction of stock index futures in China, utilizing empirical mode decomposition and radial basis function. Huang et al. [31] proposed an EMD-RBF-NN model that correlates two-phase flow rates with the volumetric heat transfer coefficient, achieving superior forecasting accuracy compared to pre-existing models. Given that the combustion process is nonlinear, using the EMD-RBF neural network for predictions could improve prediction efficiency and accuracy. However, this method has not yet been applied to the prediction of the combustion process.
This study aims to introduce an innovative modelling approach that integrates data decomposition and neural networking to scrutinize the impact of oxygen content on the combustion performance of waste cooking oil. Due to the elevated viscosity, substantial water content, and high condensation point inherent in waste cooking oil, the atomization combustion process engenders complexity. This complexity amplifies the challenge of accurately controlling and predicting the combustion process, particularly in comparison to the conventional combustion of gaseous and solid particles. The incorporation of neural networking in the biomass fuel industry remains infrequent, thus rendering the monitoring and analysis of biodiesel atomization combustion, along with the examination of combustion state characteristic changes via efficient extraction of collected flame image information, critically significant. The remaining sections of this paper are organized as follows: Section 2 elucidates the experimental apparatus system involved in oxygen-enriched swirl combustion in industrial biodiesel furnaces and kilns, as well as the protocol for combustion stability data acquisition and pretreatment. Section 3 provides a comprehensive overview of EMD-RBF-NN. Section 4 presents the prediction outcomes of CSI and compares these findings with existing neural network models. Section 5 concludes the paper with a conclusion.
2.
Biodiesel swirl atomization combustion device and data extraction
2.1. Swirl atomization combustion equipment and materials
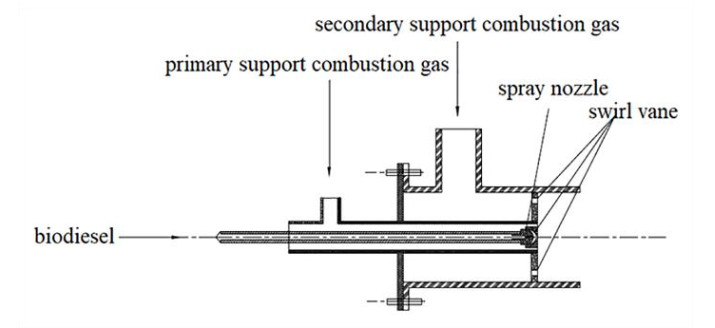
Characterized by high viscosity and inadequate atomization, biodiesel's combustion efficiency can be compromised. This study introduces a self-engineered swirl atomizer to achieve enhanced combustion efficiency. The atomizer simultaneously ensures efficient atomization while providing ample combustion-supporting gas for biomass fuel.
The burner assembly consists of three concentric layers. The innermost layer houses high-pressure liquid fuel, which undergoes primary atomization in a specialized channel, facilitated by a high-speed atomization nozzle.
The medium layer's primary function is to supply combustion air. The flow of air commences from an inlet and encounters swirl vanes at the outlet, intensifying the air pressure. This high-pressure air from the swirl vanes amalgamates with the atomized fuel from the innermost layer, enabling secondary fuel atomization due to the increased air pressure. However, the primary air outlet's limited aperture results in an insufficient quantity of air for optimal biodiesel combustion.
Addressing this, the outermost layer incorporates a secondary air channel with ample space to provide the necessary supplementary combustion-supporting gas for biodiesel combustion. Moreover, it features a ring of air baffles around the secondary air outlet, surrounded by gas outlets. This design ensures high gas flow and air velocity at the outlets, leading to more effective mixing of atomized biofuel with combustion-supporting air, thereby enhancing the combustion process.
Figure 1 depicts the nozzle employed in the biodiesel combustion experiment. Figure 2 represents the flame monitoring system positioned in the combustion chamber. Table 1 shows the basic physical parameters of the oils used for the tests.
2.2. Data acquisition and preprocessing
A flame represents the immediate manifestation of fuel combustion conditions within a furnace, furnishing rapid and definitive data pertaining to these conditions. Figure 3 delineates the evolving pattern of the flame image during the combustion process under certain operational circumstances. As digital image technology and artificial intelligence continue to advance, intelligent combustion diagnostic tools not only facilitate investigations into the mechanisms of combustion processes, but also enable the training and optimisation of models using collected combustion characteristic parameters within the furnace. This ultimately uncovers the inherent dynamics of the combustion process, thereby illuminating its combustion characteristics.
Previous research has identified that an increment in temperature and oxygen concentration elicits the following attributes in high-temperature oxygen-enriched combustion flames: 1) a progressive enhancement in flame brightness; 2) an escalating flame volume and length; 3) a systematic shift in flame colour from blue towards yellow; 4) a trend of uniformity in brightness and colour within the same image; and 5) a correlation between higher combustion efficiency and finer image texture.
In light of these characteristics, the flame feature vector, f(i, j) (where i = 1 to n-1 and j = 1 to n-1), has been established to extract the aforementioned features, which will serve as the input for the neural network.
(1) Mean value of the correlation function: ave
Matrix p reflects the correlation between a pixel and its surrounding pixels. The ave is the average value of the gray correlation function matrix. Experiments show that the better the flame burns, the finer the image texture, and the larger the ave.
(2) Information entropy based on the gray histogram: sh
The pg is the probability that pixels with grayscale "g" appear. The "g" is the grayscale range of the flame picture. Experiments indicate that the more stable the combustion, the higher the value of the information entropy based on the grayscale histogram; conversely, the less stable the combustion, the lower the entropy value.
(3) Flame area: s
There has been a great deal of research on flame area in combustion theory, which is a geometric characteristic quantity representing combustion state. The area is calculated by counting the total number of pixels with gray level greater than zero in the preprocessed image.
The th is used as the segmentation threshold of the flame image, which has different values for different images, and F(x) is a step function, which is defined as follows:
(4) Flame length: L
The flame length is also a characteristic quantity between reaction gas flow and atomization effect and combustion effect, and a geometric characteristic quantity representing combustion state.
where L is the actual length of flame, α is the actual length represented by a unit pixel, l is the pixel length of flame, and x1,x2 are the horizontal coordinates of flame head and tail pixels.
(5) The gray variance of the flame image: var
The combustion process is dynamic, potent, and intricate, as evidenced by the asymmetrical gray distribution in the associated image. Combustion stability is inversely proportional to the variability in gray levels; that is, the more stable the combustion, the lesser the gray fluctuation and the more consistent the distribution, thus allowing the portrayal of flame pulsation via gray variance. In a state of stable combustion, the variance in image gray levels is minute, encapsulating the subdued flame pulsation. Conversely, in an unstable combustion scenario, a heightened gray image variance manifests, signaling intense flame pulsation throughout the unstable combustion period. The respective mathematical representation is as follows:
In which m and n are the number of rows and columns of the flame image, and f is the total number of pixels in the image whose gray value is not 0.
(6) Gray level:gl
As combustion temperature escalates, the radiant energy discharged by the flame intensifies, resulting in an elevated gray level within the image. Therefore, it can be inferred that there exists a positive correlation between the temperature of the combustion flame and the gray level of the image. Given specific combustion conditions, a rise in combustion temperature correlates with enhanced combustion stability and an increased gray level of the flame.
(7) Image energy of flame area:Asm
A large ASM value indicates a more uniform and regular texture pattern. The more stable the flame, the smaller its pulsation, the smaller the gray level change, the more uniform the distribution, and the higher the energy.
Figure 4 illustrates the variation pattern of combustion characteristic parameters under different oxygen-enrichment conditions, with the x-axis representing length, the y-axis denoting area, and the z-axis corresponding to grayscale. Owing to the varying magnitudes and units derived from the extraction of feature quantities, an initial step of data normalization is performed. Subsequent computations, conducted in accordance with pertinent data and employing the Particle swarm optimization (PSO) algorithm, reveal that the primary result for S and ave is zero. Therefore, the representation of flame stability is formulated as follows:
In the context of this experiment, the derived image feature value indicates a direct correlation between combustion stability and the CSI index, whereby greater stability reflects a higher CSI index. During instances of extreme flame instability or flameout, the CSI oscillates between 0 and 25. A CSI range of 25 to 45 signifies generally normal combustion, whereas a CSI between 45 and 100 indicates stable combustion. Concurrently, it is imperative to note that the eigenvalues of distinct flames vary, resulting in differential impact coefficients for each eigenvalue with respect to stability.
3.
A new method based on EMD and RBF-NN
In this paper, a flame image representation method based on EMD and RBF-NN is proposed, which can be used to monitor and predict the combustion process. This combination method improves the performance of combustion conditions.
3.1. Traditional methods and models
The neural network, owing to its potent learning and classification capabilities, has effectively superseded linear regression, autocorrelation, and multivariate regression, among other statistical methodologies, finding extensive applications across diverse fields. Of particular interest is the radial basis function (RBF) neural network, renowned for its computational agility and superior convergence speed. Structurally, the RBF neural network mirrors the architecture of a feedforward neural network, comprising three distinct layers: an input layer constituted by signal source nodes, a hidden layer (also known as the radial basis layer) typified by a non-negative, radially symmetric function with local distribution and a peak at the center, and an output layer. As depicted in Figure 5, the framework of the RBF neural network exhibits a nonlinear transformation from the input layer to the hidden layer, while the transformation from the hidden layer to the output layer is linear. The radial basis function is trained by the traditional gradient descent learning algorithm, the kernel function is the Gaussian kernel function, and the center and diffusion of kernel function are obtained by the K-means clustering algorithm. Here, let x=(x1, x2,⋯xn)T be an input vector with input nodes of n (n = 5 in this paper) and ck=(ck1,ck2,⋯ckn)T be the kth node center vector in the hidden layer (k = 1, 2, ⋯, K). This kind of neural network can be represented by a parameter model, which reveals the output node calculated by the weighted sum of hidden node outputs as follows:
||x−ck|| is a transformation matrix (usually a Euclidean matrix), wik is the connecting weight vector, λ(||x−ck||) is a kernel function of the kth node, and y=(y1,y2,⋯ym)T is the output vector with the output nodes of m (m = 1 in this paper, which is the CSI).
Gaussian function is the most commonly used kernel function in the hidden layer, which will be used as the activation function. The position of kth is controled by the parameter vector ck. σk=(σk1,σk2,⋯σkn)T is the bandwidth vector of the kth, the following equation is given by:
In this paper, the RBF neural network is used to describe the nonlinear mapping fromthe input vector of the flame characteristics and Csi(t) to the output vector. However, how to determine the information of the Csi(t) in the input layer to get perfect σk of RBF-NN is also a significant problem.
EMD is the core content of the empirical mode decomposition method, which does not need any filter or wavelet basis function. Time series is originally a nonlinear wave signal, and a series of different characteristic scales of data are decomposed by EMD gradually smoothing signals of different scales or trends. Each decomposed sequence is named as an intrinsic mode function (IMF), and the lowest frequency usually represents the trend or mean value of the original signal. In this paper, the EMD process for the time series Csi(t) is given as follows: (1) Search out the local minimum and maximum values of the CSI time series. (2) The shapes of the upper envelope and lower envelope of the Csi(t) raw data series are determined by fitting extreme values. (3) Get the instantaneous average of the two envelopes: e1(t)=0.5(Emax(t)+Emin(t)). (4) Calculate the difference between Csi(t) and e1(t): d1(t)=Csi(t)-e1(t). (5) Processing d1(t): If d1(t) meets two limit conditions of IMF (the difference between the extreme value and zero crossing point in the whole data sequence is less than or equal to 1; the average value of the upper and lower envelopes is equal to 0 at any point), d1(t) will be defined as the first IMF1(t). While d1(t) does not meet the two limit conditions of IMF, let Csi(t)=d1(t) return to (1)−(4), then d1(t) cannot be repeated n times (n > 0) unless the nth repeat difference sequence d1n(t) meets the above conditions (i.e., the screening process); then, d1n(t) was defined as the first IMF, IMF1(t). Moreover the residue r1(t)=Csi(t)−IMF1(t). (6) Execute (1)−(5) only when the termination criteria are met. When the residue rn becomes a constant, monotone function or a function with only one maximum value or one minimum value, the screening process will finally end, and no more IMF can be extracted from this function. Finally, the low-pass filtering result of the signal with IMF components can be primitively indicated as
3.2. New model
Figure 6 illustrates the proposed hybrid model. As depicted, the EMD-RBF-NN model is established through two stages: (1) Information extraction: This involves the utilization of the EMD method to isolate deterministic information from the raw data sequence of the Combustion stability index (CSI). The first Intrinsic Mode Function (IMF) encapsulates a simple oscillation mode embedded within the CSI series. In the screening process applied in this research, stimuli satisfying the first restriction (the total count of extreme values and zero crossings should be identical or differ by at most one) are not granted flexibility within the engineering practice domain. Consequently, the termination standard for calculation can be delineated as follows:
The termination standard is enacted by confining the value of the standard deviation (STDn), employing the same nomenclature as used in the preceding section. Consequently, the highest frequency band intrinsic mode function (IMF) is procured for the subsequent stage. (2) Multivariable input prediction: Relying on the existing Combustion stability index (CSI) data series, the future sequence is forecasted using the radial basis function neural network (RBF-NN). The RBF-NN comprises three distinct layers: An input layer, a hidden layer, and an output layer. The data for the input layer, which comprises combustion characteristic parameters, is gleaned from the flame's characteristic parameters, and the nonlinear information is then directly dispatched to the succeeding layer. The activation function within the hidden layer facilitates the computation of the radial basis function. Eventually, the weighted sum of the hidden layer results is relayed to the output layer, generating the predicted flame stability data as the output.
3.3. Data simulation
In order to systematically verify the validity and feasibility of the technology proposed in the study, the analyzed data x(t) is expressed as the following equation,
Figure 7 shows the IMF results of Eq (15), where the time parameter t is set from 1 to 10 by 0.1, and there is no noise with any signal noise ration. The following three indicators are used to evaluate the accuracy of the model.
The MAE is used to measure the average absolute error between the predicted value and the real value on the experimental data set. For a test set containing n microblog messages, MAE is defined as:
MAPE is used to measure the relative errors between the average test value and the real value on the experimental datasets. MAPE is defined as:
RMSE is used to measure the deviation between the observed value and the true value
where ˆy(n) is the estimation of investigated time series y(n).
4.
Results and discussion
4.1. Use the mixed model to analyze the time series of the stability model
In this segment of the research, the empirical mode decomposition (EMD) method and radial basis function (RBF) are employed, along with a neural network, to model the experimental findings, which include six color feature parameters and four texture feature parameters, as outlined in Table 2. Traditional procedures typically implement wavelet decomposition to break down time series into sub-band sequences of varying directions and scales. On a uniform scale, distinct sub-bands encapsulate time series information of differing orientations. Utilizing empirical mode decomposition (EMD) as a substitute for wavelet transformation results in the attainment of the flame combustion stability index (CSI) signal and the decomposition of the intrinsic mode function (IMF), as illustrated in the Figure 8. The original time series is divided into nine IMFs. The CSI time series, owing to the ever-present combustion volatility, exhibits unsteady and non-linear features over time. Nevertheless, EMD decomposition reveals that all IMFs and final residuals demonstrate increased stability and pronounced periodicity when compared to the initial time series. This suggests that the EMD method can generate superior decomposition results. A total of 500 data points were utilized to construct the neural network model and were arbitrarily categorized in a 3:1 ratio into training and testing groups. The RBF neural network, implemented via MATLAB, incorporates two principal adjustment parameters, namely, the spread parameter and the maximum number of neurons. As depicted in the Figure 9, the model converges to an optimal state.
4.2. Analysis of prediction results of CSI under different oxygen enrichment levels
Figure 10 presents the predicted Combustion stability index (CSI) over a specified duration at varying degrees of oxygen enrichment. It is observable that despite the flame's fluctuation throughout the entire combustion process, its stability is maintained within a certain range for a specific period. This indicates the swirl atomization burner, designed in the current study, can secure continuous and stable flame combustion, provided the air and fuel quantities are sufficient. Simultaneously, a gradual increase in the degree of oxygen enrichment results in an enhanced flame stability index.
4.3. Comparison with other methods
To ascertain the efficacy and convenience of the EMD-RBF-NN diagnostic approach, this new method is juxtaposed with other predictive methodologies. The backpropagation (BP) neural network also serves as a commonly employed model for time series prediction in Figure 11. Guided by past experiences, the BP-NN, WT-BP-NN, EMD-BP-NN, and RBF-NN are utilized to compute Intrinsic Mode Functions (IMFs) across various layers. To assess the model's applicability, the EMD-NN, RBF-NN, and EMD-RBF-NN are used to predict the Combustion stability index (CSI), which constitutes 50% of the total data in the test data set. As can be inferred from Table 3, the novel method exhibits superior predictive ability when contrasted with existing techniques.
5.
Conclusions
In the present study, a hybrid PSO-EMD-RBF neural network-based model is introduced to enhance the prediction accuracy of biodiesel combustion flame stability. Based on the swirling spray combustion characteristics of biodiesel, a method for calculating flame stability was devised employing the Particle swarm optimization (PSO) algorithm alongside flame image processing techniques. Given the volatility and instability inherent in combustion processes, the empirical mode decomposition (EMD) is applied to transform the irregular flame stability sequence into a series of relatively stable components whose periodic traits are more pronounced than the original sequence, thereby mitigating the impact of noise within the data. In selecting the prediction model, the nonlinear fitting capability, self-learning, and self-adapting attributes of the radial basis function model are considered. This facilitates the projection of the future values for each component using the radial basis function model, and the aggregation of these values yields the ultimate prediction result. Calculations indicate that the Empirical Mode Decomposition-Radial Basis Function-Neural Network (EMD-RBF-NN) model substantially augments the accuracy of CSI predictions in comparison to other extant predictive models.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research was funded by [the National Natural Science Fund of China] grant number [51766007], [the National Natural Science Fund of China] grant number [51666006], NSFC--Yunnan joint fund project grant number [U1602272], and [Research Fund from State Key Laboratory of Complex Nonferrous Metal Resources Clean Utilization] grant number [CNMRCUTS1704]. Yunnan Provincial Department of Education Project [2024J0453].
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: