1.
Introduction
Multi attribute group decision making (MAGDM) is quite an interesting and eminent field of research attempting to produce arguments and techniques that determine the most favorable alternative from a set of alternatives. It is challenging for decision makers to give accurate information about options due to the complexity of the socioeconomic environment and their lack of expertise and judgment. Classical set theory deals with the information of type yes or no, that is, whether an element belongs to a set or not. On the other hand, real life situations may be imprecise or unclear, and there may be possibility other than yes or no. To tackle vague or imprecise information, in 1965, Zadeh [36] extended the concept of classical sets in the form of fuzzy sets. Fuzzy set theory permits a membership function valued in the interval [0,1]. After that, Atanassov [1] presented the intuitionistic fuzzy set (IFS) as a generalization of the fuzzy set. The IFS has both a positive and a negative membership degree, and that the sum of both these degrees is less than or equal to one.
Analysis of clusters [6], medical diagnosis problems with decision-making (DM) [14] and pattern recognition [8] are some of the fields that have used IFSs. In the success of IFSs, numerous researchers have contributed. Chen et al. [7] defined a method for the use of intuitionistic fuzzy numbers (IFNs) and interval valued intuitionistic fuzzy (IVIF) numbers in aggregation processes and to address DM challenges. The intuitionistic fuzzy Hamacher aggregation procedures were cited by Huang as being advantageous in instances involving decision-making. Khan et al. [22] defined a solution of linear and quadratic equations based on triangular linear Diophantine fuzzy numbers. Alaoui et al. [5] defined a novel analysis of fuzzy physical models by generalized fractional fuzzy operators.
In order to combine intuitionistic fuzzy data and make decisions, a variety of intuitionistic fuzzy aggregation operators have been proposed for combining different options [20]. The cumulative positive and negative membership degrees of the decision-maker may occasionally exceed one. For example, if a decision-maker assigns a positive membership degree of 0.3 and a negative membership degree of 0.9,0.3+0.9=1.2>1. Intuitionistic fuzzy sets are unable to handle this situation. Yager [34] developed the Pythagorean fuzzy set (PyFS), which includes both positive and negative membership degrees but whose square sum is equal to or less than one, to address this issue. 0.32+0.92=0.9 corresponds to the above-mentioned example. PyFS is a generalization of IFS. PyFS resolves inaccurate and uncertain information in actual MADM problems better than IFS. Since the development of PyFS, many aggregation operators have been established for Pythagorean fuzzy Dombi aggregation operators and their application in Pythagorean fuzzy multiple criteria group decision making and decision support systems [20,37]. In multiple attribute group decision-making, some generalized Pythagorean fuzzy Bonferroni mean aggregation operations are used [38]. Ren et al. [31] defined the Pythagorean fuzzy TODIM approach to multi-criteria decision making. Gou et al. [12] proposed some properties of continuous Pythagorean fuzzy information.
Zeng et al. [39] introduced the exponential intuitionistic divergence measure, envelopment analysis, preference fusion and membership improvement of intuitionistic fuzzy numbers and discussed its potential application in multi-criteria decision making in 2019. Garg et al. [13] discussed the correlation measures for cubic m-polar fuzzy sets with applications. Ayub et al. [3] proposed cubic Heronian mean Dombi aggregation operators and their application on the MADM problem. Qiyas et al. [30] presented a novel approach of linguistic intuitionistic cubic hesitant variables and their application in decision making.
In multi-attribute decision making, Hussain et al. [15] applied averaging operators based on spherical cubic fuzzy numbers. Decision support systems use cubic picture fuzzy aggregation operators [28]. Decision-making including distance measure and induced aggregation operators, as well as decision-making involving distance measures and linguistic aggregation operators are discussed in [24]. Fuzzy generalized hybrid aggregation operators and their application in fuzzy decision making, and fuzzy induced generalized aggregation operators and its application in multi-criteria decision making are discussed in [25,27]. For comparison, the author studied the cubic fuzzy Einstein aggregation operations and their application to decision-making [10]. Multi-attribute decision-making problems were solved under a cubic intuitionistic fuzzy set environment, based on Bonferroni mean operators [18], and cubic intuitionistic fuzzy aggregation operators [19]. Multi-attribute decision-making problems are solved under cubic hesitant fuzzy sets and an assessment method of prostate cancer risk classes utilizing cubic hesitant fuzzy sets similarity measure was presented by different authors [2,9,35]. The expected values of aggregation operators on cubic triangular fuzzy numbers and their use in problems involving multi-criteria are described in [32,33]. Abdullah et al. [4] defined Pythagorean cubic fuzzy Hamacher aggregation operators and their application in a green supply selection problem.
The main motivation is the extension of aggregation operators characteristics to consider a wider range of complex problems. To deal with the aggregate uncertainty expressed in the form of cubic sets, a variety of aggregation operators have been created based on the algebraic t-norm and t-conorm. Important mathematical processes called logarithmic operational rules can be used to conveniently aggregate uncertain and erroneous data. These concepts served as inspiration for us to create a cubic MAGDM approach to solve the problem within cubic sets (CSs). This method is built on the logarithmic aggregation operators and the logarithmic operations of cubic sets.
The contributions of our method are as follows:
(1) To overcome the limitations of algebraic operations and represent the interactions between various cubic sets, we developed a variety of distinct logarithmic operations for cubic sets.
(2) We developed aggregation operators for cubic information that overcome the limitations of algebraic operators. These operators are logarithmic cubic weighted averaging (log-CWA), logarithmic cubic ordered weighted averaging (log-COWA), logarithmic cubic weighted geometric (log -CWG) and logarithmic cubic ordered weighted geometric (log-COWG) operators.
(3) Using cubic information, we developed a method to handle multi-attribute decision-making scenarios.
(4) To illustrate the efficiency and dependability of the recommended cubic logarithmic aggregation operators, we used a circulation center evaluation problem.
(5) According to the data, the suggested strategy performs better and yields more accurate results when compared to the current approaches.
The remainder of the paper is organized as follows: Section 2 introduces numerous key terms, including IFS, PyFS, CS, score, and accuracy function. Section 3 discusses the logarithmic operation rules and characteristics of cubic numbers (CNs). In Section 4, logarithmic cubic averaging aggregation operators are defined. In Section 5, logarithmic cubic geometric aggregation operators are defined. The MAGDM approach is given in Section 6 based on the logarithmic cubic aggregation operators. An example is solved in Section 7 based on the logarithmic aggregation operator. In Section 8, we demonstrate the sensitivity analysis and comparison of the proposed method to other existing methods. Finally, the study's conclusion is reached in Section 8.
2.
Preliminaries
This part recaps the basic definitions of current fuzzy set extensions, which served as the study's foundation.
Definition 2.1. [1] Let ˆG≠ϕ be a universal set. Then, the set
is an IFS, where ˆWˇZ(ˆs),˘UˇZ(ˆs)∈[0,1] are the element's positive and negative membership degrees ˆs∈ˆG in ˇZ, respectively. ˆWˇZ(ˆs),˘UˇZ(ˆs) satisfy the condition, for all ˆs∈ˆG,
Definition 2.2.[29] Let ˇZ=(ˆWˇZ(ˆs),˘UˇZ(ˆs)|ˆs∈ˆG) be an IFN. Then, the score function of ˇZ is defined as;
The accuracy function of ˇZ is defined as;
Definition 2.3. [39] Let ˇZ1=((ˆWˇZ1(ˆs),˘UˇZ1(ˆs)) and ˇZ2=((ˆWˇZ2(ˆs),˘UˇZ2(ˆs)) be any two IFNs. Then, the comparison rules are defined as follows:
(1) If S(ˇZ1)>S(ˇZ2), then ˇZ1>ˇZ2.
(2) If S(ˇZ1)=S(ˇZ2) and ˆS(ˇZ1)>ˆS(ˇZ2), then ˇZ1>ˇZ2.
(3) If S(ˇZ1)=S(ˇZ2) and ˆS(ˇZ1)=ˆS(ˇZ2), then ˇZ1=ˇZ2.
2.1. Properties of fuzzy sets
Definition 2.4.[1] Let ˇZ1,ˇZ2 and ˇZ3 be a fuzzy sets. Then, the following properties of fuzzy sets are as follows:
Identity
Absorption by ϕ and U
Idempotent
De Morgan laws
Involution
Absorption
2.2. Cubic set and its operations
The cubic set is an appropriate way to deal with fuzziness. The cubic set has been extensively applied to the decision making problems. It can be defined as follows:
Definition 2.5.[10] Let ˆG≠ϕ, be a fixed set. Then, the set
is called CS, where [ˆWˇZ(ˆs),˘UˇZ(ˆs)],ˆYˇZ(ˆs) are known as the element's positive and negative membership degrees ˆs∈ˆG in ˇZ respectively, with the condition that 0≤[ˆWˇZ(ˆs),˘UˇZ(ˆs)],ˆYˇZ(ˆs)≤1.
Definition 2.6.[10] Let ˇZ=([ˆWˇZ(ˆs),˘UˇZ(ˆs)],ˆYˇZ(ˆs)|ˆs∈ˆG),ˇZ1=([ˆWˇZ1(ˆs),˘UˇZ1(ˆs)],ˆYˇZ1(ˆs)|ˆs∈ˆG) and ˇZ2=([ˆWˇZ2(ˆs),˘UˇZ2(ˆs)],ˆYˇZ2(ˆs)|ˆs∈ˆG) are any two IFSs. Then the following operations are defined:
(1) ˇZc={ˆYˇZ(ˆs),[˘UˇZ(ˆs),ˆWˇZ(ˆs)]}.
(2) ˇZ1∧ˇZ2={[min(ˆWˇZ1(ˆs),ˆWˇZ2(ˆs)),min(˘UˇZ1(ˆs),˘UˇZ2(ˆs))],max(ˆYˇZ1(ˆs),ˆYˇZ2(ˆs))}.
(3) ˇZ1∧ˇZ2={[max(ˆWˇZ1(ˆs),ˆWˇZ2(ˆs)),max(˘UˇZ1(ˆs),˘UˇZ2(ˆs))],min(ˆYˇZ1(ˆs),ˆYˇZ2(ˆs))}.
(4) υ⋅ˇZ={[1−(1−ˆWˇZ)υ,(˘UˇZ)υ],(ˆYˇZ)υ}.
(5) ˇZυ={[(ˆWˇZ)υ,1−(1−˘UˇZ)υ],1−(1−ˆYˇZ)υ}.
3.
Logarithmic aggregation information for cubic number
In this section, we define the basic operation laws, and some properties of logarithmic cubic numbers.
3.1. The logarithmic operation laws of cubic numbers
In this section, we will introduce and investigate the characteristics of certain novel logarithmic operating rules for cubic numbers. It is noted that log˘e0 in the real number system, has no meaning, and log˘e1 is not defined. As a result, we assume ˇZ≠0, where ˇZ is a CN. Also, the base of a logarithm, i.e., ˘e≠1, is in the open interval (0,1) and always a positive-real number.
Definition 3.1. Let ˆG≠ϕ be a fixed set and ˇZ=([ˆWˇZ(ˆs),˘UˇZ(ˆs)],ˆYˇZ(ˆs)) be a cubic number. Then, the logarithmic cubic number is defined as,
where, [ˆWˇZ(ˆs),˘UˇZ(ˆs)],ˆYˇZ(ˆs) are identified as positive and negative membership degrees of the element ˆs∈ˆG in ˇZ respectively, with the condition that 0≤[ˆWˇZ(ˆs),˘UˇZ(ˆs)],ˆYˇZ(ˆs)≤1. The logarithmic operational law's positive membership is thus defined as follows:
Negative membership is defined as
and the refusal degree is defined as
The operational law of log-CNs is defined next.
Definition 3.2. Let ˇZ=([ˆWˇZ(ˆs),˘UˇZ(ˆs)],ˆYˇZ(ˆs)), ˇZ1=([ˆWˇZ1(ˆs),˘UˇZ1(ˆs)],ˆYˇZ1(ˆs)) and ˇZ2=([ˆWˇZ2(ˆs),˘UˇZ2(ˆs)],ˆYˇZ2(ˆs)) be any three CNs, let υ be any scalar greater than 0. Then, the logarithmic cubic operational law is defined as follows;
3.2. Properties of logarithmic operational law for cubic numbers
We discuss the attributes of CNs based on the logarithmic operational law in this section of the article.
Theorem 3.1. Let ˇZ=([ˆWˇZ,˘UˇZ],ˆYˇZ) be any cubic number with condition 0<˘e≤[ˆW,˘U]≤1,˘e≠1. Then, prove that
Proof. For proof, see Appendix A.
Theorem 3.2.Let ˇZ=([ˆWˇZ,˘UˇZ],ˆYˇZ) be any cubic numbers with condition 0<˘e≤[ˆW,˘U]≤1,˘e≠1, Then, prove that
Proof. As we know,
Theorem 3.3. Let the collection of two cubic numbers is ˇZ1=([ˆW1,˘U1],ˆY1) and ˇZ2=([ˆW2,˘U2],ˆY2) with conditions 0<ˇe≤min([ˆW1,˘U1],[ˆW2,˘U2]) and ˇe≠1. Then, show that
Proof. For proof, see Appendix B.
Theorem 3.4. Let the collection of three cubic numbers is ˇZ1=([ˆW1,˘U1],ˆY1),ˇZ2=([ˆW2,˘U2],ˆY2) and ˇZ3=([ˆW3,˘U3],ˆY3) with conditions 0<ˇe≤min([ˆW1,˘U1],[ˆW2,˘U2]) and ˇe≠1. Then, we shows that
Proof. For proof, see Appendix C.
Theorem 3.5. Let the collection of three cubic numbers is ˇZ1=([ˆW1,˘U1],ˆY1),ˇZ2=([ˆW2,˘U2],ˆY2) and ˇZ3=([ˆW3,˘U3],ˆY3) with conditions 0<ˇe≤min([ˆW1,˘U1],[ˆW2,˘U2]) and ˇe≠1. Then, we shows that
Proof. For proof, see Appendix D.
Theorem 3.6.Let two CNs is ˇZ1=([ˆW1,˘U1],ˆY1) and ˇZ2=([ˆW2,˘U2],ˆY2) with conditions satisfy, 0<ˇe≤min([ˆW1,˘U1],[ˆW2,˘U2]) and ˇe≠1, and also let υ be any positive real number. Then,
Proof. The procedure in this case is eliminated because the proof is comparable to Theorem 3.2.
Theorem 3.7. Let ˇZ=([ˆW,˘U],ˆY) be a CN, 0<ˇe≤ˆW≤1, ˇe≠1, and υ1,υ2>0. Then, we show that
Proof. For proof, see Appendix E.
4.
Logarithmic cubic averaging aggregation operators
We defined some logarithmic cubic fuzzy averaging aggregation operators, namely, log-CWA and log-COWA, and study their features in depth in this section.
4.1. Logarithmic cubic weighted averaging aggregation operator
Definition 4.1.Let ˇZp=([ˆWˇZp,˘UˇZp],ˆYˇZp)(p=1,2,⋯,n) be a collection of cubic numbers with 0<˘ep≤[ˆWp,˘Up]≤1, and ˘ep≠1. Then, the mapping log−CWA:ˇRn⟶ˇR, is defined,
The function log-CWA is called the logarithmic cubic weighted averaging operator, where ϖ=(ϖ1,ϖ2,⋯,ϖn)T denotes the weighed vector of log˘epˇZp(p=1,2,⋯,n), such that ϖp∈[0,1], and ∑np=1ϖp=1.
Theorem 4.1. Let ˇZp=([ˆWp,˘Up],ˆYp)(p=1,2,⋯,n) be a collection of CNs with condition 0<ˇep≤[ˆWp,˘Up]≤1, and ˇep≠1. Then, using Definitions 3.1 and 3.2, we have
Proof. For proof, see Appendix F.
4.2. Properties
(1) Idempotency:Let ˇZp=([ˆWp,˘Up],ˆYp)(p=1,2,⋯,n) be a collection of cubic numbers that are equal, i.e., ˇZp=ˇZ,(p=1,2,⋯,n). Then,
where ˘e1=˘e2=...=˘en=˘e.
Proof. We have
(2) Boundedness:If ˇZp=([ˆWp,˘Up],ˆYp)(p=1,2,⋯,n) is a collection of CNs, let ˇZ−=min(ˇZ1,⋯,ˇZn) and ˇZ+=max(ˇZ1,ˇZ2,⋯,ˇZn). Then,
where ˘e1=˘e2=⋯=˘en=˘e.
Proof. Let, ˇZp=([ˆWp,˘Up],ˆYp),(p=1,2,⋯,n) be a collection of CNs and ˇZ−=min(ˇZ1,⋯,ˇZn), ˇZ+=max(ˇZ1,ˇZ2,⋯,ˇZn). We have the following inequalities.
It follows that
Therefore, we have
(3) Monotonicity: Let ˇZp=([ˆWp,˘Up],ˆYp) and ˇZ∗p=([ˆW∗p,˘U∗p],ˆY∗p),(p=1,2,⋯,n) be a collections of CNs, if [ˆWp,˘Up]≤[ˆW∗p,˘U∗p] and ˆYp≥ˆY∗p, with 0<˘ep≤min([ˆWp,˘Up],[ˆW∗p,˘U∗p])≤1, hold for any p, then
where ˘e1=˘e2=...=˘en=˘e.
Proof. Let
and
altough [ˆWˇZp,˘UˇZp]≤[ˆW∗ˇZp,˘U∗ˇZp] and ˆYˇZp≥ˆY∗ˇZp for any p, giving
Therefore, by using the score function and accuracy function, we can conclude that
4.3. Logarithmic cubic ordered weighted averaging aggregation operator
Definition 4.2.Let ˇZp=([ˆWˇZp,˘UˇZp],ˆYˇZp) where (p=1,2,...,n) be a collection of cubic numbers with 0 < \breve{e} _{p}\leq \left[ \hat{W}_{p}, \breve{U}_{p}\right] \leq 1, and \breve{e} _{p}\neq 1. Then, the mapping \log -CWA:\check{R}^{n}\longrightarrow \check{R}, is defined as
Thus, the function \log -CWA is known as the logarithmic cubic ordered weighted averaging operator, where the weighed vectors are denoted by \varpi = \left(\varpi _{1}, \varpi _{2}, ..., \varpi _{n}\right) ^{T} of \log _{\breve{e}_{p}}\check{Z}_{p}\left(p = 1, 2, ..., n\right), subject to \varpi _{{\rm{ p }}}\in \left[ 0, 1\right], and their sum is always equal to 1.
Theorem 4.2. Let \check{Z}_{p} = \left(\left[ \hat{W} _{p}, \breve{U}_{p}\right], \hat{Y}_{p}\right) \left(p = 1, ..., n\right) be a collections of CNs with 0 < \breve{e}_{p}\leq \left[ \hat{W}_{p}, \breve{U}_{p} \right] \leq 1, and \breve{e}_{p}\neq 1, that is, p = 1, 2, ..., n. Then, utilized Definition 4.2, we have
Proof. For proof, see Appendix G.
4.4. Properties
(1) Idempotency:Let \check{Z}_{p} = \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \hat{Y}_{p}\right), \left(p = 1, 2, .., n\right) be a collection of CNs are equal, i.e., \check{Z}_{p} = \check{Z}, \left(p = 1, 2, ..., n\right) . Then,
where \breve{e}_{1} = \breve{e}_{2} = ... = \breve{e}_{n} = \breve{e} .
(2) Boundedness:If \check{Z}_{p} = \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \hat{Y}_{p}\right) \left(p = 1, 2, \cdots, n\right) be a collection of CNs. Let \check{Z}^{-} = \min \left(\check{Z}_{1}, ..., \check{ Z}_{n}\right) and \check{Z}^{+} = \max \left(\check{Z}_{1}, \check{Z} _{2}, ..., \check{Z}_{n}\right) . Then,
where \breve{e}_{1} = \breve{e}_{2} = \cdots = \breve{e}_{n} = \breve{e} .
(3) Monotonicity: Let \check{Z}_{p} = \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \hat{Y}_{p}\right) and \check{Z}_{p}^{\ast } = \left(\left[ \hat{W}_{p}^{\ast }, \breve{U}_{p}^{\ast }\right], \hat{Y}_{p}^{\ast }\right), \left(p = 1, 2, \cdots, n\right) be a family of cubic numbers, if \left[ \hat{W}_{p}, \breve{U}_{p}\right] \leq \left[ \hat{W}_{p}^{\ast }, \breve{U} _{p}^{\ast }\right] and \hat{Y}_{p}\geq \hat{Y}_{p}^{\ast }, also 0 < \breve{e}_{p}\leq \min \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \left[ \hat{W}_{p}^{\ast }, \breve{U}_{p}^{\ast }\right] \right) \leq 1 , holds for any p , then
where \breve{e}_{1} = \breve{e}_{2} = \cdots = \breve{e}_{n} = \breve{e}.
5.
Logarithmic cubic geometric aggregation operators
The logarithmic cubic weighted geometric and \log -CFOWG aggregation operators, as well as their properties, are defined and explained in this portion of the paper.
5.1. Logarithmic cubic weighted geometric aggregation operator
Definition 5.1.Let \check{Z}_{p} = \left(\left[ \hat{W}_{p}, \breve{ U}_{p}\right], \hat{Y}_{p}\right) \left(p = 1, 2, \cdots, n\right) be a collection of cubic numbers with condition 0 < \breve{e}_{{\rm{ p }}}\leq \left[ \hat{W} _{p}, \breve{U}_{p}\right] \leq 1, and \breve{e}_{{\rm{ p }}}\neq 1. Then, the mapping \log -CWG:\check{R}^{n}\longrightarrow \check{R}, defined as
is called the logarithmic cubic weighted geometric operator of dimension n . Where \varpi = \left(\varpi _{1}, \cdots, \varpi _{n}\right) ^{T} are the weight vector of \log _{\breve{e}_{p}}\check{Z}_{p{\rm{\ }}}\left(p = 1, 2, \cdots, n\right) , such that \varpi _{{\rm{ p }}}\in \left[ 0, 1\right], \sum_{p = 1}^{n}\varpi _{{\rm{ p }}} = 1 . And also we have take \breve{e}_{1} = \breve{e}_{2} = \cdots = \breve{e}_{n} = \breve{e} .
Theorem 5.1. Let there be a collection of cubic numbers \check{Z} _{p} = \left(\left(\hat{W}_{p}, \breve{U}_{p}\right), \hat{Y}_{p}\right), \left(p = 1, 2, \cdots, n\right) with condition 0 < \check{e}_{p}\leq \left[ \hat{W}_{p}, \breve{U}_{p}\right] \leq 1, and \check{e}_{p}\neq 1. Then, utilizing the \log - CWG operator the aggregated value is also a logarithmic cubic number. Hence,
Proof. For proof, see Appendix H.
5.2. Properties
(1) Idempotency:Let \check{Z}_{p} = \left([\hat{W}_{p}, \breve{U} _{p}], \hat{Y}_{p}\right) \left(p = 1, 2, ..., n\right) be a collection of cubic numbers and all the CNs are equal, i.e., \check{Z}_{p} = \check{Z}, \left(p = 1, 2, ..., n\right) . Then,
where \breve{e}_{1} = \breve{e}_{2} = ... = \breve{e}_{n} = \breve{e} .
(2) Boundedness:If \check{Z}_{p} = \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \hat{Y}_{p}\right), \left(p = 1, 2, ..., n\right) is a family of CNs, let \check{Z}^{-} = \min \left(\check{Z}_{1}, ..., \check{Z} _{n}\right) and \check{Z}^{+} = \max \left(\check{Z}_{1}, \check{Z}_{2}, ..., \check{Z}_{n}\right) . Then,
where \breve{e}_{1} = \breve{e}_{2} = \cdots = \breve{e}_{n} = \breve{e} .
(3) Monotonicity: Let \check{Z}_{p} = \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \hat{Y}_{p}\right) and \check{Z}_{p}^{\ast } = \left(\left[ \hat{W}_{p}^{\ast }, \breve{U}_{p}^{\ast }\right], \hat{Y}_{p}^{\ast }\right), \left(p = 1, 2, ..., n\right) be a collections of cubic numbers. If \left[ \hat{W}_{p}, \breve{U}_{p}\right] \leq \left[ \hat{W}_{p}^{\ast }, \breve{U} _{p}^{\ast }\right] and \ \hat{Y}_{p}\geq \hat{Y}_{p}^{\ast }, with 0 < \breve{e}_{p}\leq \min \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \left[ \hat{W}_{p}^{\ast }, \breve{U}_{p}^{\ast }\right] \right) \leq 1 , holds for any p , then
where \ \breve{e}_{1} = \breve{e}_{2} = ... = \breve{e}_{n} = \breve{e}.
5.3. Logarithmic cubic ordered weighted geometric aggregation operator
Definition 5.2.Let the collection of the cubic numbers are \check{Z} _{p} = \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \hat{Y}_{p}\right) \left(p = 1, 2, ..., n\right) with condition 0 < \breve{e}_{p}\leq \left[ \hat{W }_{p}, \breve{U}_{p}\right] \leq 1, and \breve{e}_{p}\neq 1. Then, the mapping \log -COWG:\check{R}^{n}\longrightarrow \check{R} , defined as
is called the logarithmic cubic ordered weighted geometric operator of dimension n. The permutations are denoted by \left(\check{z}\left(1\right), \check{z}\left(2\right), ..., \check{z}\left(n\right) \right) of \left({\rm{ p }} = 1, 2, ..., n\right), such that \check{Z}_{\check{z}\left({\rm{ p- }}1\right) }\geq \check{Z}_{\check{z}\left({\rm{ p }}\right) }, for all p = 1, 2, ..., n . Also the weighted vectors are denoted by \varpi = \left(\varpi _{1}, \varpi _{2}, \cdots, \varpi _{n}\right) ^{T} of \log _{\breve{e} }\check{Z}_{\left(p\right) }, \left({\rm{ p }} = 1, 2, ..., n\right) , subject to \varpi _{{\rm{ p }}}\in \lbrack 0, 1], and their sum is always equal to one. And, we have \breve{e}_{1} = \breve{e}_{2} = ... = \breve{e}_{n} = \breve{e} .
Theorem 5.2. Let the collection of cubic numbers are \check{Z}_{ {\rm{ p }}} = \left(\left[ \hat{W}_{{\rm{ p }}}, \breve{U}_{{\rm{ p }}}\right], \hat{Y}_{{\rm{ p }}}\right), \left(p = 1, 2, ..., n\right) with the condition 0 < \breve{e}_{{\rm{ p }}}\leq \left[ \hat{W}_{{\rm{ p }}}, \breve{U}_{{\rm{ p }}}\right] \leq 1, and \breve{e}_{{\rm{ p }}}\neq 1. Then, by utilizing the \log - COWG operator the aggregated value is also a logarithmic CNs. Hence,
Proof. For proof, see Appendix I.
5.4. Properties
(1) Idempotency:Let there be a collection of cubic numbers are \check{Z} _{p} = \left([\hat{W}_{p}, \breve{U}_{p}], \hat{Y}_{p}\right) \left(p = 1, 2, ..., n\right) with \check{Z}_{p} = \check{Z}. Then, we show that
where \check{e}_{1} = \check{e}_{2} = ... = \check{e}_{n} = \check{e}.
(2) Boundedness:Let there be a collection of cubic numbers are \check{Z} _{p} = \left([\hat{W}_{p}, \breve{U}_{p}], \hat{Y}_{p}\right) \left(p = 1, 2, ..., n\right). \check{Z}^{-} = \min \left(\check{Z}_{1}, \check{Z }_{2}, ..., \check{Z}_{n}\right) and \check{Z}^{+} = \max \left(\check{Z} _{1}, \check{Z}_{2}, ..., \check{Z}_{n}\right). Then,
where \check{e}_{1} = \check{e}_{2} = \cdots = \check{e}_{n} = \check{e}.
(3) Monotonicity: Let \check{Z}_{p} = \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \hat{Y}_{p}\right) and \check{Z}_{p}^{\ast } = \left(\left[ \hat{W}_{p}^{\ast }, \breve{U}_{p}^{\ast }\right], \hat{Y}_{p}^{\ast }\right) \left(p = 1, 2, ..., n\right) be a collections of cubic numbers. If \ \left[ \hat{W}_{p}, \breve{U}_{p}\right] \leq \left[ \hat{W}_{p}^{\ast }, \breve{U} _{p}^{\ast }\right] and \ \hat{Y}_{p}\geq \hat{Y}_{p}^{\ast }, with 0 < \check{e}_{p}\leq \min \left(\left[ \hat{W}_{p}, \breve{U}_{p}\right], \left[ \hat{W}_{p}^{\ast }, \breve{U}_{p}^{\ast }\right] \right) \leq 1, holds for any p , then,
Definition 5.3. Let there be a collection of cubic numbers are \log _{ \check{e}}\check{Z} = \left(\left[ 1-\log _{\check{e}}\breve{U}, \log _{\check{ e}}(1-\breve{U})\right], \log _{\check{e}}(1-\hat{Y})\right).
Then, S is the score function of \log _{\breve{e}}\check{Z} , which is defined as follows:
\hat{S} be the accuracy degree of \log _{\breve{e}}\check{Z} and is defined as follows:
(1) If S\left(\log _{\breve{e}}\check{Z}_{1}\right) > S\left(\log _{\breve{ e}}\check{Z}_{2}\right), then \log _{\breve{e}}\check{Z}_{1} > \log _{\breve{ e}}\check{Z}_{2} .
(2) If S\left(\log _{\breve{e}}\check{Z}_{1}\right) = S\left(\log _{\breve{ e}}\check{Z}_{2}\right), then if \hat{S}\left(\log _{\breve{e}}\check{Z} _{1}\right) > \hat{S}\left(\log _{\breve{e}}\check{Z}_{2}\right), then \log _{\breve{e}}\check{Z}_{1} > \log _{\breve{e}}\check{Z}_{2} .
(3) If \hat{S}\left(\log _{\breve{e}}\check{Z}_{1}\right) = \hat{S}\left(\log _{\breve{e}}\check{Z}_{2}\right), then \log _{\breve{e}}\check{Z} _{1} = \log _{\breve{e}}\check{Z}_{2}.
6.
Approach for solving MAGDM problem
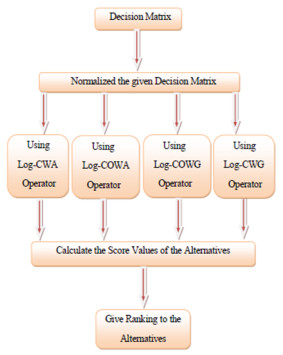
This part tackles the MAGDM problem using the previously mentioned aggregation operations. An example is given to demonstrate the superiority as well as the validity of the introduced operators in a real-life scenario. Let the finite set of m alternatives be \breve{U} = \left\{ u_{1}, u_{2}, ..., u_{m}\right\}, and the finite set of n attribute is \check{Z} = \left\{ z_{1}, z_{2}, ..., z_{n}\right\} . The weight vector of attributes is \varpi = \left(\varpi _{1}, \varpi _{2}, \cdots, \varpi _{n}\right) ^{T} , such that \varpi _{p}\in \left[ 0, 1\right], \sum_{p = 1}^{n}\varpi _{p} = 1 . Let the decision matrices (DMs) as follows:
By using the \log -CWA, \log -COWA, \log -CWG, and \log -CWG operators, we intend to solve the MAGDM issue using cubic fuzzy information using the following algorithm.
Step 1.Make the decision matrices (DMs).
Step 2.Normalize the given decision matrices (DMs).
Step 3. Use the introduced operators to combine the preferences of the DMs of various types.
Step 4.Use the Definition of the score function to calculate the score value.
Step 5.On the basis of the score function, rank all of the possibilities and choose the best one.
Figure 1 shows the algorithm of the proposed method.
7.
Illustrative example
7.1. Online study effect during Covid-19
Education plays a vital role in the development of society and individual behavior. For that purpose, the role of teachers is the most important in delivering and transferring of knowledge and experience to students in a healthy and effective environment with smoothness and easy way. The relationship of teacher to student in this sense is like a backbone in the body. If there is more effective ways and suitable environment for sharing knowledge there will be the best outcomes of it. The flow of knowledge between teacher and student plays a key role in that scenario. We have studied and observed the difference between the flow and gaining of knowledge between students and teacher before and after the Covid- 19 pandemic. We have found very vivid clues of teacher teaching effect before Covid- 19 , and the effects on students today has a clear difference.
Knowledge flow between Students and teacher before and after Covid- 19 in colleges:
R_{1} : Face to face interaction
Teacher student interaction in the classroom before Covid was face to face interaction. The teacher was teaching everything in a friendly environment with direct student interaction. However this effective way of teaching with face to face interaction has vanished because of Covid- 19 , which creates hurdles in the way of transferring knowledge from teacher to students.
R_{2} : Attention
Face to face interaction was interrupted by the arrival of Covid- 19. Before Covid, the relationship between teacher and student was so closed which was showing their strong connection whenever students lost their attention during class from their particular topic, teachers were always there to help them pay their attention again. However now, using virtual classrooms, that strong bonding between teacher and students has lost and students lose their attention. Such teaching method includes not powerful visual presentations because the teacher didn't see whether students are attentive or not. Finally, we come to the conclusion that taking classes from home fuels a disturbing environment that leads to losing attention, etc.
R_{3} : Performance
Performances of students are getting worse because of the lack of face to face interaction in the classroom between teacher and student and the lack of full attention. This badly effects students performance. They lose their vocabulary skills, fluency, sharpness, and obedience, etc. Informal environment of class at home leads to disturbed patterns of gaining knowledge that directly affects student performance.
R_{4} : Interest
Interest is something really important for achieving goals. Online classes create a situation in which students cannot hold their interest in studies. When the students pick up a cell phone and get on the internet, a lot of unwanted notifications start coming, which attract students toward unproductive things. Especially immature students can easily lose their attention to other things than studies and taking classes.
Step 1.Decision matrices given by three experts are given in Tables 1–4.
Step 2.We do not need to normalize the data because all the criteria are of the same type.
Step 3.Use the methods that have been introduced, which are listed below.
First, we utilized the \log -CWA operator, and we obtained Table 5.
Second, we utilized the \log -CWG operator, and we get Table 6.
Third, we utilized the \log -COWA operator, and we get Table 7.
Fourth, we utilized the \log -COWG operator, and we get Table 8.
Step 4.The following score values are obtained by using the score function (see Table 9).
Step 5.Thus, from the obtained score values, we get the ranking of the attributes, as shown in Table 10.
Hence, R_{2} is our best choice.
In Figure 2, we show the ranking of the alternative graphically.
8.
Sensitivity analysis
8.1. Validity test
Uncertain outcomes are a result of the fact that, when applied to the same decision making problem, several MAGDM methods provide different assessments (rankings). In order to assess the validity and reliability of the MAGDM method, we consider the following.
Test criteria on 1:The MAGDM method works well when the best alternative is kept as the default, and the non-optimal alternative is changed to a worse alternative without altering the relative importance of any decision attribute.
Test criteria on 2:Transitive qualities should be followed by an effective MAGDM strategy.
Test criteria on 3:When the MAGDM problem is divided into smaller problems and these smaller problems, are subjected to the proposed MAGDM approach for the ranking of alternatives, the MAGDM approach is effective. The cumulative rating of the options maintains consistency with the ranking of the original problem.
The following attributes are used to evaluate the suggested solution's validity.
8.2. Validity check with criteria 1
In order to assess the viability of the established technique using criteria on 1, the worst alternative R_{4}^{/} is substituted for the non-optimal alternative R_{4}^{/} for each expert in the original decision matrix, and the rating values are provided in Table 11.
Now, utilizing the \log -CWA operator in Step 3 on transferring alternative, we get the computed scores of the alternatives are S(R_{1}) = 0.234, S(R_{2}) = 0.265, S(R_{3}) = 0.223, S(R_{4}) = 0.245 . As a result, the final ranking of the options points to R_{2} as the best alternative, and the approach developed satisfies test criteria on 1.
8.3. Validity check with criteria 2 and 3
We divided the initial decision-making problem into smaller decision making problems \left(R_{1}, R_{2}, R_{3}\right), \left(R_{2}, R_{3}, R_{4}\right) and \left(R_{1}, R_{3}, R_{4}\right) using these possibilities in order to test the defined MAGDM approach with criteria 2 and 3. When we use the provided MAGDM approach to solve these subproblems, the rating of the alternatives will be R_{2} > R_{1} > R_{3}, R_{2} > R_{4} > R_{3} and R_{4} > R_{1} > R_{3} . We achieve the ultimate ranking order as R_{2} > R_{4} > R_{1} > R_{3} by adding a ranking of alternatives to the smaller problems. This shows a transitive property and is equivalent to a non-decomposed problem. As a result, the criteria 2 and 3 have same best alternative as the defined MAGDM approach.
8.4. Comparison analysis
In this part, the comparing of our suggested aggregation operators to previous information aggregation operators is expressed using [10,11,18,21] aggregation operators. The STOLs for the MAGDM problem are defined for MAGDM problems with CFNs. The results and rankings are shown in Table 12. For comparison, we have solved the same numerical example present in Section 7.1 by the existing aggregation operators in [10,11,18,21]. The results are shown in Table 12. It is determined that the best option is still the same. Consequently, the new strategy is more logical than the existing one.
We have observed the logarithmic aggregation operators, and we have suggested proposed results that are broader, are more accurate and represent a novel approach to aggregating the cubic fuzzy data. In Figure 3, we show the ranking of the alternatives using different methods.
9.
Conclusions
In this study, we presented the CNs logarithmic operating laws, which are a useful addition to the currently used cubic aggregation methods. Based on logarithmic operational principles, we derived valuable operational laws under cubic information. Then, based on the developed logarithmic operational laws, a number of cubic aggregation operators were defined, including \log -CWA, \log -CWG, \log -COWA, and \log -COWG aggregation operators. We have examined a number of prerequisites for these logarithmic aggregation operations. To show the effectiveness and consistency of the suggested cubic logarithmic aggregation operators, we developed a method to handle MAGDM problems with uncertainty in the form of cubic fuzzy information. A real life example of Online study effect during Covid-19 was given in order to assess and show the applicability of our suggested technique. In order to demonstrate the superiority and the validity of the recommended aggregation methods, we employed certain existing tools. The research shows that our proposed aggregation operator outperforms the existing method in terms of reliability and accuracy. Thus, our suggested technique, logarithmic aggregation operator, provides a novel way to identify the best option in the MAGDM decision-making problem. The theory of logarithmic aggregation operators based on the CS is a very effective and dominant idea, which can be used for aggregating the collection of information into a single set. The proposed theory can easily resolve many real-life problems: for instance, artificial intelligence in education, in Health care, in business, in manufacturing, roads, machine learning, game theory, computer science and many more. Thus, our suggested technique, logarithmic aggregation operator, provides a novel way to identify the best option in the MAGDM decision-making problem.
In the future, we extended our work to other disciplines for further research, including pattern recognition, symmetric operators, power operators, Hamacher operators, Dombi operators, Einstein operator, etc.
Acknowledgments
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work under grant code 22UQU4310396DSR45.
Conflict of interest
The authors declare that they have no conflicts of interest.










 DownLoad:
DownLoad:














