Investigating stochastic solutions for fourth order dispersive NLSE with quantic nonlinearity

Yazid Alhojilan; Islam Samir; Yazid Alhojilan; Islam Samir

doi:10.3934/math.2023776

AIMS Mathematics

2023, Volume 8, Issue 7: 15201-15213. doi: 10.3934/math.2023776

Previous Article Next Article

Research article Special Issues

Investigating stochastic solutions for fourth order dispersive NLSE with quantic nonlinearity

Yazid Alhojilan ¹,
Islam Samir ^{2
,
,}

1.
Department of Mathematics, College of Science, Qassim University, P.O. Box 6644, Buraydah 51452, Saudi Arabia
2.
Department of Physics and Mathematics Engineering, Faculty of Engineering, Ain Shams University, Cairo, Egypt

In this paper, the stochastic fourth order nonlinear Schrödinger equation with quantic nonlinearity and affected by multiplicative noise is considered. This model is used to mimic the wave propagation through optical fibers. The improved modified extended tanh method is used to extract optical solutions for the investigated model. Various types of stochastic solutions are provided such as bright soliton, dark soliton, singular soliton, singular periodic solution and Weierstrass elliptic solution. Moreover, Matlab software packages are used to introduce the effect of the multiplicative noise on the raised solutions. The noise intensity is varied to show the robust of the extracted solutions against the noise.

Keywords:

Citation: Yazid Alhojilan, Islam Samir. Investigating stochastic solutions for fourth order dispersive NLSE with quantic nonlinearity[J]. AIMS Mathematics, 2023, 8(7): 15201-15213. doi: 10.3934/math.2023776

Related Papers:

[1]	Yousef F. Alharbi, E. K. El-Shewy, Mahmoud A. E. Abdelrahman . New and effective solitary applications in Schrödinger equation via Brownian motion process with physical coefficients of fiber optics. AIMS Mathematics, 2023, 8(2): 4126-4140. doi: 10.3934/math.2023205
[2]	Islam Samir, Hamdy M. Ahmed, Wafaa Rabie, W. Abbas, Ola Mostafa . Construction optical solitons of generalized nonlinear Schrödinger equation with quintuple power-law nonlinearity using Exp-function, projective Riccati, and new generalized methods. AIMS Mathematics, 2025, 10(2): 3392-3407. doi: 10.3934/math.2025157
[3]	Hamood Ur Rehman, Aziz Ullah Awan, Sayed M. Eldin, Ifrah Iqbal . Study of optical stochastic solitons of Biswas-Arshed equation with multiplicative noise. AIMS Mathematics, 2023, 8(9): 21606-21621. doi: 10.3934/math.20231101
[4]	Da Shi, Zhao Li, Dan Chen . New traveling wave solutions, phase portrait and chaotic patterns for the dispersive concatenation model with spatio-temporal dispersion having multiplicative white noise. AIMS Mathematics, 2024, 9(9): 25732-25751. doi: 10.3934/math.20241257
[5]	Dan Chen, Da Shi, Feng Chen . Qualitative analysis and new traveling wave solutions for the stochastic Biswas-Milovic equation. AIMS Mathematics, 2025, 10(2): 4092-4119. doi: 10.3934/math.2025190
[6]	Nafissa T. Trouba, Huiying Xu, Mohamed E. M. Alngar, Reham M. A. Shohib, Haitham A. Mahmoud, Xinzhong Zhu . Soliton solutions and stability analysis of the stochastic nonlinear reaction-diffusion equation with multiplicative white noise in soliton dynamics and optical physics. AIMS Mathematics, 2025, 10(1): 1859-1881. doi: 10.3934/math.2025086
[7]	Mahmoud A. E. Abdelrahman, Wael W. Mohammed, Meshari Alesemi, Sahar Albosaily . The effect of multiplicative noise on the exact solutions of nonlinear Schrödinger equation. AIMS Mathematics, 2021, 6(3): 2970-2980. doi: 10.3934/math.2021180
[8]	F. A. Mohammed, Mohammed K. Elboree . Soliton solutions and periodic solutions for two models arises in mathematical physics. AIMS Mathematics, 2022, 7(3): 4439-4458. doi: 10.3934/math.2022247
[9]	Siru Li, Tian Xu, Ailong Wu . Existence and asymptotic properties of global solution for hybrid neutral stochastic differential delay equations with colored noise. AIMS Mathematics, 2025, 10(3): 6379-6405. doi: 10.3934/math.2025291
[10]	Mustafa Inc, Hadi Rezazadeh, Javad Vahidi, Mostafa Eslami, Mehmet Ali Akinlar, Muhammad Nasir Ali, Yu-Ming Chu . New solitary wave solutions for the conformable Klein-Gordon equation with quantic nonlinearity. AIMS Mathematics, 2020, 5(6): 6972-6984. doi: 10.3934/math.2020447

Abstract

1. Introduction

Nonlinear partial differential equations (NLPDEs) can be used to mimic many nonlinear phenomena that arise in a various scientific fields, including geology, fluid dynamics, biology, chemical physics, Optics, plasma physics and solid state physics ^{[1,2,3,4,5,6,7,8,9]}. Many researchers have recently become interested in studying the dynamics of these models ^{[10,11,12,13]}. One of the basic models of nonlinear waves is the nonlinear Schrodinger equation (NLSE) ^[14,15]. It is used in a variety of fields, including electromechanical systems ^[16], laser beams ^[17], and the theory of crystals ^[18] and solids ^[19].

General random disturbances Spontaneous emissions and Thermal fluctuations can be modeled using stochastic Schrodinger models. Many authors investigated the uniqueness and existence of stochastic NLSEs with multiplicative or additive noise. The case of additive noise is investigated in ^[20,21] while the case of multiplicative noise if reported in ^[22,23]. Both types of noises are investigated in ^[24,25]. In addition, Numerical methods are used to study the stochastic NLSE in ^[26,27].

In this context, the stochastic Fourth order NLSE with quantic nonlinearity and affected by multiplicative noise. This stochastic model has not been studied before. This model reads as:

$\begin{eqnarray} && i (H_t+\alpha_1 H_x+\alpha_3 H_{xxx})+\alpha_2 H_{xx}+\alpha_4 H_{xxxx}+\beta_1 |H|^2 H+\beta_2 |H|^4 H+\sigma H B_t = 0, \end{eqnarray}$

(1.1)

where $H_t$ represents the linear temporal evolution. $H_x$ represents the inter-modal dispersion. $H_{xxx}$ and $H_{xxxx}$ represent the third order and fourth order dispersion. $H_{xx}$ represents the group velocity dispersion. $\beta_1$ and $\beta_2$ represent the coefficients of self phase modulation effect and quantic nonlinearity. $B_t$ is the stochastic term which represents the white noise. $B(t)$ and follow the next conditions:

(i) For $t\geq0$ , $B(t)$ has continuous trajectories.

(ii) For $s < t$ , $B(t)-B(s)$ has independent increments.

(iii) $B(t)-B(s)$ has a normal distribution with variance $= t-s$ and mean $= 0$ .

This model is used to describe the wave propagation through optical fibers. This model includes the dispersion and nonlinearity effects. Dispersion is also known as wave broadening or wave spreading. Some of the optical power in a propagated wave is delayed at the fiber's output end, which results in dispersion ^[28]. Dispersion shows how optical power that enters the fiber simultaneously leaves at various moments. Because of dispersion, the optical wave width grows continually across the fiber. The output signal varies from the input signal when dispersion reaches the data rate's maximum value ^[29]. In addition, The intensity dependence of the medium's refractive index causes nonlinear effects in optical fiber. Optical soliton is a special type of solutions that can propagate to very large distance retaining its shape and speed. This optical wave is generated due to dedicated balance which occurs between the dispersion and nonlinear effects ^[30,31]. In addition, adding the noise effect to the investigated model is very necessary to show the robust of the extracted solutions against the noise. Research into all these different influences is making a huge contribution to the development of the telecommunications industry ^[29].

The nonlinear stochastic Chiral Schrödinger equation (CNLSE) in two dimensions was investigated in literature ^[32] to extract periodic envelopes, explosive, dissipative, symmetric solitons, and blow up waves. It was confirmed that the noise factor is dominant on all the wave conversion, growing and damping of envelopes and shocks. In ref ^[33], the stochastic NLSE with group velocity dispersion and self modulation nonlinear effect was studied by applying the unified solver approach to extract rational, dissipative, explosive, envelope, periodic, and localized soliton solutions.

In this current work, the improved modified extended tanh function scheme is utilized to provide optical solitons for the stochastic NLSE in (1.1). In addition, this method provide other solutions such as trigonometric, hyperbolic and exponential type solutions. The proposed method is briefly introduced in Section 2. Then, the stochastic solutions are extracted for the investigated model in Section 3. The effect of the multiplicative noise on the obtained solutions is discussed in Section 4. Finally, the work is concluded.

2. Revisitation of the technique

This section introduces the improved modified extended tanh scheme ^[34].

Considering the following NLPDE:

$\begin{equation} G(H,H_t,H_x,H_{xx},H_{xt},....) = 0, \end{equation}$

(2.1)

where $G$ is polynomial in $H(x, t)$ and its partial derivatives

Step 1: The following mathematical transformation is applied

$\begin{equation} H(x,t) = F(\xi), \; \xi = x-\lambda\; t. \end{equation}$

(2.2)

Therefore, Eq (2.1) is converted to the following ODE:

$\begin{equation} F(F,F',F'',F''',....) = 0. \end{equation}$

(2.3)

Step 2: The solutions for Eq (2.3) is supposed in the form:

$\begin{equation} F(\xi) = a_0+\sum\limits_{r = 1}^{N}{a_r A^r(\xi)}+{b_{r} A^{-r}(\xi)}, \end{equation}$

(2.4)

where $A(\xi)$ holds:

$\begin{equation} A'(\xi) = \sqrt{d_0+d_1 A(\xi)+d_2 A^2(\xi)+d_3 A^3(\xi)+d_4 A^4(\xi)}. \end{equation}$

(2.5)

By changing the values of the constants $d_0, \; d_1, \; d_2, \; d_3$ and $d_4$ , one can obtain different general solutions for Eq (2.5).

Step 3: $N$ that raised in Eq (2.4) can be evaluated by applying the balancing rule on Eq (2.3).

Step 4: Substituting by Eq (2.4) with (2.5) into (2.3), a polynomial in $A(\xi)$ is provided. Collecting the terms which have the same power together and equating them to zero, one get a system of nonlinear equations that can be solved using packages of Mathematica to determine $\lambda, a_k$ and $b_k$ .

3. Results

In this section, the improved modified extended tanh method is applied to provide stochastic solutions for the proposed model in the following form:

$\begin{equation} H(x,t) = F(\xi) e^{i(w t-k x-\sigma^2t+\sigma B(t))}, \; \xi = x-\lambda\; t. \end{equation}$

(3.1)

Substituting by (3.1) into (1.1) provides

$\begin{eqnarray} F^{(3)} \left(\alpha _3-4 \alpha _4 k\right)+F' \left(\alpha _1+4 \alpha _4 k^3-3 \alpha _3 k^2-2 \alpha _2 k-\lambda \right) = 0, \end{eqnarray}$

(3.2)

and

$\begin{eqnarray} \beta _2 F^5+\alpha _4 F^{(4)}+\beta _1 F^3+F'' \left(\alpha _2+6 \alpha _4 k^2\right)+F \left(-3 \alpha _4 k^4-\alpha _2 k^2+\alpha _1 k+\sigma ^2-w\right) = 0, \end{eqnarray}$

(3.3)

where Eq (3.2) represents the imaginary part while Eq (3.3) is the real part.

Equating the coefficients of (3.2) to zero gives

$\begin{eqnarray} && \alpha _3 = 4 \alpha _4 k,\\&& \lambda = \alpha _1-8 \alpha _4 k^3-2 \alpha _2 k. \end{eqnarray}$

(3.4)

Balancing $F^{(4)}$ with $F^5$ , we get $N = 1$ . Then, the solution of Eq (3.3) can be represented as follow:

$\begin{equation} F(\xi) = a_0+a_1 A(\xi)+\dfrac{b_1}{A(\xi)}. \end{equation}$

(3.5)

By employing Step 4 which discussed in the last section, we can obtain the next results for (1.1) :

Case 1. $d_0 = d_1 = d_3 = 0$

Result (1)

$\begin{eqnarray} && a_0 = 0,\; b_1 = 0,\; d_4 = \frac{a_1^2 \sqrt{-\beta _2}}{2 \sqrt{6} \sqrt{\alpha _4}},\; \alpha _1 = \frac{\frac{\sqrt{6} \sqrt{-\alpha _4} \beta _1 \left(k^2-d_2\right)}{\sqrt{\beta _2}}+\alpha _4 \left(-10 d_2 k^2+9 d_2^2-3 k^4\right)-\sigma ^2+w}{k},\\&& d_2 = -\frac{-\frac{\sqrt{6} \sqrt{-\alpha _4} \beta _1}{\sqrt{\beta _2}}+\alpha _2+6 \alpha _4 k^2}{10 \alpha _4}. \end{eqnarray}$

Then, we obtain the following stochastic bright soliton and singular periodic solutions for (1.1).

$\begin{eqnarray} && H(x,t) = \sqrt[4]{6} \sqrt{\frac{-\frac{\sqrt{6} \sqrt{-\alpha _4} \beta _1}{\sqrt{\beta _2}}+\alpha _2+6 \alpha _4 k^2}{5 \sqrt{\alpha _4} \sqrt{-\beta _2}}} \text{sech}\left(\frac{\sqrt{-\frac{-\frac{\sqrt{6} \sqrt{-\alpha _4} \beta _1}{\sqrt{\beta _2}}+\alpha _2+6 \alpha _4 k^2}{\alpha _4}} (x-\lambda t)}{\sqrt{10}}\right)\times e^{i(w t-k x-\sigma^2t+\sigma B(t))},\\&& \end{eqnarray}$

(3.6)

$\begin{eqnarray} && H(x,t) = \sqrt[4]{6} \sqrt{\frac{-\frac{\sqrt{6} \sqrt{\alpha _4} \beta _1}{\sqrt{-\beta _2}}+\alpha _2+6 \alpha _4 k^2}{5 \sqrt{\alpha _4} \sqrt{-\beta _2}}} \sec \left(\frac{\sqrt{\frac{-\frac{\sqrt{6} \sqrt{\alpha _4} \beta _1}{\sqrt{-\beta _2}}+\alpha _2+6 \alpha _4 k^2}{\alpha _4}} (x-\lambda t)}{\sqrt{10}}\right)\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}.\\&& \end{eqnarray}$

(3.7)

Case 2. $d_1 = d_3 = 0$

Result (1)

$\begin{eqnarray} && a_0 = 0,\; b_1 = 0,\; d_4 = \frac{a_1^2 \sqrt{-\beta _2}}{2 \sqrt{6} \sqrt{\alpha _4}},\; d_2 = -\frac{-\frac{\sqrt{6} \sqrt{-\alpha _4} \beta _1}{\sqrt{\beta _2}}+\alpha _2+6 \alpha _4 k^2}{10 \alpha _4},\; d_0 = \frac{d_2^2}{4d_4},\\&&\alpha _1 = \frac{\sqrt{6} \sqrt{\alpha _4} \sqrt{-\beta _2} \beta _1 \left(k^2-d_2\right)+\alpha _4 \beta _2 \left(-10 d_2 k^2+6 d_2^2-3 k^4\right)+\beta _2 \left(w-\sigma ^2\right)}{\beta _2 k}. \end{eqnarray}$

Then, we obtain the following stochastic dark soliton and singular periodic solutions for (1.1).

$\begin{eqnarray} && H(x,t) = \sqrt[4]{\frac{3}{2}} \sqrt{\frac{-\frac{\sqrt{6} \sqrt{-\alpha _4} \beta _1}{\sqrt{\beta _2}}+\alpha _2+6 \alpha _4 k^2}{5 \sqrt{\alpha _4} \sqrt{-\beta _2}}} \tanh \left(\frac{\sqrt{\frac{-\frac{\sqrt{6} \sqrt{-\alpha _4} \beta _1}{\sqrt{\beta _2}}+\alpha _2+6 \alpha _4 k^2}{\alpha _4}} (x-\lambda t)}{2 \sqrt{5}}\right)\times e^{i(w t-k x-\sigma^2t+\sigma B(t))},\\&& \end{eqnarray}$

(3.8)

$\begin{eqnarray} && H(x,t) = \sqrt[4]{\frac{3}{2}} \sqrt{-\frac{-\frac{\sqrt{6} \sqrt{-\alpha _4} \beta _1}{\sqrt{\beta _2}}+\alpha _2+6 \alpha _4 k^2}{5 \sqrt{\alpha _4} \sqrt{-\beta _2}}} \tan \left(\frac{\sqrt{-\frac{-\frac{\sqrt{6} \sqrt{-\alpha _4} \beta _1}{\sqrt{\beta _2}}+\alpha _2+6 \alpha _4 k^2}{\alpha _4}} (x-\lambda t)}{2 \sqrt{5}}\right)\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}.\\&& \end{eqnarray}$

(3.9)

Result (2)

$\begin{eqnarray} && a_0 = 0,\; a_1 = 0,\; \alpha _1 = \frac{6 \beta _1 b_1^2 d_2^2 d_4 \left(d_2-k^2\right)+2 \beta _2 b_1^4 d_4^2 \left(10 d_2 k^2-6 d_2^2+3 k^4\right)+3 d_2^4 \left(w-\sigma ^2\right)}{3 d_2^4 k},\\&& d_4 = \frac{\sqrt{3} \sqrt{\alpha _4} d_2^2}{b_1^2 \sqrt{-2 \beta _2}}, d_2 = \frac{-\alpha _2 \sqrt{-\beta _2}-\sqrt{6} \sqrt{\alpha _4} \beta _1-6 \alpha _4 \sqrt{-\beta _2} k^2}{10 \alpha _4 \sqrt{-\beta _2}},\; d_0 = \frac{d_2^2}{4d_4}. \end{eqnarray}$

Then, we obtain the following stochastic singular soliton and singular periodic solutions for (1.1).

$\begin{eqnarray} && H(x,t) = \sqrt[4]{\frac{3}{2}} \sqrt{\frac{-\alpha _2 \sqrt{-\beta _2}-\sqrt{6} \sqrt{\alpha _4} \beta _1-6 \alpha _4 \sqrt{-\beta _2} k^2}{5 \sqrt{\alpha _4} \beta _2}} \coth \left(\frac{\sqrt{-\frac{-\alpha _2 \sqrt{-\beta _2}-\sqrt{6} \sqrt{\alpha _4} \beta _1-6 \alpha _4 \sqrt{-\beta _2} k^2}{\alpha _4 \sqrt{-\beta _2}}} (x-\lambda t)}{2 \sqrt{5}}\right)\\&&\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}, \end{eqnarray}$

(3.10)

$\begin{eqnarray} && H(x,t) = \sqrt[4]{\frac{3}{2}} \sqrt{-\frac{-\alpha _2 \sqrt{-\beta _2}-\sqrt{6} \sqrt{\alpha _4} \beta _1-6 \alpha _4 \sqrt{-\beta _2} k^2}{5 \sqrt{\alpha _4} \beta _2}} \cot \left(\frac{\sqrt{\frac{-\alpha _2 \sqrt{-\beta _2}-\sqrt{6} \sqrt{\alpha _4} \beta _1-6 \alpha _4 \sqrt{-\beta _2} k^2}{\alpha _4 \sqrt{-\beta _2}}} (x-\lambda t)}{2 \sqrt{5}}\right)\\&&\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}. \end{eqnarray}$

(3.11)

Result (3)

$\begin{eqnarray} && a_0 = 0,\; d_4 = \frac{a_1 d_2}{2 b_1},\; \alpha _1 = \frac{-\frac{6 a_1 \beta _1 b_1 \left(2 d_2+k^2\right)}{d_2}+\frac{a_1^2 \beta _2 b_1^2 \left(-20 d_2 k^2-36 d_2^2+3 k^4\right)}{d_2^2}+6 \left(w-\sigma ^2\right)}{6 k},\\&& b_1 = -\frac{\sqrt{\frac{3}{2}} \left(\alpha _2 \sqrt{-\beta _2}+\sqrt{6} \sqrt{\alpha _4} \beta _1+6 \alpha _4 \sqrt{-\beta _2} k^2\right)}{10 a_1 \sqrt{\alpha _4} \beta _2},\; d_2 = \frac{a_1 b_1 \sqrt{-\beta _2}}{\sqrt{6} \sqrt{\alpha _4}},\; d_0 = \frac{d_2^2}{4d_4}. \end{eqnarray}$

Then, we obtain the following stochastic singular soliton and singular periodic solutions for (1.1).

$\begin{eqnarray} && H(x,t) = \Bigg\{\frac{\sqrt[4]{3} \sqrt{\frac{\sqrt{6} \beta _1+\frac{\sqrt{-\beta _2} \left(\alpha _2+6 \alpha _4 k^2\right)}{\sqrt{\alpha _4}}}{a_1 \beta _2}} \tanh \left(\frac{\sqrt{-\frac{\sqrt{6} \beta _1}{\sqrt{\alpha _4} \sqrt{-\beta _2}}-\frac{\alpha _2}{\alpha _4}-6 k^2} (x-\lambda t)}{2 \sqrt{10}}\right)}{2^{3/4} \sqrt{5}}\\&& +\sqrt{-a_1} \coth \left(\frac{\sqrt{-\frac{\sqrt{6} \beta _1}{\sqrt{\alpha _4} \sqrt{-\beta _2}}-\frac{\alpha _2}{\alpha _4}-6 k^2} (x-\lambda t)}{2 \sqrt{10}}\right)\Bigg\}\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}, \end{eqnarray}$

(3.12)

$\begin{eqnarray} && H(x,t) = \Bigg\{\frac{\sqrt[4]{3} \sqrt{-\frac{\sqrt{6} \beta _1+\frac{\sqrt{-\beta _2} \left(\alpha _2+6 \alpha _4 k^2\right)}{\sqrt{\alpha _4}}}{a_1 \beta _2}} \tan \left(\frac{\sqrt{\frac{\sqrt{6} \beta _1}{\sqrt{\alpha _4} \sqrt{-\beta _2}}+\frac{\alpha _2}{\alpha _4}+6 k^2} (x-\lambda t)}{2 \sqrt{10}}\right)}{2^{3/4} \sqrt{5}}\\&&+\sqrt{a_1} \cot \left(\frac{\sqrt{\frac{\sqrt{6} \beta _1}{\sqrt{\alpha _4} \sqrt{-\beta _2}}+\frac{\alpha _2}{\alpha _4}+6 k^2} (x-\lambda t)}{2 \sqrt{10}}\right)\Bigg\}\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}. \end{eqnarray}$

(3.13)

Case 3. $d_0 = d_1 = 0$

Result (1)

$\begin{eqnarray} && b_1 = 0,\; d_2 = \frac{a_0 d_3}{a_1},\; \alpha _1 = \frac{2 a_0^2 a_1^2 \beta _2 k^3}{d_3^2}-\frac{2 a_0 a_1 k \left(5 a_0^2 \beta _2+3 \beta _1\right)}{3 d_3}-\frac{a_0^4 \beta _2+a_0^2 \beta _1+\sigma ^2-w}{k},\\&& \alpha _2 = \frac{2 a_0 a_1 \left(-5 a_0^2 \beta _2 d_3+6 a_0 a_1 \beta _2 k^2-3 \beta _1 d_3\right)}{3 d_3^2},\; d_3 = \frac{\sqrt{2} a_0 a_1 \sqrt{-\beta _2}}{\sqrt{3 \alpha _4}},\; d_4 = \frac{d_3^2}{4d_2}. \end{eqnarray}$

Then, we obtain the following stochastic dark soliton for (1.1).

$\begin{eqnarray} && H(x,t) = \Bigg\{a_0 \left(\tanh \left(\frac{a_0 \sqrt{\frac{\sqrt{-\beta _2}}{\sqrt{\alpha _4}}} (x-\lambda t)}{2^{3/4} \sqrt[4]{3}}\right)+1\right)+a_0\Bigg\}\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}. \end{eqnarray}$

(3.14)

Case 4. $d_3 = d_4 = 0$

Result (1)

$\begin{eqnarray} && a_0 = 0,\; a_1 = 0,\; d_0 = -\frac{b_1^2 \sqrt{-\beta _2}}{2 \sqrt{6} \sqrt{\alpha _4}},\; \alpha _1 = \frac{-\frac{\sqrt{6} \sqrt{\alpha _4} \beta _1 \left(k^2-d_2\right)}{\sqrt{-\beta _2}}+\alpha _4 \left(-10 d_2 k^2+9 d_2^2-3 k^4\right)-\sigma ^2+w}{k},\\&& d_2 = \frac{-\alpha _2 \sqrt{\beta _2}-\sqrt{6} \sqrt{-\alpha _4} \beta _1-6 \alpha _4 \sqrt{\beta _2} k^2}{10 \alpha _4 \sqrt{\beta _2}},\; d_1 = 0. \end{eqnarray}$

Then, we obtain the following stochastic singular soliton and singular periodic solutions for Eq (1.1).

$\begin{eqnarray} && H(x,t) = \sqrt[4]{6} \sqrt{\frac{\alpha _2 \sqrt{\beta _2}+\sqrt{6} \sqrt{-\alpha _4} \beta _1-6 \alpha _4 \sqrt{\beta _2} k^2}{5 \sqrt{-\alpha _4} \beta _2}} \text{csch}\left(\frac{\sqrt{\frac{\alpha _2 \sqrt{\beta _2}+\sqrt{6} \sqrt{-\alpha _4} \beta _1-6 \alpha _4 \sqrt{\beta _2} k^2}{\alpha _4 \sqrt{\beta _2}}} (x-\lambda t)}{\sqrt{10}}\right)\\&&\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}, \end{eqnarray}$

(3.15)

$\begin{eqnarray} && H(x,t) = \sqrt[4]{6} \sqrt{\frac{-\alpha _2 \sqrt{\beta _2}-\sqrt{6} \sqrt{-\alpha _4} \beta _1-6 \alpha _4 \sqrt{\beta _2} k^2}{5 \sqrt{-\alpha _4} \beta _2}} \csc \left(\frac{\sqrt{-\frac{-\alpha _2 \sqrt{\beta _2}-\sqrt{6} \sqrt{-\alpha _4} \beta _1-6 \alpha _4 \sqrt{\beta _2} k^2}{\alpha _4 \sqrt{\beta _2}}} (x-\lambda t)}{\sqrt{10}}\right)\\&&\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}. \end{eqnarray}$

(3.16)

Result (2)

$\begin{eqnarray} && a_1 = 0,\; d_2 = \frac{a_0 d_1}{b_1},\; \alpha _1 = \frac{2 a_0^2 b_1^2 \beta _2 k^3}{d_1^2}-\frac{2 a_0 b_1 k \left(5 a_0^2 \beta _2+3 \beta _1\right)}{3 d_1}-\frac{a_0^4 \beta _2+a_0^2 \beta _1+\sigma ^2-w}{k},\\&& \alpha _2 = \frac{2 a_0 b_1 \left(6 a_0 b_1 \beta _2 k^2-5 a_0^2 \beta _2 d_1-3 \beta _1 d_1\right)}{3 d_1^2},\; d_1 = \frac{\sqrt{2} a_0 b_1 \sqrt{-\beta _2}}{\sqrt{3 \alpha _4}},\; d_0 = \frac{d_1^2}{4d_2}. \end{eqnarray}$

Then, we obtain the next stochastic exponential solution for (1.1).

$\begin{eqnarray} && H(x,t) = a_0 \left(1-\frac{2 b_1}{b_1-2 a_0 e^{\sqrt[4]{\frac{2}{3}} a_0 \sqrt{\frac{\sqrt{-\beta _2}}{\sqrt{\alpha _4}}} (x-\lambda t)}}\right)\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}. \end{eqnarray}$

(3.17)

Case 5. $d_2 = d_4 = 0$

Result (1)

$\begin{eqnarray} && a_1 = 0,\; d_0 = \frac{b_1^2 \sqrt{-\beta _2}}{2 \sqrt{6} \sqrt{\alpha _4}},\; d_1 = \frac{\sqrt{\frac{2}{3}} a_0 b_1 \sqrt{-\beta _2}}{\sqrt{\alpha _4}},\; d_3 = -\frac{2 \sqrt{\frac{2}{3}} a_0^3 \sqrt{-\beta _2}}{\sqrt{\alpha _4} b_1},\; a_0 = \frac{\sqrt{-\frac{6 \beta _1+\frac{\sqrt{6} \sqrt{-\beta _2} \left(6 \alpha _4 k^2-\alpha _2\right)}{\sqrt{\alpha _4}}}{\beta _2}}}{\sqrt{30}},\\&&\alpha _1 = \frac{-11 a_0^4 \beta _2+a_0^2 \left(5 \sqrt{6} \sqrt{-\alpha _4} \sqrt{\beta _2} k^2-3 \beta _1\right)-\sigma ^2+w}{k}-3 \alpha _4 k^3-\frac{\sqrt{6} \sqrt{\alpha _4} \beta _1 k}{\sqrt{-\beta _2}}. \end{eqnarray}$

Then, we obtain the next stochastic Weierstrass elliptic solution for (1.1).

$\begin{eqnarray} && H(x,t) = \Bigg\{\frac{b_1}{\wp \left(\frac{(x-t \lambda ) \sqrt{-\frac{\left(-\frac{\frac{\sqrt{6} \sqrt{-\beta _2} \left(6 k^2 \alpha _4-\alpha _2\right)}{\sqrt{\alpha _4}}+6 \beta _1}{\beta _2}\right){}^{3/2} \sqrt{-\beta _2}}{b_1 \sqrt{\alpha _4}}}}{6\ 5^{3/4}};g_2,g_3\right)}+\frac{\sqrt{-\frac{6 \beta _1+\frac{\sqrt{6} \sqrt{-\beta _2} \left(6 \alpha _4 k^2-\alpha _2\right)}{\sqrt{\alpha _4}}}{\beta _2}}}{\sqrt{30}}\Bigg\}\\&&\times e^{i(w t-k x-\sigma^2t+\sigma B(t))}, \end{eqnarray}$

(3.18)

where $g_2 = -4d_1/d_3$ and $g_3 = -4d_0/d_3$ .

4. Influence of the noise on the extracted solutions

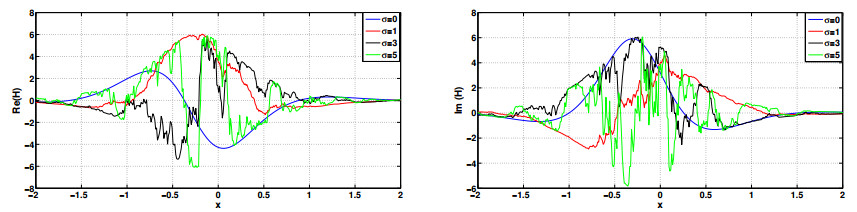
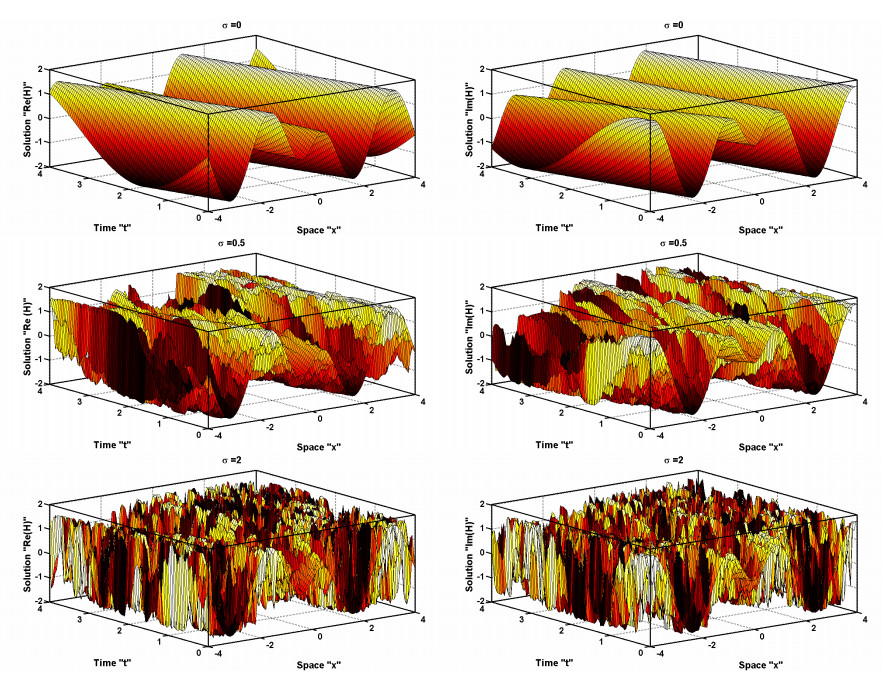
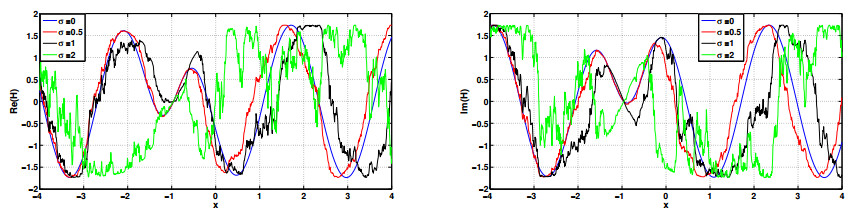
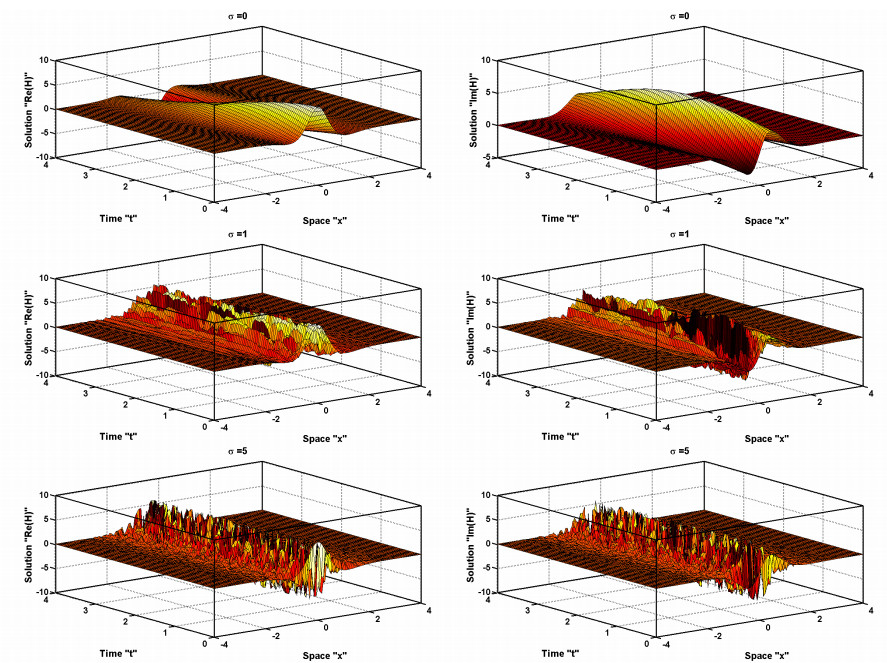
In this section, we investigate the effect of the multiplicative noise on the derived solutions. 2D and 3D simulations using different values for $\sigma$ are presented using Matlab packages. In , 3D graphical illustrations of Eq (3.6) are introduced with $\alpha _4 = -0.13, \; \alpha _2 = 2, \; \beta _2 = 0.055, \; \beta _1 = -2, \; k = -2, \; \lambda = -0.095, \; w = 1$ . In , 2D graphical illustrations of Eq (3.6) is presented using different noise intensities. In , 3D graphical illustrations of Eq (3.8) are provided with $\alpha _4 = 0.49, \; \alpha _2 = -2, \; \beta _2 = -2, \; \beta _1 = -2, \; k = -2, \; \lambda = -0.63, \; w = 1$ . In Figure 4, 2D graphical illustrations of Eq (3.8) is presented using different noise intensities. It is observed that as the noise intensity increases, the extracted wave begins to degrade. From –, we also observed that the higher level wave is more robust to noise than the lower level wave. One can notice that the propagated wave of Eq (3.6) is fully distorted when $\sigma = 5$ as shown in and while the propagated wave of Eq (3.8) is fully distorted when $\sigma = 2$ as shown in Figures 3 and 4. The signal level of the obtained solutions can be controlled to be robust against the noise by adjusting coefficients of the fourth order dispersion, group velocity dispersion, self phase modulation and the quantic nonlinearity.

Figure 1. 3D graphs of solution

$H(x, t)$ of Eq (3.6).

DownLoad: Full-Size Img PowerPoint

Figure 2. 2D graphs of solution

$H(x, t)$ of Eq (3.6).

DownLoad: Full-Size Img PowerPoint

Figure 3. 3D graphs of solution

$H(x, t)$ of Eq (3.8).

DownLoad: Full-Size Img PowerPoint

Figure 4. 2D graphs of solution

$H(x, t)$ of Eq (3.8).

DownLoad: Full-Size Img PowerPoint

5. Conclusions

In this work, The improved modified extended tanh function method is implemented successfully to investigate stochastic forth order NLSE with quantic nonlinearity and affected by multiplicative noise. Many exact optical solutions are extracted in terms of hyperbolic, trigonometric, exponential and Weierstrass elliptic solutions. This stochastic model with fourth-order dispersion and quantic nonlinearity has not been studied before. Therefore, all of these extracted solutions are new. These solutions are crucial in understanding some complex physical phenomena. The extracted solutions will be useful in future studies like coastal water motions, industrial studies, quasi particle theory, optical fiber and space plasma applications. Matlab packages are used to simulate the effect of the multiplicative noise on the derived solutions.

Acknowledgments

The researchers would like to thank the Deanship of Scientific Research, Qassim University, for funding the publication of this project.

Conflict of interest

The authors declare no conflict of interest.

References

[1]	I. Samir, N. Badra, H. M. Ahmed, A. H. Arnous, A. S. Ghanem, Solitary wave solutions and other solutions for Gilson-Pickering equation by using the modified extended mapping method, Results Phys., 36 (2022), 105427. https://doi.org/10.1016/j.rinp.2022.105427 doi: 10.1016/j.rinp.2022.105427
[2]	I. Samir, N. Badra, A. R. Seadawy, H. M. Ahmed, A. H. Arnous, Computational extracting solutions for the perturbed Gerdjikov-Ivanov equation by using improved modified extended analytical approach, J. Geom. Phys., 176 (2022), 104514. https://doi.org/10.1016/j.geomphys.2022.104514 doi: 10.1016/j.geomphys.2022.104514
[3]	A. R. Alharbi, Traveling-wave and numerical solutions to a Novikov-Veselov system via the modified mathematical methods, AIMS Math., 8 (2023), 1230–1250. https://doi.org/10.3934/math.2023062 doi: 10.3934/math.2023062
[4]	M. Sharaf, E. El-Shewy, M. Zahran, Fractional anisotropic diffusion equation in cylindrical brush model, J. Taibah Univ. Sci., 14 (2020), 1416–1420. https://doi.org/10.1080/16583655.2020.1824743 doi: 10.1080/16583655.2020.1824743
[5]	I. Samir, N. Badra, H. M. Ahmed, A. H. Arnous, Solitary wave solutions for generalized Boiti-Leon-Manna-Pempinelli equation by using improved simple equation method, Int. J. Appl. Comput. Math., 8 (2022), 1–12. https://doi.org/10.1007/s40819-022-01308-2 doi: 10.1007/s40819-022-01308-2
[6]	H. Abdelwahed, Nonlinearity contributions on critical MKP equation, J. Taibah Univ. Sci., 14 (2020), 777–782. https://doi.org/10.1080/16583655.2020.1774136 doi: 10.1080/16583655.2020.1774136
[7]	I. Samir, N. Badra, H. M. Ahmed, A. H. Arnous, Solitons in birefringent fibers for CGL equation with Hamiltonian perturbations and Kerr law nonlinearity using modified extended direct algebraic method, Commun. Nonlinear Sci., 102 (2021), 105945. https://doi.org/10.1016/j.cnsns.2021.105945 doi: 10.1016/j.cnsns.2021.105945
[8]	T. A. Nofal, I. Samir, N. Badra, A. Darwish, H. M. Ahmed, A. H. Arnous, Constructing new solitary wave solutions to the strain wave model in micro-structured solids, Alex. Engin. J., 61 (2022), 11879–11888. https://doi.org/10.1016/j.aej.2022.05.050 doi: 10.1016/j.aej.2022.05.050
[9]	I. Samir, N. Badra, A. R. Seadawy, H. M. Ahmed, A. H. Arnous, Exact wave solutions of the fourth order non-linear partial differential equation of optical fiber pulses by using different methods, Optik, 2021, 166313. https://doi.org/10.1016/j.ijleo.2021.166313
[10]	H. X. Jia, D. W. Zuo, X. H. Li, X. S. Xiang, Breather, soliton and rogue wave of a two-component derivative nonlinear Schrödinger equation, Phys. Lett. A, 405 (2021), 127426. https://doi.org/10.1016/j.physleta.2021.127426 doi: 10.1016/j.physleta.2021.127426
[11]	M. A. Abdelrahman, S. Hassan, M. Inc, The coupled nonlinear Schrödinger-type equations, Mod. Phys. Lett. B, 34 (2020), 2050078. https://doi.org/10.1142/S0217984920500785 doi: 10.1142/S0217984920500785
[12]	A. R. Alharbi, A study of traveling wave structures and numerical investigation of two-dimensional Riemann problems with their stability and accuracy, CMES-Comp. Model. Eng., 134 (2023), 2193–2209. https://doi.org/10.32604/cmes.2022.018445 doi: 10.32604/cmes.2022.018445
[13]	S. Frassu, T. Li, G. Viglialoro, Improvements and generalizations of results concerning attraction-repulsion chemotaxis models, Math. Method. Appl. Sci., 45 (2022), 11067–11078. https://doi.org/10.1002/mma.8437 doi: 10.1002/mma.8437
[14]	K. L. Geng, D. S. Mou, C. Q. Dai, Nondegenerate solitons of 2-coupled mixed derivative nonlinear Schrödinger equations, Nonlinear Dyn., 111 (2023), 603–617. https://doi.org/10.1007/s11071-022-07833-5 doi: 10.1007/s11071-022-07833-5
[15]	W. B. Bo, R. R. Wang, Y. Fang, Y. Y. Wang, C. Q. Dai, Prediction and dynamical evolution of multipole soliton families in fractional Schrödinger equation with the PT-symmetric potential and saturable nonlinearity, Nonlinear Dyn., 111 (2023), 1577–1588. https://doi.org/10.1007/s11071-022-07884-8 doi: 10.1007/s11071-022-07884-8
[16]	M. Blencowe, Quantum electromechanical systems, Phys. Rep., 395 (2004), 159–222. https://doi.org/10.1016/j.physrep.2003.12.005 doi: 10.1016/j.physrep.2003.12.005
[17]	P. Kelley, Self-focusing of optical beams, Phys. Rev. Lett., 15 (1965), 1005. https://doi.org/10.1103/PhysRevLett.15.1005 doi: 10.1103/PhysRevLett.15.1005
[18]	H. Chu, Eigen energies and eigen states of conduction electrons in pure bismuth under size and magnetic field quantizations, J. Phys. Chem. Solids, 50 (1989), 319–324. https://doi.org/10.1016/0022-3697(89)90494-0 doi: 10.1016/0022-3697(89)90494-0
[19]	N. Ashcroft, N. Mermin, Solid state physics, New York, Cengage Learning, 1976.
[20]	G. Falkovich, I. Kolokolov, V. Lebedev, S. Turitsyn, Statistics of soliton-bearing systems with additive noise, Phys. Rev. E, 63 (2001), 025601. https://doi.org/10.1103/PhysRevE.63.025601 doi: 10.1103/PhysRevE.63.025601
[21]	A. Debussche, C. Odasso, Ergodicity for a weakly damped stochastic non-linear Schrödinger equation, J. Evol. Equ., 5 (2005), 317–356. https://doi.org/10.1007/s00028-005-0195-x doi: 10.1007/s00028-005-0195-x
[22]	M. A. Abdelrahman, W. W. Mohammed, The impact of multiplicative noise on the solution of the chiral nonlinear Schrödinger equation, Phys. Scripta, 95 (2020), 085222. https://doi.org/10.1088/1402-4896/aba3ac doi: 10.1088/1402-4896/aba3ac
[23]	S. Albosaily, W. W. Mohammed, M. A. Aiyashi, M. A. Abdelrahman, Exact solutions of the (2+1)-dimensional stochastic chiral nonlinear Schrödinger equation, Symmetry, 12 (2020), 1874. https://doi.org/10.3390/sym12111874 doi: 10.3390/sym12111874
[24]	K. Cheung, R. Mosincat, Stochastic nonlinear Schrödinger equations on tori, Stoch. Partial Differ., 7 (2019), 169–208. https://doi.org/10.1007/s40072-018-0125-x doi: 10.1007/s40072-018-0125-x
[25]	A. Debussche, L. D. Menza, Numerical simulation of focusing stochastic nonlinear Schrödinger equations, Physica D, 162 (2002), 131–154. https://doi.org/10.1016/S0167-2789(01)00379-7 doi: 10.1016/S0167-2789(01)00379-7
[26]	J. Cui, J. Hong, Z. Liu, W. Zhou, Strong convergence rate of splitting schemes for stochastic nonlinear Schrödinger equations, J. Differ. Equ., 266 (2019), 5625–5663. https://doi.org/10.1016/j.jde.2018.10.034 doi: 10.1016/j.jde.2018.10.034
[27]	J. Cui, J. Hong, Z. Liu, Strong convergence rate of finite difference approximations for stochastic cubic Schrödinger equations, J. Differ. Equ., 263 (2017), 3687–3713. https://doi.org/10.1016/j.jde.2017.05.002 doi: 10.1016/j.jde.2017.05.002
[28]	Y. Fang, G. Z. Wu, X. K. Wen, Y. Y. Wang, C. Q. Dai, Predicting certain vector optical solitons via the conservation-law deep-learning method, Opt. Laser Technol., 155 (2022), 108428. https://doi.org/10.1016/j.optlastec.2022.108428 doi: 10.1016/j.optlastec.2022.108428
[29]	I. Samir, A. Abd-Elmonem, H. M. Ahmed, General solitons for eighth-order dispersive nonlinear Schrödinger equation with ninth-power law nonlinearity using improved modified extended tanh method, Opt. Quant. Electron., 55 (2023), 470. https://doi.org/10.1007/s11082-023-04753-5 doi: 10.1007/s11082-023-04753-5
[30]	R. R. Wang, Y. Y. Wang, C. Q. Dai, Influence of higher-order nonlinear effects on optical solitons of the complex Swift-Hohenberg model in the mode-locked fiber laser, Opt. Laser Technol., 152 (2022), 108103. https://doi.org/10.1016/j.optlastec.2022.108103 doi: 10.1016/j.optlastec.2022.108103
[31]	J. J. Fang, D. S. Mou, H. C. Zhang, Y. Y. Wang, Discrete fractional soliton dynamics of the fractional Ablowitz-Ladik model, Optik, 228 (2021), 166186. https://doi.org/10.1016/j.ijleo.2020.166186 doi: 10.1016/j.ijleo.2020.166186
[32]	Y. F. Alharbi, E. K. El-Shewy, M. A. Abdelrahman, Effects of Brownian noise strength on new chiral solitary structures, J. Low Freq. Noise V. A., 2022.
[33]	Y. F. Alharbi, E. El-Shewy, M. A. Abdelrahman, New and effective solitary applications in Schrödinger equation via Brownian motion process with physical coefficients of fiber optics, AIMS Math., 8 (2023), 4126–4140. https://doi.org/10.3934/math.2023205 doi: 10.3934/math.2023205
[34]	Z. Yang, B. Y. Hon, An improved modified extended tanh-function method, Z. Naturforsch. A, 61 (2006), 103–115. https://doi.org/10.1515/zna-2006-3-401 doi: 10.1515/zna-2006-3-401

This article has been cited by:

1.	Selvi Altun Durmus, Optical soliton solutions of stochastic the third-order nonlinear Schrödinger equation with multiplicative white noise via Itô calculus, 2024, 56, 1572-817X, 10.1007/s11082-024-06413-8
2.	Islam Samir, Karim K. Ahmed, Hamdy M. Ahmed, Homan Emadifar, Wafaa B. Rabie, Extraction of newly soliton wave structure of generalized stochastic NLSE with standard Brownian motion, quintuple power law of nonlinearity and nonlinear chromatic dispersion, 2024, 21, 26660326, 100232, 10.1016/j.physo.2024.100232

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1415) PDF downloads(74) Cited by(2)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(4)

AIMS Mathematics

Investigating stochastic solutions for fourth order dispersive NLSE with quantic nonlinearity

Related Papers:

Abstract

1. Introduction

2. Revisitation of the technique

3. Results

4. Influence of the noise on the extracted solutions

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Investigating stochastic solutions for fourth order dispersive NLSE with quantic nonlinearity

Related Papers:

Abstract

1. Introduction

2. Revisitation of the technique

3. Results

4. Influence of the noise on the extracted solutions

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog