Existence and asymptotic properties of global solution for hybrid neutral stochastic differential delay equations with colored noise

1.   Introduction

Numerous stochastic dynamical systems demonstrate dependencies on both current and previous states, while also integrating delayed derivatives. In order to more accurately describe and simulate such systems, neutral stochastic differential equations are commonly employed ^[1]. In practical applications, the time delay effect is a critical factor in characterizing the dynamical behavior of systems ^[2]. For instance, synaptic signal transmission in biological neural networks involves axonal conduction delay. At the same time, communication delay in industrial networked control systems also requires modeling through a delay term ^[3], such as $W(\Phi(t-\delta))$. Neutral stochastic differential delay equations (NSDDEs) with Markov switching constitute a significant class of hybrid dynamical systems ^[4]. Due to their ability to exhibit complex dynamical behavior, hybrid NSDDEs are widely applied in various fields, such as being used to simulate the signal transmission and inter-neuron interactions of neural networks in biomedicine, and for designing control systems to achieve precise control of complex systems in engineering. In recent years, the stability of hybrid NSDDEs has received much attention. There have been a number of achievements on the issue of hybrid NSDDEs ^[5].

In real-world scenarios, many dynamical systems are usually subjected to random abrupt changes caused by different kinds of environmental noise ^[6]. Typically, dynamical systems with white noise perturbations are modeled by It$\hat{\text{o}}$ stochastic differential equations (SDEs) ^[7]. Research on the stability analysis of SDEs has been abundant up to now ^[8,9]. However, sensor noise in engineering applications is usually time-correlated, and white noise models cannot accurately capture this characteristic. Moreover, the noise intensity is often related to the system state, such as the power of thermal noise in circuits varying with temperature. Therefore, introducing colored noise can better describe the spectral characteristics of real-world noise. As a result, dynamical systems with colored noise are typically described using SDEs where the noise has finite second-order moments. Such models can better capture the non-linearities and correlations that exist in many natural systems, thus enhancing the understanding and explanation of the behavior for various systems. Lately, the noise-to-state stability (NSS) of hybrid SDEs with colored noise was studied in ^[10], and the NSS of stochastic impulse-delayed systems with multiple random impulses was discussed in ^[11].

Currently, The majority of stability criteria apply only to stochastic systems where the coefficients meet the linear growth condition (LGC). Currently, The majority of stability criteria apply only to stochastic systems where the coefficients meet the linear growth condition (LGC). However, the nonlinear dynamic behaviors in real-world systems ^[12], such as the Duffing equation in mechanical vibrations or the nonlinear rate equations in chemical reaction networks, require model coefficients to satisfy polynomial growth conditions (PGC) ^[13], rather than the traditional LGC. As research has advanced, researchers have increasingly focused on the stability of highly nonlinear SDEs as research has progressed ^[14,15]. For example, the stability of hybrid variable multiple-delay SDEs, which are highly nonlinear, was considered in ^[16], and the stability of hybrid NSDDEs under PGC has been addressed in ^[17]. As we all know, these stability criteria can generally be divided into delay-independent stability (DIS) and delay-dependent stability (DDS) ^[18]. The DDS criterion contains information about time delay, considering the size of time delay, and is therefore generally less conservative than the DIS criterion, which is suitable for time delay of any size ^[19]. There are many theoretical results about DDS for SDEs ^[20,21]. Recently, the DDS of highly nonlinear hybrid NSDDEs was studied in ^[22], while the DDS criterion for hybrid NSDDEs was derived using Lyapunov functionals in ^[23].

In fields such as engineering control, biological neural networks, and environmental science, neutral stochastic differential systems are often subject to the coupled influence of multiple factors, including time delay effect, colored noise, high nonlinearity, and Markov switching mechanisms. This complexity imposes higher demands on model construction. However, existing models are largely constrained by linear growth conditions and white noise assumptions, neglecting the dynamic interplay among time delay, noise, and switching behaviors, which results in insufficient accuracy in modeling real systems. Therefore, there is an urgent practical need to develop neutral stochastic differential delay models that integrate high nonlinearity, colored noise, and Markov switching.

To better explain our purpose, consider the voltage regulation problem in power systems, where the dynamical behavior is affected by equipment failures (Markov switching) and environmental vibrations (colored noise). The system dynamics can be modeled as hybrid NSDDEs with colored noise, as follows:

where $W(\Phi(t-\delta)) = 0.1\Phi(t-\delta)$, $\pi(t)$ is a Markov chain taking values from the set $\mathcal{S}$ = $\left\{1, 2\right\}$, with $\pi(t) = 1$ representing the normal mode and $\pi(t) = 2$ representing the failure mode, and its generator matrix given by $\Gamma = \left[-3, 3; 1, -1\right]$. We generate $\xi(t)\in \mathcal{R}$ using the formula $\xi(t) = 0.5\text{cos}(2t+\varpi)$, where $\varpi$ is a uniformly distributed random variable in the interval $\left[0, 2\pi\right]$ and $\mathbb{E} \xi(t)^2\leq 0.125.$ We define

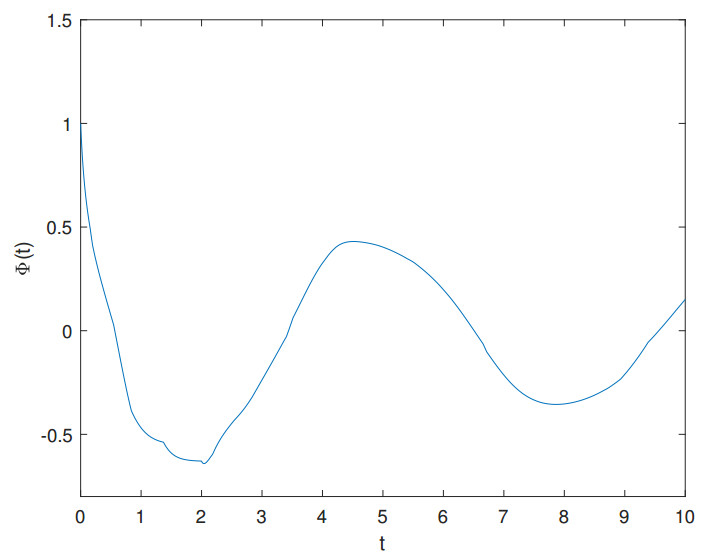
If $\delta$ takes a value of 0.015, it can be observed from Figure 1 that the highly nonlinear hybrid NSDDEs (1.1) are asymptotically stable. In contrast, if $\delta$ is set to 2, Figure 2 shows that the same highly nonlinear hybrid NSDDEs (1.1) become unstable. Put differently, the size of time delay affects the stability of system (1.1). However, for the highly nonlinear hybrid NSDDEs with colored noise, there are few DDS criteria that can be utilized to obtain a sufficient bound on the time delay $\delta$ and ensure the stability of its solution. Therefore, the focus of this paper is on exploring a class of highly nonlinear hybrid NSDDEs with colored noise and establishing applicable DDS criteria.

The primary contributions are summarized as follows: (1) Colored noise is introduced in hybrid NSDDEs, and the coefficients of hybrid NSDDEs are highly nonlinear. (2) The existence of a global solution for highly nonlinear hybrid NSDDEs with colored noise is proved under PGC. (3) The Lyapunov functional considered in this paper involves time delay, which makes our stability criteria delay-dependent and thus less conservative.

Notations: If $\Phi\in \mathcal{R}^{n}$, $\vert \Phi\vert$ represents its Euclidean norm. The set of continuous functions $\varrho:[-\delta, 0]\rightarrow \mathcal{R}^{n}$ is denoted by $C\left([-\delta, 0]; \mathcal{R}^{n}\right)$ for $\delta > 0$, with its norm defined as $\Vert\varrho\Vert = \text{sup}_{-\delta\leq u\leq 0}\vert\varrho\left(u\right)\vert$. Let $C^{1, 1}(\mathcal{R}^{n}\times \mathcal{S} \times \mathcal{R}_{+}; \mathcal{R}_{+})$ represent the family of all continuous functions $U(\Phi, i, t)$ that are continuously differentiable once with respect to $\Phi$ and $t$, respectively. The family of all quasi-polynomial functions $H(\iota)$ with non-negative continuous coefficients are defined as $\mathcal{H}(\mathcal{R}^n; \mathcal{R}_{+})$, and $H(\iota)$ is expressed as $H(\iota) = a_k\vert \iota\vert^{d_k}+a_{k-1}\vert \iota\vert^{d_{k-1}}+\dots+a_{1}\vert \iota\vert^{d_{1}}$ with $a_i\geq 0$ $(i = 1, 2, \cdots, k)$ and $d_k\geq d_{k-1}\geq\cdots\geq d_1\geq 1$. A continuous function $\beta\in C(\mathcal{R}_{+}; \mathcal{R}_{+})$ is considered to belong to the set of $\mathcal{K}$-function if it is strictly increasing and $\beta(0) = 0$. If $\beta(\cdot)$ is also radially unbounded, then it is said to belong to the set of $\mathcal{KR}$-functions. Additionally, a function $\Xi(\Phi, t)\in C(\mathcal{R}_+\times \mathcal{R}_+; \mathcal{R}_+)$ is considered to belong to the set of $\mathcal{KL}$-functions if it is a $\mathcal{K}$-function for every fixed $t$ and decreases to zero for every fixed $\Phi$ as $t\to\infty$.

2.   Model description and preliminaries

Suppose ($\Omega, \mathcal{F}, \left\{\mathcal{F}_{t}\right\}_{t\geq0}, \mathbb{P}$) is a complete probability space, where $\left\{\mathcal{F}_{t}\right\}_{t\geq0}$ is a filtration that satisfies right continuity, and $\mathcal{F}_{0}$ contains all $\mathbb{P}$-null sets. For any $t\geq 0$, let $\pi(t)$ be a right-continuous Markov chain on the complete probability space with state space $\mathcal{S} = \left\{1, 2, \dots, N\right\}$ and generator $\Gamma = [\gamma_{ij}]_{N\times N}$. Here, $\gamma_{ij}\geq 0$ and $\gamma_{ii} = -\sum_{j = 1, j\ne i}^{N}\gamma_{ij}\leq 0$.

Next, we analyze the given highly nonlinear hybrid NSDDE with colored noise

and initial condition

where $\Phi(t)\in \mathcal{R}^n$ denotes the state vector, and $\xi (t)\in \mathcal{R}^{d}$ represents colored noise. The $f\in C\big(\mathcal{R}^{n} \times \mathcal{R}^{n}\times \mathcal{S}\times$$\mathcal{R}_{+}; \mathcal{R}^{n}\big),$ $\sigma \in C\big(\mathcal{R}^{n} \times \mathcal{R}^{n}\times \mathcal{S}$ $\times \mathcal{R}_{+}; \mathcal{R}^{n\times d}\big)$ and $W\in C\left(\mathcal{R}^{n}; \mathcal{R}^{n}\right)$ denote Borel-measurable functions.

In the following, we provide some assumptions for (2.1).

Assumption 2.1. ^[17]. For any $h > 0$ and for all $\tilde{u}, \tilde{v}, \bar u, \bar v\in \mathcal{R}^{n}$, where $\vert \tilde{u}\vert\vee\vert \tilde{u}\vert\vee\vert \bar u\vert\vee\vert \bar v\vert\leq h$, there exists a constant $L_{h} > 0$ such that

with $(i, t)\in \mathcal{S}\times \mathcal{R}_{+}$.

Assumption 2.2. ^[17]. For any $\tilde{u}, \tilde{v}\in \mathcal{R}^{n}$, there are constants $Q > 0, \ \alpha_{1} > 1$ and $\alpha_{2}\geq 1$ satisfying

with $(i, t)\in \mathcal{S}\times \mathcal{R}_{+}$. Furthermore, there also is a constant $\tilde{\omega }\in(0, \frac{\sqrt{2}}{2})$ satisfying

with $W(0) = 0$.

Remark 2.1. Assumptions 2.1 and 2.2 ensure that the coefficients $f$ and $\sigma$ satisfy the local Lipschitz condition and the PGC.

Remark 2.2. Assumption 2.2 in condition (2.5) shows that the function $W$ is globally Lipschitz continuous and satisfies the LGC: $\vert W(\tilde{u})\vert\leq\tilde{\omega}\vert\tilde{u}\vert$.

Assumption 2.3 ^[10]. Given the process $\xi(t)$ is both piecewise continuous and $\mathcal{F}_{t}$-adapted. Furthermore, it satisfies $\sup_{0\leq s\leq t}\mathbb{E}\vert{\xi(t)}\vert^{2} < \infty$.

Remark 2.3. By Assumption 2.3, for any $t\geq 0$, it can be checked that $\xi(t) < \infty$ almost surely (a.s.).

For convenience, we assume that $\alpha_{1} > 1$, although it is sufficient to have only $\text{max}\left\{\alpha_{1}, \alpha_{2}\right\} > 1$. The PGC (2.4) is referred to as Assumption 2.2, and it is well-known that under Assumptions 2.1–2.3, the hybrid NSDDE (2.1) has a unique maximal local solution, but this solution may blow up in finite time. To prevent this phenomenon, some restrictions are given below.

Assumption 2.4. Let $\bar{U}\in C^{1, 1}(\mathcal{R}^{n}\times \mathcal{S}\times \mathcal{R}_{+}; \mathcal{R}_{+})$ and $H\in\mathcal{H}(\mathcal{R}^n, \mathcal{R}_{+})$. $\gamma(\cdot)\in\mathcal{KR}$ and is convex, along with $b_{1}, b_{2}, b_{3} > 0$ and $\alpha\geq 2(\alpha_{1}\vee \alpha_{2})$, such that

and

for any $(\Phi, \nu, i, t)\in \mathcal{R}^{n}\times \mathcal{R}^{n}\times \mathcal{S}\times \mathcal{R}_{+}$.

Remark 2.4. Assumption 2.4 is the key to the presence of a global solution for hybrid NSDDE (2.1) in the nonlinear scenario.

Remark 2.5. Assumption 2.4 is an improvement of Assumption 2.4 in ^[10] since this paper assumes that $W(\cdot)$ satisfies Assumption 2.1. Therefore, Assumption 2.4 is valid in this paper.

Definition 2.1. ^[24]. For $\alpha > 0$, assume that $\Xi\in\mathcal{KL}$ and $\beta\in\mathcal{K}$ exist, satisfying

where $t\in \mathcal{R}_+$ and $\eta\in\mathcal{L}_{\mathcal{F}_0}^{\alpha}(\left[-\delta, 0\right]; \mathcal{R}^n)$. Then hybrid NSDDE (2.1) is said to be NSS in the $\alpha$th moment (NSS-$\alpha$-M). In particular, when $\alpha = 2$, it is commonly referred to as NSS in the mean square.

Lemma 2.1. ^[25]. If Assumption 2.2 is satisfied and there exists a constant $\alpha\geq 1$, then

holds, where $\tilde{u}, \tilde{v}\in \mathcal{R}^{n}$.

3.   Main results

This section presents a sufficient condition for proving the existence of a unique global solution to hybrid NSDDE (2.1). Additionally, it explores the NSS and DDS criteria for global solutions.

3.1.   Noise-to-state stability

Theorem 3.1. Assuming that Assumptions 2.1–2.4 are satisfied, we can make the following assertions for hybrid NSDDE (2.1).

(ⅰ) Hybrid NSDDE (2.1) has a unique global solution on the interval $\left[-\delta, \infty\right).$

(ⅱ) The global solution satisfies

$\forall t\in \mathcal{R}_{+}$, where $\eta\in\mathcal{L}_{\mathcal{F}_0}^{\alpha}(\left[-\delta, 0\right]; \mathcal{R}^n)$ and $\bar{\lambda} > 0$ is the only solution of

where $d_k = \text{deg}(H(x))$.

(ⅲ) When $b_1 = 0$ and $\eta\in\mathcal{L}_{\mathcal{F}_0}^{\alpha}(\left[-\delta, 0\right]; \mathcal{R}^n)$, the global solution satisfies

where $t\in \mathcal{R}_+$, $M_{0} = \frac{\sqrt{ \tilde{\omega }}}{1-\sqrt{ \tilde{\omega }}}\mathbb{E}\vert\vert\eta\vert\vert^{\alpha}+\frac{1}{(1-\sqrt{ \tilde{\omega }})(1- \tilde{\omega })^{\alpha-1}}C_{\lambda}H(\vert\vert\eta\vert\vert)$. In other words, the global solution of hybrid NSDDE (2.1) is NSS-$\alpha$-M.

Proof. To better understand the proof process, we can illustrate it in three steps.

Step 1. By relying on Assumptions 2.1–2.3, it can be easily demonstrated that hybrid NSDDEs (2.1) possesses a unique maximal local solution on the interval $\left[-\delta, \varphi_{\infty}\right)$, where $\varphi_{\infty}$ represents the explosion time. We choose an integer ${\bar h}_0 > 0$ that is large enough to ensure $\vert\vert\eta\vert\vert\leq\bar h_0$. We define the stopping time $\phi_{\bar h} = \inf\left\{t\in\left[0, \varphi_{\infty}\right):\vert \Phi(t)\vert\geq \bar h\right\}$ for every integer $\bar h\geq\bar h_0$, where $\inf\emptyset = \infty$. It is an obvious fact that $\phi_{\bar h}$ increases as $\bar h\to\infty$ and $\phi_{\infty} = \lim _{\bar h\to\infty}\phi_{\bar h}\leq\varphi_{\infty}$ a.s. If $\phi_{\infty} = \infty$ a.s., in that case, there is one unique global solution for hybrid NSDDE (2.1) on the interval $\left[-\delta, \varphi_{\infty}\right)$.

We can obtain from (2.6) and (2.7) that

Based on the information about the time delay, one gets

Substituting (3.5) into (3.4) and applying the Jensen inequality, one has

with $M_1 = H((1+ \tilde{\omega })\vert\vert\eta\vert\vert)+b_3\delta H(\vert\vert\eta\vert\vert)$. Combining (2.6) and (3.6), we can deduce

Let us define $\mu_{\bar h} = \inf_{\vert y\vert\geq(1- \tilde{\omega })\bar h, t\geq 0}\vert y\vert^{\alpha}$. In accordance with the definition of $\phi_{\bar{h}}$, for $t\in[-\delta, \phi_{\bar{h}}]$, one has $\vert\Phi(t)\vert\leq\bar{h}$. We observe that

Noting that

we see that

Clearly, one obtains $\lim_{{\bar h}\to\infty}\mu_{\bar h} = \infty$. Letting ${\bar h}\to\infty$, we have $\mathbb{P}\left\{\phi_{\infty}\leq t\right\} = 0$, which in turn leads to $\mathbb{P}\left\{\phi_{\infty} > t\right\} = 1$. As we let $t\to\infty$, we find that $\mathbb{P}\left\{\phi_{\infty} = \infty\right\} = 1$, which means that $\phi_{\infty} = \infty$ a.s. Therefore, we can conclude that assertion (i) holds as required.

Step 2. Since $H\in\mathcal{H}(\mathcal{R}^n; \mathcal{R}_{+})$, we set $H(\iota) = a_k\vert \iota\vert^{d_k}+a_{k-1}\vert \iota\vert^{d_{k-1}}+\dots+a_{1}\vert \iota\vert^{d_{1}}$. Combining Lemma 2.1 and $\tilde{\omega}\in(0, \frac{\sqrt{2}}{2})$, we derive

By using the zero-point theorem and (2.6), it can be concluded that Eq (3.2) has a unique solution $\bar{\lambda} > 0$. For any $\lambda\in\left(0, \bar{\lambda}\wedge \frac{1}{2\delta}\log(\frac{1}{ \tilde{\omega }})\right]$, we get

Since

from (3.2) and (3.7), one has

From the Fatou lemma and (2.6), it follows that (3.8) yields

where $C_{\lambda} = \left[2^{d_k}+e^{\lambda\delta}\delta\left(b_3+\lambda2^{d_k-1}\right)\right]$. It is also evident from (3.9) and Lemma 2.1 that

Thus, we get

Thus,

In particular,

where $M_0 = \frac{\sqrt{ \tilde{\omega }}}{1-\sqrt{ \tilde{\omega }}}\mathbb{E}\vert\vert\eta\vert\vert^{\alpha}+\frac{1}{(1-\sqrt{ \tilde{\omega }})(1- \tilde{\omega })^{\alpha-1}}C_{\lambda}H(\vert\vert\eta\vert\vert)$. Hence, setting $t\to\infty$ yields the following inequality:

showing that assertion (ⅱ) is satisfied.

Step 3. When $b_1 = 0$, (3.10) still holds. Thus, when $b_1 = 0$, there holds

By Definition 2.1, we can easily know that the global solution of hybrid NSDDE (2.1) is NSS-$\alpha$-M. As a result, we can infer that the expected assertion (ⅲ) is valid. □

3.2.   Delay-dependent asymptotic stability

Assumption 3.1. Given that $\zeta(t)$ is both piecewise continuous and $\mathcal{F}_{t}$-adapted, one can conclude the existence of a positive scalar $\mu$ such that $\sup_{t\geq 0}\mathbb{E}\vert \xi(t)\vert^{2} < \mu$.

Remark 3.1. To discuss the asymptotic properties of the global solution for hybrid NSDDE (2.1), a stricter assumption about the colored noise $\xi(t)$, namely Assumption 3.1, is required. It is evident that when Assumption 3.1 holds, Assumption 2.3 also holds. Therefore, under the conditions that Assumptions 2.1, 2.2, 2.4, and 3.1 are satisfied, the conclusions in Theorem 3.1 still hold for hybrid NSDDE (2.1).

Next, for $t\in \mathcal{R}_+$, we define $\bar{ \Phi}_{t} = \left\{ \Phi(t+\zeta):\right.$ $\left.-2\delta\leq \zeta\leq 0\right\}$ and $\bar{ \pi}_{t} = \left\{ \pi(t+\zeta):-2\delta\leq \zeta\leq 0\right\}$. Furthermore, let $\Phi(\zeta) = \eta(-\delta)$ for $\zeta\in [-2\delta, -\delta)$ and $\pi(\zeta) = \pi_{0}$ for $\zeta\in[-2\delta, 0)$. For all $\Phi, \nu\in \mathcal{R}^n$ and $(i, t)\in \mathcal{S}\times[-2\delta, 0)$, let $f(\Phi, \nu, i, \zeta) = f(\Phi, \nu, i, 0)$ as well as $\sigma(\Phi, \nu, i, \zeta) = \sigma(\Phi, \nu, i, 0)$. Define the following delay-dependent Lyapunov functional:

where $U\in C^{1, 1}(\mathcal{R}^{n}\times \mathcal{S}\times \mathcal{R}_{+}; \mathcal{R}_{+})$ satisfies $\lim_{\vert \Phi\vert\rightarrow \infty}[\inf_{(t, i)\in \mathcal{R}_{+}\times \mathcal{S}}U(\Phi, i, t)] = \infty$, $\theta > 0$ is a constant that requires identification, and $F(u) = \delta\vert f(\Phi(u), \Phi(u-\delta), \pi(u), u)\vert^{2}+\mu\delta\vert \sigma(\Phi(u), \Phi(u-\delta), \pi(u), u)\vert^{2}$. Then, we have

where

In order to analyze the DDS of hybrid NSDDE (2.1), additional assumptions are required.

Assumption 3.2. Consider the functions $U\in C^{1, 1}(\mathcal{R}^{n}\times \mathcal{S}\times \mathcal{R}_{+}; \mathcal{R}_{+})$, $U_{1}\in \mathcal{H}(\mathcal{R}^n; \mathcal{R}_+)$, $G\in C(\mathcal{R}^{n}; \mathcal{R}_{+})$, and the constants $\beta_{i} > 0\ (i = 1, 2, 3)$ and $\vartheta_{k} > 0\ (k = 1, 2)$ satisfying

and

for all $(\Phi, \nu, i, t)\in \mathcal{R}^{n}\times \mathcal{R}^{n}\times \mathcal{S}\times \mathcal{R}_{+}$. In addition, $G$ also satisfies the following condition:

Assumption 3.3. Assume there exists a constant $L > 0$ satisfying the following inequality:

where $(\Phi, \bar { \Phi}, i, t)\in \mathcal{R}^{n}\times \mathcal{R}^{n}\times \mathcal{S}\times \mathcal{R}_{+}$.

Remark 3.2. Assumption 3.2 imposes the necessary requirement on the operator $\mathcal{L}$. Assumption 3.3 states that $f$ satisfies the Lipschitz condition.

Theorem 3.2. Under Assumptions 2.1, 2.2, 2.4, and 3.1–3.3, the condition

holds, which implies that the solution to the hybrid NSDDE (2.1) satisfies the following conditions:

Proof. Let $\rho_h = \inf\left\{t\geq 0:\vert \Phi(t)- W(\Phi(t-\delta))\vert\geq h\right\}$. Using the ordinary differential formula, we obtain

Let $\theta = L^{2}/(\vartheta_{1}(1-2 \tilde{\omega }^2))$. From Assumption 3.3, there holds

According to condition (3.17), it is not difficult to get $\theta\delta^2\leq \vartheta_{2}$. Then, combining (3.11), (3.14), and (3.21), we have

Substituting this into (3.20) gives

where

Noting that

it yields from (3.23) that

Bringing this into (3.22) leads to

As we let $h\to\infty$ and apply the Fatou lemma along with the Fubini theorem to (3.24), we derive

where

Considering that $G\in C(\mathcal{R}^n; \mathcal{R}_+)$, we can deduce from (3.25) that

On the one hand, for $t\in[0, \delta]$, one has

On the other hand, for $t > \delta$, we get

Combining (2.1) and (2.5) results in

Hence, together with Assumption 3.1, we obtain

which implies

Noting that $0 < \kappa < \frac{\sqrt{2}}{2}$, then

Hence,

where $K_3 = K_2+\frac{2 \tilde{\omega }^2\delta L^2}{(1-2 \tilde{\omega }^2)\vartheta_{1}}\sup_{-\delta\leq v\leq\delta}\mathbb{E}\vert \Phi(v)\vert^2$. Bringing (3.27) into (3.26) and letting $t\to\infty$, we derive

Applying the Fubini theorem again to (3.27) yields the result (3.18). Letting $h\to\infty$ and combining (3.20), (3.22), and (3.27), we calculate

which indicates

Hence, (3.19) holds. □

Corollary 3.1. Suppose that the conditions of Theorem 3.2 are true and that there exist two constants $d > 0$ and $\hat{\alpha} > 0$, satisfying

for any $\Phi\in \mathcal{R}^n$. Then, we can obtain the solution of the hybrid NSDDE (2.1), satisfying

Namely, hybrid NSDDE (2.1) is $H_{\infty}$-stable in $L^{\hat{\alpha}}$.

Remark 3.3. Theorem 3.1 proves that NSDDE (2.1) possesses NSS-$\alpha$-M. This result describes the asymptotic behavior of system states under the influence of noise and tends to be stable under certain conditions. Theorem 3.2 further establishes the integral boundedness of the function $U_1(\Phi)$, that is,

which demonstrates that the cumulative energy of the system state over time is finite. Corollary 3.1 states that NSDDE (2.1) is $H_{\infty}$-stable in $L^{\hat{\alpha}}$. This is a special case of Theorem 3.2. Specifically, when $d\vert \Phi\vert^{\hat{\alpha}}\leq U_1(\Phi)$, the integral boundedness of $U_{1}(\Phi(t))$ directly implies the integral boundedness of $\vert \Phi\vert^{\hat{\alpha}}$, that is,

thereby ensuring that NSDDE (2.1) is $H_{\infty}$-stable in $L^{\hat{\alpha}}$.

Next, we establish a theorem regarding the asymptotic stability in $L^{\hat{\alpha}}$ for hybrid NSDDE (2.1).

Theorem 3.3. Suppose that the conditions of Corollary 3.1 are true. If ${\hat{\alpha}}\geq2$ and $2({\hat{\alpha}}-1)\vee({\hat{\alpha}}+\alpha_1-1)\vee2({\hat{\alpha}}+\alpha_2-1)\leq \alpha$, then the solution of hybrid NSDDE (2.1) satisfies

Namely, hybrid NSDDE (2.1) is asymptotically stability in $L^{\hat{\alpha}}$.

Proof. Using this inequality $\vert \bar{a}\bar{b}\vert\leq \bar{c}\vert \bar{a}\vert^2+\frac{1}{4\bar{c}}\vert \bar{b}\vert^2$ with any $\bar{a}, \bar{b}\in \mathcal{R} \ \text{and}\ \bar{c} > 0$. For any $0\leq t_1 < t_2 < \infty$, from Assumptions 2.2 and 3.1, there holds

For any $1\leq\bar{p}\leq \alpha$, we get

which further leads to

Therefore, according to Theorem 3.1, it follows that

By applying the inequality

and (3.29), we can get

where

As a consequence, $\mathbb{E}\vert \Phi(t)- W(\Phi(t-\delta))\vert^{\hat{\alpha}}$ is uniformly continuous. Based on (3.29), one has

applying the Barbalat lemma, we have $\lim_{t\to\infty}\mathbb{E}\vert \Phi(t)- W(\Phi(t-\delta))\vert^{\hat{\alpha}} = 0$. Next, applying the following inequality

we derive

Taking $\varepsilon = \frac{ \tilde{\omega }}{1- \tilde{\omega }}$,

Then, letting $t\to\infty$, we obtain

By (3.29), one obtains $\lim_{t\to\infty}\mathbb{E}\vert \Phi(t)\vert^{\hat{\alpha}} = 0$. □

Theorem 3.4. If the conditions of Theorem 3.2 are met and there exist two positive constants $d > 0$ and $\hat{\alpha} > 0$ satisfying

then the solution of hybrid NSDDE (2.1) is almost surely asymptotically stability, i.e., $\lim_{t\to\infty} \Phi(t) = 0$ a.s.

Proof. Combined with (3.18), (3.25), and (3.27), we get

According to Fubini's theorem, we get

which means

Setting $\bar{ \Phi}(t) = \Phi(t)- W(\Phi(t-\delta))$ for $t\geq 0$ and $\rho_h = \inf\left\{t\geq 0:\vert \bar{ \Phi}(t)\vert = h\right\}$, by (3.32),

According to Corollary 3.1, we denote $K_5: = \int_{0}^{\infty}\mathbb{E}\vert \Phi(t)\vert^{\hat{\alpha}}dt < \infty$. Then, the proof follows a similar process to that of Theorem 3.3, and we obtain that

where $K_6 = 2^{{\hat{\alpha}}-1} \tilde{\omega }^{\hat{\alpha}}\delta\vert\vert\eta\vert\vert, \ K_7 = 2^{{\hat{\alpha}}-1}(1+ \tilde{\omega }^{\hat{\alpha}})$. This implies

Letting $T\to\infty$, it follows that

The remainder of the proof will be segmented into three steps. First, we assert that

If Eq (3.35) is not fulfilled, then a sufficiently small constant $\epsilon\in(0, \frac{1}{4})$ can be found which satisfies

where $\Delta_1 = \left\{\lim_{t\to\infty}\sup G(\bar{ \Phi}(t)) > 2\epsilon\right\}$. From (3.34), there exists a sufficiently large constant $l$ with $\mathbb{P}(\rho_l < \infty)\leq\epsilon$, which means that

where $\Delta_2 = \left\{\vert \bar{ \Phi}(t)\vert < l\ \text{for}\ \forall t\geq-\delta\right\}$. From (3.36) and (3.37), we can obtain

For $t\geq-\delta$, let $\varsigma(t) = \bar{ \Phi}(t\wedge\rho_l)$. It is clear that $\varsigma(t)$ is bounded and

where

For $0\leq t < \rho_l$, from (2.5), we can get

which indicates

Therefore, there holds

From Assumption 2.2 and (3.40), it can be seen that $\hat{f}(t)$ and $\hat{ \sigma}(t)$ are bounded processes, and

where all $t\geq 0$ and some $K_8 > 0$. From the definition of $\rho_l$, it is easy to get $\vert\varsigma(t)\vert\leq l$ for any $t\geq-\delta$.

Set the stopping time

Based on (3.33), as well as the definitions of $\Delta_1$ and $\Delta_2$, it follows that

For all $\omega\in\Delta_1\cap\Delta_2$ and $q\geq 1$, there are

We know that $G(\cdot)$ is uniformly continuous in $\bar{S}_l = \left\{ \Phi\in \mathcal{R}^n:\vert \Phi\vert\leq l\right\}$. It is possible to find $\tau = \tau(\epsilon) > 0$ small enough to make

We highlight that, for $\omega\in\Delta_1\cap\Delta_2$, if $\vert\varsigma(\psi_{2q-1}+v)-\varsigma(\psi_{2q-1})\vert < \tau$ for all $v\in[0, \Upsilon ]$ and some $\Upsilon > 0$, then $\psi_{2q}-\psi_{2q-1}\geq\Upsilon$. Accordingly, there exists a small enough constant $\Upsilon > 0$ and a large enough integer $q_0 > 0$ such that

By (3.38) and (3.42), there exists a constant $T$ large enough such that

If $\psi_{2q_0}\leq T$, then $\vert\varsigma(\psi_{2q_0})\vert < l$, and thus $\psi_{2q_0} < \rho_l$. So, for any $0\leq t\leq\psi_{2q_0}$, as well as $\omega\in\left\{\psi_{2q_0}\leq T\right\}$, there holds

Together with Assumption 3.1 and (3.41), for $1\leq q\leq q_0$, we obtain

Based on the Chebyshev inequality and (3.45), there holds

If $\psi_{2q_0}\leq T$, then $\psi_{2q-1}\leq T$, and combining (3.46) and (3.49) yields

Based on (3.44), this implies that

By (3.32), (3.47), and (3.50), we conclude

which conflicts with (3.45). Thus, (3.35) must hold.

The second step involves proving that

If this is false, then $\epsilon_0 = \mathbb{P}(\Delta_3) > 0$, where $\Delta_3 = \left\{\limsup_{t\to\infty}\vert \bar{ \Phi}(t)\vert > 0\right\}$. By (3.34), there exists a large enough integer $m_0 > 0$ such that $\mathbb{P}(\rho_{m_0} < \infty)\leq\frac{1}{2}\epsilon_0$. Let $\Delta_4 = \left\{\rho_{m_0} = \infty\right\}$. Then,

Note that, for any $\omega\in\Delta_3\cap\Delta_4$ and $t\geq 0$, $\bar{ \Phi}(t, \omega)$ is bounded. It is possible to find a sequence $\left\{t_i\right\}_{i\geq 1}$ satisfying $t_i\to\infty$ as well as $\bar{ \Phi}(t_i, \omega)\to \bar{ \Phi}(\omega)\ne0$ as $i\to\infty$. It is worth noting that, since $G$ is continuous, we can obtain

Therefore, for all $\omega\in\Delta_3\cap\Delta_4$,

But, this contradicts (3.35). Thus, we can obtain $\lim_{t\to\infty}\bar{ \Phi}(t) = 0$ a.s. Further, we can get

The third step involves claiming assertion (3.31). It follows from (2.5) that

Then, for any $T > 0$,

Consequently, we have

Making use of (3.51) and allowing $T\to\infty$, we get

Letting $t\to\infty$ in (3.52) and combining $\lim_{t\to\infty}\bar{ \Phi}(t) = 0$ a.s., we have

Since $\tilde{\omega }\in(0, \frac{\sqrt{2}}{2})$, and by (3.53), we obtain

□

Remark 3.4. When the noise considered in hybrid NSDDE (2.1) is white noise, we obtain that Theorems 3.2–3.4 that are consistent with those in ^[17].

Remark 3.5. In contrast to ^[10], in this paper, we develop new mathematical techniques to address the challenges posed by the neutral term, since the presence of the neutral term fundamentally alters the issue.

Remark 3.6. The nonlinear functions considered in ^[24] satisfy the linear growth condition. When $\alpha_1 = \alpha_2 = 1$ in Assumption 2.2, the PGC simplifies to the LGC, and thus the nonlinear functions under consideration throughout the paper are more universal.

4.   Numerical examples

We will validate the correctness of the theoretical results through examples in this section.

Let us examine the highly nonlinear hybrid NSDDE with colored noise (1.1). Based on the coefficients of (1.1), Assumptions 2.1–2.3, and 3.1 hold when $Q = 6$, $\alpha_1 = 3$, $\alpha_2 = 1$, $\tilde{\omega } = 0.1$ and $\mu = 0.15$. Let $\bar{U}(\Phi, t, i) = \vert \Phi\vert^6$. Then, we get

which shows

where $b_1 = 15.2968, \ b_2 = 3.7, \ b_3 = 3.5811, \bar{ \Phi} = \Phi-0.1 \nu, \ H(\Phi) = \Phi^8+ \Phi^6$, and $\gamma(\vert \xi(t)\vert^2)$ $= 0.05\vert \xi(t)\vert^{24}.$ Hence, it can be concluded that Assumption 2.4 is also fulfilled.

Define the function as follows:

By calculating, we get

From (3.12), we get

and

Moreover,

Choosing $\vartheta _{1} = 0.1$ and $\vartheta _{2} = 0.01,$ we have

and

Thus,

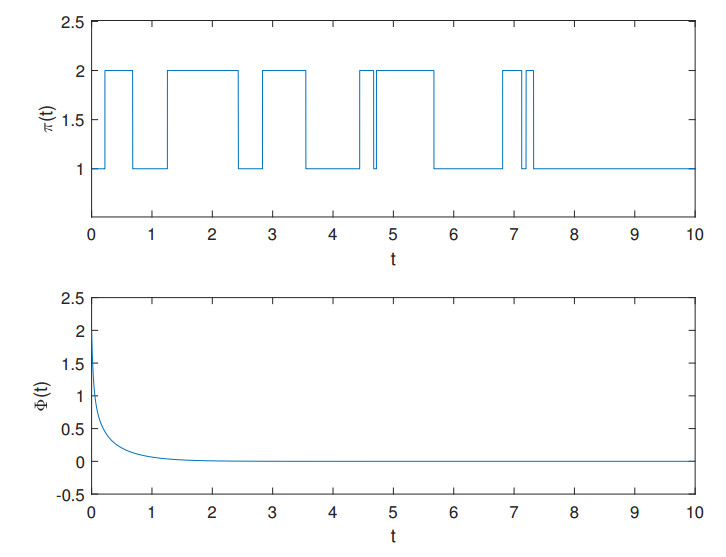
Let $\beta_{1} = 1.905$, $\beta_{2} = 1.0681$, $\beta_{3} = 0.153$, $U_1(\Phi) = \Phi^6+ \Phi^4+ \Phi^2$, and $G(\Phi) = 0.2 \Phi^6$$+0.2 \Phi^4+0.075 \Phi^2.$ It is easy to demonstrate that Assumptions 3.2 and 3.3, along with condition (3.16) when $L = 1.5$, have been satisfied. Thus, by condition (3.17), we have $\delta\leq 0.0209$. Moreover, according to Theorem 3.2, the unique global solution of (1.1) satisfies both (3.18) and (3.19). For $\hat{\alpha}\in[2, 6], \ d = 1$, by Corollary 3.1, we can get (1.1) is $H_{\infty}$-stable in $L^{\hat{\alpha}}$. Since $\alpha_1 = 3, \alpha_2 = 1$, and $\alpha = 6$, for $\hat{\alpha} = 3$, by Theorems 3.3 and 3.4, it follows that the global solution of (1.1) is asymptotically stable in $L^{\hat{\alpha}}$ and almost surely asymptotically stable. We show a computer simulation of (1.1) with $\delta = 0.02$ in Figure 3. It is obvious from Figure 3 that the global solution of (1.1) is stable.

Remark 4.1. Literature ^[24] derived NSS criteria for neutral stochastic delayed nonlinear systems, however the impact of Markov switching was not considered. On the other hand, literature ^[22] investigated the DDS of a class of multi-delay hybrid neutral SDEs, but the influence of colored noise was not addressed. Building upon these studies, this paper incorporates both Markov switching and colored noise to develop a more comprehensive stability analysis framework.

Remark 4.2. Hybrid NSDDEs with colored noise form a class of mathematical tools that can efficiently model complex dynamical systems, and are especially suitable for describing systems with stochastic, nonlinear, time delay, and Markov switching properties. In addition to power systems, hybrid NSDDEs with colored noise have applications in other areas. For example, in robotic arm motion control, hybrid NSDDEs can be used to optimize trajectory tracking performance and improve control accuracy. In finance, they can be used to model the dynamic behavior of stock prices and predict their future trends. By considering these complex factors, hybrid NSDDEs can more accurately portray the dynamic characteristics of real systems and provide strong theoretical support for system analysis and control.

5.   Conclusions

The existence of global solution of highly nonlinear hybrid NSDDEs has been proved under PGC, and the NSS-$\alpha$-M of the global solution has been obtained by inequality techniques. Furthermore, the Lyapunov function method was utilized to construct several innovative DDS criteria for highly nonlinear hybrid NSDDEs, including $H_{\infty}$-stability in $L^{\hat{\alpha}}$, asymptotic stability in $L^{\hat{\alpha}}$, and almost surely asymptotic stability. In future work, we will investigate highly nonlinear hybrid NSDDEs with multiple time delays or L$\acute{\text{e}}$vy noise ^[26], and explore the application of highly nonlinear hybrid NSDDEs to biological models ^[27,28].

Author contributions

Siru Li: Writing-original draft; Tian Xu: Writing-review and editing; Ailong Wu: Supervision, writing-review and editing. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this paper.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant 62476082.

Conflict of interest

The authors declare that there are no conflicts of interest.