Stabilization of nonlinear hybrid stochastic time-delay neural networks with Lévy noise using discrete-time feedback control

1.   Introduction

Neural networks are successful tools for pattern recognition and machine learning, but traditional neural network models tend to ignore stochasticity, which may limit their performance and applicability. Compared to traditional deterministic neural networks, stochastic neural networks (SNNs) have greater robustness, generalization, and the ability to deal with uncertainty and noise, making them more suitable for use in areas such as financial forecasting, image processing, and natural language processing. During the evolution of many real neural networks, signal transmission between neurons inevitably generates time delay. The time delay has an important impact on the stability, oscillatory characteristics, and dynamic response of SNNs. Therefore, it is significant to analyze stochastic time-delay neural networks (STDNNs). There are numerous research results on STDNNs (see, e.g., ^[1,2,3,4,5]).

The classic enforcement condition is that the network coefficients satisfy the linear growth condition. However, in practice, such a restriction is too stringent for many STDNNs. Consequently, numerous scholars have shifted their focus to researching highly nonlinear STDNNs. Recently, the stability criteria for stochastic differential delay equations (SDDEs) driven by G-Brownian motion with highly nonlinear coefficients have been studied in ^[6], the finite-time stabilization criteria for highly nonlinear stochastic coupled systems of networks have been explored in ^[7], and a delayed feedback control function has been designed in ^[8] to stabilize nonlinear hybrid STDNNs with time-varying delays. Nevertheless, the above discriminant rules can only be applied in cases where the time delay of SNNs is constant or a differentiable function. In fact, these conditions may not be natural features of real-world SNNs. For instance, piecewise constant delays or sawtooth delays often appear in either sampled data control or network-based control (see, e.g., ^[9]), and yet these time delays are clearly not differentiable. Technically, it is crucial to ensure that the time delay is not limited to a constant or differentiable function to extend the applicability and expansiveness of dynamic evolution properties.

In many circumstances, neural networks are also subject to abrupt changes in parameters and structure caused by uncontrollable external factors, which can be efficiently modeled using Markov chains. As a result, STDNNs with Markov chains, namely hybrid STDNNs, are widely used to describe more complex dynamic phenomena in networks (see, e.g., ^{[10,11,12,13]}). However, Markov chains are unable to simulate random jumps of network states. In reality, many networks experience random state jumps due to unforeseen events such as earthquakes, storms, and floods. Lévy processes can describe such random jumps well, as these processes have significant tail and peak pulses. There are several related research achievements (see, e.g., ^{[14,15,16,17]}). Lately, the stability of hybrid stochastic delayed Cohen–Grossberg neural networks driven by Lévy noise has been investigated in ^[18], and the stabilization problem for a class of hybrid SDDEs with Lévy noise has been studied in ^[19]. Hence, it is worthwhile to consider Lévy noise in hybrid STDNNs.

It is already known that the stability of SNNs may decrease or eventually turn unstable under time delay, Markov chains, and so on. It is significant to consider how to make unstable SNNs stable. Various control strategies have been advanced to achieve the stabilization of a system. For example, Li and Mao used delayed feedback control to stabilize nonlinear hybrid SDDEs in ^[20]. Li and co-workers proposed feedback control based on discrete-time observations of state and mode to stabilize hybrid SDDEs with non-differential delays in ^[21].

Note that the stabilization problem of highly nonlinear STDNNs has been discussed in ^[8], but does not take into account non-differentiable time delay. The delayed feedback controls used in ^[19,20] have considered the time lag between the time of state observation and when the corresponding control reaches the system. Still, the control functions require continuous-time observations of system state and mode; in contrast, the controller based on discrete-time state and mode observations is easier to implement in practice and relatively less costly. Inspired by the preceding discussion, the primary objective of this paper is to apply discrete-time feedback control for stabilizing nonlinear hybrid STDNNs with Lévy noise, where the time delay is non-differentiable. The major advantages of this paper can be categorized as below:

(1) The coefficients of the considered STDNNs are highly nonlinear, and the time delay is non-differentiable, which makes the results we obtained more general.

(2) The introduction of Markov chains and Lévy noise to nonlinear STDNNs makes theoretical exploration in this paper more challenging. Additionally, the feedback control employed is more practical than continuous-time feedback control because it is based on discrete-time states and mode observations.

(3) This paper develops new stabilization criteria for $H_{\infty}$ stability, asymptotic stability, and exponential stability of global solutions for nonlinear hybrid STDNNs with Lévy noise.

Notations: We denote by $\Re^n$ the $n$-dimensional Euclidean space, $\Re = \left(-\infty, +\infty\right)$, and $\Re_+ = \left[0, +\infty\right)$. For $\Phi\in \Re^n$, we define $\vert \Phi\vert$ as its Euclidean norm. Denote by $B^T$ the transpose of a vector or matrix $B$. With respect to a matrix $B$, $\vert B\vert = \sqrt{\text{trace}(B^TB)}$ denotes its trace norm. If $B$ is a symmetric real matrix, its smallest and largest eigenvalues are expressed by $\lambda_{\min}(B)$ as well as $\lambda_{\max}(B)$, respectively. The family of c$\grave{a}$dl$\grave{a}$g functions $\varrho:[-\theta, 0]\rightarrow \Re^{n}$ are denoted by $D\left([-\theta, 0]; \Re^{n}\right)$ for $\theta > 0$, with its norm defined as $\Vert\varrho\Vert = \text{sup}_{-\theta\leq u\leq 0}\vert\varrho\left(u\right)\vert$. The family of all bounded, $\mathcal{F}_0$-measurable, $D([-\theta, 0]; \Re^n)$-valued random variables is denoted as $D_{\mathcal{F}_0}^b([-\theta, 0]; \Re^n)$. For real numbers $m$ and $n$, $m\vee n = \max\left\{m, n\right\}$ as well as $m\wedge n = \min\left\{m, n\right\}$. Let $B$ be a subset of $\Omega$, and $I_B$ represents its indicator function. Specifically, $I_B(\nu) = 1$ if $\nu\in B$ and $0$ else. Suppose that $W(t) = (W_1(t), \cdots, W_m(t))$ is an $m$-dimensional Brownian motion defined in the complete probability space $(\Omega, \mathcal{F}, \left\{\mathcal{F}_{t}\right\}_{t\geq0}, \mathbb{P})$ whose associated filtration $\left\{\mathcal{F}_{t}\right\}_{t\geq0}$ satisfies the usual conditions. The Poisson random measure $N(dt, d\tau)$ is formed on $\Re_+\times Y$, where $Y = \Re^n-\left\{0\right\}$. The compensated Poisson random measure, denoted as $\tilde{N}(dt, d\tau) = N(dt, d\tau)-\vartheta(d\tau)dt$, is introduced, with $\vartheta$ being a Lévy measure that satisfies

In general, this pair $(W, N)$ is known as Lévy noise.

Remark 1.1. (2.1) describes the properties of Lévy measure $\vartheta$ for noise, ensuring that the noise exhibits appropriate heavy-tailed behavior. Specifically, the term $1\wedge\vert\tau\vert^2$ is used to regulate the noise tail, avoiding the excessive effects of tremendous noise values on the system. In physical systems, this type of noise is often used to describe phenomena with long memory or long-range dependence. In biological systems, noise sources that satisfy (2.1) are utilized to model processes with significant stochasticity.

2.   Model description and preliminaries

Let ${\pi(t), t\geq 0}$ be a right-continuous Markov chain on the probability space with state space $\mathcal{S} = \left\{1, 2, \dots, N\right\}$ and generator $\Gamma = [\gamma_{ij}]_{N\times N}$, where $\gamma_{ij}\geq 0$ and $\gamma _{ii} = -\sum_{j = 1, j\ne i}^{N}\gamma_{ij}\leq 0$. Furthermore, we assume that $\pi(\cdot), W(\cdot), \tilde{N}(\cdot, \cdot)$ are mutually independent. Generally speaking, the nonlinear hybrid STDNNs subject to Lévy noise have the following form:

where

and for any $1\leq i, j\leq n$, $a_i(\pi(t)) > 0$ and $b_{ij}(\pi(t))$ are real values. $\iota(t^-) = \lim_{u\to t}\iota(u)$, $f\in C\left(\Re^{n} \times \Re^{n}\times \mathcal{S}\times \Re_{+}; \Re^{n}\right)$, $h\in C\left(\Re^{n} \times \Re^{n}\times \mathcal{S}\times \Re_{+}; \Re^{n\times m}\right)$, $g\in C\left(\Re^{n} \times \Re^{n}\right.$ $\left.\times \mathcal{S}\times \Re_{+}\times Y; \Re^{n}\right)$, $G\in C\left(\Re^{n} \times \Re^{n}\times \mathcal{S}\times \Re_{+}\times Y; \Re^{n}\right)$. The constant $e\in (0, \infty)$ lets us clarify the meaning of 'large' and 'small' jumps in concrete applications. Additionally, $\theta_t$ is a time-varying function. Notice that the last integral term in (2.2) represents a compound Poisson process, which can be easily managed by employing techniques such as the interlacing method (see, e.g., ^[22]). Therefore, it is meaningful to focus on equations driven by continuous noise interspersed with small jumps by omitting the large jump term. Consequently, this study will focus on the reduced STDNNs with small jumps in the form

with initial condition

where $\iota(t^-) = \lim_{u\to t}\iota(u)$. Next, we will describe the required assumptions and lemmas.

Assumption 2.1. The time-varying delay $\theta_t$ is a Borel measurable function from $\Re_+$ to $[\theta_1, \theta]$ with the following properties

where $\theta_1$ and $\theta$ are constants with $0\leq\theta_1 < \theta, M_{u, \Delta} = \left\{t\in \Re^+:t-\theta_t\in[u, u+\Delta)\right\}$ as well as $\mu(\cdot)$ represents the Lebesgue measure on $\Re_+$.

Remark 2.1. It is important to note that Assumption 2.1 is indeed weaker than the condition that the time-varying delay $\theta_t$ is differentiable and its derivative is bounded by a positive constant less than 1. Furthermore, many time-varying delay functions actually satisfy Assumption 2.1. For instance, assume that $\theta_t$ is satisfying the Lipschitz condition, namely,

where $\theta_2\in\left(0, 1\right)$. For any $u\geq -\theta$, let $s = \inf\left\{t\in M_{u, \Delta}\right\}$. It is clear that $s\in M_{u, \Delta}$, that is, $u\leq s-\theta_s < u+\Delta$. If $t\geq s+\frac{\Delta}{1-\theta_2}$, then

Consequently, $t-\theta_t\leq u+\Delta$, namely, $t\notin M_{u, \Delta}$. Put differently, we have $M_{u, \Delta}\subset\left[s, s+\frac{\Delta}{1-\theta_2}\right)$, which implies $\frac{\mu(M_{u, \Delta})}{\Delta} \leq\frac{1}{1-\theta_2}$. Since this holds for any $u\geq -\theta$ and $\Delta\in\left(0, 1\right)$, Assumption 2.1 must hold with $\bar{\theta} = \frac{1}{1-\theta_2}$. This suggests, in particular, that many sawtooth delays, such as

satisfy Assumption 2.1.

Lemma 2.1. ^[19] Under Assumption 2.1 is satisfied, let $T > 0$ and $\eta$ is a c$\grave{a}$dl$\grave{a}$g function from $[-\theta, T-\theta_1]$ to $\Re_+$ with at most finite number of jumps in any finite time interval. Then

Remark 2.2. Lemma 2.2 in ^[21] demands that $\eta$ is continuous, but here the solution is c$\grave{a}$dl$\grave{a}$g. Hence we need to come up with a new lemma, that is, Lemma 2.1.

Furthermore, the coefficients of (2.3) considered are polynomially rather than linearly increasing, namely highly nonlinear. Therefore, we give the assumption as follows:

Assumption 2.2. Suppose that for any constants $h > 0$, $k, \bar{k}, l, \bar{l}\in \Re^n$ and $\vert k\vert\vee\vert \bar{k}\vert\vee\vert l\vert\vee\vert \bar{l}\vert\leq h$, there exists a constant $H_h$ satisfying

where $(i, t)\in \mathcal{S}\times \Re_+$. In addition, there are constants $H > 0, \; \beta_{1} > 1$, as well as $\beta_i\geq 1\; (2\leq i\leq 4)$ satisfying

Under Assumption 2.2, the existence and uniqueness of the maximal local solution for (2.3) can only be ensured. However, it has the potential to blow up to infinity in finite time. To escape this potential explosion, the following assumptions become necessary:

Assumption 2.3. Suppose there exist some positive constants $\alpha, \beta, \omega_1, \omega_2, \omega_3$ which make

and

hold. Furthermore, let us assume that $\omega_2 > \omega_3\bar{\theta}$. Assuming that

we obtain $q_1 > q_2\bar{\theta}$.

Assumption 2.4. ^[19] For any $L\in \Re_+$, there exists a constant $\phi_L$ so that for any $k, \bar{k}, l, \bar{l}\in \Re^n$ and $\vert k\vert\vee\vert \bar{k}\vert\vee\vert l\vert\vee\vert \bar{l}\vert\leq L$, we have

where $(i, t)\in \mathcal{S}\times \Re_+$. There are constants $\chi > 0$ and $\omega\geq 1$ so that for $0 < \vert\tau\vert < e$, satisfying

Under Assumptions 2.1–2.4, it is known that (2.3) possesses a unique global solution and $\sup_{-\theta\leq u < \infty}\mathbb{E}$ $\vert\iota(u)\vert^{\beta} < \infty$, but the stability of (2.3) is not guaranteed (see, e.g., ^[19]). Our goal is to devise a feedback control function $u(\cdot, \cdot, \cdot)$ to enable the controlled nonlinear hybrid STDNNs with Lévy noise

become stable, where $u: \Re^n\times \mathcal{S}\times \Re_+\to \Re^n$ is Borel measurable, $\iota(\sigma_{t^-}) = \lim_{u\to t}\iota(\sigma_u)$, as well as $\sigma_t = [t/\lambda]\lambda$, where $[t/\lambda]$ is the integer part of $t/\lambda$. $\lambda > 0$ denotes the duration between two consecutive observations. The assumption about the function $u(\cdot, \cdot, \cdot)$ will be made as below.

Assumption 2.5. Consider all $\iota, \kappa\in \Re^n$, suppose that there is a constant $\rho$ satisfying

where $(i, t)\in \mathcal{S}\times \Re_+$. Also suppose that $u(0, i, t) = 0$.

To deal with the discrete-time Markov chain, we introduce the lemma as follows:

Lemma 2.2. ^[21] For all $t\geq0, m > 0$, as well as $i\in \mathcal{S}$, one has

where $\bar{\gamma} = \max_{i\in \mathcal{S}}(-\gamma_{ii}).$

3.   Boundedness

Within this section, we will present a theorem establishing the existence and uniqueness of a global solution for (2.13), with the property that the solution is $L^\beta$-bounded.

Theorem 3.1. According to Assumptions 2.1–2.5, for any initial condition (2.4), the hybrid STDNNs (2.13) yield a unique global solution $\iota(t)$ on $[-\theta, \infty)$ satisfying

Proof. Define a bounded function $\varphi: \Re_+\to[0, \lambda]$ with the form

then (2.13) can be represented as

Given $\mathcal{F}(\iota) = \vert \iota\vert^\beta$, from the generalized It$\hat{\text{o}}$ formula, one has

where the specific form of $M(t)$ is not used and will not be described in detail here. The operator $L\mathcal{F}$ from $\Re^n\times \Re^n\times \Re^n\times \mathcal{S}\times \mathcal{S}\times \Re_+$ to $\Re$ is defined as

In accordance with the proof of [19, Lemma 2.7], we can find two constants $b_1, b_2 > 0$ that satisfy

Using Assumptions 2.3, 2.5, and (3.4), we can conclude that

Based on Assumption 2.3, we can pick a constant $\delta_0$ to ensure that

and further, another constant $\delta$ to satisfy

According to Young inequality, we have

where $\hat{u}$ denotes a positive constant. Therefore, we can obtain

where $U = \sup_{s\geq 0}\left[(2\hat{u}+2+\omega_1\beta+b_1+b_2)\vert s\vert^\beta-\delta_0\vert s\vert^{\alpha+\beta-2}\right]$. Since the proof closely resembles that of [21, Theorem 3.1], it is omitted here. □

Remark 3.1. $\hat{u}$ changes may occur from line to line, but their particular form is not used.

4.   Stabilization

This section discusses the stabilization characteristic of (2.13). Next, we introduce some necessary assumptions.

Assumption 4.1. Designing the control function $u: \Re^n\times \mathcal{S}\times \Re_{+}\to \Re^n$, for any $\iota, \kappa\in \Re^n$, we can find constants $p_i, \bar{p}_i\in \Re$, positive constants $\hat{p}_i, \hat{c}_i, m_i, \bar{m}_i$, as well as $c_i, \bar{c}_i, n_i, \bar{n}_i\in \Re_+(i\in \mathcal{S})$ satisfying

and

where $(i, t)\in \mathcal{S}\times \Re_{+}$, while

are nonsingular M-matrices. In addition,

where

in which

Based on the principles of M-matrix theory, we can conclude that the nonsingularity of the M-matrices $\mathcal{P}_1$ and $\mathcal{P}_2$ ensures that all $\varrho_i$ and $\bar{\varrho}_i$ defined in (4.6) are positive.

Define the function

and the function $\mathcal{L}\mathbb{V}$ by

According to (4.1)–(4.3), (4.5), (4.6), and Young inequality, we can deduce that

Assumption 4.2. Suppose that there are constants $\psi_i > 0(1\leq i\leq 9)$ to make

and

hold, where $\psi_5 > \psi_6\bar{\theta}, \psi_7\in(0, 1/\bar{\theta})$ and $\Phi\in C(\Re^n; \Re_{+})$.

Next, we describe our stabilization rules.

4.1.   $H_{\infty}$ stabilization

Theorem 4.1. Assume that Assumptions 2.1–2.5, 4.1, and 4.2 are satisfied, and let

If $\lambda$ is a sufficiently small positive constant such that

and

hold, then the solution of (2.13) satisfies

for any initial condition (2.4).

Proof. For convenience, the proof is divided into two steps.

Step 1. For $t\in \Re_{+}$, we define $\hat{\iota}_t = \left\{\iota(t+s):-2\theta\leq s\leq0\right\}$ and $\hat{\pi}_t = \left\{\pi(t+s):-2\theta\leq s\leq0\right\}$. For $\hat{\iota}_t$ and $\hat{\pi}_t$ to be well defined for $t\in[0, 2\theta]$, define $\iota(s) = \varsigma(-\theta)$ for $s\in\left[-2\theta, -\theta\right)$ and $\pi(s) = \pi_0$ for $s\in\left[-2\theta, 0\right)$. Next, we use the Lyapunov function stated below

for $t\geq 0$, where $\mathbb{V}$ has been determined by (4.7) and

For $u\in\left[-2\theta, 0\right)$, we set $f(\iota, \kappa, i, u) = f(\iota, \kappa, i, 0), g(\iota, \kappa, i, u) = g(\iota, \kappa, i, 0), u(\iota, i, u) = u(\iota, i, 0)$. Based on It$\hat{\text{o}}$ formula, it follows that

where $M(t)$ denotes the continuous local martingale with $M(0) = 0$ and $L\mathbb{V}$ is defined by

In addition, we can obtain

Together with (4.18) and (4.19), we obtain

where

Under Assumptions 2.2–2.5, 4.1, and Theorem 3.1, we can intuitively see that

Step 2. For a sufficiently large positive constant $v_0$, consider the initial value $\vert\vert\varsigma\vert\vert < v_0$. For any $v_0\leq v$, define the stopping time $\varpi_v = \inf\left\{t\geq 0:\vert\iota(t)\vert\geq v\right\}$, for $\varpi_v$ is increasing as $v\to\infty$ and $\lim_{v\to\infty}\varpi_v = \infty$. By generalized It$\hat{\text{o}}$ formula, it is possible to obtain from (4.20) that

Based on (4.22), let $v\to\infty$ and then apply the dominated convergence theorem and Fubini theorem to have

According to (4.13), (4.21), Assumptions 2.5 and 4.2, we can conclude that

Furthermore, under Assumption 2.5 and Lemma 2.2, it is concluded that

Moreover, in view of the fact that $t-\sigma_t\leq\lambda$ holds for all $t\geq 0$, it can be proved on (2.13) that

Notice that $\int_0^{t}\mathbb{E}\vert\iota(u)-\iota(\sigma_u)\vert^2du$ is the equivalent of $\int_0^{t}\mathbb{E}\vert\iota(u^-)-\iota(\sigma_{u^-})\vert^2du$. Substituting (4.25) and (4.26) into (4.24), and using (4.13) and (4.14), it can be found that

Using Lemma 2.1, we obtain

and

Therefore, we can further deduce

where $H_1 = \mathbb{U}(\hat{\iota}_0, \hat{\pi}_0, 0)+\bar{\theta}\theta\sup_{-\theta\leq u < 0}\left[\psi_6\mathbb{E}\vert\iota(u)\vert^2+\psi_7\mathbb{E}\Phi(\iota(u))\right]\leq\infty$. From (4.14) and $\psi_7\in(0, 1/\bar{\theta})$, we get

Let $t\to\infty$ and combine with (4.11) to obtain

which means that the needed assertion (4.15) holds. □

4.2.   Asymptotic stabilization

Theorem 4.2. Assuming that conditions of Theorem 4.1 hold, the solution of (2.13) satisfies

for any initial condition (2.4).

Proof. From Theorem 3.1, let $H_2 = \sup_{-\theta\leq u < \infty}\mathbb{E}\vert\iota(t)\vert^\beta < \infty$. We can prove, as (3.4) is to be shown, that there are two constants $\hat{b}_1, \hat{b}_2 > 0$ that make

For any $0\leq t_1 < t_2 < \infty$, under Assumptions 2.2, 2.3, and 2.5, with the use of It$\hat{\text{o}}$ formula, we obtain

where $\breve{a} = \max_{1\leq i\leq n}\left\{a_i\right\}, \breve{b} = \max_{1\leq i, j\leq n}\left\{b_{ij}\right\}$ and $H_3$ is a constant unrelated to $t_1$ and $t_2$. Hence, $\mathbb{E}\vert\iota(t)\vert^2$ is uniformly continuous at $t$ on $\Re_+$. This, combined with (4.15), means that

Next, fix any $\bar{\beta}\in(2, \beta)$, it is obtained from the hölder inequality

In combination with (4.28), it is implied that the required (4.27) holds. □

4.3.   Exponential stabilization

Theorem 4.3. Assume that Assumptions 2.1–2.5, 4.1, and 4.2 are satisfied, and recall that

If $\lambda > 0$ is a small enough constant to make

and

hold, then the solution of (2.13) satisfies

and

for any initial condition (2.4) and $\bar{\beta}\in[2, \beta)$.

Proof. Similarly to the proof of Theorem 4.1, for $t\geq 0$, it is shown that

and $\gamma$ is a sufficiently small positive constant. Setting $\epsilon_1 = \min_{i\in \mathcal{S}}\varrho_i, \epsilon_2 = \max_{i\in \mathcal{S}}\varrho_i, \epsilon_3 = \max_{i\in \mathcal{S}}\bar{\varrho}_i$, we have

where

Analogous to the proof of Theorem 4.1,

In addition, there is apparently

From Lemma 2.1,

Substitute (4.37) and (4.38) into (4.36) to obtain

where

as well as

Clearly,

Now, we may select a small enough constant $\gamma > 0$ to satisfy

Again reviewing (4.30) and $\lambda\leq\frac{1}{6\sqrt{2}\rho}$, from (4.39)

for any $t\in \Re_+$. Moreover, for any $\bar{\beta}\in(2, \beta)$, we have by (4.29) and (4.40) that

Thus, the required assertion (4.33) is proved.

Put $t_k = k\lambda$ for $k = 0, 1, 2, \cdots$. By Hölder inequality and Doob martingale inequality, it is possible to show that

Based on Assumptions 2.2, 2.4, and 2.5, it is possible to conclude that

where $\bar{\beta} = 2(\beta_1\vee\beta_2\vee\beta_3\vee\beta_4)$ and $H_5 > 0$ is a constant. From Assumption 2.3, we find $\bar{\beta}\in[2, \beta)$. We can obtain, by applying (4.40) and (4.41), that

where $\hat{\varepsilon} = \gamma(\beta-\bar{\beta})/(\beta-2)$ and $H_6 > 0$ is also a constant. So

It is shown by Borel–Cantelli Lemma that for almost all $\tilde{\omega}\in\Omega$, there exists an integer $k_0 = k_0(\tilde{\omega}) > 0$, which makes

Thus, we have

This means

which is the desired assertion (4.34). □

Remark 4.1. The asymptotic stability discussed in Theorem 4.2 states that the solution of system (2.13) will asymptotically converge to zero; however, its rate of decrease is not provided. In Theorem 4.3, we further show that the solution of system (2.13) converges to zero at an exponential rate.

Remark 4.2. In general, almost surely exponential stabilization cannot be obtained from exponential stabilization in $L^{\bar{\beta}}$, but it is possible in the content of this paper, as stated in Theorem 4.3.

Remark 4.3. Recently, Dong and collaborators ^[19] designed a feedback control function to stabilize highly nonlinear hybrid SDDEs with Lévy noise, which is based on continuous-time state and mode observations and difficult to implement in practice. Consequently, the feedback control function $u(\iota(\sigma_{t^-}), \pi(\sigma_t), t)$ based on discrete-time state and mode observations used in this paper is more sensible and practical.

5.   Numerical examples

An example will be given throughout this section to demonstrate the validity of theoretical results.

Example 1. Consider the nonlinear hybrid STDNNs with Lévy noise

on $t\geq 0$ and $\iota(t) = 1+\sin(t)$ for $t\in\left[-0.2, 0\right]$. The coefficients are defined by $\mathcal{A}(1) = 0.3, \mathcal{A}(2) = 0.2, \mathcal{B}(1) = 0.5, \mathcal{B}(2) = 0.6$, and

where $e = 5$, $W(t)$ is a scalar Brownian motion, the Markov chain $\pi(t)$ over the state space $\mathcal{S} = \left\{1, 2\right\}$, possessing the generator matrix $\Gamma = \left(-1, 1;1, -1\right)$, and time delay $\theta_t = 0.1\vert\sin(t)\vert+0.1$.

The Lévy measure $\vartheta$ is characterized by $\vartheta(d\tau) = a\phi(d\tau) = 0.5\times e^{-2\vert\tau\vert}d\tau$, where $a = 0.5$ represents the jump rate, $\phi(\cdot)$ is the jump distribution, and the probability density function of $\phi(\cdot)$ is $e^{-2\vert\tau\vert}$. This ensures the fulfillment of (2.1).

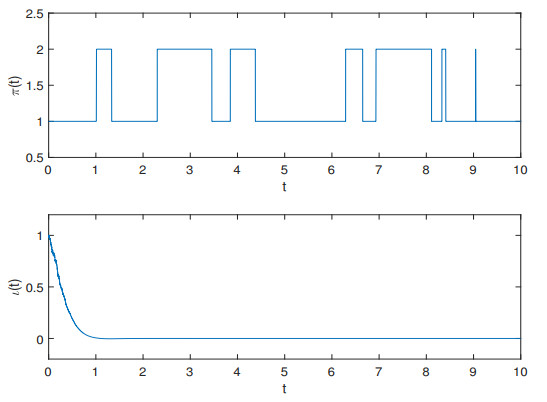
We can check that Assumption 2.1 is true when $\theta_1 = 0.1, \theta = 0.2, \bar{\theta} = 1.1111$. Assumption 2.2 holds when $\beta_1 = 3, \beta_2 = \beta_3 = \beta_4 = 2$. Assumption 2.3 holds when $\alpha = 4, \omega_1 = 0.72, \omega_2 = 0.19, \omega_3 = 0.06, q_1 = 1.0967, q_2 = 0.1867, \beta > 6$, we may then choose $\beta = 7$ and satisfy the condition $q_1 > q_2\bar{\theta}$. Figure 1 indicates that (5.1) is unstable. To make it stable, we devise the control function

clearly, $\rho = 2.5$ satisfies Assumption 2.5. The controlled nonlinear hybrid STDNNs with Lévy noise take the following form:

Due to

it follows that for $(\iota, \kappa, i, t, \tau)\in \Re\times\Re\times\mathcal{S}\times \Re_+\times Y$, we obtain

and

Hence, (4.1)–(4.3) hold when

as well as

which are both M-matrices. From (4.6), we derive

So

which satisfies (4.4). It is obvious that

As a result of (4.9), we obtain

In addition, we have

Selecting $\psi_1 = 0.2, \psi_2 = 0.01, \psi_3 = 0.3$, and $\psi_4 = 0.5$, we obtain

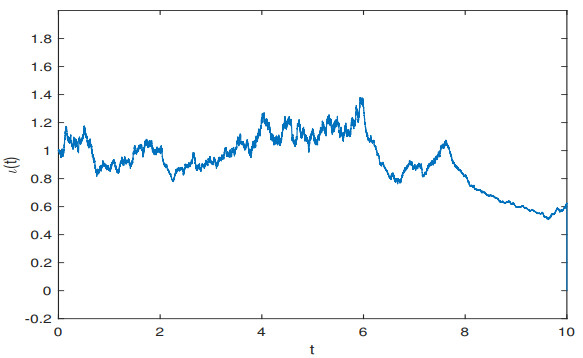
where $\Phi(\iota) = 0.8722\iota^4+0.0995\iota^6$, $\psi_5 = 0.9023, \psi_6 = 0.2251, \psi_7 = 0.1474, \psi_8 = 0.0995$, and $\psi_9 = 0.9717$. Based on Theorems 4.1 and 4.3, we have $\zeta = 106.5937$ and $\lambda\leq0.0028$. Thus, in view of Theorems 4.1–4.3, it follows that the controlled nonlinear hybrid STDNNs with Lévy noise (5.3) are $H_{\infty}$-stable, asymptotically stable, and exponentially stable in $L^{\bar{\beta}}$ for any $\bar{\beta}\in[2, 7)$. We perform a computer simulation with initial data $\iota(t) = 1+\sin(t)$ for $t\in\left[-0.2, 0\right]$ and $\pi(0) = 1$. Figure 2 shows sample paths of the Markov chain and the solution of controlled STDNNs (5.3). The simulation results apparently support our theoretical results.

6.   Conclusions

In this paper, we probe into the stabilization problem of nonlinear hybrid STDNNs with Lévy noise, whose coefficients are highly nonlinear. Unlike the constant time delay considered in ^[20] and the time delay studied in ^[8], which is a continuous function, we focus on the case where the time delay of STDNNs is time-varying and non-differentiable. We employ feedback control based on discrete-time state and mode observations to make unstable nonlinear hybrid STDNNs with Lévy noise stable. In addition, utilizing M-matrix theory and Lyapunov functional techniques, we explore the $H_{\infty}$ stability, asymptotic stability, and exponential stability of the controlled nonlinear hybrid STDNNs with Lévy noise. In future work, we will explore introducing mixed delays into highly nonlinear hybrid SNNs with Lévy noise ^[23]. Additionally, incorporating Lévy noise into metapopulation models will be considered (see, e.g., ^[24,25]), as it could enhance the realism and complexity of the models.

Author contributions

Tian Xu: Writing-original draft; Ailong Wu: Supervision, writing-review & editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant 62476082 and the Natural Science Foundation of Hubei Province of China under Grant 2021CFA080.

Conflict of interest

The authors declare that there are no conflicts of interest.