1.
Introduction
Nature's vast majority of systems-including the biological nervous system-are dynamic in that external circumstances influence it to have internal memory and behave in a specific manner. The idea of activity development may describe that through time. Time delays, both constant and time-varying, generally exist in dynamic systems, such as chemical process control systems, man-manufacturing systems, cooling systems, hydraulic systems, irrigation channels, metallurgical processes, robotics, and neural networks [1,6,8,10,11,13,14,19,22,23,24,30,31,32,35,36,39,45].
The nonlinear ordinary difference equation in discrete-time state-space form may be used to explain a general class of discrete-time systems. For discrete-time systems, it is possible to employ the nonlinear ordinary difference equation in the discrete-time state-space form to describe them. x(k+1)=f(x(k),u(k)),y(k)=h(x(k),u(k)) where x(k)∈Rn is the internal state vector, u(k)∈Rm is the control input, and y(k)∈Rp is the system output. These equations may be obtained from analyzing the dynamical system or process under study. In contrast, others may be derived from discretized or sampled continuous-time dynamics of a nonlinear system under investigation.
The study of the stability analysis of discrete-time systems with time-varying delays has emerged as a popular subject in the area of control theory during the last few years [7,12,15,17,21,25,26,27,29,33,37,38,42,44,45]. The stability of neural networks is a precondition for solving many engineering issues; it has garnered considerable attention in recent years, and many elegant solutions have been published. [11,19,22,23,34,35,39,45]. When implementing continuous-time neural networks for computer simulation, for computational or experimental reasons, it is necessary to construct a discrete-time system that is analogous to the continuous-time neural networks that should not be overlooked. [24] points out that discretization cannot consistently maintain the dynamics of the continuous-time counterpart, even for a short sample interval. As a result, it is critical to understand the dynamics of discrete-time neural networks.
Human brain activity, particularly that of neural networks, may be viewed as a very sophisticated parallel computer that is more efficient than any presently existing computer when neural networks are straightforwardly implemented in computers. In the case of neural networks, one of the most crucial characteristics is a temporal delay in the leakage term. When it comes to neural networks, the time delay in the leakage term has a significant impact on their dynamics since the system becomes unstable when there is a delay in reacting to a negative outcome; this causes the system to become unstable [5,6,15,18,20]. [6] investigated neural networks with a time delay in the leakage term and their findings on the presence and uniqueness of the equilibrium, independent of the time delay and starting circumstances, to determine whether the equilibrium exists. This means that the existence and uniqueness of the equilibrium point are unaffected by the delay in the leakage term. As a result of its importance as a helpful tool for the stability analysis of both linear and nonlinear systems, especially high-order systems, passivity theory, initially proposed in circuit analysis, has drawn a lot of attention and has been extensively investigated. Systems with passive qualities maintain their internal stability. The passivity theory has been widely used in a variety of fields, including signal processing [43], fuzzy control [16], sliding mode control [41], and networked control [4].
The problems of novel delay-range-dependent robust asymptotic stability and passivity criteria for uncertain discrete-time neural networks with interval discrete and distributed time-varying delays are introduced in this paper, which is motivated by earlier discussions. A novel delay-range-dependent stability and passivity analysis is also investigated for uncertain discrete-time neural networks with interval discrete, distributed, and leakage time-varying delays. New delay-range-dependent robust asymptotic stability and passivity criteria in terms of linear matrix inequalities (LMIs) for considered systems are obtained using a class of novel augmented Lyapunov-Krasovskii functionals (LKFs), model transformation, coefficient matrix decomposition technique, reciprocally convex combination, Leibniz-Newton formula, and use of zero equation. Also presented is an improvement in the stability and passivity criterion for discrete-time neural networks with interval time-varying delay dependent on the delay range. Theory may be shown using numerical examples, indicating that it's more effective while being less conservative. The main contributions and highlights of this paper are summarized in the following key points.
(1) The rebuilt summation inequality is used for the robust stability analysis issue for discrete-time neural networks that incorporate interval time-varying leakage, discrete and distributed delays for developing the delay-dependent criteria.
(2) We apply new inequalities to improve the stability criteria, such as Jensen inequality, coefficient matrix decomposition technique, utilization of zero equation, mixed model transformation, and reciprocally convex combination. Using the above new LKFs and the lemmas leads to less conservatism of the obtained results than in published literature, as presented via numerical examples.
(3) We present numerical examples to demonstrate the feasibility and effectiveness of the theorem.
Notations: Throughout the paper Rn denotes the n-dimensional Euclidean space; Z+={0,1,2,3,...}; N = {1, 2, 3, ...}; R(n×m) denotes the set of n×m-real matrices; AT denotes the transpose of the matrix A; A is symmetric if A=AT; In is the n×n-identity matrix; matrix A is called semi-positive definite (A≥0) if xTAx≥0, for all x∈Rn; A is positive definite (A>0) if xTAx>0, for all x≠0; A>B means A−B>0(B−A<0); A≥B means A−B≥0(B−A≤0); ρ=max{τ2,h2,M}; ∗ denotes symmetric terms in a symmetric matrix; [⋆] denote the right-side vector in a symmetric quadratic form.
2.
Problem formulation and preliminaries
Consider the following uncertain discrete-time neural network with interval time-varying leakage, discrete and distributed delays, as shown in the following system:
where x(k)=[x1(k),x2(k),…,xn(k)]T∈Rn is the system state vector, z(k) is the output vector of neuron network, w(k) is the exogenous disturbance input vector, A=diag{a1,a2,...,an} is the state feedback coefficient matrix with |ai|<1, matrices B,C,D,Az,Bz,Cz and Dz are known real constant matrices with appropriate dimensions, M∈N, ϕ(s) is the initial condition of system (2.1), τ(k) represents the leakage delay satisfying
where τ1 and τ2 denote the lower and upper bounds of τ(k). The time-varying delay h(k) satisfies
where h1 and h2 are known positive integers. There exists a constant κ>0 such that function δ(i) satisfies the following convergence condition
ΔA(k), ΔB(k),ΔC(k) and ΔD(k) represent the time-varying parameter uncertainties, and are assumed to satisfy the following linear fractional form
where Γ,H1,H2,H3 and H4 are known real constant matrices with appropriate dimensions. The uncertain matrix Δ(k) satisfies
and is said to be admissible, where E is a known matrix satisfying
and Ω(k) is an unknown time-varying matrix function satisfying
Assumption 1. For i∈{1,2,…,n}, the neuron activation functions fi(⋅), gi(⋅) in system (2.1) are continuous and bounded.
Assumption 2. For any s1,s2∈R,s1≠s2, the continuous and bounded activation functions fi(⋅) and gi(⋅) satisfy
and fi(0)=gi(0)=0, where F−i,F+i,G−i, and G+i are known real constants.
Definition 1. [28] The discrete-time system (2.1), with ω(k)=0, is said to be robust asymptotically stable if there exists a positive definite scalar function V(x(k)):Z+×Rn↦R such that
along the solution of the system (2.1) for all uncertainties.
Definition 2. [36] The discrete-time system (2.1), with ω(k)=0 and Ω(k)=0, is said to be asymptotically stable if there exists a positive definite scalar function V(x(k)):Z+×Rn↦R+ such that
along the solution of the system (2.1).
Definition 3. [32] The system (2.1) is called passive if there exists a scalar γ≥0 such that
for all k∈Z+ and for all solution of (2.1) with x(0)=0 holds.
Lemma 1. [17] Suppose that Δ(k) is given by (2.6)–(2.8). Let M,S and N be real constant matrices of appropriate dimension with M=MT. Then, the inequality
holds if and only if, for any positive real constant δ,
Lemma 2. [27] Let γ1,γ2,…,γN:Rm↦R have positive values in an open subset D of Rm. Then, the reciprocally convex combination of γi over D satisfies
subject to
Lemma 3. The following inequality holds for any α∈Rn, β∈Rm, Ξ,Y∈Rn×m, X∈Rn×n, and Z∈Rm×m,
where [XY∗Z]≥0.
Lemma 4. [8] For any positive real constant matrix M∈Rn×n, M=MT, two constants h2≥h1>0, such that the following inequalities hold:
(1) [h1∑i=1x(i)]TM[h1∑i=1x(i)]≤h1h1∑i=1xT(i)Mx(i),
(2) [k−h1−1∑i=k−h2k−h1−1∑j=ix(j)]TM[k−h1−1∑i=k−h2k−h1−1∑j=ix(j)]≤(h2−h1)(h2−h1+1)2k−h1−1∑i=k−h2k−h1−1∑j=ixT(j)Mx(j),
(3) [−h1−1∑i=h2k−1∑j=k+ix(j)]TM[−h1−1∑i=−h2k−1∑j=k+ix(j)]≤(h2−h1)(h2+h1+1)2−h1−1∑i=−h2k−1∑j=k+ixT(j)Mx(j).
Lemma 5. [25] For a given positive-definite n×n-matrix R, three given non-negative integers α,β,k satisfying α<β≤k, a vector function x(⋅)∈Rn and denoting Δx(k)=x(k+1)−x(k), we have
where
Lemma 6. Let Δx(k)∈Rn be a vector-valued function with first-order forward difference entries. Then, the following integral inequality holds for any constant matrices X,Mi∈Rn×n, i=1,2,…,5 and h(k) is discrete interval time-varying delays with 0≤h1≤h(k)≤h2,
where
Proof. From the discrete analog of the Newton-Leibniz formula, we obtain
For any constant matrices Ξ1,Ξ2∈Rn×n with zero equation (2.10),
Using Lemma 3 with α=Δx(i), β=[x(k−h1)x(k−h(k))], Y=[M1M2] and Z=[M3M4∗M5], we get
Substituting (2.13) into (2.12), then we obtain
By Eq (2.11), the following equation is true for any constant matrices Ξ1,Ξ2∈Rn×n
Similarly, we have
Finally, considering (2.14) and (2.15) together, then the summation inequality (2.9) is established. This brings the proof to a conclusion.
3.
Main results
3.1. Stability analysis for discrete-time neural network
This subsection presents a stability analysis of system (2.1) with ω(k)=0. The LMI based conditions will be derived using Lyapunov technique.
Consider the following neural network with interval leakage delay of the form
To be more specific, we will present the notations that will be used later
where Πi,j=ΠTj,i, i,j=1,2,3,…,21,
and others are equal to zero.
First of all, we examine the discrete-time neural network of the type with interval time-varying discrete, leakage, and distributed delays of the form
Theorem 1. The system (3.3) is asymptotically stable, if there exist positive definite symmetric matrices Pi,Qj,Rk,Zi, i=1,2,3,…,6,j=1,2,3,…,7, k=1,2,3,4, and any appropriate dimensional matrices Λ1,Λ2, satisfying the following LMIs
Proof. We begin by demonstrating the asymptotic stability of the system (3.3) under the constraints of the theorem. Let us partition the constant matrix A into its components
where A1,A2∈Rn×n are real constant matrices in order to improve the bounds of the discrete delay.
After that, we rewrite the system (3.3) using transformation method, so we achieve the following equivalents form:
Design and implement the following Lyapunov-Krasovskii functional as follows:
where
Evaluating the forward difference of Vi(k)(i=1,2,…,10), along the trajectory of system (3.3) is given by
Let us define for i=1,2,…,10,
where
Based on Lemma 4, the forward difference of V3(k) is calculated as
By Lemma 5, four terms from ΔV4(k) and ΔV9(k) can each be driven as
By Lemma 6, six terms from ΔV5(k) and ΔV10(k) can each be driven as
From Assumption 2, we have
and
where
where λ1i,λ2i,F−i,F+i,G−i, and G+i (i = 1, 2, ..., n) are known real constants.
According to (3.12)–(3.27), it is straightforward to see that
where ξ(k)=[xT(k),yT(k),xT(k−h(k)),xT(k−h1),xT(k−h2),k−1∑i=k−h(k)yT(i),k∑i=k−h1xT(i), 0∑i=−h1k∑j=k+ix(i),k∑i=k−h12xT(i),0∑i=−h2k−h1∑j=k+ixT(i),xT(k−τ(k)),xT(k−τ1),xT(k−τ2), k−1∑i=k−τ(k)yT(i),k∑i=k−τ1xT(i),0∑i=−τ1k∑j=k+ixT(i),k∑i=k−τ2xT(i),0∑i=−τ2k−τ1∑j=k+ixT(i),fT(x(k)), gT(x(k−h(k))),(M∑i=1δ(i)x(k−i))T]T, and Π is defined in (3.2). From (3.4)–(3.10), system (3.3) is asymptotically stable, as defined in Definition 2. The theorem is now complete in its proof.
If leakage delay term disappears, that is τ(k)=0, the neural networks system (3.3) reduces to
The delay-dependent stability criterion for the system in (3.29) can be directly deduced from Theorem 1.
We introduce the following notations for later use
where ˉΠi,j=ˉΠTj,i=Πi,j, i,j=1,2,3,…,10,19,20,21, and it is presented in the following theorem.
Theorem 2. The system (3.29) is asymptotically stable, if there exist positive definite symmetric matrices Pi,Qj,Rk,Zl, i=1,2,4=,6,j=1,2,3,…,6, k=1,2,l=1,2,3 and any appropriate dimensional matrices Λ1,Λ2, satisfying the following LMIs
Proof. Based on the same method as Theorem 1, but for this estimation we do not decompose matrix A, thereby rewriting the system (3.29) with model transformation method as the following descriptor system
Construct the following Lyapunov-Krasovskii functional as
where
When the forward difference of V(k) is calculated, it is defined as
Let us define for i=1,2,…,6,
We can estimate V1(k) as follows.
The proof after this step is omitted since it is analogous to the derivation of the Theorem 1.
When D=0, the neural networks system (3.3) becomes
The delay-dependent stability criterion for the system in (3.40) can be directly deduced from Theorem 1.
We introduce the following notations for later use
where ˆΠi,j=ˆΠTj,i=Πi,j, i,j=1,2,3,…,20, and it is presented in the following corollary.
Corollary 1. For given integers h1,h2 satisfying 0<h1≤h2, system (3.40) is asymptotically stable for 0<h1≤h(k)≤h2, if there exist positive definite matrices Pi,Qj,Rk,Zi, i=1,2,3,…,6,j=1,2,3,…,6, k=1,2,3,4, and any appropriate dimensional matrices Λ1,Λ2, satisfying the following LMIs, satisfying the following LMIs.
Proof. The proof has been skipped since it is almost identical to the derivation of Theorem 1 except that the matrix D is not included in the proof.
If leakage delay term disappears and D=0, the neural networks (3.29) becomes
The delay-dependent stability criterion for the system in (3.49) can be directly deduced from Theorem 2.
We introduce the following notations for later use
where ˆˉΠi,j=ˆˉΠTj,i=Πi,j, i,j=1,2,3,…,10,19,20, and it is presented in the following corollary.
Corollary 2. For given integers h1,h2 satisfying 0<h1≤h2, system (3.49) is asymptotically stable for 0<h1≤h(k)≤h2, if there exist positive definite matrices Pi,Qj,Rk,Zl, i=1,2,4,6,j=1,2,3,…,6,k=1,2,l=1,2,3 and any appropriate dimensional matrices Λ1,Λ2, satisfying the following LMIs
Proof. The proof is removed since it is comparable to the derivation of Theorem 2 without D and hence does not need to be included.
For system (2.1), we derive robust asymptotic stability using Theorem 1 and the following notations, which will come in handy later.
Theorem 3. The system (3.1) is robustly asymptotically stable, if there exist positive definite symmetric matrices Pi,Qj,Rk, i=1,2,…,9, j=1,2,…,5, k=1,2,…,8, any appropriate dimensional matrices J,T1,T2,Sl, Jm, Km, Mm,Nm, l=1,2,…,4, m=1,2,3 and any positive real constant δ satisfying the following LMIs
Proof. Together with LMIs of Theorem 1, by replacing A1, B, C and D in (3.4) with A1+ΔA(k), B+ΔB(k), C+ΔC(k) and D+ΔD(k) in (2.5), respectively. Then, we find that condition (3.57) is equivalent to the following condition
By using Lemma 1, we obtain that (3.64) is equivalent to the LMIs as follows
where δ is a positive real constant. From Theorem 1 and conditions (3.57)–(3.63), it follows from Definition 1 that system (3.1) is robustly asymptotically stable. This completes the proof of the theorem.
If D=0, then system (3.1) reduces to the following system
The delay-dependent stability criteria for the system in (3.66) can be directly deduced from Theorem 3.
We introduce the following notations for later use
and it is presented in the following corollary.
Corollary 3. The system (3.66) is robustly asymptotically stable, if there exist positive definite symmetric matrices Pi,Qj,Rk, i=1,2,…,9, j=1,2,…,4,k=1,2,…,8, any appropriate dimensional matrices J,T1,T2,Sl, Jm,Km,Mm,Nm, l=1,2,…,4, m=1,2,3 and any positive real constant δ such that the following LMIs hold
Proof. Together with LMI results of Corollary 1, by replacing A1 and B in (3.42) with A1+ΔA(k) and B+ΔB(k) in (2.5), respectively. Then, we find that condition (3.69) is equivalent to the following condition
By using Lemma 1, we obtain that (3.76) is equivalent to the LMI as follows
where δ is a positive real constant. From Corollary 1 and conditions (3.69)–(3.75), system (3.66) is robustly asymptotically stable. The proof is completed.
3.2. Passivity analysis for discrete-time neural network
This subsection focuses on the robust passivity analysis of the uncertain linear discrete-time system with interval discrete and distributed time-varying delays (2.1). The LMI-based conditions will be derived using the Lyapunov technique.
First and foremost, we introduce the following notations for later use
where ˘Πi,j=˘ΠTj,i=Πi,j, i,j=1,2,3,…,22,
and others are equal to zero.
Theorem 4. The system (2.1) is robustly passive, if there exist positive definite symmetric matrices Pi,Qj,Rk, i=1,2,…,10,j=1,2,…,6,k=1,2,…,8, any appropriate dimensional matrices J,T1,T2,Sl, Jm,Km,Mm,Nm, l=1,2,…,4,m=1,2,3 and any positive real constant δ,γ satisfying the following LMIs
Proof. The proof follows from Theorem 1 and Theorem 3 by choosing the Lyapunov-Krasovskii functional (3.14) and the forward differences in (3.16)–(3.27) with (2.1)–(2.8) and conditions (3.78)–(3.84), it follows that
Given a positive integer l and summing both sides of (3.85) from 0 to l with respect to k results in
Under the zero condition, we have
Therefore from (3.86), it is easy to get the inequality in Definition 3. Hence it can conclude that the system (2.1) is robustly passive. The proof of this theorem is completed.
If D=Dz=0, then system (2.1) reduces to the following system
The delay-dependent passivity criterion for the system in (3.87) can be directly deduced from Theorem 4. We introduce the following notations for later use
where ˜Πi,j=˜ΠTj,i=ˆΠi,j, i,j=1,2,3,…,21,
and others are equal to zero.
Corollary 4. The system (3.87) is robustly passive if there exist positive definite symmetric matrices Pi,Qj,Rk, i=1,2,…,9, j=1,2,…,4,6, k=1,2,…,8, any appropriate dimensional matrices J,T1,T2,Sl, Jm,Km,Mm, Nm, l=1,2,…,4, m=1,2,3 and any positive real constant δ,γ such that the following LMIs hold
Proof. The proof is omitted since it is analogous to the derivation of Theorem 4 with Definition 3.
If If leakage delay term disappears and D=Dz=0, then system (2.1) reduces to the following system
The delay-dependent passivity criterion for the system in (3.95) can be directly deduced from Theorem 4. We introduce the following notations for later use
where ˜Πi,j=˜ΠTj,i=ˆΠi,j, i,j=1,2,3,…,21,
and others are equal to zero.
Corollary 5. The system (3.95) is passive, if there exist positive definite symmetric matrices Pi,Qj,Rk, i=1,2,…,9, j=1,2,…,4,6, k=1,2,…,8, any appropriate dimensional matrices J,T1,T2,Sl, Jm,Km,Mm, Nm, l=1,2,…,4, m=1,2,3 and any positive real constant γ such that the following LMIs hold
Proof. As with the derivation of Theorem 4 with Definition 3, the proof is skipped here for simplicity's sake.
Remark 1. The problem of new delay-range-dependent asymptotic stability criteria for uncertain discrete-time neural networks with interval discrete, distributed, and leakage time-varying delays (Theorems 1–3, Corollarys 1–3) is studied. Moreover, new delay-range-dependent passivity criteria are also investigated for uncertain discrete-time neural networks with interval discrete, distributed, and leakage time-varying delays (Theorem 4, Corollarys 5 and 6). We use a mixed techniques such as new inequalities, Jensen inequality, coefficient matrix decomposition technique, utilization of zero equation, mixed model transformation, and reciprocally convex combination. Using the above new LKFs and the lemmas leads to less conservatism of the obtained results than in published literature, as presented via numerical examples.
3.3. Numerical examples for discrete-time neural network
In this part, we will provide numerical examples that will illustrate the efficacy and application of the techniques that are being discussed.
Example 1. Illustrate the effectiveness of the proposed stability criterion (Theorem 1) for the discrete-time system subjected to norm-bounded uncertainties (3.3) with parameters as follows
For the activation functions
In addition, we choose 2≤τ(k)≤8. Then, by using the MATLAB LMI Toolbox, we solve LMI (3.4)–(3.10), and the corresponding values of the permissible upper limits of h2 for a range of h1 values from 4 to 20 are also computed and given in Table 1 as follows:
Example 2. Consider system (3.29) with Theorem 2 and the following parameters as
For the activation functions
Then, by using the MATLAB LMI Toolbox, we solve LMI (3.31)–(3.34), and the corresponding values of the permissible upper limits of h2 for a range of h1 values from 4 to 20 are also computed and given in Table 2 as follows:
Example 3. Consider system (3.49) with Corollary 2 and the following parameters
For the activation functions
Table 3 lists the findings of the maximum delay limits for different h2 for system (3.49). A comparison of current outcomes with those from the past may be seen in Table 3. Table 3 shows that our findings for this particular case provide higher upper limits to the time delay than those in the references [10,13,14,30,31].
Example 4. Illustrate the effectiveness of the proposed robust stability criterion (Corollary 3) for the uncertain discrete-time system subjected to norm-bounded uncertainties, consider the following system
where |α(k)|<α. The uncertain system can be expressed in the form of (3.66) with the following parameters
For given interval [h1,h2], the values of α such that the robust asymptotic stability of this system are listed in Table 4. From the table, it is clear that the proposed robust stability criterion accommodates a higher perturbation bound for a given delay range than [3,7,29,40] without losing stability.
Example 5. Illustrate the effectiveness of the proposed stability criterion (Theorem 4) for the discrete-time system subjected to norm-bounded uncertainties (2.1) with parameters as follows
For the activation functions
In addition, we choose 2≤τ(k)≤8 and δ(i)=1,i=1,2,...,M. Using the MATHLAB tools to solve LMIs (3.78)–(3.84), and the corresponding values of the permissible upper limits of h2 for a range of h1 values from 4 to 20, we are also computed and given in Table 5 as follows:
Remark 2. An important property in discrete delayed system theory is stability which applies to analyzing properties of passivity of various discrete delayed systems. In recent years, stability and passivity properties have also been related to the different discrete delayed systems [3,7,10,13,14,29,30,31,40]. Moreover, in this work, we use refined inequality and mixed techniques to improve the stability and passivity criteria. By applying the abovementioned methods, we obtain less conservative results than the others [3,7,10,13,14,29,30,31,40].
4.
Conclusions
This paper explored discrete-time neural networks with mixed interval time-varying delays for asymptotic stability and passivity. It has also examined how discrete-time neural networks with time interval variations have resilient asymptotic stability and passivity analysis. The study was carried out using a technique that incorporated the enhanced Lyapunov-Krasovskii functional, mixed model transformation, decomposition approach of the coefficient matrix, and usage of zero equations. A novel set of delays-range-dependent robust asymptotic stability criteria was developed and constructed using LMIs. We can demonstrate numerically that our criteria are less conservative than those found in the current literature. Another numerical example has been provided to show the applicability of the discoveries that have been proposed.
Acknowledgments
This research has received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation [grant number B05F650018].
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.









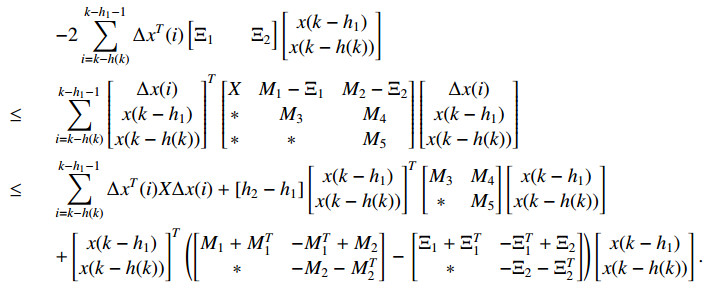
 DownLoad:
DownLoad:



