1.
Introduction
This paper considers the existence and global exponential stability of piecewise pseudo almost periodic solutions for interval general BAM neural networks with mixed time-varying delays and impulsive perturbations. The mixed time-varying delays include leakage delays and time-varying delays:
where Z+ is the set of nonnegative integers; the numbers of neurons in layers X and Y are denoted by m. xi(t) represents the state variables of the i-th neurons at time t. yj(t) represents the state variables of the j-th neurons at time t. ai(t)>0, bj(t)>0 are continuous functions and represent the decay rates of neurons in different layers, respectively. sji(t), tij(t) are the connection weights. fj(⋅,⋅), gi(⋅,⋅) represent the activation functions of the j-th and i-th units, respectively. ci(t), dj(t) represent the external inputs of the i-th neuron and the j-th neuron acting on different layers at time t, respectively. αi(t)>0, βj(t)>0 are time-varying leakage delays. τji(t)>0, δij(t)>0 are time-varying delays respectively satisfying 1−τ′ji(t)>0, 1−δ′ij(t)>0. The sequence {tk} has no finite accumulation point. Ik(⋅):Rm→R and Jk(⋅):Rm→R, k∈Z+.
The initial value conditions of the system (1.1) are as follows:
where r1=max1≤i,j≤m{supt∈R+|αi(t)|,supt∈R+|δij(t)|}, r2=max1≤i,j≤m{supt∈R+|βj(t)|,supt∈R+|τji(t)|}, φi(θ)∈C1([−r1,0],R), i=1,2,⋯,m, ψj(θ)∈C1([−r2,0],R) and j=1,2,⋯,m.
BAM neural networks have more complex dynamic behavior. They are composed of two-layer nonlinear feedback networks. Neurons in different layers are interconnected, and there is no connection between neurons in the same layer [1]. It extends the single-layer self-association learning rule to the two-layer hetero-association mode. Time delays in neural networks not only decrease the transmission speed of the networks, but may also change the stability of the networks. There have been many excellent results on the stability and bifurcation behavior of delayed neural networks [2,3,4,5,6,7,8,9]. The existence and stability of solutions for neural networks with time delays have been widely explored [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. In particular, the dynamic behavior of neural networks with leakage delays [10,12,13,24,25,27,29] is still a hot research topic.
Impulses are ubiquitous in the actual neural networks and the dynamic behavior of the neural networks are often affected by impulsive perturbations. And the study of impulsive control theory for neural networks has made a lot of advancements [11,15,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40].
Compared with the activation functions fj(⋅), gi(⋅) in BAM neural networks [10,11,13,14,15,17,19,21,22,23,24], the activation functions fj(xj,yj), gi(xj,yj) in the interval general BAM neural networks [16,17,20,21,22,24] more clearly show the connections between different layers of neurons in the networks. Ding and Huang [16] studied the existence and global robust exponential stability of equilibrium points for the following a class of interval general BAM neural networks with constant delays by using fixed-point theory and constructing suitable Lyapunov functions:
By variable transformations, fixed point theory and constructing suitable delay differential inequalities, Xu et al. [17] studied the existence, uniqueness and global exponential stability of the equilibrium point of system (1.3) with proportional delays. Given ai=ai(t), bj=bj(t), sji=sji(t) and tij=tij(t) in the system (1.3), the authors of [20] studied the existence and global exponential stability of periodic solutions for the system (1.3) on time scales by using fixed point theory and constructing suitable Lyapunov functions. Given ai=ai(t), bj=bj(t), sji=sji(t), tij=tij(t), ci=ci(t) and dj=dj(t) in the system (1.3), Duan [22] studied the existence and global exponential stability of pseudo almost periodic solutions for system (1.3) by using exponential dichotomy, fixed point theory and inequality techniques. Given ai=ai(t), bj=bj(t), sji=sji(t), tij=tij(t), ci=ci(t) and dj=dj(t) in the system (1.3), the authors of [24] studied the existence and exponential stability of almost periodic solutions for system (1.3) with leakage delays by using exponential dichotomy, fixed point theory and inequality techniques.
However, in the existing literature, we have not found any research on the dynamic behavior of interval general BAM neural networks with impulses and leakage delays. The stability of the interval general BAM neural networks may be destroyed by external perturbations and leakage delays. Therefore, the effects of leakage delays and impulsive perturbations on the dynamic behavior of interval general BAM neural networks are worth exploring.
Motivated by the above discussions, this paper studies the existence and global exponential stability of piecewise pseudo almost periodic solutions for the interval general BAM neural network described by (1.1) with mixed time-varying delays and impulsive perturbations. The mixed time-varying delays include leakage delays and time-varying delays.
Throughout this paper, let e+i=supt∈R+|ei(t)|, e−i=inft∈R+|ei(t)|, e+ij=supt∈R+|eij(t)| and e−ij=inft∈R+|eij(t)|. Let T be the set of the real sequences {tk}k∈Z+ such that σ_=infk∈Z+t1k=infk∈Z+(tk+1−tk)>0, so limk→+∞tk=+∞. For {tk}k∈Z+⊂T, assume that {tjk:tjk=tk+j−tk,k,j∈Z+} are equipotentially almost periodic and t0=0; it can be easily proved that the sequence {tjk} satisfies tjk+i−tjk=tik+j−tik and tjk−tik=tj−ik+i. And suppose that the following conditions hold.
(H1) For u1, v1, u2, v2∈R, there are nonnegative constants Pj, Qj, Hi and Ki such that |fj(u1,v1)−fj(u2,v2)|≤Pj|u1−u2|+Qj|v1−v2| and |gi(u1,v1)−gi(u2,v2)|≤Hi|u1−u2|+Ki|v1−v2|.
(H2) ai(t), bj(t)∈C(R+,R+) are almost periodic functions, and supt∈R+|ai(t)|=a+i, inft∈R+|ai(t)|=a−i, supt∈R+|bj(t)|=b+j, inft∈R+|bj(t)|=b−j. sji(t), tij(t), ci(t), dj(t):R+→R are piecewise pseudo almost periodic functions, and supt∈R+|sji(t)|=s+ji, supt∈R+|tij(t)|=t+ij, supt∈R+|ci(t)|=c+i and supt∈R+|dj(t)|=d+j.
(H3) Ik, Jk∈PAP(Z+,Rn) and there are two positive constants I, J satisfying 0<I, J<1 such that |Ik(u1)−Ik(u2)|≤I|u1−u2|, |Jk(u1)−Jk(u2)|≤J|u1−u2| for u1, u1∈R, k∈Z+.
Remark 1.1. In the existing literature on BAM neural networks, in addition to the condition (H1), the activation functions fj(⋅) and gi(⋅) are required to satisfy fj(0)=0 and gi(0)=0. In this paper, the activation functions fj(0,0)=0, gi(0,0)=0 are not required, as it only needs to meet the condition (H1).
In this paper, first, by using the exponential dichotomy of linear differential equations and the fixed point theory for contraction mapping, the existence of piecewise pseudo almost periodic solutions for system (1.1) satisfying the initial value conditions given by (1.2) is studied. And then by using mathematical methods of induction and inequality techniques, the global exponential stability of piecewise pseudo-almost periodic solutions for system (1.1) satisfying the initial value conditions given by (1.2) will be discussed.
Remark 1.2. Compared with the systems studied in [11,16,17,20,21,22,24,25], the system (1.1) studied in this paper is more general, as some classical Hopfield neural networks and BAM neural networks are special cases of the system (1.1). Duan [22] studied the effects of constant delays in the activation functions on the dynamic behavior of the system, but they did not consider the effects of leakage delays and impulsive perturbations on the dynamic behavior of the system. The mixed time-varying delays studied in this paper include not only the time-varying delays in the activation functions but also the leakage delays; the influences of impulsive perturbations on the dynamic behavior of the system are also considered. This paper not only considers the norm ‖⋅‖∞ but also ‖(⋅)′‖∞. Therefore, the results obtained in [21,22,24] are special cases of the research results in this paper.
2.
Preliminaries
This section mainly gives the necessary definitions, lemmas and notations to prove the existence and global exponential stability of the piecewise pseudo almost periodic solutions of the system described by (1.1)–(1.2).
C1(R,Rn) is the set of continuous functions with a continuous derivative, and
where ‖⋅‖∞=max1<i<msupt∈R|⋅|.
BC(R,Rn) is the set of bounded continuous functions, and (BC(R,Rn),‖⋅‖∞) is a Banach space.
Let PC(R,Rn) be the set of all piecewise continuous functions ϕ:R→Rn such that ϕ is countinuous at t for t∉{tk:k∈Z+} and that ϕ(t+k), ϕ(t−k) exist and ϕ(t−k)=ϕ(tk) for k∈Z+.
Define L∞(Z+,Rn)={u:Z+→Rn,‖u‖=supn∈Z+|u(n)|} and PAP0(Z+,Rn)={u∈L∞(Z+,Rn):limn→∞12nn∑k=−n‖u(k)‖=0}.
Definition 2.1. [34] A function f∈C(R,Rn) is called almost periodic if for ∀ϵ>0, there is L(ϵ)>0 such that every interval of length L(ϵ) contains at least a number δ∈T(f,ϵ) such that |f(t+δ)−f(t)|<ϵ for any t∈R, where T(f,ϵ)={δ∣|f(t+δ)−f(t)|<ϵ,∀t∈R}. The set of all almost periodic functions is represented by AP(R,Rn).
Definition 2.2. [35] A sequence {un} is called almost periodic if for ∀ϵ>0, there is a natural number L(ϵ) such that for k∈Z, there is at least one number q in [k,k+L(ϵ)] for which the inequality ‖un+q−un‖<ϵ holds for all n∈N. The set of all almost periodic sequences is represented by AP(Z,Rn).
Definition 2.3. [36] A function ϕ∈PC(R,Rn) is called piecewise almost periodic if the following conditions are satisfied.
● (1) {tjk}, tjk=tk+j−tk, k, j∈Z are equipotentially almost periodic, that is to say, for any ϵ>0, there is a relatively dense set in R of ϵ-almost periods that are common for any of the sequences {tjk}.
● (2) For any ϵ>0, there is a constant δ(ϵ)>0 such that, if t′ and t″ belong to the same interval of continuity of ϕ and |t′−t″|<δ, then ‖ϕ(t′)−ϕ(t″)‖<ϵ.
● (3) For any ϵ>0, there is a relatively dense set Ω(ϵ) in R such that, if ρ∈Ω(ϵ), then ‖ϕ(t+ρ)−ϕ(t)‖<ϵ for t∈R, which satisfies |t−ti|>ϵ, i∈Z.
Denote by APT(R,Rn) the set of piecewise almost periodic functions; UPC(R,Rn) is the set of the function f∈PC(R,Rn) such that f satisfies the condition (2) in Definition 2.3. Let
Obviously, PC0T(R,Rn)⊂PAP0T(R,Rn).
Definition 2.4. f∈PC(R×Ω1×Ω2,Rn) is said to be piecewise almost periodic in t uniformly in (φ,ψ)∈Ω1×Ω2 if for every compact set K1×K2⊆Ω1×Ω2, {f(⋅,φ,ψ):(φ,ψ)∈K1×K2} is uniformly bounded, and for ∀ϵ>0, there exists a relatively dense set Ω(ϵ) such that ‖f(t+τ,φ,ψ)−f(t,φ,ψ)‖≤ϵ for (φ,ψ)∈K1×K2, τ∈Ω(ϵ), and given t∈R, |t−ti|>ϵ.
Definition 2.5. [37] Sequence {un}n∈Z∈L∞(Z,Rn) is called pseudo almost periodic if there exist u1n∈AP(Z,Rn) and u2n∈PAP0(Z,Rn) such that un=u1n+u2n. The set of pseudo almost periodic sequences is denoted by PAP(Z,Rn).
Definition 2.6. [38] A function ϕ∈PC(R,Rn) is known as piecewise pseudo almost periodic if it can be disintegrated into ϕ=ϕ1+ϕ2, where ϕ1∈APT(R,Rn) and ϕ2∈PAP0T(R,Rn). The set of piecewise pseudo almost periodic functions is denoted by PAPT(R,Rn).
Lemma 2.1. [38] Let the sequence of vector-valued functions {Ii}i∈Z be pseudo almost periodic and there be a constant L>0 such that ‖Ii(u)−Ii(v)‖≤L‖u−v‖ for all u,v∈Ω,i∈Z if ϕ∈PAPT(R,X)∩UPC(R,X) such that R(ϕ)⊂Ω; then Ii(ϕ(ti)) is pseudo almost periodic.
Lemma 2.2. [39] If φ(⋅)∈PAPT(R,Rn), then φ(⋅−h)∈PAPT(R,Rn).
Lemma 2.3. [39] If φ(⋅),ψ(⋅)∈PAPT(R,R), then φ×ψ∈PAPT(R,R).
Lemma 2.4. [39] If fi(⋅)∈C(R,Rn) satisfies the Lipschitz condition, ψ(⋅)∈PAPT(R,R), ψ′(⋅)∈PAPT(R,R) and δ(⋅)∈APT(R,R) such that for all t∈R, 1−δ′(t)>0, fi(ψ(⋅−δ(⋅)))∈PAPT(R,R).
Lemma 2.5. [40] Assume that f∈PAPT(R×Ω1×Ω2,X) and the following conditions hold:
● (1) {f(t,u,v):t∈R,u∈K1,v∈K2} is bounded for every bounded subset K1×K2⊆Ω1×Ω2.
● (2) {f(t,u,v)} is uniformly continuous in each bounded subset of Ω1×Ω2 uniformly in t∈R.
If φ∈PAPT(R,X), ψ∈PAPT(R,X) such that R(φ)×R(ψ)⊂Ω1×Ω2, then f(t,φ(⋅),ψ(⋅))∈PAPT(R,X), where R(φ), R(ψ) are the ranges of φ, ψ, respectively.
Lemma 2.6. [40] Let f∈PAPT(R×Ω1×Ω2,X), φ∈PAPT(R,X), ψ∈PAPT(R,X) and R(φ)×R(ψ)⊂Ω1×Ω2. Assume that there exists a constant Lf>0 such that ‖f(t,u1,v1)−f(t,u2,v2)‖≤Lf(‖u1−u2‖+‖v1−v2‖), t∈R, u1, u2∈Ω1 and v1, v2∈Ω2. Then, f(⋅,φ(⋅),ψ(⋅))∈PAPT(R,X).
Definition 2.7. [34] Let x∈Rn and A(⋅) be an n×n continuous matrix defined on R. The linear system x′(t)=A(t)x(t) is said to admit an exponential dichotomy on R if there exist positive constants k and α and a projection P such that the fundamental solution matrix X(t) of x′(t)=A(t)x(t) satisfies the following:
Lemma 2.7. [34] Let ai(⋅) be an almost periodic function on R and M[ai]=limT→+∞∫t+Ttai(s)ds>0, i=1,2,...,n. Then, the system x′(t)=diag(−a1(t),−a2(t),...,−an(t))x(t) admits an exponential dichotomy on R.
Lemma 2.8. [41] Let A(⋅) be an almost periodic matrix function and f(⋅)∈PAP(R,Rn). If x′(t)=A(t)x(t) admits an exponential dichotomy, then the pseudo almost periodic system x′(t)=A(t)x(t)+f(t) has a unique pseudo almost periodic solution x(t), and
Definition 2.8. Let ¯z(t)=(¯x(t),¯y(t))T be the solution of system (1.1) satisfying the initial value conditions ¯ϕ=(¯φ(θ),¯ψ(θ))T. If there exist constants M≥1, η>0 such that for any solution z(t)=(x(t),y(t))T of the system (1.1) satisfying the initial value conditions ϕ=(φ(θ),ψ(θ))T, the following inequality holds
where ‖ϕ−¯ϕ‖1=max{max{‖φ‖∞,‖φ′‖∞},max{‖ψ‖∞,‖ψ′‖∞}}. Then, ¯z(t) is said to be globally exponentially stable.
3.
Existence of piecewise pseudo almost periodic solutions
This section establishes the conditions of the existence for piecewise pseudo almost periodic solutions of the system described by (1.1)–(1.2).
Lemma 3.1. Let f∈PAPT(R×Ω1×Ω2,X), φ, ψ∈PAPT(R,Rn) and R(φ)×R(ψ)⊂Ω1×Ω2. There are constants P>0, Q>0 such that for t∈R, φ, ¯φ∈Ω1, ψ, ¯ψ∈Ω2, |f(t,φ,ψ)−f(t,¯φ,¯ψ)|≤P|φ−¯φ|+Q|ψ−¯ψ| and θ(⋅)∈C(R,R). Then, f(t,φ(t−θ(⋅)),ψ), f(t,φ,ψ(t−θ(⋅)))∈PAPT(R,X) and f(t,φ(t−θ(⋅)),ψ(t−θ(⋅)))∈PAPT(R,X).
Proof. Since φ, ψ∈PAPT(R,R), then φ=φ1+φ2, ψ=ψ1+ψ2, where φ1, ψ1∈APT(R,R) and φ2, ψ2∈PAP0T(R,R). We have
where f1=f(t,φ1(t−θ(⋅)),ψ1), f2=f(t,φ1(t−θ(⋅))+φ2(t−θ(⋅)),ψ1+ψ2)−f(t,φ1(t−θ(⋅)),ψ1). From Lemmas 2.2–2.5, f1=f(t,φ1(t−θ(⋅)),ψ1)∈APT(R,R) holds. Now f2∈PAP0T(R,R) will be proved. Since
Thus f2∈PAP0T(R,R). So, f(t,φ(t−θ(⋅)),ψ)∈PAPT(R,X). In a similar way, f(t,φ,ψ(t−θ(⋅)))∈PAPT(R,X) and f(t,φ(t−θ(⋅)),ψ(t−θ(⋅)))∈PAPT(R,X). The proof is complete. □
Theorem 3.1. If conditions (H1)–(H3) are true. For any ϕ=(φ,ψ)T∈PAPT(R+,R2m) and ¯ϕ=(¯φ,¯ψ)T∈PAPT(R+,R2m), define the operator
where
Then, Φ1ϕ(⋅) is a mapping from PAPT(R+,R2m) to PAPT(R+,R2m).
Proof. By Lemmas 2.2–2.5 and Lemma 3.1, ¯Fi(t,φ,ψ)∈PAPT(R+,R); thus,
where ¯F1i(t,φ,ψ)∈APT(R+,R), ¯F2i(t,φ,ψ)∈PAP0T(R+,R).
For i=1,2,...,m, we have
Step 1: Prove that Ψ1(t)∈UPC(R+,R). Obviously, Ψ1(t)∈PC(R+,R). For t′,t″∈(tk,tk+1),k∈Z+,t″<t′,
For ∀ϵ>0, there is 0<δ<min{a−iϵ2‖¯F1i‖∞a+i,ϵ2‖¯F1i‖∞} such that for t′, t′ satisfying 0<|t′−t″|<δ, |Ψ1(t′)−Ψ1(t″)|<ϵ holds. So, Ψ1(t)∈UPC(R+,R).
Step 2: Prove that Ψ1(⋅)∈APT(R+,R). Since ¯F1i(t,φ,ψ)∈APT(R+,R), for ∀ϵ>0, there is a relatively dense set Ω(ϵ); for τ∈Ω(ϵ), t∈R+, |t−tk|>ϵ, i∈Z+ such that |¯F1i(s+τ,φ(s+τ),ψ(s+τ))−¯F1i(s,φ(s),ψ(s))|<a−iϵ. Then
Consequently, Ψ1(⋅)∈APT(R,R).
Step 3: Prove that Ψ2(⋅)∈PAP0T(R+,R). Since ¯F2i(s−u,φ(s−u),ψ(s−u)),¯F2i(s,φ(s),ψ(s))∈PAP0T(R+,R), then
Consequently, Ψ2(⋅)∈PAP0T(R+,R). So, ∫t−∞e−∫tsai(u)du¯Fi(s,φ,ψ)ds∈PAPT(R+,R). Similarly, for j=1,2,...,m, we have that ∫t−∞e−∫tsbj(u)du¯Gj(s,φ,ψ)ds∈PAPT(R+,R).
Therefore Φ1ϕ(⋅)∈PAPT(R+,R2m). □
Theorem 3.2. If conditions (H_{1}) – (H_{3}) are true, for any \phi = (\varphi, \psi)^{T}\in PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) , define the operator
Then, \Phi_{\phi}^{2}(\cdot) is a mapping from PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) to PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) .
Proof. Assume that t\in(t_{l}, t_{l+1}] , l\in\mathbb{Z}^{+} ; therefore, t-t_{k} = t-t_{l}+t_{l}-t_{k}\geq(l-k)\underline{\sigma} , and
For any \epsilon > 0 , take the positive constant \delta < \frac{\epsilon (1-e^{-a_{i}^{-}\underline{\sigma}})}{a_{i}^{+}\|I_{k}(\varphi_{i}(t_{k}))\|_{\infty}} , for t', t''\in(t_{k}, t_{k+1}), k\in\mathbb{Z}^{+}, t' < t'' , provided that |t'-t''| < \delta ; there is \zeta\in(t', t'') such that
That is, \sum\limits_{t_{k} < t}e^{-\int_{t_{k}}^{t}a_{i}(u)du}I_{k}(\varphi_{i}(t_{k}))\in UPC(\mathbb{R}^{+}, \mathbb{R}) . By Lemma 2.1 and (H_{3}) , I_{k}(\varphi_{i}(t_{k}))\in PAP(\mathbb{Z}^{+}, \mathbb{R}) . Let I_{k}(\varphi_{i}(t_{k})) = I_{k}^{1}+I_{k}^{2} , where I_{k}^{1}\in AP(\mathbb{Z}^{+}, \mathbb{R}) , I_{k}^{2}\in PAP_{0}(\mathbb{Z}^{+}, \mathbb{R}) ; then,
First, we show that \overline{I_{1}}(\cdot)\in AP_{T}(\mathbb{R}^{+}, \mathbb{R}) . Since \{t_{k}^{j}: k, j\in\mathbb{Z}^{+}\} are equipotentially almost periodic, for any \epsilon > 0 , there is a relatively dense set \Omega(\epsilon) of \mathbb{R}^{+} and Q(\epsilon) of \mathbb{Z}^{+} such that for t\in(t_{k}, t_{k+1}] , |t-t_{k}| > \epsilon , |t-t_{k+1}| > \epsilon , k\in\mathbb{Z}^{+} , \tau\in\Omega(\epsilon) , q\in Q(\epsilon) , from Lemma 35 (see [35]), we have that t+\tau > t_{k}+\tau+\epsilon > t_{k+q} and t_{k+q+1} > t_{k+1}-\epsilon+\tau > t+\tau ; so, t_{k+q} < t+\tau < t_{k+q+1} . Then
So, \overline{I_{1}}(\cdot)\in AP_{T}(\mathbb{R}^{+}, \mathbb{R}) .
Next, we show that \overline{I_{2}}(\cdot)\in PAP_{T}^{0}(\mathbb{R}^{+}, \mathbb{R}) . For k , n\in\mathbb{Z}^{+} and t\in(t_{k}, t_{k+1}] , let
since
\lim\limits_{t\rightarrow \infty}|\chi_{n}(t)| = 0 ; there is \chi_{n}(t)\in PC^{0}_{T}(\mathbb{R}, \mathbb{R}^{n})\subset PAP^{0}_{T}(\mathbb{R}, \mathbb{R}^{n}) .
Let S_{n}(t) = \sum\limits_{l = 0}^{n}\chi_{l}(t) , because
Therefore, \lim\limits_{t\rightarrow \infty}|s_{n}(t)| = 0 . So, s_{n}(t)\in PAP^{0}_{T}(\mathbb{R}, \mathbb{R}^{n}) .
And because \lim\limits_{n\rightarrow \infty}s_{n}(t) = \overline{I_{2}}(\cdot) uniformly holds on \mathbb{R}^{+} , from Lemma 2.2 in [40], \overline{I_{2}}(\cdot)\in PAP_{T}^{0}(\mathbb{R}^{+}, \mathbb{R}) holds. Therefore, \sum\limits_{t_{k} < t}e^{-\int_{t_{k}}^{t}a_{i}(u)du}I_{k}(\varphi_{i}(t_{k}))\in PAP_{T}(\mathbb{R}^{+}, \mathbb{R}) .
In the same way, \sum\limits_{t_{k} < t}e^{-\int_{t_{k}}^{t}b_{j}(u)du}J_{k}(\psi_{j}(t_{k}))\in PAP_{T}(\mathbb{R}^{+}, \mathbb{R}) can be obtained. Thus \Phi_{\phi}^{2}(\cdot)\in PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) . □
From Theorems 3.1 and 3.2, the following theorem is obtained.
Theorem 3.3. If conditions (H_{1}) – (H_{3}) are true, for any \phi = (\varphi, \psi)^{T}\in PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) and \phi' = (\varphi', \psi')^{T}\in PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) , define the operator
Then, \Phi_{\phi}(t) maps PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) into PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) , and \Phi_{\phi}'(t) maps PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) into PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) .
Theorem 3.4. Assume that conditions (H_{1}) – (H_{3}) are true and the following condition holds:
(H_4) p_{ij} = \max\{\max\{\frac{\theta_{i}}{a_{i}^{-}}+\frac{I}{1-e^{-a_{i}^{-}\underline{\sigma}}}, \frac{\theta_{i}}{a_{i}^{-}}(a_{i}^{+}+a_{i}^{-})+\frac{Ia_{i}^{+}}{1-e^{-a_{i}^{-}\underline{\sigma}}}\}, \max\{\frac{\gamma_{j}}{b_{j}^{-}}+\frac{J}{1-e^{-b_{j}^{-}\underline{\sigma}}}, \frac{\gamma_{i}}{b_{j}^{-}}(b_{j}^{+}+b_{j}^{-})+\frac{Ib_{j}^{+}}{1-e^{-b_{j}^{-}\underline{\sigma}}}\}\} < 1 ,
where \theta_{i} = a_{i}^{+}\alpha_{i}^{+} +\sum\limits_{j = 1}^{m}s_{ji}^{+}(P_{j}+Q_{j}) , \gamma_{j} = b_{j}^{+}\beta_{j}^{+}+\sum\limits_{i = 1}^{m}t_{ij}^{+}(H_{i}+K_{i}) , i, j = 1, 2, \cdots, m .
Then, there is a unique piecewise differentiable pseudo almost periodic solution of system (1.1) in the region
where \phi^{0} = (\varphi_{1}^{0}, \varphi_{2}^{0}, \cdots, \varphi_{m}^{0}, \psi_{1}^{0}, \psi_{2}^{0}, \cdots, \psi_{m}^{0})^{T} , and
Proof. It is easy to show that \mathbb{X}_{0}\subset PAP_{T}(\mathbb{R}^{+}, \mathbb{R}^{2m}) is a closed convex set. Rewrite (1.1) into the following form
We consider the following system
where
Since M[a_{i}] > 0 , M[b_{i}] > 0 , from Lemma 2.7, we have that the linear system
admits an exponential dichotomy on \mathbb{R}^{+} . Thus, by Lemma 2.8, we obtain that system (3.2) has a unique piecewise pseudo almost periodic solution, which is expressed as follows:
Let l_{i} = c_{i}^{+}+\sum\limits_{j = 1}^{m}s_{ji}^{+}|f_{j}(0, 0)| , l_{i}' = \frac{\sup\limits_{k\in\mathbb{Z}^{+}}|I_{k}(0)|}{1-e^{-a_{i}^{-}\underline{\sigma}}} , l_{j} = d_{j}^{+}+\sum\limits_{i = 1}^{m}t_{ij}^{+}|g_{i}(0, 0)| and l_{j}' = \frac{\sup\limits_{k\in\mathbb{Z}^{+}}|J_{k}(0)|}{1-e^{-b_{j}^{-}\underline{\sigma}}} . Then,
Similarly, \psi_{j}^{0}(t)\leq \frac{l_{j}}{b_{j}^{-}}+l_{j}' .
In addition,
Similarly, |(\psi_{j}^{0})'(t)|\leq \frac{l_{j}}{b_{j}^{-}}(b_{j}^{+}+b_{j}^{-})+b_{j}^{+}l_{j}' .
Therefore, \|\phi^{0}\|_{1}\leq L . For \phi\in\mathbb{X}_{0} , \|\phi\|_{1}\leq\|\phi-\phi^{0}\|_{1}+\|\phi^{0}\|_{1}\leq \frac{L}{1-p} .
We will prove that \Phi_{\phi}:\mathbb{X}_{0}\rightarrow \mathbb{X}_{0} is a contraction.
First, we prove that for any \phi\in\mathbb{X}_{0} and \Phi_{\phi}\in\mathbb{X}_{0} , let
Then,
Similarly, |G_{j}(t, \varphi, \psi)|\leq \big(b_{j}^{+}\beta_{j}^{+} +\sum\limits_{i = 1}^{m}t_{ij}^{+}(H_{i}+K_{i})\big)\|\phi\|_{1} = \gamma_{j}\|\phi\|_{1}, j = 1, 2, \cdots, m , where \theta_{i} = a_{i}^{+}\alpha_{i}^{+}+\sum\limits_{j = 1}^{m}s_{ji}^{+}(P_{j}+Q_{j}), \gamma_{j} = b_{j}^{+}\beta_{j}^{+}+\sum\limits_{i = 1}^{m}t_{ij}^{+}(H_{i}+K_{i}), i, j = 1, 2, \cdots, m .
For i = 1, 2, \cdots, m , we have
similarly, for j = 1, 2, \cdots, m , |(\Phi_{\phi}-\phi^{0})_{j}(t)|\leq(\frac{\gamma_{j}}{b_{j}^{-}}+\frac{J}{1-e^{-b_{j}^{-}\underline{\sigma}}})\|\phi\|_{1} .
Furthermore, for i = 1, 2, \cdots, m , we have
Similarly, for j = 1, 2, \cdots, m , we have
In the light of (H_{4}) , we have that \|\Phi_{\phi}-\phi^{0}\|_{1}\leq p\|\phi\|_{1} < \frac{pL}{1-p} , that is \Phi_{\phi}\in\mathbb{X}_{0} .
Next, we prove that \Phi_{\phi} is a contraction. For \phi = (\varphi_{1}, \varphi_{2}, \cdots, \varphi_{m}, \psi_{1}, \psi_{2}, \cdots, \psi_{m})^{T}, \overline{\phi} = (\overline{\varphi}_{1}, \overline{\varphi}_{2}, \cdots, \overline{\varphi}_{m}, \overline{\psi}_{1}, \overline{\psi}_{2}, \cdots, \overline{\psi}_{m})^{T}\in\mathbb{X}_{0} , it follows that
and |\overline{G}_{j}(t, \varphi, \psi)-\overline{G}_{j}(t, \overline{\varphi}, \overline{\psi})|\leq\big(b_{j}^{+}\beta_{j}^{+} +\sum\limits_{i = 1}^{m}t_{ij}^{+}(P_{i}+Q_{i})\big)\|\phi-\overline{\phi}\|_{1} = \gamma_{j}\|\phi-\overline{\phi}\|_{1}, \, \, j = 1, 2, \cdots, m .
And because
and
Similarly,
So, for i = 1, 2, \cdots, m , we have
and
Similarly, for j = 1, 2, \cdots, m , we have
By (H_{4}) , we have
which implies that \Phi_{\phi} is a contraction. Therefore, \Phi_{\phi} has a fixed point in \mathbb{X}_{0} , that is, (1.1) has a unique piecewise pseudo almost periodic solution in \mathbb{X}_{0} . This completes the proof. □
4.
Global exponential stability of piecewise pseudo almost periodic solutions
This section states and proves the sufficient conditions for the global exponential stability of piecewise pseudo almost periodic solutions of the system described by (1.1)–(1.2).
Theorem 4.1. Assume that conditions (H_{1}) – (H_{4}) are true and the following condition holds.
(H_5) For i , j = 1, 2, \cdots, m ,
Then, the piecewise pseudo almost periodic solutions of the system described by (1.1)–(1.2) is globally exponentially stable.
Proof. According to Theorem 3.4, the system (1.1) has at least one piecewise differentiable pseudo-almost periodic solution (\overline{x}_{1}(t), \overline{x}_{2}(t), \cdots, \overline{x}_{m}(t), \overline{y}_{1}(t), \overline{y}_{2}(t), \cdots, \overline{y}_{m}(t))^{T}\in X_{0} with the initial value condition \overline{\phi} = (\overline{\varphi}_{1}(\theta), \overline{\varphi}_{2}(\theta), \cdots, \overline{\varphi}_{m}(\theta), \overline{\psi}_{1}(\theta), \overline{\psi}_{2}(\theta), \cdots, \overline{\psi}_{m}(\theta))^{T} . Let
be an arbitrary solution of system (1.1) with the initial value condition
Let u_{i}(\cdot) = x_{i}(\cdot)-\overline{x}_{i}(\cdot) , v_{j}(\cdot) = y_{j}(\cdot)-\overline{y}_{j}(\cdot) ; for t\neq t_{k} and t > 0 , we have
The initial value conditions are as follows:
Multiplying e^{\int_{t_{k}}^{s}a_{i}(\tau)d\tau} on both sides of (4.1) and e^{\int_{t_{k}}^{s}b_{j}(\tau)d\tau} on both sides of (4.2), and integrating over [t_{k}, t] , we derive
Consider the following functions:
where h_{i}(s) = a_{i}^{+}\frac{e^{s\alpha_{i}^{+}}-1}{s} +\sum\limits_{j = 1}^{m}s_{ji}^{+}\big(P_{j}+Q_{j} e^{s\tau_{ji}^{+}}\big) , \overline{h}_{j}(s) = b_{j}^{+}\frac{e^{s\beta_{j}^{+}}-1}{s} +\sum\limits_{i = 1}^{m}t_{ij}^{+}\big(H_{i}e^{s\delta_{ij}^{+}}+K_{i}\big) .
For i, j = 1, 2, \cdots, m , since C_{i}(s) , D_{i}(s) are continuous on (0, a_{i}^{-}) , \overline{C}_{j}(s) , \overline{D}_{j}(s) are continuous on (0, b_{j}^{-}) , \lim\limits_{s\rightarrow 0}C_{i}(s) > 0 , \lim\limits_{s\rightarrow 0}\overline{C}_{j}(s) > 0 , \lim\limits_{s\rightarrow 0}D_{i}(s) > 0 , \lim\limits_{s\rightarrow 0}\overline{D}_{j}(s) > 0 , \lim\limits_{s\rightarrow a_{i}^{-}}C_{i}(s) < 0 , \lim\limits_{s\rightarrow a_{i}^{-}}D_{i}(s) < 0 , \lim\limits_{s\rightarrow b_{j}^{-}}\overline{C}_{j}(s) < 0 and \lim\limits_{s\rightarrow b_{j}^{-}}\overline{D}_{j}(s) < 0 . There exist constants s_{1}^{i} , s_{2}^{i}\in(0, a_{i}^{-}) and s_{3}^{j} , s_{4}^{j}\in(0, b_{j}^{-}) such that C_{i}(s_{1}^{i}) = 0 , D_{i}(s_{2}^{i}) = 0 , \overline{C}_{j}(s_{3}^{j}) = 0 and \overline{D}_{j}(s_{4}^{j}) = 0 . There exists a constant \eta\in(0, \min\limits_{1\leq i, j\leq m}\{s_{1}^{i}, s_{2}^{i}, s_{3}^{j}, s_{4}^{j}\}) such that C_{i}(\eta) > 0 , D_{i}(\eta) > 0 , \overline{C}_{j}(\eta) > 0 and \overline{D}_{j}(\eta) > 0 . Obviously, there is \eta\in(0, \min\{a_{i}^{-}, b_{j}^{-}\}) .
Take a positive sequence \{M_{k}\}_{k = 1}^{\infty} satisfying
where N_{k} = M_{k}\max\{1+I, 1+J\} , k\geq 1 , N_{0} = \max\{1+I, 1+J\} .
Let
Let \Upsilon = \|\phi-\overline{\phi}\|_{1} ; for i, j = 1, 2, \cdots, m , it is obvious that there exists a positive constant M_{0} > 1 such that the following inequalities hold
For t = t_{0}^{+} , we have
Therefore,
Now we will prove, for t\in(0, t_{1}] , l = 1, 2, \cdots, 2m , that
In order to prove that (4.6) is true, we first prove that for any \rho > 1 , t\in(0, t_{1}] , the following inequality holds:
If (4.7) is not established, there are l_{0}\in\{1, 2, \cdots, 2m\} and t'\in(0, t_{1}] such that
where t'\in(0, t_{1}] is the smallest variable such that (4.8) holds. There is a constant \sigma\geq 1 such that
and \|w_{l}(t)\|_{1} < M_{1}\rho\Upsilon e^{-\eta t}, \, \, t\in(0, t') .
For l_{0}\in\{1, 2, \cdots, m\} , let i_{0} = l_{0} ; from ( H_{5} ) and (4.3), we derive
where h_{i_{0}}(\eta) = a_{i_{0}}^{+}\frac{e^{\eta \alpha_{i_{0}}^{+}}-1}{\eta } +\sum\limits_{j = 1}^{m}s_{ji_{0}}^{+}\big(P_{j}+Q_{j} e^{\eta \tau_{ji_{0}}^{+}}\big) . Equations (4.10) and (4.11) are both in conflict with (4.9).
For l_{0}\in\{m+1, m+2, \cdots, 2m\} , let j_{0} = l_{0}-m ; similarly, from ( H_{5} ) and (4.4), we derive
where \overline{h}_{j_{0}}(\eta) = b_{j_{0}}^{+}\frac{e^{\eta \beta_{j_{0}}^{+}}-1}{\eta } +\sum\limits_{i = 1}^{m}t_{ij_{0}}^{+}\big(H_{i}e^{\eta \delta_{ij_{0}}^{+}}+K_{i}\big) . Equations (4.12) and (4.13) are both in conflict with (4.9).
Therefore, (4.8) is not valid. For t\in(0, t_{1}] , we have that (4.7) holds. Let \rho\rightarrow 1 ; for t\in(0, t_{1}] , (4.6) holds.
For t = t_{1}^{+} , we have
Therefore,
For t\in(t_{1}, t_{2}] , l = 1, 2, \cdots, 2m , we certify that
In order to prove that (4.15) is true, we first prove that for any \rho > 1 and t\in(t_{1}, t_{2}] , the following inequality holds:
If (4.16) is not established, there are l_{1}\in\{1, 2, \cdots, 2m\} and t''\in(t_{1}, t_{2}] such that
where t''\in(t_{1}, t_{2}] is the smallest variable such that (4.17) holds. There is a constant \sigma_{1}\geq 1 such that
and \|w_{l}(t)\|_{1} < M_{2}\rho\Upsilon e^{-\eta t}, t\in(t_{1}, t'') .
For l_{1}\in\{1, 2, \cdots, m\} , let i_{1} = l_{1} ; from (H_{5}) and (4.3), we derive
where h_{i_{1}}(\eta) = a_{i_{1}}^{+}\frac{e^{\eta \alpha_{i_{1}}^{+}}-1}{\eta } +\sum\limits_{j = 1}^{m}s_{ji_{1}}^{+}\big(P_{j}+Q_{j} e^{\eta \tau_{ji_{1}}^{+}}\big) . Equations (4.19) and (4.20) are both in conflict with (4.18).
For l_{1}\in\{m+1, m+2, \cdots, 2m\} , let j_{1} = l_{1}-m ; similarly, from (H_{5}) and (4.4), we derive
where \overline{h}_{j_{1}}(\eta) = b_{j_{1}}^{+}\frac{e^{\eta \beta_{j_{1}}^{+}}-1}{\eta } +\sum\limits_{i = 1}^{m}t_{ij_{1}}^{+}\big(H_{i}e^{\eta \delta_{ij_{1}}^{+}}+K_{i}\big) . Equations (4.21) and (4.22) are both in conflict with (4.18).
Therefore, (4.17) is not valid. For t\in(t_{1}, t_{2}] , we have that (4.16) holds. Let \rho\rightarrow 1 ; for t\in(t_{1}, t_{2}] , (4.15) holds.
Similar to the proof of (4.14) and (4.15), we deduce that
Let M = \sup\limits_{k\geq 1}\max\{M_{k}, N_{k-1}\} ; obviously, M > 1 ; we have
Therefore, for i, j = 1, 2, \cdots, m ,
From Definition 2.8, the piecewise pseudo almost periodic solution
of system (1.1) with the initial value conditions
is said to be globally exponentially stable. □
5.
Example
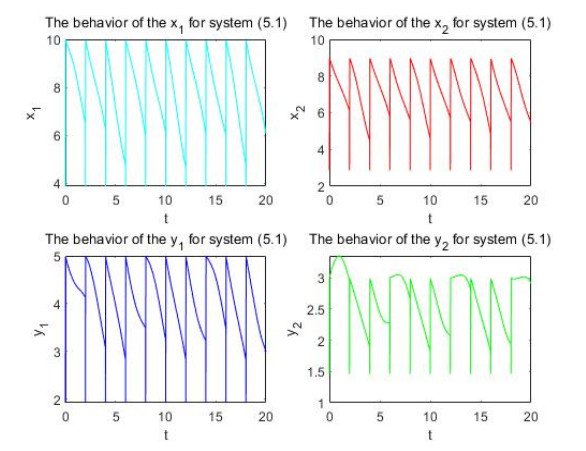
This section presents an example to illustrate the effectiveness of our results obtained in previous sections. Consider the following interval general BAM neural network with mixed time-varying delays and impulsive perturbations:
where f_{j}(x_{j}(t), y_{j}(t-\tau_{ji}(t))) = |x_{j}(t)|+|y_{j}(t-\tau_{ji}(t)|, g_{i}(x_{i}(t-\delta_{ij}(t)), y_{i}(t)) = |x_{i}(t-\delta_{ij}(t))|+|y_{i}(t)|, i, j = 1, 2 , and
Obviously,
By calculation, it is easy to acquire \underline{\sigma} = 2 , P_{j} = Q_{j} = H_{i} = K_{i} = 1 , i, j = 1, 2, \cdots, m , I = J = \frac{1}{40} and
For i, j = 1, 2, \cdots, m , p_{ij} = 0.7633 < 1 and 0.2 > \frac{11}{80} . That is, the conditions (H_1) – (H_5) are valid. From Theorems 3.4 and 4.1, system (5.1) has a piecewise pseudo almost periodic solution, which is globally exponentially stable. Computer simulations of the existence and stable behavior of the pseudo-almost periodic solutions are given in Figures 1 and 2, respectively.
6.
Conclusions
The pseudo almost periodic behaviors have been applied to the qualitative theory of differential equations. Piecewise pseudo almost periodic solutions of BAM neural networks are generalizations of almost periodic solutions, which have obvious scientific significance and application value in many fields such as signal processing, pattern recognition, associative memory, image processing and optimization problems.
This paper investigated the piecewise pseudo almost periodic solutions of the interval general BAM neural networks with mixed time-varying delays and impulsive perturbations. By employing the exponential dichotomy of linear differential equations, fixed-point theory for contraction mapping, differential inequality techniques and mathematical methods of induction, the effective conditions for the existence and global exponential stability of piecewise pseudo almost periodic solutions of system (1.1) have been established. From Theorems 3.4 and 4.1, the delays contained in the activation functions do not affect the existence and global exponential stability of piecewise pseudo almost periodic solutions of system (1.1). The existence and global exponential stability of the piecewise pseudo almost periodic solutions of the system (1.1) are determined by the negative feedback terms, leakage delays, connection weights, impulsive perturbations and the Lipschitz constants of the activation functions.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare that they have no competing interests concerning the publication of this article.









 DownLoad:
DownLoad:




