Pythagorean fuzzy incidence graphs with application in illegal wildlife trade

1.   Introduction

Graphs are useful tools for data analysis, complicated system modeling and information communication. They give us the ability to visualize and interpret data, which enables us to gain greater insights and make more rational decisions. A graph is a practical tool for understanding information about the connections between items. In operations research, system analysis and economics, graph models are widely used. Yet, in many real-life circumstances, a graph-theoretic issue may have a part that is uncertain and cannot be represented by a graph. Fuzzy models are preferable to handle problems with uncertainty. In fuzzy graph theory as well, connectivity evolved into a key idea. Connectivity is among the most essential concerns in graph theory and its applications. A difficulty that highlights the significance of connectedness in fuzzy graphs is the fact that total flow disconnection happens less frequently in physical issues than flow reduction between pairs of vertices. Understanding complex systems, optimizing resource allocation, building effective algorithms and obtaining insights into a variety of fields, ranging from social networks to biological systems, all depend on the study of connectivity in graphs.

Zadeh ^[1] developed the idea of a fuzzy subset of a set as an extension of the crisp set to indicate uncertainty. He considered the essential idea of a membership value. Since the crisp set only contains the truth values, $0$ (which means "false") and $1$ (which means "true"), it cannot be used to solve ambiguous real-life problems. A fuzzy set (FS) allowed an object to have the value of membership value within $[0, 1]$. The FS only considers a member's value of membership in a set. Atanassov ^[2] proposed the idea of intuitionistic fuzzy sets (IFSs) as a generalization of fuzzy sets. IFSs also consider the nonmembership value of a member such that the sum of membership and nonmembership values of a member is less than or equal to $1$. Xu and Yager ^[3] called $\phi = (\sigma_{\phi}, \mu_{\phi}),$ an intuitionistic fuzzy number (IFN). Yager ^[4,5] regarded Pythagorean fuzzy sets (PFSs) as a novel extension of IFSs, defined by the membership value and the nonmembership value fulfilling the condition that the sum of their squares is less than 1. PFSs are more capable than IFSs to model the uncertainties in real life decision-making problems. Yager and Abbasov ^[6] developed a relation between Pythagorean membership values and complex numbers.

Kaufmann ^[7] was the first to propose the idea of fuzzy graphs (FGs). Rosenfeld ^[8] explored a number of theoretical ideas, such as paths, cycles and connectedness in the FGs. Mathew and Sunitha ^[9] investigated node and arc connectivity in FGs. Chakraborty and Mahapatra ^[10] introduced the concept of intuitionistic fuzzy graphs (IFGs). Connectivity status of intuitionistic fuzzy graphs was discussed by Bera et al. ^[11] with application. Naz et al. ^[12] proposed the concept of Pythagorean fuzzy graphs (PFGs) along with their applications in decision-making. Akram and Naz ^[13] studied the energy of PFGs with applications. For other extensions and notations, the readers are referred to ^{[14,15,16,17]}. Akram et al. ^[18,19] illustrated connectivity concepts in m-polar fuzzy network models. Ahmad and Nawaz ^[20,21] studied connectivity in directed rough fuzzy graphs (DRFGs) and introduced the Wiener index of a DRFG. Ahmad and Batool ^[22] proposed the idea of domination in DRFGs with an application. For other applications, the readers are referred to ^{[23,24,25,26]}.

The drawback of FGs is that they provide no information concerning the impact of vertices on edges. For example, suppose vertices indicate different hostels, and edges represent the roads linking these hostels. We can create a graph to show the volume of traffic moving between the hostels. The hostel with the most guests will have the most ramps. If $S_{1}$ and $S_{2}$ are two different hostels, and $S_{1}S_{2}$ is a road connecting them, then $(S_{2}, S_{1}S_{2})$ could reveal the ramp system from the road $S_{1}S_{2}$ to the hostel $S_{2}$. The introduction of the concept of fuzzy incidence graphs was necessary to address this gap in these graphs. In interconnection networks with influenced flows, fuzzy incidence graphs are crucial. Thus, it is important to examine their connection features. Dinesh ^[27,28] proposed the concept of fuzzy incidence graphs (FIGs). Mordeson ^[29] developed the concept of incidence cut pairs in FIGs. Malik et al. ^[30] investigated complementary FIGs. Mathew and Mordeson ^[31] illustrated a variety of connectivity concepts in FIGs. They also covered other structural characteristics of FIGs. Fang et al. ^[32] discussed the connectivity index and Wiener index of FIGs. They also developed three different types of nodes in FIGs. Subsequently, Nazeer et al. ^[33] proposed the concepts of order, size, dominance and strong pair domination in FIGs. Strong and weak fuzzy incidence dominance as well as other forms of domination were also covered by them. Nazeer et al. ^[34] was the first to propose the concepts of cyclic connectivity, fuzzy incidence cycle, cyclic connectivity index and average cyclic connectivity index. For a more detailed and comprehensive study on FIGs, we may suggest ^[35] to the reader. Nazeer et al. ^[36] proposed the concept of intuitionistic fuzzy incidence graphs (IFIGs), which they describe as a generalization of FIGs with unique characteristics. In IFIGs, they discussed several types of product, such as the Cartesian product, composition, tensor product and normal product.

FIGs and IFIGs have potential applications in a wide range of sectors, particularly in those electrical, electronic and social networks where not only the edges and vertices are of interest, but additionally how they are related to one another is crucial. However, several issues in real life cannot be described using FIGs and IFIGs. We need a more general graph to handle these certain situations since FIGs and IFIGs may not handle them effectively. The Pythagorean fuzzy incidence graphs (PFIGs) would be a prominent research direction since uncertainties are well expressed using the PFSs. In interconnection networks with influenced flows, PFIGs are essential. Therefore, it is important to study their connectivity properties. Motivated by the factors above, the goal of our study is to propose a generalization of connectivity of FIGs that operate effectively in a Pythagorean fuzzy environment. The novel contributions of our study might be summed up as follows:

● The concept of incidence graph in Pythagorean fuzzy environment is introduced.

● In this work, we examine how the removal of a vertex, edge and pair from the PFIGs affects the strength of a vertex-edge pair's connectivity.

● We propose the idea of Pythagorean fuzzy incidence cycles and trees. Strong incidence pairs are used to describe Pythagorean fuzzy incidence trees and cut pairs.

● We establish the existence of the strongest incidence path between every vertex and edge. Also, we introduce some types of Pythagorean fuzzy incidence pairs, namely, $\alpha$-strong incidence pairs, $\beta$-strong incidence pairs and $\delta$-weak incidence pairs.

● The issue of illicit trafficking in wildlife is addressed by the proposed tools.

The other contents of this paper are structured as follows: In Section 2 we define Pythagorean fuzzy incidence graphs (PFIGs), incidence path and strength of incidence path. Pythagorean fuzzy incidence cycle and Pythagorean fuzzy incidence trees and a few relevant propositions are presented in Section 3. In Section 4, we discuss Pythagorean fuzzy incidence cut vertices, Pythagorean fuzzy incidence bridges and Pythagorean fuzzy incidence cut pairs in PFIG and prove several propositions on Pythagorean fuzzy incidence cut pairs. In Section 5, we define the strong Pythagorean fuzzy incidence pairs and demonstrate the types of strong Pythagorean fuzzy incidence pairs. This section also includes the concept of a strong incidence path and some results on strong Pythagorean incidence pairs. Section 6 provides an application of PFIG in illegal wildlife trade. In Section 7, a comparison between our research work and existing models is given. Lastly, in Section 8, we give some final remarks. The list of abbreviations is given in Table 1.

2.   Pythagorean fuzzy incidence graphs

In this section, we first present a few essential concepts that are relevant to this research article. We then define the Pythagorean fuzzy incidence graphs, subgraphs of Pythagorean fuzzy incidence graphs, complete Pythagorean fuzzy incidence subgraphs and the strength of connectedness between any two vertices of PFIGs. The notion of incidence graphs proposed by Dinesh ^[28] is defined below:

Definition 2.1. ^[28] An incidence graph on a non-empty set $V$ is a triplet $G = (V, E, I)$, where $E\subseteq V\times V, I\subseteq V\times E.$

Definition 2.2. ^[28] In an incidence graph $G = (V, E, I)$, if $(\check{q}, \check{t}\check{w})\in I,$ then $(\check{q}, \check{t}\check{w})$ is called a pair or incidence pair (IP).

Definition 2.3. ^[29] Let $G = (V, E, I)$ be an incidence graph. A sequence

is called a walk. It is closed if $\check{q}_{0} = \check{q}_{n}$. It is a trail if the edges are distinct and an incidence trail if the pairs are distinct. It is said to be a path if the vertices are distinct. A path is called a cycle if it is closed.

All IPs are distinct by the definition of a cycle. We consider the below sequences to be walks:

The latter is closed if $\check{q}\check{q}_{0} = \check{q}_{n}\check{q}_{n+1}$. They are called incidence paths (IPt if the vertices are distinct). According to the definition of an incidence path, if $\check{q}\check{t}$ is on the incidence path, then IPs of the type $(\check{q}, \check{q}\check{t})$ and $(\check{t}, \check{q}\check{t})$ are also on the incidence path but not an IP of the form $(\check{q}, \check{t}\check{w})$ with $\check{q}\neq \check{t}\neq \check{w}.$

Definition 2.4. ^[28] An incidence graph is said to be a connected incidence graph if every pair of vertices is connected by an incidence path. A tree is an incidence connected graph with no cycles. It is a forest if it is not connected.

Definition 2.5. ^[4,5] A Pythagorean fuzzy set (PFS) on a universe $\check{X}$ is an object of the form

where $\sigma_{\check{A}}: \check{X}\rightarrow [0, 1]$ and $\mu_{\check{A}}: \check{X}\rightarrow [0, 1]$ represent the membership and non-membership functions of $\check{A},$ respectively, such that for all $\check{x}\in \check{X}$,

$\pi_{\check{A}}(\check{x}) = \sqrt{1-(\sigma_{\check{A}}(\check{x}))^{2}-(\mu_{\check{A}}(\check{x}))^{2}}$ is called the degree of indeterminacy of element $\check{x}\in \check{X}$.

We now define a Pythagorean fuzzy incidence graph.

Definition 2.6. A PFIG on a non-empty set $V$ is an ordered triplet $\check{G} = (\check{J}, \check{K}, \check{L})$, where $\check{J} = < V, \sigma_{\check{J}}, \mu_{\check{J}} >$ is a PFS on $V$, $\check{K} = < E, \sigma_{\check{K}}, \mu_{\check{K}} >$ is a PFS on $E\subseteq V\times V$ such that

for all $\check{a}, \check{k}\in V$, and $\check{L} = < I, \sigma_{\check{L}}, \mu_{\check{L}} >$ is a PFS on $I\subseteq V\times E$ such that

for all $(\check{a}, \check{k}\check{l})\in I$.

Although pairs of the type $(\check{a}, \check{k}\check{l})$, where $\check{a}\neq \check{k} \neq \check{l}$ are allowed under the definition of PFIG, only pairs of the form $(\check{a}, \check{a}\check{k})$ will be taken into consideration.

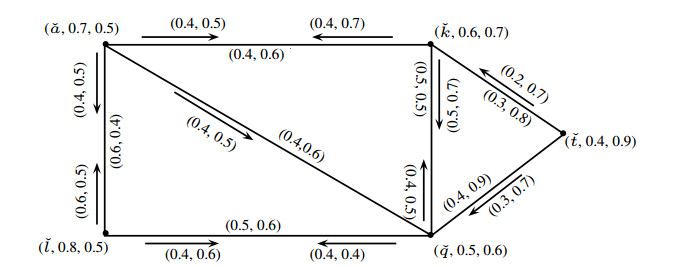
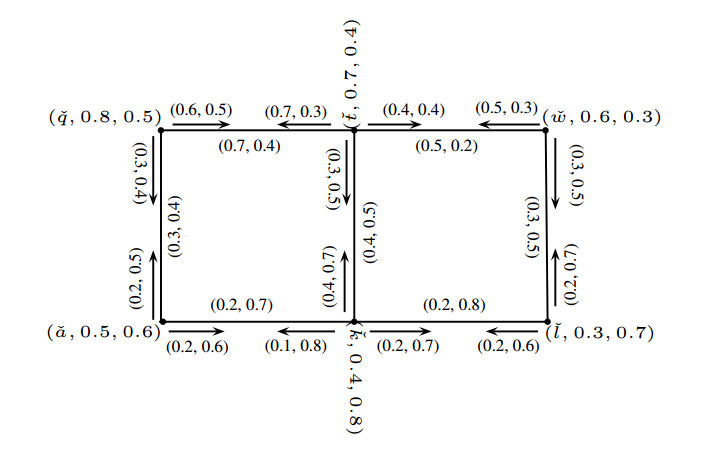
Example 2.1. Consider an incidence graph $G = (V, E, I),$ where $V = \{\check{q}, \check{t}, \check{a}, \check{k}, \check{l}\},$ $E = \{\check{a}\check{k}, \check{a}\check{l}, \check{k}\check{q}, \check{l}\check{q}, \check{a}\check{q},$$\check{k}\check{t}, \check{q}\check{t}\}\subseteq V\times V$, and $I = \{(\check{a}, \check{a}\check{k}), (\check{k}, \check{a}\check{k}), (\check{a}, \check{a}\check{l}), (\check{l}, \check{a}\check{l}), (\check{l}, \check{l}\check{q}), (\check{q}, \check{l}\check{q}), (\check{k}, \check{k}\check{q}), (\check{q}, \check{k}\check{q}), (\check{a}, \check{a}\check{q}), (\check{t}, \check{k}\check{t}), (\check{t}, \check{q}\check{t})\}$$\subseteq V\times E$. Let $\check{J}$, $\check{K}$ and $\check{L}$ be the PFSs defined on $V$, $E$ and $I$, respectively:

$\check{J} = \{(\check{q}, 0.5, 0.6), (\check{t}, 0.4, 0.9), (\check{a}, 0.7, 0.5), (\check{k}, 0.6, 0.7), (\check{l}, 0.8, 0.5)\},$ $\check{K} = \{(\check{a}\check{k}, 0.4, 0.6), (\check{a}\check{l}, 0.6, 0.4), (\check{k}\check{q}, 0.5, 0.5), (\check{l}\check{q}, 0.5, 0.6), (\check{a}\check{q}, 0.4, 0.6), (\check{k}\check{t}, 0.3, 0.8), (\check{q}\check{t}, 0.4, 0.9)\},$

$\check{L} = \{((\check{a}, \check{a}\check{k}), 0.4, 0.5), ((\check{k}, \check{a}\check{k}), 0.4, 0.7), ((\check{a}, \check{a}\check{l}), 0.4, 0.5), ((\check{l}, \check{a}\check{l}), 0.6, 0.5), ((\check{l}, \check{l}\check{q}), 0.4, 0.6), ((\check{q}, \check{l}\check{q}), 0.4,$$\; \; \; \; \; \; \; \; 0.4), ((\check{k}, \check{k}\check{q}), 0.5, 0.7), ((\check{q}, \check{k}\check{q}), 0.4, 0.5), ((\check{a}, \check{a}\check{q}), 0.4, 0.6), ((\check{t}, \check{k}\check{t}), 0.2, 0.7), ((\check{t}, \check{q}\check{t}), 0.3, 0.7)\}.$

By routine calculations, it is easy to see from Figure 1 that $\check{G} = (\check{J}, \check{K}, \check{L})$ is a PFIG.

Definition 2.7. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. The supports of $\check{J}$, $\check{K}$ and $\check{L}$, respectively, are defined below:

$supp(\check{J}) = \{\check{a}\in V\; |\; \sigma_{\check{J}}(\check{a})\neq 0\; \rm{or}\; \mu_{\check{J}}(\check{a})\neq 0\},$

$supp(\check{K}) = \{\check{a}\check{k}\in E\; |\; \sigma_{\check{K}}(\check{a}\check{k})\neq 0\; \rm{or}\; \mu_{\check{K}}(\check{a}\check{k})\neq 0\},$

$supp(\check{L}) = \{(\check{a}, \check{a}\check{k})\in V\times E\; |\; \sigma_{\check{L}}(\check{a}, \check{a}\check{k})\neq 0\; \rm{or}\; \mu_{\check{L}}(\check{a}, \check{a}\check{k})\neq 0\}$.

Definition 2.8. The incidence strength of PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is defined by $IS_{\check{G}} = (\sigma_{\check{G}}^{IS}, \mu_{\check{G}}^{IS})$, where $\sigma_{\check{G}}^{IS} = \min \{\sigma_{\check{L}}(\check{a}, \check{a}\check{k})\; |\; (\check{a}, \check{a}\check{k})\in supp(\check{L})\}$ and $\mu_{\check{G}}^{IS} = \max \{\mu_{\check{L}}(\check{a}, \check{a}\check{k})\; |\; (\check{a}, \check{a}\check{k})\in supp(\check{L})\}$.

Example 2.2. Consider a PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ as shown in Figure 2.1. Then,

$\sigma_{\check{G}}^{IS} = \min \{\sigma_{\check{L}}(\check{a}, \check{a}\check{k}), \sigma_{\check{L}}(\check{k}, \check{a}\check{k}), \sigma_{\check{L}}(\check{a}, \check{a}\check{l}), \sigma_{\check{L}}(\check{l}, \check{a}\check{l}), \sigma_{\check{L}}(\check{l}, \check{l}\check{q}), \sigma_{\check{L}}(\check{q}, \check{l}\check{q}), \sigma_{\check{L}}(\check{k}, \check{k}\check{q}), \sigma_{\check{L}}(\check{q}, \check{k}\check{q}), \sigma_{\check{L}}(\check{a}, \check{a}\check{q}), \\ \; \; \; \; \; \; \; \; \; \; \; \sigma_{\check{L}}(\check{t}, \check{k}\check{t}), \sigma_{\check{L}}(\check{t}, \check{q}\check{t})\}$ $\; \; \; \; \; \; = \min \{0.4, 0.4, 0.4, 0.6, 0.4, 0.4, 0.5, 0.4, 0.4, 0.2, 0.3\} = 0.2,$

$\mu_{\check{G}}^{IS} = \max \{\mu_{\check{L}}(\check{a}, \check{a}\check{k}), \mu_{\check{L}}(\check{k}, \check{a}\check{k}), \mu_{\check{L}}(\check{a}, \check{a}\check{l}), \mu_{\check{L}}(\check{l}, \check{a}\check{l}), \mu_{\check{L}}(\check{l}, \check{l}\check{q}), \mu_{\check{L}}(\check{q}, \check{l}\check{q}), \mu_{\check{L}}(\check{k}, \check{k}\check{q}), \mu_{\check{L}}(\check{q}, \check{k}\check{q}), \mu_{\check{L}}(\check{a}, \check{a}\check{q}), \\ \; \; \; \; \; \; \; \; \; \; \; \mu_{\check{L}}(\check{t}, \check{k}\check{t}), \mu_{\check{L}}(\check{t}, \check{q}\check{t})\}$ $\; \; \; \; \; \; = \max \{0.5, 0.7, 0.5, 0.5, 0.6, 0.4, 0.7, 0.5, 0.6, 0.7, 0.7\} = 0.7.$

Thus, the incidence strength of $\check{G}$ is $IS_{\check{G}} = (\sigma_{\check{G}}^{IS}, \mu_{\check{G}}^{IS}) = (0.2, 0.7).$

Definition 2.9. A PFIG $\check{H} = (\check{M}, \check{Q}, \check{S})$ is called a partial Pythagorean fuzzy incidence subgraph of PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ if

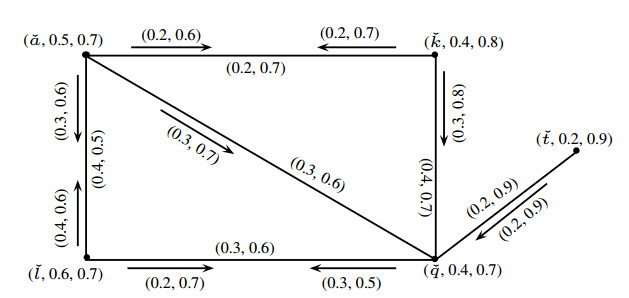
Example 2.3. Consider a PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ as shown in Figure 1. Let $\check{M} = \{(\check{q}, 0.4, 0.7), (\check{t}, 0.2, 0.9),$$(\check{a}, 0.5, 0.7), (\check{k}, 0.4, 0.8), (\check{l}, 0.6, 0.7)\},$ $\check{Q} = \{(\check{a}\check{k}, 0.2, 0.7), (\check{a}\check{l}, 0.4, 0.5), (\check{l}\check{q}, 0.3, 0.6), (\check{a}\check{q}, 0.3, 0.6), (\check{k}\check{q},$$0.4, 0.7), (\check{q}\check{t}, 0.2, 0.9)\},$ and $\check{S} = \{((\check{a}, \check{a}\check{k}), 0.2, 0.6), (\check{k}, \check{a}\check{k}), 0.2, 0.7), ((\check{a}, \check{a}\check{l}), 0.3, 0.6), ((\check{l}, \check{a}\check{l}), 0.4, 0.6),$$((\check{l}, \check{l}\check{q}), 0.2, 0.7), ((\check{q}, \check{l}\check{q}), 0.3, 0.5), ((\check{a}, \check{a}\check{q}), 0.3, 0.7), ((\check{k}, \check{k}\check{q}), 0.3, 0.8), ((\check{t}, \check{q}\check{t}), 0.2, 0.8)\}$.

By direct calculations, it is easy to see from Figure 2 that $\check{H} = (\check{M}, \check{Q}, \check{S})$ is a partial Pythagorean fuzzy incidence subgraph of $\check{G} = (\check{J}, \check{K}, \check{L})$.

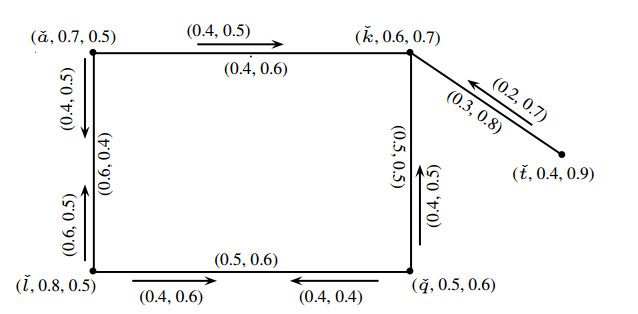
Definition 2.10. A PFIG $\check{H} = (\check{M}, \check{Q}, \check{S})$ is called a Pythagorean fuzzy incidence subgraph (PFIS) of PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ if

A PFIS $\check{H} = (\check{M}, \check{Q}, \check{S})$ is said to bea spanning Pythagorean fuzzy incidence subgraph (SPFIS) of PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ if $supp(\check{M}) = supp(\check{J})$.

Example 2.4. Consider a PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ as shown in Figure 1. A PFIS and SPFIS of $\check{G} = (\check{J}, \check{K}, \check{L})$ are shown in Figures 3 and 4, respectively.

Definition 2.11. A PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is called a complete PFIG if

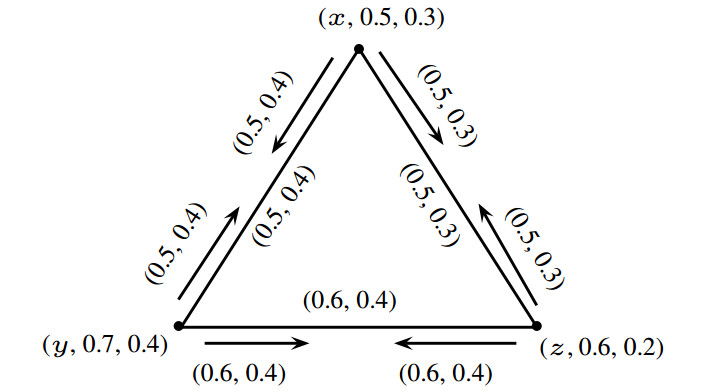
Example 2.5. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ with $\check{J} = \{(x, 0.5, 0.3), (y, 0.7, 0.4), (z, 0.6, 0.2)\}$ be a PFIG as shown in Figure 5. By routine calculations, it is easy to see that $\check{G} = (\check{J}, \check{K}, \check{L})$ is a complete PFIG.

Definition 2.12. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. An IPt is a walk of distinct vertices, edges and pairs.

Definition 2.13. The incidence strength of an IPt $\check{P}$ of PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$, denoted by $IS_{\check{P}}$, is defined by

where $\sigma_{\check{P}}^{IS} = \min \{\sigma_{\check{L}}(\check{a}, \check{a}\check{k})\; :\; (\check{a}, \check{a}\check{k})\in \check{P}\}$ and $\mu_{\check{P}}^{IS} = \max \{\mu_{\check{L}}(\check{a}, \check{a}\check{k})\; :\; (\check{a}, \check{a}\check{k})\in \check{P}\}$ are $\sigma$-incidence strength and $\mu$-incidence strength of $\check{P}$, respectively.

Example 2.6. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG as shown in Figure 6. Consider a $\check{q} - \check{l}$ IPt between vertices $\check{q}$ and $\check{l}$,

The $\sigma$-incidence strength of an IPt $\check{P}_{1}$ is given by

and the $\mu$-incidence strength of an IPt $\check{P}_{1}$ is given by

Thus, the incidence strength of an IPt $\check{P}_{1}$ is $IS_{\check{P}_{1}} = (\sigma_{\check{P}_{1}}^{IS}, \mu_{\check{P}_{1}}^{IS}) = (0.2, 0.7).$ Consider an $\check{a} - \check{t}\check{w}$ IPt between a vertex $\check{a}$ and an edge $\check{t}\check{w}$,

The $\sigma$-incidence strength of an IPt $\check{P}_{2}$ is given by

and the $\mu$-incidence strength of an IPt $\check{P}_{2}$ is given by

Thus, the incidence strength of an IPt $\check{P}_{2}$ is $IS_{\check{P}_{2}} = (\sigma_{\check{P}_{2}}^{IS}, \mu_{\check{P}_{2}}^{IS}) = (0.1, 0.8).$ Consider an $\check{a}\check{k} - \check{w}\check{l}$ IPt between edges $\check{a}\check{k}$ and $\check{w}\check{l}$,

The $\sigma$-incidence strength of an IPt $\check{P}_{3}$ is given by

and the $\mu$-incidence strength of an IPt $\check{P}_{3}$ is given by

Thus, the incidence strength of an IPt $\check{P}_{3}$ is $IS_{\check{P}_{3}} = (\sigma_{\check{P}_{3}}^{IS}, \mu_{\check{P}_{3}}^{IS}) = (0.1, 0.8).$

Definition 2.14. In a PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$, the incidence strength of connectedness between vertices $\check{a}$ and $\check{k}$, denoted by $ICONN_{\check{G}}(\check{a}, \check{k})$, is defined by

where $ICONN_{\sigma(\check{G})}(\check{a}, \check{k}) = \max \{\sigma_{\check{P}_{i}}^{IS}\}$ and $ICONN_{\mu(\check{G})}(\check{a}, \check{k}) = \min \{\mu_{\check{P}_{i}}^{IS}\}$ are $\sigma$-incidence strength and $\mu$-incidence strength of connectedness between $\check{a}$ and $\check{k}$, respectively. Here $\check{P}_{i}$ represents all possible IPts between $\check{a}$ and $\check{k}$.

We now define incidence strength of connectedness of an IPt between a vertex and an edge in PFIG.

Definition 2.15. A vertex $\check{a}$ and an edge $\check{k}\check{l}$ in a PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ are called connected if an IPt exists between them.

Definition 2.16. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. The incidence strength of connectedness between a vertex $\check{a}$ and an edge $\check{k}\check{l}$, denoted by $ICONN_{\check{G}}(\check{a}, \check{k}\check{l})$, is defined by

where $ICONN_{\sigma(\check{G})}(\check{a}, \check{k}\check{l}) = \max \{\sigma_{\check{P}_{i}}^{IS}\}$ and $ICONN_{\mu(\check{G})}(\check{a}, \check{k}\check{l}) = \min \{\mu_{\check{P}_{i}}^{IS}\}$ are $\sigma$-incidence strength and $\mu$-incidence strength of connectedness between $\check{a}$ and $\check{k}\check{l}$, respectively. Here $\check{P}_{i}$ represents all possible IPts between $\check{a}$ and $\check{k}\check{l}$.

Example 2.7. Consider a PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ as shown in Figure 6. All possible $\check{q} - \check{k}\check{l}$ IPts are

$\check{P}_{1}: \check{q}, (\check{q}, \check{q}\check{a}), \check{q}\check{a}, (\check{a}, \check{q}\check{a}), \check{a}, (\check{a}, \check{a}\check{k}),$$\check{a}\check{k}, (\check{k}, \check{a}\check{k}), \check{k}, (\check{k},$$\check{k}\check{t}), \check{k}\check{t}, \check{t}, (\check{t},$$\check{t}\check{w}), \check{t}\check{w}, (\check{w}, \check{t}\check{w}), \check{w}, (\check{w}, \check{w}\check{l}), \check{w}\check{l}, (\check{l}, \check{w}\check{l}),$$\check{l}, (\check{l}, \check{l}\check{k}), \check{l}\check{k} = \check{k}\check{l};$

$\check{P}_{2}: \check{q}, (\check{q}, \check{q}\check{t}), \check{q}\check{t}, (\check{t}, \check{q}\check{t}), \check{t}, (\check{t}, \check{t}\check{w}), \check{t}\check{w}, (\check{w}, \check{t}\check{w}), \check{w},$$(\check{w}, \check{w}\check{l}), \check{w}\check{l}, (\check{l}, \check{w}\check{l}), \check{l}, (\check{l}, \check{l}\check{k}), \check{l}\check{k} = \check{k}\check{l};$ $\check{P}_{3}: \check{q}, (\check{q}, \check{q}\check{t}), \check{q}\check{t}, (\check{t}, \check{q}\check{t}), \check{t}, (\check{t}, \check{t}\check{k}), \check{t}\check{k}, (\check{k}, \check{t}\check{k}), \check{k}, (\check{k}, \check{k}\check{l}), \check{k}\check{l};$

$\check{P}_{4}: \check{q}, (\check{q}, \check{q}\check{a}), \check{q}\check{a}, (\check{a}, \check{q}\check{a}), \check{a}, (\check{a}, \check{a}\check{k}), \check{a}\check{k}, (\check{k}, \check{a}\check{k}), \check{k}, (\check{k}, \check{k}\check{l}), \check{k}\check{l}.$

The incidence strengths of these IPts are given by

The $\sigma$-incidence strength and $\mu$-incidence strength of connectedness are given by

Thus, $ICONN_{\check{G}}(\check{q}, \check{k}\check{l}) = (ICONN_{\sigma(\check{G})}(\check{q}, \check{k}\check{l}), ICONN_{\mu(\check{G})}(\check{q}, \check{k}\check{l})) = (0.2, 0.7).$

All possible $\check{q} - \check{q}\check{a}$ IPts are

$\check{P}_{1}: \check{q}, (\check{q}, \check{q}\check{t}), \check{q}\check{t}, (\check{t}, \check{q}\check{t}), \check{t}, (\check{t}, \check{t}\check{w}), \check{t}\check{w}, (\check{w}, \check{t}\check{w}), \check{w}, (\check{w}, \check{w}\check{l}), \check{w}\check{l}, (\check{l}, \check{w}\check{l}), \check{l}, (\check{l}, \check{l}\check{k}), \check{l}\check{k}, (\check{k}, \check{l}\check{k}), \check{k}, (\check{k}, \check{k}\check{a}), \check{k}\check{a}, (\check{a}, \check{k}\check{a}), \check{a}, (\check{a}, \check{a}\check{q}), \check{a}\check{q} = \check{q}\check{a};$

$\check{P}_{2}: \check{q}, (\check{q}, \check{q}\check{t}), \check{q}\check{t}, (\check{t}, \check{q}\check{t}), \check{t}, (\check{t}, \check{t}\check{k}), \check{t}\check{k}, (\check{k}, \check{t}\check{k}), \check{k}, (\check{k}, \check{k}\check{a}), \check{k}\check{a}, (\check{a}, \check{k}\check{a}), \check{a}, (\check{a}, \check{a}\check{q}), \check{a}\check{q} = \check{q}\check{a};$

$\check{P}_{3}: \check{q}, (\check{q}, \check{q}\check{a}), \check{q}\check{a}.$

The incidence strengths of these IPts are given by

The $\sigma$-incidence strength and $\mu$-incidence strength of connectedness are given by

Thus, $ICONN_{\check{G}}(\check{q}, \check{q}\check{a}) = (ICONN_{\sigma(\check{G})}(\check{q}, \check{q}\check{a}), ICONN_{\mu(\check{G})}(\check{q}, \check{q}\check{a})) = (0.3, 0.4).$

Proposition 2.1. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG and $\check{H} = (\check{M}, \check{Q}, \check{S})$ be a PFIS of $\check{G}$. Then, for every $(\check{a}, \check{a}\check{k})\in supp(\check{S})$,

Definition 2.17. An $\check{a} - \check{k}\check{l}$ IPt $\check{P}$ in a PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is called a strongest $\check{a} - \check{k}\check{l}$ IPt if its incidence strength equals $ICONN_{\check{G}}(\check{a}, \check{k}\check{l})$, i.e., $ICONN_{\sigma(\check{G})}(\check{a}, \check{k}\check{l}) = \sigma_{\check{P}}^{IS}$ and $ICONN_{\mu(\check{G})}(\check{a}, \check{k}\check{l})$ $= \mu_{\check{P}}^{IS}$.

Remark 2.1. An IPt $\check{P}_{1}$ is said to have more incidence strength than an IPt $\check{P}_{2}$ if $\sigma_{\check{P}_{1}}^{IS} > \sigma_{\check{P}_{2}}^{IS}$, $\mu_{\check{P}_{1}}^{IS} < \mu_{\check{P}_{2}}^{IS}$. Note that the strongest IPt does not have to be unique.

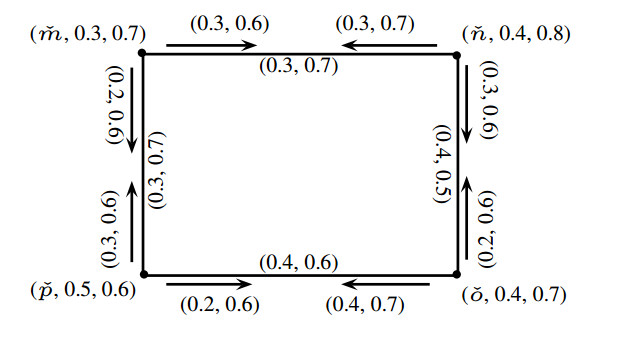
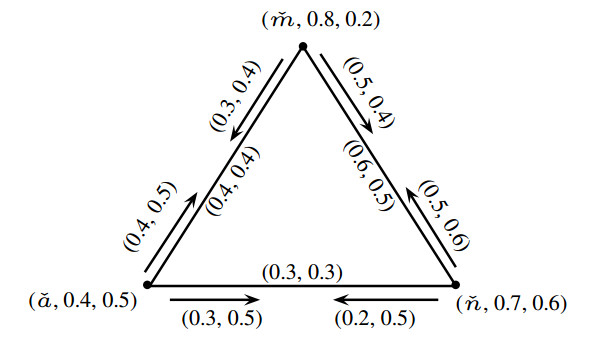
Example 2.8. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG as shown in Figure 7. All possible $\check{n} - \check{m}\check{n}$ IPts are

$\check{P}_{1}: \check{n}, (\check{n}, \check{m}\check{n}), \check{m}\check{n};$

$\check{P}_{2}: \check{n}, (\check{n}, \check{n}\check{o}), \check{n}\check{o}, (\check{o}, \check{n}\check{o}), \check{o}, (\check{o}, \check{o}\check{m}), \check{o}\check{m}, (\check{m}, \check{o}\check{m}), \check{m}, (\check{m}, \check{m}\check{n}), \check{m}\check{n};$

$\check{P}_{3}: \check{n}, (\check{n}, \check{n}\check{p}), \check{n}\check{p}, (\check{p}, \check{n}\check{p}), \check{p}, (\check{p}, \check{p}\check{m}), \check{p}\check{m}, (\check{m}, \check{p}\check{m}), \check{m}, (\check{m}, \check{m}\check{n}), \check{m}\check{n}.$

The incidence strengths of these IPts are given by

Thus, $ICONN_{\check{G}}(\check{n}, \check{m}\check{n}) = (ICONN_{\sigma(\check{G})}(\check{n}, \check{m}\check{n}), ICONN_{\mu(\check{G})}(\check{n}, \check{m}\check{n})) = (0.4, 0.6).$

The IPt $\check{P}_{2}: \check{n}, (\check{n}, \check{n}\check{o}), \check{n}\check{o}, (\check{o}, \check{n}\check{o}), \check{o}, (\check{o}, \check{o}\check{m}),$$\check{o}\check{m}, (\check{m}, \check{o}\check{m}), \check{m}, (\check{m}, \check{m}\check{n}), \check{m}\check{n}$ is a strongest $n - nm$ IPt since $ICONN_{\sigma(\check{G})}(\check{n}, \check{m}\check{n}) = \sigma_{\check{P}_{2}}^{IS}$ and $ICONN_{\mu(\check{G})}(\check{n}, \check{m}\check{n}) = \mu_{\check{P}_{2}}^{IS}$. Similarly, $\check{n}, (\check{n}, \check{n}\check{o}), \check{n}\check{o}$ is the strongest $\check{n} - \check{n}\check{o}$ IPt. Note that both $\check{p}, (\check{p}, \check{p}\check{m}), \check{m}\check{p}, (\check{m}, \check{p}\check{m}),$$\check{m}, (\check{m}, \check{m}\check{n}), \check{m}\check{n}, (\check{n}, \check{m}\check{n}), \check{n}, (\check{n}, \check{n}\check{p}), \check{n}\check{p}$ and $\check{p}, (\check{p}, \check{p}\check{m}), \check{m}\check{p}, (\check{m}, \check{p}\check{m}), \check{m}, (\check{m}, \check{m}\check{o}), \check{m}\check{o}, (\check{o}, \check{m}\check{o}), \check{o}, (\check{o}, \check{o}\check{n}), \check{o}\check{n}, (\check{n}, \check{o}\check{n}), \check{n}, (\check{n}, \check{n}\check{p}), \check{n}\check{p}$ are strongest $\check{p} - \check{n}\check{p}$ IPts.

3.   Pythagorean fuzzy incidence cycles and trees

In this section, we define the notions of Pythagorean fuzzy incidence cycles and Pythagorean fuzzy incidence trees in Pythagorean fuzzy incidence graphs and then prove several propositions. The definition of cycle of a PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is given below:

Definition 3.1. A PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a cycle if $(supp(\check{J}), supp(\check{K}), supp(\check{L}))$ is a cycle.

Definition 3.2. A PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a Pythagorean fuzzy cycle if $(supp(\check{J}), supp(\check{K}), supp(\check{L}))$ is a cycle and no unique $\check{q}\check{t}\in supp(\check{K})$ exists such that $\sigma_{\check{K}}(\check{q}\check{t}) = \min \{\sigma_{\check{K}}(\check{a}\check{k})\; |\; \check{a}\check{k}\in supp(\check{K})\}$ and $\mu_{\check{K}}(\check{q}\check{t}) = \max \{\mu_{\check{K}}(\check{a}\check{k})\; |\; \check{a}\check{k}\in supp(\check{K})\}$.

Definition 3.3. A PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a Pythagorean fuzzy incidence cycle (PFIC) if it is a Pythagorean fuzzy cycle and no unique $(\check{q}, \check{q}\check{t})\in supp(\check{L})$ exists such that

Definition 3.4. A pair $(\check{q}, \check{q}\check{t})$ is called a weakest IP of cycle $\mathfrak{C}$ if $\sigma_{\check{L}}(\check{q}, \check{q}\check{t}) = \min \{\sigma_{\check{L}}(\check{a}, \check{a}\check{k})\; |\; (\check{a}, \check{a}\check{k})\in \mathfrak{C}\}$ and $\mu_{\check{L}}(\check{q}, \check{q}\check{t}) = \max \{\mu_{\check{L}}(\check{a}, \check{a}\check{k})\; |\; (\check{a}, \check{a}\check{k})\in \mathfrak{C}\}$.

Example 3.1. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG as shown in Figure 8. Consider the walk

It is a cycle.

Since

and also $\sigma_{\check{K}}(\check{p}\check{m}) = 0.3, \mu_{\check{K}}(\check{p}\check{m}) = 0.7$. Thus, $\check{G}$ is a Pythagorean fuzzy cycle. $\check{G}$ is a PFIC since

and also $\sigma_{\check{L}}(\check{o}, \check{o}\check{p}) = \sigma_{\check{L}}(\check{m}, \check{m}\check{p}) = 0.2, \mu_{\check{L}}(\check{o}, \check{o}\check{p}) = \mu_{\check{L}}(\check{m}, \check{m}\check{p}) = 0.7$.

Definition 3.5. A connected PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a tree if $(supp(\check{J}), supp(\check{K}), supp(\check{L}))$ is a tree.

Definition 3.6. A connected PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a Pythagorean fuzzy tree if it has a Pythagorean fuzzy incidence spanning subgraph $\check{T} = (\check{M}, \check{Q}, \check{S})$ which is a tree such that for all $\check{a}\check{k}$ not in $\check{T}, \sigma_{\check{K}}(\check{a}\check{k}) < CONN_{\sigma(\check{T})}(\check{a}, \check{k})$ and $\mu_{\check{K}}(\check{a}\check{k}) > CONN_{\mu(\check{T})}(\check{a}, \check{k})$.

Definition 3.7. A connected PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a Pythagorean fuzzy incidence tree (PFIT) if it has a Pythagorean fuzzy incidence spanning subgraph $\check{T} = (\check{M}, \check{Q}, \check{S})$ which is a tree such that for every $(\check{a}, \check{a}\check{k})$ not in $\check{T}$,

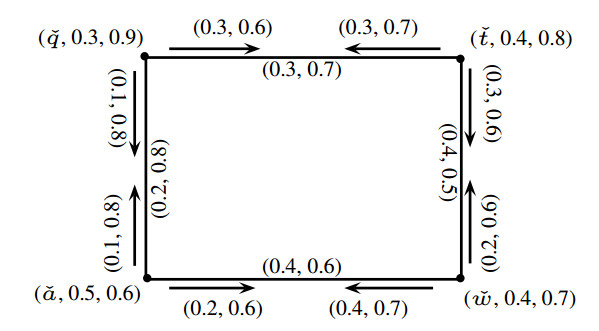
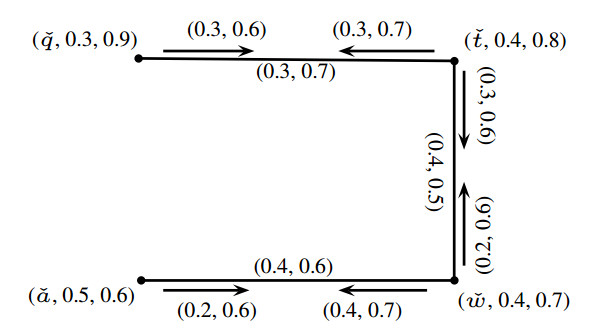
Example 3.2. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG as shown in Figure 9. It is easy to see that $\check{G}$ has a SPFIS $\check{T} = (\check{M}, \check{Q}, \check{S})$ as shown in Figure 10. This is a tree, and $CONN_{\sigma(\check{T})}(\check{q}, \check{a}) = 0.3, CONN_{\mu(\check{T})}(\check{q}, \check{a}) = 0.7$.

Since $\check{q}\check{a}\in supp(\check{K})\setminus supp(\check{Q})$ satisfies

Thus, $\check{G}$ is a Pythagorean fuzzy tree. Also, $ICONN_{\sigma(\check{T})}(\check{a}, \check{a}\check{q}) = 0.2, ICONN_{\mu(\check{T})}(\check{a}, \check{a}\check{q}) = 0.7,$ and $ICONN_{\sigma(\check{T})}(\check{q}, \check{a}\check{q}) = 0.2, ICONN_{\mu(\check{T})}(\check{q}, \check{a}\check{q}) = 0.7$. Since $(\check{a}, \check{a}\check{q})\in supp(\check{L})\setminus supp(\check{S})$,

and $(\check{q}, \check{a}\check{q})\in supp(\check{L})\setminus supp(\check{S})$,

Thus, $\check{G} = (\check{J}, \check{K}, \check{L})$ is a PFIT.

Definition 3.8. The PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a forest if $(supp(\check{J}), supp(\check{K}), supp(\check{L}))$ is a forest.

Definition 3.9. A PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a Pythagorean fuzzy forest if it has a Pythagorean fuzzy incidence spanning subgraph $\check{F} = (\check{M}, \check{Q}, \check{S})$ which is a forest such that for all $\check{a}\check{k}$ not in $\check{F}, \sigma_{\check{K}}(\check{a}\check{k}) < CONN_{\sigma(\check{F})}(\check{a}, \check{k})$ and $\mu_{\check{K}}(\check{a}\check{k}) > CONN_{\mu(\check{F})}(\check{a}, \check{k})$.

Definition 3.10. A PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a Pythagorean fuzzy incidence forest (PFIF) if it has a Pythagorean fuzzy incidence spanning subgraph $\check{F} = (\check{M}, \check{Q}, \check{S})$ which is a forest such that for every $(\check{a}, \check{a}\check{k})$ not in $\check{F}$,

Proposition 3.1. A PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is a PFIF if and only if in any cycle of $\check{G}$, there is an IP $(\check{a}, \check{a}\check{k})$ such that $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) < ICONN_{\sigma(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) > ICONN_{\mu(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k}).$

Proof. The result is trivially true if there are no cycles. Let $(\check{a}, \check{a}\check{k})\in \check{G}$ and let $(\check{a}, \check{a}\check{k})$ belong to a Pythagorean fuzzy cycle such that

Let $(\check{a}, \check{a}\check{k})$ be a weakest IP of cycle $\mathfrak{C}$, i.e.,

Then, PFIS obtained after deleting IP $(\check{a}, \check{a}\check{k})$ is a PFIF. Remove IPs in a similar manner if there are any further cycles. The removed IP will always have a lesser incidence strength than those eliminated previously at each step. The PFIS that remains after deletion of IPs is a PFIF. As a result, there is an IPt $\check{P}$ between $\check{a}$ and $\check{a}\check{k}$ such that $\sigma_{\check{P}}^{IS} > \sigma_{\check{L}}(\check{a}, \check{a}\check{k})$, $\mu_{\check{P}}^{IS} < \mu_{\check{L}}(\check{a}, \check{a}\check{k})$ and does not include $(\check{a}, \check{a}\check{k})$. If earlier deleted IPs still exist in $\check{P}$, we can use an IPt with more incidence strength to bypass them.

Conversely, if $\check{G}$ is a PFIF, and $\mathfrak{C}$ is any cycle, then by definition, there exist $(\check{a}, \check{a}\check{k})$ IPs of $\mathfrak{C}$ not in $\check{F}$ such that

where $\check{F}$ is as in the PFIF definition. □

Proposition 3.2. If there is at most one IPt between any vertex $\check{a}$ and edge $\check{a}\check{k}$ of PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ with the most incidence strength, then $\check{G}$ is a PFIF.

Proof. Let $\check{G}$ be not a PFIF. Then, by Proposition 3.1, $\exists$ a cycle $\mathfrak{C}$ in $\check{G}$ such that for all $(\check{a}, \check{a}\check{k})\in \mathfrak{C},$ $\sigma_{\check{L}}(\check{a}, \check{a}\check{k})\geq ICONN_{\sigma(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k})\leq ICONN_{\mu(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})$. Therefore $\check{a}, (\check{a}, \check{a}\check{k}), \check{a}\check{k}$ is the strongest IPt between $\check{a}$ and $\check{a}\check{k}$. Suppose $(\check{a}, \check{a}\check{k})$ is a weakest IP of cycle $\mathfrak{C}$, and then $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) = \min \{\sigma_{\check{L}}(\check{q}, \check{q}\check{t})\; |\; (\check{q}, \check{q}\check{t})\in \mathfrak{C}\}$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) = \max \{\mu_{\check{L}}(\check{q}, \check{q}\check{t})\; |\; (\check{q}, \check{q}\check{t})\in \mathfrak{C}\}$. Hence, the remaining portion of $\mathfrak{C}$ is the IPt between $\check{a}$ and $\check{a}\check{k}$ with the most incidence strength, which is a contradiction. Hence, $\check{G}$ is a PFIF. □

Proposition 3.3. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a cycle. Then, $\check{G}$ is a PFIC if and only if $\check{G}$ is not a PFIT.

Proof. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIC. Then, $\exists$ at least two IPs $(\check{a}, \check{a}\check{k})\in supp(\check{L})$ with

Let $\check{T} = (\check{M}, \check{Q}, \check{S})$ be a spanning PFIT in $\check{G} = (\check{J}, \check{K}, \check{L})$. Then{, } there exists $(\check{q}, \check{q}\check{t})$ such that $supp(\check{L})\setminus supp(\check{S}) = \{(\check{q}, \check{q}\check{t})\}$. Hence, IPt between $\check{q}$ and $\check{q}\check{t}$ in $\check{T} = (\check{M}, \check{Q}, \check{S})$ such that $\sigma_{\check{L}}(\check{q}, \check{q}\check{t}) < ICONN_{\sigma(\check{T})}(\check{q}, \check{q}\check{t})$ and $\mu_{\check{L}}(\check{q}, \check{q}\check{t}) > ICONN_{\mu(\check{T})}(\check{q}, \check{q}\check{t})$ does not exist. Thus, $\check{T} = (\check{M}, \check{Q}, \check{S})$ is not a PFIT.

Conversely, assume that $\check{G} = (\check{J}, \check{K}, \check{L})$ is not a PFIT. Since $\check{G}$ is a cycle, $\forall\; (\check{q}, \check{q}\check{t})\in supp(\check{L})$, we have a SPFIS $\check{T} = (\check{M}, \check{Q}, \check{S})$ which is a tree. $\sigma_{\check{S}}(\check{q}, \check{q}\check{t}) = 0 = \mu_{\check{S}}(\check{q}, \check{q}\check{t})$,

and $\sigma_{\check{S}}(\check{a}, \check{a}\check{k}) = \sigma_{\check{L}}(\check{a}, \check{a}\check{k}), \; \mu_{\check{S}}(\check{a}, \check{a}\check{k}) = \mu_{\check{L}}(\check{a}, \check{a}\check{k}), \; \forall\; (\check{a}, \check{a}\check{k})\in supp(\check{L})\setminus \{(\check{q}, \check{q}\check{t})\}$. Hence, IP $(\check{a}, \check{a}\check{k})$ for which $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) = \min \{\sigma_{\check{L}}(\check{q}, \check{q}\check{t})\; |\; (\check{q}, \check{q}\check{t})\in supp(\check{L})\}$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) = \max \{\mu_{\check{L}}(\check{q}, \check{q}\check{t})\; |\; (\check{q}, \check{q}\check{t})\in supp(\check{L})\}$ holds is not unique. Thus, $\check{G} = (\check{J}, \check{K}, \check{L})$ is a PFIC. □

Proposition 3.4. If $\check{G} = (\check{J}, \check{K}, \check{L})$ is a PFIT, and $\check{G}^{*} = (supp(\check{J}), supp(\check{K}), supp(\check{L}))$ is not a tree, then there exists at least one IP $(\check{a}, \check{a}\check{k})$ such that $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) < ICONNG_{\sigma(\check{G})}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) > ICONNG_{\mu(\check{G})}(\check{a}, \check{a}\check{k})$.

Proof. Since $\check{G}$ is a PFIT, there exists a SPFIS $\check{T} = (\check{M}, \check{Q}, \check{S})$ that is a tree, and for every $(\check{a}, \check{a}\check{k})\notin \check{T}$,

Also,

Thus, for every $(\check{a}, \check{a}\check{k})\notin \check{T},$

Thus, one IP $(\check{a}, \check{a}\check{k})\notin \check{T}$ exists. □

Proposition 3.5. If $\check{G} = (\check{J}, \check{K}, \check{L})$ is a PFIT, then $\check{G}$ is not a complete PFIG.

Proof. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a complete PFIG, and then for all $(\check{a}, \check{a}\check{k})$

Since $\check{G} = (\check{J}, \check{K}, \check{L})$ is a PFIT, for every $(\check{a}, \check{a}\check{k})$ not in $\check{T} = (\check{M}, \check{Q}, \check{S})$

where $\check{T} = (\check{M}, \check{Q}, \check{S})$ is a SPFIS of $\check{G} = (\check{J}, \check{K}, \check{L})$, which is a tree. Thus,

which is not possible. Hence, $\check{G} = (\check{J}, \check{K}, \check{L})$ is not a complete PFIG. □

4.   Pythagorean fuzzy incidence cut vertices, bridges and cut pairs

In this section, we define Pythagorean fuzzy incidence cut vertices, Pythagorean fuzzy incidence bridges and Pythagorean fuzzy incidence cut pairs. We also establish some results about Pythagorean fuzzy incidence cut pairs. The notion of Pythagorean fuzzy incidence cut vertices is defined below:

Definition 4.1. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. Let $\check{l}\in V$ and $\tilde{E}$ be the set difference of $E$ and the set of edges with $\check{l}$ as an end vertex. Then, $\check{l}$ is called a Pythagorean fuzzy incidence cut vertex (PFICV) of $\check{G}$, if $ICONNG_{\sigma(\check{G}\setminus \{\check{l}\})}(\check{a}, \check{a}\check{k}) < ICONNG_{\sigma(\check{G})}(\check{a}, \check{a}\check{k})$ and $ICONNG_{\mu(\check{G}\setminus \{\check{l}\})}(\check{a}, \check{a}\check{k}) > ICONNG_{\mu(\check{G})}(\check{a}, \check{a}\check{k})$ for some pair $(\check{a}, \check{a}\check{k})\in V\times \tilde{E}$ such that $\check{a}\neq \check{l}\neq \check{k}$.

Definition 4.2. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. Let $\check{q}\check{t}\in E$ and $\tilde{E} = E\setminus \{\check{q}\check{t}\}$. Then, $\check{q}\check{t}$ is called a Pythagorean fuzzy incidence bridge of $\check{G}$, if $ICONNG_{\sigma(\check{G}\setminus \{\check{q}\check{t}\})}(\check{a}, \check{a}\check{k}) < ICONNG_{\sigma(\check{G})}(\check{a}, \check{a}\check{k})$ and $ICONNG_{\mu(\check{G}\setminus \{\check{q}\check{t}\})}(\check{a}, \check{a}\check{k}) > ICONNG_{\mu(\check{G})}(\check{a}, \check{a}\check{k})$ for some pair $(\check{a}, \check{a}\check{k})\in V\times \tilde{E}$ such that $\check{a}\check{k}\neq \check{q}\check{t}$.

Definition 4.3. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. A pair $(\check{q}, \check{q}\check{t})\in supp(\check{L})$ is called a Pythagorean fuzzy incidence cut pair (PFICP) of $\check{G}$ if $ICONNG_{\sigma(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{a}, \check{a}\check{k}) < ICONNG_{\sigma(\check{G})}(\check{a}, \check{a}\check{k})$ and $ICONNG_{\mu(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{a}, \check{a}\check{k}) > ICONNG_{\mu(\check{G})}(\check{a}, \check{a}\check{k})$ for some pair $(\check{q}, \check{q}\check{t})$ in $\check{G}$.

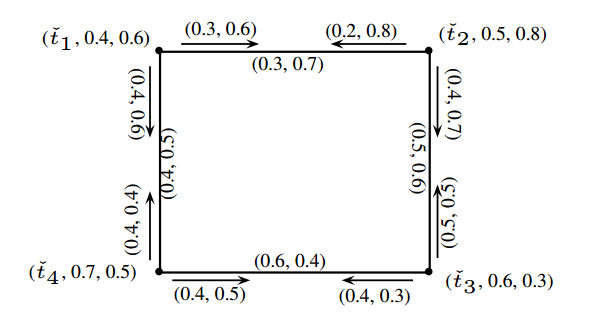
Example 4.1. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG as shown in Figure 11.

By routine calculation, it is easy to see that $\check{t}_{3}$ is PFICV, $\check{t}_{2}\check{t}_{3}, \check{t}_{3}\check{t}_{4}, \check{t}_{4}\check{t}_{1}$ are Pythagorean incidence bridges, and all incidence pairs except $(\check{t}_{2}, \check{t}_{1}\check{t}_{2})$ are PFICPs.

Proposition 4.1. If $\check{G} = (\check{J}, \check{K}, \check{L})$ is a PFIF, then the pairs of $\check{F} = (\check{M}, \check{Q}, \check{S})$ (as in Definition 3.10) are exactly the PFICPs of $\check{G}$.

Proposition 4.2. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. Then, the following statements are equivalent:

(1) $ICONNG_{\sigma(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k}) < \sigma_{\check{L}}(\check{a}, \check{a}\check{k}), ICONNG_{\mu(\check{G}\setminus\{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k}) > \mu_{\check{L}}(\check{a}, \check{a}\check{k})$.

(2) $(\check{a}, \check{a}\check{k})$ is a PFICP.

(3) $(\check{a}, \check{a}\check{k})$ is not the weakest IP of any cycle.

Proof. The following three implications are proven by contrapositive:

$(1)\Rightarrow (2)$ If $(\check{a}, \check{a}\check{k})$ is not a PFICP, then

$(2)\Rightarrow (3)$ Assume that the weakest IP in a cycle is $(\check{a}, \check{a}\check{k})$. Then, the rest of the cycle can be used as an IPt between $\check{a}$ and $\check{a}\check{k}$ to convert any IPt involving $(\check{a}, \check{a}\check{k})$ into a path not involving $(\check{a}, \check{a}\check{k})$ but at least as strong. Thus, $(\check{a}, \check{a}\check{k})$ is not a PFICP.

$(3)\Rightarrow (1)$ Let

Then, there exists an IPt $\check{P}$ between $\check{a}$ and $\check{a}\check{k}$ that does not include $(\check{a}, \check{a}\check{k})$ such that $\sigma_{\check{P}}^{IS}\geq \sigma_{\check{L}}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{P}}^{IS}\leq \mu_{\check{L}}(\check{a}, \check{a}\check{k})$. Then, the cycle formed by this IPt $\check{P}$ and $(\check{a}, \check{a}\check{k})$ has $(\check{a}, \check{a}\check{k})$ as its weakest IP. □

Proposition 4.3. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG and $(\check{a}, \check{a}\check{k})\in supp(\check{L})$. If $(\check{a}, \check{a}\check{k})$ is a PFICP, then $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) = ICONNG_{\sigma(\check{G})}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) = ICONNG_{\mu(\check{G})}(\check{a}, \check{a}\check{k})$.

Proof. Suppose $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) < ICONNG_{\sigma(\check{G})}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) > ICONNG_{\mu(\check{G})}(\check{a}, \check{a}\check{k})$. Then, a strongest $\check{a} - \check{a}\check{k}$ IPt exists between such that for all IPs $(\check{q}, \check{q}\check{t})$ in the IPt, $\sigma_{\check{L}}(\check{q}, \check{q}\check{t}) > \sigma_{\check{L}}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{L}}(\check{q}, \check{q}\check{t}) < \mu_{\check{L}}(\check{a}, \check{a}\check{k})$. Then, the cycle formed by this IPt $\check{P}$ and $(\check{a}, \check{a}\check{k})$ has $(\check{a}, \check{a}\check{k})$ as its weakest IP. Hence, $(\check{a}, \check{a}\check{k})$ is not a PFICP. □

Proposition 4.4. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. If $\check{l}$ is a common vertex of at least two PFICPs, then $\check{l}$ is a PFICV.

Proof. Let $(\check{l}, \check{a}\check{l})$ and $(\check{l}, \check{k}\check{l})$ be two PFICPs. Then, $\check{q}, \check{t}\in V$ exists such that every strongest $\check{q} - \check{t}$ IPt contains $(\check{l}, \check{a}\check{l})$. If $\check{l}\neq \check{q}$ and $\check{l}\neq \check{t}$, then $\check{l}$ is a PFICV. Let $\check{l} = \check{q}$ or $\check{l} = \check{t}$, and then every strongest $\check{q} - \check{l}$ IPt contains $(\check{l}, \check{a}\check{l})$, or every strongest $\check{l} - \check{t}$ IPt contains $(\check{l}, \check{k}\check{l})$. Assume that $\check{l}$ is not a PFICV. Then, at least one strongest IPt $\check{P}$ exists between every two vertices not containing $\check{l}$. Then, the cycle $\mathfrak{C}$ is formed by this IPt $\check{P}$ with $(\check{l}, \check{a}\check{l})$ and $(\check{l}, \check{k}\check{l}).$ We will discuss two cases:

(1) Suppose that $\check{a}, (\check{a}, \check{a}\check{l}), \check{a}\check{l}, (\check{l}, \check{a}\check{l}), \check{l}, (\check{l}, \check{l}\check{k}), \check{l}\check{k}, (\check{k}, \check{l}\check{k}), \check{k}$ is not a strongest IPt. Then, $(\check{l}, \check{a}\check{l})$ or $(\check{l}, \check{k}\check{l})$ or both will be weakest IPs of the cycle $\mathfrak{C}$, which contradicts that $(\check{l}, \check{a}\check{l})$ and $(\check{l}, \check{k}\check{l})$ are PFICPs.

(2) Suppose that $\check{P_{1}}: \check{a}, (\check{a}, \check{a}\check{l}), \check{a}\check{l}, (\check{l}, \check{a}\check{l}), \check{l}, (\check{l}, \check{l}\check{k}), \check{l}\check{k}, (\check{k}, \check{l}\check{k}), \check{k}$ is a strongest IPt joining $\check{l}$ and $\check{k}$. Then, $\sigma_{\check{P_{1}}}^{IS} = \min \{\sigma_{\check{L}}(\check{l}, \check{a}\check{l}), \sigma_{\check{L}}(\check{l}, \check{k}\check{l})\}$, and $\mu_{\check{P_{1}}}^{IS} = \max \{\mu_{\check{L}}(\check{l}, \check{a}\check{l}), \mu_{\check{L}}(\check{l}, \check{k}\check{l})\})$, the strength of IPt $\check{P}$. Thus, for all $(\check{q}, \check{q}\check{t})\in \check{P}$

and

Thus, both $(\check{l}, \check{a}\check{l})$ and $(\check{l}, \check{k}\check{l})$ are the weakest IPs of the cycle $\mathfrak{C}$, which is a contradiction.

□

Proposition 4.5. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIT. Then, the internal vertices of a SPFIS $\check{T} = (\check{M}, \check{Q}, \check{S}),$ which is a tree, are the PFICVs of $\check{G}$.

Proof. Let $\check{l}\in \check{G} = (\check{J}, \check{K}, \check{L})$ such that $\check{l}$ is not an end vertex of $\check{T}$. Then, $\check{l}$ is the common vertex of at least two IPs in $\check{T}$, which are PFICPs of $\check{G}$. Thus, by Proposition 4.4, $\check{l}$ is a PFICV. Let $\check{l}$ be an end vertex of $\check{T}$. Then, $\check{l}$ is not a PFICV, or else there would exist $\check{a}\neq \check{l}$ and $\check{k}\neq \check{l}$ such that every strongest $\check{a} - \check{k}$ IPt contains $\check{l}$, and one such IPt lies in $\check{T}$, which is impossible since $\check{l}$ is an end vertex of $\check{T}$. □

Corollary 4.1. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIT. Then, a PFICV $\check{l}$ of $\check{G}$ is the common vertex of at least two PFICPs.

5.   Connectivity in Pythagorean fuzzy incidence graphs

In this section, we first define the strong incidence pairs and weak incidence pairs in Pythagorean fuzzy incidence graphs. Then, we obtain the characterization of Pythagorean fuzzy incidence cut pairs using a-strong incidence pairs. Also, we examine the connectivity of Pythagorean fuzzy incidence graphs by various theorems.

Definition 5.1. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. An IP $(\check{q}, \check{q}\check{t})$ is said to be a strong incidence pair (SIP) if $\sigma_{\check{L}}(\check{q}, \check{q}\check{t})\geq ICONN_{\sigma(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{q}, \check{q}\check{t})$ and $\mu_{\check{L}}(\check{q}, \check{q}\check{t})\leq ICONN_{\mu(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{q}, \check{q}\check{t})$.

A SIP is called an $\alpha$-SIP if $\sigma_{\check{L}}(\check{q}, \check{q}\check{t}) > ICONN_{\sigma(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{q}, \check{q}\check{t})$ and $\mu_{\check{L}}(\check{q}, \check{q}\check{t}) < ICONN_{\mu(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{q}, \check{q}\check{t})$.

A SIP is called a $\beta$-SIP if $\sigma_{\check{L}}(\check{q}, \check{q}\check{t}) = ICONN_{\sigma(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{q}, \check{q}\check{t})$ and $\mu_{\check{L}}(\check{q}, \check{q}\check{t}) = ICONN_{\mu(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{q}, \check{q}\check{t})$.

Note that a SIP need not to be an $\alpha$-SIP or a $\beta$-SIP.

Definition 5.2. An IP $(\check{q}, \check{q}\check{t})$ is said to be a $\delta$-weak IP if $\sigma_{\check{L}}(\check{q}, \check{q}\check{t})\leq ICONN_{\sigma(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{q}, \check{q}\check{t})$ and $\mu_{\check{L}}(\check{q}, \check{q}\check{t})\geq ICONN_{\mu(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{q}, \check{q}\check{t})$.

Definition 5.3. An IP $(\check{q}, \check{q}\check{t})$ is said to be a $\delta^{*}$-IP if it is a $\delta$-weak IP with $\sigma_{\check{L}}(\check{q}, \check{q}\check{t}) > \min \{\sigma_{\check{L}}(\check{a}, \check{a}\check{k})\; |\; (\check{a}, \check{a}\check{k})\in supp(\check{L})\}$ and $\mu_{\check{L}}(\check{q}, \check{q}\check{t}) < \max \{\mu_{\check{L}}(\check{a}, \check{a}\check{k})\; |\; (\check{a}, \check{a}\check{k})\in supp(\check{L})\}.$

Example 5.1. In Figure 7. Consider an IP $(\check{m}, \check{m}\check{n})$ of $\check{G}$ with $\sigma_{\check{L}}(\check{m}, \check{m}\check{n}) = 0.4$ and $\mu_{\check{L}}(\check{m}, \check{m}\check{n}) = 0.5$. All possible $\check{m} - \check{m}\check{n}$ IPts in $\check{G}$ are

$\check{P}_{1}: \check{m}, (\check{m}, \check{m}\check{n}), \check{m}\check{n};$

$\check{P}_{2}: \check{m}, (\check{m}, \check{m}\check{p}), \check{m}\check{p}, (\check{p}, \check{m}\check{p}), \check{p}, (\check{p}, \check{p}\check{n}), \check{p}\check{n}, (\check{n}, \check{p}\check{n}), \check{n}, (\check{n}, \check{n}\check{m}), \check{n}\check{m} = \check{m}\check{n};$

$\check{P}_{3}: \check{m}, (\check{m}, \check{m}\check{o}), \check{m}\check{o}, (\check{o}, \check{m}\check{o}), \check{o}, (\check{o}, \check{o}\check{n}), \check{o}\check{n}, (\check{n}, \check{o}\check{n}), \check{n}, (\check{n}, \check{n}\check{m}), \check{n}\check{m} = \check{m}\check{n}$.

The incidence strengths of these IPts are given by

The $\sigma$-incidence strength and $\mu$-incidence strength of connectedness are given by

After the deletion of IP $(\check{m}, \check{m}\check{n})$, we have $ICONN_{\sigma(\check{G}\setminus \{(\check{m}, \check{m}\check{n})\})}(\check{m}, \check{m}\check{n}) = 0.3, ICONN_{\mu(\check{G}\setminus \{(\check{m}, \check{m}\check{n})\})}(\check{m}, \check{m}\check{n}) = 0.6.$ $\sigma_{\check{L}}(\check{m}, \check{m}\check{n}) > ICONN_{\sigma(\check{G}\setminus \{(\check{m}, \check{m}\check{n})\})}(\check{m}, \check{m}\check{n})$ and $\mu_{\check{L}}(\check{m}, \check{m}\check{n}) < ICONN_{\mu(\check{G}\setminus \{(\check{m}, \check{m}\check{n})\})}(\check{m}, \check{m}\check{n}).$ Thus, $(\check{m}, \check{m}\check{n})$ is an $\alpha$-SIP. Similarly, $(\check{p}, \check{p}\check{m}), (\check{m}, \check{m}\check{o}), (\check{n}, \check{n}\check{o}), (\check{o}, \check{o}\check{n}), (\check{m}, \check{m}\check{p}), (\check{o}, \check{o}\check{m}), (\check{n}, \check{n}\check{p})$ are SIPs. In particular, $(\check{n}, \check{n}\check{o}), (\check{o}, \check{o}\check{n}), (\check{m}, \check{m}\check{p}), (\check{o}, \check{o}\check{m}), (\check{n}, \check{n}\check{p})$ are $\alpha$-strong IPs. The IPs $(\check{p}, \check{p}\check{n}), (\check{n}, \check{n}\check{m})$ are $\delta$-weak IPs. In particular, $(\check{n}, \check{n}\check{m})$ is $\delta^{*}$-IP. There is no $\beta$-SIP in $\check{G}$.

Definition 5.4. In a PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$, an $\check{a} - \check{a}\check{k}$ IPt $\check{P}$ is called a strong IPt if all $(\check{q}, \check{q}\check{t})$ in $\check{P}$ are strong. In particular, it is called an $\alpha$-strong IPt if all the IPs in an IPt are $\alpha$-strong, and it is called a $\beta$-strong IPt if all the pairs in an IPt are $\beta$-strong. A strong IPt that is closed is called a strong incidence cycle.

Remark 5.1. In a PFIG, the strongest IPt need not be a strong IPt, and a strong IPt need not be the strongest IPt.

Example 5.2. Consider a PFIG as shown in Figure 7. The $\check{n} - \check{m}\check{n}$ IPt $\check{P}: \check{n}, (\check{n}, \check{n}\check{o}), \check{n}\check{o}, (\check{o}, \check{n}\check{o}), \check{o}, (\check{o}, \check{o}\check{m}), \check{o}\check{m}, (\check{m}, \check{o}\check{m}), \check{m}, (\check{m}, \check{m}\check{n}), \check{m}\check{n}$ is a strong IPt since all the IPs in $\check{P}$ are strong. Similarly, an $\check{p} - \check{n}\check{p}$ IPt $\tilde{P}: \check{p}, (\check{p}, \check{p}\check{m}), \check{m}\check{p}, (\check{m}, \check{p}\check{m}), \check{m}, (\check{m}, \check{m}\check{o}), \check{m}\check{o}, (\check{o}, \check{m}\check{o}), \check{o}, (\check{o}, \check{o}\check{n}), \check{o}\check{n}, (\check{n}, \check{o}\check{n}$$), \check{n}, (\check{n}, \check{n}\check{p}), \check{n}\check{p}$ is a strong IPt. Note that both $\check{P}$ and $\tilde{P}$ IPts are strong as well as strongest IPts. Now consider another strongest $\check{p} - \check{p}\check{n}$ IPt $\check{p}, (\check{p}, \check{p}\check{m}), \check{m}\check{p}, (\check{m}, \check{p}\check{m}), \check{m}, (\check{m}, \check{m}\check{n}), \check{m}\check{n}, (\check{n}, \check{m}\check{n}), \check{n}, (\check{n}, \check{n}\check{p}), \check{n}\check{p}$. This is not a strong IPt since IP $(\check{n}, \check{m}\check{n})$ is $\delta$-weak IP. The $\check{o} - \check{m}\check{o}$ IPt $\check{o}, (\check{o}, \check{o}\check{n}), \check{o}\check{n}, (\check{n}, \check{o}\check{n}), \check{n}, (\check{n}, \check{n}\check{m}),$$\check{n}\check{m}, (\check{m}, \check{n}\check{m}), \check{m}, (\check{m}, \check{m}\check{o}), \check{m}\check{o}$ is neither a strongest IPt nor a strong IPt.

Proposition 5.1. A PFIC is a strong incidence cycle.

Proof. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIC. Then, $(supp(\check{J}), supp(\check{K}), supp(\check{L}))$ is a cycle such that $\exists$ no unique $\check{q}\check{t}\in supp(\check{K})$ such that $\sigma_{\check{K}}(\check{q}\check{t}) = \min \{\sigma_{\check{K}}(\check{a}\check{k})\; |\; \check{a}\check{k}\in supp(\check{K})\}$ and $\mu_{\check{K}}(\check{q}\check{t}) = \max \{\mu_{\check{K}}(\check{a}\check{k})\; |\; \check{a}\check{k}\in supp(\check{K})\}$ and $\exists$ no unique $(\check{q}, \check{q}\check{t})\in supp(\check{L})$ such that

We have to show that each IP in $\check{G}$ is a SIP. Let $(\check{a}, \check{a}\check{k})\in supp(\check{L})$ be not a SIP. Then, it is a $\delta$-weak IP. Thus, $\sigma_{\check{L}}(\check{a}, \check{a}\check{k})\leq ICONN_{\sigma(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})$, and $\mu_{\check{L}}(\check{a}, \check{a}\check{k})\geq ICONN_{\mu(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})$. Since $(supp(\check{J}), supp(\check{K}), supp(\check{L}))$ is a cycle, every IP $(\check{q}, \check{q}\check{t})\in \check{G}\setminus \{(\check{a}, \check{a}\check{k})\}$ satisfies

which contradict that $\check{G}$ is a PFIC. Thus, $(\check{a}, \check{a}\check{k})$ is a SIP. □

Proposition 5.2. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. An IP $(\check{a}, \check{a}\check{k})$ in $\check{G}$ such that $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) = \max \{\sigma_{\check{L}}(\check{q}, \check{q}\check{t})$$\; |\; (\check{q}, \check{q}\check{t})\in supp(\check{L})\}$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) = \min \{\mu_{\check{L}}(\check{q}, \check{q}\check{t})\; |\; (\check{q}, \check{q}\check{t})\in supp(\check{L})\}$ is a SIP.

Proof. Let $\check{P}$ be an $\check{a} - \check{a}\check{k}$ IPt in $\check{G}$. Then, $\sigma_{\check{P}}^{IS}\leq \sigma_{\check{L}}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{P}}^{IS}\geq \mu_{\check{L}}(\check{a}, \check{a}\check{k})$. If $(\check{a}, \check{a}\check{k})$ is a unique IP such that $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) = \max \{\sigma_{\check{L}}(\check{q}, \check{q}\check{t})\; |\; (\check{q}, \check{q}\check{t})\in supp(\check{L})\}$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) = \min \{\mu_{\check{L}}(\check{q}, \check{q}\check{t})\; |\; (\check{q}, \check{q}\check{t})\in supp(\check{L})\}$, then for every $\check{q} - \check{q}\check{t}$ IPt $\tilde{P}$ in $\check{G}$,

where $(\check{q}, \check{q}\check{t})$ is a pair other than $(\check{a}, \check{a}\check{k})$, and hence,

Thus, $(\check{a}, \check{a}\check{k})$ is a SIP. If $(\check{a}, \check{a}\check{k})$ is not unique, then for every $\check{q} - \check{q}\check{t}$ IPt $\tilde{P}$ in $\check{G}\setminus \{(\check{a}, \check{a}\check{k})\}$, $\sigma_{\tilde{P}}^{IS} = \sigma_{\check{L}}(\check{a}, \check{a}\check{k})$, and $\mu_{\tilde{P}}^{IS} = \mu_{\check{L}}(\check{a}, \check{a}\check{k})$. If $\exists$ an $\check{a} - \check{a}\check{k}$ IPt $\check{P}$ in $\check{G}\setminus \{(\check{a}, \check{a}\check{k})\}$, then $\sigma_{\check{P}}^{IS} = \sigma_{\check{L}}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{P}}^{IS} = \mu_{\check{L}}(\check{a}, \check{a}\check{k})$. Hence $(\check{a}, \check{a}\check{k})$ is a $\beta$-SIP. Otherwise, it is an $\alpha$-SIP. □

The converse of this proposition is not necessarily true.

Example 5.3. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG as shown in Figure 12. Note that $\sigma_{\check{L}}(\check{m}, \check{m}\check{n}) = 0.5 = \max \{\sigma_{\check{L}}(\check{q}, \check{q}\check{t})\; |\; (\check{q}, \check{q}\check{t})\in supp(\check{L})\}$, and $\mu_{\check{L}}(\check{m}, \check{m}\check{n}) = 0.5 = \min \{\mu_{\check{L}}(\check{q}, \check{q}\check{t})\; |\; (\check{q}, \check{q}\check{t})\in supp(\check{L})\}$, and $(\check{m}, \check{m}\check{n})$ is a SIP. $(\check{a}, \check{m}\check{a})$ is also an $\alpha$-SIP in $\check{G}$ but $\sigma_{\check{L}}(\check{a}, \check{m}\check{a})\neq 0.5, \mu_{\check{L}}(\check{a}, \check{m}\check{a})\neq 0.4$.

Proposition 5.3. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. An IP $(\check{a}, \check{a}\check{k})$ in $\check{G}$ such that $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) = \min \{\sigma_{\check{J}}(\check{a}), \sigma_{\check{K}}(\check{a}\check{k})\}$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) = \max \{\mu_{\check{J}}(\check{a}), \mu_{\check{K}}(\check{a}\check{k})\}$ is a SIP.

Proof. Consider the PFIG $\check{G}\setminus \{(\check{a}, \check{a}\check{k})\}$. If $\check{G}\setminus \{(\check{a}, \check{a}\check{k})\}$ is disconnected, then $(\check{a}, \check{a}\check{k})$ is a PFICP, and so

Hence, $(\check{a}, \check{a}\check{k})$ is a SIP by definition. If $\check{G}\setminus \{(\check{a}, \check{a}\check{k})\}$ is connected, then $\exists$ pairs $(\check{a}, \check{a}\check{l})$ for some $\check{l}\neq \check{k}$ such that $(\check{a}, \check{a}\check{l}), (\check{k}, \check{a}\check{k})\in \check{P},$ where $\check{P}$ is an IPt between $\check{a}$ and $\check{a}\check{k}$ in $\check{G}\setminus \{(\check{a}, \check{a}\check{k})\}$. Hence,

That is, $\sigma_{\check{L}}(\check{a}, \check{a}\check{k})\geq ICONN_{\sigma(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k})\leq ICONN_{\mu(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k}).$ Hence $(\check{a}, \check{a}\check{k})$ is a SIP. □

The converse of the above proposition is not necessarily true. In Figure 7, $\sigma_{\check{L}}(\check{n}, \check{n}\check{a}) = \min \{\sigma_{\check{J}}(\check{n}), \sigma_{\check{K}}(\check{n}\check{a})\}$ and $\mu_{\check{L}}(\check{n}, \check{n}\check{a}) = \max \{\mu_{\check{J}}(\check{n}), \mu_{\check{K}}(\check{n}\check{a})\}$, and $(\check{n}, \check{n}\check{a})$ is a SIP. The IP $(\check{a}, \check{n}\check{a})$ is also a SIP but $\sigma_{\check{L}}(\check{a}, \check{n}\check{a})\neq \min \{\sigma_{\check{J}}(\check{a}), \sigma_{\check{K}}(\check{n}\check{a})\}$ and $\mu_{\check{L}}(\check{a}, \check{n}\check{a})\neq \max \{\mu_{\check{J}}(\check{a}), \mu_{\check{K}}(\check{n}\check{a})\}$.

Proposition 5.4. In a PFIG, every PFICP is a SIP.

Proof. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. Let $(\check{a}, \check{a}\check{k})\in supp(\check{L})$ be a PFICP. Then, by definition,

If possible, assume that $(\check{a}, \check{a}\check{k})$ is not a SIP. Then, $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) < ICONNG_{\sigma(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})$, and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) > ICONNG_{\mu(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k}).$ Let $\check{P}$ be a strongest $\check{a} - \check{a}\check{k}$ IPt in $\check{G}\setminus \{(\check{a}, \check{a}\check{k})\}$, and then $\check{P}$ together with $(\check{a}, \check{a}\check{k})$ forms a PFIC whose weakest IP is $(\check{a}, \check{a}\check{k})$. By Proposition 4.2, it is impossible since $(\check{a}, \check{a}\check{k})$ is a PFICP. □

Proposition 5.5. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. An IP $(\check{a}, \check{a}\check{k})$ in $\check{G}$ is a SIP if and only if $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) = ICONN_{\sigma(\check{G})}(\check{a}, \check{a}\check{k}), \mu_{\check{L}}(\check{a}, \check{a}\check{k}) = ICONN_{\mu(\check{G})}(\check{a}, \check{a}\check{k})$.

Proof. Assume that $(\check{a}, \check{a}\check{k})\in supp(\check{L})$ is a SIP. Since $\check{P}: \check{a}, (\check{a}, \check{a}\check{k}), \check{a}\check{k}$ is a IPt between $\check{a}$ and $\check{a}\check{k}$, $ICONNG_{\sigma(\check{G})}(\check{a}, \check{a}\check{k}) \geq \sigma_{\check{L}}(\check{a}, \check{a}\check{k}), ICONNG_{\mu(\check{G})}(\check{a}, \check{a}\check{k})\leq \mu_{\check{L}}(\check{a}, \check{a}\check{k})$. If $\check{P}$ is a unique IPt between $\check{a}$ and $\check{a}\check{k}$, the result is trivial. Now, let $\check{Q}$ be another IPt between $\check{a}$ and $\check{a}\check{k}$ in $\check{G}$. Then, $\check{Q}$ is an IPt in $\check{G}\setminus \{(\check{a}, \check{a}\check{k})\}$ such that $\sigma_{\check{Q}}^{IS}\leq ICONNG_{\sigma(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k}), \mu_{\check{Q}}^{IS}\geq ICONNG_{\mu(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})$. Since $(\check{a}, \check{a}\check{k})$ is a SIP, $ICONNG_{\sigma(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})\leq \sigma_{\check{L}}(\check{a}, \check{a}\check{k})$, and $ICONNG_{\mu(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k})\geq \mu_{\check{L}}(\check{a}, \check{a}\check{k}).$ Thus, $\sigma_{\check{L}}(\check{a}, \check{a}\check{k})\geq \sigma_{\check{Q}}^{IS}$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k})\leq \mu_{\check{Q}}^{IS}$. $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) = \sigma_{\check{P}}^{IS}$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) = \mu_{\check{P}}^{IS}$. Thus, $ICONN_{\sigma(\check{G})}(\check{a}, \check{a}\check{k}) = \sigma_{\check{L}}(\check{a}, \check{a}\check{k})$ and $ICONN_{\mu(\check{G})}(\check{a}, \check{a}\check{k}) = \mu_{\check{L}}(\check{a}, \check{a}\check{k})$.

Conversely, If $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) = ICONN_{\sigma(\check{G})}(\check{a}, \check{a}\check{k})$ and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) = ICONN_{\mu(\check{G})}(\check{a}, \check{a}\check{k})$, then

Hence, $(\check{a}, \check{a}\check{k})$ is a SIP. □

Proposition 5.6. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a connected PFIG. Then, there exists a SIP between any vertex $\check{a}$ and edge $\check{k}\check{l}$ in $\check{G}$.

Proposition 5.7. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG. An IP $(\check{a}, \check{a}\check{k})$ is a PFICP if and only if it is an $\alpha$-SIP.

Proof. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG and let $(\check{a}, \check{a}\check{k})\in supp(\check{L})$ be a PFICP of $\check{G}$. Then, by Proposition 4.2, $ICONNG_{\sigma(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k}) < \sigma_{\check{L}}(\check{a}, \check{a}\check{k})$, and $ICONNG_{\mu(\check{G}\setminus \{(\check{a}, \check{a}\check{k})\})}(\check{a}, \check{a}\check{k}) > \mu_{\check{L}}(\check{a}, \check{a}\check{k})$. Thus, $(\check{a}, \check{a}\check{k})$ is an $\alpha$-SIP.

Conversely, assume that $(\check{a}, \check{a}\check{k})$ is an $\alpha$-SIP. Then, by definition, $\check{P}: \check{a}, (\check{a}, \check{a}\check{k}), \check{a}\check{k}$ is the unique strongest $\check{a} - \check{a}\check{k}$ IPt, and so

Hence, $(\check{a}, \check{a}\check{k})$ is a PFICP. □

Proposition 5.8. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIT. An IP $(\check{q}, \check{q}\check{t})$ in $\check{G}$ is a SIP if and only if $(\check{q}, \check{q}\check{t})\in \check{T}$, where $\check{T} = (\check{M}, \check{Q}, \check{S})$ is a tree in the definition of PFIT.

Proof. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIT and let $\check{T} = (\check{M}, \check{Q}, \check{S})$ be a tree such that for every $(\check{a}, \check{a}\check{k})\notin \check{T}$, $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) < ICONN_{\sigma(\check{T})}(\check{a}, \check{a}\check{k})$, and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) > ICONN_{\mu(\check{T})}(\check{a}, \check{a}\check{k})$. Let $(\check{q}, \check{q}\check{t})$ be a strong IP. If $(\check{q}, \check{q}\check{t})\notin \check{T}$, then $\sigma_{\check{L}}(\check{q}, \check{q}\check{t}) < ICONN_{\sigma(\check{T})}(\check{q}, \check{q}\check{t})$, and $\mu_{\check{L}}(\check{q}, \check{q}\check{t}) > ICONN_{\mu(\check{T})}(\check{q}, \check{q}\check{t})$. Since $(\check{q}, \check{q}\check{t})$ is a SIP,

Since $(\check{q}, \check{q}\check{t})\notin \check{T}$, $\check{T}$ is PFIS of $\check{G}\setminus (\check{q}, \check{q}\check{t})$, and hence

which is a contradiction.

Conversely, assume that $(\check{q}, \check{q}\check{t})\in supp(\check{L})$. By Proposition 4.1, $(\check{q}, \check{q}\check{t})$ is a PFICP. By Proposition 5.7, $(\check{q}, \check{q}\check{t})$ is a SIP. □

Proposition 5.9. A connected PFIG is a PFIT if and only if it has no $\beta$-SIP.

Proof. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a connected PFIG. If $\check{G}$ is PFIT, then $\exists$ a unique $\check{T} = (\check{M}, \check{Q}, \check{S})$ so that every $(\check{a}, \check{a}\check{k})\in \check{T}$ is PFICP and hence is an $\alpha$-SIP. By definition of a PFIT, all $(\check{q}, \check{q}\check{t})$ such that $(\check{q}, \check{q}\check{t})\in \check{G}$ but $(\check{q}, \check{q}\check{t})\notin \check{T}$ are $\delta$-weak IPs. Thus, $\check{G}$ has no $\beta$-SIP.

Conversely, assume that $\check{G}$ has $\beta$-SIP. If $\check{G}$ has no cycles, then $\check{G}$ is a PFIT. Now, let $\mathfrak{C}$ be a cycle in $\check{G}$. Then, $\mathfrak{C}$ has only an $\alpha$-SIP and $\delta$-weak IP. All pairs of $\mathfrak{C}$ cannot be $\alpha$-SIPs. Hence, in every cycle of $\check{G}$ $\exists$ a unique $\delta$-weak IP. By Proposition 3.1, $\check{G}$ is a PFIT. □

Proposition 5.10. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a connected PFIG. $\check{G}$ is a PFIT if and only if there exists a unique strong IPt between any vertex and edge. In particular, this IPt will be an $\alpha$-strong IPt.

Proof. Let $\check{G}$ be a PFIT. Then, by Proposition 5.6, there exists a strong IPt $\check{P}$ between any vertex $\check{a}\in supp(\check{J})$ and edge $\check{k}\check{l}\in supp(\check{K})$. By Proposition 5.8, this IPt $\check{P}$ lies entirely in the associated maximum spanning tree $\check{T} = (\check{M}, \check{Q}, \check{S})$, and such IPt is unique since $\check{T}$ is a tree. Since $\check{T}$ has no $\beta$-SIPs, this IPt will be an $\alpha$-strong IPt.

Conversely, suppose $\exists$ a unique strong IPt between any vertex and edge of $\check{G}$. Let $\check{G}$ be not a PFIT, and then there is a cycle $\mathfrak{C}$ in $\check{G}$ such that for every $(\check{a}, \check{a}\check{k})\in \mathfrak{C},$

That is, every IP $(\check{a}, \check{a}\check{k})\in \check{L}$ is a SIP, which is a contradiction to our assumption that the strong IPt is unique. □

Proposition 5.11. Let $\check{G} = (\check{J}, \check{K}, \check{L})$ be a PFIG and let $\check{P}$ be a strong IPt between $\check{q}$ and $\check{q}\check{t}$. Then, $\check{P}$ is a strongest $\check{q} - \check{q}\check{t}$ IPt in the following cases:

(1) $\check{P}$ contains only $\alpha$-SIPs. {(1)} $\check{P}$ is a unique strong $\check{q} - \check{q}\check{t}$ IPt.

(2) Incidence strengths of all $\check{q} - \check{q}\check{t}$ IPts in $\check{G}$ are equal.

Proposition 5.12. A complete PFIG has no $\delta$-weak IPs.

Proof. Suppose that $(\check{q}, \check{q}\check{t})$ is a $\delta$-weak IP of a complete PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$. Then,

Thus, there exists a stronger IPt $\check{P}$ than path $\tilde{P}: \check{q}, (\check{q}, \check{q}\check{t}), \check{q}\check{t}$ between $\check{q}$ and $\check{q}\check{t}$ in $\check{G}$. Then,

That is, for every $(\check{a}, \check{a}\check{k})\in \check{P}$, $\sigma_{\check{L}}(\check{a}, \check{a}\check{k}) > \sigma_{\check{L}}(\check{q}, \check{q}\check{t})$, and $\mu_{\check{L}}(\check{a}, \check{a}\check{k}) < \mu_{\check{L}}(\check{q}, \check{q}\check{t})$. Let $\check{w}$ be the first vertex in $\check{P}$ after $\check{q}$. Then $\sigma_{\check{L}}(\check{q}, \check{q}\check{w}) > \sigma_{\check{L}}(\check{q}, \check{q}\check{t})$, and $\mu_{\check{L}}(\check{q}, \check{q}\check{w}) < \mu_{\check{L}}(\check{q}, \check{q}\check{t})$. This is not possible as $\sigma_{\check{L}}(\check{q}, \check{q}\check{w}) = \min \{\sigma_{\check{J}}(u), \sigma_{\check{K}}(uw)\} = \sigma_{\check{L}}(\check{q}, \check{q}\check{t})$, and $\mu_{\check{L}}(\check{q}, \check{q}\check{w}) = \max \{\mu_{\check{J}}(u), \mu_{\check{K}}(uw)\} = \mu_{\check{L}}(\check{q}, \check{q}\check{t})$. Thus, $\check{G}$ has no $\delta$-weak IP. □

6.   Application: Recognition of countries participating in illegal wildlife trade

Graph theory has expanded greatly as a result of a wide variety of applications in optimization issues, combinatorial issues, linguistics, chemistry, physics and other fields. In this section, we describe a real-world application of PFIGs.

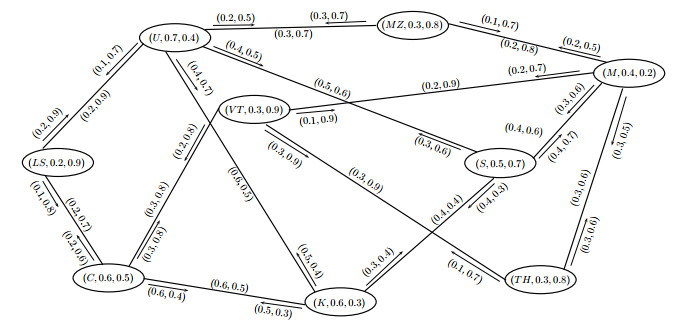
Due to the numerous benefits of wildlife on human life, wildlife trading is getting more popular with the increase of population. People in many countries are accustomed to a lifestyle that fuels the demand for wildlife. Wildlife crime is seen as a low-risk, high-reward dirty industry, currently estimated to be the fourth most profitable global crime, after the trafficking of drugs, humans and firearms. From the Americas to Asia to Africa, wildlife trade is unfortunately still common in many continents. It is a big business, bringing in estimated billions of dollars of illegal revenue. The golden triangle of Laos, Thailand and Myanmar is a global hub for illegal wildlife trade and trafficking. China is the largest importer of illegal wildlife and animal products, driving demands for animals from around the world. Wildlife trade alone is a major threat to some species, but its impact is frequently made worse by habitat loss and other pressures. Criminals mostly devise many creative ways to transport illegal wildlife focusing on the path of processing and sale. It is difficult for law enforcement to find concealed ways. So, police should be aware of the latest trends in the illegal wildlife trade market. We can use the PFIG to highlight the safest path chosen by dangerous international networks for illegal wildlife trade between two countries and can also tell the removal of which country reduces the safety of that path. Consider a few countries of the world, where illegal wildlife trade is a major threat to wildlife, in the following set: $\check{W} = \{South\; Africa, Mozambique, Kenya, Uganda, China,$$Myanmar, Thailand, Laos, Vietnam\}$. PFS $\check{J}$ defined on set $\check{W}$ is presented in Table 2.

In Table 2, $\sigma_{\check{J}}$ indicates law enforcement efforts of the country for illegal wildlife trade, $\mu_{\check{J}}$ indicates the involvement of the country in organized illegal wildlife trade, and the neutral approach of the country to illegal wildlife trade can be considered as a degree of indeterminacy. We define PFS $\check{K}$ on $\check{Z}\subseteq \check{W}\times \check{W}$ in Table 3. An element of PFS $\check{K}$ represents illegal wildlife trade between those two countries.

In Table 3, $\sigma_{\check{K}}$ indicates the rate of illegal wildlife trade between countries, and $\mu_{\check{K}}$ indicates the rate of the world's negative thinking or disliking for that illegal wildlife trade. Membership and non-membership values of each pair of countries are according to $\sigma_{\check{K}}(\check{a}\check{k})\leq \min \{\sigma_{\check{J}}(\check{a}), \sigma_{\check{J}}(\check{k})\}, \mu_{\check{K}}(\check{a}\check{k})\leq \max \{\mu_{\check{J}}(\check{a}), \mu_{\check{J}}(\check{k})\}$ and $(\sigma_{\check{K}}(\check{a}\check{k}))^{2}+ (\mu_{\check{K}}(\check{a}\check{k}))^{2}\leq 1$ for all $\check{a}, \check{k}\in \check{W}$. Let us use the following alphabets for country names:

S = South Africa, MZ = Mozambique, K = Kenya, U = Uganda, C = China, M = Myanmar, TH = Thailand, LS = Laos, VT = Vietnam. Now, we define a PFS $\check{L}$ on $\check{Y}\subseteq \check{W}\times \check{Z}$ in Table 4.

Trafficking routes for illegal wildlife frequently do not follow direct lines between source and destination countries; they can be circuitous and involve multiple transit stages. Let $\sigma_{\check{L}}(VT, (VT, TH))$ and $\mu_{\check{L}}(VT, (VT, TH))$ represent the degree of safety and degree of risk for illegal wildlife trade, respectively, to use Vietnam as a source country, travel on $(VT, TH)$ and arrive at destination country Thailand. Similarly, the membership and non-membership values of the other pairs of PFIGs are shown in Table 4. Membership and non-membership values of each pair of countries are according to $\sigma_{\check{L}}(\check{a}, \check{a}\check{k})\leq \min \{\sigma_{\check{J}}(\check{a}), \sigma_{\check{K}}(\check{a}, \check{a}\check{k})\}, \mu_{\check{L}}(\check{a}, \check{a}\check{k})\leq \max \{\mu_{\check{J}}(\check{a}), \mu_{\check{K}}(\check{a}, \check{a}\check{k})\}$ and $(\sigma_{\check{L}}(\check{a}, \check{a}\check{k}))^{2}+ (\mu_{\check{L}}(\check{a}, \check{a}\check{k}))^{2}\leq 1$ for all $(\check{a}, \check{a}\check{k})\in \check{W}\times \check{Z}$. PFIG $\check{G} = (\check{J}, \check{K}, \check{L})$ is shown in Figure 13.

To make clear how the values in Table 5 are obtained, we show a calculation example for the bold entry $(K, (K, C))$ in Table 5. The possible incidence paths are as follows:

The incidence strengths of these IPts are given by

The $\sigma$-incidence strength and $\mu$-incidence strength of connectedness are given by

Thus, $ICONN_{\check{G}}(K, (K, C)) = (ICONN_{\sigma(\check{G})}(K, (K, C)), ICONN_{\mu(\check{G})}(K, (K, C))) = (0.5, 0.3).$

If we remove the pair $(K, (K, C))$ from the graph, then

$\sigma_{\check{L}}(K, (K, C)) > ICONN_{\sigma(\check{G}\setminus \{(K, (K, C))\})}(K, (K, C)), \; \rm{and}\; \mu_{\check{L}}(K, (K, C)) < ICONN_{\mu(\check{G}\setminus \{(K, (K, C))\})}(K, (K, C)).$ Thus, $(K, (K, C))$ is an $\alpha$-SIP and so by Proposition 5.7 is a PFICP of $\check{G}$.

$\sigma_{\check{L}}(\check{a}, \check{a}\check{k})$, and $\mu_{\check{L}}(\check{a}, \check{a}\check{k})$ represent the degree of safety and degree of risk of IPts between $\check{a}$ and $\check{k}$. Then, $ICONN_{\check{G}}(\check{a}, \check{a}\check{k})$ represents the IPt with the highest safety and smallest risk among all such IPts. Hence such an IPt is the safest path to travel.

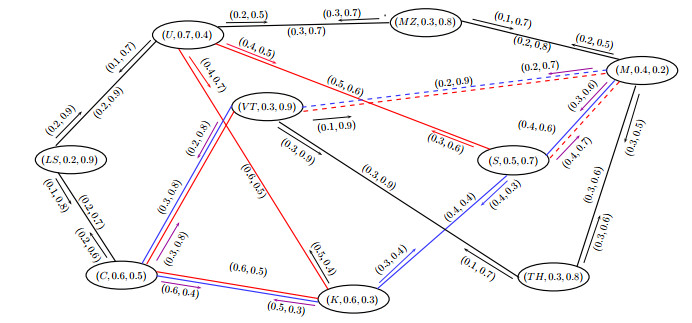
The incidence strength of connectedness between a vertex $\check{a}$ and an edge $\check{a}\check{k}$ of $\check{G} = (\check{J}, \check{K}, \check{L})$ are calculated in Table 5. Suppose $(\check{q}, \check{q}\check{t})$ is a PFICP. Then, $(\check{a}, \check{a}\check{k})$ exists such that $ICONNG_{\sigma(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{a}, \check{a}\check{k}) < ICONNG_{\sigma(\check{G})}(\check{a}, \check{a}\check{k})$ and $ICONNG_{\mu(\check{G}\setminus \{(\check{q}, \check{q}\check{t})\})}(\check{a}, \check{a}\check{k}) > ICONNG_{\mu(\check{G})}(\check{a}, \check{a}\check{k})$. Thus, the removal of pair $(\check{q}, \check{q}\check{t})$ would make the path less safe. There are two safest IPts between from VT to (VT, M) with $ICONN_{\check{G}}(VT, (VT, M)) = (0.2, 0.8)$ such as:

These paths are shown in Figure 14. Let us remove PFICP $(C, (C, K))$ from $\check{G}$. Then, $ICONNG_{(\check{G}-\{(C, (C, K))\})}(VT, (VT, M)) = (0.1, 0.9)$. Thus, removal of $(C, (C, K))$ reduces the safety of the path. Similarly, removal of pairs $(C, (C, LS)), (U, (U, S)), (K, (K, C)), (M, (M, S)), (K, (K, U)), (U, (U, K)), (M, (M, TH)),$ $(TH, (M, TH)), (V, (V, C)), (C, (C, V)), (U, (U, MZ)), (M, (M, MZ)), (S, (S, K))$ and $(M, (M, VT))$ reduce the safety of the path.

7.   Comparative analysis

In this section, we compare our suggested model to existing models to determine its validity and superiority. In comparison to FS and IFS, PFS is a more powerful model for handling uncertainty. FSs address the ambiguity of belongingness, whereas IFSs provide information regarding the hesitancy of a statement. A PFS effectively handles uncertain data by extending the range for the assignment of membership and non-membership values. In Figure 13, a PFIG indicates a network of illegal wildlife trade in nine different countries, South Africa, Mozambique, Kenya, Uganda, China, Myanmar, Thailand, Laos and Vietnam. The edge between any two countries represents the illegal wildlife trade between those two countries, and the membership and non-membership values indicate the rate of illegal wildlife trade between countries and the rate of the world's negative thinking or disliking of that illegal wildlife trade, respectively. Moreover, let $\sigma_{\check{L}}(C_{1}, (C_{1}C_{2}))$ and $\mu_{\check{L}}(C_{1}, (C_{1}C_{2}))$, represent the degree of safety and degree of risk for illegal wildlife trade, respectively, to use $C_{1}$ as a source country, travel on $(C_{1}C_{2})$ and arrive at destination country $C_{2}$. The $ICONN_{\check{G}}(C_{1}, (C_{1}C_{2}))$ represents the IPt with the highest safety and smallest risk among all such IPts. In the case of graphs, incidence pairs are not present, and thus graphs do not provide any information about the safety of the path. In the case of incidence graphs, the membership value of each incidence pair is $1$, and thus $ICONN_{\check{G}}(C_{1}, (C_{1}C_{2})) = 1$ for all incidence pairs of the network. Hence, we cannot determine the safest path to travel. In the case of fuzzy incidence graphs, the nonmembership value of each pair is missing, and thus the $ICONN_{\check{G}}(C_{1}, (C_{1}C_{2}))$ does not provide any information about how risky the path is to travel on. In the case of IFIGs, $\sigma_{\check{J}}(C_{1})+ \mu_{\check{J}}(C_{1})\leq 1$, for each $C_{1}$. Thus, in the case of $(South Africa, 0.5, 0.7)$, $0.5+ 0.7\nleq 1$, and hence IFIGs do not have the ability to handle such information. Similarly, all the other concepts in fuzzy incidence graph structure as fuzzy incidence cycle, fuzzy incidence tree, fuzzy incidence cut vertices, fuzzy incidence bridges, fuzzy incidence cut pairs, and strong incidence pairs, use only the membership value of the problem. Nevertheless, in real-life scenarios where the non-satisfactory factor is also present, the fuzzy incidence graph model fails to illustrate non-satisfactory factors along with satisfactory factors. In comparison to fuzzy incidence graphs, Pythagorean fuzzy incidence graphs offer a more comprehensive description of relationships between objects. Problems where an element does not belong to a particular subset or where the degree of exclusion varies, can be modeled using nonmembership values. This adaptability enables more precise modeling of challenging real-world scenarios.

8.   Conclusions

One of the key factors that affect a network is connectivity. Particularly in real life, connectivity is essential for problems like internet routing and transport network flow. We introduce the idea of PFIGs in this article. We discussed the strength IPt between a vertex and an edge in PFIGs. We also proposed the concepts of PFICs and PFITs and provided some important related results. We illustrated the notions of PFICVs and PFICPs in PFIG and proved essential propositions concerning PFICPs. We discussed $\alpha$-strong, $\beta$-strong and $\delta$-weak IPs. We proved that any vertex and edge have a strong IPt between them. Moreover, we used strong pairs to characterize various Pythagorean incidence structures. We also obtained the characterization of PFICs using $\alpha$-SIPs and determined the relation between PFITs and $\alpha$-SIPs. Finally, we provided an application of PFIGs in the illegal wildlife trade network.

This research work can be further extended to include the analysis of (1) connectivity indices of PFIGs, (2) cyclic connectivity index of PFIGs, (3) average cyclic connectivity index of PFIGs and (4) Wiener index of PFIGs.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Large Group Research Project under grant number (R.G.P.2/181/44).

Conflict of interest

The authors declare no conflict of interest.