Bond incident degree indices of stepwise irregular graphs

1.   Introduction

In recent decades, smart windows with advanced architectural glass coatings are widely used to provide the comfortable daylight and thermal environment indoors. Such windows are an important component to improve the energy efficiency of the buildings ^[1,2,3,4]. Chromogenic and other materials potentially applicable in the smart windows for filtering the solar radiation have a variety of mechanisms for changing the light transmission depending on change in the ambient conditions or under the influence of electric current (Table 1). As well as glasses with liquid crystal coatings and suspended particle devices, chromogenic glazings are the next generation of solar control smart glasses after low-emissivity glasses having a high reflectance of infrared radiation.

The window entirely covered by smart technology, when it is switched to opaque mode, attenuates transmitting not only direct solar radiation but also diffused and reflected radiation. However, to achieve the comfortable indoor conditions, it is desirable to protect the room dependently on the position of the Sun relative to the window from the direct sunlight only, and transmit the diffuse sky light and the light reflected from the surface of the Earth and the surrounding buildings (the reflected radiation (albedo) is then also diffused). At present, such a regulation of the light transmission of a window depending on the incidence angle of the solar beams is impossible without blinds or other daylight redistribution devices ^[114], static angular-selective shading systems ^[115] with a micro-perforated screen, a tubular shading structure, and an expanded metal mesh, or automatically controlled active window shades ^[116]. Thin films with inclined columnar microstructure ^[117,118] have an angular selectivity of optical transmittance in narrow angular ranges and only in certain spectral ranges and cannot optimally control the light transmission in the continuous spectrum of solar radiation when the Sun moves in wide angular ranges.

Applications of angular-selective filtering of solar radiation are constantly expanding, although they do not yet affect the area of smart windows. Optical filter based on angular-selective photonic structure is used to increase the path length of radiation in a solar cell ^[119]. Different concepts to realize angular-selective thin-film filters are compared regarding their limits for efficiency and power output per unit area of the solar cells ^[120]. Potential benefit of adaptive spatial optical filter to secure key generation is quantified for various strengths of turbulence, sky radiances, and pointing angles ^[121]. For effective control of solar radiation passing into the room, it is necessary to know the daily and annual changes in the radiation intensity depending on the geographical latitude. Daylight-factor, radiosity and ray tracing methods are used to calculate the daylight distribution in rooms with solar shadings and light redirecting devices ^[122]. Meteorological observations database for locations throughout the world are given in the handbooks ^[123,124]. On this basis, the methods for calculating solar radiation data are developed ^{[125,126,127,128,129]}.

Thus, smart glasses currently used in windows regulate the temperature, insolation and illumination level indoors, but cannot provide the angular-selective light transmission of the windows dynamically adapted to the position of the Sun. Without the additional use of blinds or other devices, the smart window can not attenuate only direct solar radiation, passing diffused one. Meanwhile, glare and too bright surfaces indoors arise mainly due to the direct sunlight, and the diffused light should preferably pass through the window to create a comfortable environment. A grating optical filter proposed for smart windows ^{[130,131,132,133,134,135,136,137,138,139,140,141,142,143,144]} provides the angular-selective light transmission depending on the position of the Sun relative to the window without using blinds, etc. The relative positions of two filter’s gratings consisting of alternating transmissive and non-transmissive strips allows you to protect the room from the direct sunlight in a preset range of incidence angles of the solar beams, while transmitting the diffused light. Such a method of angular regulation of the light transmission is patented by the author (RU Patents 2509324 and 2677069). The grating filter transmits only the desired part of the incident radiation with no change or, optionally, with a change in its spectrum, in different incidence-angle ranges, reflecting, absorbing, or scattering the rest of the light. Non-transmissive strips of the filter may hinder the view through the window and can be applied to vertical windows not used for viewing, to inclined windows and skylights. To ensure sufficient visibility it is more preferable to create the non-transmissive strips by the photochromic, thermochromic, electrochromic or other smart technologies.

Materials section is devoted to an overview of chromogenic and other materials most promising for the use in smart windows. Design of the grating optical filter, methods for calculating its geometrical parameters and light transmission characteristics and some results of calculation by these methods are demonstrated in grating optical filters section. Conclusions and prospects of the field section provides comparative assessment of the potential of different chromogenic and other materials for the use in grating filters, conclusions and future prospects of the field.

2.   Materials

The prior art on the chromogenic and other technologies (Table 1) shows that photochromics, thermochromics, thermotropics, gasochromics and electrochromics are the most promising for the use in smart windows (including the windows with grating filters) compared to other chromogenics, such as ionochromics, acidichromics, halochromics, solvatochromics, hygrochromics (hydrochromics), mechanochromics (piezochromics, tribochromics), etc. There are some other smart technologies such as nanocrystal in-glass composites, elastomer deformation tunable, electrokinetic pixel, liquid crystal devices, suspended particle devices and liquid infill windows, also having the prospects for using in the conventional smart windows entire covered with active layers. These technologies, with the exception of liquid infill windows, are also applicable to the grating optical filters for smart windows.

2.2.   Photochromic materials

The photochromism ^{[7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]} phenomenon discovered at the end of the 19th century is a reversible color change of organic and inorganic compounds under the influence of ultraviolet and shortwave visible radiation. Due to the reversible reactions of photoisomerization, photocyclization, tautomerization, etc., accompanied by a significant change in the structure of the compound its two different states have different absorption spectra. An enormous amount of new concepts and developments in the field of photochromic glasses highly promising for applications have been provided in ^[13]. Review ^[17] summarizes the design and preparation of photochromic (PC) hybrid materials, and particularly those based on the incorporation of organic molecules in organic-inorganic matrices by the sol-gel method.

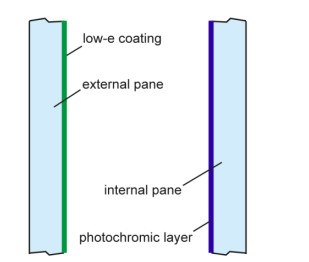
The possibility of applying thin-film coatings on the window pane (Figure 1) is an important advantage of photochromic materials for the use in smart windows. The photochromic properties of polymeric thin films ^[12], thin amorphous ^[10,11] and polycrystalline ^[11] metal oxide layers have been investigated. The visible light transmittance of photochromic materials based on silver halogenides having a very convenient kinetics of photochemical reactions varies on average from 0.7 in the bleached state to 0.25 in the darkened state ^[9]. The solar transmittance of the photochromic device with a TiO₂ sol-gel layer decreases from 57% to 7.5% in under three minutes ^[19].

The double glazing system with a commercial low-e glass (Solarban 70XL, starphire, 5.7 mm) and a PC layer prepared by embedding organic dyes, 1, 2-b Naphthopyran, in sol-gel based organic-inorganic mesoporous coating matrix ^[20], has the distinct reduction in visible light transmittance (24.6% of tinted state versus 65.0% of clear state) and solar transmittance (11.5% of tinted state versus 25.1% of clear state).

Some photochromic materials are capable of an additional color change ^{[24,25,26,27,28,29,30]} caused by a flow of ions through the material (ionochromism) or by alternatively exposing a film of photochromic material with HCl and NH₃ gases (acidochromism). Ionochromic ^[25,26,27] and acidochromic substances ^[28,29,30] are not promising for the use in photochromic smart windows (ion flows are applied in electrochromic windows only).

For the wide application of photochromic technologies in architectural glazing, it is necessary to increase the cyclicality of the photoswitches of materials experiencing irreversible photochemical and thermal reactions, as well as the stability of their photoinduced forms. For commercialization of photochromic windows, it is also necessary to increase their cost-effectiveness, strength and durability. Research in these areas continues in recent years ^{[18,19,20,21,22,23]}.

2.2.   Thermochromic and thermotropic materials

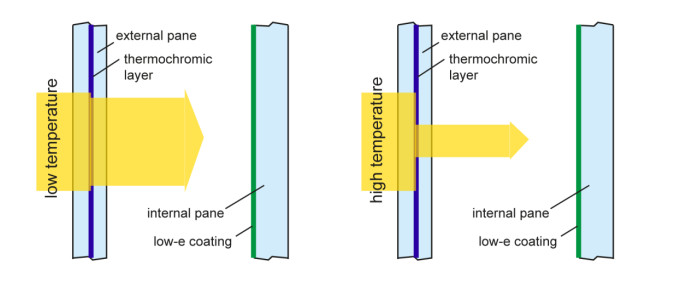
Thermochromic materials ^{[31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,110]} display a color change responding to changes in external temperature, so smart windows based on them can control the solar radiation indoors (Figure 2). The theory of metal-insulator transitions in VO₂, Ti₂O₃ and Ti_2-xV_xO₃ leading to the appearance of a thermochromic effect has been discussed in the 1970s ^[31]. Continuous thermochromism as a gradual color change occurs over a range of temperatures, and discontinuous thermochromism involves a structural phase change with instantaneous color change at the transition temperature. Vanadium dioxide is one of the most promising thermochromic materials for the future smart window applications due to its self-regulating nature and potentially simple implementation ^[42]. For commercialization of this material, it needs to be addressed some drawbacks. Thin VO₂ film integrated into a silver-containing low emissivity coating to enhance the visible transmittance shows the unique combination of a high transmittance of 58.2% in its low temperature state, a solar transmittance variation of 7.1% with the added benefit of a low emissivity of 10% ^[42]. The plot of transition temperature as function of tungsten concentration in W_xV_1-xO₂ single crystals shows that the transition temperature between 20 and 25 ℃ ideal for the thermochromic window with an energy-efficient benefit is possible at tungsten concentrations between 1.2% and 1.05% ^[36]. The smart window fabricated by coating rare earth/W-codoped VO₂ nanoparticles onto glass exhibits reducing the phase transition temperature from ~68 to 40.8 ℃ and 31.9 ℃ at the integrated visible light transmission 40% and 63% and the solar modulating ability 6.3% and 3.6%, respectively ^[49].

In addition to the inorganic thermochromic materials, such properties can appear in different classes of polymers. The actual status of development in adaptive solar control by use of thermotropic and organic thermochromic materials for application in smart windows has been reviewed in detail in ^[60]. Ligand-exchange thermochromic system integrated in a thin film has a gradual reduce of the transmittance from 54% to 4.5% in the visible range and from 22.5% to 4.5% in the solar range when the temperature increases from 25 to 85 ℃ ^[60]. Thermochromic composites introduced into polyolefin matrices show the visible transmittance decrease from 61% to 34% and the solar transmittance decrease from 68% to 62%. For the typical thermochromic materials, the reduction of light transmission in correspondence of transparent and opaque states when coupled with a clear glass is from 55-60% to 5-13%, and the reduction of solar heat gain is from 0.36-0.37 to 0.12-0.17 with switching times in the order of a few minutes ^[110].

Thermotropic materials ^[60,61,62] exhibit a temperature dependent change of the light scattering and reflective properties, but not the color change. Especially active studies of these materials began in the 1990s. The thermotropics, acting on the basis of reflective (back scattering) effects, are more advantageous due to partially preventing solar irradiation from entering the building. Due to a phase separation or phase transition upon reaching the switching temperature of a thermotropic system consisting of at least two components, a difference between the refractive indices of these components appears and the incident solar radiation is scattered and reflected at the interface between components ^[60]. This review provides the following data on decreasing the visible normal-hemispherical transmittance: (1) from 92% at 20 ℃ to 30% at 90 ℃ for a 400 μm thick film of the thermally crosslinked phase-separating polymer blend; (2) from 92% at 25 ℃ to 6% at 50 ℃ for a 1 mm thick layer of the phase-separating thermotropic gel; (3) from 58% at 20 ℃ to 10% at 42 ℃ for a polymeric hydrogel with added nanoparticles at their size of 630 nm; (4) from 82% (solar transmittance) at 25 ℃ to 57% at 95 ℃ for a 2 mm thick layer of the phase transition polymer blend; (5) from 58% to 22% for a 120 μm thick film of the polyolefine with thermotropic additives.

Thermochromic and thermotropic windows are very advanced, yet simplest, smart technology available and are quickly commercializing throughout the world. To justify their incremental cost above a conventional window it needs to increase the long-term stability of glazing units and their energy saving potential due to improving thermochromic and thermotropic properties of materials. Research conducting in the past few years, are aimed also at solving these problems ^{[46,47,48,49,50,51,52,53,54,55,56,57,58,59,62]}.

2.3.   Gasochromic materials

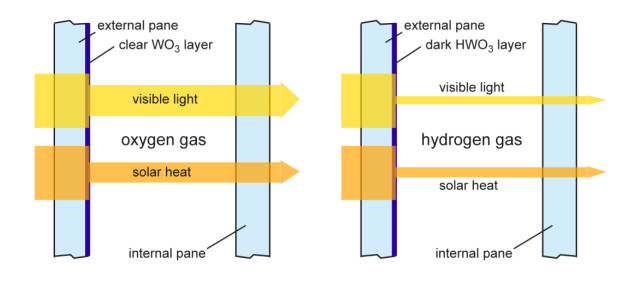
Gasochromic windows have potential to achieve the ultimate aim of combining the use of renewable energy with user comfort ^[18]. Gasochromic materials ^{[4,65,66,67,68]} relate to the class of chemochromics ^[63,64] displaying a color change responding to chemical changes or reactions. One of the internal surfaces of a double glazed unit is coated by a gasochromic thin film reversibly switching its optical transmittance upon alternating exposure to diluted hydrogen and oxygen gases. For example, a tungsten oxide reacting with hydrogen increases scattering and absorption properties due to blue coloration. Oxygen causes a reversible effect to achieve the transparent state of the film (Figure 3).

Advantage of the gasochromic window is ability to control the depth and speed of coloration by the choice of film thickness and the change of hydrogen concentration. However, such a window needs a hydrogen and oxygen generating system. Visible transmittance of the tungsten oxide film can vary between 0.10-0.59 with a solar heat gain coefficient range of 0.12-0.46, and switching speeds are 20 s to color and less than a minute to bleach ^[65]. One of the latest results ^[68] shows that the transmittance of the Pt-WO₃ gasochromic films upon exposure to hydrogen was reduced from approximately 80% to 10%, the switching time of the films was as fast as 5 s, and the switching durability of the films was preserved for over 1500 cycles.

2.4.   Electrochromic materials

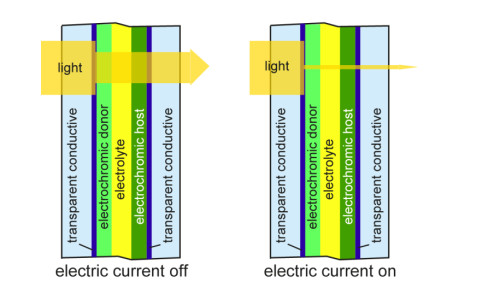
Unlike the chromogenics discussed above, electrochromic materials ^{[85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101]} change their optical properties under the influence of a low electrical voltage. An electrochromic window unit consists of few microns thick five-layer coating (transparent conductive/electrochromic donor/ion conductive electrolyte/electrochromic host/transparent conductive) interposed between two glass substrates (Figure 4). Reversible transporting of coloration ions (most commonly lithium or hydrogen) between the donor and host electrochromic layers through the central electrolyte layer cases darkening (coloration) and bleaching processes at the change in electrical polarity. The electrochromic window remains transparent (with no strong degradation in visibility) across the switching range, and can be changed gradually between bleached and fully colored states dependently on voltage. Some types of electrochromic windows need no voltage to maintain the desired colored state long time after switching to this state. Another type slowly goes to bleached state when powered off. Electrochromism among the tungsten and other transition metal oxides, inorganic non-oxide materials has been discussed in detail in ^[85] as a comprehensive foundation and reference work for studies within the rapidly expanding field of electrochromic thin films for smart windows. Many types of polymer electrolytes widely used in electrochromic devices and other applications have been reviewed in ^[88]. Electrochromic devices consisting of electron accumulation layer (counter-electrode, Li_xV₂O₅), an ion conductor layer (or electrolyte, usually LiAlF₄), an electrode layer (commonly tungsten trioxide WO₃ or niobium pentoxide Nb₂O₅, although many more metal oxides display electrochromism), and two outer layers made of transparent conductive oxides (TCO) are presented in ^[4].

The visible transmittance of typical electrochromic windows ranges from 0.02 to 0.80 ^[98], the solar heat gain coefficient ranges from 0.1 to 0.5. A recently designed monolithic solid-state organic-inorganic hybrid electrochromic device with indium tin oxide/tungsten oxide/nafion/indium tin oxide thin layers, “growed” on single glass or flexible plastic substrate by a cheap and facile process without any lamination step and fully at room temperature condition showed optical contrast of 49% (at 650 nm), switching response time of 30 s and very low electric energy absorption (of about 80 mJ/cm²) required to achieve a complete and homogeneous coloration (90% of optical modulation) ^[96]. This electrochromic technology outperforms all the others, with overall yearly energy savings as high as 40 kW·h/m²·yr (referred to window surface) in the hottest climates, assuming the clear glazings as benchmark.

A tutorial overview of a technology that is currently introduced in buildings ^[97] discusses a web-coated electrochromic device in the form of 0.4 mm thick foil (polyester/conductor/nickel oxide/electrolyte/tungsten oxide/conductor/polyester) for glass lamination, and touches on possibilities to combine electrochromism with other functionalities such as thermochromic control of solar energy transmittance, energy generation and storage, photocatalytic purification of indoor air. Electrochromic batteries that do not require external voltages to trigger coloration/de-coloration processes ^[98], in contrast to all other electrochromic technologies, are highly-promising in the realization of energy-efficient devices. Low-cost and flexible single-layer all-in-one electrochromic devices with polymer gel electrolyte incorporated into electrochromic mixtures (consisting of hydroxyalkyl viologens and hydroquinone or ferrocene electron mediators) exhibited low driving voltages (0.9 V for a ferrocene based device, 1.5 V for a hydroquinone based device), high optical contrast (up to 82%) and satisfactory coloration efficiency (>240 cm²·C⁻¹) ^[99]. Hydrides with switchable optical properties discovered in 1996 ^[86] are in research and development as non-conventional electrochromics having potential advantages in terms of energy performance, temperature stability, glare control and privacy due to switching to a reflective state rather than absorbing state. Rare earth and transition metals can be converted to transparent hydrides by injection of hydrogen from the gas or solid phase. Another electrochromic device having the reversible change of optical states between clear transparent and silver-mirror due to silver deposition at introducing the formation of AgBr_n^1-n in the electrolyte solution showed reducing the transmittance from 0.78 to 0.11 at 700 nm ^[95].

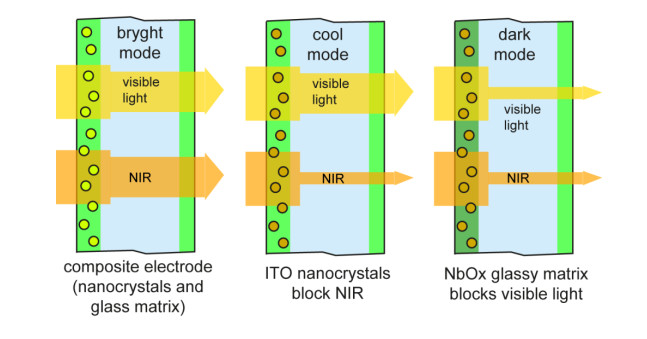
Nanocrystal in-glass composites window (Figure 5) represents, at the moment, the most promising electrochromic emerging technology ^[4,102,103]. It was first developed by researchers at the University of California, Berkeley, using indium tin-oxide (ITO) nanocrystals embedded in a glassy matrix of niobium oxide (NbO_x) and represents an evolution of the so called NIR-switching electrochromics, a technology that allows to control NIR radiation without blocking visible light transmission.

Nanocrystal in-glass composites proper dual-band electrochromic operation: the nanocrystal in-glass electrochromic film operates by absorbing Li⁺ ions and losing electrons from a donor layer and darkening accordingly, akin to conventional EC glass. At open circuit voltage (4.0 V) both nanocrystals and glass matrix are in a clear state. However, a voltage reduction to 2.3 V at first increases ions carriers in the plasmonic nanocrystals alone, which are responsible for blocking NIR radiation. Then, turning the voltage down to 1.5 V additionally triggers the reduction of the NbO_x glass matrix, which in turn blocks visible light as well (Figure 5). Hence, this system allows for a triple switching configuration: a “bright mode” where visible light and NIR enter undisturbed; a “cool mode” that blocks NIR while allowing visible light in; and finally a “dark mode” that limits both heat and natural light entering the room.

Electrochromic glazing is the most mature and effective active dynamic glass technology for buildings, however its wide spread use is still marred by a number of drawbacks, both technical and economical, and its operation versatility has also room for further improvement ^[4]. In recent years, a wider range of electrochromic materials are studied to overcome these shortcomings ^{[92,93,94,95,96,97,98,99,100,101]}.

2.5.   Other electrically operating technologies

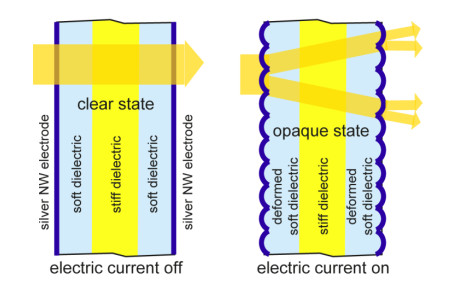
Like electrochromic windows, elastomer deformation tunable and electrokinetic pixel windows, polymer-dispersed liquid crystal (PDLC) windows and suspended-particle devices (SPD) also function under the influence of an electrical voltage. An elastomer-deformation tunable window^[4,84] presented in Figure 6 is a dynamic glazing technology (developed at Harvard School of Engineering), having different properties and characterizing by the possibility to vary from a clear state to a tinted opaque state, without vision trough, able to diffuse light ^[4]. This mechanochromic technology exploits geometric deformation of the glazed surface to control light scattering, turning the opacity of the window from clear to opaque or any state in between. This effect is achieved by sandwiching the glass or polymer pane between two transparent dielectric elastomer layers, which are sprayed with a network of electrically conducting silver nanowires (Figure 6). When voltage is applied to the window, nanowires are energized and turn into electrodes, which tend to move toward each other by Coulombic forces squeezing and deforming the two elastomer layers below. The process requires less than a second to complete. The application of this technology in the glass manufacturing industry should be facilitated by its cheaper manufacturing process, which employs elastomer sheets already available in large format rolls and foregoes the slow and expensive vacuum deposition required by most current, chemical-based dynamic glazing in favor of a simpler spraying or peeling of the silver nanowire layer. This process would also be easily scalable to larger architectural applications ^[4].

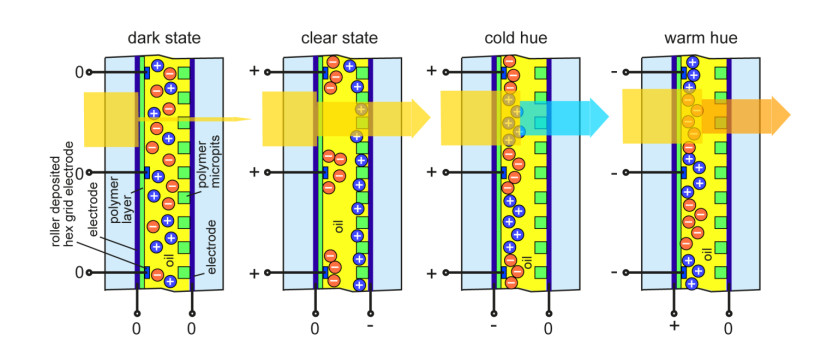
Electrokinetic pixel window technology ^[4,111], devised by Researchers at the University of Cincinnati, in collaboration with Hewlett Packard and EMD/Merck, controls the colored particles movement via electrophoresis to modulate separately both transmission and hue of entering light. The system employs two planar electrodes, controlling an electrophoretic dispersion of particles of 2 biprimary, complementary colors characterized by opposite electrical charges ^[4]. Key to the system is an additional, third electrode shaped as a hexagonal grid that creates a mesh of honeycomb cells, 500 mm in side. Additionally, the bottom planar electrode features polymer-replicated micro-pits able to trap color particles as needed and inhibit their chromatic spread (Figure 7). Each of the electrodes can be separately charged, drawing particles of the specific color towards the upper electrode, the inferior one or onto the perimeter one according to the positive or negative charge supplied.

This way it is possible to obtain a neutral, dark state (no electrodes charged, both color particles mixed in uniform dispersion) or a neutral clear state (color particles compacted towards the perimeter electrode and in the lower electrode micro-pits, no color dispersion). At the same time, a cold hue (blue particles dispersed, yellow particles compacted around the perimeter electrode) or a warm one (yellow particles dispersed, blue particles accumulated around the perimeter electrode) can be achieved. Switching between control states requires ±25 V and 10 s, whereas each can be maintained with a low holding voltage of ±10 V. Testing of a Cyan-Red colloidal dispersion achieved visible transmittance values of 75% in its clear state and 22% in dark state ^[4].

Liquid crystal windows ^{[104,105,106,107,108,109,110]} are investigating from 1980s. The brief review of industrial development and market situation of PDLC technology ^[106] suggests that this field has become the subject of worldwide demand and growth again. Liquid crystal devices consist of a double sheet of glass within which is located a polymer matrix film sandwiched between two electrical conductors of transparent thin plastic film (Figure 8). Within the film tiny liquid crystal spheres with a diameter of the same order of magnitude as the wavelength of visible radiation are dispersed. In the absence of electrical stimulus the liquid crystals have a disordered arrangement and the light rays undergo random diffractions so glazed elements appear white and translucent; on the other hand, when an electric field is applied, the liquid crystals align in the same direction ensuring the transparency of the panels. The degree of transparency can be controlled by the voltage applied. The light transmittance of liquid crystal glazing in the active state does not normally exceed 70%, while in the off state is about 50%. The solar factor reduction is usually between 0.69 and 0.55 ^[110].

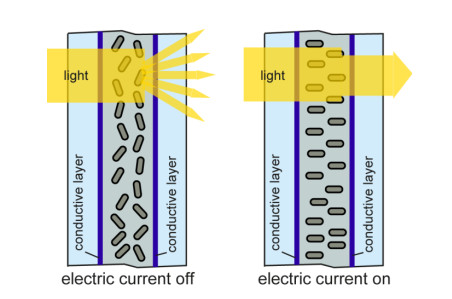
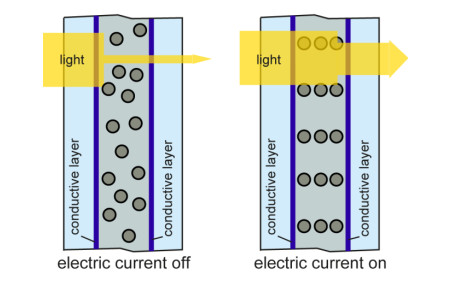
SPD smart glasses developed by Research Frontiers Inc. are also a promising energy control technology. SPD consist of a double sheet of glass within which is located a layer of thin laminate of suspended particles similar to rods immersed in a fluid, placed between two electrical conductors of transparent thin plastic film (Figure 9). When the power is turned on, the suspended rod particles align, light passes through and the SPD smart glass panel clears. When the power is switched off the suspended rod particles are randomly oriented blocking the light and the glass appears opaque. In this way, SPD glass can lighten or darken, allowing instantaneous control of the amount of light and heat passing through. SPD smart glass, when dark, can block up to 99.4% of the visible radiation ^[110].

Although the elastomer deformation and electrokinetic pixel window technologies, as well as suspended particle devices, have prospects for using at fully glazing of conventional smart windows, in grating optical filters, the possibility of their use is limited for small widths of the active strips of gratings. The liquid crystal panels are the most promising for the construction of interior privacy partitions.

3.   Grating optical filters

3.1.   Design concepts and principle of operation

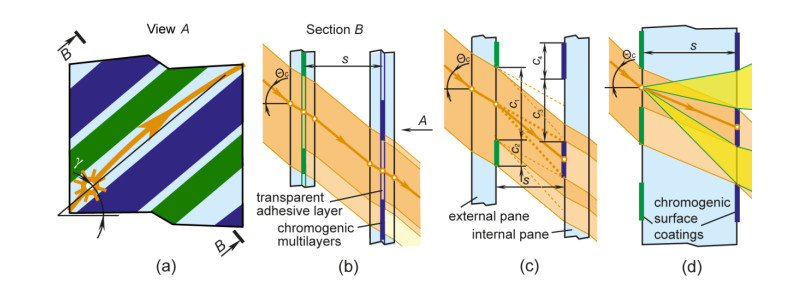
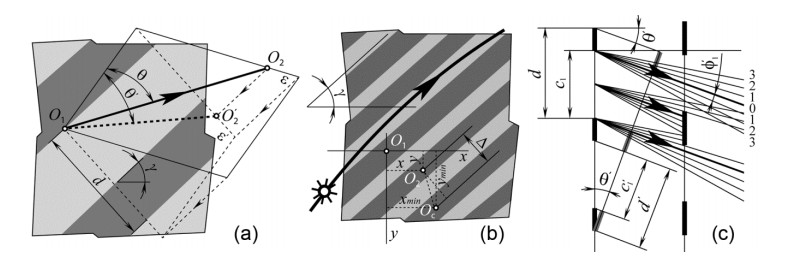
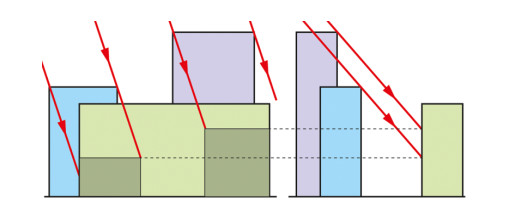
Design concepts of grating optical filters for smart windows are presented in Figure 10. An optical filter with thin-film grating layers formed by alternating directionally transmissive and non-transmissive (absorptive, reflective, or scattering) parallel strips on both surfaces of a glass sheet substrate (Figure 10d) has been proposed originally in ^{[130,131,132,133]}. The alternating strips of millimeters widths can be made by any of the known methods of surface processing, including gluing a film with pre-deposited strips on it to the substrate surface. The directional light transmission of the filter depends on widths of the transmissive strips c₁ and c₃, widths of the non-transmissive strips c₂ and c₄, as well as distance between gratings s (the thickness of glass in this case). Just as a diffraction grating, the gratings we form here are characterized by the period, that is, the total width of the two adjacent strips (c₁ + c₂ and c₃ + c₄). For the uniform regulation of light transmission over the entire area of the window, the periods of two gratings must be equal: c₁ + c₂ = c₃ + c₄.

The filter with two thin-film gratings on different panes of a double glazed window (Figure 10c) has been presented initially in ^[134,135]. The strips are sloped at an angle ${\rm{ \mathsf{ γ} }}$ (Figure 10a) to be adapted to the Sun’s trajectory relative to the window. Figure 10b shows the section of a window in a plane perpendicular to the gratings, strips of which interposed between the glass substrates and consist of multilayer coatings. The similar sections are shown in Figure 10c, d. A shift of the input and output gratings relative to each other is determined by a characteristic angle of the filter ${\Theta _c}$ between a beam passing through the centers of the strips of both gratings, and the horisontal. If this beam falls into the center of the non-transmissive strip of the output gratings, the filter has a minimum transmittance in some angular range symmetrically around the characteristic angle (when c₁ > c₄, Figure 10c) or zero transmittance at the characteristic angle (when c₁ = c₄, Figure 10d). If the beam falls into the center of the transmissive strip, the filter has a maximum transmittance in some angular range symmetrically around the characteristic angle (Figure 10b).

As a static passive device, the grating filter with non-transmissive and non-switchable strips has clear limitations impairing the view through the window compared to adaptive and/or dynamic switching windows. Therefore filters with reflective, absorptive or scattering strips can only be applied to windows that are not used for viewing, and also to skylights. A combination of the angular selectivity of the grating filter and adaptive/responsive technologies discussed in materials section would be preferred to use. In this case, the strips of the gratings, switched to an active (darkened) state due to environmental parameters or when an electric current is applied, will obstruct the view only when protection from the intensive solar radiation is necessary (just like a window fully glazed with smart glass or a conventional window system with blinds) and will not interfere with the view during the rest of the time, being in an inactive (bleached) state.

Grating filter attenuates the direct sunlight completely at a preset characteristic incidence angle (Figure 10d) or partially in an angular range symmetrically around the characteristic angle (such range with equal minimum transmittance is highlighted in Figure 10c by dashed lines). Figure 10d shows two of several angular ranges in which the diffused beams falling into the same point at different incidence angles pass through the transmissive strips of the output gratings. Protection not only from the direct light, but also partially from the diffused light is possible when c₄ > c₁. Since the filter has two gratings, it is possible to use two different smart technologies in one window. It is advisable to use, for example, the reflective chromogenics in the input gratings and the scattering or absorptive chromogenics in the output gratings ^[134].

If the filter’s gratings located on different panes of double or triple glazed windows as in Figure 10b, c the optimal widths of the strips vary from a few millimeters to tens of millimeters ^[141], and for single glazing (Figure 10d) these widths are several millimeters ^[131]. At such widths of the strips that are much larger than wavelengths of the visible light, the problems due to diffraction, dispersion and other wave phenomena do not arise, unlike diffraction gratings. This is similar to blinds and other devices, in the use of which these harmful phenomena are also not occur. The effect of diffraction on the directional transmittance of grating optical filters with angular-selective light transmission designed for single and double glazed smart windows have been investigated in ^[143].

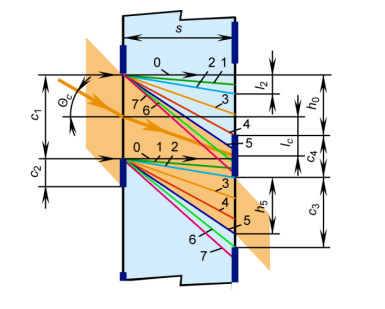
In Figure 11, the refracted beams labeled 1-7 indicate the boundaries of the incident collimated radiation that passes through the input surface of the filter within the limits of a single period of the gratings. The beams labeled 0 indicate such boundaries at a normal incidence angle. For the plane-parallel filter, a bandwidth h is the width of the part of the transmissive strips on the output surface, through which the refracted beams pass within the limits of a single period (h₀ and h₅ are indicated for beams 0 and 5, respectively). The bandwidth is defined through the angular dependence of the offset l of the refracted beam on the output surface with respect to the non-refracted beam 0 at the normal incidence angle (l₂ and l_c are indicated for beam 2 and the beam incident at the characteristic angle ${\Theta _c}$, respectively).

The intensity of light transmitted through the input gratings is reduced with increasing incidence angle. However, the ratio of transmitted intensity to incident intensity for all angles is the same and is equal to the ratio of the width of the transmissive strip to the period of the input gratings. The widths of the alternating strips on the output gratings and their shift relative to the input gratings provide selective light transmission that depends on the range of the incidence angle. As the incidence angle changes, the proportion of radiation that passes through both gratings of the filter also changes. The ratio of the intensity transmitted through the filter to the incident intensity is equal to the ratio of the bandwidth depending on the incidence angle to the period of the gratings. Angular-selective filtering of the intensity of the radiation distinguishes this filter from neutral-density filters, which evenly reduce the transmitted intensity, independently on the incidence angle.

3.2.   Method for calculating the angular dependence of light transmittance of grating filter

The angular dependence of the directional light transmittance of the filter is calculated by a graphic-analytical method ^[133]. The theoretical transmittance ${\rm{ \mathsf{ τ} }}$ of the plane-parallel filter is calculated by: ${\rm{ \mathsf{ τ} }}$ = h/(c₁ + c₂). The offset function (an angular dependence of the offset) was obtained ^[130] taking into account Snell’s law: l = ssin $\Theta$ /(n² − sin² $\Theta$)^1/2, where $\Theta$ is the incidence angle and n is the refractive index of the glass. Figure 11 shows that with increasing incidence angles from 0° to the angle that corresponds to the refracted beam 2, the bandwidth is reduced. When analyzing the position of the beam 1, which is located in this angular range, we obtain the following equation for calculating the bandwidth: h = 0.5c₁ − 0.5c₄ + l_c − l. Since the relation 0.5c₁ + l = 0.5c₄ + l_c holds when beam 2 passes through the lower edge of the absorptive strip on the output gratings, the offset is calculated as l = −0.5c₁ + 0.5c₄ + l_c. The corresponding incidence angle is extremal. With a further increase in the incidence angle, the bandwidth is unchanged and is equal to h = c₁ − c₄ (including for the refracted beam 3 corresponding to the characteristic angle of the filter). The precise value of the extremal incidence angle is determined by substituting the calculated offset l of the refracted beam 2 into $\Theta$ = arcsin[nl/(s² + l²)^1/2].

Using a similar analysis of Figure 11, the equations for calculating the bandwidth in other ranges of the incidence angles are obtained:

(1) Between the refracted beams 4 and 6 as well as for beam 5, it increases according to the relation h = 0.5c₁ − 0.5c₄ − l_c + l.

(2) Between the refracted beams 6 and 7, it is unchanged and h = c₃.

The refracted beam 7 corresponds to the incidence angle 90° at the given refractive index. The equations for calculating the offsets of the refracted beams at the extremal incidence angles are obtained by equating the calculated bandwidths for two adjacent areas: l = 0.5c₁ − 0.5c₄ + l_c for beam 4 and l = −0.5c₁ + c₃ + 0.5c₄ + l_c for beam 6.

The offset function exists and is continuous in the incidence angle range from 0° to 90° for possible values of the refractive index of the glass (1.47 < n < 1.76) and increases continuously ^[130]. The offset functions for the refracted beams are plotted in Figure 12 for various refractive indices and distances between gratings. The first and second derivatives of the offset function are given by:

Both derivatives by Eqs 1 and 2 exist and are continuous in the angular range 0°-90°. For the second derivative, we have determined the points of inflection (indicated in Figure 12) of the offset function; the positions of these points are determined only by the refractive index and is independent on the distance between gratings. For n = 1.8 (curve 4), there is no point of inflection because the second derivative cannot be zero in the angular range 0°-90° (the maximal refractive index, for which the point of inflection exists, is n = 1.73). In the range of incidence angles from 0° to the angles corresponding to the points of inflection, the second derivatives are positive (displacement functions are concave upward); further, up to 90°, the second derivatives are negative (concave downward).

In spite of the fact that the offset functions have concave and convex regions, a nearly linear dependence of the offset on the beam incidence angles is observed in the angular range from 0° to 60°-70°; the angles for which the bending becomes noticeable (Figure 12) decrease with increasing refractive index.

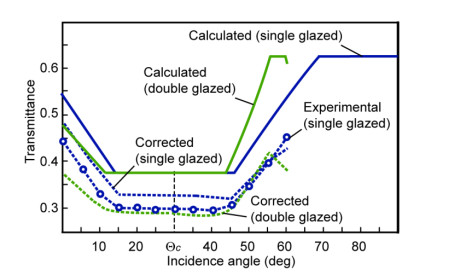
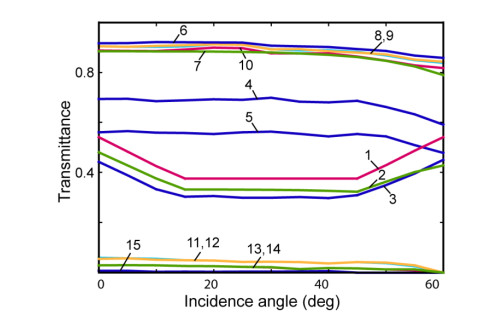
The angular dependence of the directional light transmittance of the filter with thin-film coatings on different panes of a double glazed window (Figure 10c) was calculated in ^[134]. To form the gratings of a triple glazed window, the internal surfaces of either of the two chambers are used. Figure 13 exhibits angular characteristics of the light transmission of the filters applied to the single and double glazed windows. For the single glazing, the filter characteristic was calculated at parameters: ${\Theta _c}$ = 30°, c₁ = 3 mm, c₂ = 1 mm, c₃ = 2.5 mm, c₄ = 1.5 mm, s = 4 mm, n = 1.5.

The corrected characteristic was calculated taking into account the reflection according to Fresnel equations, as well as the absorption according to Bouguer-Lambert law ^[131] by Eq 3:

where ${\rm{ \mathsf{ α} }}$ is the natural absorptance of the glass, ${\rm{ \mathsf{ ρ} }}$ is the reflectance of the glass surfaces. Figure 13 shows the characteristic corrected according to this equation, as well as the experimental characteristic in the angular range 0°-60° obtained for a sample of this filter ^[131].

For a double glazed window (Figure 10c), the beam offset function is simpler than for single glazing: l = stan$\Theta$. By graphic-analytical calculating the filter with parameters ${\Theta _c}$ = 40.8°, c₁ = 24 mm, c₂ = 8 mm, c₃ = 20 mm, c₄ = 12 mm, and s = 16 mm, five angular ranges with identical parameters of the change in the bandwidth were specified:

(1) In the angular range 0°-11.44° (l = −0.5c1 + 0.5c₄ + l_c) it decreases: h = 0.5c₁ − 0.5c₄ + l_c − l.

(2) In the angular range 11.44°-43.6° (l = 0.5c₁ − 0.5c₄ + l_c) it has a minimum: h = c₁ − c₄.

(3) In the angular range 43.6°-55.45° (l = −0.5c₁ + c₃ + 0.5c₄ + l_c) it increases: h = 0.5c₁ − 0.5c₄ − l_c + l.

(4) In the angular range 55.45°-59.57° (l = 0.5c₁ + 0.5c₄ + l_c) it has a maximum: h = c₃.

(5) In the angular range 59.57°-60° it decreases: h = 0.5c₁ + c₃ + 0.5c₄ + l_c − l.

Equations for calculating the offset of the beam at the extreme incidence angles defined by $\Theta$ = arctan(l/s) are shown in parentheses. Graphic-analytical calculation was carried out (Figure 13) only up to the incidence angle of 60°, because filtering of the solar radiation is not relevant at the larger angles. Corrected filter characteristic for double glazing, shown in Figure 13, is calculated by Eq 4:

where ${{{\rm{ \mathsf{ α} }}_1}}$ and ${{{\rm{ \mathsf{ α} }}_2}}$ are the natural absorptances, s₁ and s₂ are the thicknesses, n₁ and n₂ are the refractive indices of the external and internal panes of double glazing, respectively.

3.3.   Calculated and experimental angular characteristics of light transmittance

Method for calculating the directional light transmittance of the filter with thin-film grating layers formed by alternating transmissive and absorptive (zero transmittance) parallel strips on both surfaces of a glass sheet substrate has been confirmed by the numerical simulation and experiments ^[131,132]. Calculated angular characteristics of 20 filters with different geometrical parameters when the incidence angle is changed in range from 0° to 90° in a plane perpendicular to the gratings have alternating sections with decreasing, constant minimum, increasing and constant maximum transmittance. In the angular range 0°-60° a broken and virtually linear dependence is observed for all the filters. The sloped sections in this range have insignificant curvature and inflection points, at large angles the curvature increases (this shows the effect of the sinusoidal dependence of the offset function—up to 60°, it is almost linear). The influence of reflection and other physical factors becomes stronger at larger angles, however, there is less demand for practical application at these angles. In Figure 14, the calculated, corrected and experimental angular characteristics of light transmittance of the filter with parameters ${\Theta _c}$ = 30°, c₁ = 3 mm, c₂ = 1 mm, c₃ = 2.5 mm, c₄ = 1.5 mm, s = 4 mm and n = 1.5 ^[131] are presented, as well as of the clean glass samples, glasses with a clean film and glasses with a black film indifferent variations.

The calculated values of the transmittance are in good agreement with the experimental data in the angular range 0°-60° for 7 filters with different geometrical parameters ^[131]. The mean deviations of the experimental data for these filter samples do not exceed 4%, and the maximum deviation is 5.6%. When characteristics of 7 filters were compared for the incidence angles up to 60°, it became clear what needs to be taken into account to ensure the pre-specified characteristics of the transmittance:

-To make the transmittance increase faster in the same angular range, it is necessary to reduce the period of the gratings.

-The angular characteristic is virtually symmetrical relative to the characteristic angle of the filter.

-By choosing the widths of the alternating strips, it is possible to minimize or maximize the transmittance for different values of the characteristic angle, or for different angular ranges symmetric relative to this angle.

-If the transmissive and absorptive strips on the output gratings are interchanged, the characteristics are axially symmetric relative to the horizontal.

-For an equidistant shift of the characteristics over the angular ranges, the characteristic angle of the filter needs to be varied.

3.4.   Methods for determining the optimum slope angle of filter’s gratings

Horizontal and vertical blinds are the best devices for controlling the transmitted solar radiation depending on the incidence angle of sunlight. The most significant advantage of the grating optical filter over blinds is that the alternating strips of the gratings can be applied to the window pane at any angle—the most optimal for the window with the given azimuth A₀ of orientation to the cardinal. The filter can provide a minimum or maximum light transmission in a predetermined range of the incidence angles. By optimizing of solar radiation filtering it is mainly required to minimize transmission in the hottest period of the year. In filter’s gratings, it can be used strips reflecting or absorbing only infrared or ultraviolet spectrum part of the solar radiation with the aim of window’s visibility maintaining. The optimum slope angle of the gratings at given thickness and refractive index of the glass, the latitude and longitude of location is determined according to the following algorithm ^{[134,135,138]}.

(1) The elevation H and the azimuth A of the Sun are calculated (by one of the numerous computer programs) for every hour relative to the zenith position of the Sun on days of the spring or autumn equinox and the summer and winter solstice.

(2) The azimuth of the Sun${\rm{ \mathsf{ α} }}$ for a given window, measured from the perpendicular to the plane of the window at the point of incidence is equal to: ${\rm{ \mathsf{ α} }}$ = A − A₀.

(3) The incidence angle of the beam on the vertical plane window is calculated by the special case of first cosine theorem for the trihedral angle when the dihedral angle in front of the desired plane angle is 90°: cos$\Theta$ = cosHcos ${\rm{ \mathsf{ α} }}$. The incidence angle is:$\Theta$ = arccos[cosHcos(A − A₀)].

(4) The refraction angle is calculated by Snell’s Law: $\Theta_n$ = arcsin(sin$\Theta$/n).

(5) For a single glazed window (Figure 15a), the coordinates x and y of the output surface trace of the point 0 of incidence onto the input surface of the filter are determined by: x = stan${\rm{ \mathsf{ β} }}$ and y = $- \left\{ {{\mathop{\rm stan}\nolimits} \left({{\Theta _n} - |{\rm{ \mathsf{ β} }}|} \right)/\cos {\rm{ \mathsf{ β} }}} \right\}$, where ${\rm{ \mathsf{ β} }}$ is the refraction angle corresponding to the azimuthal incidence angle ${\rm{ \mathsf{ α} }}$, calculated from proportion: ${\rm{ \mathsf{ β} }}$ = $\Theta_n {\rm{ \mathsf{ α} }}$/ $\Theta$ ^[134]Coordinates of incidence point’s traces are determined every hour for days of equinox and solstice. For a double glazed window (Figure 15b), the coordinates are determined by: x = stan${\rm{ \mathsf{ α} }}$ and $y =- \{ {\mathop{\rm stan}\nolimits} (\Theta - |{\rm{ \mathsf{ α} }}|)/\cos {\rm{ \mathsf{ α} }}\}$ ^[138].

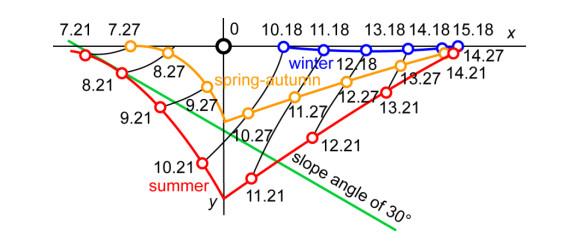
(6) The trajectories of the output surface trace of the point of incidence are plotted for the days of equinoxes and solstices. Figure 16 shows an example of such trajectories for a window with azimuth of 120° for the city of Orenburg, Russia (the latitude of 51°46'N, the longitude of 55°06'E, GMT + 05:00). The trajectories are calculated for the days of the vernal equinox (21.03.2013), summer (21.06.2013) and winter (21.12.2013) solstice at s = 4 mm and n = 1.5.

(7) The isochrones are plotted through the traces with the identical time. The trajectory of the point traces is symmetric with respect to the vertical for a window with the south orientation. Thus, the point of incidence on the input surface, depending on the time of day and season leaves the traces on the output surface on the complex and changing trajectory.

(8) The date and time with the maximal Sun protection requirements are set to determine the optimum angle of the filter gratings slope. In Figure 16, the optimum slope angle is indicated for the 15 of July (for the middle of the hottest period for the city of Orenburg) for the zenith location of the Sun. The lines of the slope are drawn along the normals to the isochrones in the points found by interpolating between the spring-autumn and summer trajectories for the 15 of July.

The developed algorithm ^[134] enables to optimize solar radiation filtering according to the orientation of a particular window to the cardinal and the known motion trajectory of the Sun relative to it. This algorithm was updated in ^[138] by selecting a date for calculation taking into account the local climate. As such a date the middle of the hottest period of the year or the day with the maximum solar radiation can be taken. Next, the time of zenith position of the Sun and the time with maximum solar radiation are determined for the selected date. The maximum solar radiation falls on the upper atmosphere at the noon. However, the transparency of the atmosphere significantly affects the daily course of radiation, especially in the summer months. The atmosphere is less transparent in the afternoon due to its higher dustiness and humidity and the emergence of convective cloudiness. Therefore, the maximum intensity of direct radiation in summer occurs in the morning hours. The updated algorithm ^[138] differs from the previous one starting from point 6.

(6) The trajectories of the output surface trace of the point of incidence are plotted for the selected date through the hourly points with the calculated coordinates x and y. These trajectories will be approximately symmetric with respect to a line passing through the point corresponding to the time when the azimuths of the Sun and window are equal (x = 0 in Figure 17). The precise symmetry is only for a window with the azimuth of 180°, when the trajectory of the Sun relative to the window is symmetric. For such a window the strips of the filter’s gratings should be horizontal.

(7) The line of symmetry of the trace trajectory is plotted for a certain time, for example, for the time with maximum solar radiation as in Figure 17. The angle between the perpendicular to this line of symmetry plotted through the corresponding point of the trace trajectory and the horizontal is the optimum slope angle of the filter’s gratings on the window pane.

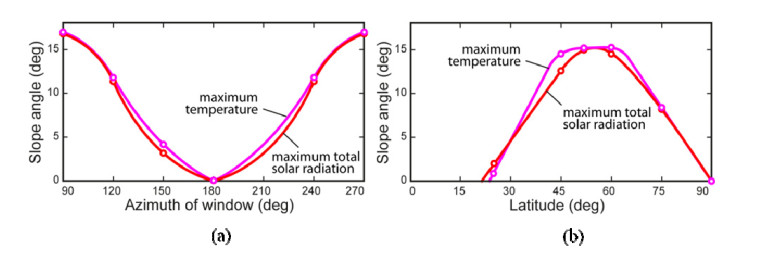
In Figure 17, the optimum angles of filter’s gratings slope for different dates are shown for single (s = 4 mm and n = 1.5) and double (s = 16 mm and n = 1.5) glazed windows with the azimuths of 120°. Calculations were carried out also at the different refractive indices of the glass, distances between filter’s gratings and azimuths of the window, as well as at the different latitudes for the longitude of the city of Orenburg (55°06'E) ^[138]. Figure 18a demonstrates the dependencies of the optimum angle on the azimuth for the maximum solar radiation and the middle of the hottest period. The maximum difference between them is 22%. The dependences of the optimum slope angle on the latitude are presented in Figure 18b for the double glazed window with azimuth of 120°.

In ^[136,139], a new more effective method to determine the optimum slope angle of filter’s gratings was presented.

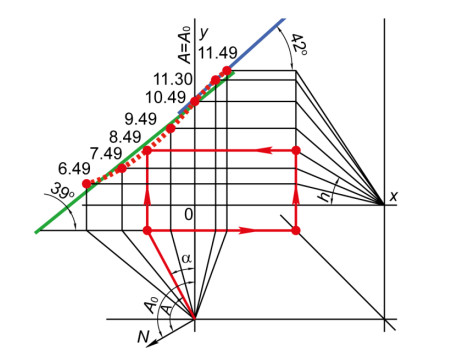
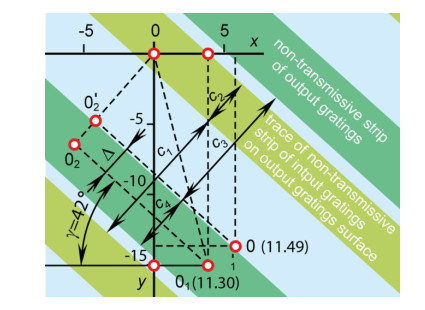
(1) By one of the many computer programs taking into account the geographical coordinates of the building, elevation H and azimuth A of the Sun are calculated for the selected date through every minute (hour, etc.) relative to the time when the azimuth of the Sun and the azimuth A₀ (0° ≤ A₀ < 360°) of the window are equal (A = A₀). At this time, the solar beams fall in the plane perpendicular to the window (y-axis in Figure 19). The trajectory of the Sun’s motion relative to window with azimuth of 120° and slope angles of filter’s gratings on a window pane are determined in Figure 19 for the city of Orenburg at 15.07.2015 (middle of the hottest period in Orenburg).

(2) The azimuth of the Sun measured from the perpendicular to the window is calculated by:${\rm{ \mathsf{ α} }}$ = A − A₀. For further calculations, only the azimuths within −70° ≤${\rm{ \mathsf{ α} }}$≤ +70° should be taken because of the increase in reflectance at large incidence angles.

(3) The incidence angle is calculated by: cos$\Theta$ = cosHcos${\rm{ \mathsf{ α} }}$. The incidence angle is equal: $\Theta$ = arccos(cosHcos${\rm{ \mathsf{ α} }}$). Only the angles $\Theta$ ≤ 70° should be taken for further calculations.

(4) Values of the coordinates of trace of trajectory of the Sun on vertical plane of the window are calculated in the range of incidence angles $\Theta$ ≤ 70°: x = tan${\rm{ \mathsf{ α} }}$; y = tanH. Based on the results of calculations, the trace of the trajectory of the Sun is plotted (dashed line in Figure 19). The calculated points are indicated through every hour relative to 10 h 49 min (the time at A = A₀), and also for 11 h 30 min (the time of maximum solar radiation). For 8 h 49 min at the azimuth A and the elevation H of the Sun, the arrows show order of obtaining the point of “trace” of the Sun on the plane of the window.

(5) If a required time t_min of the minimum light transmittance of the window is preset (usually it is the time of maximum solar radiation) an equation of the curved trajectory is found through determined points of the trajectory in a selected time interval (for example, t_min ± 30 min). The equation of function can be found using the nonparametric regression analysis. Derivative of the obtained function is calculated for the point at t_min. This derivative is equal to angular coefficient k_tan of the line tangent to the trajectory for the point at t_min. Desired optimal slope angle ${\rm{ \mathsf{ γ} }}_{\rm{tan}}$ of the filter’s gratings on the window pane obtained by making a tangent is equal to: ${\rm{ \mathsf{ γ} }}_{\rm{tan}}$ = arctank_tan (42º in Figure 19).

If the time t_min is not initially set, linear approximation of the curved trajectory is performed and equation of the straight line is found: y_app = k_appx_app + b_app. Using k_app = tan${\rm{ \mathsf{ γ} }}_{\rm{app}}$, desired optimal slope angle ${\rm{ \mathsf{ γ} }}_{\rm{app}}$ of the filter’s gratings obtained by approximation is equal to: ${\rm{ \mathsf{ γ} }}_{\rm{app}}$ = arctank_app (39º in Figure 19). The determined slope angles are adapted to the trajectory of the Sun’s motion relative to window. Table 2 shows the computational results of the slope angles of the filter’s gratings for 6 different azimuths of the windows according to this method by the linear approximation ^[141]. Calculations are carried out for the double glazed window at the distance between gratings s = 16 mm on the day (15.06.2018) and the time (11 h 30 min) of maximum solar radiation in the city of Orenburg. As the azimuth of the window increases from 90° to 180°, the slope angle of the filter’s gratings decreases from 44° to 0°.

The slope angles of filter’s gratings determined according to the initial algorithm ^{[134,135,138]} are smaller than by the new algorithm ^[136,139]. The new algorithm is universal and suitable for windows with any glazing (by the initial algorithm, the angles for the single and double glazed windows are different), as well as for devices with sloped shading elements, for example, for zebra blinds with sloped strips. For the south window with the azimuth of 180°, the angles are the same since the Sun’s trajectory in this case is symmetric with respect to the zenith position of the Sun.

3.5.   Methods for determining the characteristic angle of the filter

Since the angular characteristic of the light transmission of the filter is virtually symmetrical relative to its characteristic angle ^{[131,133,134]}, for a given characteristic, the characteristic angle can be determined graphically from the line of symmetry between the areas of decreasing and increasing transmission (Figure 13). After determining the optimum angle of the filter gratings slope it is necessary to find its geometric parameters to meet the angular-selective characteristic of the light transmission required to the particular window. They are calculated according to the following algorithm ^[134].

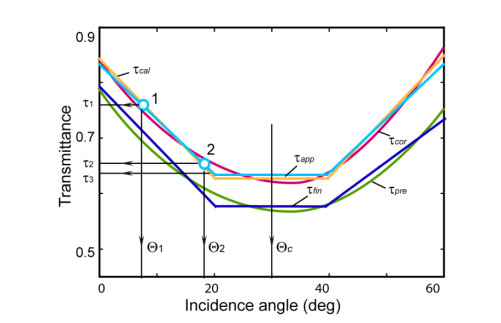
(1) The pre-specified angular-selective characteristic of the filter is shown in Figure 20 as a dependency of the light transmittance ${{\rm{ \mathsf{ τ} }}_{pre}}$ on the incidence angle $\Theta$.

(2) The pre-specified characteristic is corrected taking into account the angular dependence of the reflectance and absorptance. The corrected characteristic of light transmission of the filter is shown in Figure 20 by line ${{\rm{ \mathsf{ τ} }}_{cor}}$. The values are calculated by: ${{\rm{ \mathsf{ τ} }}_{cor}}$ = ${{\rm{ \mathsf{ τ} }}_{pre}}$ / ${{\rm{ \mathsf{ τ} }}_{raw}}$, where ${{\rm{ \mathsf{ τ} }}_{raw}}$ is the transmittance of a raw glass calculated by Eq 3 or 4.

(3) The corrected line ${{\rm{ \mathsf{ τ} }}_{cor}}$ is replaced by a polygonal line ${{\rm{ \mathsf{ τ} }}_{app}}$ as a result of piecewise linear approximation. Figure 13 shows that the calculated characteristics of the light transmission are close to the polygonal lines. The horizontal areas with the minimum and maximum light transmission are calculated, respectively, by:

The sloped areas with the increasing and decreasing transmittance are calculated for the single and double glazed windows, respectively, by:

where ${\rm{ \mathsf{ θ} }}$ is the projection of the incidence angle on a plane perpendicular to the gratings (Section B in Figure 10). Eqs 5-10 were obtained from the calculation equations of the graphic-analytical method given in method for calculating the angular dependence of light transmittance of grating filter subsection.

(4) The value of the filter characteristic angle ${\Theta _c}$ is determined graphically on the vertical axis of symmetry between the decreasing and increasing areas of the polygonal line ${{\rm{ \mathsf{ τ} }}_{app}}$ (Figure 20). This symmetry of the values of light transmittance is the result of reversing the signs before the summands in Eqs 7-10.

A new method is developed ^{[136,141,142]} to optimize the characteristic angle of the filter at preset date and time of day taking into account orientation of the window to the cardinal, the latitude of the building, the seasonal and daily distribution of the solar radiation intensity. The characteristic angle is determined as a projection of the incidence angle on a plane perpendicular to the strips of the gratings (Section B in Figure 10) for the single and double glazed window, respectively, by Eqs 11 and 12:

where ${\rm{ \mathsf{ α} }}$ = A - A₀. To calculate the characteristic angle, the values of the azimuth and elevation of the Sun are taken for the time when a minimum directional light transmission is required.

Determination of projections of the traces of the incidence point on the input gratings surface on a plane perpendicular to the strips of the filter’s gratings is shown in Figure 21 at the characteristic angle and an arbitrary incidence angle. The characteristic angles of filters for the different azimuths of the windows calculated by Eq 12 ^[141] are demonstrated in Table 2. In Figure 21, the arrangement of the strips is shown at 11 h 49 min.

The shift $\Delta$ between filter’s gratings at the characteristic angle and arbitrary incidence angle provides the calculation of the bandwidth of the filter at this arbitrary incidence angle.

3.2.   Methods for determining the widths of strips of filter’s gratings

For a given angular characteristic of the light transmission of the filter (Figure 20), the widths of the alternating strips of filter’s gratings are calculated according to the following initial algorithm ^[134].

(1) The values of the widths of the strips c₁, c₂, c₃ and c₄ are determined by solving a system of four equations, one of which is the equation of the periods of the input and output gratings: c₁ + c₂ = c₃ + c₄. Other three equations are based on Eqs 5-10 for areas of the line ${{\rm{ \mathsf{ τ} }}_{app}}$ (Figure 20). The transmittances ${{\rm{ \mathsf{ τ} }}_1}$ and ${{\rm{ \mathsf{ τ} }}_2}$ at the angles ${\Theta _1}$ and ${\Theta _2}$ are determined graphically for two arbitrary points 1 and 2 on the sloping area of the line ${{\rm{ \mathsf{ τ} }}_{app}}$. Eq 8 or 10 for the decreasing area is used twice with the substitution of the found values. Eq 5 for the area with the constant minimum light transmittance is applied as the fourth equation by the substitution of the appropriate value ${{\rm{ \mathsf{ τ} }}_3}$, defined in Figure 20.

(2) Graphic-analytical calculation by Eqs 5-10 is carried out for a filter with the determined geometric parameters c₁, c₂, c₃, c₄ and ${\Theta _c}$. Figure 20 shows the calculated characteristic ${{\rm{ \mathsf{ τ} }}_{cal}}$, which may differ from the line ${{\rm{ \mathsf{ τ} }}_{app}}$ if the values c₁, c₂, c₃, c₄ and ${\Theta _c}$ determined by solving the system of four equations are rounded.

(3) The final (actual) angular characteristic of the filter ${{\rm{ \mathsf{ τ} }}_{fin}}$ with the accepted geometric parameters is obtained by the correction taking into account the angular dependence of the reflectance and absorptance by: ${{\rm{ \mathsf{ τ} }}_{fin}}$ = ${{\rm{ \mathsf{ τ} }}_{cal}}$ ${{\rm{ \mathsf{ τ} }}_{raw}}$.

By a new method ^{[136,141,142]}, the theoretical values of required minimum ${{\rm{ \mathsf{ τ} }}_{\min }}$ and maximum ${{\rm{ \mathsf{ τ} }}_{\max }}$ transmittances are preset to optimize the geometric parameters of the filter at preset date and time of day taking into account orientation of the window to the cardinal, the latitude of the building, the seasonal and daily distribution of the solar radiation intensity. The minimum and maximum theoretical light transmittances are preset taking into account Eqs 5 and 6. The widths of the strips are calculated by:

where ${\Theta _{av}}$ is the preset average incidence angle (${\Theta _{av}}$ < ${\Theta _c}$) at which the directional light transmittance of the filter should have the average value ${{\rm{ \mathsf{ τ} }}_{av}}$ = 0.5(${{\rm{ \mathsf{ τ} }}_{\min }}$ + ${{\rm{ \mathsf{ τ} }}_{\min }}$), ${{\rm{ \mathsf{ τ} }}_{\min }}$ and ${{\rm{ \mathsf{ τ} }}_{\max }}$ are the preset minimum and maximum theoretical transmittances (without taking into account the reflection and absorption).

The widths of all strips of both gratings decrease with the increasing average angle as can be seen from Eqs 13 and 14. Selection of the average incidence angle predetermines the widths of the alternating angular ranges with decreasing, minimum, increasing and maximum light transmittances, of which the theoretical angular characteristic of the filter consists (Figure 13).

The widths of the strips calculated ^[141] by Eqs 14-17 for the double glazed window with the azimuth of 120° at the distance between gratings s = 16 mm on the day (15.06.2018) and the time (11 h 30 min) of maximum solar radiation in the city of Orenburg at the different average incidence angles and light transmittances are presented in Table 3.

The minimum and maximum required transmittances ${{\rm{ \mathsf{ τ} }}_{r\min }}$ and ${{\rm{ \mathsf{ τ} }}_{r\max }}$ are calculated by Eq 18 at ${{\rm{ \mathsf{ α} }}_a}$ = 0.01 mm⁻¹ and n = 1.5 by correcting the theoretical light transmittances ${\rm{ \mathsf{ τ} }}$ taking into account the reflection according to Fresnel equations, as well as the absorption according to Bouguer-Lambert law:

where $\Theta_I$ is the incidence angle of the solar beams at the time, when a minimum light transmission is required (i.e. at the characteristic angle); $\Theta_{in}$ is the corresponding refractive angle; ${{\rm{ \mathsf{ α} }}_a}$ is the natural absorptance of glass, mm⁻¹; ${s_\sum }$ is the total thickness of all panes, mm. The exponent of the first multiplier in the denominator is 2, 4 and 6 for single, double and triple glazed windows, respectively.

For the experimental confirmation of calculated optimal geometric parameters of the filter, a model of the double glazed window with gratings has been made ^[141]. The experiments have been carried out in the city of Orenburg, Russia on June 15 (the day of maximum solar radiation in Orenburg), 2018, from 6 h 49 min up to 13 h 19 min The corresponding optimal filter parameters have been determined for a double glazed window with the azimuth of orientation of 120° and the distance between the gratings of 16 mm to provide the minimum light transmittance of the window at 11 h 30 min (the time of maximum solar radiation in the city of Orenburg). The calculated, corrected, and experimental angular characteristics of the filters at the average incidence angle of 19.807° and two different light transmittances (from Table 3) are presented in Figure 22. The experimental data are in good agreement with the corrected (theoretical) values.

Thus, all the optimal geometrical parameters of the filter providing a minimum light transmission in a predetermined range of the incidence angles are determined.

3.7.   Methods for calculating the angular and temporal characteristics of light transmittance

The theoretical angular characteristic of the filter is a dependence of its theoretical light transmittance on the incidence angle changing in a plane perpendicular to the gratings (Section B in Figure 10) when the light source moves only in this plane, unlike the Sun. The angular ranges with the constant minimum and maximum transmittances are calculated by Eqs 5 and 6. The decreasing and increasing transmittances are calculated by Eqs 7 and 8 for single glazing and by Eqs 9 and 10 for double glazing.

The theoretical temporal characteristic is a dependence of the theoretical transmittance on the time of day when the light source (the Sun) has a complicated trajectory. The ranges with the constant minimum and maximum transmittances are calculated also by Eqs 5 and 6. Decreasing and increasing transmittances are calculated ^[141,142] by:

where $\Delta$ is the shift between the traces of the input gratings on the surface of the output gratings at the characteristic angle and an arbitrary incidence angle. This shift is determined for a single and double glazed window, respectively, by ^[142]:

where $\Theta$ and $\Theta_{i}$ are the incidence angles; $\Theta_n$ and $\Theta_{in}$ are the corresponding refractive angles at the time, when a minimum or maximum transmission is required, and an arbitrary time, respectively.

The corrected characteristics of the transmittance ${{\rm{ \mathsf{ τ} }}_{cor}}$ are calculated taking into account the reflection according to Fresnel equations, as well as the absorption according to Bouguer-Lambert law by Eq 18.

All the above equations are suitable for calculating the transmittance of the filter with gratings having the non-transmissive (zero transmittance) strips. When using chromogenic strips, some calculation equations should be changed. A filter, chromogenic strips of which are switched to the colored (darkened) state, in addition to transmitting the direct light through the transmissive strips of both gratings (i.e. through clear glass), can transmit the colored direct light through the chromogenic strips if this applied technology is not light scattering or reflective. After transformations of Eqs 5 and 6, the minimum and maximum transmittances are calculated by ^[142]:

where ${\rm{ \mathsf{ τ} }}_{chr1}$ and ${\rm{ \mathsf{ τ} }}_{chr2}$ are the directional transmittances (at normal incidence) of the chromogenic strips of the input and output gratings in their colored state, respectively.

After transformations of Eqs 7-10, taking into account the partial transmission of the chromogenic strips, the decreasing and increasing transmittances are calculated for single and double glazings, respectively, by ^[142]:

From Eq 19, the decreasing and increasing transmittances depending on the time of day are calculated by ^[142]:

The visible light transmittance of chromogenic glasses in the bleached state is comparable or less than that of the clear glass. Such transmittance of a smart window with the grating filter will exceed that for a conventional chromogenic smart window, since the total area of all chromogenic strips of both gratings is less than the total area of the conventional window.

3.8.   Angular and temporal characteristics of light transmittance of smart windows

The theoretical angular characteristic of the light transmittance of the filter with absorptive strips is calculated by Eqs 5-10. It shows changing the transmittance of the smart window in a plane perpendicular to the gratings (Section B in Figure 10), and can illustrate a dependence of the transmittance on projections of the real incidence angles on this plane. This characteristic is corrected by Eq 18 at the natural absorptance of the glass ${{\rm{ \mathsf{ α} }}_a}$ = 0.01 mm⁻¹ and the total thickness of all panes ${s_\sum }$ = 8 mm. The angular characteristics of the light transmittance of the filter with thermochromic strips (${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.34, thermochromic composites introduced into polyolefin matrices ^[60]) instead of absorptive strips are calculated by Eqs 22-27 and corrected by Eq 18. The characteristic of a window fully covered with thermochromic layer is calculated by Eq 18 at ${\rm{ \mathsf{ τ} }}$ = 0.34.

The angular characteristics of the solar transmittance of the filter with thermochromic strips (${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.62, thermochromic composites introduced into polyolefin matrices ^[60]) are calculated by Eqs 22-27 and corrected by Eq 18. The characteristic of a window fully covered with thermochromic layer is calculated by Eq 18 at ${\rm{ \mathsf{ τ} }}$ = 0.62.

The theoretical and corrected temporal characteristics of the light and solar transmittance are calculated in a time interval from 6 h 49 min to 12 h 19 min (later than 12 h 19 min the real incidence angles of the solar beams exceed 70°). The minimum and maximum theoretical light transmittance of the window with absorptive strips is calculated by Eqs 5 and 6. The decreasing and increasing transmittances are calculated by Eq 19 substituting the shifts calculated by Eq 20 or 21.The incidence angles of the solar beams and corresponding refractive angles are determined every half hour relative to the time when the azimuths of the Sun and the window are equal (10 h 49 min) and for the time with the required minimum light transmission (11 h 30 min). The corrected characteristic is calculated by Eq 18.

The temporal characteristics of the light transmittance of the window with thermochromic strips are calculated by Eqs 20-23 and 28 and corrected by Eq 18 for two cases: (1) ${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.34 (thermochromic composites introduced into polyolefin matrices ^[60]) and (2) ${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.045 (ligand-exchange thermochromic system integrated in a thin film ^[60]). The temporal characteristics of the light transmittance of the window fully covered with chromogenic layer (${{\rm{ \mathsf{ τ} }}_{chr}}$ = 0.34 and ${{\rm{ \mathsf{ τ} }}_{chr}}$ = 0.045) are calculated by Eq 18 at the corresponding incidence and refractive angles.

The temporal characteristics of the solar transmittance of the window with thermochromic strips are calculated by Eqs 20-23 and 28 and corrected by Eq 18 for the same two materials at ${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.62 and ${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.045. The temporal characteristics of the light transmittance of the window fully covered with chromogenic layer (${{\rm{ \mathsf{ τ} }}_{chr}}$ = 0.62 and ${{\rm{ \mathsf{ τ} }}_{chr}}$ = 0.045) are calculated by Eq 18.

The geometrical parameters of the filter calculated according to methods for determining the widths of strips of filter’s gratings subsection are the optimum slope angle of filter’s gratings of 42°, the characteristic angle of 28.71°, the widths of the strips of c₁ = 11.25, c₂ = 3.75, c₃ = 6 and c₄ = 9 mm.

Figure 23 shows the theoretical and corrected angular characteristics calculated in ^[142] for light (Figure 23a) and solar (Figure 23b) transmittances of a filter with thermochromic and absorptive strips and a window fully covered with thermochromic layer. The characteristics of the thermochromic filter and thermochromic layer are given for the colored state of the thermochromic material.

Distinction between all theoretical characteristics and their corrections increases with an increase in the incidence angle due to a nonlinear increase in the reflectance and absorptance. The calculated filter has the widths of the transmissive strips of the input gratings, which exceed the widths of the absorptive and thermochromic strips of the output gratings (c₁ > c₄, as in Figure 10c), therefore the theoretical transmittance is minimum in some angular range symmetrically around the characteristic angle (lines 1 and 3 in Figure 23a, line 1 in Figure 23b). The light transmittance of the filter with chromogenic strips is significantly higher than the filter with absorptive strips due to transmitting the direct sunlight through chromogenic strips additionally and selecting the material with high value of the visible light transmittance (${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.34) in its colored state.

When comparing the corrected characteristics of a chromogenic grating filter (lines 4 in Figure 23a and 2 in Figure 23b) and a layer of the same chromogenic material fully covering the window (lines 5 and 3 in Figure 23a, b), it can be seen that the filter provides a minimum of the light transmittance in a preset angular range symmetrically around the characteristic angle, while the transmittance of the window with the chromogenic layer just smoothly decreases with the increasing incidence angle. As a periodic structure, the filter also has other minimums of the transmittance at large incidence angles when the Sun protection is irrelevant due to an increase in the reflectance and absorptance. Moreover, with the initial selection of the angular range with the required minimum transmittance during the highest intensity of solar radiation and high temperature, in the adjacent angular ranges, the chromogenic strips will be in the bleached state under the influence of ambient stimulative conditions or with forced switching in the case of electrochromic materials.

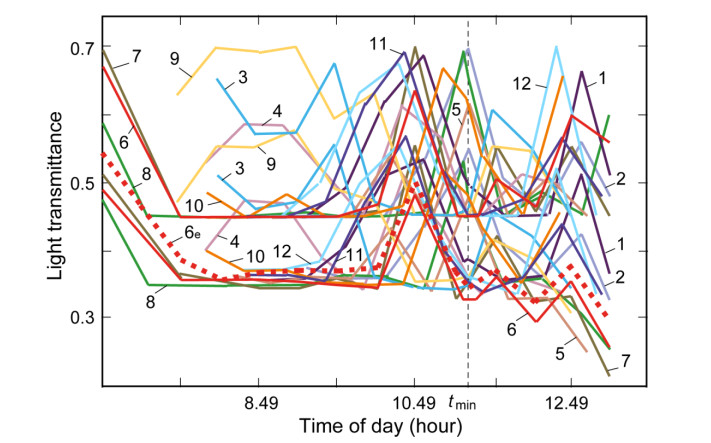
Figure 24 presents the temporal characteristics of the theoretical and corrected light (Figure 24a) and solar (Figure 24b) transmittances of the windows with absorptive and thermochromic strips and the window fully covered with thermochromic layer calculated in ^[142]. The characteristics are shown for the colored state of the thermochromic strips and layer according to the calculation results without taking into account the fact that they can be switched to the bleached state.

The characteristics with a gradual change in the incidence angles on the plane perpendicular to the gratings, shown in Figure 23, are valid only for the eastern and western windows of buildings located on the equator. In all other cases, due to a simultaneous change in the azimuth and the elevation of the Sun, the transmittance of the window depends on the projections of the real incidence angles of the solar beams on the plane perpendicular to the gratings ^[134,136]. The values of these projections, taking into account the slope angle of the filter’s gratings adapted to the trajectory of the Sun relative to a window (Figure 10a), can increase or decrease repeatedly during the day. Therefore, the ranges of angular (Figure 23) and temporal (Figure 24) characteristics with the same minimum transmittance significantly differ. The temporal characteristics of the windows with filters have two time intervals with minimum transmittance, the first of which is very long. However, in the morning hours with low intensity of ultraviolet and shortwave visible solar radiation and low temperature, the chromogenic (photochromic or thermochromic/thermotropic) strips should be switched to the bleached state and the filter will function only at a later time, providing the required minimum transmittance at preset time 11 h 30 min and, in this case, in some time interval around it. This time duration depends not only on ratio of the widths of strips (as for angular characteristics), but also on the change in the real incidence angles. The required time duration can be achieved by numerical simulation, setting different values of the average incidence angle. The functioning of the filter is much easier when using gasochromic or electrochromic materials, as they can be switched between bleached and colored state at any time.

The temporal characteristics of the light and solar transmittance of the window fully covered with chromogenic layer are not as smooth and monotonically decreasing as its angular characteristics, since the real incidence angles of the solar beams do not change monotonically. In the time interval when the chromogenic layer fully covering the window is most likely to be switched to the colored state (from 10 h 49 min to 12 h 19 min), its temporal characteristics are decreasing (lines 5 in Figure 24) or almost unchanged (lines 6).

The light transmittance of the filter with chromogenic strips (line 2 in Figure 24a) is significantly higher than the filter with absorptive strips (line 8) for the material with a high value of the visible light transmittance of ${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.34 in its colored state. At a low its value (${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.045, line 4), this excess is negligible and exists only due to additional transmitting the direct sunlight through chromogenic strips. Vice versa, the excess of the light and solar transmittance of the filter with chromogenic strips over the transmittance of the window fully covered with the same chromogenic layer is greater for the material with a low value of the transmittance (${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.045, lines 4 compared to lines 6 in Figure 24) than the material with a high its value (${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.34 and ${{\rm{ \mathsf{ τ} }}_{chr{\rm{1}}}}$ = ${{\rm{ \mathsf{ τ} }}_{chr{\rm{2}}}}$ = 0.62, lines 2 in Figure 24a, b compared to lines 5). Here the reason is the smaller total area of all chromogenic strips of both gratings of the filter than the total area of the chromogenic window.

In Figure 24, both light and solar transmittances (lines 2 and 4) have two explicit minimums (excepting line 2 in Figure 24b for a material with very high solar transmittance of 0.62), during the first of which (partially or entirely) it is desirable to switch the chromogenic strips to the bleached state. When choosing photochromic, thermochromic, etc. materials for both gratings, we should take into account external conditions that affect the switching mode. For materials switching by electric current, programmable switches can be used.

With a pre-selected time of 11 h 30 min for a minimum required transmittance, the maximum is observed at 10 h 49 min (when the azimuths of the Sun and the window are equal), since the shift between the traces of the input gratings on the surface of the output gratings by Eq 20 or 21 has a maximum value. In the same time interval (from 10 h 49 min to 12 h 19 min in Figure 24), the values of the maximums and minimums of transmittance and the ratios between them depend on the light and solar transmittance of the selected material in the colored state of the strips (lines 2 and 4 in Figure 24).

To expand the angular ranges with increasing, decreasing, or constant transmittance, it is necessary to increase the period of the gratings, as it was proved computationally and experimentally in ^[131]. According to Eqs 13-17, the widths of all strips, therefore, the period increase with the decreasing average angle. That is, with the same times of the maximums of transmittance (10 h 49 min and 12 h 19 min), the time interval with a constant minimum of transmittance can be increased by the decrease in the average angle. With the same widths of the strips of gratings and other parameters, to change the times of the maximums of transmittance, it is necessary to change the characteristic angle of the filter (according to Eqs 7-10 and 24-27), i.e., to choose a different time with a required minimum of transmittance (according to Eqs 11 and 12).

Thereby, switching the chromogenic strips to the bleached state at the required time by choosing the suitable material is an important advantage of using chromogenic strips instead of absorptive ones, which significantly increases transmission at low intensity of solar radiation and low temperature. In the colored state of chromogenic strips having the different transmittance depending on the material used (lines 2 and 4 in Figure 24 in the time interval from 10 h 49 min to 12 h 19 min), the ratio between the transmission of direct and diffused radiation varies additionally. In addition to the angular ranges shown in Figure 10d for the diffused “non colored” beams passing through the transmissive strips of the output gratings, the diffused beams will also partially pass through the chromogenic strips of both gratings and create more comfortable daylighting.

The main advantage of a smart window with chromogenic filter over a conventional chromogenic smart window is the angular selectivity of its transmittance (lines 2 and 3 in Figure 23). The transmittance of the conventional window decreases with the increasing incidence angle only due to an increase in the reflectance and absorptance. The filter additionally regulates the transmittance of the window with a change in the incidence angle due to the gratings. Since the incidence angles of the solar beams change over time, the angular selectivity of the filter also causes a temporary change in the transmittance of the filter. Comparison of lines 2 and 4 in Figure 24 for filters of different chromogenic materials with lines 5 and 6 for conventional windows made of the same materials, respectively, shows that the transmittance control is more pronounced at the low transmittance of material in the colored state. At very high values (0.62 for the solar transmittance in Figure 24b), lines 2 and 5 are only slightly different.

In the colored state of chromogenic material, a conventional smart window passes diffused light only through the chromogenic layer fully covering the window, and a window with chromogenic filter, in addition, also passes diffused light through transmissive strips of pure glass, as shown in Figure 10d. In the bleached state, the chromogenic material slightly reduces the transmittance of a window compared to pure glass. Therefore, the window with filter has a higher visible light and solar transmittance because of the smaller total area ^[131,141] of all chromogenic strips of both gratings than the total area of the conventional chromogenic window. According to the results obtained for the widths of the strips in methods for determining the widths of strips of filter’s gratings subsection, this area is 15% smaller.

Thus, the analysis of the use of chromogenic technologies in the filters with angular selectivity of the transmission and the results of calculation of their angular and temporal characteristics of the light and solar transmittance according to the modified method confirm the advantages of a smart window with chromogenic filter above (1) a window with a filter with absorptive strips (ability to switch the chromogenic strips to the bleached state and increase transmission at low intensity of solar radiation and low temperature, increased comfort of daylighting due to an additional variation of the ratio between the transmission of direct and diffused radiation), (2) a conventional chromogenic smart window (angular selectivity of the transmittance, possibility to transmit the diffused light when attenuating the direct light in the colored state, the higher visible light and solar transmittance in the bleached state).

3.9.   Numerical simulation of the light transmittance of smart window for 12 months

A numerical simulation of the light transmission of a smart window with integrated optical filter for 12 months have been performed ^[137] to demonstrate the possibility to provide dynamic control of daylighting and solar energy throughout the year without human intervention and the use of daylight redirection devices. Calculations of the theoretical and corrected temporal characteristics of the light transmittance have been carried out for a filter with geometric parameters shown in Tables 2 and 3: the slope angle of filter’s gratings of 42°, the characteristic angle of the filter of 28.71°, the average incidence angle of 19.807°, the widths of the strips of c₁ = 6.4286, c₂ = 2.1429, c₃ = 6 and c₄ = 2.5714 mm. These parameters were determined at the given minimum (${{\rm{ \mathsf{ τ} }}_{\min }}$ = 0.45) and maximum (${{\rm{ \mathsf{ τ} }}_{\max }}$ = 0.7) theoretical transmittance for a double glazed window with the azimuth of 120° at the distance between the gratings s = 16 mm per day and the time of the maximum solar radiation in Orenburg.

The results of calculations of the elevation and azimuth of the Sun, the difference between the azimuths of the Sun and the window, the incidence angles of the solar beams, the coordinates of the traces of the point of incidence of the solar beams on the output surface, the theoretical and corrected transmittances of the filter depending on the time of day for the 15th day of each month. The theoretical and corrected temporal characteristics of the filter are shown in Figure 25. Line 6e shows the results of experiments on a double glazed window model conducted on June 15, 2019 in Orenburg. All geometric parameters of the model correspond to the values accepted for calculations.

According to Eq 18, the distinction between the theoretical and corrected transmittances depends only on the incidence angle. The characteristics presented in Figure 25 show that this distinction increases with the increasing incidence angle. The time of day when the azimuths of the Sun and the window are equal, as well as the daylight hours and the corresponding time intervals selected to approximate the trajectory of the Sun, differ from month to month.

Values of the corrected transmittance are minimal for the pre-set time (11 h 30 min) and the date (15.06.2018) of the maximum solar radiation. The only exception is lower values at large incidence angles of the solar beams, which is explained by an increase in the reflectance. The average values of the theoretical and corrected light transmittances of the filter at the corresponding time intervals for the warmest months ^[137] are presented in Table 4. These data demonstrate the minimum transmittance in June, as well as in May and July, when protection from solar radiation is most in demand.

The experimental results are in good agreement with the calculated data. According to Figure 25 it can be seen that the largest deviations (up to 16%) between the corrected calculated (lower line 6) and experimental (line 6e) transmittances are observed at large incidence angles of the solar beams, which is explained by an increase in the reflectance and absorptance.

Thus, smart window with integrated optical filter with parameters determined by the methods described above, provides angular-selective control of daylighting and solar energy during the movement of the Sun without human intervention and the use of daylight redirection devices throughout the year. Such a smart window has the minimum light transmission at a given date and time of the day and differs from blinds and other similar devices. The calculations have been performed for gratings with transmissive and non-transmissive strips, therefore, in the cold season, the filter can also have light transmission minimums (Figure 25), since the gratings are periodic structures. Therefore, instead of non-transmissive (reflective, absorptive or scattering) strips, it is advisable to use strips using chromogenic and other technologies described in materials section and angular and temporal characteristics of light transmittance of smart windows subsection. In this case, in the cold season, the filter will let in as much light and solar energy as possible.

3.10.   Diffraction in the grating optical filters with angular-selective light transmission

Since with the increasing incidence angle of parallel beams onto the gratings their period decrease, diffraction limitations can occur even in gratings with millimeter periods or more. In ^[143], the influence of diffraction on the angular-selective directional light transmission of grating optical filters with periods of up to tens of millimeters designed for single and double glazed smart windows, have been investigated.

To calculate the filter parameters at a complex trajectory of the Sun’s motion, the projection of the angle ${\rm{ \mathsf{ θ} }}$ between the beam passing through the input gratings (in Figure 26a this angle belongs to the plane of incidence${\rm{ \mathsf{ ε} }}$) and the perpendicular to the window on the plane ${\rm{ \mathsf{ ε} }}'$ is determined. The plane ${\rm{ \mathsf{ ε} }}'$ is perpendicular to the strips of the gratings. For single glazing, this angle is equal to the refractive angle ${\rm{ \mathsf{ θ} }}$ = arcsin(sin$\Theta$/n). For double glazing, it is equal to the incidence angle ${\rm{ \mathsf{ θ} }}$ = $\Theta$. The projection ${\rm{ \mathsf{ θ} }}$' of the refractive or incidence angle ${\rm{ \mathsf{ θ} }}$ is determined by:

Figure 26b shows a diagram of a smart window with sloped gratings adapted to the trajectory of the Sun in relation to the window, and the coordinates of the traces of the point of incidence O₁ at the characteristic (O_с) and arbitrary (O₂) incidence angles. To calculate the characteristic angle according to Eq 29, we take the values x = x_min and у = у_min, calculated for the values of the azimuth of the Sun and the incidence angle, corresponding to the time of the maximum solar radiation, when the directional light transmission of the window should have a minimum value. The arrangement of the strips in Figure 26b corresponds to the characteristic angle of incidence when the incidence point O₁ is in the middle of the transmissive strip of the input gratings, and its trace O_c is in the middle of the non-transmissive strip of the output gratings. Figure 26b shows the shift $\Delta$ between the traces of the input gratings in the plane of the output gratings for the characteristic angle ${\Theta _c}$ and an arbitrary incidence angle $\Theta$ (the projection of the distance between points O₂ and O_c on a plane perpendicular to the strips of the gratings).

It is known that with an oblique incidence of parallel beams onto the gratings, the diffraction pattern is observed on a plane perpendicular to the incident beams. In the simplest case, when the incidence angle of the beams onto the plane of the grating changes, and the direction of the beams always remains perpendicular to the slits of the diffraction grating (Figure 11), the period of the grating d decreases according to: d' = dcos $\Theta$. However, in our case, it must be taken into account that the incidence angles of the solar beams simultaneously change both in the azimuthal (horizontal) and vertical plane. In addition, the gratings of the filter are located at an angle ${\rm{ \mathsf{ γ} }}$ to the horizontal.

The periods of the input and output gratings are d = с₁ + с₂ = с₃ + с₄. The diffraction pattern after the passage of parallel beams through the input gratings will be observed with a decrease in the period of these gratings according to: d' = dcos${\rm{ \mathsf{ θ} }}$' (Figure 26c).The widths of the strips of the input gratings will decrease proportionally. With the oblique incidence of parallel beams, the width of the transmissive strip and the period of the gratings (after transformations, taking into account Eq 29) will be, respectively:

In Figure 26c, the plane of incidence of the solar beams at a given instant of time (plane ${\rm{ \mathsf{ ε} }}$ in Figure 26a) is projected onto the plane perpendicular to the strips of the gratings (plane ${\rm{ \mathsf{ ε} }}'$ in Figure 26a). The directions of the intensity maxima up to the third order and the projection ${\rm{ \mathsf{ ϕ} }}$₁' of the diffraction angle corresponding to the first-order maximum are conventionally shown.

According to the well-known diffraction grating equation, after the passage of sunlight through the input gratings with the number of slits, i.e. transmissive strips, N, light intensity I(${\rm{ \mathsf{ ϕ} }}$) at diffraction angle ${\rm{ \mathsf{ ϕ} }}$ will be equal to:

where I₀ is the light intensity in the direction of the main diffraction maximum, ${\rm{ \mathsf{ λ} }}$ is the wavelength.

When determining the directional transmittance by Eqs 5, 6 and 19 and correcting it by Eq 18, diffraction is not taken into account. The concept of “directional light transmission” is permissible only at very small diffraction angles ${\rm{ \mathsf{ ϕ} }}$, which can be observed when the grating period is significantly larger than the wavelength. Calculations show ^[131,136] that the grating periods of optical filters for windows exceed the wavelengths of visible light by four orders of magnitude for single glazing and five orders of magnitude for double glazing. In accordance with the equation d' = dcos${\rm{ \mathsf{ θ} }}$', the influence of diffraction increases with the increasing incidence angles of the solar beams, especially when approaching “sliding” beams, that is, to incidence angles of 90°. However, at such incidence angles, the solar beams passing through the window structure fall into the area in close proximity to the window and there is no need to control the light transmission.

The directions of intensity maxima are determined from the condition d'(sin${\rm{ \mathsf{ ϕ} }}_m$ − sin${\rm{ \mathsf{ θ} }}$) = m${\rm{ \mathsf{ λ} }}$, where m is the order of the maximum. This expression is valid for an unlimited grating, however, in window constructions the number of periods is quite large and is about 50 for double glazing and 375 for single glazing. The intensity corresponding to the diffraction angle ${\rm{ \mathsf{ ϕ} }}_m$ is calculated by Eq 32.

With a significant excess of the grating period over the light wavelength and, accordingly, at small diffraction angles, the total intensity after passing through the input gratings is equal to: I_pas1 = с₁I_fal/d, where I_fal is the intensity of the falling light. This intensity is the sum of the light intensity in the direction of the main maximum and the diffracted light intensity I_pas1 = I₀ + I_dif, where I₀ = (с₁/d)²I_fal. Then the total intensity of the transmitted light is equal to:

where the second term in parentheses indicates the fraction of diffracted light.

The intensity of diffracted light is related to the intensity I_fal of the light incident on the input gratings by the ratio:

The maximum intensity of the diffracted light according to this expression is achieved at с₁ = 0.5d, i.e., when the widths of the transmissive and non-transmissive strips of the gratings are equal с₁ = с₂.

At small diffraction angles, the solar radiation transmitted through the input gratings can be considered directed (not scattered). For window structures, the scattered diffracted light is acceptable in view of the fact that protection from the solar radiation cannot simultaneously provide good visibility through the window.

The propagation of a parallel beam of light transmitted through the gratings can be considered straightforward and obeying geometric optics at distances from the gratings r < < D²/${\rm{ \mathsf{ λ} }}$, where D is the beam diameter. For real window structures and the distances between the input and output filter gratings, this inequality is fully satisfied.

The light diffracted in the input gratings partially passes through the transmissive strips of the output gratings (Figure 26c), the rest is blocked by non-transmissive strips. Accordingly, the light transmittance calculated by Eqs 5, 6 and 19 and corrected by Eq 18 decreases. Let us evaluate the decrease in the transmittance due to diffraction at distances of the maximum wavelength of visible radiation of 780 nm from the two edges of the non-transmissive strip of the output gratings within one its period. At large distances, the influence of diffraction can be neglected. The intensity of diffracted light will decrease in comparison with that calculated by Eq 34 by the amount of (2 × 780/d)²I_fal. Then the intensity of the light diffracted on the input gratings and passing through the output gratings is (with a length dimension in mm):

Thus, it follows from Eqs 33-35 that the intensity of the light transmitted through the input gratings and reaching the output gratings taking into account diffraction losses is equal to:

Excluding diffraction loss:

The ratio of the expressions in parentheses in Eqs 36 and 37 shows a decrease in the transmittance of the filter due to diffraction by the input gratings.

The projection of the distance of 780 nm from the edge of the non-transmissive strip of the output gratings onto the plane of Figure 26c with a distance s between the filter gratings is defined by Eq 38:

Then the projection ${\rm{ \mathsf{ ϕ} }}$' of the diffraction angle ${\rm{ \mathsf{ ϕ} }}$ at a distance of 780 nm from the edge of the strip is defined by Eq 39:

The diffraction angle ${\rm{ \mathsf{ ϕ} }}$ is determined by:

where from:

The orders of intensity maxima within the angle ${\rm{ \mathsf{ ϕ} }}$ are determined from the condition d'sin${\rm{ \mathsf{ ϕ} }}_m$ = ± m${\rm{ \mathsf{ λ} }}$. The corresponding intensity maxima and intensity in the direction of the angle ${\rm{ \mathsf{ ϕ} }}$ are determined by Eq 32.

The corrected directional transmittance calculated by Eq 18 is equal to the ratio of the intensity passing through the output gratings to the intensity incident on the input gratings: ${{\rm{ \mathsf{ τ} }}_{cor}}$ = I_pas/I_fal (without taking into account the losses of diffracted light at the edges of the non-transmissive strips of the output gratings). When accounting for diffraction by Eqs 36 and 37 in Eq 18, the corresponding diffraction factor is added to calculate the light transmittance:

Diffraction on the output gratings does not affect the value of the transmittance, however, the fraction of diffracted (scattered) light will increase. According to Eq 42, the diffraction limits of the incidence angles and the widths of the transmissive and non-transmissive strips of the input gratings are estimated at which the influence of the diffraction factor can be neglected.

In ^[143], the effect of diffraction on the light transmission of the optical filter with the parameters described in numerical simulation of the light transmittance of smart window for 12 months section was estimated. At the incidence angles of the solar beams greater than 70°, the reflectance sharply increases, as well as transmitted beams fall into the area near the window, i.e. there is no need for control the light transmission. With the accepted parameters of the filter, the incidence angle is $\Theta$ = 69.9842° at 12 h 49 min At this angle, the width of the transmissive strip of the input gratings and the grating period by Eqs 30 and 31 are equal to с₁' = 6.3193 and d' = 8.4258 mm.

The total intensity of the light transmitted through the input gratings, according to the equation I_pas1 = с₁I_fal/d is equal to I_pas1 = 0.75I_fal. It consists of the light intensity in the direction of the main maximum I₀ = 0.5625I_fal and the diffracted light intensity I_dif = 0.1875I_fal (according to Eqs 33 and 34).

The diffraction angle at the distance of 780 nm from the edge of the non-transmissive strip of the output gratings according to Eq 41 is ${\rm{ \mathsf{ ϕ} }}$ = 0.0017°. The maxima of the first and second orders from the condition d'sin${\rm{ \mathsf{ ϕ} }}_m$ = ± m${\rm{ \mathsf{ λ} }}$ at ${\rm{ \mathsf{ λ} }}$ = 780 nm are ${\rm{ \mathsf{ ϕ} }}$₁ = 0.0053° and ${\rm{ \mathsf{ ϕ} }}$₂ = 0.0106°. Within the angle ${\rm{ \mathsf{ ϕ} }}$there are no intensity maxima, except for the main maximum. The intensities calculated by Eq 32 at N = 50 corresponding to the diffraction angles ${\rm{ \mathsf{ ϕ} }}$, ${\rm{ \mathsf{ ϕ} }}$₁ and ${\rm{ \mathsf{ ϕ} }}$₂ are equal to: I(${\rm{ \mathsf{ ϕ} }}$) = 0.5849I₀, I(${\rm{ \mathsf{ ϕ} }}$₁) = 0.0169I₀ and I(${\rm{ \mathsf{ ϕ} }}$₂) = 0.0132I₀.

The main diffraction maximum is sharp (75% of the total intensity of the light transmitted through the input gratings) and narrow—of the order of the wavelength on the plane of the output gratings (from a comparison of the diffraction angle ${\rm{ \mathsf{ ϕ} }}$ = 0.0017° and the direction of the minimum between the zeroth and first order maxima ${\rm{ \mathsf{ ϕ} }}$₁/2 = 0.00265°).

The shift between the traces of the input gratings in the plane of the output gratings for the characteristic angle ${\Theta _c}$ and incidence angle $\Theta$ = 69.9842° according to Eq 21 is $\Delta$ = 11.78 mm. The theoretical light transmittance according to Eq 19 is ${\rm{ \mathsf{ τ} }}$ = 0.5973.

According to Eqs 18 and 42, the corrected light transmittance was calculated without taking into account and taking into account diffraction. In both cases, they are equal to ${{\rm{ \mathsf{ τ} }}_{cor}}$ = 0.3783. The transmittances are practically the same, because the diffraction factor in Eq 42 is 0.9999998. At the incidence angle of $\Theta$ = 69.9842°, the value of the diffraction factor in Eq 42 would be comparable with the multiplication of the second and third factors estimating the contribution of reflection and absorption, at the widths of the strips of several nanometers, which is impossible in the considered window constructions. With the widths of the strips used for the calculation at the incidence angles of 85°, 87° and 89°, the corrected light transmittance without and taking into account diffraction is, respectively, 0.0848, 0.0365 and 0.005, i.e., when approaching the incidence angle of 90°, the transmittance tends to zero.

For a single glazed window with a distance between the gratings (glass thickness) s = 4 mm and widths of the strips c₁ = 3, c₂ = 1, c₃ = 2.5 and c₄ = 1.5 mm (a filter with such parameters has been considered in ^[131]), the diffraction factor in Eq 42 is 0.9999992 and the influence of diffraction can also be neglected.

3.11.   Novel building typology with optimal daylighting

A novel building typology consisting in the use of the grating optical filters in the smart windows to achieve comfortable conditions of natural lighting and insolation indoors has been presented in ^[140]. The problems of ensuring comfortable conditions will always be relevant, including in the cities of the future, since without their optimal solution it is impossible to imagine a building that fully corresponds to the concept of “smart home”. For a separate building, these problems could be solved quite simply by choosing the maximum area of light openings for the northern sector, the minimum for the southern, and the middle for the eastern and western sectors. However, from an architectural and artistic point of view, such a building with different window sizes on different facades can hardly be called a successful solution. It would be even more difficult to imagine a similar approach for a complex of buildings, given their mutual influence on the distribution of sunlight. In modern conditions for a building with identical windows, problems are solved with the use of blinds and other devices for redistributing light fluxes.

The use of low-emission coatings, chromogenic and other advanced technologies in windows is constantly expanding, especially due to a gradual decrease in cost, that is, the future lies with such technologies. The disadvantage of such windows is the inability to transmit scattered sunlight when blocking direct radiation. Discomfort in the room is caused by direct rays, and in the active state, smart windows also cease to transmit scattered rays. The functioning of such windows does not take into account the position of the Sun in the sky, that is, the incidence angles of the solar beams onto the window, although at some angles protection is not required even from direct beams.

A novel approach to the use of chromogenic technologies in the smart windows is that thin-film chromogenic coating is applied not over the entire area of one surface of pane, as in conventional smart windows, but in the form of parallel strips on two surfaces of the one or two panes, from which a grating optical filter with angular selectivity consists. Figure 27 demonstrates the principles of using the smart windows with optical filters on an example of a complex of three buildings by dividing the building’s facade into shading and lighting zones, taking into account two opposing buildings. All three buildings are located in parallel, the paths of solar beams are shown for the time of the maximum solar radiation at the selected calculating date (usually this is the middle of the hottest period of the year or the day of the maximum solar radiation). At this time, the illuminated part of the facade of the building needs the maximum Sun protection, that is, the light transmission of the smart windows with activated chromogenic strips should be minimal, and for the shaded part of the facade it is possible to use smart windows with a relatively large light transmission (in extreme cases, in this area you can apply conventional windows).

Thus, in this case, for the considered facade of the building, it is advisable to use smart windows of two types that differ from each other in the level of light transmission. The slope angles of the gratings of both types must be the same, since they are designed for the same facade. The characteristic angles of the filters must also be the same due to the same incidence angles of the solar beams. However, the ratio of the widths of the transmissive and chromogenic strips will be different.

The widths of the directionally transmissive strips of the output gratings are calculated for single and double/triple glazed windows, respectively, by Eqs 13 and 14. Numerical simulation ^[141] shows that for the same value of this width, in order to increase the light transmission of the filter, it is necessary to reduce the period of the gratings. Similarly, taking into account the surrounding buildings, smart windows are calculated for all the facades of the building, with the exception of the northern sector, where the Sun protection is not required. The dimensions of the windows of all the facades will be the same, and the thin-film coatings of the filters will not violate the aesthetic appearance. In addition, the absence of blinds and other devices will even improve the aesthetic properties of windows, especially panoramic ones. Ergonomic properties will also improve (there is no need to constantly adjust the position of the blinds lamellas, since a smart window with an optical filter self-adapts to the position of the Sun), as well as environmental factors (lack of window construction elements, for example, blinds requiring replacement with subsequent disposal). Smart windows with optical filters will cost more than conventional windows, but they also perform additional functions of angular regulation of light transmission and save money on the purchase of light redistribution devices, their installation and operation.

During seasonal and daily movement of shaded and illuminated sections of the facade, smart windows of two corresponding types will function in a less optimal mode, since their parameters are calculated for the time with the most required Sun protection, when the intensity of solar radiation is maximum.

The proposed building typology is best suited for a complex of buildings in which people are mostly in the daytime, that is, for public buildings such as offices, classrooms, libraries, mega malls, etc. The considered approach is applicable not only for newly designing buildings, but also for reconstructing old buildings with replacing windows.

4.   Conclusions and prospects of the field

Smart windows with advanced architectural glass technologies having a variety of mechanisms for changing the light transmission depending on change in the ambient conditions or under the influence of electric current have been reviewed. Photochromic, thermochromic, thermotropic, gasochromic and electrochromic technologies, as well as nanocrystal in-glass composites, elastomer deformation tunable, electrokinetic pixel, liquid crystal and suspended particle devices, are the most promising for the use in the conventional smart windows entire covered with active layers. These technologies are also applicable to the grating optical filters for smart windows with additional function of angular filtering the solar radiation without using the blinds or other light redistribution devices.

Design of the grating filter, methods for calculating its geometrical parameters and light transmission characteristics and some results of calculation by these methods have been demonstrated. Unlike the conventional smart window, such a window with the filter blocks the direct sunlight partially or completely in a preset range of the incidence angles of the solar beams and transmits the diffused light providing more comfortable daylighting indoors. Calculated angular and temporal characteristics of the light transmittance demonstrate the angular selectivity of the transmission of a smart window with grating optical filter compared to a conventional smart window.

Each of the chromogenic or other smart technology has its own advantages and disadvantages and is being continuously developed. The possibility of their use in the grating filters depends on the complexity of applying thin-film surface coatings (using masks, etc.) or multilayer coatings interposed between two glass sheets, but there is no fundamental difference from the fabrication of conventional smart windows. Wide thin-film photochromic, gasochromic, thermochromic or thermotropic strips on the inner surfaces of a double or triple glazing chamber (Figure 10c) will be more technologically in the fabrication than narrower strips on both surfaces of a single glazing (Figure 10d), as well as multilayer strips with electrochromics, thermochromics or thermotropics interposed between glass sheets (Figure 10b). Various methods of physical vapor deposition and all other well-known coating methods can be applicable for fabricating the gratings with varying degree of the manufacturability. Self-adhesive window films with pre-applied chromogenic gratings are promising for the renovation of existing window systems.

The total cost of a window with two gratings will increase compared to a conventional smart window with a single chromogenic surface due to the use of masks or other technological complications. However, for such a window, a smaller amount of chromogenic materials will be required, since the total area of all chromogenic strips of both gratings will be less than the area of the window ^[131,141] fully covered with the chromogenic layer. In addition, the window with grating filter will be more effective due to a new function of the angular selectivity of transmission improving the indoor environment. By reducing the cost of air conditioning in the hot season, like a conventional chromogenic window, the filter additionally improves lighting conditions due to the transmission of diffused solar radiation. All this contributes to the commercialization of smart windows with filters in the future, especially considering that chromogenic technology is actively developing and becoming cheaper.

Based on smart glass technologies ^{[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30 ,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49 ,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77 ,78,79,80,81,82,83,84,85,86,87,88,89,90,91 ,92,93,94,95,96,97,98,99,100,101, 102, 103, 104, 105 , 106, 107, 108, 109, 110, 111, 112, 113]} and developed grating optical filters ^{[130,131,132,133,134,135,136,137,138,139,141,142,143,144]}, a novel building typology has been proposed in ^[140]. The fundamental principle of such a typology is the building, the windows of each facade of which (excluding facades in the northern sector, where the Sun protection is not required) have filters with the individual slope of the gratings and the relative position of the two gratings, calculated taking into account the azimuths of the windows, as well as the different light transmittances in different zones of each the facade, determined by the shading of these facades with the surrounding buildings.

Having the optimal light transmission in each facade, the windows of these facades can be of the same dimensions, and the thin-film coatings of the filters will not violate the aesthetic appearance, along with the absence of blinds or other devices. Due to self-adaptation of the filter to the position of the Sun, such a smart window is more ergonomic compared to the blinds whose lamellas need adjustment. Lack of the additional window construction elements requiring replacement with subsequent disposal improves the environmental protection.

Thus, the prospects of the field of both smart windows in general and grating filters in particular are confirmed by the possibility of further developing the comfort of daylighting and insolation of rooms in the “smart homes” of the future.

Acknowledgments

This study was supported by the Research Institute of Building Physics of the Russian Academy of Architecture and Construction Sciences (project number 2020-7.6.9.).

Conflict of interest

none