Modified function projective synchronization of master-slave neural networks with mixed interval time-varying delays via intermittent feedback control

1.   Introduction

Neural networks (NNs) have been a fascinating topic during the last decade and have been intensively researched. A neural network is a calculation model spurred by the organic brain organizations in the cerebrum with a mix of neurons and neurotransmitters. There have been widely applied in many aspects, such as software engineering, physics, psychology, biology, artificial intelligence (AI), and electrical engineering. On the other hand, due to the connecting of neurons, the state of neural network nodes tends to be consistent with time. So there are many research studies on the synchronization of neural networks have been applied in many areas, including neural computing, image processing, traffic systems, and secure communication.

Since the restricted interchange speed of neurons and amplifiers can lead to network instability or inconstancy, time delays are always required for neural networks. As a result, as stated in ^{[1,2,3,4,5,6,7,8,9,10,11,12]}, neural networks incorporating time delay have garnered a lot of study attention. Time delay is a natural phenomenon that always occurs in neural networks. Note that the latency of information processing and the limited speed of information transmission between neurons causes the discrete time delay ^{[1,2,3,4,5,6,7,8,9]}. On the other hand, since the variety of sizes and lengths of the axon, nerve impulses are distributed, which causes the distributed time delay ^[13]. Such delays frequently lead to system instability, oscillation, and decreased performance. Therefore, time delays cannot be avoided in the analysis of stability and performance for neural networks, and many researchers have studied neural networks with distributed and discrete time delays ^[11,12]. In 2018, Zhou and Cai investigated the synchronization of two delayed neural networks using intermittent feedback control, In 2016, Balasundaram, Raja, Zhu, Chandrasekaran and Zhou investigated discrete-time stochastic recurrent neural networks with multiple time-varying leakage terms and impulsive effects, and ^[7] investigated the synchronization of chaotic neural networks with discrete time-varying leakage terms and impulsive effects using delayed exponential synchronization.

Recently, synchronization has been a hot topic in neural networks with delays. Synchronization is a term that refers to the process of weaving the threads of execution of several tasks together without destroying shared data or causing deadlocks or race conditions. Synchronization also occurs between network nodes to ensure that send and receive streams operate correctly and that information does not collide. Projective synchronization ^{[12,13,14,15,16,17]}, cluster synchronization ^{[18,19,20,21]}, general decay synchronization ^[22], quasi synchronization ^[23], complete synchronization ^[24], lag synchronization ^[25], finite-time synchronization ^[26], and outer synchronization ^[27,28] are some of the types of synchronization that have been defined. Function projective synchronization is characterized that the master and slave systems could be synchronized up to a scaling function. Function projective synchronization is a more general definition than that of projective synchronization. It could be used to get more secure communication in applications because it is evident that the unpredictability of the scaling function in function projective synchronization can enhance communication security, such as ^[29]. In ^[30], Cai, Hao, and Liu examined how to use intermittent control to accomplish exponential synchronization of two chaotic systems with delays using intermittent control. In ^[31], Xing, Jiang, and Hu utilized Lyapunov functional theory, mathematical induction, and an inequality technique to provide intermittent synchronization for delayed recurrent neural networks. To the best of the author's knowledge, no publication has been made on a neural network's proposed exponential function projective synchronization.

To date, many effective control approaches to study the stabilization problem of time delay systems have been put forward, including continuous state-feedback control and discontinuous state-feedback control. In recent years, discontinuous feedback control, such as switch control, impulsive control, and intermittent control, has received wide attention. Especially intermittent control was proposed in the seminal paper in ^[32] and has aroused a great deal of interest due to its broad potential applications in various practical systems ^{[33,34,35,36]}, such as economy, transportation, communication, manufacturing, etc. Compared with continuous control, intermittent control is more economical and practical when the system output is measured intermittently rather than continuously. Compared with impulsive control, intermittent control is easier to implement in practical applications and process control because it has a nonzero control width. However, impulsive control is activated only at some isolated instants. Owing to those merits, intermittent control has become a hot control method in various fields and achieved many results ^[37,38,39]. The intermittent control strategy also finds applications in physiological modeling, networked control systems, transportation, economy, communication, and manufacturing, among others ^{[40,41,42,43]}. The problem of exponential synchronization for the complex dynamical network with mixed time-varying under periodically intermittent control was studied in ^[44]. In ^[45], the problem of projective synchronization of a hyperchaotic system under periodically intermittent control has been investigated. On the other hand, nonperiodically (aperiodically) intermittent control permits us to vary both the constant and the control width ^[46,47]. In ^[48], Pecora and Carroll presented the master-slave approach for synchronizing two identical chaotic systems with differing beginning circumstances in recent years. Aperiodic intermittent control is more practicable than intermittent control regularly. In ^[12], Abdurahman, Jiang, and Teng investigated the synchronization of impulsive neural networks with heterogeneous time-varying delays using projective function synchronization. The Lyapunov stability theory, the periodically hybrid intermittent feedback control technique, the differential inequality method, and inductive mathematics were used to derive the theoretical result in ^[49], which examined the synchronization of master-slave neural networks with mixed time-varying delays. Later in ^[50], the exponential synchronization of chaotic neural networks with time-varying delay was studied using an intermittent output feedback approach. However, there is room for improvement. No study has been published on function projective synchronization for master-slave neural networks with mixed interval time-varying delays via intermittent feedback control.

Motivated by the above discussion, we have considered the issue of modified function projective synchronization for master-slave neural networks with mixed time-varying delays in this paper. The neural networks may not be synchronized when a controller is not added to the infrastructure of individual nodes. Hence the controlled synchronization of neural networks is a rather important topic in both theoretical research and practical applications, such as feedback control ^[51], intermittent control ^[31]. We have considered periodically intermittent control and feedback control in this paper. Intermittent control is to control systems via discontinuous control inputs at a control period. In some cases, it can be impossible to use only the synchronization of neural networks at all times. Therefore, using synchronization of neural networks in some intervals may prove more cost-effective than synchronization of neural networks at all times. As a result of the above, we will study the intermittent feedback controller with mixed time-varying delays, including both discrete interval and distributed time-varying delays representing two time-varying differential functions $\sigma_1(t)$ and $\sigma_2(t)$ are treated as continuous functions belonging to the specified interval. These delays have upper and lower bounds required to find the function derivative, similar to the time delay in ^[12]. Developing a novel Lyapunov-Krasovskii functional and linear transformation technique, employing the lower bound and upper bound lemma for the reciprocally convex approach, novel criteria for the master system's synchronization with the slave system derived in terms of linear matrix inequalities (LMIs). Additionally, this study disproves the commonly held notion that the upper bound of the delay-derivation upper bound of time-varying delay must be less than 1. Finally, simulated examples are offered to demonstrate the use and benefits of the proposed techniques.

This paper is organized as follows. Section 2 contains model descriptions and preliminaries. Section 3 introduces several criteria for establishing modified function projective synchronization across master-slave neural networks with heterogeneous time-varying delays. Finally, Section 4 uses numerical examples to demonstrate the utility of the theoretical result.

2.   Problem formulation and preliminaries

The following notation will use in this paper: $\mathbb{R}$ indicates the set of real numbers, $\mathbb{R}^+$ denotes the set of all real non-negative numbers, $\mathbb{R}^n$ denotes the set of $n$-dimensional real spaces equipped with the Euclidean vector norm $\Arrowvert \centerdot \Arrowvert$, and $\mathbb{R}^{n\times m}$ denote the space of all matrices of $n\times m$-dimensional. $A^T$ is denoted the transpose of matrix $A$, $A$ is symmetric if $A = A^T,$ $\lambda_{\text{max}}(A)$ and $\lambda_{\text{min}}(A)$ signify the maximum and minimum eigenvalues, respectively, of matrix $A$. $I$ denotes the identity matrix with the appropriate dimensions. The symbol $\star$ always denotes the symmetric block in a symmetric matrix.

Consider the neural networks model shown below, which incorporates both interval and distributed time-varying delays:

where $x(t) = [x_1(t), x_2(t), ..., x_n(t)] \in \mathbb{R}^n$ and $y(t) = [y_1(t), y_2(t), ..., y_n(t)] \in \mathbb{R}^n$ are the master system's state vector and the slave system's state vector, respectively, $n$ is the number of neurons, $C\in \mathbb{R}^{n\times n}$ is a positive matrix, $A\in \mathbb{R}^{n\times n}, \ B\in \mathbb{R}^{n\times n}$ and $D \in \mathbb{R}^{n\times n}$ represent the connection weight matrices. $U(t)$ represents the control input that will be designed. The initial conditions $\psi(t)$ and $\varphi(t)$ denote continuous vector-value initial functions, $h(t)$ and $\sigma_i(t) \ (i = 1, 2)$ denoted the interval discrete time-varying delay and interval distributed time-varying delay, respectively, $h_2, \rho_2$ is the upper bound of $h(t)$ and $\sigma_i(i = 1, 2),$ respectively.

Assumptions include the following:

(A.1) The delay functions $h(t):\mathbb{R}^+\rightarrow \mathbb{R}^+,$ and $\sigma_i(t):\mathbb{R}^+\rightarrow \mathbb{R}^+$ satisfy $0 \leqslant h_1 \leqslant h(t) \leqslant h_2,$ and $0\leqslant \rho_1 \leqslant \sigma_1(t) \leqslant \sigma_2(t) \leqslant \rho_2,$ respectively, where $0 \leqslant \dot{h}(t) \leqslant \mu \leqslant \infty,$ $0\leqslant h_1 \leqslant h_2,$ $0 \leqslant \rho_1 \leqslant \rho_2, t\in \mathbb{R}^+$ and $\mu > 0$ are given real constants.

(A.2) For the activation functions $f_1(\cdot), \ f_2(\cdot)$ and $f_3(\cdot)$ with $f_1(0) = f_2(0) = f_3(0) = 0,$ assume there are three matrices with positive diagonals. $\epsilon_1, \ \epsilon_2$ and $\epsilon_3,$ there hold

where $y_h = y(t-h(t)), \ x_h = x(t-h(t)).$

The master system (1) is said to achieve exponential function projective synchronization with the slave system (2) if there exists a continuously differentiable positive scaling function $\alpha(t) > 0$ such that

where $\Arrowvert \cdot \Arrowvert$ stand for the Euclidean vector norm and $x(t)\in \mathbb{R}^n$ can be equilibrium point.

By defining the error signal as $e(t) = y(t)-\alpha(t)x(t)$, we obtain the following synchronized error system for master-slave neural networks:

We design the following periodically intermittent feedback controller:

where

where $n\in \mathbb{Z^+},$ $M$ and $G$ are constant matrix and $J$ is a control gain metrices, $\Omega$ is the control period, $0\leqslant \ell \leqslant \Omega,$ and $\ell$ is the so-called control width.

Substituting intermittent feedback controller (4) for the error system of master-slave neural networks (3), the closed-loop system shown below demonstrates the findings:

where

and $\lambda(t) = \varphi(t)-\alpha(t)\psi(t)$ is the error system's starting state (3).

Remark 1. When $\alpha(t) = 1$ or $\alpha(t) = -1$ is used as the scaling function, the synchronization issue is simplified to complete synchronization or anti-synchronization. When $\alpha(t) = 0$, the synchronization issue becomes a chaos management challenge.

To establish our primary findings, we will require the following definitions and lemmas.

Definition 2.1. ^[12] Error system for master-slave neural network with mixed interval time-varying delays (5), which including both discrete interval and distributed interval time-varying delay is said to achieve exponential function projective synchronization (EFPS) if there exists $L\geqslant 1, \ \lambda > 0$ and a continuously differentiable positive scaling function $\alpha(t) > 0$ such that

where $\Arrowvert \cdot \Arrowvert$ stands for the Euclidean vector norm.

Remark 2. The neural networks will achieve function projective synchronization if the scaling function $\alpha(t)$ is a function of $t$. Many different types of synchronization are included in the function projective synchronization, when $\alpha(t) = \alpha$ or $\alpha(t) = 1,$ the function projective synchronization is reduced to projective synchronization or common synchronization proposed in ^[15,16,17] and ^[52,53], respectively. It is worth pointing out that there was no exponential function projective synchronization for master-slave neural networks with intermittent feedback control shown in the system (5).

Lemma 2.1. ^[54] For any constant symmetric positive matrix $M > 0$ scalar $d > 0$ and vector function $Z:[0, d]\rightarrow \mathbb{R}^n,$ such that the integrations concerned are well defined, the following inequality holds:

Lemma 2.2. ^[55] Define the function $\Phi(\gamma, H)$ as follows for all vectors $\sigma \in \mathbb{R}^\mathit{\text{p}}:$

for a pair of positive integers $q, \ p$ and a scalar $\gamma\in (0, 1),$ a matrix with a positive definite value $H\in \mathbb{R}^{\mathit{\text{q}}\times \mathit{\text{p}}},$ two matrices $W_1$ and $W_2\in \mathbb{R}^{\mathit{\text{q}}\times \mathit{\text{p}}},$ if a matrix $K\in \mathbb{R}^{\mathit{\text{q}}\times \mathit{\text{q}}}$ exists such that

consequently, the following inequality is true:

Lemma 2.3. ^[56] (Schur's complement) Given matrices $X, Y$ and $Z$ with $X^T = X$ and $Z^T = Z,$ then

is equivalent to one of the following condition

(1) $X < 0$ and $Z-Y^TX^{-1}Y < 0,$

(2) $Z < 0$ and $X-YZ^{-1}Y^T < 0.$

Remark 3. In this paper, distributed delays $\sigma_1(t)$ and $\sigma_2(t)$ are included in the system (5), which is more general and flexible than the previous research ^[57,58,59]. Then, these results can be established as new criterion LMIs.

The goal of this work is to create the controller with the structure (4) that is capable of exponentially synchronizing the master system (1) and the slave system (2). Furthermore, we are interested in developing a feedback gain matrix $J$ that is exponentially stable for the controlled error system (5).

3.   Main results

In this section, we will evaluate the modified function projective synchronization of the master systems (1) and the slave system (2) utilizing suitable Lyapunov-Krasovskii functionals method, Jensen's inequality, the reciprocally convex technique's lower bound lemma, and piecewise analytic method.

Theorem 3.1. The master system (1) and the slave system (2) achieve exponential function projective synchronization under periodically intermittent feedback controller (4), for given scalar $0 < \alpha < \beta$ there exist n$\times$n-symmetric positive definite matrices $P, \ Q_1, \ Q_2, \ Q_3, \ S_1, \ S_2, \ R,$ n$\times$n-matrices $W_1, W_2$ and $J$ such that the following inequalities hold:

where

Proof. We considered the following Lyapunov-Krasovskii functional:

where

It is easy to check that

where

Calculating the derivative of $V(t, x_t)$ with respect to $t$ along the error system's trajectory (5) indicates that

then, we obtain that

By using Lemmas 2.1 and 2.2, it is shown that there exists a matrix $K$ such that $\hat{S}_1 > 0$ and $\hat{S}_2 > 0$, respectively, and the following inequality is proven:

Similarly, it holds that

and by use of Lemma 2.1, we obtain

where

As a result of (A.2), it is apparent that

Case I. For $t\in [n\Omega, n\Omega+\ell),$ the slave system is executed inside control windows, which enables the intermittent feedback control to function.

From (5) and (17)–(23), we obtain

The following zero equation is derived.

From (24) and (25), we have

If $\Gamma < 0$, then we get

Integrating the above inequality for $t \in [n\Omega, n\Omega+\ell), n \in \mathbb{Z}^+,$ yields the following result:

which implies

Case II. For $[n\Omega+\ell, (n+1)\Omega),$ the slave system is running in free windows, and the intermittent output feedback control is disabled.

We are able to do similar estimation as we did for Case I, we have the following

If (11) satisfies the matrix inequality (30) and is equivalent to $\Delta < 0$, we get

therefore, when $t\in[n\Omega+\ell, (n+1)\Omega), n\in \mathbb{Z}^+,$ we get

Combination with (29) and (32), we can obtain

Thus, for $t\in[n\Omega, n\Omega+\ell), \ n\in \mathbb{Z}^+,$ by (28) and (33), we get

and for $t\in [n\Omega+\ell, (n+1)\Omega), \ n\in \mathbb{Z}^+,$ by (29), (32) and (33), we have

From (34) and (35), we obtain that

where

Furthermore, as a result of (16), we get

and

So, we get from (36)–(38) that

then

By Definition 2.1, the master system (1) can be exponential function projective synchronized with the slave system (2) under the intermittent feedback controller (4). The proof is completed.

Remark 4. If $\Omega = \ell$ in condition (14), the intermittent feedback controller (4) immediately transforms into a continuous output feedback controller in the Theorem 3.1 is met.

Remark 5. If $\alpha(t) = 1, \ D = 0, \ \hat{S}_1 = 0, \ Q_1 = 0, \ R = 0, \ h_1 = 0, \ \rho_1 = \rho_2 = 0$ and $\hat{f}_3(\cdot) = 0,$ the closed-loop system (5) turns into form

proposed by ^[50], and the assumption (A.1) can be reduced the case, that is

To address this situation, we define

Then, a similar method used in Theorem 3.1 is used to produce Corollary 3.1.

Corollary 3.1. Assume (41) is satisfied. For given scalar $\alpha > 0$ and $\beta > 0,$ there exist n$\times$n-symmetry matrices $P, \ Q_2, \ Q_3, \ S_2,$ n$\times$n-matrix $W_2$ and $J$ such that conditions (10) and (11), the controller error system is exponentially stable, and the following inequalities are hold:

where

Proof. From (15), we can get

Calculating the derivative of $V(t, x_t)$ with respect to $t$, it can be deduced that

For case $t\in [n\Omega, n\Omega+\ell)$, from (17)–(25) and (40), we have

If $\tilde{\Gamma} < 0$, then (44) is equivalent to (42).

Similarly, for case $t\in [n\Omega+\ell, (n+1)\Omega)$ is equivalent to (43).

Note that the controller gain matrix $J$ cannot be derived directly based on Theorem 3.1 since they are coupled with the positive definite matrix $P$ in (10) and (11). In order to calculate the controller gain matrix, we apply the partition matrix method to get the following conclusion.

Theorem 3.2. Assume a situation $(0 < \phi \leq 1),$ and $\phi \mu < 1,$ the controlled error system (5) is exponentially function projective stable, if $\alpha > 0$ and $\beta > 0.$ There are n$\times$n-symmetric positive definite matrices $Z, \ \hat{Q}_1, \ \hat{Q}_2, \ \hat{Q}_3, \ \hat{S}_1, \ \hat{S}_2, \ \hat{R}, \mathit{\text{n}}\times\mathit{\text{n-}}\mathit{\text{matrices}}\ \hat{W}_1, \hat{W}_2, \ K,$ and an inverse n$\times$n-matrix $V$ respectively, such that the following inequalities hold:

where

Additionally, the controller (4) intended gain matrix is provided by $J = KV^{-1}.$

Proof. Denote $Z = P^{-1},$ $\chi = \text{diag}\{Z, Z, Z, Z, Z, Z, Z, I, I, I \}.$ The inequalitie (10) obtained by pre and post multiplying the matrices $Z^T$ and $Z$, respectively, using the idea of congruence transformation, are equivalent to

then

Similarly, the inequality (11) is equivalent to

then

where

From, $\bar{\gamma}_{1, 1}$ and the others are defined in Theorem 3.2. If a real matrix $V$ exists that satisfies (49) let $K = JV$, then we have

and apply the Schur complement lemma, from (50), we get

the linear matrix inequalities (LMIs) (52) is equivalent to LMI-based conditions in (45). Similarly, from (51), we get

where

and linear matrix inequalities (LMIs) (53) is equivalent to (46). The proof is completed.

Remark 6. In Theorem 3.2, the periodically intermittent feedback control gain matrix is obtained using the partition matrix method and elementary transformation of matrix and condition (50). In particular, the partition matrix method provides a powerful tool to solve the problem of coupling between matrices.

4.   Numerical examples

Example 4.1. Consider the following 2-dimensional neural networks with mixed interval time-varying delays:

From the Theorem 3.2, we let $h_1 = 0.05, \ h_2 = 0.1, \ \rho_1 = 0.05, \ \rho_2 = 0.1, \ \alpha = 0.3, \ \beta = 3.2, \ \mu = 1.3$ and $\phi = 0.5, \ h(t) = \dfrac{e^t}{e^t+1}, \ \sigma_1(t) = 0.05+0.05\sin(t), \ \sigma_2(t) = 0.08+0.02\sin(t).$

For the period width $\Omega = 2$ and $\ell = 1.9,$ consider the condition (14) yields

By applying the MATLAB, Theorem 3.2 may be solved in the following ways. Following that, the controller gain is set

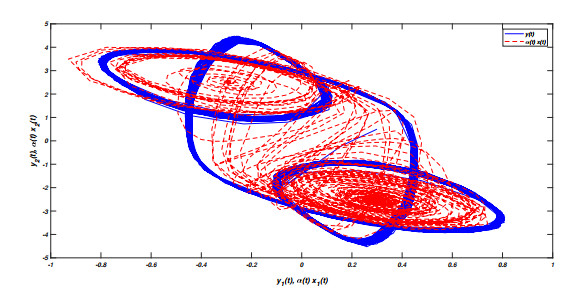
Figure 1 shows the trajectory of master system (1) and slave system (2) with the time-varying scaling function $\alpha(t) = 0.8+0.2\sin \dfrac{0.5\pi t}{15}.$ Figure 2 shows The trajectories of $e_1(t)$ and $e_2(t)$ without the controller. Figure 3 shows the trajectories of $e_1(t)$ and $e_2(t)$ with the controller and the modified function projective synchronization error trajectories of $e_1(t)$ and $e_2(t)$ of the master-slave neural networks with intermittent feedback control is shown in Figure 4.

Example 4.2. Consider the following 3-dimensional neural networks with mixed interval time-varying delays:

then, the controller gain is

As a result of Theorem 3.2, the system (1) under the direction of the controller (4) with the provided parameters is exponential function projective synchronized.

Figure 5 shows the trajectory of the master system (1) and slave system (2) with the time-varying scaling function $\alpha(t) = 0.8+0.2\sin\dfrac{0.5}{15}\pi t$. Figure 6 shows the trajectories of $e_1(t), e_2(t)$ and $e_3(t)$ of the master-slave neural networks without the controller. Figure 7 shows the trajectories of $e_1(t), e_2(t)$ and $e_3(t)$ of the master-slave neural networks with the controller. The modified function projective synchronization error trajectories of $e_1(t),$ $e_2(t)$ and $e_3(t)$ of the master-slave neural networks with intermittent control is shown in Figure 8.

Remark 7. In this paper, we have developed a model of the master-slave neural networks to be more comprehensive and general than the previous paper. As a result, there are no results to compare with our paper. However, we have offered examples to show our work, and we can reduce the system model from our work to compare it. Our model is more general than others ^{[12,29,30,45,49,50,57,59]}. By Remark 5, a novel Lyapunov-Krasovskii functional, the reciprocally convex approach, and Jensen's inequality, we gain less conservative results when compared with the other work ^[50], as shown in Corollary 3.1.

Remark 8. The periodically intermittent feedback controller presented in this paper is more general and efficient than ^[60,61] because the controller does not have to run all the time. Moreover, distributed delays $\sigma_1(t)$ and $\sigma_2(t)$ are included in the system (5), which is more general and flexible than ^[62,63,64], which this study disproves the commonly held notion that the upper bound of the delay-derivation upper bound of time-varying delay must be less than $1$.

Remark 9. There is room to improve this work in that constant matrices $M$ and $G$ are required for calculating the controller. Moreover, in the future topic, it is very challenging to apply some lemmas or Lyapunov-Krasovskii functional used in this paper into memristive neural networks ^[65,66] to achieve improved stability criteria, which are applied in the next generation computer ^[67,68].

5.   Conclusions

The periodically intermittent control of modified function projective synchronization of master-slave neural networks was studied between discrete intervals and distributed time-varying delays. The development of suitable Lyapunov-Krasovskii functionals uses the lower bound lemma for reciprocally convex approach. Moreover, it still uses the application of the piecewise analysis method, periodically intermittent control and mathematical induction. The sufficient conditions for modified function projective synchronization of master-slave neural network systems were derived in terms of LMIs. The intermittent feedback controller designed can guarantee modified function projective synchronization of the error system. Finally, numerical simulations were presented to illustrate the efficacy of the suggested theoretical conclusions.

Acknowledgments

This project is funded by National Research Council of Thailand (NRCT) and Khon Kaen University: N42A650291.

Conflict of interest

The authors of this research study disclose that they have no conflicts of interest.