1.
Introduction
Provision of clean water for the ever-growing population remains a challenge [1,2]. The problem has been exacerbated by environmental pollution, climate change and rising demands for water [3,4,5]. The generation of high quantities of solid and liquid wastes, which are beyond critical levels and low preparedness on how to deal with the wastes among the populace has further worsened the situation. More than 80% of municipal wastewater is released into freshwater bodies untreated while industries dump millions of tons of pollutants in freshwater bodies and land resources resulting to their pollution [6,7]. The situation is dire in poor developing countries where, effluents are released to the environment without any treatment [8]. Fayomi and others [9] noted that 90% of sewage in developing countries is released in watercourses without any treatment resulting to extensive environmental pollution. In developing countries of Africa such as Kenya [10] and Nigeria [1], more than 70% of the population do not treat water from freshwater sources prior to consumption, which poses a public health concern and risk to waterborne diseases. A data gap on wastewater generation levels in developing and developed countries exists although there is consensus that a large share of the sewage is released in watercourses untreated [11].
The infrastructure to treat wastewater is limited even with increased production of municipal and industrial effluent [9,12,13]. The effluents are reservoirs of organic and inorganic water pollutants [14,15,16,17]. Such pollutants deteriorate the quality of water in addition to negatively affecting human health and ecosystems due to their highly toxic, non-biodegradable and persistent nature [17,18]. For these reasons, significant efforts have been made to enhance wastewater treatment using techniques such as chemical precipitation, photocatalytic oxidation, flotation, coagulation, flocculation and adsorption in conventional approaches including sequencing batch reactor, activated sludge and membrane bioreactor methods [15,16,19]. The conventional methods combine biological, physical and chemical operations and processes to decontaminate wastewater. The methods are based on centralized conveyance of wastewater to treatment plants or to individual treatment systems where appropriate [20].
Centralized and individual wastewater treatment systems are financially inefficient to maintain. Operations and maintenance costs of the former are higher due to requirements to transport and store waste in spacious areas in addition to technical staff requirements for operations and processing [21]. Decentralized treatment systems on the other hand, are easy to maintain but cannot process large quantities of wastewater [21]. Wastewater treatment approaches used are engineering intensive, high-energy consuming, oversized and have sophisticated designs, which contributes to their high failure rate and exorbitant operations and maintenance costs [22,23]. In addition, the methods are not effective in complete elimination of emerging contaminants and endocrine disrupting chemicals found in wastewater [24,25]. The effectiveness of wastewater treatment measures is influenced by the economy, stability, efficiency and energy access so that each approach has its own merits and demerits based on the pollutant being eliminated [26]. The differences in the quality of raw wastewater, equipment used, operational skills applied, chemicals used in treatment, operations, testing and monitoring of treatment plants influence the success of wastewater decontamination [27]. The interplay of these factors complicates wastewater treatment processes and therefore, the necessity for an optimal treatment technology.
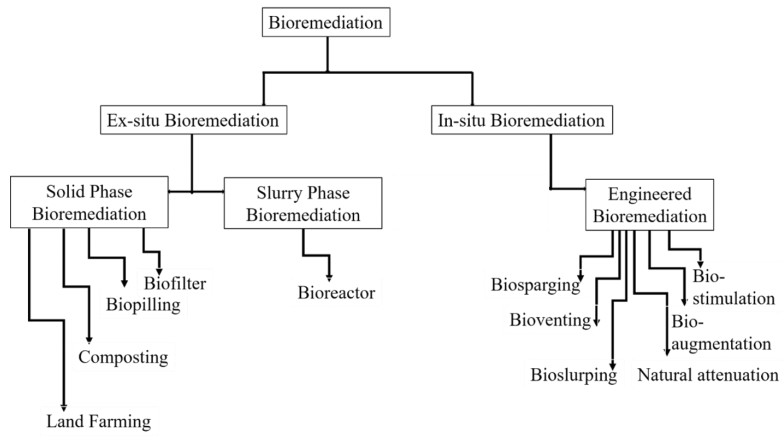
Most recently, bioremediation that involves the application of natural biological activity to decontaminate, destroy or transform harmful substances to harmless ones has been proposed for wastewater treatment [15,18,26]. The technology has effectively eliminated pollutants found in soils, aquaculture, freshwater and marine ecosystems [17,28]. Bioremediation involves the use of both aerobic and anaerobic fungi, microalgae, protozoa and bacteria to detoxify, immobilize, eradicate or degrade chemical contaminants found in wastewater [29,30]. The microbes used in the process are isolated and identified in freezing ice environs, deep sea, animals, plants, soil and water and as such, have a ubiquitous nature. Their availability in large numbers and the high affinity to a variety of pollutants makes the microorganisms suitable cleaners of the environment [29]. The eco-friendly and cost-effective nature of bioremediation processes promotes the high preference to use the technology. By being energy efficient, the technology prevents the burning of fossil fuels associated with greenhouse gas emissions and ultimately, climate change. Some authors have associated bioremediation to reduced greenhouse gas emissions [31] and the restoration of polluted land and water resources [32], which has a positive effect on climate change mitigation and adaptation. Lorenzo [33] highlighted that biodegradation of pollutants though slow and yet to be implemented in large scale; is a green process with the potential to control climate change by decontaminating wastewater to a useful resource and eliminating the growing global water scarcity. Some of the bioremediation approaches used in decontaminating wastewater are as shown in Figure 1.
Bioremediation requires engineering techniques but not to the intensive extent of conventional treatment approaches [34]. Human intervention is also key in establishing the optimal microbe mix and match for best bioremediation results. Therefore, there is need to understand the various approaches used in bioremediation of wastewater, their advantages and disadvantages and optimization approaches that can enhance pollutant remediation in future. In researching on bioremediation, a large gap exists between field and laboratory research, which deters applicability of the technique in environmental pollutant elimination. This observation is because most bioremediation studies are done at laboratory level to evaluate the microbial potential and effectiveness to contaminant remediation [34]. The laboratory experiments involve collecting samples of wastewater for bioremediation testing. The samples are few in most cases to reduce research costs and hence, not representative of the actual pollution extent. The resultant findings are also not representative of the actual remediation capacity. For these reasons, only few of the laboratory findings have been transferred for field applications over the last decade. Where field applications have been done, they are still at trial experiments, which are small-scale in nature [35]. According to Sharma and Kumar [17], field applications of bioremediation are limited by lengthy protocols of approval by regulating authorities that involve risk assessment of the technology. In this mini-review, applications of bioremediation in wastewater treatment are explored to understand merits, demerits, challenges and prospects of the technology. The aim of the review is to enhance the applications of the technique in field settings, which are apparently limited in practice. In addition, the review makes suggestions on establishing a proper pollutant-microbe mix and bioremediation technique, which will optimize wastewater decontamination outcomes in the near future.
2.
Factors that influence bioremediation in wastewater
Bioremediation processes can be either ex-situ or in-situ (Figure 1). In ex-situ bioremediation, wastewater treatment occurs some other place other than the production site while in-situ bioremediation is at the original site through biological systems. Ex-situ bioremediation can also be carried out in-situ to prevent environmental pollution. For instance, a consortium of Scedosporium apiospermum H2 and Aspergillus ochraceus H16 fungal species was used to decontaminate pollutants in oil mill wastewater by applying both composting (ex-situ) and bioaugmentation (in-situ) processes and decreased ecotoxicity and phytotoxicity was reported [35]. The preference to either in- or ex-situ approach of bioremediation is influenced by a number of biotic and abiotic factors that control the growth of microorganisms used and ultimately, the biological processes that the microbes regulate during environmental clean-up [36]. These factors are as summarized in Table 1 [37,38] and can be classified into two: - 1) physicochemica l and 2) biological factors.
2.1. Physicochemical factors
The age of the organometallic ions in wastewater, temperature, presence or absence of electron donors and electron acceptors, ionic strength, solubility, redox potential and pH are some of the physicochemical factors that influence wastewater treatment via bioremediation [39]. Akpor et al. [40] summarizes these factors as the inherent characteristics of the wastewater effluent targeted for bioremediation. The factors influence processes such as biosorption by regulating the charge on the surface of a microbial cells and the isoelectric point of the wastewater in which decontamination is occurring [41]. Through biosorption, microbes can accumulate pollutants such as heavy metals via physicochemical or metabolic-based pathways of uptake. Changes in the physicochemical factors of wastewater also influence the ionic state of ligands such as the amino, phosphoryl and carboxyl groups during bioremediation processes. Specifically changes in redox potential, pH and solubility influence the transformation of heavy metal ions in wastewater to insoluble forms [42]. Adsorption of wastewater contaminants by microbes during remediation is pH- dependent so that higher alkaline pH favors precipitation while lower pH levels favor attraction of contaminants to microbial surfaces [36]. Once adsorption has occurred on the microbes, decontamination of wastewater is possible. Optimum temperatures, which vary based on the microbe used for bioremediation and range between 25-29 ℃ [43], favor microbial metabolism and enzymatic activity, which promotes bioremediation. Additionally, optimum temperatures enhance solubility and improve the bioavailability of heavy metal pollutants present in wastewater [39] Lower temperatures slow down microbial enzyme activity while higher temperatures result to protein denaturation and ultimately, enzyme inhibition. According to Das and Chandran [44], temperature influences pollutant chemistry in wastewater bioremediation and regulates the diversity and physiology of the microbes used. The presence and addition of nutrients (nitrogen, carbon and phosphorous) that facilitate microbial growth and their reproduction enhances bioremediation in the processes of biostimulation and bioaugmentation. The addition of such nutrients in some bioremediation processes improves the efficacy of the process [45]. According to Abatenh et al. [41], such nutrients optimize the C: N: P ratio and promote the degradation of hydrocarbons in addition to increasing the metabolic activity of pollutant degrading microbes. Although nutrient addition promotes the growth of heterotrophic microbes important in wastewater decontamination, their excessive use could be counterproductive rather than bio-stimulative as Ogbeh et al. [45] argued. The presence of enough moisture for microbes favors biodegradation processes. In a study focusing on bioremediation of hydrocarbons in wastewater, adequate moisture content was shown to favor pollutant removal by enhancing microbial activity [46]. The authors also noted that low moisture inhibits microbial activity while excess water created microbial resistance against oxygen diffusion reducing the efficacy of bioremediation processes.
2.2. Biological factors
The biological factors that influence wastewater treatment through bioremediation manifest during implementation of the technique and emanate from the inherent characteristics of the microbes used [39]. The characteristics include the presence of plasmid-encoded genes that enhance substrate specificity during contaminant bioremediation and encode specific enzymes that degrade a number of substrates in the case of bacteria [36]. Chemotaxis, often manifested by bacteria as the movement of the microbe to a direction of suitable gradient is another innate behavior that influences bioremediation of recalcitrant organic pollutants [47]. In this case, bacterial cells move towards the pollutants owing to their increased concentrations or following the trigger of activity by some of their enzymes. The phenomenon enhances the biodegradation and bioavailability efficiency of recalcitrant contaminants in wastewater enhancing bioremediation outcomes [47,48]. Chemotaxis, which is either positive or negative from a chemical gradient also enables microbes to grow, reproduce and survive in polluted waters, which improves their activity and efficacy in bioremediation [49]. The ability of microbes to exist in interactive networks of multiple species (consortiums) is an enhancer to complete bioremediation of certain pollutants such as organohalides [29]. A microbial consortium of Staphylococcus, Stremptomyces, Bacillus, Actinomycetes and Pseudomonas species to decontaminate wastewater sourced from a centralized treatment plant was reported to have higher removal efficacy for chemical and biological oxygen demand at more than 90% compared to individual microbes with about 50% efficacy rates [50]. A consortium of Aspergillus ochraceus H2 and Scedosporium apiospermum H16 reduced the polyphenolic content of olive mill wastewater from 2.6 to < 1 toxicity units following ex-situ and in-situ bioremediation [35].
The nature of some microbes to have optimal activity in the presence or absence of oxygen is another innate factor that influences bioremediation. Anaerobic microbes unlike aerobic ones use co-metabolic substrates for energy and other electron acceptors as well as organic carbon to degrade recalcitrant pollutants rather than oxygen [51]. The success of either anaerobic or aerobic bioremediation however depends on the target pollutant. In one study, bioremediation efficacy of crude oil from wastewater was higher using aerobic rather than anaerobic microbes [52]. Other authors suggested that anaerobic bioremediation favors decontamination of recalcitrant pollutants though most bioremediation systems use aerobic microorganisms [20,53]. The toxic pressure that pollutants exert on microorganisms also triggers the microbes' enzymatic activity hence initiating bioremediation processes such as is the case in degradation of xenobiotics [41].
Enzyme activity also plays a crucial role in decontamination of wastewater pollutants [48]. Some of the enzyme classes with an important role in bioremediation include cytochrome P450, dehalogenases, dehydrogenases, hydrolases, proteases, lipases and oxidoreductases (laccases and peroxidases) [54]. The enzymes enhance bioremediation through processes such as ring-opening, pollutant elimination, reduction and oxidation reactions. The cytochrome P450 family of enzymes metabolizes chemicals such as xenobiotics, steroids and fatty acids that have are adsorbed by microbes from wastewater [55]. Laccases function by producing radicals through reduction of oxygen found in polluted water and also cleave rings found in aromatic pollutants [56]. Dehalogenases eliminate halogens in wastewater through cleavage of carbon-halogen bonds [54]. Dehyrogenases provide energy for microorganisms used in bioremediation by catalyzing the oxidation of organic compounds [57]. Hydrolases and proteases catalyze the breakdown of fats and proteins respectively [58]. Transesterification and esterification to breakdown lipids in wastewater is catalyzed by lipases [54]. Oxidoreductases such as peroxidases and laccases also have high thermal stability and redox potential, which makes them effective in elimination of dyes, phenolic contaminants such as pharmaceuticals and bisphenols as well as organic pollutants of wastewater [59,60].
Immobilization, which serves to reduce and prevent the movement of microbial cells and their respective enzymes to preserve their catalytic and viability functions is another biological factor influencing pollutant remediation in wastewater [61]. Immobilization explores the natural ability of microbes to form biofilms on material surfaces. Microbes and biocatalysts are anchored on inert carriers that allow media interchange to improve their bioremediation ability and reusability [62]. Processes used in immobilization include copolymerization, covalent binding, atomization, gelation, adsorption, encapsulation and entrapment [63]. Consequently, the processes speed up pollutant elimination and reduce costs affiliated with using many biocatalysts. Immobilization has been applied in enhanced removal of dyes, aromatic hydrocarbons and phenolic compounds in wastewater treatment [61,62].
3.
Role of microbes in wastewater bioremediation
As shown in Figure 1, bioremediation can occur in a number of approaches including attenuation, biostimulation and bioaugmentation. In the case of wastewater decontamination, autotrophic and heterotrophic bacteria as well as fungi, protozoa and algae to a smaller extent are introduced in biological treatment processes [64]. The microbes survive in wastewater polluted environs because they readily use its noxious components as energy sources [48,53]. The heterotrophic microbes biodegrade pollutants in wastewater using it as an electron donor to respire. In this case, nitrates and sulfates among other nutrients in wastewater are the electron acceptors under anoxic, anaerobic or aerobic conditions. Autotrophic microbes oxidize ammonia to nitrite or nitrates for energy use while alkaline components of wastewater such as dissolved organic compounds including hydroxyacids, steroids, saccharides and aromatic compounds are used as the sources of carbon. Alternative sources of energy for some microbes can be from solar energy and chemicals in the case of phototrophic and chemotrophic microorganisms, respectively [65]. Hydrocarbons and organic matter as carbon sources enhance the growth and reproduction of microbes used in bioremediation processes [51]. The specific functions of both bacteria and fungi in decontaminating wastewater are discussed in subsequent sections.
3.1. Role of microbes in removal of heavy metals from wastewater
Microbes adopt using various mechanisms to survive and interact with organic metals in wastewater in addition to withstanding the high metal toxicity levels [66,67]. Some of the mechanisms include production of exopolysaccharide and metallothioneins, production of enzymes, extrusion and biotransformation [68,69]. To detoxify and resist metals, microbes also produce metal chelators and biosurfactants, oxidate, demethylate, and decrease metals and metal ligands mechanically [70].
Through extracellular chemical precipitation, volatilization and valence conversion, microbes can also decontaminate metals [83]. These mechanisms are possible because microbes have a negative charge on their surfaces owing to an anionic structure in which metals that are cationic can bind. Through biosorption, the uptake of heavy metals by microorganisms can be either through metabolism-based bioaccumulation or by metabolism-free biosorption [84,85]. The latter occurs outside the cells while the former, involves transformation and sequestration of metal species based on their redox potential within the cell. Decontamination of wastewater off heavy metals can also occur through the complexation of the cations in the cell cytoplasm via a variety of compounds. It is the ability of microbes to accumulate heavy metals intracellularly that has been exploited in effluent treatment by bioremediation [39]. Metals can also be sequestered extracellularly by their accumulation in the periplasm and their subsequent transformation to insoluble compounds [86]. Microbes such as bacteria adsorb metal cations using ionizable hydroxyl, phosphate, amino and carboxyl groups found in their cell wall and plasma membrane [87]. The methylation of toxic heavy metals to increase their lipophilicity decontaminates pollutants off wastewater by their ability to permeate cell membranes of microbes for bioaccumulation [70]. Reduction of heavy metals to transform them to harmless substances by using the contaminants as electron acceptors and donors to produce energy and through enzymatic activity is another mechanism of bioremediation reported in the detoxification of chromium and mercury [39,88]. Specific examples of microbes and the metals they decontaminate from wastewater are as shown in Table 2.
Although microbes decompose heavy metals to decontaminate wastewater completely and with high efficacy, this bioremediation approach is insufficient at large-scale [89]. Some authors agreed with this suggestion claiming that the process results to production of large quantities of sludge whose nature is toxic [90]. At large scale, bioremediation of heavy metals would be more costlier owing to the addition of nutrients prerequisite to enhance enzymatic activity and uptake of such toxins [68]. Consequently, the chemical and biological oxygen demand in the wastewater would increase. Selvi et al. [91] highlighted that most large-scale bioremediation projects are limited to single method applications, have low efficacies, cost inefficiencies and are prone to failure. To modify the bioremediation of heavy metals in wastewater to industrial scale, biotechnological modifications to the process through bio-stimulation and genetic engineering must be applied [89].
3.2. Role of microbes in removal of dyes from wastewater
Textile effluents contains various contaminants and mixed dyes. The dyes color the initial raw materials used in making textiles. The dyes have aromatic structures that make them resistant and recalcitrant to degradation using conventional approaches of wastewater treatment [92]. Bioremediation techniques such as biodegradation, bioaccumulation and biosorption are hence used in biological decolorization of the dyes in such effluents [41]. In biosorption, dead or living microbes are used to adsorb the dyes while bioaccumulation and biosorption involves intracellular sequestration of dyes by microorganisms from effluents. Biodegradation is the enzymatic mineralization and decolorization of dyes found in wastewater. In most cases, enzymes produced by bacterial and fungal species are responsible for removal of selected dyes from textile effluents. Radia and Romana [93] suggested that dye removal from textile wastewater occurs either through enzymatic and cellular biodegradation or via microbial biomass adsorption. The authors further argued that biodegradation of textile effluents to remove the dyes is more superior than biosorption and adsoprtion since it has higher efficacy comparatively. The effectiveness of the textile effluent bioremediation mechanisms is influenced by factors such as the dye concentration, temperature and pH of affected waters, and the microorganisms used [92]. Some of the bacterial and fungal species used to decolorize dyes from textile effluent and their specific targets are as shown in Table 3.
3.3. Role of microbes in removal of hydrocarbons in wastewater
Bioremediation of hydrocarbons such as oil is dependent on the quantities and specific nature of the pollutants in wastewater. Petroleum based hydrocarbons that are the commonest in wastewater occur in four forms: - resins, asphaltenes, aromatics and saturated compounds [44]. Saturated and aromatic hydrocarbons are refractory to bioremediate since microorganisms have low attacking capacity to their chemical bonds hence cannot degrade them unless they have the ability to produce biosurfactants or through biostimulation. Barathi and Vasudevan [105] noted that some polycyclic aromatic hydrocarbons cannot be degraded at all through bioremediation. The mechanism of hydrocarbon pollutant bioremediation involves the use of aerobic microbes. The process begins with an intracellular attack by peroxidases and oxygenases, which trigger the step-by-step conversions of the organic pollutants to intermediates of the tricarboxylic acid cycle that are less noxious [106]. The microbes can also biodegrade hydrocarbons by producing biosurfactants and by attaching themselves on substrates [44]. Biosurfactants are surface-active biomolecules produced extracellularly by microbes such as P. aeruginosa, B. subtilis, Acenitobacter and Candisa bombicola to reduce the surface tension of water-hydrocarbon interfaces and solubilize hydrocarbons, increase their bioavailability and mobility for enhanced bioremediation [107]. Some of the microorganisms involved in bioremediation of hydrocarbons are as shown in Table 4.
The biodegradation of hydrocarbons just as other pollutants is very difficult to implement at industrial scale. The observation is attributable to the fact that hydrocarbon degradation at natural settings is propagated by indigenous microbes. The microbes usually have high carbon and energy demand for growth and reproductive purposes. In addition, the presence of hydrocarbons particularly, petroleum-based ones in the microbes' bulk environs makes them physiologically stressed [108]. By biodegradation, such stress is relieved as Kleindienst et al. [109] highlighted. The indigenous microbes also have varied catalytic pathways some of which are not specific or compatible to hydrocarbon decomposition. To alleviate the limited effectiveness of the microorganisms in hydrocarbon removal from wastewater and enhance large-scale applications, joint use of microbes in consortiums could optimize results. Some bacterial consortiums have been used to decontaminate crude oil [110,111] and diesel oil [112] with an efficacy of more than 80% in pilot field applications.
4.
A literature review on the specific applications of bioremediation in wastewater treatment
4.1. Treatment of industrial effluent
Industrial wastewater is a significant source of toxic environmental pollutants whose levels are on the rise due to the growing urbanization and technological advancements in the industrialization era [123]. Such wastewater is sourced from food, dairy, desalination, leather tanning, electroplating, automobile, metal finishing, petroleum and textile dyeing industries and results to heavy metal pollution [19]. Application of microorganisms including algae, bacteria and fungi has been reported as effective in the treatment of the toxic industrial effluent [124]. According to Dubey et al. [125], cyanobacteria species such as Nodularia sp., Oscillatoria sp., Cyanothece sp., and Synechococcus sp. are effective in industrial wastewater treatment. The removal efficacy for the cyanobacterial species was between 68% and 99%. The Cyanothece, Nostoc, Nodularia, Arthrospira, Desmodesmus, Oscillatoria, Chlamudomonas, Phormidium, Botryococcus etc autotrophic species of algae have been effectively used in phycoremediation of industrial effluents although the efficacy rates were not specified for the microbes. [126,127]. Organic matter present in aerobic wastewater treatment systems favors the growth of heterotrophs. They compete for oxygen better than the nitrifying microbes that are slow growing and low yielding. It is for this reason Alteromonas sp., Gliocladium virens, Corius versicolor and Phanerochaete chrysosporium are used in bioremediation of pulp and paper mill effluents [128,129]. The biological removal of color was achieved by the degradation of polymeric lignin and also the production of laccases and peroxidases to catalyze the reaction. The efficiency for removal was at 42% [128]. Annika et al. [130] also confirmed that P. aeruginosa and Brevibacillus choshinensis were able to decolorize textile effluent in the presence of glucose within a week. In the study, decolorization of the dyes from textile effluent as a result of bioremediation was measured by estimating phytotoxicity in Triticum spp., Brassica juncea and Vigna radiate plant species. Dye decolorization from the effluent was inversely proportional to phytotoxicity. Other species that had high efficacy in bioremediating textile effluents include B. licheniformes and P. putida [131]. In the study, the bacterial species reduced heavy metals such as lead, nickel, chromium, cadmium and copper by 93.5%, 89.46%, 83.52%, 80.7% and 93.5%, respectively. In particular, the Pseudomonas species were shown to biodegrade tannery wastes that had aromatic and aliphatic hydrocarbons and are normally refractory [124]. The species were more effective on decontaminating the wastewater during the dry season when their concentration was higher at 5.4×107 cfu/ml compared to the rainy season that had 9.6×104 cfu/ml bacterial load.
Biochemical oxygen demand (BOD), (which the quantity of oxygen consumed by microorganisms including bacteria during aerobic decomposition of organic matter at specified temperature) and chemical oxygen demand (COD), (which is the quantity of dissolved oxygen needed to stabilize and oxidize inorganic and organic content of a specified solution) are common indicators of the strength of wastewater. A number of microbes have been shown to significantly reduce COD and BOD levels in wastewater. Acinetobacter calcoaceticus and P. putida for instance, could remove 70%-80% of lignin and COD, respectively in addition to decolorizing dyes in paper mill and kraft pulp effluent by more than 60% in a continuous bioreactor [132]. In another study by Chandra [133], Enterobacter sp., Citrobacter sp.,
and P. putida were 82%-99.8%, 96.8^ and 97% effective in removal of heavy metals, BOD/COD and in textile effluent decolorization, respectively. Maghsoodi Vida et al. [134] reported a 70.7% and 69.5% effectiveness in COD reduction in textile effluent by Coccus and Bacillus bacterial species. Contents of tannery effluent were rendered safe for disposal and non-toxic following biodegradation by Pseudomonas sp. [135]. The authors reported a removal efficacy of 70.9% and 76.7% for BOD and COD, respectively. A consortium of Micrococcus, Arthrobacter, Pseudomonas and Bacillus species also reduced COD and BOD by 95% from steel industry effluents [136]. More than 60% reductions in COD and BOD from sugar mill effluents were reported after biodegradation using Escherichia coli, Enterobacter aeruginosa, Klebsiella pneumonia, B. cereus and Staphylococcus aureus [137]. Using Micrococcus, Arthrobacter, Pesudomonas and Bacillus species, steel effluent bioremediation was successful and COD and BOD reduction was up to 95% efficient [138]. Gradual reduction in BOD and COD in sewage water was also reported following bioremediation using Scendesmus spp. and Chlorella minutissima microalgal species [139]. The efficacy rate of removal was measured at 95% for BOD and 90% for COD.
Unlike the positive results obtained on using microbes to cleanse wastewater, Buaisha et al. [19] argued that in activated sludge systems, heavy metal removal via bioremediation was inefficient at high concentrations of the metals. At elevated concentrations some metals result to cell break-off unlike in low concentrations where they serve as micronutrients. With cell break-off, some microbial enzymes are inhibited irreversibly leading to low bioremediation efficacy. In an assay on onsite wastewater treatment, which is energy saving, Mirra et al. [20] agreed that microbes and their nutritional demands can make bioremediation processes expensive, lead to production of filamentous bacterial especially in activated sludge systems and hence, the need to monitor their oxygen uptake rates to optimize the process and success rate of field applications of the technology. Ojha et al. [48] also reported that bioremediation rates are slower especially when biodegrading refractory pollutants of wastewater and the microbes used could have low metabolic capacity to attack the chemical bonds and decontaminate such wastewater contaminants, which limits field application of bioremediation. Kedia and Sharma [138] suggested the need to incorporate bio-stimulation and genetic engineering technologies to enhance the outcome of field applications of bioremediation. In bio-stimulation, nutrients that are electron acceptors and enhance rate limiting reactions such as carbon, oxygen, nitrogen and phosphorus are added to promote bioremediation. Ojha et al. [48] who supported the use of genetic engineering to enhance bioremediation outcomes suggested the use of degradative and reporter genes whose role is to encode contaminant decomposing proteins and monitor pollution levels, respectively to enhance bioremediation efficacy. The authors argued that the biotechnological modifications of genetic engineering and bio-stimulation enhanced enzyme activity and provided microbes with essentials nutrients for growth and reproduction in the polluted wastewater, which resulted to speedier bioremediation outcomes. Mer operon for instance, which is a genetically engineered mercury resistant microbe was shown to have 100% efficacy in cleansing wastewater off the heavy metal [139].
4.2. Treatment of municipal wastewater
Municipal wastewater contains disease causing pathogens, toxic heavy metal elements and pharmaceutical wastes, sludge, plastics, organic and inorganic compounds [16,19]. In addition, wastewater contains endocrine disrupting chemicals and other degradation resistant chemicals sourced from the use of pharmaceuticals, personal care products, plasticizers and heat stabilizers [140]. Some of these pollutants cannot be removed via conventional water treatment approaches hence the use of microbes through bioaugmentation biological processes [141]. In bioaugmentation, microbes that can biodegrade recalcitrant pollutants in wastewater are added [142]. The use of Pseudomonas sp. from activated sludge was reported to remove phenolic compounds from wastewater with an efficacy rate between 48%-94% within 40 hours [143]. A bacteria consortium of P. putida, E. cloacae and Gordonia sp. proved effective in removal of total organic carbon in municipal wastewater with an efficiency rate of 80% to 84% [144]. In less than twelve days, a consortium of Bacillus sp., P. aeruginosa and Acinetobacter calcoaceticus removed lipid and BOD content from lipid-rich wastewater by more than 98% [145]. Hesnawi et al.
[141] also reported 42%, 52%, 54% and 70% removal of TOC from municipal wastewater using P. aeruginosa, B. laterosponus, B. subtilis and SludgeHammer (a commercial bacteria), respectively.
Fungal species have also been used in the treatment of municipal wastewater and in particular, elimination of recalcitrant contaminants [140]. Trametes versicolor completely detoxified municipal wastewater off parabens in two days [146]. Trametes hirstula and T. versicolor significantly reduced low concentrations (20-500 ng/l) of pharmaceutical contaminants in wastewater completely [147]. Removal efficacy was enhanced using laccases and through biosorption. Selenium contaminated municipal wastewater was effectively treated with Alternaria alternata and Ascomycota sp. making fungi important bioremediators of heavy metals [148]. In this case, the removal rate was at 0.5-0.7 ug/l daily to achieve a 17% reduction of Selenium within a week. The removal efficacy rose to 0.9 ug/l daily on bio-stimulation.
Microalgae have also been reported to remove toxic contents of wastewater according to Nag et al. [149]. In the study [149], Scenedesmus sp., Chlorella sp., Phormidium sp. and Oscillatoria sp. were used for bioremediation. Nitrogen and phosphorus removal was 79.6% effective while COD, ammonia and TOC removal rate was at 90.8%, 93.9% and 86%, respectively [149]. Dunaliella and Chlorella species were found to reduce the COD and BOD of domestic wastewater by more than 65% [150]. Significant reductions in nitrates, phosphate and COD resulted following the treatment of municipal wastewater with Scenedesmus and Chlorella species [151]. Chlorella species had 70%, 98.2% and 84.2% reduction efficacy for phosphates, nitrates and COD, respectively while Scenedesmus sp. had 80.5%, 99.7% and 95% reduction efficacies for the pollutants in respective order. Nitrogen and phosphorous from municipal wastewater were reduced by 90% of their initial concentrations using S. rubescens and C. vulgaris
[152]. Heavy metals were also absorbed from wastewater using a consortium of S. obliquus and C. pyrenoidosa as well as Sprirulina and Spirogyra species [72]. The removal efficacy was 98.83% for selenium, 99.73% for manganese, 98.3% for chromium and 99.73% for iron.
To improve the activity of microbes used during bioremediation of municipal wastewater, a number of modifications on the treatment systems can be done. The adoption of the upflow anaerobic sludge blanket (UASB) technology that is processed by anaerobic microbes and uses a methane generating digestor has been shown to improve bioremediation efficacy. With optimization of its hydraulic retention and temperature, UASB reactors cleared COD from municipal wastewater in a period of 6 hours [153]. The fixed bed membrane bioreactor (FBMBR) technique is another bioremediation approach with high capacity to decontaminate COD, nitrogen, nitrates and ammonium from municipal wastewater with an efficacy rate of more than 90% [154]. The two methods combined with phycoremediation will enhance the in-situ treatment of sewage wastewater [153].
5.
Merits and demerits of bioremediation in wastewater treatment
Autochthonous microbes found in contaminated environs hold the key to detoxify wastewater through biodegradation and bioremediation techniques. Once the techniques are conducted in optimal environmental conditions, they can be effective, environmentally friendly and cost saving according to Azubuike et al. [155] and in comparison, to conventional physicochemical methods [19,20], which are costlier and result to generation of toxic sludge. Crini and Lichtfouse [156] also pointed out that the technology is simple, well accepted by environmentalists and the public and economically attractive. The technology has been hailed for its positive effects towards climate change adaptation [32,33]. This is because large quantities of different varieties of species as pure cultures or in the form of consortiums can be used to degrade contaminants in wastewater [48,157]. Some of the bioremediation successes achieved with regards to wastewater treatment include removal of suspended solids, BOD, COD, biodegradable matter, heavy metals, hydrocarbons and also emergent contaminants [14,15]. Using microbial degradation, micro and nano plastics that were previously perceived to be refractory can now be eliminated from the environment [158]. In this case, micro-plastics are fragments of a diameter below 5 mm while nano-plastics have a < 100 nm diameter [159]. The process of their degradation depends on the microbes used and the enzymatic pathways used. Zhou et al. [158] studied the targeted chemical bonds during depolymerization of micro and nano-plastics based on a variety of microbes and enzymes used. The transformation of some organic contaminants to harmless substances such as ethane, water and carbon dioxide is a great advantage of bioremediation approaches [29]. Ex-situ approaches of bioremediation are time and labor efficient since they do not require preliminary assessment of polluted sites prior to implementation of decontamination works unlike conventional approaches [155]. The installation and maintenance costs of some bioremediation approaches are low considering the ubiquitous and diverse nature of microorganisms used [29].
Despite the advantages, bioremediation techniques have a number of limitations. Depending on the pollution site, some contaminants cannot be transformed to non-toxic forms. In some cases, such as the bioremediation of hydrocarbons, biodegradation can stop at intermediate cycling of the pollutants resulting to more noxious or immobile products, which can be resistant to further degradation [29]. Such a phenomenon could occur due to changes in the characteristics of bioremediators or physicochemical conditions, which do not favor microbial or enzymatic activities [48]. The addition of electron donors and acceptors as well as nutrients resulting to profuse microorganism growth in the process of biostimulation depends on the environmental conditions of the polluted site, which regulate the technology's potentiality [155]. The technology is therefore site-specific in addition to requiring constant scientific observation. Goswami et al. [42] also noted that the efficacy of biostimulation is limited when contaminants are recalcitrant. Ogbeh et al. [45] also highlighted that addition of nutrients in excess is counterproductive to bioremediation outcomes. Such a phenomenon occurs if the added nutrients do not have the required micronutrients, enhance degradation of added nutrients rather than targeted pollutants and are toxic to indigenous microbes in the wastewater [160]. Some of the pollutants in wastewater such as heavy metals can limit the activity of indigenous microbes by producing toxins and resulting to low bioremediation efficacy [39]. In activated sludge systems, high quantities of heavy metals in particular copper, was reported to reduce the systems' effectiveness, caused cell break off and irreversible inactivation of enzymes, which reduced bioremediation efficacy [19]. Some microorganisms are not able to acclimatize in some wastewater pollutants such as heavy metals, recalcitrant and aromatic compounds due to their toxicity resulting to the deactivation or slow activity of the remediation process [157]. The need to create optimal environs for the survival of microbes, the slow nature of the technique, the uncontrolled degradation of some products and production of sludge are also limitations of bioremediation [156]. Some ex-situ bioremediation processes such as landfarming have low efficacy for inorganic pollutants, require microbial optimization prior to implementation, excavation and large operating spaces for favorable results [155]. It is therefore necessary to advance knowledge on the inherent mechanisms of bioremediation particularly, the decomposition of pollutants in wastewater and its effect on the enzymatic processes that regulate bioremediation. Such information is key in choosing the most appropriate technique and best microbial consortia with the highest efficacy based on the specific characteristics of the targeted wastewater.
6.
Bioremediations prospects
Despite the obvious advantages and the empirical evidence associated with bioremediation highlighted in this study, the approach is yet to provide convincing results with regards to wastewater and environmental cleanup as well as applications at field settings. Most of the studies evaluated in this review show that the focus is on identifying and testing of microbes with bioremediation potential at experimental level rather than the actual application of the microbes in large scale pollutant remediation [161]. While testing, identifying and isolating the bioremediators is a major step towards practical bioremediation, field application of bioremediation processes are limited. This is because 99% of the microbes identified as bioremediators cannot be cultured in laboratory conditions a phenomenon known as the "great plate count anomaly" [157]. In addition, conditions of microbial growth at laboratory setting are controlled unlike in field settings where the microorganisms are sensitive to environmental changes such as the characteristics of the targeted wastewater, its pH, redox potential, nutrient availability and environmental temperature variations [39,40,45]. The targeted contaminants for bioremediation should be available to microbes to enable the process. This is however dependent on their specific characteristics of microorganisms and the presence of bio-stimulants in some cases in addition to the specific wastewater characteristics and the system used for bioremediation. In highlighting these factors, Azubuike et al. [155] advocated for in-situ techniques such as bioinventing and biosparging that are less costly compared to ex-situ techniques such as biopilling, landfarming, windrow and bioreactors, which are expensive to setup and have low efficacy for refractory pollutants of wastewater. Consequently, recovery of isolates used for biodegradation processes is challenging. The extent of pollution and the pollutants present in wastewater also influence the success of bioremediation. Bioremediation of recalcitrant compounds including aromatic hydrocarbons, pharmaceuticals, halogenated compounds and polyethylene terephthalate found in wastewater is slow since most microbes cannot metabolize them or produce enzymes that enable their biodegradation [162].
Future research should therefore invest in applying bioinformatically-based mutagenesis and rational protein engineering to make novel enzymes and improve existent ones towards higher bioremediation efficacy [163]. Such biotechnological approaches coupled with the use of microbial consortia and genetic engineering techniques can optimize on a microbial mix-match specific to a given pollutant found in wastewater in addition to enabling large scale application of bioremediation. The use of the recombinant DNA advancements will enable the creation of whole microbial communities with bettered pollutant remediation [138]. However, the interaction of the engineered microbial communities with indigenous microorganisms is yet to be understood hence the need to undertake advanced research to clarify the grey areas in future [164]. By harnessing less understood microbes of the environment for bioremediation and in integrating eco-evolutionary principles in biotechnology, effective enzymes and degradation pathways of wastewater pollutants can be discovered as Borchert et al. [157] asserted. The combined use of genetic engineering and nanotechnology is another growing prospect in bioremediation set to increase efficacy and speed up the process [165]. Nanotechnology integrated with microbes was reported to be a green technique to alleviate pollutants such as heavy metals, bisphenol and dyes from industrial effluents with high efficacy [166].
Considering the limitations of bioremediation such as low population, nutritive inadequacies, lack of microorganisms with required biodegradation capacities, incompatibility of microbes with targeted pollutants and lack of contaminant bioavailability, there is need to invest in regulated bioaugmentation and biostimulation to speed up and enhance efficacy of the technique [29,155]. The latter entails the addition of substrates and/or nutrients in wastewaters to trigger activity of autochthonous microorganisms. However, the addition of the substances should be moderate since their excessive use results to suppressed microbial diversity and metabolic activity [167]. Contrary, addition of low levels of nutrients results to low activity and prolonged process [19]. Bioaugmentation on the other hand, serves to introduce new microbes with biodegradative capacity in addition to naturally occurring ones in wastewater. The aim is to make consortiums whose synergistic effects are likely to induce improved bioremediation efficacy according to Bhattacharya et al. [168]. The procedures must be undertaken with caution since they could lead to unhealthy competition between exogenous and endogenous microbes and a subsequent introduction of pathogens in the wastewater and the environment as well as low survival of the inoculums [39]. Additionally, bioaugmentation among other modifications could increase the overall cost of bioremediation processes making them financially inefficient compared to other conventional wastewater treatment approaches. Biosurfactants, which are bioemulsifiers can also be used to enhance availability of pollutants such as polyaromatic hydrocarbons to microbes and ultimately, biodegradation efficacy. The biomolecules reduce surface tension on hydrocarbon-water bonds enabling their solubilization and subsequent bioavailability for biodegradation [107]. The use of biosurfactants should be regulated to avoid increased cost of large-scale bioremediation [44,116]. Simultaneous application of multiple bioremediation approaches is highly recommended since it increases efficacy [169]. Therefore, future bioremediation research should focus on optimizing the enzyme activity of microbes used, identifying the best microorganisms to use, ensuring their compatibility to target environs and environmental conditions of wastewater polluted areas and their speedier efficacy with minimal waste production. Such modifications are ongoing using UASB and FBMBR technologies combined with other biotechnologies. At field settings, wastewater treatment processes via bioremediation has high potential but requires site-specific modifications to suit the targeted environs.
7.
Conclusions
Bioremediation is shown to be a revolutionary and growing approach of cleaning up wastewater. The technique is applied both ex-situ and in-situ using varied microorganisms to cleanse pollutants from industrial and municipal effluents as shown using empirical case studies. The efficacy of bioremediation processes was found to be varied and dependent on the specific microbes used, physicochemical and biological factors and the targeted pollutants. Some pollutants were biodegraded or detoxified completely while some were refractory. To improve the effectiveness of the process, this review made several suggestions for future studies. These include the use of biostimulants, bioaugmentation, addition of biosurfactants and the simultaneous use of microbial consortiums and different bioremediation approaches. Genetic engineering advancements incorporating recombinant DNA techniques were recommended for production of microbial communities with high affinity and resilience to recalcitrant pollutants and containing enzymes that enhance the degradation of such contaminants in future studies. Research on optimal microbe mixes and appropriate physicochemical and biological factors to bioremediate refractory pollutants should be prioritized to improve efficacy and reduce the cost of the technology. Biotechnological modifications on bioremediation will enhance the transfer of laboratory findings to field applications using the right mix and match of microbes based on the targeted wastewater pollutant. Additionally, large-scale application of bioremediation in wastewater treatment, which is at nascent stages will greatly progress through the advancements. The advancements should be implemented cautiously to prevent unhealthy competition of engineered microbes with autochthonous ones, which could lead to production of toxins and ultimately, reverse the gains of bioremediation for wastewater treatment. Optimization of environs where bioremediation occurs was recommended to enhance microbial survival, their metabolic and enzymatic activity towards effective wastewater decontamination. The findings of this review therefore advocate for further research on the uptake of bioremediation to enable large-scale field applications of the technology with greater efficacy in wastewater pollutant decontamination.
Acknowledgments
The authors would like to thank the University of Johannesburg for the support offered to complete this research.
Conflict of interest
The authors hereby declare no conflicts of interest in this research.









 DownLoad:
DownLoad: