Weighted pseudo almost periodic solutions of octonion-valued neural networks with mixed time-varying delays and leakage delays

1.   Introduction

Lung cancer is a prevalent cancer globally and a major cause of cancer deaths, responsible for 18% of cancer-related mortality and 11% of cancer cases^[1,2,3,4]. It not only affects the health and quality of life of millions of people but also places a tremendous burden on global healthcare systems. The occurrence of lung cancer stems from gene mutations and unregulated growth control, leading to abnormal cell proliferation^[5]. These abnormally proliferating cells gradually form tumors, which can infiltrate nearby tissues and metastasize.

Lung cancer risk factors are smoking, occupational hazards, air pollution, and genetics. Smoking is the most significant causative factor, greatly increasing the likelihood of developing the disease^[6]. Additionally, prolonged exposure to air pollution, radiation, and chemicals like heavy metals can also raise lung cancer risk^[7]. People working in the mining, construction, and chemical industries face higher risks due to occupational exposure^[8]. Genetic factors also play a role in some cases, with individuals having a family history of lung cancer being at a higher risk^[9]. These factors together raise the likelihood of lung cancer.

The metastasis and spread of cancer cells are among the primary reasons why lung cancer is so deadly ^[10]. Cancer cells spread via the blood and lymphatic systems, such as the brain, bones, and liver, forming metastatic tumors^[11]. These tumors severely disrupt the structure and function of the affected organs and weaken the immune system, leading to decreased resistance and making patients more susceptible to infections and other diseases^[12]. The presence of metastatic tumors not only affects the patient's quality of life but also makes treatment more complex and difficult, thereby further increasing the mortality rate of lung cancer.

Cancer treatments encompass chemotherapy, immunotherapy, targeted therapy, radiation, and surgical procedures^[13,14]. Surgery is suitable for early-stage lung cancer and involves removing the tumor and affected tissues to control the disease^[15]. Radiation therapy uses high-energy rays to kill cancer cells and is often combined with surgery or chemotherapy. Chemotherapy uses drugs to kill or inhibit the growth of cancer cells and is applicable for advanced lung cancer or as adjuvant therapy after surgery^[16]. Targeted therapy employs specific drugs to attack the genes or proteins of cancer cells, reducing damage to normal cells^[17]. Immunotherapy, an emerging treatment method, boosts the immune system to identify and destroy cancer cells. In order to quickly develop effective treatment strategies, we need to thoroughly study the interaction mechanisms between cancer cells and other cells.

Some researchers have attempted to investigate the interactions between tumor cells and immune cells using mathematical models to better understand the dynamic characteristics of cancer^{[18,19,20,21,22]}. These models not only capture the interactions between different cell types but also account for factors such as immune evasion, changes in the tumor microenvironment, and the effects of drug treatments. By simulating tumor progression under various environmental and therapeutic conditions, researchers can predict the trajectory of tumor development, evaluate treatment efficacy, and provide support for personalized treatment strategies^[23]. These models are particularly valuable in the context of immunotherapy, targeted therapy, and other emerging treatments as they help optimize therapeutic approaches, minimize side effects, and promote more precise cancer treatment.

With the development of fractional calculus, its application in modeling cancer growth has become increasingly widespread^{[24,25,26,27,28]}. In particular, the Caputo derivative, which can more accurately describe systems with memory effects and historical dependence, has shown significant advantages in simulating complex biological processes^[26]. Studies have shown that fractional-order models, when analyzing the impact of chemotherapy on cancer cell growth, align better with experimental data and more accurately reflect the interactions between cancer cells, chemotherapy drugs, and immune cells compared to integer-order models^[29,30,31]. Since fractional-order models can capture the non-locality and long-term memory effects of the system, they have demonstrated higher precision and effectiveness in cancer modeling, drawing increasing attention from researchers.

Lung cancer, as a high-mortality cancer, has attracted many researchers who use fractional-order mathematical models to analyze the dynamic behavior of its cells and their interactions with other cells^{[32,33,34,35,36]}. Amilo et al.^[34] established a Nablara discrete fractional-order model, revealing how the growth of lung epithelial cells and their interactions with immune cells promote the increase in the number of lung cancer cells. At the same time, they combined immunotherapy with targeted therapy to analyze the effects of these two treatment strategies on cancer cells and explored in-depth the role of genetic mutations in the spread of cancer cells^[35]. In addition, Özköse et al.^[36] developed a model that includes lung cancer tumor cells, lung cancer stem cells, CD8+ T cells, interleukin-12 (IL-12), and natural immune cells, studying the dynamic relationships between these factors and cell types. The results showed that after tumor formation, an increase in the number of CD8+ T cells significantly reduced the numbers of cancer stem cells and tumor cells.

In the aforementioned studies, the dynamic interactions between cancer cells and immune cells, as well as the effects of different treatment strategies on cancer cells, have been effectively modeled. However, optimizing these interactions during the treatment process to achieve the best therapeutic outcomes remains an important and unresolved issue. To address this, many researchers have focused on optimal control under various treatment strategies, aiming to determine the best control policies to inhibit cancer growth and spread through mathematical models^{[37,38,39,40,41,42]}. For example, one study analyzed the optimal treatment plan combining chemotherapy with a healthy lifestyle, and the results showed that this combination enhances the effectiveness of chemotherapy and reduces side effects ^[43]. Another study explored the optimal combination of surgery and programmed cell death ligand 1 (PD-L1) monoclonal antibody immunotherapy in the treatment of lung cancer, and the findings also indicated that the combined therapy significantly improves patient prognosis compared to single treatments^[44]. Through these studies, researchers aim to provide more precise guidance for clinical treatment and optimize therapeutic outcomes.

This paper establishes a Caputo fractional-order model for lung cancer, aiming to explore the dynamics of lung cancer from two key aspects. First, the model focuses on the complex interactions between lung cancer cells, immune cells, healthy cells, and metastatic cancer cells, revealing the underlying mechanisms involved in tumor growth and cancer cell metastasis. Second, the model incorporates surgery and immunotherapy as intervention factors to evaluate the impact of different treatment strategies on tumor growth rate, immune response, and other dynamic changes. Through these studies, this paper aims to provide theoretical support for lung cancer treatment, enhance the understanding of tumor evolution under different treatment interventions, and provide scientific guidance for optimizing clinical treatment strategies.

The key contributions and innovations of this paper are as follows:

a. Unlike ^[37], the new model presented in this paper takes into account the interaction between healthy cells and tumor cells in nutrient competition. This competitive mechanism inhibits tumor cell growth, leading to a more comprehensive description of its growth dynamics.

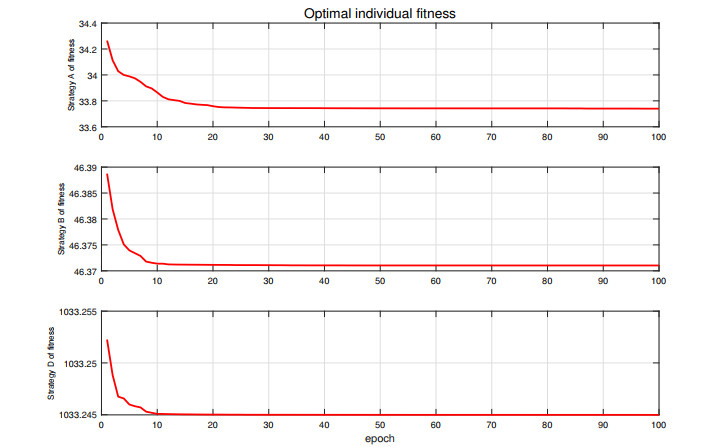
b. Existing research on fractional-order optimization control often overlooks the time-dependent changes in control parameters and the performance of the objective function under different treatment strategies^[38,39,40]. This paper analyzes these issues through numerical simulations and demonstrates the impact of different treatment strategies on control parameters and the objective function, as shown in Figures 1 and 2.

c. Based on real data regarding the changes in cancer cells in lung cancer patients, we evaluated the model parameters using the least squares method and performed curve fitting.

The remainder of this paper is organized as follows: Section 2 introduces the model construction and key definitions. Section 3 analyzes the conditions for the existence and uniqueness of the solution. Section 4 explores the stability theorems of the equilibrium points. Section 5 investigates the combined optimization strategy of surgery and immunotherapy, proposing the conditions for the existence of an optimal solution and deriving its expression. Section 6 validates the theory through numerical simulations. Section 7 performs parameter evaluation and curve fitting using real data. Finally, Section 8 summarizes the main conclusions of this paper.

2.   Model formulation and preliminaries

2.1.   Model formulation

Bashkirtseva et al. ^[23] developed a three-dimensional system based on the Lotka-Volterra competition model to study the dynamic interactions between tumor cells, immune cells, and healthy cells. The system considers the competition between healthy cells and tumor cells and introduces the stimulatory effect of tumor cell proliferation on immune cell proliferation. Specifically, tumor cell proliferation stimulates the growth of immune cells, but the proliferation of immune cells is not unlimited. Therefore, the authors use a second-type functional response function to describe this relationship. The system is

where $T$, $H$, and $E$ represent tumor cells, healthy cells, and immune cells, respectively. $r_i$ and $k_i$ ($i = 1, 2, 3$) denote the growth rate and the maximum carrying capacity of each cell type. $a_{12}$ represents the competition coefficient between healthy cells and tumor cells, $a_{13}$ represents the killing rate of tumor cells by effector cells, $a_{21}$ represents the rate at which tumor cells inactivate healthy cells, $a_{31}$ represents the rate at which tumor cells kill immune cells, and $d_3$ represents the death rate of immune cells.

Meanwhile, in order to investigate the interactions between lung cancer cells, immune cells, and disseminated cancer cells, Amilo et al.^[37] developed a three-dimensional system. In this system, in addition to considering the stimulatory effect of cancer cell proliferation on the immune system, it also takes into account the natural proliferation rate of immune cells in the absence of cancer cells. This three-dimensional system is

where $N(t)$, $P(t)$, and $I(t)$ represent the number of lung cancer cells, disseminated cancer cells, and immune cells, respectively. $\lambda$, $K$, $\mu$, and ${{\beta }_{1}}$ denote the growth rate of lung cancer cells, carrying capacity, spread rate, and the rate at which immune cells eliminate cancer cells. ${{\phi }_{1}}$, ${{\phi }_{2}}$, and ${{\phi }_{3}}$ are the factors influencing immune cells. ${{\beta }_{2}}$ indicates the rate at which cancer cells kill immune cells, while $\gamma$, $\delta$, and ${{\beta }_{3}}$ represent the spread rate, death rate of disseminated cancer cells, and the rate at which immune cells destroy them. The fractional order of the Caputo derivative $\alpha$ ranges from $0 < \alpha \le 1$.

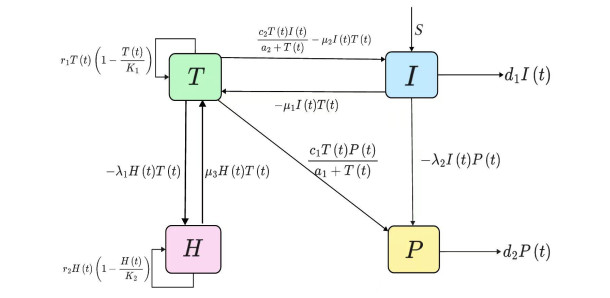
Inspired by systems (2.1) and (2.2) and considering that when the number of cancer cells becomes too high, the lack of nutrients or oxygen may lead to the death or slowed proliferation of cancer cells, resulting in a gradual reduction in the rate of cancer cell spread and eventually leading to stabilization. To better describe this phenomenon, we use a second-order functional response function to model the dynamic process of cancer cell diffusion. This function effectively simulates the rapid spread of cancer cells in the early stages, and as the number of tumor cells increases, resource limitations gradually become apparent, causing the diffusion rate to slow down and eventually stabilize. Therefore, we have established a four-dimensional fractional-order system that includes lung cancer cells, immune cells, healthy cells, and diffusing cancer cells to analyze the dynamic behaviors of these cells, as schematically shown in Figure 3. The specific form of the system is as follows:

where $T(t)$, $I(t)$, $H(t)$, and $P(t)$, respectively, represent the tumor cell density, immune cell density, healthy cell density, and tumor cell density diffused out at time $t$ in the lungs. Other parameters are detailed in Table 1. To better understand the following content, we will first introduce some basic definitions and concepts.

2.2.   Preliminaries

Definition 2.1. ^[33] The Riemann-Liouville fractional integral is given by

where $\alpha > 0$ and $\Gamma(\cdot)$ is the Gamma function.

Definition 2.2. ^[33] The Caputo derivative is given by:

To simplify the notation, we use $D^\alpha h(t)$ to represent the Caputo derivative operator ${}_0^C D_t^\alpha h(t)$.

Definition 2.3. ^[37] Let $(X, d)$ be a metric space and $T: X \rightarrow X$ be a function. If there exists a constant $0 \leq k < 1$ such that for any $x, y \in X$ the following holds, $d(T(x), T(y)) \leq k \cdot d(x, y),$ then $T$ is called a Banach contraction.

Definition 2.4. ^[37] If a function $f: \mathbb{R}^n \rightarrow \mathbb{R}^m$ on a set $D \subseteq \mathbb{R}^n$ has a constant $K \geq 0$ such that for any two points $x$ and $y$ in $D$ it holds that $|f(x) - f(y)| \leq K |x - y|$, then the function is Lipschitz continuous on $D$.

Definition 2.5. ^[37] The Laplace transform of the Caputo fractional derivative is given by the following formula:

3.   The existence and positivity of solutions

We first focus on the existence and uniqueness of the solution to system (2.3). Since directly proving the solution to system (2.3) is challenging, we will transform it into

where

According to ^[33], we can provide the following definition:

Definition 3.1. ^[33] Let ${{C}^{*}}\left[0, a \right]$ be the set of continuous column vectors $X\left(t \right)$, where the components $T(t)$, $I(t)$, $H(t)$, and $P(t)$ of $X\left(t \right)$ are continuous functions on the interval $\left[0, a \right]$. The norm of $X\in {{C}^{*}}\left[0, a \right]$ is defined as follows:

if $t > \varepsilon \ge m$, it can be represented as $C_{\varepsilon }^{*}\left[0, a \right]$ and ${{C}_{\varepsilon }}\left[0, a \right]$.

Definition 3.2. ^[33] If $X\in {{C}^{*}}\left[0, a \right]$ satisfies the following conditions:

(1) $\left(t, X\left(t \right) \right)\in B$, $t\in \left[0, a \right]$, where $B = \left[0, a \right]\times L$,

${{e}_{1}}$, ${{e}_{2}}$, ${{e}_{3}}$, and ${{e}_{1}}$ are real numbers.

(2) $X\left(t \right)$ satisfies the initial value problem (3.1).

At this point, $X\left(t \right)$ is called the solution to initial value problem (3.1).

Theorem 3.1. For the initial value problem (3.1), there exists a unique solution $X\in {{C}^{*}}\left[0, a \right]$.

Proof. Based on the relevant properties of Caputo fractional order, (3.1) can be reformulated as

Thus,

Let $F:{{C}^{*}}\left[0, a \right]\to {{C}^{*}}\left[0, a \right]$, and we obtain

then

This suggests

When $N\to \infty$, we have

and

Based on the definition of operator F in Eq (3.4) having a unique fixed point, it follows that Eq (3.3) exists a unique solution $X \in {{C}^{*}}\left[0, \tau \right]$. From Eq (3.3), we can deduce that

and

This implies that $X\in C_{\varepsilon }^{*}[0, a]$. From (3.3), we can deduce

Therefore, the initial value problem of Eq (3.3) corresponds to the solution of Eq (3.1).

Theorem 3.2. The solution of system (2.3) is positively invariant in the set

and

That is, if $X\left(0 \right) > 0$, then the model remains greater than zero for $t > 0$.

Proof. Obviously,

We can derive the following conclusion from the first equation of system (2.3)

Let

and

Therefore, we can obtain

Next, by applying the Laplace transform to (3.5), we derive

Based on the Laplace transform of the Caputo fractional derivative, we have

and

Thus,

By applying the inverse Laplace transform,

As each term on the right side of Eq (3.6) is a positive constant, $T(t)$ is positive for any $t > 0$. The positivity of the remaining three variables in system (2.3) can be proven similarly to $T(t)$.

4.   The existence and stability of equilibria

In this section, we will investigate the equilibria of system (2.3). First, we analyze the equilibria in the absence of tumor cells. Second, we explore the equilibria when tumor cells coexist with other cell populations. Finally, we examine the local stability of these equilibria under different parameter conditions. Based on

we can obtain two equilibria without tumor cells, denoted as ${{E}_{1}} = \left(0, \frac{s}{{{d}_{1}}}, 0, 0 \right)$ and ${{E}_{2}} = \left(0, \frac{s}{{{d}_{1}}}, {{K}_{2}}, 0 \right)$.

Basic Reproduction Number: As an important indicator for assessing the progression of cancer, we will then apply the next-generation matrix^[51,52] method for calculation, namely,

where $F = \frac{\partial \mathcal{F}}{\partial T}$ and $V = \frac{\partial \mathcal{V}}{\partial T}$. It follows from (2.3) that

and

After substituting ${{E}_{1}}$ and ${{E}_{2}}$, we get

and

Therefore, it can be concluded that

Next, we will analyze the existence of equilibria of system (2.3) when $T\ne 0$. According to the first equation of system (4.1), we can derive

From the second equation of system (4.1), we have

From the third equation of system (4.1), it can be deduced that

Based on the fourth equation of system (4.1), we can obtain

Therefore, system (2.3) has an interior equilibrium ${{E}_{3}} = \left({{T}^{*}}, {{I}^{*}}, {{H}^{*}}, {{P}^{*}} \right)$.

4.1.   Local stability analysis of ${E}_{2}$

This section examines the local stability of tumor-free equilibria.

Lemma 4.1. If ${{r}_{1}} < {{\mu }_{1}}\frac{s}{{{d}_{1}}}+{{\lambda }_{1}}{{K}_{2}}$, equilibrium point ${E}_{2}$ exhibits local asymptotic stability.

Proof. The Jacobian matrix of system (2.3) is

Thus, the Jacobian matrix at ${{E}_{1}}$ is

Obviously, the eigenvalues of matrix ${{J}_{{{E}_{2}}}}$ are

This means that when ${{r}_{1}} < {{\mu }_{1}}\frac{s}{{{d}_{1}}}+{{\lambda }_{1}}{{K}_{2}}$, ${{E}_{2}}$ exhibits local asymptotic stability.

4.2.   Local stability analysis of ${E}_{3}$

Next, we will examine the local stability of the internal equilibria.

Lemma 4.2. If ${{C}_{1}} > 0,$ ${{C}_{2}} > 0,$ ${{C}_{3}} > 0$, and ${{C}_{4}} > 0$, then ${{E}_{3}}$ is locally asymptotically stable.

Proof. The Jacobian matrix at ${{E}_{3}}$ is

where

Therefore, the characteristic polynomial of matrix ${{J}_{{{E}_{3}}}}$ is

Through calculation, we can obtain

According to the Hurwitz criterion^[37], if ${{C}_{1}} > 0,$ ${{C}_{2}} > 0,$ ${{C}_{3}} > 0$, and ${{C}_{4}} > 0$, then ${{E}_{3}}$ is locally asymptotically stable, where

5.   Optimization control

We will continue to formulate a fractional-order optimal control problem, targeting model (2.3), and study and design an optimal control strategy. By analyzing the basic reproduction number, it is evident that parameters $r_1$ and $\mu_1$ play critical roles in tumor control. To effectively regulate tumor cell numbers, we need to decrease $r_1$ while enhancing $\mu_1$. This will achieve the goal of reducing tumor density and minimizing control costs. This approach not only improves treatment efficacy but also reduces the burden on patients while controlling the tumor.

In our optimal control problem, we introduce two control functions: $u_1(t)$ and $u_2(t)$. Here, $u_1(t)$ represents surgical treatment and $u_2(t)$ represents immunotherapy. Surgical treatment reduces the number of tumor cells by directly removing tumor tissue, while immunotherapy boosts the immune system's ability to target cancer cells. Through these measures, our aim is to minimize the objective function, thereby achieving optimal treatment outcomes while controlling costs.

From the above description, we introduce the following control model on the basis of the existing system (2.3) to address this issue more systematically. This model considers both the dynamic interaction between tumor cells and immune cells, as well as the effects of surgery and immunotherapy, aiming to achieve effective tumor control through optimized control strategies.

The initial condition is $T\left(0 \right) = {{T}_{0}}$, $I\left(0 \right) = {{I}_{0}}$, $H\left(0 \right) = {{H}_{0}}$, and $P\left(0 \right) = {{P}_{0}}$. Our objective function is as follows:

$D_1$ and $D_2$ are both positive constants, representing the weights of the control measures' costs in the objective function. Meanwhile, we define the following control set:

where ${{u}_{i}}$ is measurable.

The main challenge is to discover an optimal control solution $(u_{1}^{*}, u_{2}^{*})$ that minimizes the objective function $\mathbb{J}\left({{u}_{1}}, {{u}_{2}} \right)$. Therefore, our initial focus will be on exploring the existence of this optimal control solution.

Theorem 5.1. If these conditions are all fulfilled:

(1) The control set $\mathbb{U}$ contains at least one element.

(2) The control set is both convex and closed.

(3) The righthand side of system (5.1) is subject to linear constraints on the state and control variables.

(4) The objective function's integrand exhibits convexity.

(5) Exist a constant $\sigma$ and two positive numbers $k_1$ and $k_2$ such that the integrated function $G\left(T, {{u}_{1}}, {{u}_{2}}, t \right)$ satisfies

then a set of controls $u_{1}^{*}, u_{2}^{*}\in \mathbb{U}$ can be found such that

Proof. According to the existence of bounded system solutions in Lukes' literature^[53], condition (1) holds, and based on the definition of the control set, condition (2) also holds. Our focus is on proving the last three conditions, and below is the proof for condition (3).

By simplifying (5.1), we obtain

where

and

Obviously, we can find a constant ${{e}^{*}}$ such that

Let

and

According to the Hölder inequality^[54], we can derive

Therefore, we have

where

This implies

where $\eta = \max \{\theta, \left\| N \right\|\} < \infty.$ Therefore, M is Lipschitz continuous. This implies that condition (3) is satisfied.

Next, we will demonstrate condition (4). Let

where $\vec{u} = \left({{u}_{1}}, {{u}_{2}} \right)\in \mathbb{U}, \vec{w} = \left({{w}_{1}}, {{w}_{2}} \right)\in \mathbb{U}$, and $0\le \beta \le 1.$ To prove that $S$ is convex, it suffices to demonstrate

namely,

According to the definition of convex functions,

Derived through simplification,

Finally, our proof of condition (5) is as follows:

As $S\left(t, T, \vec{u} \right)$ is a convex function, therefore,

In this case, if we choose ${{\varphi }_{1}} = \frac{1}{2}\min \{{{D}_{1}}, {{D}_{2}}\}$, ${{\varphi }_{2}} > 0$, and $\varsigma = 2$, then condition (5) is also satisfied.

Theorem 5.2. In the optimal control problem formulated by Eqs (5.1) and (5.2), if ${{u}^{*}} = \left(u_{1}^{*}, u_{2}^{*} \right)$, ${{X}^{*}} = \left({{T}^{*}}, {{I}^{*}}, {{H}^{*}}, {{P}^{*}} \right)$ is the optimal solution, then there exists an adjoint variable ${{\delta }_{i}}, \ i = 1, 2, 3, 4$ such that

and the intercept condition is ${{\delta }_{i}}\left({{t}_{f}} \right) = 0$. The optimal control solution is

Proof. We begin by defining the Lagrangian function $Z_1$ and the Hamiltonian function $Z_2$ as follows:

where ${{\delta }_{i}}, i = 1, 2, 3, 4$ is the adjoint variable. By further applying the Pontryagin maximum principle ^[37], the following state equation can be derived:

simultaneously satisfying the transversality condition

According to the necessary conditions of the control equation,

Therefore, the optimal control solution ${{u}^{*}} = \left(u_{1}^{*}, u_{2}^{*} \right)$ is

As a result of $u_{1}^{*}\left(t \right), u_{1}^{*}\left(t \right)\in \mathbb{U}$, the expression for the optimal control solution is

6.   Numerical simulation and biological significance

In this section, we will conduct numerical simulations to validate the theoretical derivations and assess the model's accuracy. Additionally, we will discuss the complex dynamic behaviors of the system under different parameters and conditions. These simulations help in understanding the stability and response characteristics of the system and reveal various dynamic phenomena that may be encountered in practical applications. Through numerical simulations, we can intuitively observe and explain the nonlinear characteristics of the system, providing a reference for further research and applications. In the following figures, when $K_1 = 100$, we set the initial values to ^[10,12,15,2]; when $K_1 = 10$, the initial values are set to ^[5,6,7,2].

6.1.   Stability analysis of system (2.3)

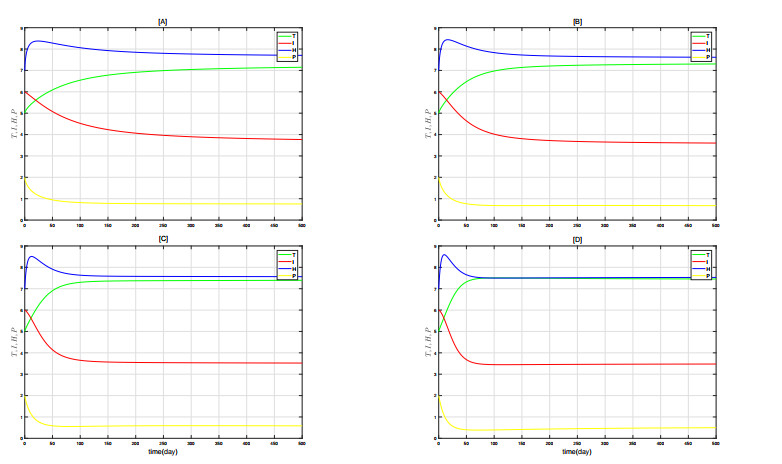
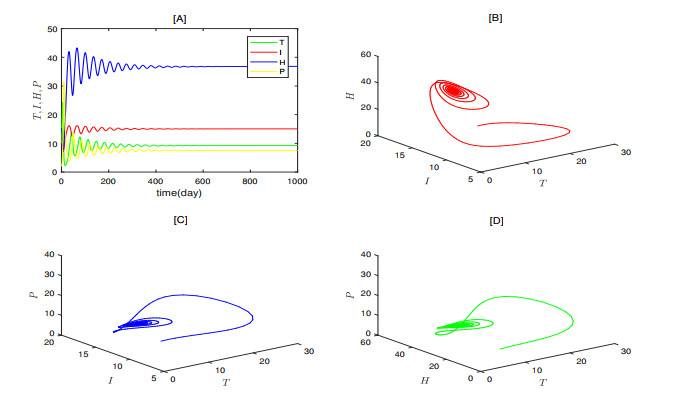
From Figure 4, it can be seen that in the initial period, both tumor cells and healthy cells increase due to the immune system not being severely compromised. However, as time progresses, the immune system becomes increasingly damaged, and cancer cells continue to proliferate and absorb a large amount of nutrients, leading to a decrease in healthy cells. Eventually, the four state variables stabilize. Additionally, when $\alpha$ increases, the number of healthy cells and cancer cells at equilibrium becomes closer and when $\alpha = 1$, their numbers are almost equal. This indicates that $\alpha$ has a significant impact on the stability of system (2.3).

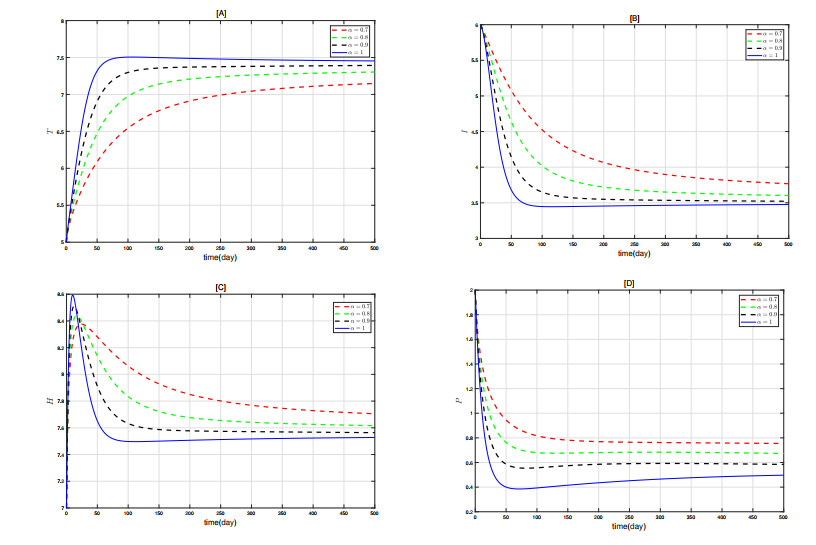
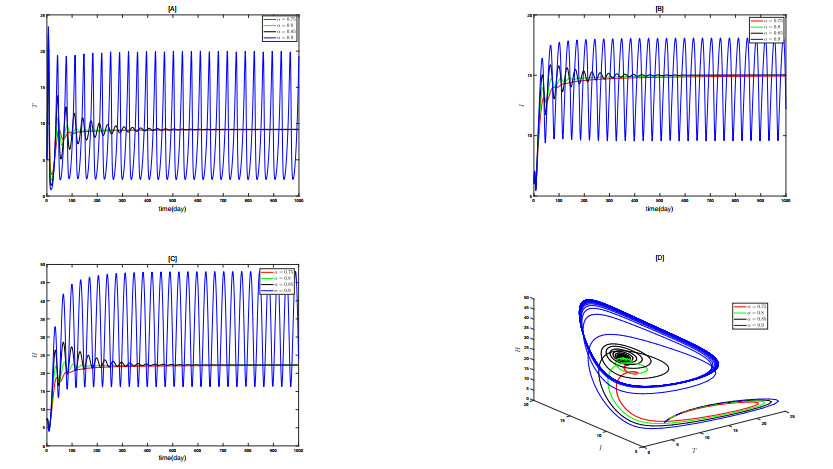
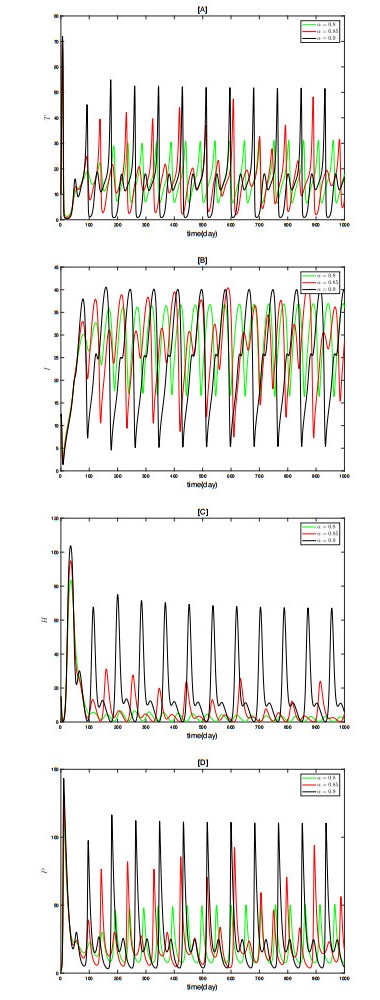
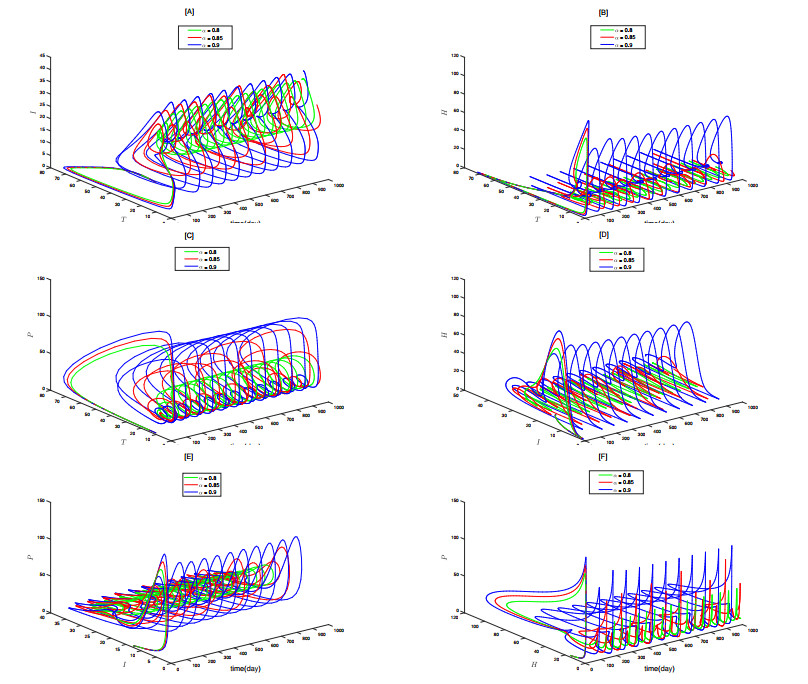
To better analyze the impact of $\alpha$ on each state variable, Figure 5 presents the time series of the same state variable under different $\alpha$ values. From Figure 5[A], it can be seen that as $\alpha$ increases, the number of tumor cells at equilibrium continuously rises, indicating that higher $\alpha$ values accelerate the growth of tumor cells. Figures 5[B–D] show that as $\alpha$ increases, the number of immune cells, healthy cells, and metastatic cancer cells at equilibrium continuously decreases. However, it is noteworthy that the maximum number of healthy cells that can be reached is also higher with larger $\alpha$ values, possibly due to the stronger protective effect on healthy cells during the initial stages. These results indicate that $\alpha$ has a significant overall impact on the system and that fractional-order models have an advantage in capturing the dynamic behavior of the system, making them more suitable for predicting and analyzing complex scenarios.

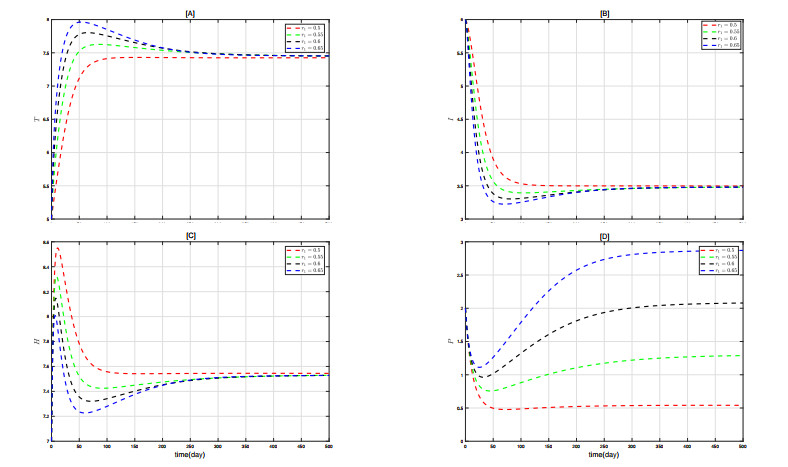
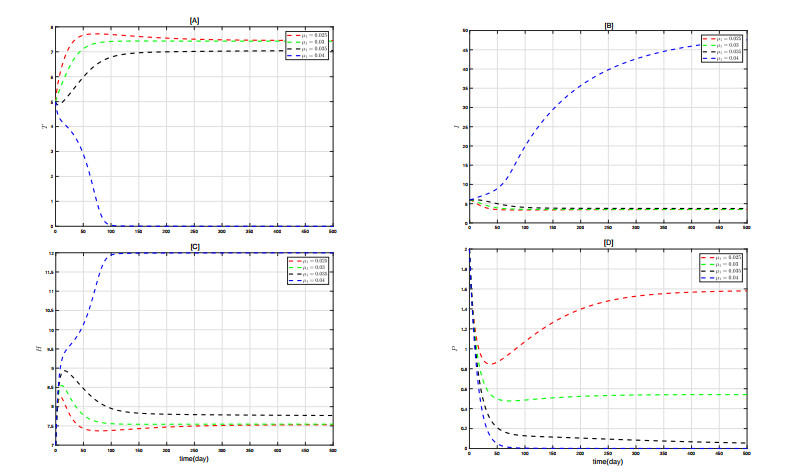
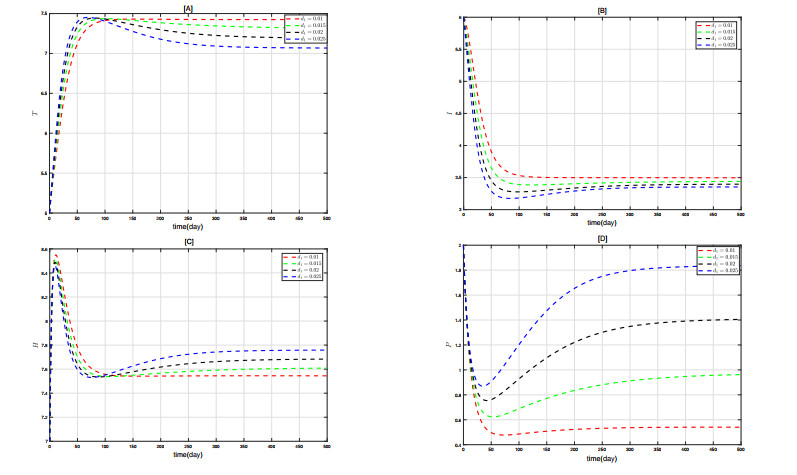
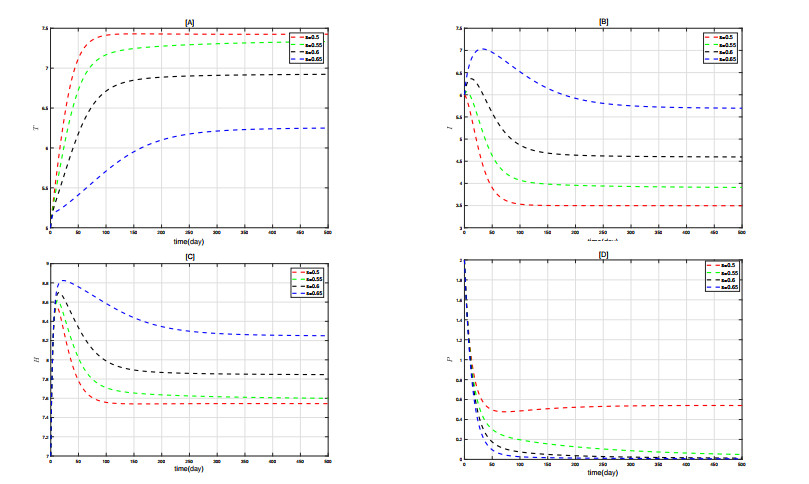
The basic reproduction number is crucial in cancer treatment. To delve deeper into the effects of different parameters in the basic regeneration expression on state variables, Figures 6–9 respectively show the comparative impacts of varying $r_1$, $\mu_1$, $d_1$, and $s$ on each state variable. From the figures, it can be seen that as $r_1$ increases, the quantities of state variables $T$ and $P$ at equilibrium gradually increase, while $I$ and $H$ gradually decrease. Conversely, increases in $\mu_1$ and $s$ have the opposite effect of $r_1$, leading to decreases in $T$ and $P$ quantities and increases in $I$ and $H$ quantities.

Notably, in Figure 8[A], during the initial period, as $d_1$ increases, $T$ continuously increases while $H$ gradually decreases. This is due to the high death rate of immune cells, resulting in a sharp decrease in their number. However, over time, the increase in tumor cells stimulates the proliferation of immune cells. As a result, the proliferation rate of immune cells far exceeds their death rate, leading to a higher immune cell production rate with larger $d_1$ values, ultimately reducing the number of tumor cells.

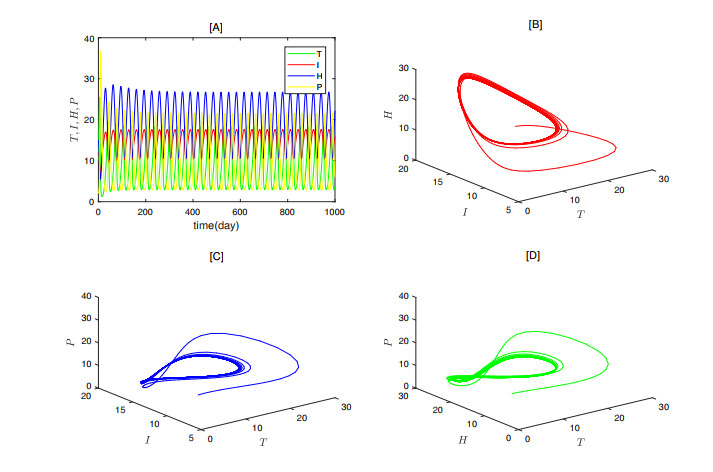
Figure 10 shows the time series and phase plots of the nodes. Subsequently, by fixing other parameters and adjusting $\alpha$ from 0.84 to 0.9, the state variables no longer stabilize at the nodes but exhibit periodic fluctuations, eventually settling into a limit cycle, as shown in Figure 11. This indicates that as $\alpha$ changes, the system (2.3) transitions from one stable state to another, with increasingly complex dynamic behavior. To more clearly analyze the impact of $\alpha$ changes on the system dynamics, Figure 12 presents the time series and phase plots of each state variable under different $\alpha$ values, providing a more intuitive validation of our analysis.

6.2.   The chaos analysis of system (2.3)

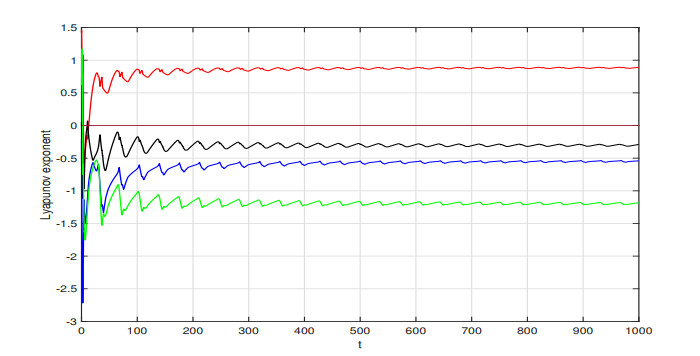
Next, we will analyze the existence of chaos in system (2.3). First, we computed the Lyapunov exponent of system (2.3), which is a numerical feature that represents the average exponential divergence rate of nearby trajectories in phase space and is one of the key indicators for identifying chaotic motion. The Lyapunov exponents of system (2.3) are shown in Table 2 and Figure 13. By observing the Lyapunov exponents, we can see that since there is a positive Lyapunov exponent, the system is expected to exhibit chaotic behavior within the parameter range specified in Table 2.

Additionally, the dimension of a chaotic attractor serves as a key numerical measure for assessing its characteristics. In this study, we use the Lyapunov dimension to quantify the chaotic attractor's dimension in system (2.3)^[55]. The calculation formula is

where $\sum\limits_{i = 1}^{j}{L{{E}_{i}}} > 0$ and $\sum\limits_{i = 1}^{j}{L{{E}_{i}}+L{{E}_{j+1}} < 0}$. For model (2.3), it follows from $LE_T = 0.8918$, $LE_I = -0.2897$, $LE_H = -0.2897$, and $LE_P = -1.1829$ that $LE_T+LE_I+LE_H = 0.06077 > 0$ and $LE_T+LE_I+LE_H+LE_P = -1.12213 < 0$. Therefore, the Lyapunov dimension is ${{d}_{L}}\approx 3.05137$, indicating that the model is a fractal with a dimension between 3 and 4.

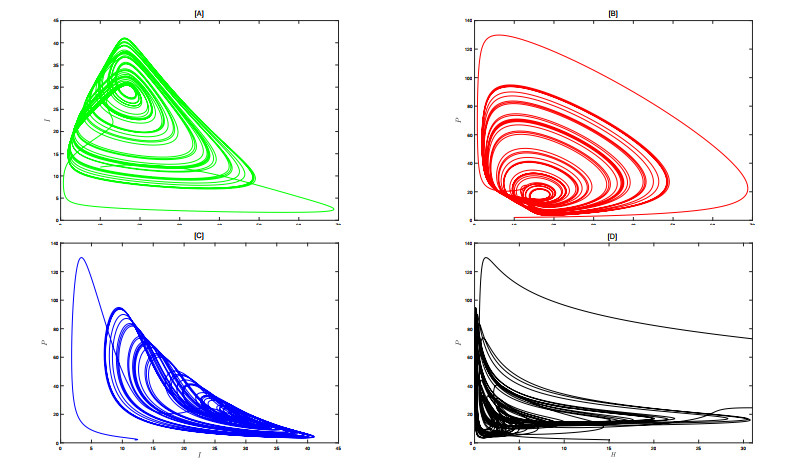
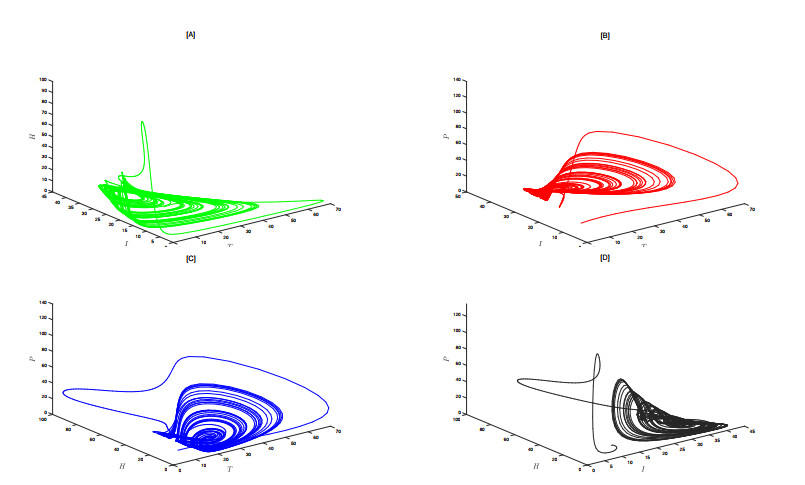
To further investigate the chaotic phenomena in system (2.3), we selected a new set of parameters and continuously adjusted the value of $\alpha$. We found that the system tends to exhibit chaos when $\alpha$ is around 0.85, as shown in Figure 14. To more intuitively demonstrate the presence of chaos, we plotted two-dimensional phase diagrams of some combinations of state variables (Figure 15), three-dimensional phase diagrams of combinations of three state variables (Figure 16), and three-dimensional plots of two state variables over time (Figure 17). Chaotic phenomena can be explained by the irregular division of tumor cells and the complex dynamic relationships between cells. When the system exhibits chaos, the unpredictability and extreme sensitivity of chaotic behavior make cancer treatment more complex and challenging.

6.3.   Bifurcation analysis of system (2.3)

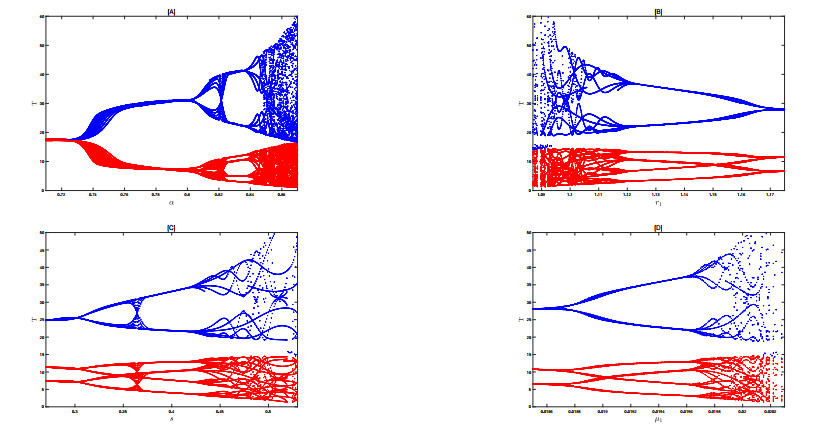
Combining the above analysis, it can be observed that varying the value of $\alpha$ leads to a transition of system (2.3) from chaotic behavior to a stable limit cycle, suggesting the presence of bifurcations within system (2.3). From a dynamical systems perspective, bifurcation refers to a phenomenon in which the continuous variation of a parameter causes a sudden and significant change in the system's behavior, thereby altering its dynamical properties. Bifurcation diagrams are crucial tools for analyzing how system properties change with respect to parameter variations, and they aid in uncovering the underlying dynamics of the system. In this study, four parameters are chosen as bifurcation parameters, and their relationships with the system state variable $T$ are examined. The corresponding bifurcation diagrams are presented in Figure 18.

Figure 18[A, C, D] illustrates the occurrence of period-doubling bifurcations in system (2.3) under specific parameter values $\alpha = 0.8$, $s = 0.3$, and $\mu_1 = 0.00187$. In Figure 18[A], a period-doubling bifurcation is observed when $r_1 = 1.12$, and the relationship between the chaotic state and the intensity of immunotherapy $\mu_1$ is also evident. Before $\mu_1 = 0.0196$, the system exhibits period-doubling bifurcations, transitioning into chaotic behavior thereafter. This suggests that even small variations in these parameters can significantly influence the system's dynamic behavior. Therefore, in cancer treatment, adjusting these parameters could lead to more effective therapeutic strategies. For instance, the value of $r_1$ can be altered through surgery, while $\mu_1$ can be regulated via immunotherapy. Next, we will conduct numerical simulations to investigate the effects of these two treatment methods on cancer, providing further insight into their role and effectiveness in modulating system parameters.

6.4.   Numerical analysis of optimal control

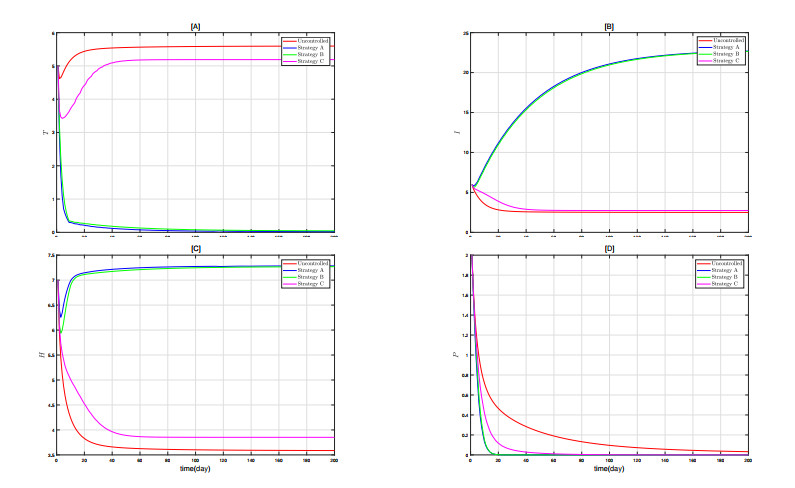
We designate the treatment method combining surgery and immunotherapy as Treatment Strategy A, surgery alone as Treatment Strategy B, and immunotherapy alone as Treatment Strategy C. Figure 1 shows the time series of the control parameter $u_i(i = 1, 2)$ under the three treatment strategies. From Figure 1[A], it can be seen that in the comprehensive Treatment Strategy A, the highest intensity of treatment is not required, and as the treatment progresses, the intensity gradually decreases, eventually reaching a very small value.

Interestingly, in the early stages of treatment, surgery dominates, while over time, immunotherapy becomes increasingly important. This aligns with real-world scenarios, where in the early stages, a larger number of tumor cells are present and surgery is used to remove most of the tumor, while the remaining tumor cells are eliminated through immunotherapy. This indicates that through comprehensive treatment, cancer can be effectively controlled without requiring extremely high treatment intensity, gradually reducing the treatment intensity and improving the sustainability and effectiveness of the treatment.

Figure 1[B] illustrates the scenario where only surgical treatment is performed. Compared to treatment strategy A, surgical treatment requires a higher intensity of treatment initially, and the treatment intensity remains higher even when it stabilizes in the later stages. This presents several issues: The high intensity of treatment not only demands a lot from doctors but also requires highly advanced medical facilities, increasing the complexity of the treatment. Therefore, the advantages of comprehensive treatment are particularly prominent, as it can reduce the intensity of treatment while improving the sustainability and effectiveness of the treatment.

Figure 1[C] shows the time series of the control function when only immunotherapy is administered. It can be seen that immunotherapy alone requires a period of high-intensity treatment, and the intensity remains relatively high in the later stages, which could result in higher costs. Therefore, among these three treatment strategies, treatment strategy A is preferred, as it can reduce the overall treatment intensity while improving treatment efficacy and sustainability.

After analyzing the treatment intensity under the three treatment strategies, we further examined their impact on the objective function, as shown in Figure 2. The objective function reflects the overall effect and cost of the treatment. From the figure, it can be seen that the objective function value for treatment strategy A is the lowest, indicating that the combined treatment (surgery and immunotherapy) is optimal in terms of effectiveness and cost. In contrast, the objective function value for treatment strategy B (surgery only) is higher. Although surgical treatment is effective in some aspects, it requires a higher initial treatment intensity, resulting in higher overall costs and less favorable outcomes.

The objective function value for treatment strategy C (immunotherapy only) is the highest, suggesting that immunotherapy alone not only requires a prolonged period of high-intensity treatment but also incurs higher costs. Considering both the treatment effect and cost, treatment strategy A is clearly superior to the other two strategies. This indicates that combining surgery and immunotherapy can achieve the best treatment outcomes while reducing treatment intensity and costs. Future research and practical treatments should focus on combined treatment. Finally, Figure 19 presents the time series of various state variables under different control strategies. It can be seen that treatment strategy A has the best control effect on cancer cells, followed by treatment strategy B, while treatment strategy C shows relatively poorer results, although all strategies are better than no treatment at all. Specifically, treatment strategy A not only significantly reduces the number of cancer cells but also effectively protects the immune system and healthy cells. In contrast, treatment strategy B is slightly less effective in controlling cancer cells than strategy A but still performs significantly better than strategy C and no treatment.

Moreover, although treatment strategy C is not as effective as the other two strategies, it still manages to control the growth of cancer cells to some extent and better protects healthy cells and the immune system compared to no treatment. This indicates that although single treatment methods (such as immunotherapy alone) have limited effectiveness, they still have some therapeutic value.

Overall, treatment strategy A, by combining surgery and immunotherapy, achieves the best results, not only excelling in inhibiting cancer cells but also maximizing the protection of the immune system and healthy cells. Although treatment strategy B is not as effective as strategy A, it still provides significant therapeutic benefits. Treatment strategy C, despite being weaker, still has its role as an adjunctive treatment. Therefore, in practical applications, comprehensive treatment strategy A should be prioritized to achieve the best clinical outcomes and patient prognosis.

7.   Real data example

Parameter estimation (PE) is crucial in the identification and validation of cancer models. The occurrence and progression of cancer involve various complex biological processes, and accurately translating these processes into mathematical models is a significant challenge. Through PE, model parameters can be determined using real data within a reasonable range, ensuring that the model can more accurately represent the biological characteristics of cancer. Accurate PE not only improves the predictive accuracy of the model but also helps reveal the underlying biological mechanisms of cancer progression, providing stronger support for clinical decision-making, ultimately driving the optimization and personalized development of cancer treatment plans.

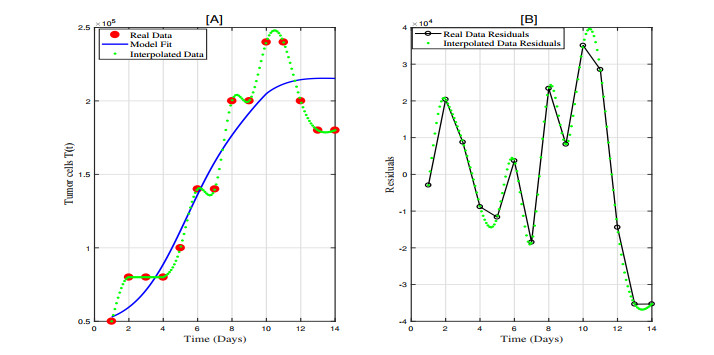
In this section, we used real data on the growth of lung cancer cells over 14 days from a patient at Kayseri Erciyes University Hospital, with specific data points including 50, 000, 80, 000, 80, 000, 80, 000, 100, 000, 140, 000, 140, 000, 200, 000, 200, 000, 240, 000, 240, 000, 200, 000, 180, 000, and 180, 000, as mentioned in reference ^[33]. Given the limited real data points and the relatively large number of model parameters, we used interpolation to increase the number of data points for fitting and then applied the least squares method. The specific fitting process and details are as follows:

Step 1: First, define the real experimental data, including the time series and tumor cell count. Since the experimental data points are limited, which makes it difficult to fully capture the changes in tumor cell growth, we use spline interpolation to generate more data points, allowing for a more accurate reflection of tumor cell growth at different stages.

Step 2: Second, initialize the model parameters, such as tumor growth rate, carrying capacity, etc., and set reasonable upper and lower bounds for each parameter to ensure the optimization results are biologically plausible. At the same time, configure the parameters of the least squares optimizer, such as the maximum number of iterations and convergence tolerance, to ensure the stability of the optimization process.

Step 3: Next, the lsqcurvefit function is employed to optimize the parameters by minimizing the sum of squared residuals between the model predictions and experimental data, thereby improving the fitting accuracy. Additionally, the Akaike information criterion and the Bayesian information criterion are used to mitigate the risk of overfitting.

Step 4: Finally, a comparison plot of the fitting results is created, showing the real data points, interpolated data, and the model's predicted curve. Additionally, a residual analysis plot is generated to evaluate the model's prediction bias at different time periods, as shown in Figure 20.

Using this method, the optimal fitting parameter value at $\alpha = 0.9$ was obtained, with the specific results shown in Table 3. In Figure 20[A], the optimal fitting curve is presented, where red points represent the observed real data, the blue curve represents the fitted curve, and green points indicate the interpolated data points. Figure 20[B] shows the residual analysis, where smaller differences from zero indicate better fitting performance. As seen in Figure 20, the fitting performance is relatively good between days 0–9, while it worsens between days 9–14. This may be due to larger fluctuations in the later data and the significant influence of the estimated parameter values on the fitting process. This also suggests that different prediction strategies should be applied based on the data characteristics of different stages when making predictions.

8.   Conclusions

Cancer treatment remains a significant challenge. This paper introduces a new Caputo fractional-order model to describe the progression of lung cancer. The model includes tumor cells, immune cells, healthy cells, and the spread of tumor cells from the lungs to surrounding organs. The main objective of this paper is to analyze the complex dynamic behaviors between these cell populations and assess the impact of different treatment strategies on cancer cell growth. By incorporating Caputo fractional-order differential equations, we are able to capture the complex interactions between cells more accurately. Compared to traditional integer-order models, the fractional-order model has a clear advantage in describing the memory effects and genetic characteristics of biological systems. Its flexibility and accuracy make it better suited for simulating the growth and spread dynamics of tumor cells.

Our model not only considers the growth of lung tumors but also includes the process of tumor cell dissemination to surrounding organs. This spread is crucial in the progression of lung cancer, and an accurate model to predict tumor dissemination is essential for devising effective treatment strategies. Additionally, the dynamic changes of immune cells and healthy cells included in the model help us understand the role of the immune system in tumor progression and the impact of different treatment regimens on the immune system.

We investigated the system's solutions to ensure that subsequent research is both reasonable and biologically meaningful, focusing on their existence, uniqueness, and positivity. First, we discussed the existence and stability conditions of tumor-free equilibria and internal equilibria. Furthermore, we calculated the basic reproduction number to determine whether the tumor will deteriorate. These analyses lay the theoretical foundation for introducing control terms and conducting numerical simulations in subsequent studies, particularly in selecting sensitive parameters, laying the groundwork for analyzing how parameters affect the system.

Considering the different impacts of surgery and immunotherapy on tumors, we introduced control parameters into the model. Surgical treatment directly affects the natural growth rate $r_1$ of tumor cells, while immunotherapy increases the killing rate $\mu_1$ of immune cells against tumor cells. By incorporating control parameters into these two aspects, we can simulate the effects of surgery and immunotherapy on the system. After introducing the control terms, we first theoretically proved the necessary conditions for the existence of optimal control solutions and then used Pontryagin's maximum principle to calculate the expressions for the optimal solutions.

We used numerical simulations to verify the correctness of the above theoretical derivations and explored some complex dynamic behaviors that are difficult to prove theoretically. First, we studied the system without the control terms and analyzed the effects of key parameters $\alpha$, $r_1$, and $\mu_1$ on the system's dynamics. The results showed that small variations in these parameters significantly affect the system's dynamic behavior. Since fractional-order systems exhibit more complex dynamic behaviors, they are more suitable for predicting the growth of tumor cells.

By continuously adjusting the parameters, we found that the system stabilizes at a node, as shown in Figure 8. This is a positive signal for cancer patients, indicating a lower number of cancer cells and higher numbers of healthy and immune cells. This suggests that as long as the immune system is strong enough, it can control tumor cells at a low level and ensure normal immune function, even if it cannot completely eliminate the tumor cells. Therefore, regular exercise and a consistent daily routine are crucial for both cancer prevention and treatment.

When only modifying $\alpha$, the system transitions from a stable node to a stable limit cycle, as illustrated in Figure 9. Further parameter adjustments lead to chaotic phenomena, which can be explained by the irregular proliferation of tumor cells and the complex dynamic interactions between cells. Chaotic behavior is detrimental to cancer treatment because it complicates monitoring cell growth, necessitating multiple treatment approaches to stabilize the condition before devising a reasonable treatment strategy. Analysis shows that the system may exhibit bifurcation phenomena. Therefore, we selected $r_1$, $\mu_1$, $\alpha$, and $s$ as bifurcation parameters and plotted the corresponding period-doubling or period-halving bifurcation diagrams. These diagrams indicate that small perturbations in these parameters can shift the system from one state to another, highlighting the importance of closely monitoring these parameter changes during cancer treatment.

After introducing controls, we studied three treatment strategies: simultaneous surgery and immunotherapy (Strategy A), surgery alone (Strategy B), and immunotherapy alone (Strategy C). Through numerical simulations, we evaluated the required control intensity, the size of the objective function, and the dynamic changes of each state variable for these three treatment strategies during the treatment process. The results showed that the combined treatment strategy performed best in terms of treatment intensity, efficacy, and cost, consistent with theoretical predictions. Surgery treatment was the next most effective, followed by immunotherapy. Regardless of the treatment strategy adopted, all were more effective than no treatment.

To validate the accuracy of the model, we used real data from lung cancer patients, recording the changes in cancer cells over a 14-day period. Given the limited amount of real data, we first applied spline interpolation to augment the dataset, then estimated parameters using the least squares method and performed curve fitting. Figure 18[A] shows the fitting results when $\alpha = 0.9$, while Figure 18[B] presents the residual analysis between the real data and the fitted data. It can be observed that the model fits well in the early stages, but the deviation increases in the later stages. This indicates that while the model effectively captures the trend of cancer cell changes, there are potential limitations in its ability to predict changes over longer periods.

Considering that in actual treatment processes, the monitored data may have a certain time delay, we plan to introduce time-delay parameters in future research. This will make the model more accurately reflect the dynamic processes in clinical treatment, simulating and predicting changes in tumor cells, immune cells, and healthy cells. By calibrating with actual clinical data, we can optimize treatment strategies, improve treatment outcomes, and reduce side effects and costs, thus providing more scientific theoretical support and effective clinical guidance for cancer treatment. Ultimately, this will help enhance patient outcomes.

Author contributions

Xingxiao Wu: Software, Writing; Lidong Huang: Idea, Methodology; Zhang Shan: Formal analysis; Wenjie Qin: Project Administration and Review Editing. All authors read and approved the final manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by National Natural Science Foundation of China (Nos. 12261104, 12361104), the Youth Talent Program of Xingdian Talent Support Plan (No. XDYC-QNRC-2022-0708), and the Yunnan Provincial Basic Research Program Project (Nos. 202401AT070036, 202301AT070016).

Conflict of interest

Declare that there are no conflicts of interest regarding the publication of this paper.