Approximate controllability of second-order neutral stochastic differential evolution systems with random impulsive effect and state-dependent delay

1.   Introduction

As an essential topic in modern control theory, controllability plays an important role in designing control systems. Approximate controllability is frequently considered by researchers because it is relatively easier to realize than exact controllability, especially in infinite dimensional systems. Therefore, approximate controllability problems for various types of control systems have been investigated in many articles. Additionally, second-order differential equations have attracted more attention due to their applications in physics, mechanics, and engineering ^[8,9]. Recently, there are several investigations about approximate controllability to second-order abstract differential equations. For example, the approximate controllability of second-order differential equations with finite delay and the impulsive integro-differential equations have been discussed in ^[16]. A set of sufficient conditions for the evolution of second-order nonlocal neutral differential inclusions to be approximately controllable have been established in ^[28]. Palanisamy et al. ^[21] studied the following second-order neutral stochastic differential:

Authors constructed a Cauchy sequence by means of the range condition, and then obtained the sufficient conditions of its approximate controllability.

In many science engineering fields, differential equations with delay are usually used to simulate dynamic systems. Application of delay differential equations in the field of biological sciences have been explored by Rihan in his monograph ^[23]. Bellen et al. ^[4] established a numerical scheme to analyze the stability of differential equations with time delay. Some researchers have noticed that the time delay may not always be a constant; it may change with the state of the system. Differential equations with state-dependent delay arise from applications and have attracted increasing attention from scholars. B$\acute{\text{e}}$lair ^[3] considered the population model with state-dependent delay. Hern$\acute{\text{a}}$ndez et al. ^[11] discussed the existence, uniqueness, and approximate controllability of solutions of first-order differential equations based on state-dependent delay. Ravichandran et al. ^[22] combined the fixed point theorem and resolvent operator to deduce the exact controllability of solutions of neutral integro-differential equations with state-dependent delay, and further deduced the continuous dependence of the system. The scholar of ^[19,20] discussed the stability and existence of periodic solutions of state-dependent delay differential equations, respectively.

On the other hand, impulse perturbations are ubiquitous in natural phenomena. Stochastic impulsive differential equations have attracted considerable attention in current research. For the approximate controllability problem of second-order neutral stochastic impulsive systems, we refer the readers to ^[14,26] and the references therein. Very recently, Huang et al. ^[13] considered the following second-order neutral impulsive stochastic equations with state-dependent delay and a Poisson jump:

where the history $x_t:(-\infty, 0]\rightarrow H, \; x_t(\theta) = x(t+\theta), \; t\geq0,$ belongs to the phase space $\mathcal{B}$, $\rho: J\times \mathcal{B}\rightarrow H$, $I_k, \; \tilde{I}_k: \mathcal{B}\rightarrow H (k = 1, 2, \ldots)$, and $\Delta x(t_k)$ represents the jump of the function $x$ at $t_k$. Using Sadovskii's fixed point theorem, Lipschitz continuity, and phase space theory, the existence of a system solution was proved, and then the sufficient conditions of the approximate controllability to the system were established.

However, systems with determining impulse occurrence time may not adequately describe the characteristics of some complex phenomena in real life. It is significant to study the systems with the influence of random impulses, which means its impulse occurrence time is a group of random sequences. So, the system with random impulses fairly differs from that with determining impulses. In recent years, there are several articles devoted to the existence, uniqueness, and other quantitative and qualitative properties of mild solutions of random impulsive differential equations. Guo et al. ^[10] obtained the existence of mild solutions of first-order Hamiltonian stochastic impulsive differential equations by using a variational method and Legendre transformation. Jose et al. ^[15] deduced the existence of solutions of integro-differential equations with random impulses through the Banach fixed point theorem and appropriate estimation. Existence and Hyers-Ulam stability of stochastic functional differential equations with random impulses and finite delays were investigated in ^[17]. In ^[25], the following second-order neutral random impulsive stochastic equation was considered:

The form of the solution of the equation was derived by Laplace transformation, and then the existence of the solution was verified by noncompact measures and M$\ddot{\text{o}}$nch's fixed point theory. Then, the exponential stability was given accordingly. Yang et al. ^[33] proved the existence of solutions of random impulsive partial differential equations by using noncompact semigroup theory. Recently, the existence of upper and lower solutions to second-order random impulsive differential equations with a boundary value problem has been considered in ^[18]. In the latest research ^[5,30,31], random impulses have been introduced into network models, chaotic systems, and so on. Stability, control, and its application issues have been studied.

With the continuous advancement of the theory of random impulsive differential systems, great progress has been made, but there is still much space for research on the approximate controllability of random impulsive differential systems. Based on the previous cited works of ^[13,21,25], we study the existence and approximate controllability of mild solutions to second-order neutral stochastic differential equations with random impulsive and state-dependent delay, as follows:

where $x(\cdot)$ takes value in a Hilbert space $X$ with the norm $\|\cdot\|$. $A$ is the infinitesimal generator of a strongly continuous cosine operator $C(t)$ on $X$. $u(\cdot)$ is the control function and $u(\cdot)\in {{L}^{2}}(J, {{L}^{2}}(\Omega, U))$. $B$ is a bounded linear operator from $U$ to $X$. Suppose $K$ is another Hilbert space, and $W(t)$ is a given $K-$valued Wiener process with a finite trace $Q$. The functions $f$, $g:J\times \mathcal{B}\rightarrow X$, and $\eta:J\times \mathcal{B}\rightarrow L_{Q}(K, X)$, where $L_{Q}(K, X)$ is the space of all $Q$-Hilbert-Schmidt operators. Function ${{x}_{t}}:(-\infty, 0]\to X$, ${{x}_{t}}(s) = x(t+s)$ belongs to some phase space $\mathcal{B}$, and $x_{\rho(t, x_t)}$ stands for time delay depending on the state $\rho(t, x_t)$, where $\rho:J\times \mathcal{B}\rightarrow (-\infty, T]$ is a continuous function. $x\left(\xi _{k}^{-} \right)$ represents the left limit of $x({{\xi }_{k}})$. Suppose $\xi _0 = 0$ and $\{{{\xi }_{k}}\}$ is an increasing sequence, that is, $0 = {{\xi }_{0}} < {{\xi }_{1}} < \cdots < {{\xi }_{k}} < \infty$, satisfying $\xi _k = \xi _{k-1}+\varepsilon _k, \; (k = 1, 2, \cdots)$. $\{{\varepsilon }_{k}\}$ is a sequence of random variables mutually independent from $\Omega$ to ${{D}_{k}} = (0, {{d}_{k}})$, where $0 < d_k < \infty$. $q_k$ maps $D_k$ into $\mathbb{R}$ for each $k = 1, 2, \cdots$. Assume that $\varphi \in \mathcal{B}$ and $\psi \in X$ are independent with ${\varepsilon }_{k}$.

The main motivations and contributions in this paper are as follows:

(ⅰ) We consider the existence and approximate controllability problem to a class of second-order impulsive stochastic differential equations with state-dependent delay, which is a more realistic abstract wave equation involving the Wiener process and random impulses sequences. As far as we know, there are very few studies of such issues.

(ⅱ) To prove the main result, we employ evolution operator theory, stochastic analysis skills, the inequality technique, the Ascoli-Azela theorem, and combine the measure of noncompactness under a stochastic case. Then corresponding sufficient conditions of existence of a mild solution result have been established.

(ⅲ) We further discuss the approximate controllability of Eqs (1.1)–(1.3) based on the main technique in ^[21]. Compared with ^[21], we considered the random impulsive effect and state-dependent delay. We extend the corresponding conditions to the random impulse system. This method is different from ^[13]. We also briefly analyzed the conclusion of the approximate controllability of the mild solution to the system under nonlocal conditions.

(ⅳ) Two examples are given to show the effectiveness of the results.

The framework of this paper is as follows: In Section 2, we give some notation and preparatory knowledge adopted from ^[2,6,7,27] and so on. In Section 3, some assumptions are given to verify the existence of solutions of differential systems. In Section 4, we study the approximate controllability of random impulsive neutral stochastic differential equations, and give proper assumptions on the premise that the corresponding equations are approximately controllable, and then obtain sufficient conditions for the approximate controllability of the system. Section 5 proves the approximate controllability of second-order differential equations under nonlocal conditions. We give examples to verify the theoretical results of this paper in Section 6.

2.   Preliminaries

Let $\left(\Omega, \mathcal{F}, \{\mathcal{F}_t\}_{t\ge 0}, P \right)$ be a complete probability space with flow, ${\omega}\in\Omega$. $K$ and $X$ are both real separable Hilbert spaces. Let $Q:K\to K$ be a symmetric nonnegative trace family operator with $Tr(Q) = \sum\limits_{n = 1}^{\infty }{{{\lambda }_{n}}} < \infty$, where $\{{{\lambda }_{n}}\}_{n = 1}^{\infty }$ is a nonnegative eigenvalue sequence of operator $Q$. Let $\{{{f}_{n}}\}_{n = 1}^{\infty }$ be a set of complete orthogonal bases in space $K$, and then $Q{f}_{n} = {\lambda }_{n}{f}_{n}$. Assume $\beta _n(t)$ is a sequence of real-valued one-dimensional standard Wiener process defined on $\left(\Omega, \mathcal{F}, \{\mathcal{F}_t\}_{t\ge 0}, P \right)$. $W(t) = \sum\limits_{n = 1}^{\infty}\sqrt{\lambda_{n}}\beta_{n}(t)f_n(t)$ is called a $Q$-Wiener process. Assume $\mathcal{F}_t = \sigma(W(s):0\leq s\leq t)$. Denote $L(K, X)$ as the space of all bounded operators from $K$ to $X$. An operator $\varphi\in L(K, X)$ is called a $Q$-Hilbert Schmidt operator if $\|\varphi\|_{Q} < \infty$, where $\|\cdot\|_{Q}$ is defined by

Let $L_{Q}(K, X)$ denote the space of all $Q$-Hilbert Schmidt operators. The completion $L_{Q}(K, X)$ of $L(K, X)$ with respect to the topology induced by the norm $\|\varphi\|_{Q}^2 = < \varphi, \varphi >$ is a Hilbert space. Assume ${{L}^{2}}(\Omega, X)$ is the set of all strongly measurable and mean integrable $X$-valued random variables with norm ${{\left\| x \right\|}_{{{L}^{2}}}} = {{(E{{\left\| x \right\|}^{2}})}^{1/2}}$, where $E$ stands for expectation define as $E(x) = \int_{\varOmega}{x(\omega)dP}$, and then ${{L}^{2}}(\Omega, X)$ is a Banach space. The subset $L_{0}^{2}(\Omega, X)$ is defined as $L_{0}^{2}\left(\Omega, X \right) = \{x\in L^2\left(\Omega, X \right) :x\ \text{is}\; \mathcal{F}_0$-$\text{measurable}\}$.

The family of bounded linear operators $\left\{ C(t), t\in \mathbb{R} \right\}$ is called a strongly continuous cosine family, if

(ⅰ) $C\left(s+t \right) +C\left(s-t \right) = 2C\left(s \right) C\left(t \right)$ for all $s$, $t\in \mathbb{R};$

(ⅱ) $C(0) = I$;

(ⅲ) $C(t)x$ is continuous in $t$ on $\mathbb{R}$ for each fixed $x\in X$.

The strongly continuous sine family $\left\{ S(t), t\in \mathbb{R} \right\}$ associated with the cosine family is defined by $S(t)x = \int_{0}^{t}{C(s)xds}, \; x\in X, \; t\in \mathbb{R}$. For more details on the theory of the cosine function of operators, one can see ^[27].

Referring to ^[12], the axioms of phase space $\mathcal{B}$ can be established.

Definition 2.1. ^[12] Assume phase space $\mathcal{B}$ consists of all ${{\mathcal{F}}_{0}}-$adapted functions from $(-\infty, 0]$ to X with seminorm ${{\left\| \cdot \right\|}_{\mathcal{B}}}$, and then the following axiomatic conditions hold:

1) If $x:(-\infty, \gamma +a]\to X, a > 0$, such that ${{x}_{\gamma }}\in \mathcal{B}$ and ${{\left. x \right|}_{[\gamma, \gamma +a]}}\in C([\gamma, \gamma +a]; X)$, then for every $t\in [\gamma, \gamma +a]$, the following conditions hold:

(a) ${{x}_{t}}\in \mathcal{B}$;

(b) $\left\| x(t) \right\|\le K{{\left\| {{x}_{t}} \right\|}_{\mathcal{B}}}$;

(c) $\lVert x_t \rVert _{\mathcal{B}}\le R\left(t-\gamma \right) \underset{\gamma \le s\le t}{sup}E\lVert x\left(s \right) \rVert +T\left(t+\gamma \right) E\lVert x_{\gamma} \rVert _{\mathcal{B}}$;

where $K > 0$ is a constant, $R(\cdot), \; T(\cdot):[0, +\infty)\to [1, +\infty)$, $R(\cdot)$ is continuous, $T(\cdot)$ is locally bounded, and then $K, \; R(\cdot)$, and $T(\cdot)$ have no concern with $x(\cdot)$.

2) The space $\mathcal{B}$ is complete.

We denote $\mathcal{D}\mathcal{P}\mathcal{C}([a, b], {{L}^{2}}\left(\Omega, X \right))$ as the set of all piecewise continuous functions, with a first derivative, mapping the interval $[a, b]$ to ${{L}^{2}}\left(\Omega, X \right)$ and ${{\mathcal{F}}_{t}}$-adapted processes. If $x\in \mathcal{D}\mathcal{P}\mathcal{C}((-\infty, T], {{L}^{2}}\left(\Omega, X \right))$, then $x$ is continuous as $t\ne {{\xi }_{k}}$, $x(\xi _{k}^{-}) = x({{\xi }_{k}})$, and $x(\xi _{k}^{+})$ exists, $k = 1, 2, \cdots, n$. Then $(\mathcal{D}\mathcal{P}\mathcal{C}, {{\left\| \cdot \right\|}_{\mathcal{D}\mathcal{P}\mathcal{C}}})$ is a Banach space with norm

where the estimate of $\left\| x_t \right\|_{\mathcal{B}}$ is given by the following lemma.

Lemma 2.1. ^[32] Let $x:(-\infty, T]\to X$ be an ${{\mathcal{F}}_{t}}$-adapted process such that ${{\mathcal{F}}_{0}}$-adapted process ${{x}_{0}} = \varphi (t)\in L_{0}^{2}(\Omega, \mathcal{B}), {{\left. x \right|}_{J}}\in \mathcal{D}\mathcal{P}\mathcal{C}(J, {{L}^{2}}(\Omega, X))$, and then

where ${{T}_{m}} = \sup\limits_{t \in J} T(t)$ and ${{R}_{m}} = \sup\limits_{t \in J} R(t)$.

Lemma 2.2. ^[7] Note map $m :J\to X$ is an arbitrary $L_Q\left(K, X \right)$-valued predictable process, and then for every $t\in J, \; p\ge 2$, the following inequality holds:

where $C_p = \left(\frac{p\left(p-1 \right)}{2} \right) ^{\frac{p}{2}}$.

Now, we introduce the definition and properties of the non-compactness measure used in the theoretical proof of this paper.

Definition 2.2. ^[2] $\beta \left(\cdot \right)$ represents the Hausdorff non-compactness measure (NCM), which is defined on bounded subset $\mathcal{D}$ of the Banach space by

Lemma 2.3. ^[2] There exists nonempty bounded subsets $\mathcal{C}, \mathcal{D}\subseteq X$, where $X$ is a real separable space, and then the following properties hold:

$(i)$ $\beta \left(\mathcal{D} \right) = 0$ iff $\mathcal{D}$ is pre-compact on $X$.

$(ii)$ $\beta \left(\mathcal{D} \right) = \beta \left(\overline{\mathcal{D}} \right) = \beta \left({conv}\left(\mathcal{D} \right) \right)$, where $\overline{\mathcal{D}}$ and ${conv}\left(\mathcal{D} \right)$ are for the closure and convex hull of $\mathcal{D}$, respectively.

$(iii)$ If $\mathcal{C}\subseteq \mathcal{D}$, then $\beta \left(\mathcal{C} \right) \le \beta \left(\mathcal{D} \right)$.

$(iv)$ $\beta \left(\left\{ \kappa \right\} \cup \mathcal{D} \right) = \beta \left(\mathcal{D} \right)$, for all $\kappa \in X$.

$(v)$ $\beta \left(\mathcal{C}+\mathcal{D} \right) \le \beta \left(\mathcal{C} \right) +\beta \left(\mathcal{D} \right)$, where $\mathcal{C}+\mathcal{D} = \left\{ \kappa +\iota; \kappa \in \mathcal{C}, \iota \in \mathcal{D} \right\}$.

$(vi)$ $\beta \left(\mathcal{C}\cup \mathcal{D} \right) \le \max \left\{ \beta \left(\mathcal{C} \right), \; \beta \left(\mathcal{D} \right) \right\}$.

$(vii)$ $\beta \left(\mu \mathcal{D} \right) \le \left| \mu \right|\beta \left(\mathcal{D} \right), \; \mu \in \mathbb{R}$.

Lemma 2.4. ^[2] For bounded and equicontinuous set $\mathcal{D}\subseteq L^2(\Omega, X)$, $\beta \left(\mathcal{D} \right)$ is continuous on $J$, and $\beta \left(\mathcal{D} \right) = \sup\limits_{t\in J}\beta \left(\mathcal{D}\left(t \right) \right)$.

Lemma 2.5. ^[2] Suppose sequence $\left\{ x^n \right\} _{n = 1}^{\infty}$ relating to Bochner integrable functions maps $J$ to $L^2(\Omega, X)$, and then $\mathcal{D} = \left\{ x^n \right\} _{n = 1}^{\infty}$ is a bounded and countable set, and $\beta \left(\mathcal{D}\left(t \right)\right)$ is a Lebegue integral on $L^2(\Omega, X)$, which satisfies

Lemma 2.6. ^[24] If the set $\mathcal{D}\subset L^p(J, L_Q(K, H))$, $W(t)$ is a $Q$-Wiener process, then for any $p\geq2$, $t\in [0, T]$, Hausdorff NCM $\beta$ satisfies

where

Remark 2.1. Specially, when $p = 2$,

Lemma 2.7. ^[6] Let $\alpha \in \mathbb{R}^+$, $m \left(\cdot \right)$ be nonnegative continuous function. If there is

then,

3.   Existence of mild solutions

In this section, the existence of mild solutions of evolution systems (1.1)–(1.3) will be derived.

Definition 3.1. ^[25] An ${{\mathcal{F}}_{t}}$-adapted process $x:(-\infty, T] \to X$ is a mild solution of systems (1.1)–(1.3) if ${{x}_{t}}, \; x_{\rho(t, x_t)}\in \mathcal{B}$, ${{\left. x \right|}_{J}}\in \mathcal{D}\mathcal{P}\mathcal{C}(J, L^2(\Omega, X))$, and

(ⅰ) ${{x}_{0}} = \varphi(t) \in L_{0}^{2}(\Omega, \mathcal{B})$ for $t\in(-\infty, 0];$

(ⅱ) $x'(0) = \psi(t)\in L_{0}^{2}(\Omega, X)$ for $t\in J$;

(ⅲ) The function $g\left(t, x_t \right)$ is continuous and $f\left(t, x_{\rho \left(t, x_t \right)} \right)$ and $\eta \left(t, x_{\rho \left(t, x_t \right)} \right)$ are integrable. For given $T\in (0, \infty)$, $x(t)$ satisfies:

where $\prod\limits_{j = i}^k{q_j\left(\varepsilon _j \right)} = q_k\left(\varepsilon _k \right) q_{k-1}\left(\varepsilon _{k-1} \right) \cdots q_i\left(\varepsilon _i \right)$, and $\delta _A\left(t \right)$ is the index function, that is,

To acquire the desired results, we give the following assumptions:

$({H}_{1})$: For every ${{v}_{1}}, {{v}_{2}}\in \mathcal{B}, \; t\in J$, there exists positive constant ${{L}_{1}}$ such that

where ${{L}_{1}} = \sup\limits_{t \in J} E\left\{ {{\left\| g(t, 0) \right\|}^{2}}, {{\left\| f(t, 0) \right\|}^{2}}, {{Tr(Q)\left\| \eta (t, 0) \right\|}^{2}} \right\}$.

(${{H}_{2}}$): $E\left\{ \underset{i, k}{\mathop{\max }}\, \prod\limits_{j = i}^{k}{\left\| {{q}_{j}}({{\varepsilon }_{j}}) \right\|} \right\}$ is uniformly bounded, and there is $\tilde{M} > 0$ such that

for every ${{\varepsilon }_{j}}, \; j = 1, 2, \cdots$.

(${{H}_{3}}$): $C(t)$ and $S(t)$ are continuous in the uniform operator topology for every $t > 0$, and there exists constants ${{M}_{1}}, {{M}_{2}} > 0$ such that

(${{H}_{4}}$): We assume function $\rho :J\times \mathcal{B}\rightarrow \left(-\infty, T \right]$ is continuous. Function $t\to {{\varphi }_{t}}$ maps set $\Re ({{\rho }^{-}}) = \left\{ \rho (s, \varsigma)\le 0, \rho (s, \varsigma):(s, \varsigma)\in J\times \mathcal{B} \right\}$ to $\mathcal{B}$. There exists a continuous and bounded function ${{D}^{\varphi }}:\Re ({{\rho }^{-}})\to (0, \infty)$ such that

$(H_5)$: The functions $g, \; f :J\times\mathcal{B}\rightarrow L^2\left(\varOmega, X \right)$ and $\eta:J\times \mathcal{B}\rightarrow L_Q\left(K, L^2\left(\varOmega, X \right) \right)$ have the following properties:

($a$) The functions $g\left(t, \cdot \right), \; f\left(t, \cdot \right) :\mathcal{B}\rightarrow L^2\left(\varOmega, X \right)$, and $\eta\left(t, \cdot \right) :\mathcal{B}\rightarrow L_Q\left(K, L^2\left(\varOmega, X \right) \right)$ are continuous for every $t\in J$, and for $v\in \mathcal{B}$, $g\left(\cdot, v \right), \; f\left(\cdot, v \right) :J\rightarrow L^2\left(\varOmega, X \right)$, and $\eta\left(\cdot, v \right) :J\rightarrow L_Q\left(K, L^2\left(\varOmega, X \right) \right)$ are measurable.

($b$) There is integrable function $n_h\in L^1\left(J, \mathbb{R}^+ \right)$ and continuous nondecreasing function $\mathcal{P}_h:\mathbb{R}^+\rightarrow \mathbb{R}^+$ such that

($c$) There exists $L_h\in L^1\left(J, \mathbb{R}^+ \right)$ and any bounded set $\mathcal{D}\subseteq L^2\left(\varOmega, X \right)$ such that Hausdorff NCM $\beta$ satisfies:

where it is effective for functions $g, \; f$, and $\eta$ to replace $h$ in ($b$) and ($c$).

Lemma 3.1. ^[1] Let $x\in\mathcal{D}\mathcal{P}\mathcal{C}((-\infty, T], X)$, such that ${x}_{0} = \varphi$ and $x'(0) = \psi$, and then

where ${{\bar{D}}^{\varphi }} = \sup \left\{ {{D}^{\varphi }}(t):t\in \Re ({{\rho }^{-}}) \right\}$.

Theorem 3.1. If hypotheses (${{H}_{1}}$)–(${{H}_{5}}$) are satisfied, then evolution systems (1.1)–(1.3) have at least one mild solution.

Proof: Define the function $z:(-\infty, T]\to X$ by

Then, we denote the function $\bar{x}$ that satisfies Definition 3.1, and can be decomposed as $\bar{x} = x(t)+z(t)$ for $t\in J$. From Lemmas 2.1 and 3.1, it is easy to get:

where $c_1 = 4R_m^2\tilde{M}M_1E\lVert \varphi(0) \rVert ^2+4T_m^2E\|\varphi\|^2_\mathcal{B}$;

where $c_2 = 4R_m^2\tilde{M}M_1E\lVert \varphi(0) \rVert ^2+4(T_m+{{\bar{D}}^{\varphi }})^2E\|\varphi\|^2_\mathcal{B}$.

Let $Y = \left\{ x\in \mathcal{D}\mathcal{P}\mathcal{C}:x(0) = 0 \right\}$ be a space endowed with a uniform convergence topology. Denote ${{B}_{r}}(0, Y) = \left\{ x\in Y:E{{\left\| x \right\|}^{2}}\le r \right\}$ for $r > 0$. Define operator $\theta :Y\to Y$, such that $(\theta x)(t) = 0$ as $t\in (-\infty, 0]$, and

Now, we show that operator $\theta$ has a fixed point by the following steps.

Step 1. We first prove that there exists an $r$ such that $\theta$ maps $B_r$ into $B_r$. Without loss of generality, let $E\lVert \left(\theta x \right) \left(t \right) \rVert ^2 > r$, and then

Both sides of the above formula are divided by $r$ at the same time, and it is not difficult to find

Then, there is

where

Similarly, $\underset{{r\rightarrow \infty}}{\lim}\frac{\mathcal{P}_f\left(2R_{m}^{2}r+c_2 \right)}{r} = \underset{{r\rightarrow \infty}}{\lim}\frac{\mathcal{P}_\eta \left(2R_{m}^{2}r+c_2 \right)}{r} = 0$. Thus, $1\le 0$, which is obviously contradictory. Accordingly, there exists an $r > 0$ such that $\theta \left(B_r \right) \subseteq B_r$.

Step 2. ${{\theta }}:Y\to Y$ is continuous. Assume $\left\{ {{x}^{n}} \right\}_{n = 0}^{+\infty }\subseteq Y$ such that ${{x}^{n}}\to x$, as $n\to \infty$. Let control function $u(\cdot)$ is continuous, and then

where $x^n\rightarrow x$ implies $\bar{x}^n\rightarrow \bar{x}$. Since $B$ is a bounded linear operator and $\left\| {{u}_{{{\bar{x}}^{n}}}}(s)-{{u}_{\bar{x}}}(s) \right\|\to 0$ as ${\bar{x}^{n}}-\bar{x}\to 0$, then $B({{u}_{{{{\bar{x}}}^{n}}}}(s)-{{u}_{{\bar{x}}}}(s))\to 0$ as $\bar{x}^n\to \bar{x}$. In view of the continuity of $g(t, \cdot), \; f(t, \cdot)$, and $\eta(t, \cdot)$, we have

Step 3. We prove that ${{\theta }({B}_{r}})$ is equicontinuous on every $[\xi_k, \xi_{k+1}), (k = 1, 2, \cdots)$. Denote

Let $\xi_k\le {{t}_{1}} < {{t}_{2}} < \xi_{k+1}$, and then as ${{t}_{1}}\to {{t}_{2}}$,

and then,

By the continuity of $C(t)$ and $S(t)$, $E{{\left\| ({{\theta }}x)({{t}_{1}})-({{\theta }}x)({{t}_{2}}) \right\|}^{2}} \to 0$ as ${{t}_{1}}\to {{t}_{2}}$, which means that ${{\theta }}$ is equicontinuous.

Step 4. Let $\mathcal{O} = \left\{ x_m \right\} _{m = 1}^{\infty}.$ We demonstrate $\mathcal{O}\left(t \right) = \left\{ x_m\left(t \right)| x_m\in B_r(J), m = 1, 2, \cdots \right\}$ is relatively compact. Let $x_{m+1} = \theta x_m, m = 0, 1, 2, \cdots$. According to the properties of the Hausdorff NCM in Lemma 2.3, we have

Subsequently,

where $\mathfrak{A} = 2\max \left\{ 1, \tilde{M} \right\} R_{m}\left(M_1\bar{L}_g+M_2\bar{L}_f+M_2\bar{L}_\eta\sqrt{Tr(Q)}\right)$.

We acquire $\beta \left(\mathcal{O}\left(t \right) \right) \le \mathfrak{A}\int_0^t{\beta \left(\mathcal{O}\left(s \right) \right) ds}$. Due to Lemma 2.7, we have $\beta \left(\mathcal{O}\left(t \right) \right) \le 0$, and then we can deduce that $\beta \left(\mathcal{O}\left(t \right) \right) = 0$, which implies $\mathcal{O}(t)$ is relatively compact. Combining Steps 1–3, $\mathcal{O}$ is uniformly bounded and equicontinuous. Thus, $\beta \left(\mathcal{O} \right) = \underset{t\in J}{sup}\beta \left(\mathcal{O}\left(t \right) \right)$ and $\mathcal{O}$ is relatively compact. From the Ascoli-Azela Theorem, there apparently exists a convergent subsequence of $\left\{ x_m \right\} _{m = 0}^{\infty}$ and $\hat{x}$ such that $\underset{m\rightarrow \infty}{\lim}x_m = \hat{x}$. In addition, operator $\theta$ is continuous, and then,

Therefore, $\hat{x}\in \mathcal{B}_r\left(0, Y \right)$ is called the fixed point of $\theta$, which is also the mild solution of systems (1.1)–(1.3).

4.   Approximate controllability

In this section, we deduce the approximate controllability of systems (1.1)–(1.3).

Definition 4.1. ^[21] Let $x(T, u)$ be a mild solution of evolution systems (1.1)–(1.3) corresponding to the control $u$ at terminal time $T$. Set

denotes the reachable set of the systems (1.1)–(1.3) at terminal time $T$. If $\overline{\mathcal{R}(T)} = L^2(\Omega, X)$, then systems (1.1)–(1.3) are said to be approximately controllable on $J$.

Now, define the Nemytskil operator $\varGamma :\mathcal{DPC}\left(J, X \right) \rightarrow L^2\left(J, X \right)$ related to the nonlinear function $f$ by

Definition 4.2. Define $\Xi$ and bounded linear operators

and then,

where $h_1\in L^2(J, X)$ and $h_2\in L^2(J, L_Q(K, X))$.

Similarly, we give the following assumptions to verify the approximate controllability of systems (1.1)–(1.3).

(${{H}_{6}}$): Systems (1.1*)–(1.3*) denote systems corresponding to (1.1)–(1.3) with $f = 0$ and $\eta = 0$, and $\mathcal{R}_T\left(0, 0 \right)$ is the reachable set of the systems (1.1*)–(1.3*) at terminal time $T$. Systems (1.1*)–(1.3*) are approximately controllable, i.e., $\overline{\mathcal{R}_T\left(0, 0 \right) } = L^2(\Omega, X)$.

(${{H}_{7}}$): (ⅰ) For every $\varepsilon > 0$, $h_1\in L^2(J, X)$, and $h_2\in L^2(J, L_Q(K, X))$, there exists a control function $u\in {{L}^{2}}(J, {{L}^{2}}(\Omega, U))$ such that

(ⅱ) $\qquad \qquad \qquad \qquad \qquad E{{\left\| Bu \right\|}_{{{L}^{2}(J, X)}}^2}\le C(E{\left\| h_1 \right\|}_{{{L}^{2}(J, X)}}^2+{E\left\| h_2 \right\|}_{{{L}^{2}(J, X)}}^2)$,

where $C$ is a constant independent of $h_1$ and $h_2$.

(ⅲ) $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad 2C{{L}_{1}}R_{m}^{2}TL' < 1$,

where

Lemma 4.1. Any mild solution of systems (1.1)–(1.3) satisfies the following inequality if hypotheses (${{H}_{1}}$)–(${{H}_{5}}$) hold:

where $x^m (m = 1, 2)$ is the solution of systems (1.1)–(1.3) related to control ${{u}_{m}}(m = 1, 2)$.

Proof: ${x}^{m}$ has the following form

So, for ${{x}^{1}}, {{x}^{2}}\in X$, we obtain that

Therefore,

The proof is complete.

Now, we prove the approximate controllability of systems (1.1)–(1.3).

Theorem 4.1. Suppose that Lemma 4.1 and hypotheses $({{H}_{6}})$–$({{H}_{7}})$ hold. Then, systems (1.1)–(1.3) are approximately controllable.

Proof: We can obtain the equivalent condition of approximate controllability of systems (1.1)–(1.3) from Definition 4.1.

For any desired state of the terminal $\omega \in X$, $\forall \varepsilon > 0$, if there exists a control function ${{u}_{\varepsilon }}\in {{L}^{2}}(J, {{L}^{2}}(\Omega, U))$ such that the mild solution of systems (1.1)–(1.3) satisfy:

where ${{x}_{\varepsilon }} = x(\cdot, {{u}_{\varepsilon }})$, then systems (1.1)–(1.3) are approximately controllable.

Due to $\overline{\mathcal{R}_T\left(0, 0 \right) }\subset \overline{\mathcal{R}(T)}$, let $\omega \in \overline{\mathcal{R}_T\left(0, 0 \right) }$, and we construct a sequence that converges to $\omega$. According to (${{H}_{6}}$), systems (1.1*)–(1.3*) are approximately controllable. So, for $\forall \varepsilon > 0$, there exists $u\in {{L}^{2}}(J, {{L}^{2}}(\Omega, U))$ and $n\in \mathbb{Z}^+$ such that

Let ${{x}^1}\in L^2(\Omega, X)$ be a mild solution of systems (1.1)–(1.3) under control ${{u}_{1}}$. Because of $({{H}_{7}})(i)$, there exists ${{u}_{2}}\in {{L}^{2}}(J, {{L}^{2}}(\Omega, U))$ such that

Combining (4.1) and (4.2), we have

By using $({{H}_{7}})\; (i)$ again, there exists control function $v_2$ such that

Based on hypothesis $({{H}_{7}})\; (ii)$ and Lemma 4.1, we have

Set ${{u}_{3}} = {{u}_{2}}-{{v}_{2}}$, and combine (4.3) and (4.4),

By mathematical induction, we construct ${{u}_{n+1}} = {{u}_{n}}-{{v}_{n}}\in {{L}^{2}}(J, {{L}^{2}}(\Omega, U))$ satisfying

and

Due to $({{H}_{7}})\; (iii)$, we infer that $\{B{{u}_{n}}\}_{n = 1}^{\infty }$ is Cauchy and convergent. Then, for $\forall \varepsilon > 0$, there exists positive integer number $N$, $n > N$ such that

Hence,

In summary, systems (1.1)–(1.3) are approximately controllable.

5.   Nonlocal conditions

In this section, we study the approximate controllability of second-order stochastic differential equations with nonlocal conditions.

In order to get the result, it is necessary to give some properties of functions ${\mathcal{H}_{1}}$ and ${\mathcal{H}_{2}}$.

(${{H}_{8}}$): ${\mathcal{H}_{1}}, {\mathcal{H}_{2}}$ are continuous and compact, and satisfy the following conditions.

$(a)$ For any $x, y\in \mathcal{B}$,

($b$) There are integrable functions $n_{\mathcal{H}_{1}}, n_{\mathcal{H}_{2}}\in L^1\left(J, \mathbb{R}^+ \right)$, and continuous nondecreasing functions $\mathcal{P}_{\mathcal{H}_{1}}, \mathcal{P}_{\mathcal{H}_{2}}:\mathbb{R}^+\rightarrow \mathbb{R}^+$, such that

Definition 5.1. An ${{\mathcal{F}}_{t}}$-adapted process $x:(-\infty, T] \to X$ is a mild solution of systems (5.1)–(5.3), if ${{x}_{t}}, \; x_{\rho(t, x_t)}\in \mathcal{B}$, ${{\left. x \right|}_{J}}\in \mathcal{D}\mathcal{P}\mathcal{C}(J, L^2(\Omega, X))$, and

(ⅰ) ${{x}_{0}} = \varphi(t)+\mathcal{H}_1(x) \in L_{0}^{2}(\Omega, \mathcal{B})$ for $t\in(-\infty, 0];$

(ⅱ) $x'(0) = \psi(t)+\mathcal{H}_2(x)\in L_{0}^{2}(\Omega, X)$ for $t\in J$;

(ⅲ) The function $g\left(t, x_t \right)$ is continuous and $f\left(t, x_{\rho \left(t, x_t \right)} \right)$ and $\eta \left(t, x_{\rho \left(t, x_t \right)} \right)$ are integrable. For given $T\in (0, \infty)$, $x(t)$ satisfies

and then, the ${{\mathcal{F}}_{t}}$-adapted stochastic process $x:(-\infty, T]\to X$ is called a mild solution to systems (5.1)–(5.3).

Theorem 5.1. If $({{H}_{1}})$–$({{H}_{8}})$ are established, referring to the proof process of Theorems 3.1 and 4.1, then evolution systems (5.1)–(5.3) are approximately controllable.

6.   Examples

Example 1. In order to verify the abstract conclusions, we give the following hyperbolic wave equations with impulse at random moments:

where ${{\rho }_{1}}:[0, \infty)\to [0, \infty)$ and ${{\rho }_{2}}:[0, \infty)\to [0, \infty)$ are continuous functions. $c_1, \; c_2$, and $c_3$ are suitable functions. $\beta (t)$ denotes a standard cylindrical Wiener process in Hilbert space $K = {{L}^{2}}([0, \pi])$ defined on a stochastic space $\left(\Omega, \mathcal{F}, P \right)$. Let $\varepsilon_k$ be a random variable defined on $D_k\equiv (0, d_k)$, where $0 < d_k < +\infty$, for $k = 1, 2, \cdots.$ Suppose $\varepsilon_i$ and $\varepsilon_j$ are independent of each other as $i\neq j$ for $i, j = 1, 2, \cdots$. $\xi_0 = t_0 = 0$ and $\xi_k = \xi_{k-1}+\varepsilon_k$ for $k = 1, 2, \cdots$. $p$ is a function regarding $k$.

Let $Z = K = {{L}^{2}}([0, \pi])$ and define operator $A:D(A)\subset Z\to Z$ as $Ax = x''$, where

Operator $A$ has a discrete spectrum, and its eigenvalue is $-{{n}^{2}}$ and $e_n = \sqrt{\frac{2}{\pi}}e^{inz}, \; n\in \mathbb{Z}$. $\{C(t):t\in \mathbb{R}\}$ is a family of strongly continuous cosine operators, and $A$ is its infinitesimal generator. Then

The correlative sine family $S(t)$ is given by

It is easy to infer ${{\left\| S(t) \right\|}^{2}}\le 1$ and ${{\left\| C(t) \right\|}^{2}}\le 1$. Hence, $C(t)$ and $S(t)$ are uniformly bounded for $t\in \mathbb{R}$.

$\mathcal{B}$ is a phase space with norm $\lVert \mu \rVert _{\mathcal{B}} = \underset{\theta \le 0}{sup}\lVert \mu \left(\theta \right) \rVert$, and define $\mathcal{B}$ as a set of bounded and uniformly continuous functions from $(-\infty, 0]$ to $Z$. Define the functions $g, \; f:J\times \mathcal{B}\rightarrow L^2\left(\varOmega, Z \right), \; \eta :J\times \mathcal{B}\rightarrow L_Q\left(K, L^2(\Omega, Z) \right), \; \rho :J\times \mathcal{B}\rightarrow \left(0, \infty \right), \; z_{t}:\text{J}\rightarrow L^2\left(\varOmega, Z \right),$ and $q_k({{\varepsilon }_{k}})$,

In this way, we can rewrite the equations (6.1)–(6.5) in the form of (1.1)–(1.3). In order to get controllable results, we need to make the following assumptions.

($a$) Continuous functions $c_1, c_2, c_3:\mathbb{R}\rightarrow \mathbb{R}$ satisfy:

($b$) $E\left\{ \underset{i, k}{\max}\lVert \prod\limits_{j = i}^k{p\left(j \right) \varepsilon _j } \rVert ^2 \right\} < \infty$.

($c$) $D^{\varphi}:\Re \left(\rho ^- \right) \rightarrow \varphi _t$ is continuous, and

($d$) For $\left(t, \mu \right) \in \left(-\infty, 0 \right] \times \mathcal{B}$,

where $G(\mu)(y) = \int_{-\infty }^{0}{{{c}_{3}}(s)\mu (s, y)ds}$, $h_g, \; h_f$ and $h_{\eta}$ are integral, and $\mathcal{G}_g, \; \mathcal{G}_f$ and $\mathcal{G}_\eta$ are all positive continuous nondecreasing functions.

Under the above conditions, for every $t\in \left[0, 1\right]$, $\mu _1, \mu _2\in \mathcal{B}$,

For arbitrary bounded set $\mathcal{D}\in \mathcal{B}$,

Similarly, $E\lVert f\left(t, \mu _1 \right) -f\left(t, \mu _2 \right) \rVert ^2\le l_g\lVert \mu _1-\mu _2 \rVert _{\mathcal{B}}^2$, and for arbitrary bounded set $\mathcal{D}\in \mathcal{B}$,

Suppose $b$ follows the Lipschitz condition:

Let $G$ be bounded,

For arbitrary bounded set $\mathcal{D}\in \mathcal{B}$,

Assume $L_1 = max\{l_g, l_f, Tr(Q)l_{\gamma}\lVert G \rVert\}$, and then conditions ($H_1$) and ($H_5$) hold.

Define $U = \left\{ u:u = \sum\limits_{n = 2}^{\infty}{u_ne_n}\; with\; \sum\limits_{n = 2}^{\infty}{u_{n}^{2}} < \infty \right\}$. $B:U \rightarrow L^2\left(\varOmega, X \right)$ and $Bu = 2u_2e_1+\sum\limits_{n = 2}^{\infty}{u_ne_n}$. Then assumption ($H_7$) holds. For a more detailed explanation, see ^[34]. Then, as the related systems with $f = 0$ and $\eta = 0$ are approximately controllable, based on Theorem 4.1, systems (6.1)–(6.5) are approximately controllable.

Example 2. We then provide a numerical example to further prove the feasibility of the theoretical results.

where $\beta (t)$ denotes a standard one-dimensional Wiener process. Let $\tau_k$ be a random variable following the exponential distribution. We assume $A = 1, \; T = 30$ and $J = [0, 30]$.

We choose the state of terminal time $T$ as $x(T) = 5$. For every $h_1\in L^2(J, X), \; h_2\in L^2(J, L_Q\left(K, X \right))$, let

Let $B = 1$, and we choose control function $u$ as $\varPhi _1u = \phi _1h_1+\varPhi _1h_2.$

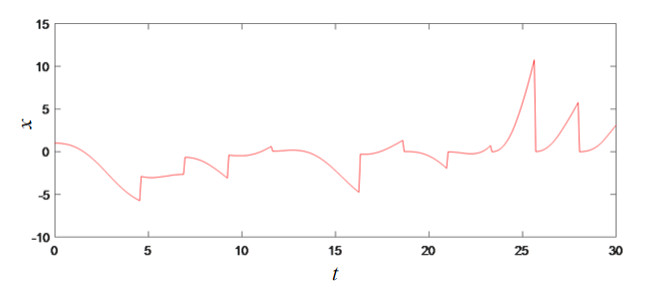
Figure 1 shows a sample path of the systems (6.6)–(6.8) with $Bu = 0$, and it can see that the systems (6.6)–(6.8) are not equal to $5$ at $t = 30$. Figure 2 shows a sample path of the systems (6.6)–(6.8) under control $u$. It can be seen that the state value of systems (6.6)–(6.8) is very close to $5$ and the error is very small.

7.   Conclusions

In this paper, we pay attention to the existence and approximate controllability of mild solutions to systems (1.1)–(1.3), which can be abstracted from the second-order stochastic wave equation and extended to more general random impulses cases. To obtain the result of existence, we applied evolution operator theory, stochastic analysis skills, and the measure of noncompactness. Then, under some appropriate conditions, the approximate controllability was established. Further, we considered relevant conclusions under the nonlocal conditions. At the end of this paper, two examples were given to show the effectiveness of the results. Our work may generalize some existing results on this topic.

Stochastic differential systems with random impulsive effect have applications in many practical problems, and there are many relative problem worth studying. In recent reference ^[29], Vinodkumar et al. discussed the existence, uniqueness, and stability of solutions of fractional differential equations with random impulses. As we know, the literature related to approximate controllability of fractional stochastic differential systems with random impulses remains very limited. In later work, we will continue to consider approximate controllability of fractional impulsive stochastic differential systems under the interference of various random factors such as random sequence, fractional Brownian motion, or Rosenblatt process.

Author contributions

Chunli You: conceptualization, methodology, investigation, and writing-original draft; Linxin Shu: methodology, project administration, and writing-review and editing; Xiao-Bao Shu: resources, supervision, technical support. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This work is supported by the Jiangxi Provincial Department of Education Science and Technology Foundation (No. GJJ2201122).

Conflict of interest

The authors declare that there are no conflicts of interest.