Non-fragile ${H_\infty }$ filter design for uncertain neutral Markovian jump systems with time-varying delays

1.   Introduction

In many practical systems, there are often sudden problems involving various noises, environmental disturbances, equipment failures, and maintenance. These factors can lead to sudden changes in system parameters and structure. Thus, for such complex problems, establishing an appropriate system model is essential. In order to solve such problems, Krasovskii and Lidskii first proposed Markovian jump systems ^[1]. Markovian jump systems as stochastic systems are also important mixing systems, and they are widely used in the fields of economics, biomedicine, manufacturing, power, aerospace, and networking ^[2,3,4,5]. Over the past decades, Markovian jump systems have been studied, focusing on the stability, control, and filtering of the system. In ^[6,7,8], the stability of neutral Markovian jump systems and stochastic singular Markovian jump systems were considered. In ^[9,10,11,12], problems of finite time ${H_\infty }$ control, robust and non-fragile ${H_\infty }$ control, and delay dependent control for Markovian jump systems with time-varying delays were studied. The problem of non-fragile ${H_\infty }$ filter design for a class of discrete singular Markovian jump systems with time-varying delays and measurement misspecification was considered based on extended passive theory in ^[13]. In ^[14], the problem of finite region asynchronous dissipative control was considered, with more attention paid to the transient behavior of a class of two-dimensional fuzzy Markovian jump systems. The problem of asynchronous deconvolution filter design for 2-D Markovian jump systems with random packet losses was addressed in ^[15].

Filtering is an important method for estimating system state information when the system is subject to disturbances. Filtering problems are fundamental in areas such as control and signal processing. Kalman and ${H_\infty }$ filtering are the more popular filtering methods. The Kalman filter is applicable when the disturbance in the system is Gaussian white noise or spectral density noise. The disadvantage of the Kalman filter is that if the understanding of the noise model or the measured noise is not accurate enough, these limit the scope of applications of the Kalman filtering technique. The ${H_\infty }$ filter applies to any signal where the measured noise is of bounded energy, and it does not have to require that the noise be Gaussian white noise. Therefore, ${H_\infty }$ filtering is widely used in many fields. The Riccati equation method and the linear matrix inequality (LMI) method are more popularly used in ${H_\infty }$ filter design. Among them, the Riccati equation method is widely used in systems with norm-bounded uncertainties, and the solution is relatively simple. However, the Riccati equation method uses an iterative approach and does not have a standardized solution, so it is relatively conservative ^[16]. The LMI method is more practical and less conservative than the Riccati method and is therefore widely used ^[17,18,19]. Through the study, it was found that either using classical optimal control to study system stability or using it to design controllers may lead to the emergence of fragile phenomena in the controllers, thereby leading to a decrease in the performance of the closed-loop system obtained by adding the controller, even making it difficult to maintain stability. Thus, the problem of non-fragile filtering has attracted the interest of scholars, and some research results have been obtained ^{[20,21,22,23,24,25]}.

As is well known, time delays arise frequently in a variety of engineering systems, such as manufacturing systems, communication systems, networked control systems, chemical processing, and biological systems ^{[13,26,27,32]}. In fact, time delays are one of the most important reasons for system instability and poor performance. In recent decades, the study of stability and control of delayed systems has attracted the attention of many scholars. In ^[28], the stability analysis of time delay systems was investigated using single/multiple integral inequalities. The delay-dependent ${L_2} - {L_\infty }$ filtering problem for stochastic systems with time delays was investigated in ^[29]. ^[30] discussed the delay-dependent ${H_\infty }$ filtering problem for a class of singular Markovian jump delay systems. Parameter uncertainties, like time delay, often lead to significant deterioration or even instability in the performance of the corresponding system. Therefore, it is necessary and reasonable to consider time delay and parameter uncertainties in the study of various control systems, including Markovian jump systems. Markovian jump systems with time delay and uncertainties have also been extensively studied ^[25,31,32].

Neutral delay as a special kind of time delay appears in the derivative of the system state. Since neutral systems can describe both the system state and the time delay of state differentiation, many control system models can be well modeled as neutral systems ^[33]. Thus, the neutral Markovian jump systems are also studied. For example, in ^[34], by utilizing the Lyapunov-Krasovskii generalization method, the problem of state estimation for uncertain neutral time-delay systems with Markovian jump parameters was studied. The robust ${H_\infty }$ filtering problem for uncertain Markovian jump-neutral distributed delay systems was studied in ^[35]. The problem of designing asynchronous ${H_\infty }$ controllers for neutral singular Markovian jump systems under dynamic event-triggered parties was studied in ^[36]. The existence of time delay affects the performance and stability of the dynamic system. Both state delay and neutral delay imply increased difficulty in modeling and controlling the system, and require more advanced control strategies and methods to deal with the time delay of the system. The mixed-delay-dependent ${L_2} - {L_\infty }$ filter design for a class of neutral stochastic systems with time-varying delay was discussed in ^[37]. The problem of robust stability and ${H_\infty }$ filter design for neutral stochastic neural networks with parameter uncertainties and time delay was considered in ^[38]. In ^[39], the problem of robust ${H_\infty }$ filter design for a class of uncertain fuzzy-neutral stochastic systems with time-delay was investigated using the Takagi-Sugeno (T-S) fuzzy model. In recent years, there has been more research on filters for Markovian jump systems, but the problem of non-fragile ${H_\infty }$ filtering of Markovian jump systems with neutral delay has rarely been reported.

Based on the above discussions, this paper discusses the problem of non-fragile ${H_\infty }$ filter design for Markovian jump systems with parameter uncertainties and two kinds of time-varying delay. Mode-dependent non-fragile ${H_\infty }$ filters are obtained by utilizing delay and mode-dependent Lyapunov-Krasovskii functions and an integral inequality technique. The main contributions of this paper are as follows:

(1) The state delay and neutral delay are considered simultaneously for filtering design of uncertain Markovian jump systems.

(2) The designed filter is a non-fragile filter. Specifically, non-fragile ${H_\infty }$ filter is robust to parameter uncertainties and external disturbances.

(3) The non-fragile ${H_\infty }$ filtering conditions for uncertain Markovian jump systems with time-varying neutral delay and state delay are shown in terms of strict LMIs, which can be solved directly with the LMI toolbox and yield non-fragile ${H_\infty }$ filter parameters.

The remainder of this paper is organized as follows. The non-fragile ${H_\infty }$ filter design for uncertain neutral Markovian jump systems with time-varying delays problem formulation and preliminaries is formulated in Section 2. Section 3 presents stability analysis and the non-fragile ${H_\infty }$ filter design. Two numerical examples are provided in Section 4, and then we conclude this paper in Section 5.

Notation: $\left({\Omega, F, \, P\, } \right)$ is a complete probability space, where $\Omega$ represents the sample space, $F$ represents the $\sigma$ -algebra of a subset of the sample space, and $P$ represents the probability measure of $F$. ${L_2}[0, \, \infty)$ is a square-integrable vector function in the $[0, \, \infty)$ space. $\varepsilon \left\{ \cdot \right\}$ represents the mathematical expectation operator with respect to the given probability measure $P$. The symbol $\left(* \right)$ represents a term induced by symmetry in the linear matrix inequality (LMI). $X > 0\left({X \geqslant 0} \right)$ represents a positive definite (semi-positive) matrix, and $X < 0\left({X \leqslant 0} \right)$ represents a negative definite (semi-negative) matrix.

2.   Problem formulation and preliminaries

Given a complete probability space $\left({\Omega, F, \, P\, } \right),$ we consider the following uncertain neutral Markovian jump systems with time-varying delays:

where $x(t) \in {\mathbb{R}^n}$ is the state vector, $y(t) \in {\mathbb{R}^r}$ is the measurement output vector, $\omega (t) \in {R^p}$ is the disturbance input vector, which belongs to ${L_2}[0, \, \infty)$, and $z(t) \in {\mathbb{R}^q}$ is the signal vector to be estimated.

$h\, (t)\,$ and $d(t)\,$ are the time-varying delays which satisfy

$\varphi \, (t)$ is a continuous real-valued initial function defined in the interval $[ - b, 0],$ where $b = \max \{ d, h\, \}$ is satisfied.

$\left\{ {{r_t}} \right\}$ is a Markov process with right-continuous trajectories, taking values in a finite set ${r_t} = i \in M = \left\{ {1, \; 2, \; ..., \; N} \right\}$. The transition rate matrix $\Pi = \left\{ {{\lambda _{ij}}} \right\}$ is given by

where $\rho > 0, \; \mathop {\lim }\limits_{\rho \to 0} \frac{{o\left(\rho \right)}}{\rho } = 0,$ and ${\lambda _{ij}} \geqslant 0$ for $i \ne j$ is the transition rate from mode $i$ at time $t$ to mode $j$ at time $t + \rho$, satisfying

For each ${r_t} \in M$,

where $A({r}_{t}), {A}_{d}({r}_{t}), {A}_{h}({r}_{t}), C({r}_{t}), {C}_{d}({r}_{t}), D({r}_{t}), {D}_{d}({r}_{t}), {G}_{1}({r}_{t}), {G}_{2}({r}_{t}),$ and ${G_3}({r_t})$ are known real constant matrices of appropriate dimensions, and where $\Delta A(t, {r_t})$ and $\Delta {A_d}(t, {r_t})$ satisfy

where $F(t, {r_t}), \; {r_t} \in M$ are unknown matrices with Lebesgue measure satisfying

and ${H_1}({r_t}), \; {K_1}({r_t}), \; and\; {K_2}({r_t}), \; {r_t} \in M,$ are known constant matrices with appropriate dimensions.

For convenience, for each $\; {r_t} = i \in M$, $A\, (t, {r_t})$ is replaced by ${A_i}(t),$ ${G_1}({r_t})$ is replaced by ${G_{1i}},$ etc.

Now we consider a non-fragile filter for system (2.1) as follows:

where ${x_f}(t) \in {\mathbb{R}^n}$ is the filter state vector; ${z_f}(t) \in {\mathbb{R}^q}$ is the filter output vector; ${A_f}(t, {r_t}), \; {B_f}(t, {r_t})\; ,\;$ ${C_f}(t, {r_t})$ are the filter parameter matrices with appropriate dimension, for ${r_t} \in M$

where

and ${H_2}({r_t}), \; {K_3}({r_t}), \; and\; {K_4}({r_t}), \; {r_t} \in M,$ are known constant matrices with appropriate dimensions.

Let

Then, we have the filtering error system

where

The non-fragile ${H_\infty }$ filtering problem can be described as follows.

Problem description: Given the uncertain neutral Markovian jump system (2.1) with parameter uncertainties (2.6), find a non-fragile filter (2.8) such that the filtering error system (2.11) is stochastically stable and satisfies the following ${H_\infty }$ performance:

where $\gamma$ is a given positive scalar.

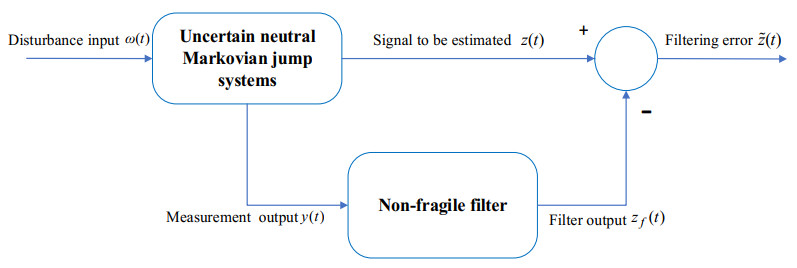
Figure 1 shows a flowchart describing non-fragile ${H_\infty }$ filtering of uncertain neutral Markovian jump systems with time-varying delays.

To support the research in this paper, the main definitions and lemmas used are presented in the following.

Definition 1. ^[7] The filtering error system (2.11) is said to be stochastically stable if for $\varphi (t) \in {\mathbb{R}^n}$ defined in the interval $\left[ { - b, \, 0} \right]$ and ${r_0} \in M,$

where $\tilde x(\alpha, \varphi, {r_0})$ is the solution to the filtering error system (2.11) under the initial conditions.

Definition 2. ^[40] Under zero initial conditions, the filtering error system (2.11) satisfies the ${H_\infty }$ performance level $\gamma > 0$, if for all nonzero $\omega (t) \in {L_2}\left[ {0, \infty } \right)$, the following inequality holds:

Lemma 1. ^[41] For any matrices $Q \in {\mathbb{R}^{n \times n}}$ and $Z \in {\mathbb{R}^{n \times n}}$ satisfying $\left[ {\begin{array}{*{20}{c}} Q & Z \\ {{Z^T}} & Q \end{array}} \right] \geqslant 0$ and a scalar $d > 0$, there is satisfying $0 \leqslant d(t) \leqslant d,$ such that the following integrals are well defined, then

where

Lemma 2. ($Bellman - Gronwall$) Let $k\;$ and $f$ be continuous real-valued functions on $\left[ {a, \, b} \right]$ and the function $g$ be integrable and nonnegative on $\left[ {a, \, b} \right]$.

If

such that

if $f(t)$ is a monotone non-decreasing function, then

Lemma 3. (Schur Complement Lemma) If the matrices ${S_{11}} = S_{11}^T$, ${S_{22}} = S_{22}^T,$ and ${S_{12}}$ are symmetric matrices with appropriate dimensions, then the following LMIs are equivalent:

(1) $S = \left[\begin{array}{cc}{S}_{11} & {S}_{12} \\ {S}_{12}^{T} & {S}_{22}\end{array}\right] < 0$

(2) ${S}_{11} < 0, {S}_{22}-{S}_{12}^{T}{S}_{11}^{-1}{S}_{12} < 0$

(3) ${S}_{22} < 0, {S}_{11}-{S}_{12}{S}_{22}^{-1}{S}_{12}^{T} < 0$

Lemma 4. ^[11] Given appropriate dimensions, the matrices ${\Pi _{1i}}$, ${\Pi _{2i}},$ and ${\Pi _{3i}}$, with ${\Pi _{1i}} = \Pi _{1i}^T$ for all $F(t)$ satisfying ${F^T}(t)F(t) \leqslant I,$ then

if and only if there exists a scalar a $\varepsilon > 0$ such that

In the following chapters, we base our analysis on the Lyapunov-Krasovskii functions to provide stability conditions for the filtering error system (2.11). Furthermore, we derive delay-dependent conditions for the existence of the non-fragile filter (2.8) and obtain sufficient conditions for the filtering error system (2.11) to be stochastically stabilized and achieve a certain ${H_\infty }$ performance level $\gamma > 0.$

3.   Main results

3.1.   Stability analysis

Theorem 1. Given the scalars $\gamma > 0, \; b > 0, \; d > 0, \; h > 0, \; \bar d > 0,$ and $\bar h > 0,$ the filtering error system (2.11) is stochastically stable if there exist matrices ${P}_{i} > 0, {Q}_{1i} > 0, {Q}_{2i} > 0, {Q}_{3} > 0, {Q}_{4} > 0, {R}_{1} > 0, {R}_{2} > 0,$ ${R_{3i}} > 0,$ ${R_4} > 0,$ and ${Z_i}$ such that the following matrix inequalities hold for all $i \in M$ :

where

Proof. We will prove the stochastic stability of the filtering error system (2.11). First, we define a new process $\left\{ {\left({{{\tilde x}_t}, \; {r_t}} \right), \; t \geqslant 0} \right\}$ using $\left\{ {{{\tilde x}_t} = x(t + \theta), \; - 2b \leqslant \theta \leqslant 0} \right\}$, and then $\left\{ {\left({{{\tilde x}_t}, \; {r_t}} \right), \; t \geqslant b} \right\}$ is a Markov process with initial state $\left(\phi (·), {r}_{0}\right)$. Further, for all ${r_t} = i \in M$, choose a stochastic Lyapunov-Krasovskii function candidate for system (2.11) as

where

Let $L$ be the weak infinitesimal generator of the stochastic process $\left\{ {\left({{{\tilde x}_t}, \; {r_t}} \right), \; t \geqslant b} \right\}$. Based on (3.1.1)–(3.1.4), we obtain

According to Lemma 1, we have

where

When $\omega (t) = 0$, we can obtain that

where

and we can find that (3.1.5) guarantees ${\Xi _i} < 0$, which implies that there exists a scalar $a > 0$ such that

for all ${\tilde x_t} \ne 0$. Then, for any $t \geqslant b$, by Dynkin's formula, we have

such that

Based on the filtering error system (2.11), for all $t > 0$ there exists scalars ${K_1} \geqslant 0, \; {K_2} \geqslant 0, \; and\; {K_3} \geqslant 0$ such that

where ${K_1} = \mathop {\max }\limits_{i \in M} \{ \left| {{{\tilde A}_i}} \right|, \left| {{{\tilde A}_{di}}} \right|, \left| {{{\tilde A}_{hi}}} \right|\}$. Then, for any $0 \leqslant t \leqslant b$, one obtains

Utilizing Lemma 2 (Gronwall-Bellman Lemma), we obtain

which implies

Using Eqs (3.1.6)–(3.1.20), we have

where $\; {K_4} \geqslant 0$, and there exists a scalar $\alpha \geqslant 0$ such that

According to Definition 1, we obtained that the filtering error system (2.11) with $\omega (t) = 0$ is stochastically stabilized.

Remark 1. In the stability analysis, by using Lyapunov stability theory and integral inequality techniques, stability of uncertain neutral Markovian jump systems is guaranteed. It is worth noting that the proof of the conditions in the definition is obtained using Dynkin's formula and the Gronwall-Bellman Lemma. The proof process is similar to that of ^[12,41].

3.2.   Non-fragile ${H_\infty }$ filter design

This paper investigates the problem of non-fragile ${H_\infty }$ filter design for neutral Markovian jump systems. Therefore, sufficient conditions are obtained for the filtering error system to have a ${H_\infty }$ performance level $\gamma$, and this condition is used to further find out the filtering parameters of the filter (2.8).

Theorem 2. The filtering error system (2.11) is stochastically stable and has an ${H_\infty }$ performance level $\gamma$ if there exist matrices ${P_i} > 0, \; {Q_{1i}} > 0, \; {Q_{2i}} > 0, \; {Q_3} > 0, \; {Q_4} > 0, \; {R_1} > 0, {R_2} > 0, \;$ ${R_{3i}} > 0, \; {R_4} > 0,$ and ${Z_i}$ such that the following matrix inequality holds for all $i \in M$ :

where ${\Omega _{i16}} = {P_i}{\tilde G_i}$.

Proof. By applying the Schur complement lemma, we known that the matrix inequality (3.2.1) can ensure (3.1.5). Consequently, the filtering error system (2.11) with $\omega (t) = 0$ is stochastically stable by Theorem 1. When $\omega (t) \ne 0$, under zero initial conditions the performance function $J$ is as follows:

Define

If $J$ satisfies condition $J < 0$, then the filtering error system (2.11) is stochastically stable and meets the given ${H_\infty }$ performance level $\gamma$.

If the inequality (3.2.2) holds, then $J < 0$.

where

If ${\tilde \Xi _i}$ satisfies condition ${\tilde \Xi _i} < 0$, then the filtering error system (2.11) satisfies ${H_\infty }$ performance level $\gamma$, and system (2.1) is stochastically stable in the presence of a non-fragile ${H_\infty }$ filter (2.8).

According to Eq (3.2.2), we have

Therefore, for any $T > 0$, the following inequality is satisfied:

Letting $T \to \infty$, we have

and then the filtering error system (2.11) can satisfy Definition 2.

Next, we begin to design a non-fragile ${H_\infty }$ filter for system (2.1).

Theorem 3. Given scalars $\gamma > 0, \; b > 0, \; d > 0, \; h > 0, \; \bar d > 0$ and $\bar h > 0$, suppose there exist matrices ${P_{1i}} > 0, \; {P_{3i}} > 0, {\tilde Q_{1i}} > 0, \;$ ${\tilde{Q}}_{2i} > 0, {\tilde{Q}}_{3} > 0, {\tilde{Q}}_{4} > 0, {\tilde{R}}_{1} > 0, {\tilde{R}}_{2} > 0, {\tilde{R}}_{3i} > 0, {\tilde{R}}_{4} > 0, {P}_{2i}, {X}_{1i}, {X}_{2i}, {X}_{3i}, {X}_{4i}$ $X, \; {Z_{1i}}, \; {Z_{2i}}, \;$ ${Z_{3i}}, \; {Z_{4i}}, \; {\tilde A_{fi}}, \; {\tilde B_{fi}},$ and ${\tilde C_{fi}}$, where $X$ is a non-singular matrix, such that the following linear matrix inequalities hold for all $i \in M$ :

where

where

Then, there exists a mode-dependent ${H_\infty }$ filter (2.8) such that the filtering error system (2.11) is stochastically stable with a ${H_\infty }$ performance level $\gamma$. Moreover, the desired parameters of the mode-dependent filter are given by

Proof.

Select the following matrix

where

Pre- and post-multiplying ${\theta _i}$ by the matrix ${\Phi _i}$ and its transposition, respectively, gives

and for any $i \in M$, we can obtain

Thus, ${\theta _i} < 0$ implies ${\tilde \Xi _i} < 0$ such that

where

According to Lemma 4, for any ${\varepsilon _{1i}} > 0, \; {\varepsilon _{2i}} > 0, \; {\varepsilon _{3i}} > 0, \; and\; {\tilde \theta _i} < 0$, we have the following inequality:

Choosing the matrices in ${\tilde \theta _i}$ as

and connecting those with (3.1.1)–(3.1.4) and (3.2.1), we obtain conditions (3.2.3)–(3.2.8) and filter parameters (3.2.11) in Theorem 3. This completes the proof.

Remark 2. In Theorem 3, using the linear matrix inequality method, non-fragile ${H_\infty }$ filtering conditions for uncertain neutral Markovian jump systems with time-varying state delay and neutral delay are given, where the non-fragile ${H_\infty }$ filtering conditions are mode- and delay-dependent strictly linear matrix inequalities to represent and obtain the mode-dependent filter parameters. These parameters can be solved directly with the LMI toolbox.

4.   Numerical example

In this section, we use the LMI toolbox, solving for the values of the filter parameters. Using filter parameters and other known parameters, we can construct figures of system state, filter state, and filtering errors in order to verify the feasibility and validity of theoretical results.

Example 1. Consider the neutral Markovian jump system (2.1) with two modes and system parameters as follows:

Using the parameters above to solve the linear matrix inequalities (3.2.3)–(3.2.8) in Theorem 3, we obtain the ${H_\infty }$ performance level $\gamma$ in Table 1.

In Table 1, it can be seen that there is a significant difference between the performance level obtained in this paper and the performance level in reference ^[40]. The ${H_\infty }$ performance level $\gamma$ in this paper is smaller. This implies that the system proposed in this paper has stronger stability and better robustness. Furthermore, the performance of the non-fragile ${H_\infty }$ filter designed in this paper is better than the robust ${H_\infty }$ filter proposed in ^[40]. The filter designed in this paper includes uncertainty terms, therefore demonstrating a stronger resistance to uncertainties and parameter variations.

Letting $d = 0.2, \; h = 0.4, \; \bar d = 0.3, \; \bar h = 0.2$, and using Eq (3.2.11), we obtain the following mode-dependent filter parameters:

When the transition rate matrix $\prod$ is known, the Markovian jump modes ${r_t}$ for the initial mode ${r_0} = 1$ is shown in Figure 2. Choosing the initial value $x({t_0}) = {\left[ {\begin{array}{*{20}{c}} {0.08} & { - 0.05} \end{array}} \right]^T}$, the time-varying delays are $d(t) = \max \{ 0.3\sin (t), 0.2\}$ and $h(t) = \max \{ 0.2\sin (t), 0.4\}$, the disturbance input $\omega (t) = \sin (t){e^{ - 0.06t}}$, and Figures 3–5 show the system state $x(t)$, filtering state ${x_f}(t)$, signal to be estimated $z(t)$, filter output ${z_f}(t)$, and filtering error $\tilde z(t)$, respectively. From Figures 2–5, it can be seen that when the two subsystems are switched according to Markovian jump modes, the obtained filter tracks the real state smoothly, and can rapidly converge to zero over time. The filtering error system is guaranteed to be stochastically stable. Finally, it can be verified that our designed non-fragile ${H_\infty }$ filter is feasible.

Example 2. Consider the partial element equivalent circuit (PEEC) model ^[42] described by neutral Markovian jump system (2.1) with the following parameters:

Let $d = 0.25, \; h = 0.2, \; \bar d = 0.35, \; \bar h = 0.25,$ and using the parameters above to solve the linear matrix inequalities (3.2.3)–(3.2.8) in Theorem 3, we obtain the ${H_\infty }$ performance level ${\gamma _{\min }} = 0.9595$ and mode-dependent filter parameters as follows:

The Markovian jump modes ${r_t}$ for the initial mode ${r_0} = 1$ is shown in Figure 6. Choosing the initial value $x({t_0}) = {\left[ {\begin{array}{*{20}{c}} {0.02} & {0.01} & { - 0.01} \end{array}} \right]^T}$, the time-varying delays are $d(t) = \max \{ 0.35\sin (t), 0.25\}$ and $h(t) = \max \{ 0.25\sin (t), 0.2\}$, the disturbance input $\omega (t) = \sin (t){e^{ - 0.05t}}$, Figure 7 shows the PEEC model system state $x(t)$, Figure 8 shows the state estimation ${x_f}(t)$, and Figure 9 shows the filtering error.

5.   Conclusions

The problem of non-fragile ${H_\infty }$ filtering for uncertain neutral Markovian jump time-delay systems with known transition jump rates is investigated in this paper. Using the Lyapunov-Krasovskii function and integral inequality technique, a novel delay and mode dependent stability criterion was derived. Using the linear matrix inequality method, a sufficient condition for the existence of the filter is given, and a mode dependent non-fragile ${H_\infty }$ filter satisfying the ${H_\infty }$ performance level $\gamma$ was designed. Two numerical examples have been provided to illustrate the effectiveness and usefulness of the results. In the future, the non-fragile ${H_\infty }$ filtering and control problems for uncertain neutral type singular Markovian jump systems with time-varying delays will be considered.

Author contributions

All authors contributed equally to this work. All authors read and approved the final manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work presented in this paper is supported by the NSFC under the grants 61462087 and 61751316 and the Special Education Project of Xinjiang under the grant 2022D03029.

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.