Convergence results for cyclic-orbital contraction in a more generalized setting with application

1.   Introduction

Cardiovascular disease (CVD) is a common kind of illness that is mainly caused by heart problems. CVD is characterized by shortness of breath, physical weakness, swollen feet, and exhaustion. A few risk factors of CVD include a high fat percentage, smoking, inactive lifestyles, and high blood pressure ^[1]. According to the World Health Organization (WHO), the foremost reason for death is CVD, which kills 18 million persons a year. Coronary artery disease is a type of heart disease ^[2]. As an outcome, stroke and heart disease are considered as main public health concerns. Clinicians regularly use angiography to analyze CVD. The use of analytical techniques, the expertise of doctors, and other resources are insufficient in underdeveloped states; therefore, this diagnosis procedure consumes more time and is expensive, requiring the investigation of numerous variables ^[3]. Recently, heart disease has become the most dangerous medical topic because the death toll from CVD has risen. Prediction helps in the primary recognition of the disease, as well as be the most effective action. In medical diagnostics, the use of machine learning (ML) has become popular ^[4]. ML has been recognized to enhance the classification and identification of diseases by providing information to aid medical experts in determining and identifying illnesses, supporting human health, and reducing the death rate ^[5]. When defining the prospect of a disease occurrence, ML classification techniques are frequently utilized.

ML is the capability of computers to learn without being automated ^[6]. Generally, in the artificial intelligence (AI) model, computers learn from preceding experiences and then information. The quantity of data is growing quickly, so it is essential to professionally handle data. Occasionally, it becomes quite complex for human beings to physically remove valuable info from raw data due to their imprecision, alikeness, changeability, and uncertainty ^[7]. This is where ML is beneficial. With an excess of information in big data, its demand is on high growth, as it acquires more precise, helpful, and steady info from raw data. One of the chief aims of ML is to permit machines to study without being methodically automated. ML has been curiously innovative in numerous areas such as pre-processing methods and learning procedures during the last few years ^[8]. Deep learning (DL) originated on artificial neural networks (ANNs), which are an important technique to deliver appropriate algorithmic structures. DL permits computational methods that are collected from numerous processing layers to learn data illustrations with numerous stages of concepts and needs little work by hand ^[9]. DL methodology established great latency in dissimilar fields of health care, as well as showed outstanding performance in natural language processing (NLP), computer vision (CV), removal of automated health records, health modalities, and sensor data analytics ^[10].

This study introduces a new Nature Inspired Metaheuristic Algorithm with Deep Learning for Healthcare Data Analysis (NIMADL-HDA) technique. The NIMADL-HDA technique examines healthcare data to recognize and classify CVD. In the presented NIMADL-HDA technique, Z-score normalization is initially performed to normalize the input data. In addition, the NIMADL-HDA technique makes use of a barnacle mating optimizer (BMO) for the feature selection (FS) process. For healthcare data classification, a convolutional long short-term memory (CLSTM) model can be employed. At last, the prairie dog optimization (PDO) algorithm can be exploited for the optimal hyperparameter selection process. The experimentation outcome analysis of the NIMADL-HDA methodology was tested on a benchmark healthcare dataset. Designed for healthcare data analysis, the NIMADL-HDA technique offers several key contributions:

• An automated NIMADL-HDA method including BMO-based feature subset selection, CLSTM-based classification, and PDO-based hyperparameter tuning has been proposed for CVD classification. To the best of our knowledge, the NIMADL-HDA method has never existed in the literature.

• BMO contributes to the model's efficacy by providing an optimum subset of applicable features for healthcare data analysis, thereby enhancing interpretability and reducing dimensionality.

• CLSTM captures the temporal dependency in healthcare information, which is crucial to analyzing medical sensor data or time-series patient information and improving the model's capability to recognize trends and patterns over time.

• PDO contributes to efficiently enhance the hyperparameters, which ensures the finetuning of the model for better performance on healthcare data.

2.   Related works

Khanna et al. ^[11] developed an innovative internet of things (IoT) and DL-permitted healthcare disease diagnosis (IoTDL-HDD) technique. This methodology uses a bidirectional long short term memory (BiLSTM) feature extraction model to remove valuable feature vectors from signals of electrocardiograms (ECG). To improve the efficacy of the BiLSTM model, the artificial flora optimization (AFO) methodology used hyperparameter optimization. Additionally, a fuzzy deep neural network (FDNN) classification algorithm was used to convey the appropriate class labels to signals of ECG. Rath et al. ^[12] identified appropriate DL and ML technologies and proposed and tested essential classification methods proposed. The Generative Adversarial Network (GAN) technique was selected by the main aim to handle imbalanced facts by creating and employing extra false information for recognition purposes. Additionally, an ensemble technique employing LSTM and GAN has been presented.

In ^[13], a Fog-based cardiac health recognition framework, termed FogDLearner, has been developed. FogDLearner uses spread resources to identify a person's cardiac health deprived of cooperating Quality of Service (QoS) and correctness. FogDLearner executes a DL based classification algorithm to forecast the cardiac health of the user. The planned structure is estimated on the PureEdgeSim simulator. In ^[14], a DL-based system, chiefly a convolutional neural network (CNN) with BiLSTM, was developed. The most appropriate features were only nominated through FS, which is skilled at ranking and choosing features that are extremely valued in the provided illness dataset. Afterwards, the CNN + BiLSTM-based hybrid DL technique was employed to forecast CVD.

Hussain et al. ^[15] developed a new DL architecture that employed one-dimensional CNNs to detect healthy and non-healthy individuals with balanced datasets to decrease the limits of the traditional ML model. Many medical parameters were utilized to estimate danger contour in patients, which were sustained in the initial analysis. Numerous regularization models were applied to avoid overfitting in the presented method. Bensenane et al. ^[16] projected a decision support system-based system (DSS) to create an analysis of CVD. It employed DL techniques that categorized ECG signals. Therefore, a dual-stage LSTM-based NN framework with ample pre-processing of ECG signals planned as an analysis-assisted method for cardiac arrhythmia recognition depends on an ECG signal study.

In ^[17], a smart healthcare method was proposed that employed ensemble DL and feature fusion techniques. First, the feature fusion model integrates removed features to make valuable healthcare information. Second, the data gain method removed irrelevant and redundant features. Additionally, the restricted prospect tactic calculated a precise feature load for every class. Lastly, the ensemble DL method was trained for heart illness forecast. Najafi et al. ^[18] presented an effectual and precise method that employed ANNs, FS, and multiple-criteria decision-making (MCDM) models. Suitable features were chosen by employing 5 FS models. Then, the three ANNs for the CVD forecast were applied. Furthermore, a Particle Swarm Optimizer (PSO) was utilized. A new combined weighting model that utilized the Best worst method (BWM) and the Method based on the Removal Effects of Criteria (MEREC) were developed.

The research gap in healthcare data classification highlights the urgent necessity for advanced methodologies in hyperparameter tuning and feature selection. Existing techniques often lack a comprehensive approach to address the intricate nature of healthcare datasets that are considered by diverse feature types and a high dimensionality. Insufficient attention to the feature selection method results in interpretability and a sub-optimal model performance. Moreover, the absence of systematic hyperparameter tuning hampers the capability of models to adapt to the unique features of healthcare information, which limits the generalization over different healthcare scenarios. Connecting this gap needs the development of robust methods that incorporates advanced hyperparameter tuning strategies and efficient FS mechanisms, which ensures the creation of interpretable and accurate healthcare classification techniques that are crucial for informed medical decision-making.

3.   The proposed model

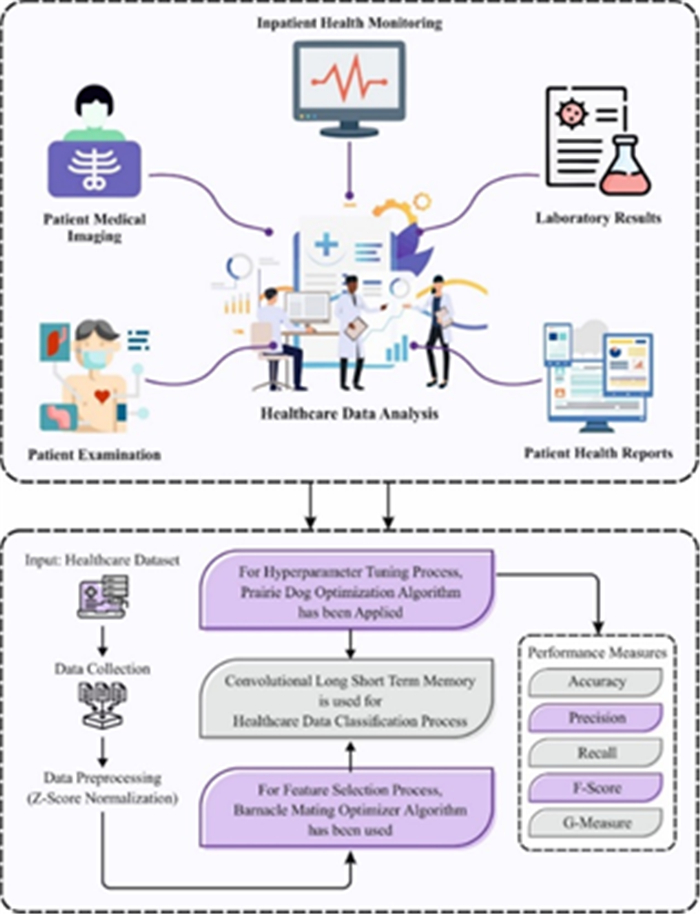
In this research, we focus on the development of the NIMADL-HDA technique. The NIMADL-HDA technique examines healthcare data to recognize and classify CVD. The presented NIMADL-HDA technique is comprised of Z-score normalization, BMO-based FS, CLSTM-based recognition, and PDO-based hyperparameter tuning. Figure 1 exemplifies the workflow of the NIMADL-HDA technique.

Figure 1.  Workflow of NIMADL-HDA technique.

DownLoad: Full-Size Img PowerPoint

3.1.   Z-score normalization

Z-score normalization is also recognized as a standardization technique. It is a statistical model that is employed to change and rescale information by conveying every data point's value in terms of standard deviations from the mean of the dataset. This procedure includes deducting the mean of a dataset from every data point and separating the result by the standard deviation (SD). The resultant z-scores offer a standardized measure of how many SDs a specific data point is from the mean. Z-score normalization is usually used in many areas, such as ML and statistics, to ensure that variables with dissimilar measures and units are on a similar scale, thus simplifying meaningful contrasts and analyses through various datasets.

3.2.   BMO based feature selection

In this stage, the NIMADL-HDA technique makes use of BMO for the FS process. Barnacles generally originate and strongly fuse to solid matter such as ships, rocks, corals, and even sea turtles ^[19]. They are hermaphroditic animals which contain both male and female reproduction methods. One of the exclusive features of barnacles is their penis size, which stretches numerous times when equated to the span of their body (7 to 8 times).

The mating performance of barnacles occurs in dual methods such as normal copulation and a sperm‐cast. The male barnacle will hit the female barnacle for normal copulation and then the mating procedure occurs. The sperm cast takes place to reproduce insulated barnacles. This is completed by liquidating fertilized eggs into the aquatic environment. This performance produces novel offspring that become a vision in an overview of BMO to crack optimization difficulties.

Comparable to other evolutionary methods such as a genetic algorithm (GA), BMO utilizes the same technique to have the selection procedure of parents reproduced to generate novel offspring. However, the method of the answer is dissimilar when equaled to the GA, which is deprived of employing any familiar range such as a tournament, roulette wheels, and much more. The assortment process for the reproduced barnacle's parents is completed depending on the simplification instructions mentioned below:

• Barnacles are generally recognized as hermaphroditic animals and denote those female barnacles capable of being composted by many male barnacles; it is expected one other barnacle reproduces each barnacle. It mainly evades the algorithm's difficulty.

• The value of $pl$ is required to be usual by the user; a collection of the barnacle's parents is complete arbitrarily. A value of $pl$ is a control parameter in which the consumer can attain noble optimizer outcomes away from the amount of barnacles and the maximal iterations.

• The Hardy‐Weinberg model employed in an assortment of the barnacle's parents is inside the array of $pl$. Otherwise, the sperm‐cast procedure is executed to gain novel offspring.

3.2.1.   Barnacles' new off‐springs generation

The group of novel offspring is directed by a standard of Hardy-Weinberg's idea. The description is measured by Eqs (1) and (2):

where $k = |barnacI{e}_{-}m-barncI{e}_{-}d|,$ $p$ refers to a usually dispersed pseudo-random amount, $q = (1-p),$ and ${x}_{barnacl{e}_{-}m}^{N}$ and ${x}_{barnacl{e}_{-}d}^{N}$ denote randomly selected variables for the barnacle's parents (Mum and Dad), correspondingly. $rand\left(\right)$ signifies a random amount array between zero to one $\left(0\sim 1\right)$. By mentioning these equations, $p$ and $q$ signify the inheritance percentage from the individual barnacle's parents. For instance, let's say $p$ is produced to be 0.80. It specifies that the novel offspring receive 80% of Mum's features and 20% of Dad's features. Eq (1) is essentially preserved as an optimizing exploitation procedure, whereas Eq (2) is preserved as an exploration procedure of the advanced BMO. Additionally, it is valuable to remark that the exploration procedure (sperm‐cast) is only related to the barnacle's mum, and the expected sperm is unconstrained from other barnacles.

3.2.2.   Sorting best barnacles

In case of classification among the barnacles, many populaces get folded from the primary populace. Similar to the GA procedure, the BMO too requires a sorting procedure. In this procedure, the optimal outcome for a definite iteration is found at the top of the doubled populace. Then, it is measured for the next generation whereas the bottom half is dead.

When it comes to designing an optimization approach, the fitness function (FF) remains the key feature that must be taken into account ^[20]. Both the objectives must be considered while assessing a solution; meanwhile, FS is a multi-objective optimization issue. The fitness of the feature subset can be defined by the classifier accuracy (maximum) and the number of features selected (minimum). The most common approach for multi‐objective formulation is aggregation. In the proposed technique, the main aim is combined into a solitary objective; therefore, the present load recognizes every objective importance:

In Eq (3), the fitness value of a subset $X$ is represented as the $Fitness\left(X\right),$ t classifier error rate by applying features selected in the $X$ subset, which is denoted by $E\left(X\right)$. The number of features selected and original features in the dataset are $\left|R\right|$ and $\left|N\right|$, respectively, and $\alpha \in \left[\mathrm{0, 1}\right]$ and $\beta = \left(1-\alpha \right)$ are the weights of the classifier error and the reduction ratio of $\alpha$ and $\beta$, respetively. The solution representation is an additional factor that must be taken into account when designing an optimization approach to address the FS problems. In this study, the feature subset is characterized by a binary vector of $N$ components, where the overall amount of features in a unique dataset is represented as $N$. Every dimension has a binary value ($0$ or $1$), where 1 specifies that the corresponding feature is selected and 0 denotes that it is not selected.

3.3.   Classification using CLSTM model

For healthcare data classification, the CLSTM model can be employed. The CLSTM is different from the LSTM network, which handles data communication within the cell over gates, namely forget $\left({f}_{t}\right)$, input $\left({i}_{t}\right)$, and output $\left({o}_{t}\right)$ ^[21]. The discrete gates switch information to join and upgrade the in cell state (CS), which selectively hold or remove information via gates. If the input gate is activated, then the input will be gathered into a cell. If the forget gate starts, then the preceding CS is forgotten. The output gate organizes if the cell output is conveyed to the last hidden layer (HL). CLSTM completely varies from LSTM because it uses convolution processes rather than matrix multiplication in the "input‐to‐state", as well as "state‐to‐state" fragments and its inputs ${X}_{1}, \dots, {X}_{t}$, unit outputs ${C}_{1}, \dots, {C}_{t}$, and HL ${\mathcal{H}}_{1}, \dots, {\mathcal{H}}_{i}$; the forget gate $\left({f}_{t}\right)$, the input gate (i), and the output gate (o) are entirely three-dimensional tensors. The benefit of this technique is that it can eliminate a huge amount of spatial terminated features and resolve the problem of the time requirement of information, thereby removing spatial information to understand the joint forming of the time and spatial data. Figure 2 depicts the framework of CLSTM.

Figure 2.  Architecture of CLSTM.

DownLoad: Full-Size Img PowerPoint

The transfer relations among every CLSTM gate are exposed by Eq (4), whereas ${I}_{t}$ denotes the input gate, ${f}_{t}$ denotes the forget gate, ${C}_{t}$ signifies the cell state, ${o}_{t}$ represents the output gate, ${\mathcal{H}}_{t}$ represents the HL output, "*" symbolizes the convolution operator, $"\mathrm{◯}"$ embodies the Hadamard product, and $\sigma$ represents the sigmoid activation function. Eq (4) shows the formula for this initiation function. The CLSTM technique employs a peephole LSTM construction based on the number of peeps that utilizes the cells to compute the forgotten and input doors so as to hold the data. The forget gate controls and removes the information that is redundantly measured, recollects the beneficial data and then transfers it back. The sustained information arrives at the input gate, information to be upgraded is defined via the sigmoid layer, and novel cell information is obtained via the $\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}$ layer to upgrade the cell. At last, the final output of the CLSTM part is obtained by multiplying the sigmoid information in the output gate with the memory cell data via $tanh$.

3.4.   Hyperparameter tuning

At last, the PDO algorithm can be exploited for the optimal hyperparameter selection process. The PDO algorithm chooses the following hyperparameters: learning rate, number of epochs, and batch size. The PDO technique is an optimization algorithm that pretends to search the activity of prairie dogs (PD) ^[22]. PD is involved in social actions such as hunting, constructing caves, preserving caves, and protection against hunters every day. Therefore, depending on the daily actions of PD, a PDO technique is separated into 4-time stages. Then, we separate the exploitation and exploration depending on a fixed mirror existence.

3.4.1.   Population initialization

The hunting action of every PD is symbolized by $1\times \mathrm{ }\mathrm{d}\mathrm{i}\mathrm{m}$ in the spatial dimension. To avert PD from opposing their trajectory, upper‐bound is represented by $UB$ and lower‐bound is represented by $LB$ to limit the movement range of PD. The set of every PD in dissimilar places is an optimal solution to a problem.

3.4.2.   Exploration stage

During the first period, the location of PD in foraging actions is connected to food sources $\rho$, current excellence of food, and location of arbitrarily created PDs. $\rho$ is a fixed food source alarm at 0.1 Khz. In a calculated method, the quality of existing food is definite as the efficiency of estimation presently acquired the finest solution $eCBes{t}_{i, j}$. The position of a randomly created PD is defined as the random collective effect $CP{D}_{i, j}$. The calculation expression is shown below:

where $GBes{t}_{i, j}$ is the global optimum solution gained so far, $\Delta$ is a very small number that represents variances among PD, and $rP{D}_{ij}$ denotes positions of random solution. Therefore, an equation to upgrade the position of PD searching for food is mentioned below:

From the above expression, Levy represents a Levy distribution with intermittent jumps. After discovering novel food sources, PD's dig and construct new caves around them. At this time, the position of the PD is connected to their dig force DS of caves. The upgraded equation for the DS is mentioned below:

where $r$ is converted among ‐l and 1 according to the equivalence of the present iteration number, $t$ denotes the current iteration number, and $T$ refers to the maximal iteration number. During the second period, Eq (10) displays an upgrade in a location of PD

3.4.3.   Exploitation stage

During 3rd time stage, PD refers to the excellence of the present food source $\varepsilon$ and the increasing effect of all PDs to arbitrarily upgrade their locations. In the calculated method, the quality of the existing food source $\varepsilon$ is a small number labeled as the quality of the food source. The procedure for upgrading the location of PD is shown below:

where rand represents a random number amongst $0$ and 1. During the foraging procedure of PDs, predators frequently attack them. Therefore, a predator attack is described as a predatory effect of PE. The $PE$ calculation equation is given below:

Upgrade the position of PD during the 4th period in Eq (13):

The novel PDO technique mimics the performance of PDs in hunting, digging, and avoiding natural enemies, thus separating the performance of PDs into 4 time periods, where $\rho$ refers to the food sources alarm, $CP{D}_{i, j}$ is a cumulative effect of all PDs, DS signifies the strength of burrowing, $\varepsilon$ is quality of the food sources, and PE denotes the predatory effect of predators regularly apprising the location to discover improved food sources. Eq (14) reviews the upgraded positions of PDs at four time periods.

The fitness selection is a significant factor that influences the performance of the PDO method. The hyperparameter selection procedure includes a solution encoding model to estimate the efficiency of candidate solutions. In this work, the PDO methodology reflects the accurateness as the main standard to design FF as expressed below:

where TP represents a true positive and FP represents a false positive value.

4.   Result analysis and discussions

In this section, the healthcare data classification result of the NIMADL-HDA technique will be examined in detail. The NIMADL-HDA technique was tested using a healthcare dataset ^[23], which combines the Cleveland, Hungarian, Switzerland, Long Beach, and Stalog Heart datasets. Table 1 represents the details of a database.

Table 1.  Details on database.

Classes	No. of Instances
Normal	561
Disease Affected	629
Total Number of Instances	1190

---

 | Show Table

DownLoad: CSV

Figure 3 validates the confusion matrices formed by the NIMADL-HDA model undernumerous epochs. The results suggest that the NIMADL-HDA method has an effective detection of normal and disease-affected classes.

Figure 3.  Confusion matrices of NIMADL-HDA technique (a-f) Epochs 500–3000.

DownLoad: Full-Size Img PowerPoint

Table 2 and Figure 4 report the general disease detection results of the NIMADL-HDA method under varying numbers of epochs. The results show that the NIMADL-HDA model properly recognize normal and disease-affected samples.

Figure 4.  Disease detection outcome of NIMADL-HDA technique (a-f) Epochs 500–3000.

DownLoad: Full-Size Img PowerPoint

Table 2.  Disease detection outcome of NIMADL-HDA technique under various epochs.

Class	Accuracybal	Precision	Recall	F-Score	G-Measure
Epoch-500
Normal	99.11	99.29	99.11	99.20	99.20
Disease Affected	99.36	99.21	99.36	99.29	99.29
Average	99.24	99.25	99.24	99.24	99.24
Epoch-1000
Normal	99.29	99.46	99.29	99.38	99.38
Disease Affected	99.52	99.37	99.52	99.44	99.44
Average	99.41	99.41	99.41	99.41	99.41
Epoch-1500
Normal	99.29	99.11	99.29	99.20	99.20
Disease Affected	99.21	99.36	99.21	99.28	99.28
Average	99.25	99.24	99.25	99.24	99.24
Epoch-2000
Normal	98.93	99.28	98.93	99.11	99.11
Disease Affected	99.36	99.05	99.36	99.21	99.21
Average	99.15	99.17	99.15	99.16	99.16
Epoch-2500
Normal	99.29	99.64	99.29	99.46	99.46
Disease Affected	99.68	99.37	99.68	99.52	99.52
Average	99.48	99.50	99.48	99.49	99.49
Epoch-3000
Normal	98.75	99.82	98.75	99.28	99.28
Disease Affected	99.84	98.90	99.84	99.37	99.37
Average	99.30	99.36	99.30	99.33	99.33

---

 | Show Table

DownLoad: CSV

In Figure 5, an average detection result of the NIMADL-HDA technique is portrayed under a varying number of epochs. The obtained values highlight that the NIMADL-HDA technique properly accomplishes a classification performance. With 500 epochs, the NIMADL-HDA technique gains an average $acc{u}_{bal}$ of 99.24%, $pre{c}_{n}$ of 99.25%, $rec{a}_{l}$ of 99.24%, ${F}_{score}$ of 99.24%, and ${G}_{measure}$ of 99.24%. Meanwhile, with 1500 epochs, the NIMADL-HDA methodology gains an average $acc{u}_{bal}$ of 99.25%, $pre{c}_{n}$ of 99.24%, $rec{a}_{l}$ of 99.25%, ${F}_{score}$ of 99.24%, and ${G}_{measure}$ of 99.24%. Besides, with 2500 epochs, the NIMADL-HDA method gains an average $acc{u}_{bal}$ of 99.48%, $pre{c}_{n}$ of 99.50%, $rec{a}_{l}$ of 99.48%, ${F}_{score}$ of 99.49%, and ${G}_{measure}$ of 99.49%. At last, with 3000 epochs, the NIMADL-HDA method gains an average $acc{u}_{bal}$ of 99.30%, $pre{c}_{n}$ of 99.36%, $rec{a}_{l}$ of 99.30%, ${F}_{score}$ of 99.33%, and ${G}_{measure}$ of 99.33%.

As shown in Figure 6, the training and validation accuracy curves of the NIMADL-HDA method below epoch-2500 deliver valuable insights into the performance of the NIMADL-HDA approach over multiple epochs. These curves highlight the vital insights into the learning procedure and the model's ability to simplify. Additionally, it is noticeable that there is a consistent development in training (TR) and testing (TS) accurateness over increasing epochs. Moreover, the model's capability to learn and identify patterns within both TR and TS datasets is highlighted. The growing testing accurateness recommends that the model not only adjusts to the training data, but also excels in creating precise forecasts on before-hidden data, thus highlighting its robust generalization abilities.

Figure 5.  Average outcome of NIMADL-HDA technique under various epochs.

DownLoad: Full-Size Img PowerPoint

Figure 6.  $Acc{u}_{y}$ curve of NIMADL-HDA technique under epoch 2500.

DownLoad: Full-Size Img PowerPoint

In Figure 7, we signify an inclusive view of TR and TS loss values for the NIMADL-HDA methodology under epoch-2500. The TR loss progressively decreases as the model enhances its weights to reduce classification errors on both the TR and TS datasets. These loss curves offer a perfect picture of how well the model supports the training data, thus highlighting its aptitude to professionally hold patterns in both datasets. It is valuable to note that the NIMADL-HDA model constantly enhances its parameters to diminish discrepancies between predictions and genuine training labels.

Figure 7.  Loss curve of NIMADL-HDA technique under epoch 2500.

DownLoad: Full-Size Img PowerPoint

With respect to the precision-recall (PR) curve, as assumed in Figure 8, the results confirm that the NIMADL-HDA approach under epoch-2500 gradually achieves greater PR values through each class. The results highlight the effective capability of the model to discriminate dissimilar classes, thus highlighting its efficiency in the detection of class labels.

Figure 8.  PR curve of NIMADL-HDA technique under epoch 2500.

DownLoad: Full-Size Img PowerPoint

In Figure 9, we present Receiver Operating Characteristic (ROC) curves formed by the NIMADL-HDA model under epoch-2500, which is best at distinguishing between classes. These curves offer valuable insights into the balance among TPR and FPR across dissimilar classification thresholds and epochs. The outcomes highlight the precise classification performance below dissimilar class labels, thus underlining its performance in tackling dissimilar classification tasks.

Figure 9.  ROC curve of NIMADL-HDA technique under epoch 2500.

DownLoad: Full-Size Img PowerPoint

Table 2 reports a detailed comparison study of the NIMADL-HDA technique with other models ^[24,25,26]. In Figure 10, a comparative result of NIMADL-HDA methodology is reported in terms of $acc{u}_{y}$. Based on $acc{u}_{y}$, the results indicate that the NIMADL-HDA model extents a higher $acc{u}_{y}$ of 99.48%, while the ACVD-HBOMDL, SC, J48, ANN, Bagging, REPTree, and SVM models obtain lower $acc{u}_{y}$ values of 99.39%, 98.86%, 97.60%, 95.55%, 94.99%, 92.91%, and 84.49%, respectively.

Table 3.  Comparative outcome of NIMADL-HDA approach with other methods ^[24,25,26].

Methods	Accuracy	Precision	Recall	F-Score
NIMADL-HDA	99.48	99.50	99.48	99.49
ACVD-HBOMDL	99.39	99.44	99.39	99.41
SC Algorithm	98.86	98.42	97.60	98.12
J48 Algorithm	97.60	97.52	98.42	98.21
ANN Algorithm	95.55	95.16	94.85	95.27
Bagging Algorithm	94.99	94.38	94.69	94.42
REPTree Algorithm	92.91	92.92	92.47	93.18
SVM Algorithm	84.49	84.95	83.95	83.99

---

 | Show Table

DownLoad: CSV

Figure 10.  $Acc{u}_{y}$ outcome of NIMADL-HDA approach with other methods.

DownLoad: Full-Size Img PowerPoint

In Figure 11, a comparative result of the NIMADL-HDA model is conveyed in terms of $pre{c}_{n}$, $rec{a}_{l}$, and ${F}_{score}$. Depending on $pre{c}_{n}$, the results designate that the NIMADL-HDA model attains a greater $pre{c}_{n}$ of 99.50%, while the ACVD-HBOMDL, SC, J48, ANN, Bagging, REPTree, and SVM techniques attain lower $pre{c}_{n}$ values of 99.44%, 98.42%, 97.52%, 95.16%, 94.38%, 92.92%, and 84.95%, respectively. Besides, based on $rec{a}_{l}$, the results show that the NIMADL-HDA methodology reached an advanced $rec{a}_{l}$ of 99.48%, while the ACVD-HBOMDL, SC, J48, ANN, Bagging, REPTree, and SVM methods acquired lower $rec{a}_{l}$ values of 99.39%, 97.60%, 98.42%, 94.85%, 94.69%, 92.47%, and 83.95%, respectively. Lastly, based on ${F}_{score}$, the results indicate that the NIMADL-HDA model reached a higher ${F}_{score}$ of 99.49%, while the ACVD-HBOMDL, SC, J48, ANN, Bagging, REPTree, and SVM models acquired lower ${F}_{score}$ values of 99.41%, 98.12%, 98.21%, 95.27%, 94.42%, 93.18%, and 83.99%, respectively.

Figure 11.  Comparative outcome of NIMADL-HDA approach with other methods ^[24,25,26].

DownLoad: Full-Size Img PowerPoint

We have carried out an experiment to ensure the performance enhancement made by feature selection and the hyperparameter tuning process. The overall results of the NIMADL-HAD technique (with FS and hyperparameter tuning) with BMOA-CLSTM (without FS) and CLSTM (without FS and hyperparameter tuning) are depicted in Table 4 and Figure 12, respectively. The results indicate that the NIMADL-HDA model outperforms the other ones with a maximum performance due to the integration of the FS and hyperparameter tuning process.

Table 4.  Comparative outcome of NIMADL-HDA approach with CLSTM and BMOA-CLSTM model.

Measures (%)
Models	Accuracy	Precision	Recall	F-Score
NIMADL-HDA	99.48	99.50	99.48	99.49
BMOA-CLSTM	98.76	98.89	98.65	98.32
CLSTM	97.15	98.08	97.12	97.96

---

 | Show Table

DownLoad: CSV

Figure 12.  Comparative outcome of NIMADL-HDA approach before and after FS with hyperparameter tuning process.

DownLoad: Full-Size Img PowerPoint

The NIMADL-HDA method excels over existing techniques in healthcare data analyses due to its innovative incorporation of bio-inspired optimization techniques, adaptive FS using the BMO, the CLSTM-based classifier, and effective hyperparameter tuning with the PDO method. Thus, the NIMADL-HDA technique can be applied for enhanced detection processes in the healthcare environment.

5.   Conclusions

In this paper, we focused on the design and improvement of the NIMADL-HDA technique. The NIMADL-HDA technique examines healthcare data to recognize and classify CVD. The presented NIMADL-HDA technique is comprised of Z-score normalization, BMO-based FS, CLSTM-based detection, and PDO-based hyperparameter tuning. In the developed NIMADL-HDA technique, Z-score normalization was initially performed to normalize the input data. In addition, the NIMADL-HDA technique made use of a BMO-based FS process. For healthcare data classification, the CLSTM model was employed. Finally, a PDO algorithm was exploited to optimize the hyperparameter selection procedure. An experimental result analysis of the NIMADL-HDA technique was tested on a benchmark healthcare dataset. The acquired outcomes stated that the NIMADL-HDA technique reached an effectual performance over other models.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work, under the General Research Funding program grant code (NU/DRP/SERC/12/23).

Conflict of interest

The authors declare that they have no conflict of interest. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.