$ M- $truncated optical soliton and their characteristics to a nonlinear equation governing the certain instabilities of modulated wave trains

Abdullahi Yusuf; Tukur A. Sulaiman; Mustafa Inc; Sayed Abdel-Khalek; K. H. Mahmoud; Abdullahi Yusuf; Tukur A. Sulaiman; Mustafa Inc; Sayed Abdel-Khalek; K. H. Mahmoud

doi:10.3934/math.2021535

AIMS Mathematics

2021, Volume 6, Issue 9: 9207-9221. doi: 10.3934/math.2021535

Previous Article Next Article

Research article Special Issues

$M-$ truncated optical soliton and their characteristics to a nonlinear equation governing the certain instabilities of modulated wave trains

1.
Department of Computer Engineering, Biruni University, Istanbul, Turkey
2.
Department of Mathematics, Federal University Dutse, Jigawa, Nigeria
3.
Department of Mathematics, Science Faculty, Firat University Elazig, Turkey
4.
Department of Medical Research, China Medical University Hospital, China Medical University, 40402 Taichung, Taiwan
5.
Department of Mathematics, College of Science, P.O. Box 11099, Taif University, Taif 21944, Saudi Arabia
6.
Department of Physics, College of Khurma University College, Taif University, P.O. Box11099, Taif 21944, Saudi Arabia

Received: 11 December 2020 Accepted: 20 May 2021 Published: 21 June 2021
MSC : 35A09, 35E05

This study investigates the nonlinear Hamiltonian amplitude equation by using two analytical techniques, namely; the extended sinh-Gordon equation expansion method, and the extended rational sine-cosine/sinh-cosh methods. Some important wave solutions are successfully constructed, such as dark, bright, combined dark-bright, singular solitons, periodic and singular periodic wave solutions. The physical features of the acquired solutions are plotted to depict the clear dynamical behaviour of the reported results. All the acquired solutions have satisfied the original equation.

Keywords:

Hamiltonian amplitude equation,
extended sinh-Gordon method,
extended rational sine-cosine/sinh-cosh,
optical solitons,
M-truncated derivative

Citation: Abdullahi Yusuf, Tukur A. Sulaiman, Mustafa Inc, Sayed Abdel-Khalek, K. H. Mahmoud. $M-$ truncated optical soliton and their characteristics to a nonlinear equation governing the certain instabilities of modulated wave trains[J]. AIMS Mathematics, 2021, 6(9): 9207-9221. doi: 10.3934/math.2021535

Related Papers:

[1]	Chun Huang, Zhao Li . New soliton solutions of the conformal time derivative generalized $ q $-deformed sinh-Gordon equation. AIMS Mathematics, 2024, 9(2): 4194-4204. doi: 10.3934/math.2024206
[2]	Khalid K. Ali, Mohamed S. Mohamed, M. Maneea . Exploring optical soliton solutions of the time fractional q-deformed Sinh-Gordon equation using a semi-analytic method. AIMS Mathematics, 2023, 8(11): 27947-27968. doi: 10.3934/math.20231429
[3]	Junjie Li, Gurpreet Singh, Onur Alp İlhan, Jalil Manafian, Yusif S. Gasimov . Modulational instability, multiple Exp-function method, SIVP, solitary and cross-kink solutions for the generalized KP equation. AIMS Mathematics, 2021, 6(7): 7555-7584. doi: 10.3934/math.2021441
[4]	Abeer S. Khalifa, Hamdy M. Ahmed, Niveen M. Badra, Wafaa B. Rabie, Farah M. Al-Askar, Wael W. Mohammed . New soliton wave structure and modulation instability analysis for nonlinear Schrödinger equation with cubic, quintic, septic, and nonic nonlinearities. AIMS Mathematics, 2024, 9(9): 26166-26181. doi: 10.3934/math.20241278
[5]	Mahmoud Soliman, Hamdy M. Ahmed, Niveen Badra, Taher A. Nofal, Islam Samir . Highly dispersive gap solitons for conformable fractional model in optical fibers with dispersive reflectivity solutions using the modified extended direct algebraic method. AIMS Mathematics, 2024, 9(9): 25205-25222. doi: 10.3934/math.20241229
[6]	Mahmoud Soliman, Hamdy M. Ahmed, Niveen Badra, M. Elsaid Ramadan, Islam Samir, Soliman Alkhatib . Influence of the $ \beta $-fractional derivative on optical soliton solutions of the pure-quartic nonlinear Schrödinger equation with weak nonlocality. AIMS Mathematics, 2025, 10(3): 7489-7508. doi: 10.3934/math.2025344
[7]	Abdul Mateen, Ghulam Hussain Tipu, Loredana Ciurdariu, Fengping Yao . Analytical soliton solutions of the Kairat-Ⅱ equation using the Kumar–Malik and extended hyperbolic function methods. AIMS Mathematics, 2025, 10(4): 8721-8752. doi: 10.3934/math.2025400
[8]	Azzh Saad Alshehry, Safyan Mukhtar, Ali M. Mahnashi . Optical fractals and Hump soliton structures in integrable Kuralay-Ⅱ system. AIMS Mathematics, 2024, 9(10): 28058-28078. doi: 10.3934/math.20241361
[9]	Emad H. M. Zahran, Omar Abu Arqub, Ahmet Bekir, Marwan Abukhaled . New diverse types of soliton solutions to the Radhakrishnan-Kundu-Lakshmanan equation. AIMS Mathematics, 2023, 8(4): 8985-9008. doi: 10.3934/math.2023450
[10]	Ahmed M. Elsherbeny, Taher A. Nofal, Yakup Yıldırım, Ahmed H. Arnous . New solitary waveforms and their dynamics in the stochastic generalized Chen–Lee–Liu model. AIMS Mathematics, 2025, 10(3): 5197-5235. doi: 10.3934/math.2025239

Abstract

1. Introduction

A key practice in nonlinear physics has been the study of both the formation and interaction of localized waves, including plasma physics, fluid dynamics, Bose-Einstein condensates and photonics, over the last few decades. Among different types of nonlinaer localized waves, solitons are the most representative and ideal testbed to investigate nonlinear wave interactions due to their intrinsic particle-like properties during propagation ^[1,2]. The position and phase shift interaction-induced displacement is typically independent of the relative phases of the solitons in the envelope. The dynamics of collisions in the region of interaction, however, depend strongly on the relative levels. The wave magnitude then evolves at the central collision point from the sum of the amplitudes of the two solitons to their distinction, respectively. A wide range of theoretical theories, computational simulations and experimental observations have already been recorded for such interactions with solitons and their possible synchronization ^[3,4,5]. In general, nonlinear Evolution Equations (NLEEs) are used to model social processes and structures of natural phenomena. In various fields of science and engineering, nonlinear wave phenomena exist, including fluid mechanics, chemical dynamics, plasma physics, solid-state physics, nonlinear optics, and population models. In nonlinear science, the precise wave outcomes of NLEEs play a crucial role, since they give us a lot of insight into the physical characteristics of the problem and can provide more physical details to support additional applications. In recent years, people have been fascinated by the precise and numerical solutions of NLEEs since they are increasingly becoming more used in various scientific fields to explain complex nonlinear phenomena. Via differential equations, some real-world problems are converted into mathematical equations.

The quest for soliton outcomes has been of significant importance in the understanding of nonlinear phenomena in recent years. Soliton's theory has been strengthened in recent decades in order to explain the meaning of impossibility in ordinary and partial differential equations ^{[6,7,8,9,10,11,12,13,14]}. The nonlinear Schrödinger equation (NLSEs) has been studied in various equations to demonstrate Soliton propagating molecules in an optical fiber, which has a variety of physical applications especially in plasma physics and nonlinear optics. There are several variants of the NLSEs; these forms, such as Kaup-Newell, Chen-Lee-Liu, and Gerdjikov-Ivanov equations, are the recently determined forms. The equation Kaup-Newell ^[15] has various forms. The equations can be modified to each other by Guage transformation ^[16]. Transformations can not sustain the reduction in the dispersion issue ^{[17,18,19,20]}. Conditions and integrations are highly dynamic and cannot be precisely planned. They need impartial investigation, therefore. In order to overcome these categorized NLSEs, a large number of numerical and exact moving wave mathematical schemes have been identified ^{[21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]}.

In this paper we consider the Hamiltonian amplitude equation with the M-truncated order " $\mu$ " given by ^[44]

$\begin{equation} i \mathscr{D}_{M, x}^{\mu, \zeta}\chi+\mathscr{D}_{M, t}^{2\mu, \zeta}\chi-2\sigma |\chi|^{2}\chi-\delta \mathscr{D}_{M, t}^{\mu, \zeta}\mathscr{D}_{M, x}^{\mu, \zeta}\chi_{xt} = 0,\;\;\;0 < \mu\le 1, \end{equation}$

(1.1)

where $\sigma\pm 1$ is the coefficient of the nonlinear term, $\delta < 1$ is the coefficients of the dispersionless term, $\zeta$ is a nonzero real number, and $\mathscr{D}_{M, *}^{\mu, \zeta}\chi$ represents the truncated $M$ -fractional derivative of $\chi$ with respect to $x$ and/or $t$ . Non-linearity arises when the change of the output is not proportional to the change of the input. Dispersion means that waves of different wavelength propagate at different phase velocities. The phase velocity of a wave is the rate at which the wave propagates in some medium. This is the velocity at which the phase of any one frequency component of the wave travels. Studies have shown that when the dispersion effect and nonlinear effect of the medium reach a stable equilibrium, the pulse can maintain its shape and velocity in the form of solitons during the transmission process ^[45].

Equation (1.1) was introduced in ^[46]. The term $\chi(x, t)$ is the unknown complex envelope function of $x$ and $t$ . This equation governs certain instabilities of modulated wave trains; the addition of the term $-\delta\chi_{xt}$ overcomes the ill-posedness of the unstable NLSEs. The equation is apparently not integrable, but a Hamiltonian analogue of the Kuramoto–Sivashinsky equation, which arises in dissipative system.

2. Applications

Here, we acquire the optical solitons of the Hamiltonian amplitude equation with M-truncated derivative by using the extended sinh-Gordon equation expansion method ^[47] and the and the extended rational sine-cosine/sinh-cosh methods ^[48].

Consider the following fractional wave transformation:

$\begin{equation} \begin{split} \chi(x,t) = \phi(\xi)e^{i\varphi},\;\;\xi = \frac{\eta \Gamma (\zeta +1) \left(q t^{\mu }+P x^{\mu }\right)}{\mu },\;\;\varphi = \frac{\Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }. \end{split} \end{equation}$

(2.1)

Plugging Eq (2.1) into (1.1), provides the following nonlinear ordinary differential equation

$\begin{equation} \begin{split} \eta ^2 q (\delta P-q)\phi''+2 \sigma\phi^{3}+(\rho ^2-\delta \rho r+r)\phi = 0 \end{split} \end{equation}$

(2.2)

from the real part, and the constraint condition

$\begin{equation} \begin{split} q = \frac{\delta \rho P-P}{2 \rho -\delta r}. \end{split} \end{equation}$

(2.3)

from the imaginary part.

2.1. Application of the extended sinh-Gordon equation expansion method

Here, we present the application of the extended sinh-Gordon equation expansion method to (1.1).

Balancing the terms $\phi''$ and $\phi^3$ , we get $n = 1$ . With $n = 1$ , we have the following test functions ^[47]:

$\begin{equation} \phi(\theta) = \gamma_{1}\sinh(\theta)+\lambda_{1}\cosh(\theta)+\lambda_{0}, \end{equation}$

(2.4)

$\begin{equation} \phi(\xi) = \pm \gamma_{1}\;i\;\rm{sech}(\xi)\pm \lambda_{1}\tanh(\xi)+\lambda_{0}, \end{equation}$

(2.5)

and

$\begin{equation} \phi(\xi) = \pm \gamma_{1}\;\rm{csch}(\xi)\pm \lambda_{1}\coth(\xi)+\lambda_{0}. \end{equation}$

(2.6)

Plugging Eq (2.4) and its second derivative alongside $\theta' = \sinh(\theta)$ into Eq (2.2), provides an equation with hyperbolic functions power. We collect a set of algebraic equations by equating each summation of the coefficients of the hyperbolic functions of the same power to zero. We simplify the set of algebraic equations and secured the values of the parameters involved. To reach the solutions of Eq (1.1), we substitute the values of the parameters into any of Eqs (2.5) and (2.6).

Ⅰ: For

$\lambda_0 = 0,\;\lambda_1 = -\frac{\sqrt{-\left(\rho ^2-\delta \rho r+r\right)}}{\sqrt{2} \sqrt{\sigma }},\;\gamma_1 = -\frac{\sqrt{-\left(\rho ^2-\delta \rho r+r\right)}}{\sqrt{2} \sqrt{\sigma }},\;\eta = -\frac{\sqrt{-2 \rho ^2+2 \delta \rho r-2 r}}{\sqrt{q (q-\delta P)}},$

we reveal the combined dark-bright soliton

$\begin{equation} \begin{split} \chi_{1.1}(x,t) = \frac{1}{2} \sqrt{\frac{|-2 \rho ^2+2 \delta \rho r-2 r|}{\sigma }} \Bigg(\tanh \left(\frac{\Gamma (\zeta +1) \sqrt{|-2 \rho ^2+2 \delta \rho r-2 r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)\\-i \rm{sech}\left(\frac{\sqrt{|-2 \rho ^2+2 \delta \rho r-2 r|} \left(\Gamma (\zeta +1) \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)\Bigg)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }} \end{split} \end{equation}$

(2.7)

and the combined singular soliton

$\begin{equation} \begin{split} \chi_{1.2}(x,t) = \frac{1}{2} \left(-\sqrt{\frac{|-2 \rho ^2+2 \delta \rho r-2 r|}{\sigma }}\right) \Bigg(-\coth \left(\frac{\Gamma (\zeta +1) \sqrt{|-2 \rho ^2+2 \delta \rho r-2 r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)\\-\rm{csch}\left(\frac{\Gamma (\zeta +1) \sqrt{|-2 \rho ^2+2 \delta \rho r-2 r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)\Bigg)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.8)

Ⅱ: For

$\lambda_0 = 0,\;\lambda_1 = 0,\;\gamma_1 = -\frac{\sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{\sigma }},\;\eta = -\frac{\sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{q (q-\delta P)}},$

we reveal the bright soliton

$\begin{equation} \begin{split} \chi_{2.1}(x,t) = -\sqrt{\frac{-\rho ^2+\delta \rho r-r}{\sigma }} \rm{sech}\left(\frac{\Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }} \end{split} \end{equation}$

(2.9)

and the singular soliton

$\begin{equation} \begin{split} \chi_{2.2}(x,t) = \sqrt{\frac{\rho ^2-\delta \rho r+r}{\sigma }} \rm{csch}\left(\frac{\Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.10)

Ⅲ: For

$\lambda_0 = 0,\;\lambda_1 = \frac{i \sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{2} \sqrt{\sigma }},\;;\gamma_1 = 0;\eta = \frac{\sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{2 \delta q P-2 q^2}},$

we get the dark soliton

$\begin{equation} \begin{split} \chi_{3.1}(x,t) = \sqrt{-\frac{\rho ^2-\delta \rho r+r}{2 \sigma }} \tanh \left(\frac{\Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{2 \delta P (\delta \rho P-P)}{2 \rho -\delta r}-\frac{2 (\delta \rho P-P)^2}{(2 \rho -\delta r)^2}\Big|}}\right)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }} \end{split} \end{equation}$

(2.11)

and the singular soliton

$\begin{equation} \begin{split} \chi_{3.2}(x,t) = \sqrt{-\frac{\rho ^2-\delta \rho r+r}{2 \sigma }} \coth \left(\frac{\Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{2 \delta P (\delta \rho P-P)}{2 \rho -\delta r}-\frac{2 (\delta \rho P-P)^2}{(2 \rho -\delta r)^2}\Big|}}\right)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.12)

2.2. Application of the extended rational sine-cosine/sinh-cosh methods

Here, we present the application of the extended rational sine-cosine/sinh-cosh methods to (1.1).

Consider the following as the first test function to Eq (2.2):

$\begin{equation} \begin{split} \phi(\xi) = \frac{\lambda_{0}\sin( \xi)}{\lambda_{2}+\lambda_{1}\cos(\xi)}. \end{split} \end{equation}$

(2.13)

Putting Eq (2.13) into Eq (2.2), provides a polynomial functions. Setting the coefficients of the powers of $\cos(\xi)$ gives a system of algebraic equations. Solving the set of algebraic equations provides the following set of values to the unknown coefficients:

Ⅰ: For

$\lambda_0 = -\frac{i \lambda_1 \sqrt{r (\delta \rho -1)-\rho ^2}}{\sqrt{2} \sqrt{\sigma }},\;\lambda_2 = 0,\;\eta = -\frac{\sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{2} \sqrt{q (q-\delta P)}},$

we reveal the singular periodic wave solution

$\begin{equation} \begin{split} \chi_{I}(x,t) = \sqrt{-\frac{r (\delta \rho -1)-\rho ^2}{2 \sigma }} \tan \left(\frac{\Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\sqrt{2} \mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.14)

Ⅱ: For

$\lambda_0 = \frac{i \lambda_1 \sqrt{r (\delta \rho -1)-\rho ^2}}{\sqrt{2} \sqrt{\sigma }},\;\lambda_2 = \lambda_1,\;\eta = -\frac{\sqrt{2} \sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{q (q-\delta P)}},$

we reveal the singular periodic wave solution

$\begin{equation} \begin{split} \chi_{II}(x,t) = -\frac{\sqrt{-\frac{r (\delta \rho -1)-\rho ^2}{2 \sigma }} \sin \left(\frac{\sqrt{2} \Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)}{\cos \left(\frac{\sqrt{2} \Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)+1}e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.15)

Consider the following as the second test function to Eq (2.2):

$\begin{equation} \begin{split} \phi(\xi) = \frac{\lambda_{0}\cos(\xi)}{\lambda_{2}+\lambda_{1}\sin(\xi)}. \end{split} \end{equation}$

(2.16)

Putting Eq (2.16) into Eq (2.2), provides a polynomial functions. Setting the coefficients of the powers of $\sin(\xi)$ gives a system of algebraic equations. Solving the set of algebraic equations provides the following set of values to the unknown coefficients:

Ⅰ: For

$\lambda_0 = -\frac{i \lambda_1 \sqrt{r (\delta \rho -1)-\rho ^2}}{\sqrt{2} \sqrt{\sigma }},\;\lambda_2 = 0,\;\eta = -\frac{\sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{2} \sqrt{q (q-\delta P)}},$

we reveal the singular periodic wave solution

$\begin{equation} \begin{split} \chi_{I}(x,t) = \sqrt{-\frac{r (\delta \rho -1)-\rho ^2}{\sigma }} \cot \left(\frac{\Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\sqrt{2} \mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.17)

Ⅱ: For

$\lambda_0 = -\frac{i \lambda_1 \sqrt{r (\delta \rho -1)-\rho ^2}}{\sqrt{2} \sqrt{\sigma }},\;\lambda_2 = \lambda_1,\;\eta = -\frac{\sqrt{2} \sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{q (q-\delta P)}},$

we reveal the singular periodic wave solution

$\begin{equation} \begin{split} \chi_{II}(x,t) = -\frac{\sqrt{-\frac{r (\delta \rho -1)-\rho ^2}{2 \sigma }} \cos \left(\frac{\sqrt{2} \Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)}{1-\sin \left(\frac{\sqrt{2} \Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)}e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.18)

Consider the following as the third test function to Eq (2.2):

$\begin{equation} \begin{split} \phi(\xi) = \frac{\lambda_{0}\sinh(\xi)}{\lambda_{2}+\lambda_{1}\cosh(\xi)}. \end{split} \end{equation}$

(2.19)

Putting Eq (2.19) into Eq (2.2), provides a polynomial functions. Setting the coefficients of the powers of $\cosh(\xi)$ gives a system of algebraic equations. Solving the set of algebraic equations provides the following set of values to the unknown coefficients:

Ⅰ: For

$\lambda_0 = \frac{\lambda_1 \sqrt{r (\delta \rho -1)-\rho ^2}}{\sqrt{2} \sqrt{\sigma }},\;\lambda_2 = 0,\;\eta = -\frac{\sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{2 \delta q P-2 q^2}},$

we reveal the dark soliton

$\begin{equation} \begin{split} \chi_{I}(x,t) = -\sqrt{\Big|\frac{r (\delta \rho -1)-\rho ^2}{2 \sigma }\Big|} \tanh \left(\frac{\Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{2 \delta P (\delta \rho P-P)}{2 \rho -\delta r}-\frac{2 (\delta \rho P-P)^2}{(2 \rho -\delta r)^2}\Big|}}\right)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.20)

Ⅱ: For

$\lambda_0 = -\frac{\lambda_1 \sqrt{r (\delta \rho -1)-\rho ^2}}{\sqrt{2} \sqrt{\sigma }},\;\lambda_2 = \lambda_1;\eta = -\frac{\sqrt{-2 \rho ^2+2 \delta \rho r-2 r}}{\sqrt{q (q-\delta P)}},$

we reveal the periodic wave solution

$\begin{equation} \begin{split} \chi_{II}(x,t) = \frac{\sqrt{\frac{r (\delta \rho -1)-\rho ^2}{2 \sigma }} \sinh \left(\frac{\Gamma (\zeta +1) \sqrt{|-2 \rho ^2+2 \delta \rho r-2 r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)}{\cosh \left(\frac{\Gamma (\zeta +1) \sqrt{|-2 \rho ^2+2 \delta \rho r-2 r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)+1}e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.21)

Consider the following as the fourth test function to Eq (2.2):

$\begin{equation} \begin{split} \phi(\xi) = \frac{\lambda_{0}\cosh(\xi)}{\lambda_{2}+\lambda_{1}\sinh(\xi)}. \end{split} \end{equation}$

(2.22)

Putting Eq (2.22) into Eq (2.2), provides a polynomial functions. Setting the coefficients of the powers of $\sinh(\xi)$ gives a system of algebraic equations. Solving the set of algebraic equations provides the following set of values to the unknown coefficients:

Ⅰ: For

$\lambda_0 = -\frac{\lambda_1 \sqrt{r (\delta \rho -1)-\rho ^2}}{\sqrt{2} \sqrt{\sigma }},\;\lambda_2 = 0;\eta = -\frac{\sqrt{\rho ^2-\delta \rho r+r}}{\sqrt{2 \delta q P-2 q^2}},$

we reveal the singular soliton

$\begin{equation} \begin{split} \chi_{I}(x,t) = \sqrt{\frac{r (\delta \rho -1)-\rho ^2}{2 \sigma }} \coth \left(\frac{\Gamma (\zeta +1) \sqrt{|\rho ^2-\delta \rho r+r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{2 \delta P (\delta \rho P-P)}{2 \rho -\delta r}-\frac{2 (\delta \rho P-P)^2}{(2 \rho -\delta r)^2}\Big|}}\right)e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.23)

Ⅱ: For

$\lambda_0 = \frac{\lambda_1 \sqrt{r (\delta \rho -1)-\rho ^2}}{\sqrt{2} \sqrt{\sigma }},\;\lambda_2 = -i \lambda_1,\;\eta = -\frac{\sqrt{-2 \rho ^2+2 \delta \rho r-2 r}}{\sqrt{q (q-\delta P)}},$

we reveal the periodic wave solution

$\begin{equation} \begin{split} \chi_{II}(x,t) = \frac{\sqrt{\frac{r (\delta \rho -1)-\rho ^2}{2 \sigma }} \cosh \left(\frac{\Gamma (\zeta +1) \sqrt{|-2 \rho ^2+2 \delta \rho r-2 r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)}{-\sinh \left(\frac{\Gamma (\zeta +1) \sqrt{|-2 \rho ^2+2 \delta \rho r-2 r|} \left(\frac{t^{\mu } (\delta \rho P-P)}{2 \rho -\delta r}+P x^{\mu }\right)}{\mu \sqrt{\Big|\frac{(\delta \rho P-P) \left(\frac{\delta \rho P-P}{2 \rho -\delta r}-\delta P\right)}{2 \rho -\delta r}\Big|}}\right)-i}e^{\frac{i \Gamma (\zeta +1) \left(r x^{\mu }+\rho t^{\mu }\right)}{\mu }}. \end{split} \end{equation}$

(2.24)

3. Physical interpretation

As it was presented in the preceding section, two analytical approaches were used in securing the optical solitons to the fractional Hamiltonian amplitude equation. To have a clear physical view to the features of the reported results in this study, numerical simulations are performed via the 3-dimensional and contour graphs by a careful choice of the parameters' values involved. The dynamics of the reported solutions is analyze based on the choice of the fractional values $\mu$ .

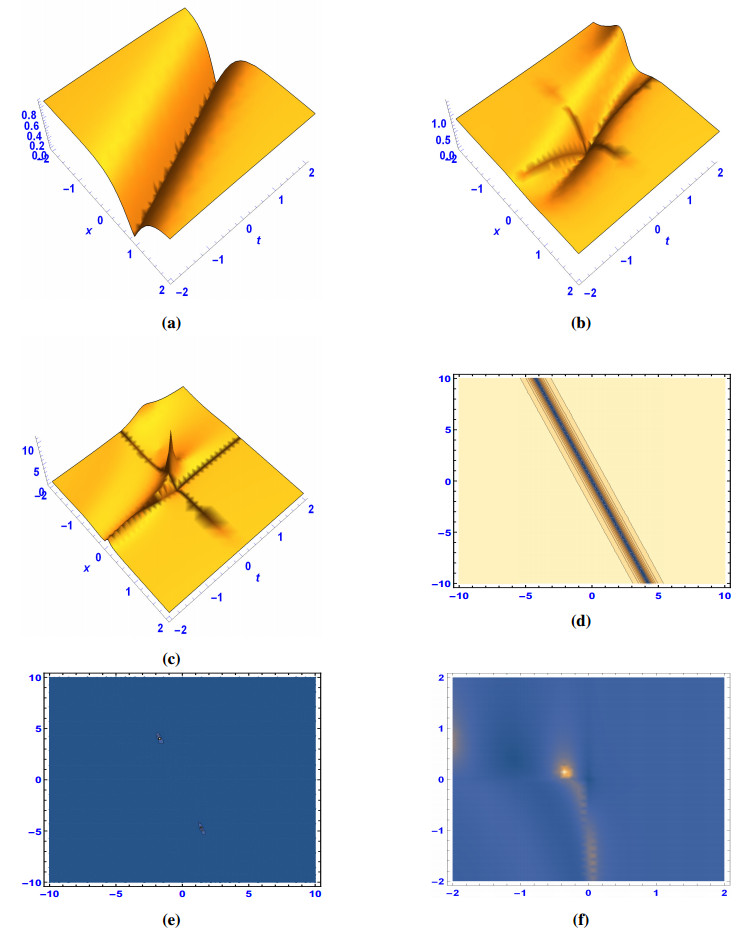
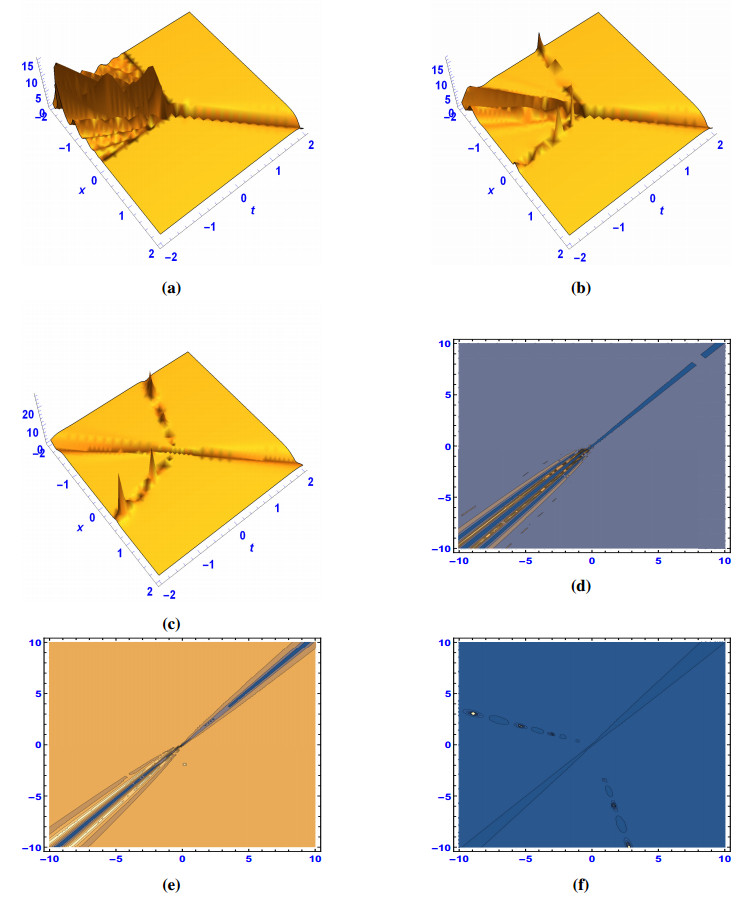
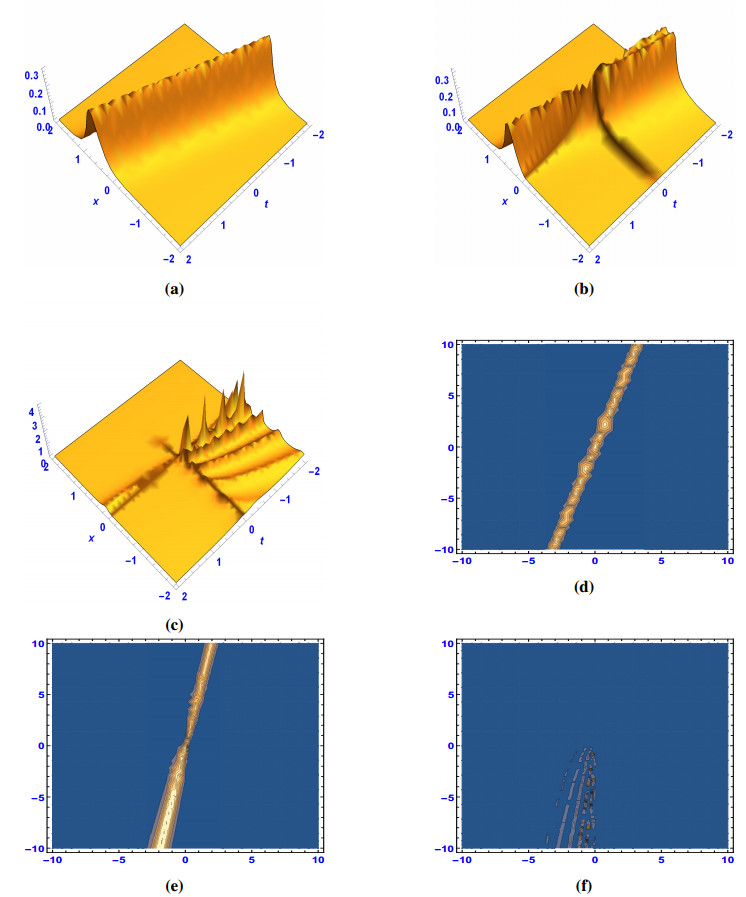
displays the shape of bright-soliton at $\mu = 1$ . When $\mu = 0.7$ , solution (2.9) maintains its dark-soliton shape with shork-shock, and changes to short-shock waves at $\mu = 0.5$ . displays the shape of dark-soliton at $\mu = 1$ . When $\mu = 0.9$ , solution (2.11) maintains its bright-soliton shape with shork-shock, and changes to short-shock waves at $\mu = 0.5$ . portrays the shock-periodic wave shape at three different fractional values of $\mu$ .

Figure 1. The 3-dimensional and contour graphs of solution (2.9) at

$r = 1, \; \delta = 0.9, \; \rho = 0.62, \; P = 0.86, \; \sigma = -1, \; \zeta = 3.57$ , and different fractional values of

$\mu$ , for (a, d)

$\mu = 1$ , for (b, c)

$\mu = 0.7$ , for (c, f)

$\mu = 0.5$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. The 3-dimensional and contour graphs of solution (2.11) at

$r = 1.71, \; \delta = 0.5, \; \rho = -0.54, \; P = 0.44, \; \sigma = 1, \; \zeta = 1.33$ , and different fractional values of

$\mu$ , for (a, d)

$\mu = 1$ , for (b, c)

$\mu = 0.9$ , for (c, f)

$\mu = 0.5$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. The 3-dimensional and contour graphs of solution (2.21) at

$r = 1.71, \; \delta = -2, \; \rho = -0.54, \; P = 0.44, \; \sigma = -1, \; \zeta = 1.33$ , and different fractional values of

$\mu$ , for (a, d)

$\mu = 1$ , for (b, c)

$\mu = 0.85$ , for (c, f)

$\mu = 0.56$ .

DownLoad: Full-Size Img PowerPoint

4. Results and discussion

We investigated the Hamiltonian amplitude equation that governs certain instabilities of modulated wave trains. We have successfully reached some important wave solutions to this nonlinear model such as the dark, bright, combined dark-bright, singular solitons, periodic and singular periodic wave solutions. It is known that dark soliton describes the solitary waves with lower intensity than the background, bright soliton describes the solitary waves whose peak intensity is larger than the background and the singular soliton solutions is a solitary wave with discontinuous derivatives; examples of such solitary waves include compactions, which have finite (compact) support, and peakons, whose peaks have a discontinuous first derivative ^[49,50].

Moreover, results presented in this study have some important physical meaning, for instance, the hyperbolic sine arises in the gravitational potential of a cylinder and the calculation of the Roche limit, the hyperbolic cosine function is the shape of a hanging cable (the so-called CATENARY), the hyperbolic tangent arises in the calculation of magnetic moment and rapidity of special relativity, the hyperbolic secant arises in the profile of a laminar jet and the hyperbolic cotangent arises in the Langevin function for magnetic polarization ^[51].

5. Conclusions

In this study the Hamiltonian amplitude equation have been investigated comprehensively with the aid of two efficient analytical schemes namely; the extended sinh-Gordon equation expansion method and the and the extended rational sine-cosine/sinh-cosh methods. To this end, so many different solitons and other solutions with an interesting behavior have been established. The physical characteristics of the acquired solutions are plotted in order to provide a good perspective of their features. To investigate the interpretation of complex physical phenomena, the results obtained can be used in different branches of science. It is also worth noting that the original equation has been satisfied by all the recorded solutions. The two techniques are very vehement in constructing novel solutions to nonlinear partial differential equations.

Acknowledgment

The authors would like to acknowledge the financial support of Taif University Researchers Supporting Project number (TURSP-2020/162), Taif University, Taif, Saudi Arabia.

Conflict of interest

The authors declare no conflict of interest.

References

[1]	T. Dauxois, M. Peyrard, Physics of solitons, Cambridge: Cambridge University Press, 2006.
[2]	Y. Kivshar, G. Agrawal, Optical solitons: from fibers to photonic crystals, London: Academic Press, 2003.
[3]	F. M. Mitschke, L. F. Mollenaurer, Experimental observation of interaction forces between solitons in optical fibers, Opt. Lett., 12 (1987), 355–357. doi: 10.1364/OL.12.000355
[4]	A. Antikainen, M. Erkintalo, J. Dudley, G. Genty, On the phase-dependent manifestation of optical rogue waves, Nonlinearity, 25 (2012), R73. doi: 10.1088/0951-7715/25/7/R73
[5]	M. Islam, C. Soccolich, J. Gordon, Ultrafast digital soliton logic gates, Opt. Quant. Electron., 24 (1992), S1215–S1235. doi: 10.1007/BF00624671
[6]	J. D. Gibbon, A survey of the origins and physical importance of soliton equations, Philos. T. R. Soc. A, 315 (1985), 335–365.
[7]	A. Yusuf, Symmetry analysis, invariant subspace and conservation laws of the equation for fluid flow in porous media, Int. J. Geom. Methods M., 17 (2020), 2050173.
[8]	T. A. Sulaiman, A. Yusuf, F. Tchier, M. Inc, FMO Tawfiq and F Bousbahi. Lie-Bäcklund symmetries, analytical solutions and conservation laws to the more general (2+1)-dimensional Boussinesq equation, Results Phys., 22 (2021), 103850. doi: 10.1016/j.rinp.2021.103850
[9]	A. I. Aliyu, Y. Li, M. Inc, A. Yusuf, B. Almohsen, Dynamics of solitons to the coupled sine-Gordon equation in nonlinear optics, Int. J. Mod. Phys. B, 35 (2021), 2150043. doi: 10.1142/S0217979221500430
[10]	H. I. Abdel-Gawad, M. Tantawy, M. Inc, A. Yusuf, Construction of rogue waves and conservation laws of the complex coupled Kadomtsev–Petviashvili equation, Int. J. Mod. Phys. B, 34 (2020), 2050115. doi: 10.1142/S0217979220501155
[11]	S. Singh, R. Sakthivel, M. Inc, A. Yusuf, K. Murugesan, Computing wave solutions and conservation laws of conformable time-fractional Gardner and Benjamin–Ono equations, Pramana-J. Phys., 95 (2021), 43. doi: 10.1007/s12043-020-02070-0
[12]	M. Arshad, A. R. Seadawy, D. Lu, Modulation stability and dispersive optical soliton solutions of higher order nonlinear Schrödinger equation and its applications in mono-mode optical fibers, Superlattice. Microst., 113 (2018), 419–429. doi: 10.1016/j.spmi.2017.11.022
[13]	D. Lu, C. L. Liu, A sub-ODE method for generalized Gardner and BBM equation with nonlinear terms of any order, Appl. Math. Comput., 217 (2010), 1404–1407.
[14]	M. Arshad, A. R. Seadawy, D. Lu, Elliptic function and Solitary Wave Solutions of higherorder nonlinear Schrödinger dynamical equation with fourth-order dispersion and cubicquintic nonlinearity and its stability, Eur. Phys. J. Plus, 132 (2017), 371. doi: 10.1140/epjp/i2017-11655-9
[15]	D. J. Kaup, A. C. Newell, An exact solution for a derivative nonlinear Schrödinger equation, J. Math. Phys., 19 (1978), 798–801. doi: 10.1063/1.523737
[16]	M. Wadati, K. Sogo, Gauge transformations in soliton theory, J. Phys. Soc. Jpn., 52 (1983), 394–398. doi: 10.1143/JPSJ.52.394
[17]	S. Xu, J. He, L. Wang, The Darboux transformation of the derivative nonlinear Schrödinger equation, J. Phys. A: Math. Theor., 44 (2011), 305203. doi: 10.1088/1751-8113/44/30/305203
[18]	D. Lu, B. Hong, New exact solutions for the (2 + 1)-dimensional generalized Broer-Kaup system, Appl. Math. Comput., 199 (2008), 572–580.
[19]	W. Liu, Y. Zhang, J. He, Rogue wave on a periodic background for Kaup-Newell equation, Rom. Rep. Phys., 70 (2018), 106.
[20]	G. P. Agrawal, Nonlinear fiber optics, 5 Eds., New York, 2013.
[21]	W. Maliet, Solitary wave solutions of nonlinear wave equation, Am. J. Phys., 60 (1992), 650–654. doi: 10.1119/1.17120
[22]	M. J. Ablowitz, P. A. Clarkson, Solitons, nonlinear evolution equations and inverse scattering, New York: Cambridge University Press, 1991.
[23]	R. Hirota, Exact solutions of the Korteweg-de Vries equation for multiple collisions of solitons, Phys. Rev. Lett., 27 (1971), 1192–1194. doi: 10.1103/PhysRevLett.27.1192
[24]	H. Rezazadeh, M. Inc, D. Baleanu, New Solitary Wave Solutions for Variants of (3+1)-Dimensional Wazwaz-Benjamin-Bona-Mahony Equations, Front. Phys., 8 (2020), 332. doi: 10.3389/fphy.2020.00332
[25]	M. Inc, H. Rezazadeh, J. Vahidi, M. Eslami, M. A. Akinlar, M. N. Ali, et al., New solitary wave solutions for the conformable Klein-Gordon equation with quantic nonlinearity, AIMS Mathematics, 5 (2020), 6972–6984. doi: 10.3934/math.2020447
[26]	S. Zhang, T. Xia, A generalized F-expansion method with symbolic computation exactly solving Broer-Kaup equations, Appl. Math. Comput., 189 (2007), 836–843.
[27]	Q. Zhao, L. H. Wu, Darboux transformation and explicit solutions to the generalized TD equation, Appl. Math. Lett., 67 (2017), 1–6. doi: 10.1016/j.aml.2016.11.012
[28]	D. B. Belobo, T. Dase, Solitary and Jacobi elliptic wave solutions of the generalized Benjamin-Bona-Mahony equation, Commun. Nonlinear Sci., 48 (2017), 270–277. doi: 10.1016/j.cnsns.2017.01.001
[29]	M. Arshad, D. Lu, M. Ur Rehman, I. Ahmed, A. M. Sultan, Optical solitary wave and elliptic function solutions of Fokas-Lenells equation in presence of perturbation terms and its modulation instability, Phys. Scripta, 94 (2019), 105202. doi: 10.1088/1402-4896/ab1791
[30]	W. P. Zhong, R. H. Xie, M. Belic, N. Petrovic, G. Chen, L. Yi, Exact spatial soliton solutions of the two-dimensional generalized nonlinear Schrödinger equation with distributed coefficients, Phys. Rev. A, 78 (2008), 023821. doi: 10.1103/PhysRevA.78.023821
[31]	W. P. Zhong, M. R. Belic, Y. Lu, T. Huang, Traveling and solitary wave solutions to the one-dimensional Gross-Pitaevskii equation, Phys. Rev. E, 81 (2010), 016605. doi: 10.1103/PhysRevE.81.016605
[32]	W. Zhong, W. P. Zhong, M. R. Belic, G. Cai, Embedded solitons in the (2 + 1)-dimensional sine-Gordon equation, Nonlinear Dynam., 100 (2020), 1519–1526. doi: 10.1007/s11071-020-05561-2
[33]	J. Manaan, M. F. Aghdaei, M. Khalilian, R. S. Jeddi, Application of the generalized G-expansion method for nonlinear PDEs to obtaining soliton wave solution, Optik, 135 (2017), 395–406. doi: 10.1016/j.ijleo.2017.01.078
[34]	M. Arshad, D. Lu, J. Wang, (N +1)-dimensional fractional reduced differential transform method for fractional order partial differential equations, Commun. Nonlinear Sci., 48 (2017), 509–519. doi: 10.1016/j.cnsns.2017.01.018
[35]	S. A. Khuri, A. Sayfy, Generalizing the variational iteration method for BVPs: proper setting of the correction functional, Appl. Math. Lett., 68 (2017), 68–75. doi: 10.1016/j.aml.2016.11.018
[36]	N. Savaissou, G. Betchewe, H. Rezazadeh, A. Bekir, S. Y. Doka, Exact optical solitons to the perturbed nonlinear Schrödinger equation with dual-power law of nonlinearity, Opt. Quant. Electron., 52 (2020), 1–16. doi: 10.1007/s11082-019-2116-1
[37]	N. Nasreen, D. Lu, M. Arshad, Optical solitons of nonlinear Schrödinger equation with second order spatiotemporal dispersion and its modulation instability, Optik, 161 (2018), 221–229. doi: 10.1016/j.ijleo.2018.02.043
[38]	Z. Pinar, H. Rezazadeh, M. Eslami, Generalized logistic equation method for Kerr law and dual power law Schrödinger equations, Opt. Quant. Electron., 52 (2020), 1–16. doi: 10.1007/s11082-019-2116-1
[39]	J. Y. Yang, W. X. Ma, Conservation laws of a perturbed Kaup-Newell equation, Mod. Phys. Lett. B, 30 (2016), 1650381. doi: 10.1142/S0217984916503814
[40]	M. A. Akbar, L. Akinyemi, S. W. Shao, A. Jhangeer, H. Rezazadeh, M. M. A. Khater, et al., Soliton solutions to the Boussinesq equation through sine-Gordon method and Kudryashov method, Results Phys., 25 (2021), 104228. doi: 10.1016/j.rinp.2021.104228
[41]	L. Akinyemi, M. Şenol, H. Rezazadeh, H. Ahmad, H. Wang, Abundant optical soliton solutions for an integrable (2+1)-dimensional nonlinear conformable Schrodinger system, Results Phys., 25 (2021), 104177. doi: 10.1016/j.rinp.2021.104177
[42]	J. C. He, Z. Y. Cong, Comment on revision of Kaup-Newell's works on IST for DNLS equation, Commun. Theor. Phys., 50 (2008), 1369–1374. doi: 10.1088/0253-6102/50/6/26
[43]	M. O. Al-Amr, New applications of reduced differential transform method, Alex. Eng. J., 53 (2014), 243–247. doi: 10.1016/j.aej.2014.06.005
[44]	S. Kumar, K. Singh, R. K. Gupta, Coupled Higgs field equation and Hamiltonian amplitude equation: Lie classical approach and $(G'/G)$ -expansion method, Pramana-J. Phys., 79 (2012), 41–60. doi: 10.1007/s12043-012-0284-7
[45]	C. Y. Yang, W. Y. Li, W. T. Yu, M. L. Liu, Y. J. Zhang, G. L. Ma, et al., Amplification, reshaping, fission and annihilation of optical solitons in dispersion decreasing fiber, Nonlinear Dynam., 92 (2018), 203–213. doi: 10.1007/s11071-018-4049-9
[46]	M. Wadati, H, Segur, M. J. Ablowitz, A new Hamiltonian amplitude equation governing modulated wave instabilities, J. Phys. Soc. Jpn., 61 (1992), 1187. doi: 10.1143/JPSJ.61.1187
[47]	X. L. Yang, J. S. Tang, Travelling wave solutions for Konopelchenko-Dubrovsky equation using an extended sinh-Gordon equation expansion method, Commun. Theor. Phys., 50 (2008), 1047. doi: 10.1088/0253-6102/50/5/06
[48]	N. Mahaka, G. Akram, Extension of rational sine-cosine and rational sinh-cosh techniques to extract solutions for the perturbed NLSE with Kerr law nonlinearity, Eur. Phys. J. Plus, 134 (2019), 159. doi: 10.1140/epjp/i2019-12545-x
[49]	A. C. Scott, Encyclopedia of nonlinear science, Routledge, Taylor and Francis Group, New York, 2005.
[50]	P. Rosenau, What is a Compacton?, Notices of the AMS, 52 (2005), 738–739.
[51]	E. W. Weisstein, Concise Encyclopedia of Mathematics, New York: CRC Press, 2002.

This article has been cited by:

1.	Usman Younas, T. A. Sulaiman, Jingli Ren, Propagation of M-truncated optical pulses in nonlinear optics, 2023, 55, 0306-8919, 10.1007/s11082-022-04344-w
2.	Saima Arshed, Ghazala Akram, Maasoomah Sadaf, Muhammad Bilal Riaz, Adam Wojciechowski, Shou-Fu Tian, Solitary wave behavior of (2+1)-dimensional Chaffee-Infante equation, 2023, 18, 1932-6203, e0276961, 10.1371/journal.pone.0276961
3.	U.H.M. Zaman, Mohammad Asif Arefin, M. Ali Akbar, M. Hafiz Uddin, Comprehensive dynamic-type multi-soliton solutions to the fractional order nonlinear evolution equation in ocean engineering, 2024, 15, 20904479, 102935, 10.1016/j.asej.2024.102935
4.	Ahu ERCAN, Fractional approach for Dirac operator involving M-truncated derivative, 2023, 73, 1303-5991, 259, 10.31801/cfsuasmas.1316623
5.	Mst. Shekha Khatun, M.F. Hoque, M. Zulfikar Ali, Hadi rezazadeh, Abundant dynamical structure of solutions to truncated M-fractional modified Korteweg–de Vries model: Effects of dispersion, nonlinearity and fractionality, 2023, 52, 22113797, 106777, 10.1016/j.rinp.2023.106777

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(2688) PDF downloads(102) Cited by(5)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(3)

AIMS Mathematics

$M-$ truncated optical soliton and their characteristics to a nonlinear equation governing the certain instabilities of modulated wave trains

Related Papers:

Abstract

1. Introduction

2. Applications

2.1. Application of the extended sinh-Gordon equation expansion method

2.2. Application of the extended rational sine-cosine/sinh-cosh methods

3. Physical interpretation

4. Results and discussion

5. Conclusions

Acknowledgment

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

M− M- truncated optical soliton and their characteristics to a nonlinear equation governing the certain instabilities of modulated wave trains

Related Papers:

Abstract

1. Introduction

2. Applications

2.1. Application of the extended sinh-Gordon equation expansion method

2.2. Application of the extended rational sine-cosine/sinh-cosh methods

3. Physical interpretation

4. Results and discussion

5. Conclusions

Acknowledgment

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

$M-$ truncated optical soliton and their characteristics to a nonlinear equation governing the certain instabilities of modulated wave trains