New diverse types of soliton solutions to the Radhakrishnan-Kundu-Lakshmanan equation

Emad H. M. Zahran; Omar Abu Arqub; Ahmet Bekir; Marwan Abukhaled; Emad H. M. Zahran; Omar Abu Arqub; Ahmet Bekir; Marwan Abukhaled

doi:10.3934/math.2023450

AIMS Mathematics

2023, Volume 8, Issue 4: 8985-9008. doi: 10.3934/math.2023450

Previous Article Next Article

Research article Special Issues

New diverse types of soliton solutions to the Radhakrishnan-Kundu-Lakshmanan equation

1.
Department of Mathematical and Physical Engineering, Benha University, Faculty of Engineering, Shubra, Egypt
2.
Department of Mathematics, Faculty of Science, Al-Balqa Applied University, Jordan
3.
Neighbourhood of Akcaglan, Imarli Street, 28/4, 26030, Eskisehir, Turkey
4.
Department of Mathematics and Statistics, American University of Sharjah, United Arab Emirates

Received: 28 October 2022 Revised: 11 January 2023 Accepted: 18 January 2023 Published: 10 February 2023
MSC : 35C07, 35Q51, 83C15

The main purpose of this study was to produce abundant new types of soliton solutions for the Radhakrishnan-Kundu-Lakshmanan equation that represents unstable optical solitons that emerge from optical propagations through the use of birefringent fibers. These new types of soliton solutions have behaviors that are bright, dark, W-shaped, M-shaped, periodic trigonometric, and hyperbolic and were not realized before by any other method. These new forms have been detected by using four different techniques, which are, the extended simple equation method, the Paul-Painlevé approach method, the Ricatti-Bernoulli-sub ODE, and the solitary wave ansatz method. These new solitons will be arranged to create a soliton catalog with new impressive behaviors and they will contribute to future studies not only for this model but also for the optical propagations through birefringent fiber.

Keywords:

Citation: Emad H. M. Zahran, Omar Abu Arqub, Ahmet Bekir, Marwan Abukhaled. New diverse types of soliton solutions to the Radhakrishnan-Kundu-Lakshmanan equation[J]. AIMS Mathematics, 2023, 8(4): 8985-9008. doi: 10.3934/math.2023450

Related Papers:

[1]	Tekin Toplu, Mahir Kadakal, İmdat İşcan . On n-Polynomial convexity and some related inequalities. AIMS Mathematics, 2020, 5(2): 1304-1318. doi: 10.3934/math.2020089
[2]	Muhammad Tariq, Soubhagya Kumar Sahoo, Jamshed Nasir, Hassen Aydi, Habes Alsamir . Some Ostrowski type inequalities via $n$ -polynomial exponentially $s$ -convex functions and their applications. AIMS Mathematics, 2021, 6(12): 13272-13290. doi: 10.3934/math.2021768
[3]	Haoliang Fu, Muhammad Shoaib Saleem, Waqas Nazeer, Mamoona Ghafoor, Peigen Li . On Hermite-Hadamard type inequalities for $n$ -polynomial convex stochastic processes. AIMS Mathematics, 2021, 6(6): 6322-6339. doi: 10.3934/math.2021371
[4]	Attazar Bakht, Matloob Anwar . Ostrowski and Hermite-Hadamard type inequalities via $(\alpha-s)$ exponential type convex functions with applications. AIMS Mathematics, 2024, 9(10): 28130-28149. doi: 10.3934/math.20241364
[5]	Serap Özcan, Saad Ihsan Butt, Sanja Tipurić-Spužević, Bandar Bin Mohsin . Construction of new fractional inequalities via generalized $n$ -fractional polynomial $s$ -type convexity. AIMS Mathematics, 2024, 9(9): 23924-23944. doi: 10.3934/math.20241163
[6]	Shuang-Shuang Zhou, Saima Rashid, Muhammad Aslam Noor, Khalida Inayat Noor, Farhat Safdar, Yu-Ming Chu . New Hermite-Hadamard type inequalities for exponentially convex functions and applications. AIMS Mathematics, 2020, 5(6): 6874-6901. doi: 10.3934/math.2020441
[7]	Khuram Ali Khan, Shaista Ayaz, İmdat İşcan, Nehad Ali Shah, Wajaree Weera . Applications of Hölder-İşcan inequality for $n$ -times differentiable $(s, m)$ -convex functions. AIMS Mathematics, 2023, 8(1): 1620-1635. doi: 10.3934/math.2023082
[8]	Jamshed Nasir, Shahid Qaisar, Saad Ihsan Butt, Hassen Aydi, Manuel De la Sen . Hermite-Hadamard like inequalities for fractional integral operator via convexity and quasi-convexity with their applications. AIMS Mathematics, 2022, 7(3): 3418-3439. doi: 10.3934/math.2022190
[9]	Hu Ge-JiLe, Saima Rashid, Muhammad Aslam Noor, Arshiya Suhail, Yu-Ming Chu . Some unified bounds for exponentially $tgs$ -convex functions governed by conformable fractional operators. AIMS Mathematics, 2020, 5(6): 6108-6123. doi: 10.3934/math.2020392
[10]	Thongchai Botmart, Soubhagya Kumar Sahoo, Bibhakar Kodamasingh, Muhammad Amer Latif, Fahd Jarad, Artion Kashuri . Certain midpoint-type Fejér and Hermite-Hadamard inclusions involving fractional integrals with an exponential function in kernel. AIMS Mathematics, 2023, 8(3): 5616-5638. doi: 10.3934/math.2023283

Abstract

1. Introduction

In recent years, fractional calculus (FC) has been successfully applied to describe the mathematical issues in real materials ^[1,2]. For instance, ^[3] provided the representation of the constitutive relationship (RCR) of the fractional mechanical element with fractional derivative (FD) of the Riemann-Liouville type, and ^[4] presented its generalised form. In ^[5], the RCR with FC of the Liouville-Caputo type was taken into consideration. It has been demonstrated that the local fractional derivative is a wonderful mathematical tool for addressing fractal issues and some challenging natural phenomena ^[6,7]. The Caputo-Fabrizio type's RCR through fractional derivative was introduced in ^[8]. The study of fractional differential equations has expanded owing to the Caputo-Fabrizio fractional derivative. The nonsingular kernel of the new derivative ^[9], is what makes it so beautiful. The Caputo-Fabrizio derivative has the same additional motivating characteristics of heterogeneity and configuration ^[10,11] with different scales as it does in the Caputo and Riemann-Liouville fractional derivatives despite being created through the convolution of an ordinary derivative and an exponential function. In the past two years, numerous studies related to the the new Caputo-Fabrizio fractional derivative have been published. It has been shown that modelling using the fractional derivative of the Atangana-Baleanu has a brief random walk. Additionally, it has been found that the Mittag-Leffler function is a more significant and practical filter tool than the power and exponential law functions, making the Atangana-Baleanu fractional derivative in the sense of Caputo an effective mathematical tool for simulating more difficult real-world problems ^[12,13].

Using partial differential equations, it is possible to express a specific relationship between its partial derivatives (PDEs) and an unknown function. PDEs may be found in almost every field of engineering and research. In recent years, the application of PDEs in fields such as finance, biology, image graphics and processing, and social sciences has risen. As a result, when certain independent variables interact with one another in each of the above-mentioned fields, appropriate functions in these variables may be established, allowing for the modelling of a variety of processes via the use of equations for the related functions ^[14,15,16]. The study of PDEs has various elements. The traditional method, which dominated the nineteenth century, was to develop procedures for identifying explicit answers ^[17,18,19]. Theoretical PDE analysis offers a wide range of applications. It's worth noting that there are certain really difficult equations that even supercomputers can't solve. All one can do in these situations is attempt to get qualitative data. Moreover, the formulation of the equation, as well as its associated side conditions, is significant. A model of a physical or technical issue is frequently used to generate the equation. It is not immediately clear that the model is continuous in the view that it results to a solved PDE ^[20,21,22]. Furthermore, in most circumstances, it is preferable that the answer be one of a kind and stable under minor data disruptions. Theoretical comprehension of the equation aids in determining whether or not these requirements are satisfied. Several methods for solving classical PDEs have already been suggested, and several solutions have been discovered ^{[23,24,25,26,27,28,29]}.

The propagation of shallow water is represented by numerous well-known integral models, such as the Boussinesq equation, KdV equation, Whitham-Broer-Kaup equation, and others. Whitham, Broer, and Kaup ^{[30,31,32,33,34]} created non-linear Whitham-Broer-Kaup equations employing the Boussinesq approximation

$\begin{equation} \left\{\begin{array}{l} \psi_{\tau}+\psi \psi_{\upsilon}+\varphi_{\upsilon}+q \psi_{\upsilon\upsilon } = 0 \\ \varphi_{\tau}+\varphi \psi_{\upsilon}+\psi \varphi_{\upsilon}-q \varphi_{\upsilon\upsilon}+p \psi_{\upsilon\upsilon\upsilon} = 0, \end{array}\right. \end{equation}$

(1.1)

where $\psi = \psi(\upsilon, \tau), \varphi = \varphi(\upsilon, \tau)$ represents the velocity of horizontal and fluid height, which fluctuates substantially from equilibriums, and $q, p$ are constants made up of many diffusion power. Wang and Zheng ^[32] implemented riccati sub-equation method to obtain the result of fractional order Whitham-Broer-Kaup equations. The analytical and numerical methods have been applied to find the solutions of Whitham-Broer-Kaup equations, such as reduced differential transform method, residual power series method (1.1), finite element method ^[35], power-series method^[36], the finite difference approach ^[37], the exponential-function technique ^[38], the variation iteration technique, the homotopy perturbation technique, the homotopy analysis technique and others ^[39,40,41].

Adomian introduced the Adomian decomposition approach in 1980, which is an effective approach for locating numeric and explicit solutions to a wide variety of differential equations that describe physical conditions. This method is applicable to initial value problems, boundary value problems, partial and ordinary differential equations, including linear and nonlinear equations, and stochastic systems. The Natural transform decomposition method is constructed by combining the Adomian decomposition method with the Natural transform method (NTDM). NTDM has also been used to analyze fractional-order non-linear partial differential equations numerically in a number of articles ^[42,43,44].

In this research, we use NTDM in combination with two different derivatives to investigate the general as well as numerical solution of the coupled system of Whitham-Broer-Kaup equations of fractional order, as inspired by the above papers. NTDM is a simple and effective technique that does not require any perturbation. We compare our suggested method's results to those of other well-known approaches like the variational iteration method, Adomain decomposition method, and Optimal homoptoy analysis method. We can observe that the proposed method is superior to the previously discussed methods for finding nonlinear fractional order partial differential equation solutions. We use Maple to perform the calculations. The suggested techniques' convergence is also ensured by extending the concept mentioned in ^[45,46].

2. Basic definitions

Fractional derivatives and integrals have a great number of properties and definitions. We propose changes to some basic fractional calculus definitions and preliminaries used in this study.

Definition 2.1. The Riemann-Liouville integral of order fraction for a function $j\in C_{\wp}, \wp\geq-1$ , is given as ^[47,48,49]

$\begin{equation} \begin{split} I^{{{\varrho}}}j(\eta) = &\frac{1}{\Gamma({{\varrho}})}\int_{0}^{\eta}(\eta-\wp)^{{{\varrho}}-1}j(\wp)d\wp, \ \ {{\varrho}} > 0, \ \ \eta > 0.\\ and \ \ I^{0}j(\eta) = &j(\eta). \end{split} \end{equation}$

(2.1)

Definition 2.2. The derivative with order fraction for $j(\eta)$ in Caputo manner is stated as ^[47,48,49]

$\begin{equation} \begin{split} D_{\eta}^{{{\varrho}}}j(\eta) = I^{{m}-{{\varrho}}}D^{{m}}j(\eta) = \frac{1}{{m}-{{\varrho}}}\int_{0}^{\eta}(\eta-\wp)^{{m}-{{\varrho}}-1}j^{({m})}(\wp)d\wp, \end{split} \end{equation}$

(2.2)

for ${m}-1 < {{\varrho}}\leq {m}, \ \ {m}\in N, \ \ \eta > 0, j\in C^{{m}}_{\wp}, \wp\geq-1$ .

Definition 2.3. The derivative with order fraction for $j(\eta)$ in CF sense is stated as ^[47]

$\begin{equation} \begin{split} D_{\eta}^{{{\varrho}}}j(\eta) = \frac{F({{\varrho}})}{1-{{\varrho}}}\int^{\eta}_{0}\exp\left(\frac{-{{\varrho}}(\eta-\wp)}{1-{{\varrho}}}\right)D(j(\wp))d\wp, \end{split} \end{equation}$

(2.3)

having $0 < {{\varrho}} < 1$ and $F({{\varrho}})$ is a normalization function having $F(0) = F(1) = 1$ .

Definition 2.4. The derivative with order fraction for $j(\eta)$ in ABC sense is stated as ^[47]

$\begin{equation} \begin{split} D_{\eta}^{{{\varrho}}}j(\eta) = \frac{B({{\varrho}})}{1-{{\varrho}}}\int^{\eta}_{0}E_{{{\varrho}}}\left(\frac{-{{\varrho}}(\eta-\wp)}{1-{{\varrho}}}\right)D(j(\wp))d\wp, \end{split} \end{equation}$

(2.4)

having $0 < {{\varrho}} < 1$ , $B(\varrho)$ is normalization function and $E_{{{\varrho}}}(z) = \sum_{m = 0}^{\infty}\frac{z^{m}}{\Gamma({m}{{\varrho}}+1)}$ is the Mittag-Leffler function.

Definition 2.5. For a function $\psi(\tau)$ , the natural transform (NT) is stated as

$\begin{equation} \begin{split} \mathbf{N}(\psi(\tau)) = \mathcal{U}({\kappa}, {{\ell}}) = \int_{-\infty}^{\infty}e^{-\kappa\tau}\psi(\ell\tau)d\tau, \ \ \kappa , \ell\in (-\infty, \infty), \end{split} \end{equation}$

(2.5)

and for $\tau\in(0, \infty)$ , the NT of $\psi(\tau)$ is stated as

$\begin{equation} \begin{split} \mathbf{N}(\psi(\tau)H(\tau)) = \mathbf{N}^{+} = \mathcal{U}^{+}({\kappa}, {{\ell}}) = \int_{0}^{\infty}e^{-\kappa\tau}\psi(\ell\tau)d\tau, \ \ \kappa , \ell\in (0, \infty), \end{split} \end{equation}$

(2.6)

where $H(\tau)$ is the Heaviside function.

Definition 2.6. For the function $\psi({\kappa}, {{\ell}})$ , the inverse NT is stated as

$\begin{equation} \begin{split} \mathbf{N}^{-1}[\mathcal{U}({\kappa}, {{\ell}})] = \psi(\tau), \ \ \forall \tau\geq0. \end{split} \end{equation}$

(2.7)

Lemma 2.7. If the NT of $\psi_{1}(\tau)$ and $\psi_{2}(\tau)$ are $\mathcal{U}_{1}({\kappa}, {{\ell}})$ and $\mathcal{U}_{2}({\kappa}, {{\ell}})$ respectively, so

$\begin{equation} \begin{split} \mathbf{N}[c_{1}\psi_{1}(\tau)+c_{2}\psi_{2}(\tau)] = c_{1}\mathbf{N}[\psi_{1}(\tau)]+c_{2}\mathbf{N}[\psi_{2}(\tau)] = c_{1}\mathcal{U}_{1}({\kappa}, {{\ell}})+c_{2}\mathcal{U}_{2}({\kappa}, {{\ell}}), \end{split} \end{equation}$

(2.8)

having $c_{1}$ and $c_{2}$ constants.

Lemma 2.8. If $\psi_{1}(\tau)$ and $\psi_{2}(\tau)$ are the inverse NT of $\psi_{1}({\kappa}, {{\ell}})$ and $\psi_{2}({\kappa}, {{\ell}})$ respectively, so

$\begin{equation} \mathcal\{N\}^{-1}[c_{1}\mathcal{U}_{1}({\kappa}, {{\ell}})+c_{2}\mathcal{U}_{2}({\kappa}, {{\ell}})] = c_{1}\mathbf{N}^{-1}[\mathcal{U}_{1}({\kappa}, {{\ell}})]+c_{2}\mathbf{N}^{-1}[\mathcal{U}_{2}({\kappa}, {{\ell}})] = c_{1}\psi_{1}(\tau)+c_{2}\psi_{2}(\tau), \end{equation}$

(2.9)

having $c_{1}$ and $c_{2}$ constants.

Definition 2.9. The NT of $D_{\tau}^{{{\varrho}}}\psi(\tau)$ in Caputo sense is stated as ^[47]

$\begin{equation} \mathbf{N}[D_{\tau}^{{{\varrho}}}\psi(\tau)] = \left(\frac{\kappa}{{\ell}}\right)^{{{\varrho}}}\left(\mathbf{N}[\psi(\tau)]-\left(\frac{1}{\kappa}\right)\psi(0)\right). \end{equation}$

(2.10)

Definition 2.10. The NT of $D_{\tau}^{{{\varrho}}}\psi(\tau)$ in CF sense is stated as ^[47]

$\begin{equation} \mathbf{N}[D_{\tau}^{{{\varrho}}}\psi(\tau)] = \frac{1}{1-{{\varrho}}+{{\varrho}}(\frac{{\ell}}{\kappa})}\left(\mathbf{N}[\psi(\tau)]-\left(\frac{1}{\kappa}\right)\psi(0)\right). \end{equation}$

(2.11)

Definition 2.11. The NT of $D_{\tau}^{{{\varrho}}}\psi(\tau)$ in ABC sense is stated as ^[47]

$\begin{equation} \begin{split} \mathbf{N}[D_{\tau}^{{{\varrho}}}\psi(\tau)] = \frac{M[{{\varrho}}]}{1-{{\varrho}}+{{\varrho}}(\frac{{\ell}}{\kappa})^{{{\varrho}}}}\left(\mathbf{N}[\psi(\tau)]-\left(\frac{1}{\kappa}\right)\psi(0)\right), \end{split} \end{equation}$

(2.12)

with $M[{{\varrho}}]$ denoting a normalization function.

3. General implementation of method

Consider the fractional partial differential equation

$\begin{equation} \begin{split} D_{\tau}^{{{\varrho}}}\psi(\upsilon, \tau) = \mathcal{L}(\psi(\upsilon, \tau))+{N}(\psi(\upsilon, \tau))+h(\upsilon, \tau) = M(\upsilon, \tau), \end{split} \end{equation}$

(3.1)

with the initial condition

$\begin{equation} \begin{split} \psi(\upsilon, 0) = \phi(\upsilon), \end{split} \end{equation}$

(3.2)

which $\mathcal{L}$ is linear, ${N}$ non-linear functions and sources function $h(\upsilon, \tau)$ .

3.1. Case I $(NTDM_{CF})$

The fractional CF derivative and natural transformation, Eq (3.1) can be stated as,

$\begin{equation} \begin{split} \frac{1}{p({{\varrho}}, {{\ell}}, {\kappa})}\left(\mathbf{N}[\psi(\upsilon, \tau)]-\frac{\phi(\upsilon)}{\kappa}\right) = \mathbf{N}[M(\upsilon, \tau)], \end{split} \end{equation}$

(3.3)

with

$\begin{equation} \begin{split} p({{\varrho}}, {{\ell}}, {\kappa}) = 1-{{\varrho}}+{{\varrho}}(\frac{{\ell}}{\kappa}). \end{split} \end{equation}$

(3.4)

On employing natural inverse transformation, we get

$\begin{equation} \begin{split} \psi(\upsilon, \tau) = \mathbf{N}^{-1}\left(\frac{\phi(\upsilon)}{\kappa}+p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[M(\upsilon, \tau)]\right). \end{split} \end{equation}$

(3.5)

Thus, for $\psi(\upsilon, \tau)$ , the series type solution is given as

$\begin{equation} \begin{split} \psi(\upsilon, \tau) = \sum\limits_{i = 0}^{\infty}\psi_{i}(\upsilon, \tau), \end{split} \end{equation}$

(3.6)

and ${N}(\psi(\upsilon, \tau))$ can be decomposed as

$\begin{equation} \begin{split} {N}(\psi(\upsilon, \tau)) = \sum\limits_{i = 0}^{\infty}A_{i}(\psi_{0}, ..., \psi_{i}), \end{split} \end{equation}$

(3.7)

the Adomian polynomials $A_{i}$ is given as

$A_{n} = \frac{1}{n!} \frac{d^n}{d\varepsilon^n}{N} (t, \Sigma_{k = 0}^n \varepsilon^k \psi_k)|_{\varepsilon = 0.}$

Putting Eqs (3.7) and (3.6) into (3.5), we obtain

$\begin{equation} \begin{split} \sum\limits_{i = 0}^{\infty}\psi_{i}(\upsilon, \tau) = &\mathbf{N}^{-1}\left(\frac{\phi(\upsilon)}{\kappa}+p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[h(\upsilon, \tau)]\right)\\ &+\mathbf{N}^{-1}\left(p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\sum\limits_{i = 0}^{\infty}\mathcal{L}(\psi_{i}(\upsilon, \tau))+A_{\tau}\right]\right). \end{split} \end{equation}$

(3.8)

From (3.8), we get,

$\begin{equation} \begin{split} \psi_{0}^{CF}(\upsilon, \tau) = &\mathbf{N}^{-1}\left(\frac{\phi(\upsilon)}{\kappa}+p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[h(\upsilon, \tau)]\right), \\ \psi_{1}^{CF}(\upsilon, \tau) = &\mathbf{N}^{-1}\left(p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\mathcal{L}(\psi_{0}(\upsilon, \tau))+A_{0}\right]\right), \\ &\vdots\\ \psi_{l+1}^{CF}(\upsilon, \tau) = &\mathbf{N}^{-1}\left(p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\mathcal{L}(\psi_{l}(\upsilon, \tau))+A_{l}\right]\right), \ \ l = 1, 2, 3, \cdots.\\ \end{split} \end{equation}$

(3.9)

Thus, we obtain the result of (3.1) by putting (3.9) into (3.6) applying $NTDM_{CF},$

$\begin{equation} \begin{split} \psi^{CF}(\upsilon, \tau) = \psi_{0}^{CF}(\upsilon, \tau)+\psi_{1}^{CF}(\upsilon, \tau)+\psi_{2}^{CF}(\upsilon, \tau)+\cdots. \end{split} \end{equation}$

(3.10)

3.2. Case II $(NTDM_{ABC})$

The fractional ABC derivative and natural transformation, Eq (3.1) is given as,

$\begin{equation} \begin{split} \frac{1}{q({{\varrho}}, {{\ell}}, {\kappa})}\left(\mathbf{N}[\psi(\upsilon, \tau)]-\frac{\phi(\upsilon)}{\kappa}\right) = \mathbf{N}[M(\upsilon, \tau)], \end{split} \end{equation}$

(3.11)

with

$\begin{equation} \begin{split} q({{\varrho}}, {{\ell}}, {\kappa}) = \frac{1-{{\varrho}}+{{\varrho}}(\frac{{\ell}}{\kappa})^{{{\varrho}}}}{B({{\varrho}})}. \end{split} \end{equation}$

(3.12)

On employing natural inverse transformation, we get

$\begin{equation} \begin{split} \psi(\upsilon, \tau) = \mathbf{N}^{-1}\left(\frac{\phi(\upsilon)}{\kappa}+q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[M(\upsilon, \tau)]\right). \end{split} \end{equation}$

(3.13)

The Adomain decomposition, we obtain as

$\begin{equation} \begin{split} \sum\limits_{i = 0}^{\infty}\psi_{i}(\upsilon, \tau) = &\mathbf{N}^{-1}\left(\frac{\phi(\upsilon)}{\kappa}+q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[h(\upsilon, \tau)]\right)\\ &+\mathbf{N}^{-1}\left(q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\sum\limits_{i = 0}^{\infty}\mathcal{L}(\psi_{i}(\upsilon, \tau))+A_{\tau}\right]\right). \end{split} \end{equation}$

(3.14)

From (3.8), we get,

$\begin{equation} \begin{split} \psi_{0}^{ABC}(\upsilon, \tau) = &\mathbf{N}^{-1}\left(\frac{\phi(\upsilon)}{\kappa}+q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[h(\upsilon, \tau)]\right), \\ \psi_{1}^{ABC}(\upsilon, \tau) = &\mathbf{N}^{-1}\left(q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\mathcal{L}(\psi_{0}(\upsilon, \tau))+A_{0}\right]\right), \\ &\vdots\\ \psi_{l+1}^{ABC}(\upsilon, \tau) = &\mathbf{N}^{-1}\left(q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\mathcal{L}(\psi_{l}(\upsilon, \tau))+A_{l}\right]\right), \ \ l = 1, 2, 3, \cdots.\\ \end{split} \end{equation}$

(3.15)

Thus, we obtain the result of (3.1), by applying $NTDM_{ABC}$

$\begin{equation} \begin{split} \psi^{ABC}(\upsilon, \tau) = \psi_{0}^{ABC}(\upsilon, \tau)+\psi_{1}^{ABC}(\upsilon, \tau)+\psi_{2}^{ABC}(\upsilon, \tau)+\cdots. \end{split} \end{equation}$

(3.16)

4. Convergence analysis

In this part, we give the uniqueness and convergence of the $NTDM_{ABC}$ and $NTDM_{CF}$ .

Theorem 4.1. Let $|\mathcal{L}(\psi)-\mathcal{L}(\psi^{*})| < \gamma_{1}|\psi-\psi^{*}|$ and $|{N}(\psi)-{N}(\psi^{*})| < \gamma_{2}|\psi-\psi^{*}|$ , where $\psi: = \psi(\wp, \tau)$ and $\psi^{*}: = \psi^{*}(\wp, \tau)$ are values of two different functions and $\gamma_{1}$ , $\gamma_{2}$ are Lipschitz constants.

$\mathcal{L}$ and ${N}$ are the operators stated in (3.1). Then for $NTDM_{CF}$ the solution of (3.1) is unique when $0 < (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}} \tau) < 1$ for all $\tau.$

Proof. Let $H = (C[J], ||.||)$ having norm $||\phi(\tau)|| = {max}_{\tau\in J}|\phi(\tau)|$ is the Banach space, $\forall$ continuous function over the interval $J = [0, T].$ Let $I:H\rightarrow H$ a non-linear mapping, with

$\psi^{C}_{l+1} = \psi^{C}_{0}+\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[\mathcal{L}(\psi_{l}(\wp, \tau))+{N}(\psi_{l}(\wp, \tau))]], \ \ l\geq0.$

$\begin{equation} \begin{split} ||I(\psi)-I(\psi^{*})||&\leq max_{\tau\in J}|\mathbf{N}^{-1}\Big[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[\mathcal{L}(\psi)-\mathcal{L}(\psi^{*})]\\ &+p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[{N}(\psi)-{N}(\psi^{*})]|\Big]\\ &\leq max_{\tau\in J}\Big[\gamma_{1}\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[|\psi-\psi^{*}|]]\\ &+\gamma_{2}\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[|\psi-\psi^{*}|]]\Big]\\ &\leq max_{\tau\in J}(\gamma_{1}+\gamma_{2})\left[\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}|\psi-\psi^{*}|]\right]\\ &\leq(\gamma_{1}+\gamma_{2})\left[\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}||\psi-\psi^{*}||]\right]\\ & = (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}} \tau)||\psi-\psi^{*}||. \end{split} \end{equation}$

(4.1)

So, I is contraction as $0 < (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}} \tau) < 1$ . The solution of (3.1) is unique as according to Banach fixed point theorem.

Theorem 4.2. As according to the above theorem, the solution of (3.1) is unique for $NTDM_{ABC}$ when $0 < (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}}\frac{\tau^{\varrho}}{\Gamma(\varrho+1)}) < 1$ for all $\tau.$

Proof. As from above theorem let $H = (C[J], ||.||)$ be the Banach space, $\forall$ continuous function over the interval $J.$ Let $I:H\rightarrow H$ is non-linear mapping, with

$\psi^{C}_{l+1} = \psi^{C}_{0}+\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[\mathcal{L}(\psi_{l}(\wp, \tau))+{N}(\psi_{l}(\wp, \tau))]], \ \ l\geq0.$

$\begin{equation} \begin{split} ||I(\psi)-I(\psi^{*})||&\leq max_{\tau\in J}|\mathbf{N}^{-1}\Big[q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[\mathcal{L}(\psi)-\mathcal{L}(\psi^{*})]\\ &+q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[{N}(\psi)-{N}(\psi^{*})]|\Big]\\ &\leq max_{\tau\in J}\Big[\gamma_{1}\mathbf{N}^{-1}[q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[|\psi-\psi^{*}|]]\\ &+\gamma_{2}\mathbf{N}^{-1}[q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[|\psi-\psi^{*}|]]\Big]\\ &\leq max_{\tau\in J}(\gamma_{1}+\gamma_{2})\left[\mathbf{N}^{-1}[q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}|\psi-\psi^{*}|]\right]\\ &\leq(\gamma_{1}+\gamma_{2})\left[\mathbf{N}^{-1}[q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}||\psi-\psi^{*}||]\right]\\ & = (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}}\frac{\tau^{{{\varrho}}}}{\Gamma{{({\varrho}}+1)}})||\psi-\psi^{*}||. \end{split} \end{equation}$

(4.2)

So, I is contraction as $0 < (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}}\frac{\tau^{{{\varrho}}}}{\Gamma{{({\varrho}}+1)}}) < 1$ . The solution of (3.1) is unique as according to Banach fixed point theorem.

Theorem 4.3. Let $\mathcal{L}$ and ${N}$ are a Lipschitz functions as stated in the above theorems, then the $NTDM_{CF}$ solution of (3.1) is convergent.

Proof. Suppose $H$ be the Banach space determined above and let $\psi_{m} = \sum_{r = 0}^{m}\psi_{r}(\wp, \tau)$ . To prove that $\psi_{m}$ is a Cauchy sequence in H. Let,

$\begin{equation} \begin{split} ||\psi_{m}-\psi_{n}||& = max_{\tau\in J}|\sum\limits_{r = n+1}^{m}\psi_{r}|, \ \ n = 1, 2, 3, \cdots\\ &\leq max_{\tau\in J} \left|\mathbf{N}^{-1}\left[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\sum\limits_{r = n+1}^{m}(\mathcal{L}(\psi_{r-1})+{N}(\psi_{r-1}))\right]\right]\right|\\ & = max_{\tau\in J} \left|\mathbf{N}^{-1}\left[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\sum\limits_{r = n+1}^{m-1}(\mathcal{L}(\psi_{r})+{N}(\psi_{r}))\right]\right]\right|\\ &\leq max_{\tau\in J}|\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[(\mathcal{L}(\psi_{m-1})-\mathcal{L}(\psi_{n-1})+{N}(\psi_{m-1})-{N}(\psi_{n-1}))]]|\\ &\leq\gamma_{1}max_{\tau\in J}|\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[(\mathcal{L}(\psi_{m-1})-\mathcal{L}(\psi_{n-1}))]]|\\ &+\gamma_{2}max_{\tau\in J}|\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[({N}(\psi_{m-1})-{N}(\psi_{n-1}))]]|\\ & = (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}} \tau)||\psi_{m-1}-\psi_{n-1}||. \end{split} \end{equation}$

(4.3)

Let $m = n+1$ , then

$\begin{equation} \begin{split} ||\psi_{n+1}-\psi_{n}||\leq \gamma||\psi_{n}-\psi_{n-1}||\leq \gamma^{2}||\psi_{n-1}\psi_{n-2}||\leq \cdots \leq \gamma^{n}||\psi_{1}-\psi_{0}||, \end{split} \end{equation}$

(4.4)

where $\gamma = (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}} \tau)$ . Thus, we get

$\begin{equation} \begin{split} ||\psi_{m}-\psi_{n}||&\leq||\psi_{n+1}-\psi_{n}||+||\psi_{n+2}\psi_{n+1}||+\cdots+||\psi_{m}-\psi_{m-1}||, \\ &(\gamma^{n}+\gamma^{n+1}+\cdots+\gamma^{m-1})||\psi_{1}-\psi_{0}||\\ &\leq \gamma^{n}\left(\frac{1-\gamma^{m-n}}{1-\gamma}\right)||\psi_{1}||. \end{split} \end{equation}$

(4.5)

As $0 < \gamma < 1$ , we have $1-\gamma^{m-n} < 1$ . Thus,

$\begin{equation} \begin{split} ||\psi_{m}-\psi_{n}||\leq \frac{\gamma^{n}}{1-\gamma}max_{\tau\in J}||\psi_{1}||. \end{split} \end{equation}$

(4.6)

Since $||\psi_{1}|| < \infty, \ \ ||\psi_{m}-\psi_{n}||\rightarrow 0$ when $n \rightarrow \infty$ . As a result, $\psi_m$ is a Cauchy sequence in H, stated that the series $\psi_m$ is convergent.

Theorem 4.4. Let $\mathcal{L}$ and ${N}$ are a Lipschitz functions as stated in the above theorems, then the $NTDM_{ABC}$ solution of (3.1) is convergent.

Proof. Suppose $\psi_{m} = \sum_{r = 0}^{m}\psi_{r}(\wp, \tau)$ . To prove that $\psi_{m}$ is a Cauchy sequence in H. Let,

$\begin{align} \begin{split} ||\psi_{m}-\psi_{n}||& = max_{\tau\in J}|\sum\limits_{r = n+1}^{m}\psi_{r}|, \ \ n = 1, 2, 3, \cdots\\ &\leq max_{\tau\in J} \left|\mathbf{N}^{-1}\left[q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\sum\limits_{r = n+1}^{m}(\mathcal{L}(\psi_{r-1})+{N}(\psi_{r-1}))\right]\right]\right|\\ & = max_{\tau\in J} \left|\mathbf{N}^{-1}\left[q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}\left[\sum\limits_{r = n+1}^{m-1}(\mathcal{L}(\psi_{r})+{N}(u_{r}))\right]\right]\right|\\ &\leq max_{\tau\in J}|\mathbf{N}^{-1}[q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[(\mathcal{L}(\psi_{m-1})-\mathcal{L}(\psi_{n-1})+{N}(\psi_{m-1})-{N}(\psi_{n-1}))]]|\\ &\leq\gamma_{1}max_{\tau\in J}|\mathbf{N}^{-1}[q({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[(\mathcal{L}(\psi_{m-1})-\mathcal{L}(\psi_{n-1}))]]|\\ &+\gamma_{2}max_{\tau\in J}|\mathbf{N}^{-1}[p({{\varrho}}, {{\ell}}, {\kappa})\mathbf{N}[({N}(\psi_{m-1})-{N}(\psi_{n-1}))]]|\\\nonumber & = (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}}\frac{\tau^{{{\varrho}}}}{\Gamma({{\varrho}}+1)})||\psi_{m-1}-\psi_{n-1}||. \end{split} \end{align}$

(4.7)

Suppose $m = n+1$ , thus

$\begin{equation} \begin{split} ||\psi_{n+1}-\psi_{n}||\leq \gamma||\psi_{n}-\psi_{n-1}||\leq \gamma^{2}||\psi_{n-1}-\psi_{n-2}||\leq \cdots \leq \gamma^{n}||\psi_{1}-\psi_{0}||, \end{split} \end{equation}$

(4.8)

with $\gamma = (\gamma_{1}+\gamma_{2})(1-{{\varrho}}+{{\varrho}}\frac{\tau^{{{\varrho}}}}{\Gamma({{\varrho}}+1)})$ . Thus, we get

$\begin{equation} \begin{split} ||\psi_{m}-\psi_{n}||&\leq||\psi_{n+1}-\psi_{n}||+||\psi_{n+2}-\psi_{n+1}||+\cdots+||\psi_{m}-\psi_{m-1}||, \\ &\leq(\gamma^{n}+\gamma^{n+1}+\cdots+\gamma^{m-1})||\psi_{1}-\psi_{0}||\\ &\leq \gamma^{n}\left(\frac{1-\gamma^{m-n}}{1-\gamma}\right)||\psi_{1}||. \end{split} \end{equation}$

(4.9)

As $0 < \gamma < 1$ , we have $1-\gamma^{m-n} < 1$ . Thus,

$\begin{equation} \begin{split} ||\psi_{m}-\psi_{n}||\leq \frac{\gamma^{n}}{1-\gamma}max_{\tau\in J}||\psi_{1}||. \end{split} \end{equation}$

(4.10)

Since $||\psi_{1}|| < \infty, \ \ ||\psi_{m}-\psi_{n}||\rightarrow 0$ when $n \rightarrow \infty$ . As a result, $\psi_m$ is a Cauchy sequence in H, stated that the series $\psi_m$ is convergent.

5. Applications

Example 1. Consider the fractional-order system of Whitham-Broer-Kaup equations is given as

$\begin{array}{l} D_{{\tau}}^{\varrho}\psi(\upsilon, \tau)+{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}} = 0, \ \ 0 < \varrho \leq 1, \quad -1 < {\tau} \leq 1, \quad -10 \leq {\upsilon} \leq 10, \\ D_{{\tau}}^{\varrho}\varphi(\upsilon, \tau)+{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+3\frac{\partial^3{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^3}}-\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}} = 0, \end{array}$

(5.1)

the initial condition

$\begin{equation} \begin{split} &\psi({\upsilon}, 0) = \frac{1}{2}-8\tanh(-2{\upsilon}), \\ &\varphi({\upsilon}, 0) = 16-16\tanh^2(-2{\upsilon}). \end{split} \end{equation}$

(5.2)

On employing natural transform, we have

$\begin{equation} \begin{split} &{\mathbf{N}}[D_{\tau}^{\varrho}\psi({\upsilon}, {\tau})] = -{\mathbf{N}}\left[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\right], \\ &{\mathbf{N}}[D_{\tau}^{\varrho}\varphi({\upsilon}, {\tau})] = -{\mathbf{N}}\left[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+3\frac{\partial^3{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^3}}-\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\right], \end{split} \end{equation}$

(5.3)

Thus, we have

$\begin{equation} \begin{split} \frac{1}{\kappa^{\varrho}}{\mathbf{N}}[\psi({\upsilon}, {\tau})]-{\kappa}^{2-\varrho}{{\psi}({\upsilon}, 0)}& = -{\mathbf{N}}\Bigg[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg], \\ \frac{1}{\kappa^{\varrho}}{\mathbf{N}}[\varphi({\upsilon}, {\tau})]-{\kappa}^{2-\varrho}{{\psi}({\upsilon}, 0)}& = -{\mathbf{N}}\Bigg[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\\ &+3\frac{\partial^3{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^3}}-\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg].\\ \end{split} \end{equation}$

(5.4)

On simplification we have

$\begin{array}{l} {\mathbf{N}}[\psi({\upsilon}, {\tau})] = {{\kappa}^{2}}\Bigg[\frac{1}{2}-8\tanh(-2{\upsilon})\Bigg]-\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}{\mathbf{N}}\Bigg[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\\ +\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg], \\ {\mathbf{N}}[\varphi({\upsilon}, {\tau})] = {{\kappa}^{2}}\Bigg[16-16\tanh^2(-2{\upsilon})\Bigg]-\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}{\mathbf{N}}\Bigg[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\\ +3\frac{\partial^3{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^3}}-\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg].\end{array}$

(5.5)

Using the inverse natural transform, we get

$\begin{equation} \begin{split} \psi({\upsilon}, {\tau})& = \Bigg[\frac{1}{2}-8\tanh(-2{\upsilon})\Bigg]\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}\mathbf{N}\Bigg\{{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg\}\Bigg], \\ \varphi({\upsilon}, {\tau})& = \Bigg[16-16\tanh^2(-2{\upsilon})\Bigg]\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}\mathbf{N}\Bigg\{{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\\ &+3\frac{\partial^3{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^3}}-\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg\}\Bigg].\\ \end{split} \end{equation}$

(5.6)

5.1. $NTDM_{CF}$ solution

The series form solution for the unknown term $\psi(\upsilon, \tau)$ and $\varphi(\upsilon, \tau)$ is given as

$\begin{equation} \psi({\upsilon}, {\tau}) = \sum\limits_{{l} = 0}^{\infty}\psi_{{l}}({\upsilon}, {\tau}) \quad and \quad \varphi({\upsilon}, {\tau}) = \sum\limits_{{l} = 0}^{\infty}\psi_{{l}}({\upsilon}, {\tau}) . \end{equation}$

(5.7)

The non-linear functions define by Adomian polynomials are given as $\psi\psi_{\upsilon} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ , $\psi\varphi_{\upsilon} = \sum_{m = 0}^{\infty}\mathcal{B}_m$ and $\varphi\psi_{\upsilon} = \sum_{m = 0}^{\infty}\mathcal{C}_m$ , thus by means of these functions Eq (5.6) can be calculated as

$\begin{equation} \begin{split} \sum\limits_{{l} = 0}^{\infty}\psi_{{l}+1}({\upsilon}, {\tau})& = \frac{1}{2}-8\tanh(-2{\upsilon})\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}\mathbf{N}\Bigg\{\sum\limits_{{l} = 0}^{\infty}\mathcal A_{{l}}\\ &+\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg\}\Bigg], \\ \sum\limits_{{l} = 0}^{\infty}\varphi_{{l}+1}({\upsilon}, {\tau})& = 16-16\tanh^2(-2{\upsilon})\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}\mathbf{N}\Bigg\{\sum\limits_{{l} = 0}^{\infty}\mathcal B_{{l}}+\sum\limits_{{l} = 0}^{\infty}\mathcal C_{{l}}\\ &+3\frac{\partial^3{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^3}}-\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg\}\Bigg].\\ \end{split} \end{equation}$

(5.8)

Both side comparison of Eq (5.8), we achieve

$\begin{equation*} \begin{split} &\psi_{0}({\upsilon}, {\tau}) = \frac{1}{2}-8\tanh(-2{\upsilon}), \\ &\varphi_{0}({\upsilon}, {\tau}) = 16-16\tanh^2(-2{\upsilon}), \\ \end{split} \end{equation*}$

$\begin{equation} \begin{split} &\psi_{1}({\upsilon}, {\tau}) = -8\sec h^2(-2{\upsilon})\left(\varrho(\tau-1)+1\right), \\ &\varphi_{1}({\upsilon}, {\tau}) = -32{\rm{sech}}^2(-2{\upsilon})\tanh(-2{\upsilon})\left(\varrho(\tau-1)+1\right), \\ \end{split} \end{equation}$

(5.9)

$\begin{equation} \begin{split} \psi_{2}({\upsilon}, {\tau})& = -16{\rm{sech}}^2(-2{\upsilon})\Big(4{\rm{sech}}^2(-2{\upsilon})\\ &-8\tanh^2(-2{\upsilon})+3\tanh(-2{\upsilon})\Big)\Big((1-\varrho)^{2}\\ &+2\varrho(1-\varrho)\tau+\frac{\varrho^{2}\tau^2}{2}\Big), \\ \varphi_{2}({\upsilon}, {\tau})& = -32\sec h^2(-2{\upsilon})\{40\sec h^2(-2{\upsilon})\tanh(-2{\upsilon})\\ &+96\tanh(-2{\upsilon})-2\tanh^2(-2{\upsilon}) -32\tanh^3(-2{\upsilon})\\ &-25\sec h^2(-2{\upsilon})\}\Big((1-\varrho)^{2}+2\varrho(1-\varrho)\tau+\frac{\varrho^{2}\tau^2}{2}\Big).\\ \end{split} \end{equation}$

(5.10)

Thus, for $\psi_{{l}}$ and $\varphi_{{l}}$ with $({l}\geq3)$ the remaining terms are simply calculate. So, the result in series type is as

(5.11)

5.2. $NDM_{ABC}$ solution

The series form solution for the unknown term $\psi(\upsilon, \tau)$ and $\varphi(\upsilon, \tau)$ is given as

$\begin{equation} \begin{split} &\psi({\upsilon}, {\tau}) = \sum\limits_{{l} = 0}^{\infty}\psi_{{l}}({\upsilon}, {\tau}), \\ &\varphi({\upsilon}, {\tau}) = \sum\limits_{{l} = 0}^{\infty}\psi_{{l}}({\upsilon}, {\tau}).\\ \end{split} \end{equation}$

(5.12)

The non-linear functions by mean of Adomian polynomials is given as $\psi\psi_{{\upsilon}} = \sum_{{l} = 0}^{\infty}\mathcal A_{{l}}$ and $\psi^{2}\psi_{{\upsilon}} = \sum_{{l} = 0}^{\infty}\mathcal B_{{l}}$ , thus by mean of these functions Eq (5.6) can be calculated as

$\begin{equation} \begin{split} \sum\limits_{{l} = 0}^{\infty}\psi_{{l}+1}({\upsilon}, {\tau})& = \frac{1}{2}-8\tanh(-2{\upsilon})\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{\ell^\varrho(\kappa^\varrho+\varrho(\ell^\varrho-{\kappa}^\varrho))}{{\kappa}^{2\varrho}}\mathbf{N}\Bigg\{\sum\limits_{{l} = 0}^{\infty}\mathcal A_{{l}}+\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg\}\Bigg], \\ \sum\limits_{{l} = 0}^{\infty}\varphi_{{l}+1}({\upsilon}, {\tau})& = 16-16\tanh^2(-2{\upsilon})\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{\ell^\varrho(\kappa^\varrho+\varrho(\ell^\varrho-{\kappa}^\varrho))}{{\kappa}^{2\varrho}}\mathbf{N}\Bigg\{\sum\limits_{{l} = 0}^{\infty}\mathcal B_{{l}}+\sum\limits_{{l} = 0}^{\infty}\mathcal C_{{l}}+3\frac{\partial^3{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^3}}-\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg\}\Bigg].\\ \end{split} \end{equation}$

(5.13)

Both side comparison of Eq (5.13), we get

$\begin{equation*} \begin{split} &\psi_{0}({\upsilon}, {\tau}) = \frac{1}{2}-8\tanh(-2{\upsilon}), \\ &\varphi_{0}({\upsilon}, {\tau}) = 16-16\tanh^2(-2{\upsilon}), \\ \end{split} \end{equation*}$

$\begin{equation} \begin{split} &\psi_{1}({\upsilon}, {\tau}) = -8{\rm{sech}}^2(-2{\upsilon})\left(1-\varrho+\frac{\varrho\tau^\varrho}{\Gamma(\varrho+1)}\right), \\ &\varphi_{1}({\upsilon}, {\tau}) = -32{\rm{sech}}^2(-2{\upsilon})\tanh(-2{\upsilon})\left(1-\varrho+\frac{\varrho\tau^\varrho}{\Gamma(\varrho+1)}\right), \\ \end{split} \end{equation}$

(5.14)

$\begin{equation} \begin{split} \psi_{2}({\upsilon}, {\tau})& = -16\sec h^2(-2{\upsilon})\left(4\sec h^2(-2{\upsilon})-8\tanh^2(-2{\upsilon})+3\tanh(-2{\upsilon}) \right) \Bigg[\frac{\varrho^{2}\tau^{2\varrho}}{\Gamma(2\varrho+1)}\\ &+2\varrho(1-\varrho)\frac{\tau^{\varrho}}{\Gamma(\varrho+1)}+(1-\varrho)^{2}\Bigg], \\ \varphi_{2}({\upsilon}, {\tau})& = -32\sec h^2(-2{\upsilon})\{40\sec h^2(-2{\upsilon})\tanh(-2{\upsilon})+96\tanh(-2{\upsilon})-2\tanh^2(-2{\upsilon})\\ &-32\tanh^3(-2{\upsilon})-25\sec h^2(-2{\upsilon})\}\left[\frac{\varrho^{2}\tau^{2\varrho}}{\Gamma(2\varrho+1)}+2\varrho(1-\varrho)\frac{\tau^{\varrho}}{\Gamma(\varrho+1)}+(1-\varrho)^{2}\right].\\ \end{split} \end{equation}$

(5.15)

Thus, for $\psi_{{l}}$ with $({l}\geq3)$ the remaining component are simply calculated. So, the series form solution is given as

$\begin{equation} \begin{split} \psi({\upsilon}, {\tau})& = \sum\limits_{{l} = 0}^{\infty}\psi_{{l}}({\upsilon}, {\tau}) = \psi_{0}({\upsilon}, {\tau})+\psi_{1}({\upsilon}, {\tau})+\psi_{2}({\upsilon}, {\tau})+\cdots, \\ \psi({\upsilon}, {\tau})& = \frac{1}{2}-8\tanh(-2{\upsilon})-8{\rm{sech}}^2(-2{\upsilon})\left(1-\varrho+\frac{\varrho\tau^\varrho}{\Gamma(\varrho+1)}\right)\\ &-16\sec h^2(-2{\upsilon})\Bigg(4\sec h^2(-2{\upsilon})-8\tanh^2(-2{\upsilon})\\ &+3\tanh(-2{\upsilon}) \Bigg)\left[\frac{\varrho^{2}\tau^{2\varrho}}{\Gamma(2\varrho+1)}+2\varrho(1-\varrho)\frac{\tau^{\varrho}}{\Gamma(\varrho+1)}+(1-\varrho)^{2}\right]+\cdots.\\ \varphi({\upsilon}, {\tau})& = \sum\limits_{{l} = 0}^{\infty}\varphi_{{l}}({\upsilon}, {\tau}) = \varphi_{0}({\upsilon}, {\tau})+\varphi_{1}({\upsilon}, {\tau})+\varphi_{2}({\upsilon}, {\tau})+\cdots, \\ \varphi({\upsilon}, {\tau})& = 16-16\tanh^2(-2{\upsilon})-32{\rm{sech}}^2(-2{\upsilon})\tanh(-2{\upsilon})\left(1-\varrho+\frac{\varrho\tau^\varrho}{\Gamma(\varrho+1)}\right)\\ &-32\sec h^2(-2{\upsilon})\{40\sec h^2(-2{\upsilon})\tanh(-2{\upsilon})+96\tanh(-2{\upsilon})-2\tanh^2(-2{\upsilon})\\ &-32\tanh^3(-2{\upsilon})-25\sec h^2(-2{\upsilon})\}\Bigg[\frac{\varrho^{2}\tau^{2\varrho}}{\Gamma(2\varrho+1)}+2\varrho(1-\varrho)\frac{\tau^{\varrho}}{\Gamma(\varrho+1)}+(1-\varrho)^{2}\Bigg]+\cdots.\\ \end{split} \end{equation}$

(5.16)

The exact result is

$\begin{equation} \begin{split} &\psi({\upsilon}, {\tau}) = \frac{1}{2}-8\tanh\left\{-2\left({\upsilon}-\frac{{\tau}}{2}\right)\right\}, \\ &\varphi({\upsilon}, {\tau}) = 16-16\tanh^2\left\{-2\left({\upsilon}-\frac{{\tau}}{2}\right)\right\}.\\ \end{split} \end{equation}$

(5.17)

Example 2. Consider the fractional-order system of Whitham-Broer-Kaup equations is given as

$\begin{equation} \begin{split} &D_{{\tau}}^{\varrho}\psi(\upsilon, \tau)+{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{1}{2}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}} = 0, \\ &D_{{\tau}}^{\varrho}\varphi(\upsilon, \tau)+{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}-\frac{1}{2}\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}} = 0, \\ &0 < \varrho \leq 1, \quad -1 < {\tau} \leq 1, \quad -10 \leq {\upsilon} \leq 10, \end{split} \end{equation}$

(5.18)

with the initial condition

$\begin{equation} \begin{split} &\psi({\upsilon}, 0) = \lambda-\kappa\coth[\kappa({\upsilon}+\theta)], \\ &\varphi({\upsilon}, 0) = -\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]. \end{split} \end{equation}$

(5.19)

On employing natural transform, we have

$\begin{equation} \begin{split} &{\mathbf{N}}[D_{\tau}^{\varrho}\psi({\upsilon}, {\tau})] = -{\mathbf{N}}\left[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{1}{2}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\right], \\ &{\mathbf{N}}[D_{\tau}^{\varrho}\varphi({\upsilon}, {\tau})] = -{\mathbf{N}}\left[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}-\frac{1}{2}\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\right]. \end{split} \end{equation}$

(5.20)

Thus, we have

$\begin{equation} \begin{split} &\frac{1}{\kappa^{\varrho}}{\mathbf{N}}[\psi({\upsilon}, {\tau})]-{\kappa}^{2-\varrho}{{\psi}({\upsilon}, 0)} = -{\mathbf{N}}\Bigg[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{1}{2}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg], \\ &\frac{1}{\kappa^{\varrho}}{\mathbf{N}}[\varphi({\upsilon}, {\tau})]-{\kappa}^{2-\varrho}{{\psi}({\upsilon}, 0)} = -{\mathbf{N}}\Bigg[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}-\frac{1}{2}\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg].\\ \end{split} \end{equation}$

(5.21)

On simplification we have

$\begin{equation} \begin{split} {\mathbf{N}}[\psi({\upsilon}, {\tau})]& = {{\kappa}^{2}}\Bigg[\lambda-\kappa\coth[\kappa({\upsilon}+\theta)]\Bigg]-\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}{\mathbf{N}}\Bigg[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\\ &+\frac{1}{2}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg], \\ {\mathbf{N}}[\varphi({\upsilon}, {\tau})]& = {{\kappa}^{2}}\Bigg[-\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\Bigg]-\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}{\mathbf{N}}\Bigg[{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\\ &+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}-\frac{1}{2}\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg].\\ \end{split} \end{equation}$

(5.22)

Using the inverse natural transform, we have

$\begin{equation} \begin{split} \psi({\upsilon}, {\tau})& = \Bigg[\lambda-\kappa\coth[\kappa({\upsilon}+\theta)]\Bigg]\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}\mathbf{N}\Bigg\{{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{1}{2}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg\}\Bigg], \\ \varphi({\upsilon}, {\tau})& = \Bigg[-\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\Bigg]\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}\mathbf{N}\Bigg\{{{\psi({\upsilon}, {\tau})}}\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+{{\varphi({\upsilon}, {\tau})}}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}-\frac{1}{2}\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg\}\Bigg].\\ \end{split} \end{equation}$

(5.23)

5.3. $NDM_{CF}$ solution

The series form solution for the unknown term $\psi(\upsilon, \tau)$ and $\varphi(\upsilon, \tau)$ is given as

(5.24)

The non-linear functions by Adomian polynomials is given as $\psi\psi_{\upsilon} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ , $\psi\varphi_{\upsilon} = \sum_{m = 0}^{\infty}\mathcal{B}_m$ and $\varphi\psi_{\upsilon} = \sum_{m = 0}^{\infty}\mathcal{C}_m$ , thus by mean of these functions Eq (5.23) can be calculated as

$\begin{equation} \begin{split} \sum\limits_{{l} = 0}^{\infty}\psi_{{l}+1}({\upsilon}, {\tau})& = \lambda-\kappa\coth[\kappa({\upsilon}+\theta)]\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}\mathbf{N}\Bigg\{\sum\limits_{{l} = 0}^{\infty}\mathcal A_{{l}}+\frac{1}{2}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg\}\Bigg], \\ \sum\limits_{{l} = 0}^{\infty}\varphi_{{l}+1}({\upsilon}, {\tau})& = -\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\\ &-{\mathbf{N}}^{-1}\Bigg[\frac{{{\varrho}}(\kappa-\varrho({\kappa}-{{\varrho}}))}{{\kappa}^2}\mathbf{N}\Bigg\{\sum\limits_{{l} = 0}^{\infty}\mathcal B_{{l}}+\sum\limits_{{l} = 0}^{\infty}\mathcal C_{{l}}-\frac{1}{2}\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg\}\Bigg].\\ \end{split} \end{equation}$

(5.25)

Both sides comparisons of Eq (5.25), we achieve

$\begin{equation*} \begin{split} &\psi_{0}({\upsilon}, {\tau}) = \lambda-\kappa\coth[\kappa({\upsilon}+\theta)], \\ &\varphi_{0}({\upsilon}, {\tau}) = -\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)], \\ \end{split} \end{equation*}$

$\begin{equation} \begin{split} &\psi_{1}({\upsilon}, {\tau}) = -\lambda\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\left(\varrho(\tau-1)+1\right), \\ &\varphi_{1}({\upsilon}, {\tau}) = -\lambda\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\coth[\kappa({\upsilon}+\theta)]\left(\varrho(\tau-1)+1\right), \end{split} \end{equation}$

(5.26)

$\begin{equation} \begin{split} \psi_{2}({\upsilon}, {\tau})& = \lambda\kappa^4 {csch}^2[\kappa({\upsilon}+\theta)]\Big\{{2\lambda\kappa}\Big\{(1-{\varrho})^{2}3{\varrho}{{\tau}}+(1-{\varrho})^{3}+\frac{3{\varrho}^{2}(1-{\varrho}){{\tau}}^{2}}{2}+\frac{{\varrho}^{3}{{\tau}}^{3}}{3!}\Big\}\\ &-{(3\coth^2([\kappa({\upsilon}+\theta)]-1))}\Big((1-\varrho)^{2}+2\varrho(1-\varrho)\tau+\frac{\varrho^{2}\tau^2}{2}\Big)\Big\}, \\ \varphi_{2}({\upsilon}, {\tau})& = [2\lambda\kappa^5 {csch}^2[\kappa({\upsilon}+\theta)]]\left[{\lambda\kappa {csch}^2(3\coth^2([\kappa({\upsilon}+\theta)]-1))}\Big\{(1-{\varrho})^{2}3{\varrho}{{\tau}}+\right.\\ &\left.+(1-{\varrho})^{3} \frac{3{\varrho}^{2}(1-{\varrho}){{\tau}}^{2}}{2}+\frac{{\varrho}^{3}{{\tau}}^{3}}{3!}\Big\}+\frac{2\lambda\kappa {csch}^2\coth^2([\kappa({\upsilon}+\theta)]){\tau}^{3\varrho}}{\Gamma(\varrho+1)\Gamma(3\varrho+1)}\right.\\ &\left.-{2\lambda\coth(3 {csch}^2([\kappa({\upsilon}+\theta)]-1))}\Big((1-\varrho)^{2}+2\varrho(1-\varrho)\tau+\frac{\varrho^{2}\tau^2}{2}\Big)\right]. \end{split} \end{equation}$

(5.27)

Thus, for $\psi_{{l}}$ and $\varphi_{{l}}$ with $({l}\geq3)$ the remaining terms are simply calculate. So, the series form solution is as

$\begin{equation} \begin{split} \psi({\upsilon}, {\tau})& = \sum\limits_{{l} = 0}^{\infty}\psi_{{l}}({\upsilon}, {\tau}) = \psi_{0}({\upsilon}, {\tau})+\psi_{1}({\upsilon}, {\tau})+\psi_{2}({\upsilon}, {\tau})+\cdots, \\ \psi({\upsilon}, {\tau})& = \lambda-\kappa\coth[\kappa({\upsilon}+\theta)]-\lambda\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\left(\varrho(\tau-1)+1\right)\\ &+\lambda\kappa^4 {csch}^2[\kappa({\upsilon}+\theta)]\Big\{{2\lambda\kappa}\Big\{(1-{\varrho})^{2}3{\varrho}{{\tau}}+(1-{\varrho})^{3}+\frac{3{\varrho}^{2}(1-{\varrho}){{\tau}}^{2}}{2}+\frac{{\varrho}^{3}{{\tau}}^{3}}{3!}\Big\}\\ &-{(3\coth^2([\kappa({\upsilon}+\theta)]-1))}\Big((1-\varrho)^{2}+2\varrho(1-\varrho)\tau+\frac{\varrho^{2}\tau^2}{2}\Big)\Big\}+\cdots.\\ \varphi({\upsilon}, {\tau})& = \sum\limits_{{l} = 0}^{\infty}\varphi_{{l}}({\upsilon}, {\tau}) = \varphi_{0}({\upsilon}, {\tau})+\varphi_{1}({\upsilon}, {\tau})+\varphi_{2}({\upsilon}, {\tau})+\cdots, \\ \varphi({\upsilon}, {\tau})& = -\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]-\lambda\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\coth[\kappa({\upsilon}+\theta)]\left(\varrho(\tau-1)+1\right)\\ &+[2\lambda\kappa^5 {csch}^2[\kappa({\upsilon}+\theta)]]\Bigg[{\lambda\kappa {csch}^2(3\coth^2([\kappa({\upsilon}+\theta)]-1))}\Big\{(1-{\varrho})^{2}3{\varrho}{{\tau}}\\ &+(1-{\varrho})^{3}+\frac{3{\varrho}^{2}(1-{\varrho}){{\tau}}^{2}}{2}+\frac{{\varrho}^{3}{{\tau}}^{3}}{3!}\Big\}+\frac{2\lambda\kappa {csch}^2\coth^2([\kappa({\upsilon}+\theta)]){\tau}^{3\varrho}}{\Gamma(\varrho+1)\Gamma(3\varrho+1)}\\ &-{2\lambda \coth(3 {csch}^2([\kappa({\upsilon}+\theta)]-1))}\Big((1-\varrho)^{2}+2\varrho(1-\varrho)\tau+\frac{\varrho^{2}\tau^2}{2}\Big)\Bigg]+\cdots. \end{split} \end{equation}$

(5.28)

5.4. $NDM_{ABC}$ solution

The series form solution for the unknown term $\psi(\upsilon, \tau)$ and $\varphi(\upsilon, \tau)$ is given as

(5.29)

The non-linear function by mean of Adomian polynomials are define as $\psi\psi_{{\upsilon}} = \sum_{{l} = 0}^{\infty}\mathcal A_{{l}}$ and $\psi^{2}\psi_{{\upsilon}} = \sum_{{l} = 0}^{\infty}\mathcal B_{{l}}$ , thus by mean of these function Eq (5.23) can be calculated as

$\begin{equation} \begin{split} \sum\limits_{{l} = 0}^{\infty}\psi_{{l}+1}({\upsilon}, {\tau})& = \lambda-\kappa\coth[\kappa({\upsilon}+\theta)]\\ &+{\mathbf{N}}^{-1}\Bigg[\frac{\ell^\varrho(\kappa^\varrho+\varrho(\ell^\varrho-{\kappa}^\varrho))}{{\kappa}^{2\varrho}}\mathbf{N}\Bigg\{\sum\limits_{{l} = 0}^{\infty}\mathcal A_{{l}}+\frac{1}{2}\frac{\partial{{\psi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}+\frac{\partial{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}}}\Bigg\}\Bigg], \\ \sum\limits_{{l} = 0}^{\infty}\varphi_{{l}+1}({\upsilon}, {\tau})& = -\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\\ &+{\mathbf{N}}^{-1}\Bigg[\frac{\ell^\varrho(\kappa^\varrho+\varrho(\ell^\varrho-{\kappa}^\varrho))}{{\kappa}^{2\varrho}}\mathbf{N}\Bigg\{\sum\limits_{{l} = 0}^{\infty}\mathcal B_{{l}}+\sum\limits_{{l} = 0}^{\infty}\mathcal C_{{l}}-\frac{1}{2}\frac{\partial^2{{\varphi({\upsilon}, {\tau})}}}{\partial{{\upsilon}^2}}\Bigg\}\Bigg].\\ \end{split} \end{equation}$

(5.30)

Both side comparison of Eq (5.30), we achieve

$\begin{equation} \begin{split} &\psi_{1}({\upsilon}, {\tau}) = -\lambda\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\left(1-\varrho+\frac{\varrho\tau^\varrho}{\Gamma(\varrho+1)}\right), \\ &\varphi_{1}({\upsilon}, {\tau}) = -\lambda\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\coth[\kappa({\upsilon}+\theta)]\left(1-\varrho+\frac{\varrho\tau^\varrho}{\Gamma(\varrho+1)}\right), \\ \end{split} \end{equation}$

(5.31)

$\begin{equation} \begin{split} \psi_{2}({\upsilon}, {\tau})& = \lambda\kappa^4 {csch}^2[\kappa({\upsilon}+\theta)]\Big\{{2\lambda\kappa}\Big\{(1-{\varrho})^{2}3{\varrho}{{\tau}}+(1-{\varrho})^{3}+\frac{3{\varrho}^{2}(1-{\varrho}){{\tau}}^{2}}{2}+\frac{{\varrho}^{3}{{\tau}}^{3}}{3!}\Big\}\\ &-{(3\coth^2([\kappa({\upsilon}+\theta)]-1))}\left[\frac{\varrho^{2}\tau^{2\varrho}}{\Gamma(2\varrho+1)}+2\varrho(1-\varrho)\frac{\tau^{\varrho}}{\Gamma(\varrho+1)}+(1-\varrho)^{2}\right]\Big\}, \\ \varphi_{2}({\upsilon}, {\tau})& = [2\lambda\kappa^5 {csch}^2[\kappa({\upsilon}+\theta)]]\Bigg[{\lambda\kappa {csch}^2(3\coth^2([\kappa({\upsilon}+\theta)]-1))}\Big\{(1-{\varrho})^{2}3{\varrho}{{\tau}}+(1-{\varrho})^{3}\\ &+\frac{3{\varrho}^{2}(1-{\varrho}){{\tau}}^{2}}{2}+\frac{{\varrho}^{3}{{\tau}}^{3}}{3!}\Big\}+\frac{2\lambda\kappa {csch}^2\coth^2([\kappa({\upsilon}+\theta)]){\tau}^{3\varrho}}{\Gamma(\varrho+1)\Gamma(3\varrho+1)}\\ &-{2\lambda \coth(3 {csch}^2([\kappa({\upsilon}+\theta)]-1))}\Bigg[\frac{\varrho^{2}\tau^{2\varrho}}{\Gamma(2\varrho+1)}+2\varrho(1-\varrho)\frac{\tau^{\varrho}}{\Gamma(\varrho+1)}+(1-\varrho)^{2}\Bigg]\Bigg].\\ \end{split} \end{equation}$

(5.32)

Thus, for $\psi_{{l}}$ and $\varphi_{{l}}$ with $({l}\geq3)$ , the remaining terms are simply calculated. So, the series form solution is as

$\begin{array}{l}\psi({\upsilon}, {\tau}) = \sum\limits_{{l} = 0}^{\infty}\psi_{{l}}({\upsilon}, {\tau}) = \psi_{0}({\upsilon}, {\tau})+\psi_{1}({\upsilon}, {\tau})+\psi_{2}({\upsilon}, {\tau})+\cdots, \\ \psi({\upsilon}, {\tau}) = \lambda-\kappa\coth[\kappa({\upsilon}+\theta)]-\lambda\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\left(1-\varrho+\frac{\varrho\tau^\varrho}{\Gamma(\varrho+1)}\right)\\ +\lambda\kappa^4 {csch}^2[\kappa({\upsilon}+\theta)]\Big\{{2\lambda\kappa}\Big\{(1-{\varrho})^{2}3{\varrho}{{\tau}}+(1-{\varrho})^{3}+\frac{3{\varrho}^{2}(1-{\varrho}){{\tau}}^{2}}{2}+\frac{{\varrho}^{3}{{\tau}}^{3}}{3!}\Big\}\\ -{(3\coth^2([\kappa({\upsilon}+\theta)]-1))}\Bigg[\frac{\varrho^{2}\tau^{2\varrho}}{\Gamma(2\varrho+1)}+2\varrho(1-\varrho)\frac{\tau^{\varrho}}{\Gamma(\varrho+1)}+(1-\varrho)^{2}\Bigg]\Big\}+\cdots.\\ \varphi({\upsilon}, {\tau}) = \sum\limits_{{l} = 0}^{\infty}\varphi_{{l}}({\upsilon}, {\tau}) = \varphi_{0}({\upsilon}, {\tau})+\varphi_{1}({\upsilon}, {\tau})+\varphi_{2}({\upsilon}, {\tau})+\cdots, \\ \varphi({\upsilon}, {\tau}) = -\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]-\lambda\kappa^2 {csch}^2[\kappa({\upsilon}+\theta)]\coth[\kappa({\upsilon}+\theta)]\left(1-\varrho+\frac{\varrho\tau^\varrho}{\Gamma(\varrho+1)}\right)\\ +[2\lambda\kappa^5 {csch}^2[\kappa({\upsilon}+\theta)]]\Bigg[{\lambda\kappa {csch}^2(3\coth^2([\kappa({\upsilon}+\theta)]-1))}\Big\{(1-{\varrho})^{2}3{\varrho}{{\tau}}+(1-{\varrho})^{3}\\ +\frac{3{\varrho}^{2}(1-{\varrho}){{\tau}}^{2}}{2}+\frac{{\varrho}^{3}{{\tau}}^{3}}{3!}\Big\}+\frac{2\lambda\kappa {csch}^2\coth^2([\kappa({\upsilon}+\theta)]){\tau}^{3\varrho}}{\Gamma(\varrho+1)\Gamma(3\varrho+1)}\\ -{2\lambda \coth(3 {csch}^2([\kappa({\upsilon}+\theta)]-1))}\Bigg[\frac{\varrho^{2}\tau^{2\varrho}}{\Gamma(2\varrho+1)}+2\varrho(1-\varrho)\frac{\tau^{\varrho}}{\Gamma(\varrho+1)}+(1-\varrho)^{2}\Bigg]\Bigg]+\cdots. \end{array}$

(5.33)

We achieve the series type result at integer-order $\varrho = 1, \kappa = 0.1$ , $\lambda = 0.005$ , $\theta = 10$ , as

$\begin{aligned} \psi(\upsilon, \tau) = & 0.005-0.1 \operatorname{coth}(0.1 \upsilon+10)-0.0005 {csch}^{2}(0.1 \upsilon+10) \tau\\ &+5 \times 10^{-7} {csch}^{2}(0.1 \upsilon+10) 0.003 \tau^{3} \\ &\left.-0.5\left(3 \operatorname{coth}^{2}(0.1 \upsilon+10)-1 .\right)\right) \tau^{2}, \\ \varphi(\upsilon, \tau) = &-0.01 {csch}^{2}(0.1 \upsilon+10)-0.000010 {csch}^{2}(0.1 \upsilon+10) \\ &\times \operatorname{coth}(0.1 \upsilon+10) \tau+1.0 \times 10^{-7} {csch}^{2}(0.1 \upsilon+10)\\ &\times \left[8.3 \times 10^{-5} \tau^{3} {csch}^{2}(0.1 \upsilon+10)(3 \operatorname{coth}(0.1 \upsilon+10)-1) \right.\\ &\left.-\tau^{2} \operatorname{coth}(0.1 \upsilon+10)\left(3 {csch}^{2}(0.1 \upsilon+10)-1\right) \right.\\ &\left.+1.6 \times 10^{-4} \tau^{3} {cosec} h^{2}(0.1 \upsilon+10) \operatorname{coth}(0.1 \upsilon+10)\right] . \end{aligned}$

The exact result of Eq (5.18) at $\varrho = 1$ , and taking $\kappa = 0.1$ , $\lambda = 0.005$ , $\theta = 10$ ,

$\begin{equation} \begin{split} &\psi({\upsilon}, {\tau}) = =\lambda-\kappa\coth[\kappa({\upsilon}+\theta-\lambda {\tau})], \\ &{\varphi({\upsilon}, {\tau})} = -\kappa^2 {csch}^2[\kappa({\upsilon}+\theta-\lambda {\tau})]. \end{split} \end{equation}$

(5.34)

6. Numerical results and discussion

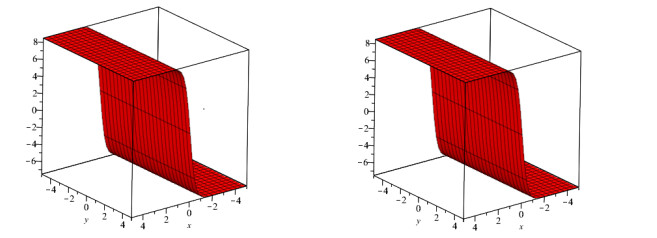
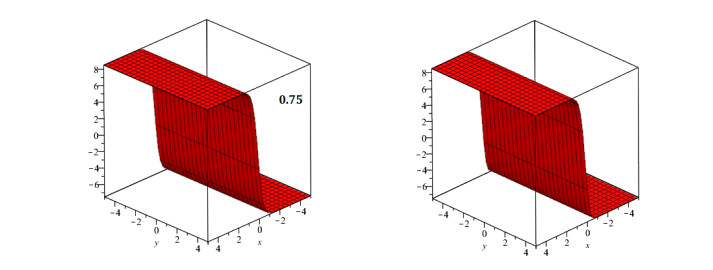
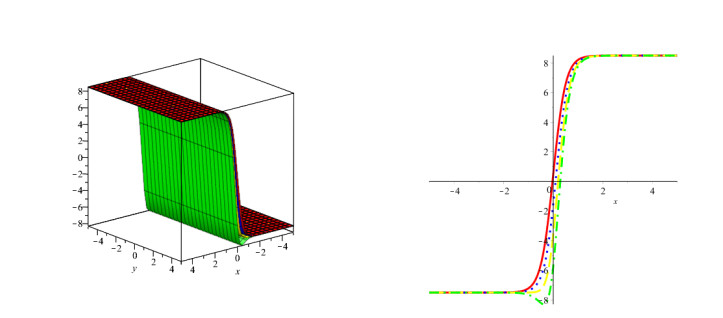
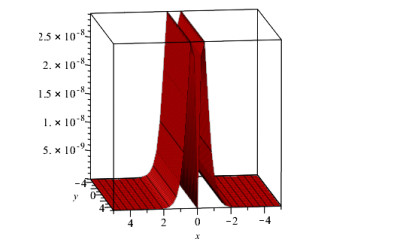
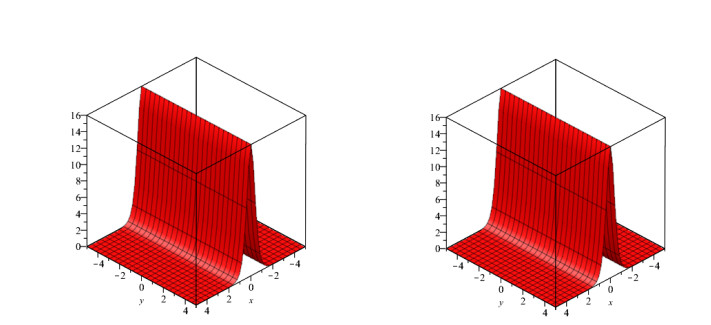
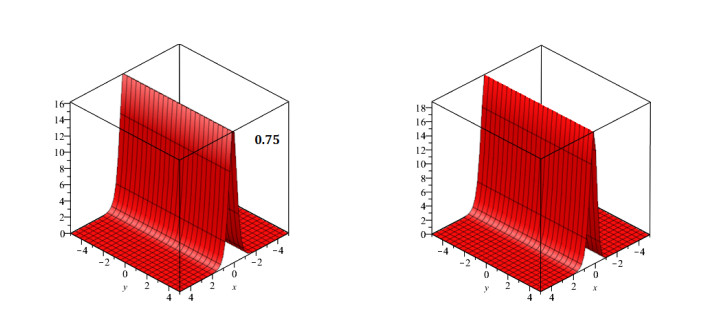
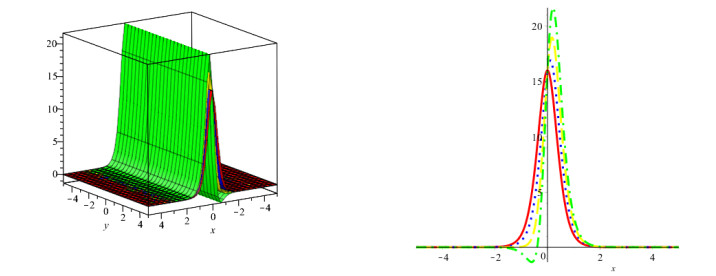
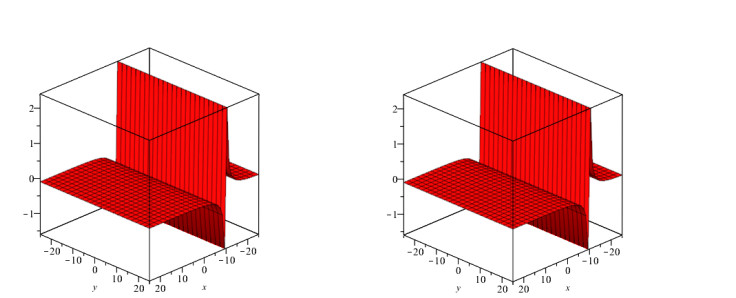
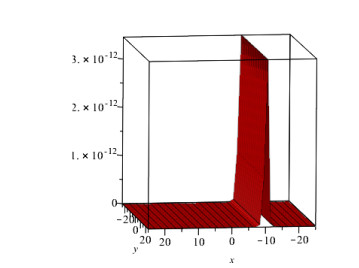
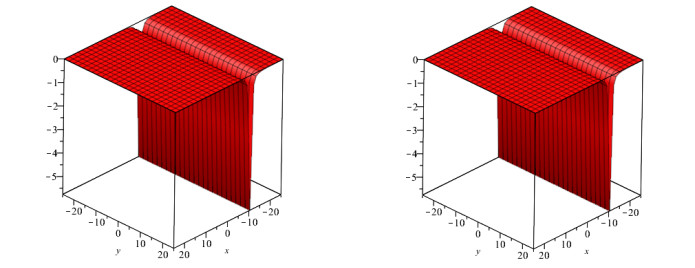
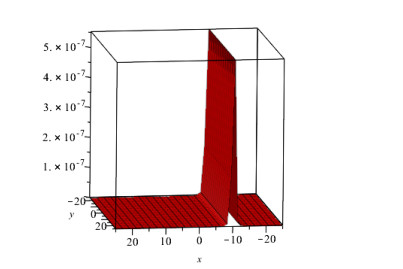
In this study, we investigated the numerical solution of coupled fractional Whitham-Broer-Kaup equation systems using two novel approaches. For any order and different values of the space and time variables, numerical data for the coupled fractional Whitham-Broer-Kaup equations can be found using Maple. We create numerical simulations for system 1 at various $\upsilon$ and $\tau$ values in Tables 1 and 2. The Adomian decomposition approach, variational iteration method, optimal homotopy asymptotic method, and natural decomposition method are numerically compared in Tables 3 and in terms of absolute error. and display the results of calculations performed for the coupled system taken into account in Problem 2. We can conclude that the Natural decomposition approach yields more accurate results based on the data in the tables above. For $\psi(\upsilon, \tau)$ of Problem 1, shows the behavior of the exact and Natural decomposition approach result, while shows the behavior of the analytical result at various fractional-orders of $\varrho$ . shows the solution to the equation $\psi(\upsilon, \tau)$ in various fractional orders, whereas shows the absolute error. The behavior of the exact and analytical solutions for $\varphi(\upsilon, \tau)$ is shown in , while the behavior of the analytical result at various fractional orders of $\varrho$ is shown in and . The behavior of the exact and analytical solution for $\psi(\upsilon, \tau)$ is depicted in , while the absolute error for Problem 2 is shown in . Similarly, the behavior of the exact and analytical solution for $\varphi(\upsilon, \tau)$ is depicted in Figure 10, while the absolute error is shown in Figure 11 for Problem 2.

Table 1. The suggested techniques result for

$\psi({\upsilon}, {\tau})$ at various fractional-orders of Example 1.

$({\upsilon}, {\tau})$	$\psi({\upsilon}, {\tau})$ at ${ \varrho }=$ 0.6	$\psi({\upsilon}, {\tau})$ at ${ \varrho }=$ 0.8	$(NTDM_{ABC})$ at ${ \varrho }=$ 1	$(NTDM_{CF})$ at ${ \varrho }=$ 1	Exact solution
(0.2, 0.01)	3.538802	3.538856	3.538907	3.538907	3.538907
(0.4, 0.02)	5.811722	5.811755	5.811846	5.811846	5.811846
(0.6, 0.03)	7.168821	7.168876	7.168992	7.168992	7.168992
(0.2, 0.01)	3.525702	3.525764	3.525891	3.525891	3.525891
(0.4, 0.02)	5.803176	5.803245	5.803337	5.803337	5.803337
(0.6, 0.03)	7.164207	7.164278	7.164348	7.164348	7.164348
(0.2, 0.01)	3.537413	3.537498	3.537537	3.537537	3.537537
(0.4, 0.02)	5.810812	5.810856	5.810952	5.810952	5.810952
(0.6, 0.03)	7.168423	7.168479	7.168504	7.168504	7.168504
(0.2, 0.01)	3.536701	3.536746	3.536853	3.536853	3.536853
(0.4, 0.02)	5.810411	5.810466	5.810504	5.810504	5.810504
(0.6, 0.03)	7.168112	7.168160	7.168260	7.168260	7.168260
(0.2, 0.01)	3.536076	3.536134	3.536168	3.536168	3.536168
(0.4, 0.02)	5.810002	5.810010	5.810057	5.810057	5.810057
(0.6, 0.03)	7.168000	7.168002	7.168016	7.168016	7.168016

| Show Table

DownLoad: CSV

Table 2. The suggested techniques solution for

$\varphi({\upsilon}, {\tau})$ at various fractional-orders of Example 1.

$({\upsilon}, {\tau})$	$\varphi({\upsilon}, {\tau})$ at ${ \varrho }=$ 0.6	$\varphi({\upsilon}, {\tau})$ at ${ \varrho }=$ 0.8	$(NTDM_{ABC})$ at ${ \varrho }=$ 1	$(NTDM_{CF})$ at ${ \varrho }=$ 1	Exact solution
(0.2, 0.01)	13.691122	13.691178	13.691260	13.691260	13.691260
(0.4, 0.02)	8.946002	8.946023	8.946070	8.946070	8.946070
(0.6, 0.03)	4.881079	4.881103	4.881133	4.881133	4.881133
(0.2, 0.01)	13.710837	13.710898	13.710995	13.710995	13.710995
(0.4, 0.02)	8.968516	8.968579	8.968653	8.968653	8.968653
(0.6, 0.03)	4.896526	4.896588	4.896615	4.896615	4.896615
(0.2, 0.01)	13.693268	13.693302	13.693340	13.693340	13.693340
(0.4, 0.02)	8.948378	8.948412	8.948446	8.948446	8.948446
(0.6, 0.03)	4.882679	4.882705	4.882761	4.882761	4.882761
(0.2, 0.01)	13.694302	13.694323	13.694380	13.694380	13.694380
(0.4, 0.02)	8.949587	8.949612	8.949634	8.949634	8.949634
(0.6, 0.03)	4.883501	4.883525	4.883575	4.883575	4.883575
(0.2, 0.01)	13.695389	13.695402	13.695420	13.695420	13.695420
(0.4, 0.02)	8.950736	8.950778	8.950823	8.950823	8.950823
(0.6, 0.03)	4.884288	4.884326	4.884389	4.884389	4.884389

| Show Table

DownLoad: CSV

Table 3. Absolute Error (AE) comparison for

$\psi({\upsilon}, {\tau})$ at

${\varrho = 1}$ obtained by different techniques.

$({\upsilon}, {\tau})$	AE Of ADM ^[50]	AE Of VIM ^[51]	AE Of OHAM ^[52]	AE of $(NTDM_{ABC})$	AE of $(NTDM_{CF})$
(0.1, 0.2)	1.05983 ${ \times }10^{-5}$	1.34144 ${ \times }10^{-6}$	1.18169 ${ \times }10^{-7}$	1.45621 ${ \times }10^{-10}$	1.45621 ${ \times }10^{-10}$
(0.1, 0.4)	9.75585 ${ \times }10^{-6}$	3.78688 ${ \times }10^{-6}$	3.15656 ${ \times }10^{-7}$	2.95673 ${ \times }10^{-09}$	2.95673 ${ \times }10^{-09}$
(0.1, 0.6)	8.77423 ${ \times }10^{-6}$	6.27984 ${ \times }10^{-6}$	4.92412 ${ \times }10^{-7}$	1.10432 ${ \times }10^{-8}$	1.10432 ${ \times }10^{-8}$
(0.2, 0.2)	4.37319 ${ \times }10^{-5}$	1.38978 ${ \times }10^{-6}$	1.12395 ${ \times }10^{-7}$	1.44301 ${ \times }10^{-10}$	1.44301 ${ \times }10^{-10}$
(0.2, 0.4)	3.82189 ${ \times }10^{-5}$	3.51189 ${ \times }10^{-6}$	2.86457 ${ \times }10^{-6}$	2.35213 ${ \times }10^{-09}$	2.35213 ${ \times }10^{-09}$
(0.2, 0.6)	3.51272 ${ \times }10^{-5}$	6.10117 ${ \times }10^{-5}$	4.51245 ${ \times }10^{-6}$	1.02145 ${ \times }10^{-08}$	1.02145 ${ \times }10^{-08}$
(0.3, 0.2)	9.62833 ${ \times }10^{-5}$	1.25698 ${ \times }10^{-5}$	1.13664 ${ \times }10^{-6}$	2.27511 ${ \times }10^{-10}$	2.27511 ${ \times }10^{-10}$
(0.3, 0.4)	8.84418 ${ \times }10^{-5}$	3.61977 ${ \times }10^{-5}$	2.62353 ${ \times }10^{-6}$	2.02314 ${ \times }10^{-09}$	2.02314 ${ \times }10^{-09}$
(0.3, 0.6)	8.33563 ${ \times }10^{-5}$	5.96721 ${ \times }10^{-5}$	4.46642 ${ \times }10^{-6}$	1.03541 ${ \times }10^{-08}$	1.03541 ${ \times }10^{-08}$
(0.4, 0.2)	1.86687 ${ \times }10^{-4}$	1.24938 ${ \times }10^{-5}$	9.24537 ${ \times }10^{-5}$	1.32601 ${ \times }10^{-10}$	1.32601 ${ \times }10^{-10}$
(0.4, 0.4)	1.72542 ${ \times }10^{-4}$	3.52859 ${ \times }10^{-5}$	2.63564 ${ \times }10^{-5}$	1.11427 ${ \times }10^{-09}$	1.11427 ${ \times }10^{-09}$
(0.4, 0.6)	1.58687 ${ \times }10^{-4}$	5.81821 ${ \times }10^{-5}$	4.65446 ${ \times }10^{-5}$	1.87965 ${ \times }10^{-08}$	1.87965 ${ \times }10^{-08}$
(0.5, 0.2)	2.88628 ${ \times }10^{-4}$	1.21847 ${ \times }10^{-5}$	9.72736 ${ \times }10^{-5}$	1.78145 ${ \times }10^{-10}$	1.78145 ${ \times }10^{-10}$
(0.5, 0.4)	2.47825 ${ \times }10^{-4}$	3.44373 ${ \times }10^{-5}$	2.33457 ${ \times }10^{-5}$	1.43901 ${ \times }10^{-09}$	1.43901 ${ \times }10^{-09}$
(0.5, 0.6)	2.47295 ${ \times }10^{-4}$	5.47346 ${ \times }10^{-5}$	4.38895 ${ \times }10^{-5}$	1.43421 ${ \times }10^{-08}$	1.43421 ${ \times }10^{-08}$

| Show Table

DownLoad: CSV

Table 4. Absolute Error (AE) comparison for

$\varphi({\upsilon}, {\tau})$ at

${\varrho = 1}$ obtained by different techniques.

$({\upsilon, \tau})$	AE Of ADM ^[50]	AE Of VIM ^[51]	AE Of OHAM ^[52]	AE of $(NTDM_{ABC})$	AE of $(NTDM_{CF})$
(0.1, 0.2)	6.52318 ${ \times }10^{-4}$	1.23581 ${ \times }10^{-5}$	5.72451 ${ \times }10^{-6}$	1.73281 ${ \times }10^{-10}$	1.73281 ${ \times }10^{-10}$
(0.1, 0.4)	5.87694 ${ \times }10^{-4}$	3.53456 ${ \times }10^{-5}$	3.24632 ${ \times }10^{-6}$	2.00931 ${ \times }10^{-09}$	2.00931 ${ \times }10^{-09}$
(0.1, 0.6)	5.72618 ${ \times }10^{-4}$	5.63261 ${ \times }10^{-5}$	3.38923 ${ \times }10^{-6}$	1.08631 ${ \times }10^{-08}$	1.08631 ${ \times }10^{-08}$
(0.2, 0.2)	1.44292 ${ \times }10^{-3}$	1.18127 ${ \times }10^{-5}$	5.45771 ${ \times }10^{-6}$	1.11621 ${ \times }10^{-10}$	1.11621 ${ \times }10^{-10}$
(0.2, 0.4)	1.33452 ${ \times }10^{-3}$	3.34512 ${ \times }10^{-5}$	2.86341 ${ \times }10^{-5}$	2.07941 ${ \times }10^{-09}$	2.07941 ${ \times }10^{-09}$
(0.2, 0.6)	1.25527 ${ \times }10^{-3}$	5.47838 ${ \times }10^{-5}$	2.82545 ${ \times }10^{-5}$	1.03361 ${ \times }10^{-08}$	1.03361 ${ \times }10^{-08}$
(0.3, 0.2)	2.14563 ${ \times }10^{-3}$	1.14848 ${ \times }10^{-5}$	5.36746 ${ \times }10^{-5}$	1.16031 ${ \times }10^{-10}$	1.16031 ${ \times }10^{-10}$
(0.3, 0.4)	1.84963 ${ \times }10^{-3}$	3.22828 ${ \times }10^{-5}$	2.74231 ${ \times }10^{-5}$	2.006841 ${ \times }10^{-09}$	2.006841 ${ \times }10^{-09}$
(0.3, 0.6)	1.72318 ${ \times }10^{-3}$	5.32558 ${ \times }10^{-4}$	2.66463 ${ \times }10^{-5}$	2.86931 ${ \times }10^{-08}$	2.86931 ${ \times }10^{-08}$
(0.4, 0.2)	2.98211 ${ \times }10^{-3}$	1.11468 ${ \times }10^{-4}$	5.23838 ${ \times }10^{-5}$	4.09741 ${ \times }10^{-10}$	4.09741 ${ \times }10^{-10}$
(0.4, 0.4)	2.59845 ${ \times }10^{-3}$	3.13456 ${ \times }10^{-4}$	2.72338 ${ \times }10^{-3}$	3.16439 ${ \times }10^{-09}$	3.16439 ${ \times }10^{-09}$
(0.4, 0.6)	2.61896 ${ \times }10^{-3}$	5.15382 ${ \times }10^{-3}$	2.54328 ${ \times }10^{-3}$	1.00693 ${ \times }10^{-09}$	1.00693 ${ \times }10^{-09}$
(0.5, 0.2)	3.84384 ${ \times }10^{-3}$	9.86396 ${ \times }10^{-3}$	4.83832 ${ \times }10^{-3}$	1.00631 ${ \times }10^{-10}$	1.00631 ${ \times }10^{-10}$
(0.5, 0.4)	3.58728 ${ \times }10^{-3}$	2.84228 ${ \times }10^{-3}$	2.84563 ${ \times }10^{-3}$	2.12692 ${ \times }10^{-09}$	2.12692 ${ \times }10^{-09}$
(0.5, 0.6)	3.35348 ${ \times }10^{-3}$	4.72446 ${ \times }10^{-3}$	2.52741 ${ \times }10^{-3}$	1.00471 ${ \times }10^{-09}$	1.00471 ${ \times }10^{-09}$

| Show Table

DownLoad: CSV

Table 5. The suggested techniques result for

$\psi({\upsilon}, {\tau})$ at various fractional-orders of Example 2.

$({\upsilon}, {\tau})$	$\psi({\upsilon}, {\tau})$ at ${ \varrho }=$ 0.5	$\psi({\upsilon}, {\tau})$ at ${ \varrho }=$ 0.75	$(NTDM_{ABC})$ at ${ \varrho }=$ 1	$(NTDM_{CF})$ at ${ \varrho }=$ 1	Exact result
(0.2, 0.01)	-0.124902	-0.124896	-0.124892	-0.124892	-0.124892
(0.4, 0.01)	-0.123585	-0.123568	-0.123553	-0.123553	-0.123553
(0.6, 0.01)	-0.122297	-0.122292	-0.122280	-0.122280	-0.122280
(0.2, 0.02)	-0.124908	-0.124898	-0.124892	-0.124892	-0.124892
(0.4, 0.02)	-0.123597	-0.123578	-0.123553	-0.123553	-0.123553
(0.6, 0.02)	-0.122299	-0.122293	-0.122280	-0.122280	-0.122280
(0.2, 0.03)	-0.124909	-0.124899	-0.124892	-0.124892	-0.124892
(0.4, 0.03)	-0.123586	-0.123568	-0.123553	-0.123553	-0.123553
(0.6, 0.03)	-0.122299	-0.122289	-0.122280	-0.122280	-0.122280
(0.2, 0.04)	-0.124908	-0.124896	-0.124892	-0.124892	-0.124892
(0.4, 0.04)	-0.123589	-0.123576	-0.123553	-0.123553	-0.123553
(0.6, 0.04)	-0.122296	-0.122288	-0.122280	-0.122280	-0.122280
(0.2, 0.05)	-0.124905	-0.124897	-0.124892	-0.124892	-0.124892
(0.4, 0.05)	-0.123578	-0.123564	-0.123553	-0.123553	-0.123553
(0.6, 0.05)	-0.122298	-0.122290	-0.122280	-0.122280	-0.122280

| Show Table

DownLoad: CSV

Table 6. The suggested techniques result for

$\varphi({\upsilon}, {\tau})$ at various fractional-orders of Example 2.

$({\upsilon}, {\tau})$	$\varphi({\upsilon}, {\tau})$ at ${ \varrho }=$ 0.5	$\varphi({\upsilon}, {\tau})$ at ${ \varrho }=$ 0.75	$(NTDM_{ABC})$ at ${ \varrho }=$ 1	$(NTDM_{CF})$ at ${ \varrho }=$ 1	Exact result
(0.2, 0.01)	-0.006894	-0.006886	-0.006872	-0.006872	-0.006872
(0.4, 0.01)	-0.006546	-0.006537	-0.006525	-0.006525	-0.006525
(0.6, 0.01)	-0.006219	-0.006213	-0.006200	-0.006200	-0.006200
(0.2, 0.02)	-0.006894	-0.006885	-0.006872	-0.006872	-0.006872
(0.4, 0.02)	-0.006542	-0.006534	-0.006525	-0.006525	-0.006525
(0.6, 0.02)	-0.006219	-0.006213	-0.006200	-0.006200	-0.006200
(0.2, 0.03)	-0.006889	-0.006882	-0.006872	-0.006872	-0.006872
(0.4, 0.03)	-0.006543	-0.006536	-0.006525	-0.006525	-0.006525
(0.6, 0.03)	-0.006216	-0.006208	-0.006200	-0.006200	-0.006200
(0.2, 0.04)	-0.006889	-0.006881	-0.006872	-0.006872	-0.006872
(0.4, 0.04)	-0.006541	-0.006532	-0.006525	-0.006525	-0.006525
(0.6, 0.04)	-0.006218	-0.006207	-0.006200	-0.006200	-0.006200
(0.2, 0.05)	-0.006889	-0.006883	-0.006872	-0.006872	-0.006872
(0.4, 0.05)	-0.006546	-0.006538	-0.006525	-0.006525	-0.006525
(0.6, 0.05)	-0.006223	-0.006213	-0.006200	-0.006200	-0.006200

| Show Table

DownLoad: CSV

Figure 1. The actual and analytic solutions for

$\psi({\upsilon}, {\tau})$ at

$\varrho = 1$ of Example

$1$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. The analytic result for

$\psi({\upsilon}, {\tau})$ at

$\varrho = 0.8, 0.6$ of Example

$1$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. The analytic solution graph at different value of

$\varrho$ for

$\psi({\upsilon}, {\tau})$ of Example

$1$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. The absolute error for

$\psi({\upsilon}, {\tau})$ of Example

$1$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. The actual and analytic result for

$\varphi({\upsilon}, {\tau})$ at

$\varrho = 1$ of Example

$1$ .

DownLoad: Full-Size Img PowerPoint

Figure 6. The analytic result graph for

$\varphi({\upsilon}, {\tau})$ at

$\varrho = 0.8, 0.6$ of Example

$1$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. The analytic result graph at different value of

$\varrho$ for

$\varphi({\upsilon}, {\tau})$ of Example

$1$ .

DownLoad: Full-Size Img PowerPoint

Figure 8. The exact and analytic solutions graph for

$\psi({\upsilon}, {\tau})$ at

$\varrho = 1$ of Example

$2$ .

DownLoad: Full-Size Img PowerPoint

Figure 9. The absolute error for

$\psi({\upsilon}, {\tau})$ of Example

$2$ .

DownLoad: Full-Size Img PowerPoint

Figure 10. The exact and analytic solutions for

$\varphi({\upsilon}, {\tau})$ at

$\varrho = 1$ of Example

$2$ .

DownLoad: Full-Size Img PowerPoint

Figure 11. The absolute error for

$\varphi({\upsilon}, {\tau})$ of Example

$2$ .

DownLoad: Full-Size Img PowerPoint

7. Conclusions

The Atangana-Baleanu and Caputo-Fabrizio operators are used in this work to attempt a semi-analytic solution of fractional Whitham-Broer-Kaup equations. To show and confirm the efficiency of the recommended technique, two examples are solved. The numerical results show that the proposed method for solving time-fractional Whitham-Broer-Kaup equations is quite effective and accurate. According to numerical data, the method is very effective and reliable for getting close solutions for nonlinear fractional partial differential equations. Compared to other analytical methods, the proposed method is a quick and easy way to look into the numerical solution of nonlinear coupled systems of fractional partial differential equations. The proposed method gives solutions in the form of a series that is more accurate and take less time to figure out. The calculated results have been displayed graphically and in tables. For both considerably coupled systems, computations were done to determine the absolute error. Several computational solutions are contrasted with well-known analytical methods and the precise results at $\varrho = 1$ . Fewer calculations and more precision are two advantages of the present approaches. Lastly, we can say that the proposed approaches are very effective and useful and that they can be used to study any nonlinear problems that come up in complex phenomena.

Conflict of interest

The authors declare that they have no competing interests.

References

[1]	A. Bekir, E. H. M. Zahran, Bright and dark soliton solutions for the complex Kundu-Eckhaus equation, Optik, 223 (2020), 165233. https://doi.org/10.1016/j.ijleo.2020.165233 doi: 10.1016/j.ijleo.2020.165233
[2]	A. Bekir, E. H. M. Zahran, Three distinct and impressive visions for the soliton solutions to the higher-order nonlinear Schrö dinger equation, Optik, 228 (2021), 166157. https://doi.org/10.1016/j.ijleo.2020.166157 doi: 10.1016/j.ijleo.2020.166157
[3]	A. Bekir, E. H. M. Zahran, New vision for the soliton solutions to the complex Hirota-dynamical model, Phys. Scripta, 96 (2021), 055212. https://doi.org/10.1088/1402-4896/abe889 doi: 10.1088/1402-4896/abe889
[4]	A. Biswas, 1-soliton solution of the K (m, n) equation with generalized evolution, Phys. Lett. A, 372 (2008), 4601–4602. https://doi.org/10.1016/j.physleta.2008.05.002 doi: 10.1016/j.physleta.2008.05.002
[5]	H. Triki, A. M. Wazwaz, Bright and dark soliton solutions for a K (m, n) equation with t-dependent coefficients, Phys. Lett. A, 373 (2009), 2162–2165. https://doi.org/10.1016/j.physleta.2009.04.029 doi: 10.1016/j.physleta.2009.04.029
[6]	H. Triki, A. M. Wazwaz, Bright and dark solitons for a generalized Korteweg-de Vries-modified Korteweg-de Vries equation with high-order nonlinear terms and time-dependent coefficients, Can. J. Phys., 89 (2011), 253–259. https://doi.org/10.1139/P11-015 doi: 10.1139/P11-015
[7]	N. A. Kudryashov, The Painlevé approach for finding solitary wave solutions of nonlinear non-integrable differential equations, Optik, 183 (2019), 642–649. https://doi.org/10.1016/j.ijleo.2019.02.087 doi: 10.1016/j.ijleo.2019.02.087
[8]	A. Bekir, E. H. M. Zahran, Optical soliton solutions of the thin-film ferro-electric materials equation according to the Painlevé approach, Opt. Quantum Electron., 53 (2021), 118. https://doi.org/10.1007/s11082-021-02754-w doi: 10.1007/s11082-021-02754-w
[9]	A. Bekir, E. H. M. Zahran, Painlevé approach and its applications to get new exact solutions of three biological models instead of its numerical solutions, Int. J. Mod. Phys. B, 34 (2020), 2050270. https://doi.org/10.1142/S0217979220502707 doi: 10.1142/S0217979220502707
[10]	A. Bekir, E. H. M. Zahran, New visions of the soliton solutions to the modified nonlinear Schrodinger equation, Optik, 232 (2021), 166539. https://doi.org/10.1016/j.ijleo.2021.166539 doi: 10.1016/j.ijleo.2021.166539
[11]	M. S. M. Shehata, H. Rezazadeh, E. H. M. Zahran, E. Tala-Tebue, A. Bekir, New optical soliton solutions of the perturbed Fokas-Lenells equation, Commun. Theor. Phys., 71 (2019), 1275c1280. https://doi.org/10.1088/0253-6102/71/11/1275 doi: 10.1088/0253-6102/71/11/1275
[12]	A. Bekir, E. H. M. Zahran, New multiple-different impressive perceptions for the solitary solution to the magneto-optic waveguides with anti-cubic nonlinearity, Optik, 240 (2021), 166939. https://doi.org/10.1016/j.ijleo.2021.166939 doi: 10.1016/j.ijleo.2021.166939
[13]	A. Biswas, Y. Yildirim, E. Yasar, M. F. Mahmood, A. S. Alshomrani, Q. Zhou, et al., Optical soliton perturbation for Radhakrishnan-Kundu-Lakshmanan equation with a couple of integration schemes, Optik, 163 (2018), 126–136. https://doi.org/10.1016/j.ijleo.2018.02.109
[14]	N. A. Kudryashov, D. V. Safonova, A. Biswas, Painleve analysis and a solution to the traveling wave reduction of the Radhakrishnan-Kundu-Lakshmanan equation, Regul. Chaotic Dyn., 24 (2019), 607–614. https://doi.org/10.1134/S1560354719060029 doi: 10.1134/S1560354719060029
[15]	H. U. Rehman, M. S. Saleem, A. M. Sultan, M. Iftikhar, Comments on dynamics of optical solitons with Radhakrishnan-Kundu-Lakshmanan model via two reliable integration schemes, Optik, 178 (2019), 557–566. https://doi.org/10.1016/j.ijleo.2018.12.010 doi: 10.1016/j.ijleo.2018.12.010
[16]	T. A. Sulaiman, H. Bulut, G. Yel, S. S. Atas, Optical solitons to the fractional perturbed Radhakrishnan-Kundu-Lakshmanan model, Opt. Quant. Electron., 50 (2018), 372. https://doi.org/10.1007/s11082-018-1641-7 doi: 10.1007/s11082-018-1641-7
[17]	B. Sturdevant, D. A. Lott, A. Biswas, Topological 1-soliton solution of the generalized Radhakrishnan, Kundu, Lakshmanan equation with nonlinear dispersion, Mod. Phys. Lett. B, 24 (2010), 1825–1831. https://doi.org/10.1142/S0217984910024109 doi: 10.1142/S0217984910024109
[18]	S. Arshed, A. Biswas, P. Guggilla, A. S. Alshomrani, Optical solitons for Radhakrishnan-Kundu-Lakshmanan equation with full nonlinearity, Phys. Lett. A, 384 (2020), 126191. https://doi.org/10.1016/j.physleta.2019.126191 doi: 10.1016/j.physleta.2019.126191
[19]	A. Bansal, A. Biswas, M. F. Mahmood, Q. Zhou, M. Mirzazadeh, A. S. Alshomrani, et al., Optical soliton perturbation with Radhakrishnan-Kundu-Lakshmanan equation by Lie group analysis, Optik, 163 (2018), 137–141. https://doi.org/10.1016/j.ijleo.2018.02.104
[20]	A. Biswas, 1-soliton solution of the generalized Radhakrishnan, Kundu, Lakshmanan equation, Phys. Lett. A, 373 (2009), 2546–2548. https://doi.org/10.1016/j.physleta.2009.05.010 doi: 10.1016/j.physleta.2009.05.010
[21]	A. Biswas, Optical soliton perturbation with Radhakrishnan-Kundu-Lakshmanan equation by traveling wave hypothesis, Optik, 171 (2018), 217–220. https://doi.org/10.1016/j.ijleo.2018.06.043 doi: 10.1016/j.ijleo.2018.06.043
[22]	A. Biswas, M. Ekici, A. Sonmezoglu, A. S. Alshomrani, Optical solitons with Radhakrishnan, Kundu, Lakshmanan equation by extended trial function scheme, Optik, 160 (2018), 415–427. https://doi.org/10.1016/j.ijleo.2018.02.017 doi: 10.1016/j.ijleo.2018.02.017
[23]	N. A. Kudryashov, The Radhakrishnan-Kundu-Lakshmanan equation with arbitrary refractive index and its exact solutions, Optik, 238 (2021), 166738. https://doi.org/10.1016/j.ijleo.2021.166738 doi: 10.1016/j.ijleo.2021.166738
[24]	D. D. Ganji, A. Asgari, Z. Z. Ganji, Exp-function based solution of nonlinear Radhakrishnan, Kundu and Laskshmanan (RKL) equation, Acta Appl. Math., 104 (2008), 201–209. https://doi.org/10.1007/s10440-008-9252-0 doi: 10.1007/s10440-008-9252-0
[25]	O. Gonzalez-Gaxiola, A. Biswas, Optical solitons with Radhakrishnan-Kundu-Lakshmanan equation by Laplace-Adomian decomposition method, Optik, 179 (2019), 434–442. https://doi.org/10.1016/j.ijleo.2018.10.173 doi: 10.1016/j.ijleo.2018.10.173
[26]	A. Neirameh, Soliton solutions modeling of generalized Radhakrishnan-Kundu-Lakshmanan equation, J. Appl. Phys., 8 (2018), 71–80. https://doi.org/10.22051/JAP.2019.21375.1099 doi: 10.22051/JAP.2019.21375.1099
[27]	S. S. Singh, Solutions of Kudryashov-Sinelshchikov equation and generalized Radhakrishnan-Kundu-Lakshmanan equation by the first integral method, Int. J. Phys. Res., 4 (2016), 37–42. https://doi.org/10.14419/ijpr.v4i2.6202 doi: 10.14419/ijpr.v4i2.6202
[28]	B. Ghanbari, J. F. Gómez-Aguilar, Optical soliton solutions for the nonlinear Radhakrishnan-Kundu-Lakshmanan equation, Mod. Phys. Lett. B, 33 (2019), 1950402. https://doi.org/10.1142/S0217984919504025 doi: 10.1142/S0217984919504025
[29]	S. Rehman, J. Ahmad, Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing, Alex. Eng. J., 60 (2021), 1339–1354. https://doi.org/10.1016/j.aej.2020.10.055 doi: 10.1016/j.aej.2020.10.055
[30]	Y. Yıldırım, A. Biswas, M. Ekici, H. Triki, O. Gonzalez-Gaxiol, A. K. Alzahrani, et al., Optical solitons in birefringent fibers for Radhakrishnan-Kundu-Lakshmanan equation with five prolific integration norms, Optik, 208 (2020), 164550. https://doi.org/10.1016/j.ijleo.2020.164550 doi: 10.1016/j.ijleo.2020.164550
[31]	Y. Yıldırım, A. Biswas, Q. Zhou, A. S. Alshomrani, M. R. Belic, Optical solitons in birefringentfibers for Radhakrishnan-Kundu-Lakshmanan equation with acouple of strategic integration architectures, Chin. J. Phys., 65 (2020), 341–354. https://doi.org/10.1016/j.cjph.2020.02.029 doi: 10.1016/j.cjph.2020.02.029
[32]	J. H. He, Exp-function method for fractional differential equations, Int. J. Nonlinear Sci. Numer. Simul., 14 (2013), 363–366. https://doi.org/10.1515/ijnsns-2011-0132 doi: 10.1515/ijnsns-2011-0132
[33]	Y. Tian, J. Liu, A modified exp-function method for fractional partial differential equations, Therm. Sci., 25 (2021), 1237–1241. https://doi.org/10.2298/TSCI200428017T doi: 10.2298/TSCI200428017T
[34]	F. Y. Ji, C. H. He, J. J. Zhang, A fractal Boussinesq equation for nonlinear transverse vibration of a nanofiber-reinforced concrete pillar, Appl. Math. Modell., 82 (2020) 437–448. https://doi.org/10.1016/j.apm.2020.01.027 doi: 10.1016/j.apm.2020.01.027
[35]	J. H. He, N. Qie, C. H. He, Solitary waves travelling along an unsmooth boundary, Results Phys., 24 (2021), 104104. https://doi.org/10.1016/j.rinp.2021.104104 doi: 10.1016/j.rinp.2021.104104
[36]	J. H. He, W. F. Hou, C. H. He, T. Saeed, T. Hayat, Variational approach to fractal solitary waves, Fractals, 29 (2021), 2150199. https://doi.org/10.1142/S0218348X21501991 doi: 10.1142/S0218348X21501991
[37]	C. X. Liu, Periodic solution of fractal Phi-4 equation, Therm. Sci., 25 (2021), 1345–1350 https://doi.org/10.2298/TSCI200502032L
[38]	J. H. He, E. D. Yusry, Periodic property of the time-fractional Kundu-Mukherjee-Naskar equation, Results Phys., 19 (2020), 103345. https://doi.org/10.1016/j.rinp.2020.103345 doi: 10.1016/j.rinp.2020.103345
[39]	J. H. He, Variational principle and periodic solution of the Kundu-Mukherjee-Naskar equation, Results Phys., 17 (2020), 103031. https://doi.org/10.1016/j.rinp.2020.103031 doi: 10.1016/j.rinp.2020.103031
[40]	J. H. He, W. F. Hou, N. Qie, K. A. Gepreel, A. H. Shirazi, H. M. Sedighi, Hamiltonian-based frequency-amplitude formulation for nonlinear oscillators, Facta Univ. Ser. Mech. Eng., 19 (2021), 199–208. https://doi.org/10.22190/FUME201205002H doi: 10.22190/FUME201205002H
[41]	Y. Zhao, Y. B. Lei, Y. X. Xu, S. L. Xu, H. Triki, A. Biswas, et al., Vector spatiotemporal solitons and their memory features in cold rydberg gases, Chin. Phys. Lett., 39 (2022), 034202. https://doi.org/10.1088/0256-307X/39/3/034202 doi: 10.1088/0256-307X/39/3/034202
[42]	S. L. Xu, Y. B. Lei, J. T. Du, Y. Zhao, R. Hua, J. H. Zeng, Three-dimensional quantum droplets in spin-orbit-coupled Bose-Einstein condensates, Chaos Solitons Fract., 164 (2022), 112665. https://doi.org/10.1016/j.chaos.2022.112665 doi: 10.1016/j.chaos.2022.112665
[43]	K. Y. Huang, Y. Zhao, S. Q. Wu, S. L. Xu, M. R. Belic, B. A. Malomed, Quantum squeezing of vector slow-light solitons in a coherent atomic system, Chaos Solitons Fract., 163 (2022), 112557. https://doi.org/10.1016/j.chaos.2022.112557 doi: 10.1016/j.chaos.2022.112557
[44]	T. A. Nofal, Simple equation method for nonlinear partial differential equations and its applications, J. Egypt. Math. Soc., 24 (2016), 204–209. https://doi.org/10.1016/j.joems.2015.05.006 doi: 10.1016/j.joems.2015.05.006
[45]	N. A. Kudryashov, V. B. Loguinova, Extended simplest equation method for nonlinear differential equations, Appl. Math. Comput., 205 (2008), 396–402. https://doi.org/10.1016/j.amc.2008.08.019 doi: 10.1016/j.amc.2008.08.019
[46]	Y. L. Ma, C. B. Li, Q. Wang, A series of abundant exact travelling wave solutions for a modified generalized Vakhnenko equation using auxiliary equation method, Appl. Math. Comput., 211 (2009), 102–107. https://doi.org/10.1016/j.amc.2009.01.036 doi: 10.1016/j.amc.2009.01.036
[47]	G. B. Whitham, Comments on periodic waves and solitons, IMA J. Appl. Math., 32 (1984), 353–366. https://doi.org/10.1093/imamat/32.1-3.353 doi: 10.1093/imamat/32.1-3.353

This article has been cited by:

Muhammad Aslam Noor, Khalida Inayat Noor, Mixed Variational Inequalities and Nonconvex Analysis, 2024, 2581-8147, 873, 10.34198/ejms.14524.8731029

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)