Wave dynamics for the new generalized (3+1)-D Painlevé-type nonlinear evolution equation using efficient techniques

Jamilu Sabi'u; Sekson Sirisubtawee; Surattana Sungnul; Mustafa Inc; Jamilu Sabi'u; Sekson Sirisubtawee; Surattana Sungnul; Mustafa Inc

doi:10.3934/math.20241552

AIMS Mathematics

2024, Volume 9, Issue 11: 32366-32398. doi: 10.3934/math.20241552

Previous Article Next Article

Research article Special Issues

Wave dynamics for the new generalized (3+1)-D Painlevé-type nonlinear evolution equation using efficient techniques

1.
Department of Mathematics, Yusuf Maitama Sule University, Kano, Nigeria
2.
Department of Mathematics, Faculty of Applied Science, King Mongkut's University of Technology North Bangkok, Bangkok 10800, Thailand
3.
Department of Mathematics, Firat University, 23119 Elazig, Turkey
4.
Department of Computer Engineering, Biruni University, 34010 Istanbul, Turkey

Received: 10 August 2024 Revised: 03 November 2024 Accepted: 08 November 2024 Published: 15 November 2024
MSC : 35A08, 35C07, 35C08, 35C09, 35Dxx

In this paper, diverse wave solutions for the newly introduced (3+1)-dimensional Painlevé-type evolution equation were derived using the improved generalized Riccati equation and generalized Kudryashov methods. This equation is now widely used in soliton theory, nonlinear wave theory, and plasma physics to study instabilities and the evolution of plasma waves. Using these methods, combined with wave transformation and homogeneous balancing techniques, we obtained concise and general wave solutions for the Painlevé-type equation. These solutions included rational exponential, trigonometric, and hyperbolic function solutions. Some of the obtained solutions for the Painlevé-type equation were plotted in terms of 3D, 2D, and contour graphs to depict the various exciting wave patterns that can occur. As the value of the amplitude increased in the investigated solutions, we observed the evolution of dark and bright solutions into rogue waves in the forms of Kuztnetsov-Ma breather and Peregrine-like solitons. Other exciting wave patterns observed in this work included the evolution of kink and multiple wave solitons at different time levels. We believe that the solutions obtained in this paper were concise and more general than existing ones and will be of great use in the study of solitons, nonlinear waves, and plasma physics.

Keywords:

Painlevé-type equation,
improved generalized Riccati equation method,
soliton theory,
generalized Kudryashov method,
multiple soliton

Citation: Jamilu Sabi'u, Sekson Sirisubtawee, Surattana Sungnul, Mustafa Inc. Wave dynamics for the new generalized (3+1)-D Painlevé-type nonlinear evolution equation using efficient techniques[J]. AIMS Mathematics, 2024, 9(11): 32366-32398. doi: 10.3934/math.20241552

Related Papers:

[1]	Ghazala Akram, Saima Arshed, Maasoomah Sadaf, Hajra Mariyam, Muhammad Nauman Aslam, Riaz Ahmad, Ilyas Khan, Jawaher Alzahrani . Abundant solitary wave solutions of Gardner's equation using three effective integration techniques. AIMS Mathematics, 2023, 8(4): 8171-8184. doi: 10.3934/math.2023413
[2]	Nafissa T. Trouba, Huiying Xu, Mohamed E. M. Alngar, Reham M. A. Shohib, Haitham A. Mahmoud, Xinzhong Zhu . Soliton solutions and stability analysis of the stochastic nonlinear reaction-diffusion equation with multiplicative white noise in soliton dynamics and optical physics. AIMS Mathematics, 2025, 10(1): 1859-1881. doi: 10.3934/math.2025086
[3]	Emad H. M. Zahran, Omar Abu Arqub, Ahmet Bekir, Marwan Abukhaled . New diverse types of soliton solutions to the Radhakrishnan-Kundu-Lakshmanan equation. AIMS Mathematics, 2023, 8(4): 8985-9008. doi: 10.3934/math.2023450
[4]	Elsayed M. E. Zayed, Mona El-Shater, Khaled A. E. Alurrfi, Ahmed H. Arnous, Nehad Ali Shah, Jae Dong Chung . Dispersive optical soliton solutions with the concatenation model incorporating quintic order dispersion using three distinct schemes. AIMS Mathematics, 2024, 9(4): 8961-8980. doi: 10.3934/math.2024437
[5]	Naher Mohammed A. Alsafri, Hamad Zogan . Probing the diversity of kink solitons in nonlinear generalised Zakharov-Kuznetsov-Benjamin-Bona-Mahony dynamical model. AIMS Mathematics, 2024, 9(12): 34886-34905. doi: 10.3934/math.20241661
[6]	Mohammed Aly Abdou, Loubna Ouahid, Saud Owyed, A. M. Abdel-Baset, Mustafa Inc, Mehmet Ali Akinlar, Yu-Ming Chu . Explicit solutions to the Sharma-Tasso-Olver equation. AIMS Mathematics, 2020, 5(6): 7272-7284. doi: 10.3934/math.2020465
[7]	Ahmed A. Gaber, Abdul-Majid Wazwaz . Dynamic wave solutions for (2+1)-dimensional DJKM equation in plasma physics. AIMS Mathematics, 2024, 9(3): 6060-6072. doi: 10.3934/math.2024296
[8]	Muhammad Imran Asjad, Sheikh Zain Majid, Waqas Ali Faridi, Sayed M. Eldin . Sensitive analysis of soliton solutions of nonlinear Landau-Ginzburg-Higgs equation with generalized projective Riccati method. AIMS Mathematics, 2023, 8(5): 10210-10227. doi: 10.3934/math.2023517
[9]	Islam Samir, Hamdy M. Ahmed, Wafaa Rabie, W. Abbas, Ola Mostafa . Construction optical solitons of generalized nonlinear Schrödinger equation with quintuple power-law nonlinearity using Exp-function, projective Riccati, and new generalized methods. AIMS Mathematics, 2025, 10(2): 3392-3407. doi: 10.3934/math.2025157
[10]	Khudhayr A. Rashedi, Saima Noor, Tariq S. Alshammari, Imran Khan . Lump and kink soliton phenomena of Vakhnenko equation. AIMS Mathematics, 2024, 9(8): 21079-21093. doi: 10.3934/math.20241024

Abstract

1. Introduction

Nonlinear evolution equations are partial differential equations (PDEs) used to simulate the temporal development of a physical process or system. These equations can be found in all branches of pure and applied sciences, engineering, and social sciences. The most popular among these PDEs include the Navier-Stokes equation ^[1], Korteweg-de Vries equation ^[2], Camassa-Holm equation ^[3], Estevez-Mansfield-Clarkson equation ^[4], Boussinesq equation ^[5], Jimbo-Miwa equation ^[6], Burgers equation ^[7], and Kadomtsev-Petviashvili equation ^[8]. Solitons are known for their outstanding ability to balance the effects of dispersion and nonlinearity, to maintain their stability, and to travel over a long distance without experiencing severe distortion. These characteristics have made solitons an effective tool for data transfer in optical communication. Dispersive solitons, also known as optical solitons, are one of the main components of high-speed fiber optic communication systems. Furthermore, understanding the theory of solitons may be used to regulate and improve difficult situations, such as preventing coastal erosion, maximizing wave energy extraction, and developing efficient wave forecasting techniques ^[9,10]. Rogue waves are space-time solitary waves with a large amplitude that can inflict significant and unanticipated damage to people and valuable assets in and near coastal areas. This has prompted scientists to investigate the fundamental physics of rogue waves and to develop methods for predicting and preventing rogue wave incidents ^{[11,12,13,14]}.

The generalized (3+1)-D Painlevé-type nonlinear evolution equation (3DPTE) has been developed recently as a model for solitons and related wave phenomena. Based on an assumption of soliton dispersion, Mohan et al. ^[15] proposed an equation that controls the parameters in rogue waves and related dynamical structures. The new equation is as follows:

$\begin{equation} q_{xxxy}+c_1q_{yt}+c_2(qq_x)_y+c_3q_{xx}+c_4q_{zz} = 0, \end{equation}$

(1.1)

where $q = q(x, y, z, t)$ and $c_1, c_2, c_3$ , and $c_4$ are assumed to be real constants. Also, $x, y$ , and $z$ are spatial variables and $t$ is time. This new and unique generalized equation can be used in soliton theory, theory of nonlinear waves, and plasma physics to represent the evolution of instabilities and plasma waves; see ^[15] for more details on the significance of this new equation and its uniqueness compared to existing equations in the literature. The equation is integrable according to the Painlevé integrability test. It can also have localized solutions such as solitons, lumps, breathers, and others ^[16].

Many scientists have now focused their attention on investigating the solutions to this equation and other underlying physical phenomena associated with it; for example, various unique methodologies have been developed to obtain solutions to this equation and prove its integrability. Some reviews are as follows: The exp $(-\Phi (\xi))$ -expansion and tanh-function methods have been used to produce various solutions to the 3DPTE ^[17]. The N-rogue generalized wave expression for extraction of solutions using the modified Hirota technique was fully studied in ^[18]. Exponential rational function solutions have also been obtained for the 3DPTE model via the generalized exponential function technique ^[19]. The integrability and soliton solution have been obtained using the novel bilinear Bäcklund transformation and Hirota bilinear form methods ^[20]. Rogue wave solutions with center parameters have been derived through the generalized direct formula scheme ^[21]. Moreover, using the Hirota bilinear method, the one, two, and three solitons for the 3DPTE have been extracted ^[22].

There are many novel approaches for solving nonlinear evolution equations, ranging from numerical, semi-analytical, and analytical methods. Moreover, some of the most commonly utilized numerical schemes are the probabilistic numerical scheme ^[23], the Bayesian numerical methods ^[24], the energy methods for free boundary problems ^[25], the modified method of approximate solutions ^[26], the novel mesh-free methods ^[27], the empirical inter-scale finite element method ^[28], the semi-analytical method of lines ^[29], and the nonstandard finite difference method ^[30]. However, this study focuses on solitary wave techniques for deriving exact solutions to nonlinear PDEs. Popular examples of these techniques include the modified simple equation technique ^[31], the rational function technique ^[32], the exponential function technique ^[33], the extended tanh-function approach ^[34], the generalized hyperbolic-function scheme ^[35], the generalized Kudryashov technique ^[36], the improved Sadar subequation methods ^[37,38], the auxiliary equation technique ^[39], the generalized Riccati equation techniques ^[40], the modified Jacobi elliptic function method ^[41], the extended direct algebra methods ^[42,43], and others. Now, motivated by the above techniques for deriving solitary wave solutions of the 3DPTE, we will use the improved generalized Riccati equation (IGRE) method ^[43] and the generalized Kudryashov (GK) method ^[44] to derive more concise and generalized solitary wave solutions for the new generalized 3DPTE equation. The IGRE method is efficient and reliable for producing succinct and more general hyperbolic and trigonometric function solutions to nonlinear PDEs, while the GK method is robust in establishing succinct and general rational and exponential function solutions to nonlinear PDEs.

The remaining sections of this paper are organized as follows. In Section 2, a brief description is given of the procedures of the IGRE and GK methods. In Section 3, the two methods are applied to derive solitary wave solutions of the Painlevé equation. In Section 4, graphs of some selected solutions are plotted to illustrate various soliton structures. Finally, Section 5 contains the conclusions for the paper.

2. Description of the IGRE and the GK methods

This section briefly describes the IGRE and GK methods for solving general nonlinear PDEs (NPDEs). The two improved methods are developed based on the fact that the solutions of many nonlinear equations can be represented by a finite series of $\tanh$ functions. This acted as a motivation to Fan in ^[34] to replace the $\tanh$ function with the solution of the Riccati equation:

$\begin{equation} \Omega'(\xi) = m+\Omega^2(\xi), \end{equation}$

(2.1)

where $m$ is a parameter to be determined. This idea yielded various solitary wave solutions for the NPDEs. Apart from the different forms of the periodic and singular solutions, the sign of $m$ in the Riccati equation also determines the number and type of traveling wave solutions for the NPDEs. In the same vein, Kudryashov ^[45] proposed his method by replacing the $\tanh$ function with the solution of Eq (2.7). These methods proved to be robust and reliable methods for finding different solutions of the NPDEs. The IGRE method provides the solution of the NPDEs using the generalized Riccati equation in Eq (2.5), and the GK method is based on the idea of representing the solution of nonlinear equation by a finite series of rational functions. Now we are going to provide the detail procedures for the IGRE and GK methods for solving general nonlinear NPDEs. For any given NPDE of the form:

$\begin{equation} M(q, q_{t}, q_x, q_{x,t}, q_{xx},\ldots) = 0, \end{equation}$

(2.2)

we apply a wave variable of the form $\xi = a_1x+a_2y+a_3z+a_4 t,$ where $a_1, a_2, a_3, a_4$ are constants, and then let $u(\xi) = q(x, y, z, t)$ . This will convert Eq (2.2) into an ordinary differential equation:

$\begin{equation} N(u, u'(\xi),u''(\xi),\ldots) = 0, \end{equation}$

(2.3)

where $u'(\xi) = \frac{du(\xi)}{d\xi}, \, u''(\xi) = \frac{d^2u(\xi)}{d\xi^2},$ and so on. We next assume that the solution of Eq (2.3) is of the form:

$\begin{equation} u(\xi) = \sum\limits_{i = 0}^{N}b_i\Omega^i(\xi), \end{equation}$

(2.4)

where $b_i$ for all $i = 1, 2, \ldots, N$ will be determined later with $b_N\neq 0$ , and $N$ will be calculated using the homogeneous balancing method (HBM), that is, by balancing the highest derivative term with the nonlinear term in Eq (2.3). As the next step in the IGRE method, the function $\Omega(\xi)$ is assumed to satisfy the following generalized Riccati equation:

$\begin{equation} \Omega'(\xi) = m_2\Omega^2(\xi)+m_1\Omega(\xi)+m_0,\quad \end{equation}$

(2.5)

where $m_0, m_1$ , s and $m_2$ are constants. Equation 2.5 has many solutions; see ^[37] for the different solutions of Eq (2.5).

Alternatively, as the next step in the GK method, the solution of Eq (2.3) is assumed to be of the form:

$\begin{equation} u(\xi) = \frac{\sum\nolimits_{i = 0}^{P}b_i\Omega^i(\xi)}{\sum\nolimits_{j = 0}^{Q}f_j\Omega^j(\xi)}, \end{equation}$

(2.6)

where $b_i \; (i = 0, 1, ..., P)$ and $f_j \; (j = 0, 1, ..., Q)$ will be determined later such that $b_P \neq 0$ and $f_Q \neq 0$ . The integers $P$ and $Q$ will be calculated using the HBM. Moreover, the function $\Omega(\xi)$ is assumed to satisfy

$\begin{equation} \Omega'(\xi) = \Omega^2(\xi)-\Omega(\xi). \end{equation}$

(2.7)

It is not difficult to see that the function

$\begin{equation} \Omega(\xi) = \frac{1}{1+\exp(\xi)} \end{equation}$

(2.8)

satisfies Eq (2.7). Details on the GK method can be found in ^[44].

The two methods described here will be applied to derive new wave solutions to the 3DPTE in the following section. These methods have proved to be effective for analyzing a wide range of traveling wave solutions for nonlinear PDEs, including exponential, rational, trigonometric, and hyperbolic function solutions with interesting wave profile patterns. This is the primary basis for their selection in this work.

3. Applications of the IGRE and the GK methods

This section contains a range of wave solutions for the 3DPTE in Eq (1.1) using the IGRE and the GK methods. We begin by transforming Eq (1.1) into a nonlinear ordinary differential equation (NODE) via the following wave transformation:

$\begin{equation} u(\xi) = q(x,y,z,t), \quad \xi = a_1x+a_2y+a_3z+a_4 t. \end{equation}$

(3.1)

Then, we have

$\begin{equation} a_1^2 c_3u^{\prime\prime}+a_1a_2c_2uu^{\prime\prime}+a_2a_4c_1u^{\prime\prime}+a_3^2c_4u^{\prime\prime}+a_1a_2c_2\left(u^{\prime}\right)^2+a_1^3a_2u^{(4)} = 0. \end{equation}$

(3.2)

Next, we determine the values of the balance numbers $N$ , $P$ , and $Q$ using HBM to implement the methods described in Section 2.

3.1. Solitary wave solutions using the IGRE method

In this section, the IGRE method is used to obtain solitary wave solutions to the 3DPTE. Now, balancing the terms $u^{(4)}$ with $\left(u^{\prime}\right)^2$ , we get $N = 2$ . By putting $N = 2$ into Eq (2.4), we have

$\begin{equation} u(\xi) = b_0+b_1\Omega(\xi)+b_2\Omega^2(\xi). \end{equation}$

(3.3)

Substituting Eq (3.3) into Eq (3.2) by using Eq (2.5) and setting the coefficients of $\Omega^i(\xi)$ to zero, we obtain the equations:

$\begin{eqnarray} \begin{aligned} \Omega^0(\xi):\quad& 8 a_1^{3}a_{{2}}b_{{1}}m_0^{2}m_{{1}}m_2+ a_1^{3 }a_{{2}}b_{{1}}m_0m_{{1}}^{3}+16 a_1^{3}a_{{2}}b_{{2}}m_ {{0}}^{3}m_2+14 a_1^{3}a_{{2}}b_{{2}}m_0^{2}m_{{1}} ^{2}\\&+a_{{1}}a_{{2}}b_{{0}}b_{{1}}c_{{2}}m_0m_{{1}}+2 a_{{1}}a_{{ 2}}b_{{0}}b_{{2}}c_{{2}}m_0^{2}+a_{{1}}a_{{2}}b_1^{2}c_{{2 }}m_0^{2}+ a_1^{2}b_{{1}}c_{{3}}m_0m_{{1}}+2 a_1 ^{2}b_{{2}}c_{{3}}m_0^{2}\\&+a_{{2}}a_{{4}}b_{{1}}c_{{1}}m_0m_{ {1}}+2 a_{{2}}a_{{4}}b_{{2}}c_{{1}}m_0^{2}+a_{{3}}^{2}b_{{1}} c_{{4}}m_0m_{{1}}+2 a_{{3}}^{2}b_{{2}}c_{{4}}m_0^{2} = 0,\\ \Omega^1(\xi):\quad& 16 a_1^{3}a_{{2}}b_{{1}}m_0^{2}m_2^{2}+22 a_{{1}} ^{3}a_{{2}}b_{{1}}m_0m_{{1}}^{2}m_2+ a_1^{3}a_{{2}}b_{ {1}}m_{{1}}^{4}+120 a_1^{3}a_{{2}}b_{{2}}m_0^{2}m_{{1}} m_2\\&+30 a_1^{3}a_{{2}}b_{{2}}m_0m_{{1}}^{3}+2 a_{{1}} a_{{2}}b_{{0}}b_{{1}}c_{{2}}m_0m_2+a_{{1}}a_{{2}}b_{{0}}b_{{1} }c_{{2}}m_{{1}}^{2}+6 a_{{1}}a_{{2}}b_{{0}}b_{{2}}c_{{2}}m_0m_{ {1}}\\&+3 a_{{1}}a_{{2}}b_1^{2}c_{{2}}m_0m_{{1}}+6 a_{{1}}a_{ {2}}b_{{1}}b_{{2}}c_{{2}}m_0^{2}+2 a_1^{2}b_{{1}}c_{{3}}m _{{0}}m_2+ a_1^{2}b_{{1}}c_{{3}}m_{{1}}^{2}+6 a_1^{2 }b_{{2}}c_{{3}}m_0m_{{1}}\\&+2 a_{{2}}a_{{4}}b_{{1}}c_{{1}}m_0m_ {{2}}+a_{{2}}a_{{4}}b_{{1}}c_{{1}}m_{{1}}^{2}+6 a_{{2}}a_{{4}}b_{{2 }}c_{{1}}m_0m_{{1}}+2 a_{{3}}^{2}b_{{1}}c_{{4}}m_0m_2+ a_{{3}}^{2}b_{{1}}c_{{4}}m_{{1}}^{2}\\&+6 a_{{3}}^{2}b_{{2}}c_{{4}} m_0m_{{1}} = 0,\\ \Omega^2(\xi):\quad& 60 a_1^{3}a_{{2}}b_{{1}}m_0m_{{1}}m_2^{2}+15 a_{{1} }^{3}a_{{2}}b_{{1}}m_{{1}}^{3}m_2+136 a_1^{3}a_{{2}}b_{{ 2}}m_0^{2}{m_2}^{2}+232 a_1^{3}a_{{2}}b_{{2}}m_0 m_{{1}}^{2}m_2\\&+16 a_1^{3}a_{{2}}b_{{2}}m_{{1}}^{4}+3 a_ {{1}}a_{{2}}b_{{0}}b_{{1}}c_{{2}}m_{{1}}m_2+8 a_{{1}}a_{{2}}b_{{0 }}b_{{2}}c_{{2}}m_0m_2+4 a_{{1}}a_{{2}}b_{{0}}b_{{2}}c_{{2}} m_{{1}}^{2}\\&+4 a_{{1}}a_{{2}}b_1^{2}c_{{2}}m_0m_2+2 a_ {{1}}a_{{2}}b_1^{2}c_{{2}}m_{{1}}^{2}+15 a_{{1}}a_{{2}}b_{{1} }b_{{2}}c_{{2}}m_0m_{{1}}+6 a_{{1}}a_{{2}}b_{{2}}^{2}c_{{2}}m_ {{0}}^{2}\\&+3 a_1^{2}b_{{1}}c_{{3}}m_{{1}}m_2+8 a_1^{ 2}b_{{2}}c_{{3}}m_0m_2+4 a_1^{2}b_{{2}}c_{{3}}{m_{{1}}} ^{2}+3 a_{{2}}a_{{4}}b_{{1}}c_{{1}}m_{{1}}m_2+8 a_{{2}}a_{{4}}b_ {{2}}c_{{1}}m_0m_2\\&+4 a_{{2}}a_{{4}}b_{{2}}c_{{1}}m_{{1}}^{2 }+3 a_{{3}}^{2}b_{{1}}c_{{4}}m_{{1}}m_2+8 a_{{3}}^{2}b_{{2}} c_{{4}}m_0m_2+4 a_{{3}}^{2}b_{{2}}c_{{4}}m_{{1}}^{2} = 0,\\ \Omega^3(\xi):\quad& 40 a_1^{3}a_{{2}}b_{{1}}m_0m_2^{3}+50 a_1^{3}a _{{2}}b_{{1}}m_{{1}}^{2}m_2^{2}+440 a_1^{3}a_{{2}}b_{{2 }}m_0m_{{1}}m_2^{2}+130 a_1^{3}a_{{2}}b_{{2}}m_{{1}} ^{3}m_2\\&+2 a_{{1}}a_{{2}}b_{{0}}b_{{1}}c_{{2}}m_2^{2}+10 a _{{1}}a_{{2}}b_{{0}}b_{{2}}c_{{2}}m_{{1}}m_2+5 a_{{1}}a_{{2}}b_{ {1}}^{2}c_{{2}}m_{{1}}m_2+18 a_{{1}}a_{{2}}b_{{1}}b_{{2}}c_{{2}} m_0m_2\\&+9 a_{{1}}a_{{2}}b_{{1}}b_{{2}}c_{{2}}m_{{1}}^{2}+14 a_{{1}}a_{{2}}b_{{2}}^{2}c_{{2}}m_0m_{{1}}+2 a_1^{2}b_{ {1}}c_{{3}}m_2^{2}+10 a_1^{2}b_{{2}}c_{{3}}m_{{1}}m_2 +2 a_{{2}}a_{{4}}b_{{1}}c_{{1}}m_2^{2}\\&+10 a_{{2}}a_{{4}}b_{{2} }c_{{1}}m_{{1}}m_2+2 a_{{3}}^{2}b_{{1}}c_{{4}}m_2^{2}+10 a_{{3}}^{2}b_{{2}}c_{{4}}m_{{1}}m_2 = 0,\\ \Omega^4(\xi):\quad& 60 a_1^{3}a_{{2}}b_{{1}}m_{{1}}m_2^{3}+240 a_1^{3} a_{{2}}b_{{2}}m_0m_2^{3}+330 a_1^{3}a_{{2}}b_{{2}}m_ {{1}}^{2}m_2^{2}+6 a_{{1}}a_{{2}}b_{{0}}b_{{2}}c_{{2}}m_2 ^{2}\\&+3 a_{{1}}a_{{2}}b_1^{2}c_{{2}}m_2^{2}+21 a_{{1}}a_ {{2}}b_{{1}}b_{{2}}c_{{2}}m_{{1}}m_2+16 a_{{1}}a_{{2}}b_{{2}}^{ 2}c_{{2}}m_0m_2+8 a_{{1}}a_{{2}}b_{{2}}^{2}c_{{2}}m_{{1}} ^{2}\\&+6 a_1^{2}b_{{2}}c_{{3}}m_2^{2}+6 a_{{2}}a_{{4}}b_{{ 2}}c_{{1}}m_2^{2}+6 a_{{3}}^{2}b_{{2}}c_{{4}}m_2^{2} = 0,\\ \Omega^5(\xi):\quad& 24 a_1^{3}a_{{2}}b_{{1}}m_2^{4}+336 a_1^{3}a_{{2}} b_{{2}}m_{{1}}m_2^{3}+12 a_{{1}}a_{{2}}b_{{1}}b_{{2}}c_{{2}}m_ {{2}}^{2}+18 a_{{1}}a_{{2}}b_{{2}}^{2}c_{{2}}m_{{1}}m_2 = 0,\\ \Omega^6(\xi):\quad& 120 a_1^{3}a_{{2}}b_{{2}}m_2^{4}+10 a_{{1}}a_{{2}}b_{{2 }}^{2}c_{{2}}m_2^{2} = 0. \end{aligned} \end{eqnarray}$

(3.4)

Upon solving the above equations using Maple, we obtain the following solution:

$\begin{equation} \begin{aligned} &b_0 = b_0, \quad b_1 = b_1, \quad b_2 = {\frac {-12 m_2^{2} a_1^{2}}{c_2}}, \quad m_1 = -{\frac {b_{{1}}c_{{2}}}{12m_2 a_1^{2}}},\quad m_0 = m_0,\quad m_2 = m_2, \quad a_1 = a_1, \\& a_4 = -{\frac {1152 a_1^{4}a_{{2}}m_0m_2^ {3}+144 a_1^{2}a_{{2}}b_{{0}}c_{{2}}m_2^{2}+144 a_{{1}} ^{3}c_{{3}}m_2^{2}+144 a_{{1}}a_{{3}}^{2}c_{{4}}m_2^{2 }+a_{{2}}b_1^{2}c_2^{2}}{144m_2^{2}a_{{1}}c_{{1}}a_{{2} }}}. \end{aligned} \end{equation}$

(3.5)

We consider the following two cases.

Case 1: When ${\frac {b_1^{2}c_2^{2}}{m_{ {2}}^{2} a_1^{4}}}-576 m_0m_2\geq0.$ Substituting Eq (3.5) into Eq (3.3) and using the solutions of Eq (2.5), we obtain the following hyperbolic function solutions for PDE (1.1):

$\begin{equation} \begin{aligned} q_1 = &\frac{ \left( 576 a_1^{8}m_0m_2^{5}- a_1^{4}b_{ {1}}^{2}c_2^{2}m_2^{2} \right) \left( \tanh \left( \frac{1}{24} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{ {2}}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{ 2}}{48m_2^{4} a_1^{6}c_2}\\& +\frac{48 b_{{0}}m_2^{4} a_1^{6}c_{{2}}+ a_1^{4}b_1^{2 }c_2^{2}m_2^{2}}{48m_2^{4} a_1^{6}c_2}, \end{aligned} \end{equation}$

(3.6)

$\begin{equation} \begin{aligned} q_2 = &\frac{ \left( 576 a_1^{8}m_0m_2^{5}- a_1^{4}b_{ {1}}^{2}c_2^{2}m_2^{2} \right) \left( \coth \left( \frac{1}{24} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{ {2}}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{ 2}}{48m_2^{4} a_1^{6}c_2}\\& +\frac{48 b_{{0}}m_2^{4} a_1^{6}c_{{2}}+ a_1^{4}b_1^{2 }c_2^{2}m_2^{2}}{48m_2^{4} a_1^{6}c_2}, \end{aligned} \end{equation}$

(3.7)

$\begin{equation} \begin{aligned} q_3 = &\frac{1}{24 m_2^{2} a_1^{2} \left( \cosh \left( \frac{1}{12} \sqrt {-{ \frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_2^{ 2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}c_2}\\ &\times\left( \begin{aligned} & 576 i\sinh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_0m_{ {2}}^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) a_1^{4}m_0m_2^{3}\\ &+288 \left( \cosh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_{{0 }}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4} }}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2} a_1^{4}m_0 m_2^{3}\\ &+24 b_{{0}}m_2^{2} a_1^{2}c_{{2}} \left( \cosh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_0m_2^ {3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\ &-576 a_1^{4}m_0m_{{ 2}}^{3}-i\sinh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_0 m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}} } \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) b_1^{2}c_2^{2}+b_{{1}}^{2}c_2^{2} \end{aligned} \right), \end{aligned} \end{equation}$

(3.8)

$\begin{equation} \begin{aligned} q_4 = &\frac{1}{24c_{{2}} \left( \cosh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_ {{0}}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^ {4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) -1 \right) m_2^{2} a_1^{2}}\\ &\times\left( \begin{aligned} & 288 \cosh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) a_1^{4}m_0m_2^{3}+ 288 a_1^{4}m_0m_2^{3}\\ &+24 \cosh \left( \frac{1}{12} \sqrt {- {\frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_2^ {2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) a _1^{2}b_{{0}}c_{{2}}m_2^{2}-24 b_{{0}}m_2^{2}a_{{1} }^{2}c_{{2}}\\&-b_1^{2}c_2^{2} \end{aligned} \right), \end{aligned} \end{equation}$

(3.9)

$\begin{equation} \begin{aligned} q_5 = &\frac{1}{ \cosh \left( \frac{1}{48}\sqrt {-{\frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2}a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) ^{2}}\\&\times \frac{1}{\left( \cosh \left( \frac{1}{48}\sqrt {-{\frac {576 a_1^{4}m _{{0}}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2}a_1 ^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) ^{2}-1\right)m_2^{2}a_1^{2}c_{{2}}}\\ &\times\left( \begin{aligned} & 12 \left( \cosh \left( \frac{1}{48} \sqrt {-{\frac {576 a_1^{4}m_{{0 }}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4} }}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{4} a_1^{4}m_0 m_2^{3}\\&+ \left( \cosh \left( \frac{1}{48} \sqrt {-{\frac {576 a_{{1}} ^{4}m_0m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2}a_ {{1}}^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{4} a_1^ {2}b_{{0}}c_{{2}}m_2^{2}\\&-12 \left( \cosh \left( \frac{1}{48} \sqrt {- {\frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_2^ {2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2} a_1^{4}m_0m_2^{3}\\&-b_{{0}}m_2^{2}a_ {{1}}^{2}c_{{2}} \left( \cosh \left( \frac{1}{48} \sqrt {-{\frac {576 a_{{ 1}}^{4}m_0m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\&+3 a_ {{1}}^{4}m_0m_2^{3}-{\frac {1}{192}} b_1^{2}c_{{2}} ^{2} \end{aligned} \right), \end{aligned} \end{equation}$

(3.10)

$\begin{equation} \begin{aligned} q_6 = &\frac{1}{24 m_2^{2} a_1^{2} \left( p\sinh \left( \frac{1}{12} \sqrt {- {\frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_2^ {2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) +s \right) ^{2}c_2}\\ &\times\left( \begin{aligned} & 288 \left( \cosh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_{{0 }}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4} }}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}p^{2} a_1^{4} m_0m_2^{3}\\&+\sqrt {-{\frac { \left( 576 a_1^{4}m_0 m_2^{3}-b_1^{2}c_2^{2} \right) \left( p^{2}+s^{ 2} \right) }{m_2^{2} a_1^{4}}}}\sqrt {-{\frac {576 a_{{1} }^{4}m_0m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2}a _{{1}}^{4}}}}\\&\times\cosh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_{ {0}}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{ 4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) p a_1^{4}m_2^{2}\\&+24 \left( \cosh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_0 m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}} } \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}p^{2} a_1^{2}b_ {{0}}c_{{2}}m_2^{2}\\&+288 s^{2} a_1^{4}m_0m_2^{3}+48 \sinh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m_0m_2^{3}-b_1^{2} c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) ps a_1^{2}b_{{0}}c_{{2}}m_2^{2}\\&-24 p^{2}a_{{1} }^{2}b_{{0}}c_{{2}}m_2^{2}+24 s^{2} a_1^{2}b_{{0}}c_{{2 }}m_2^{2}+288 p^{2} a_1^{4}m_0m_2^{3 }\\&+\sinh \left( \frac{1}{12} \sqrt {-{\frac {576 a_1^{4}m _{{0}}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1 ^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) psb_1^{2}c_2^{2}- p^{2}b_1^{2}c_2^{2} \end{aligned} \right), \end{aligned} \end{equation}$

(3.11)

$\begin{equation} \begin{aligned} q_7 = & b_0+\left(24 m_0\cosh \left( \frac{1}{24} \sqrt {-576 m_0m_2+{\frac {b_{ {1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}b_{{1}}\right) \Big/\\ &\left( \begin{aligned} & \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}}\sinh \left( \frac{1}{24} \sqrt {-576 m_0m_2+ {\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}\\&+b_{{1}}c_{{2}} \cosh \left( \frac{1}{24} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c _{{2}}^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \end{aligned} \right)\\&-\left(6912 m_0^{2} \left( \cosh \left( \frac{1}{24} \sqrt {-576 m_0m_{{ 2}}+{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}m_2^{4} a_1^ {6}\right)\Big/\\ &\left( \begin{aligned} & \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2} }{m_2^{2} a_1^{4}}}}\sinh \left( \frac{1}{24} \sqrt {-576 m_0 m_2+{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4} }}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}\\&+b_{{1}}c_{{2 }}\cosh \left( \frac{1}{24} \sqrt {-576 m_0m_2+{\frac {b_1^{2} c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \end{aligned} \right) ^{2}c_{{2}}, \end{aligned} \end{equation}$

(3.12)

$\begin{equation} \begin{aligned} q_8 = & b_0+\left(24 m_0\sinh \left( \frac{1}{24} \sqrt {-576 m_0m_2+{\frac {b_{ {1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}b_{{1}}\right) \Big/\\ &\left( \begin{aligned} & \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}}\cosh \left( \frac{1}{24} \sqrt {-576 m_0m_2+ {\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}\\&+b_{{1}}c_{{2}} \sinh \left( \frac{1}{24} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c _{{2}}^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \end{aligned} \right)\\&-\left(6912 m_0^{2} \left( \sinh \left( \frac{1}{24} \sqrt {-576 m_0m_{{ 2}}+{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}m_2^{4} a_1^ {6}\right)\Big/\\ &\left( \begin{aligned} & \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2} }{m_2^{2} a_1^{4}}}}\cosh \left( \frac{1}{24} \sqrt {-576 m_0 m_2+{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4} }}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}\\&+b_{{1}}c_{{2 }}\sinh \left( \frac{1}{24} \sqrt {-576 m_0m_2+{\frac {b_1^{2} c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \end{aligned} \right) ^{2}c_{{2}}, \end{aligned} \end{equation}$

(3.13)

$\begin{equation} \begin{aligned} q_9 = & b_0+\left(24 m_0\sinh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac {b_{ {1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}b_{{1}} \right) \Big/\\ &\left( \begin{aligned} & b_{{1}}c_{{2}}\sinh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac { b_{{1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)\\& +m_2 a_1^{2} \left( 1+\cosh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) \\&\times\sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}} \end{aligned} \right)\\&-\left(6912 m_0^{2} \left( \sinh \left( \frac{1}{12} \sqrt {-576 m_0m_{{ 2}}+{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}m_2^{4} a_1^ {6}\right)\Big/\\ &\left( \begin{aligned} & b_{{1}}c_{{2}}\sinh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac { b_{{1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \\&+m_2 a_1^{2} \left( 1+\cosh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) \\&\times\sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}} \end{aligned} \right) ^{2}c_{{2}}, \end{aligned} \end{equation}$

(3.14)

$\begin{equation} \begin{aligned} q_{10} = & b_0+\left(24 m_0\cosh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac {b_{ {1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}b_{{1}} \right) \Big/\\ &\left( \begin{aligned} & b_{{1}}c_{{2}}\cosh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac { b_{{1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)\\& +m_2 a_1^{2} \left( i+\sinh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) \\&\times\sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}} \end{aligned} \right)\\&-\left(6912 m_0^{2} \left( \cosh \left( \frac{1}{12} \sqrt {-576 m_0m_{{ 2}}+{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}m_2^{4} a_1^ {6}\right)\Big/\\ &\left( \begin{aligned} & b_{{1}}c_{{2}}\cosh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac { b_{{1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \\&+m_2 a_1^{2} \left( i+\sinh \left( \frac{1}{12} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) \\&\times\sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}} \end{aligned} \right) ^{2}c_{{2}}, \end{aligned} \end{equation}$

(3.15)

$\begin{equation*} \begin{aligned} q_{11} = &b_0-192 m_0^{2} \left( \sinh \left( \frac{1}{48} \sqrt {-576 m_0m_{{2 }}+{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\&\times \left( \cosh \left( 1/ 48 \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m _{{2}}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}m_2^{2} a_1^{2} \Big/\\ &\left( \begin{aligned} & \frac{1}{6} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}} \left( \cosh \left( \frac{1}{48} \sqrt {-576 m_ {{0}}m_2+{\frac {b_1^{2}c_2^{2}}{m_2^{2}a_{{1}} ^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\&+\frac{1}{6 {{m_2} a_1^{2}}}\times b_{{1}}c_ {{2}}\sinh \left( \frac{1}{48} \sqrt {-576 m_0m_2+{\frac {b_1^ {2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \\&\times\cosh \left( \frac{1}{48} \sqrt {-576 m_0m_2+{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)\\&-\frac{1}{12} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{m_{{2 }}^{2} a_1^{4}}}} \end{aligned} \right)^2c_2 \end{aligned} \end{equation*}$

$\begin{equation} \begin{aligned} &+4 m_0\sinh \left( \frac{1}{48} \sqrt {-576 m_0m_2+{\frac {b_{{ 1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \\&\times\cosh \left( \frac{1}{48} \sqrt {-576 m_0m_2+{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) b_{{1}}\Big/\\ &\left( \begin{aligned} &\frac{1}{6} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}} \left( \cosh \left( \frac{1}{48} \sqrt {-576 m_ {{0}}m_2+{\frac {b_1^{2}c_2^{2}}{m_2^{2}a_{{1}} ^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\&+\frac{1}{6m_2a_1^2}\times b_{{1}}c_{{2}}\sinh \left( \frac{1}{48} \sqrt {-576 m_0m_2+{\frac { b_{{1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)\\&\times \cosh \left( \frac{1}{48} \sqrt {-576 m_0m_2+{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)\\&-\frac{1}{12} \sqrt {-576 m_0m_2+{\frac {b_1^{2}c_2^{2}} {m_2^{2} a_1^{4}}}} \end{aligned} \right). \end{aligned} \end{equation}$

(3.16)

Case 2: When $576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}\geq0.$ In this case, the following trigonometric function solutions can be obtained by substituting Eq (3.5) into Eq (3.3) and using the solutions of Eq (2.5).

$\begin{equation} \begin{aligned} q_{12} = &\frac{\left( \tan \left( \frac{1}{24} \sqrt {576 m_0m_2-{\frac {b_1 ^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}b_1^{2}c_2^{2}-48 b_{{0}} m_2^{2} a_1^{2}c_{{2}}-b_1^{2}c_2^{2} }{48 m_2^{2} a_1^{2}c_{{2}}}\\&-\frac{576 \left( \tan \left( \frac{1}{24} \sqrt {{\frac {576 a_1^{4}m_{{0} }m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}} }} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2} a_1^{4}m_0 m_2^{3}}{48 m_2^{2} a_1^{2}c_{{2}}}, \end{aligned} \end{equation}$

(3.17)

$\begin{equation} \begin{aligned} q_{13} = &\frac{\left( \cot \left( \frac{1}{24} \sqrt {576 m_0m_2-{\frac {b_1 ^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}b_1^{2}c_2^{2}-48 b_{{0}} m_2^{2} a_1^{2}c_{{2}}-b_1^{2}c_2^{2} }{48 m_2^{2} a_1^{2}c_{{2}}}\\&-\frac{576 \left( \cot \left( \frac{1}{24} \sqrt {{\frac {576 a_1^{4}m_{{0} }m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}} }} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2} a_1^{4}m_0 m_2^{3}}{48 m_2^{2} a_1^{2}c_{{2}}}, \end{aligned} \end{equation}$

(3.18)

$\begin{equation} \begin{aligned} q_{14} = &-\frac{1}{24 m_2^{2} a_1^{2} \left( \cos \left( \frac{1}{12} \sqrt {{ \frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_2^{ 2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}c_2}\\ &\times\left( \begin{aligned} & -288 \left( \cos \left( \frac{1}{12} \sqrt {{\frac {576 a_1^{4}m_{{0 }}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4} }}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2} a_1^{4}m_0 m_2^{3}\\&+576 \sin \left( \frac{1}{12} \sqrt {{\frac {576 a_1^{4}m_0m_{{2} }^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) a_1^{4}m_0m_2^{3}\\&-24 b_{{0}}m_2^{2} a_1^{2}c_{{2}} \left( \cos \left( \frac{1}{12} \sqrt {{\frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_ {{2}}^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\&+576 a_1^{4}m_0m_2^{3}-\sin \left( \frac{1}{12} \sqrt {{\frac {576 a_1^{4}m_0m_2^{3}-b _{{1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t + C \right) \right) b_1^{2}c_2^{2}-b_1^{2}c_2^{ 2} \end{aligned} \right), \end{aligned} \end{equation}$

(3.19)

$\begin{equation} \begin{aligned} q_{15} = &\frac{1}{24c_{{2}} \left( \cos \left( \frac{1}{12} \sqrt {{\frac {576 a_1^{4}m_{{0 }}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4} }}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) -1 \right) m_2^{2} a_1 ^{2}}\\ &\times\left( \begin{aligned} &288 \cos \left( \frac{1}{12} \sqrt {{\frac {576 a_1^{4}m_0m_{{2} }^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) a_1^{4}m_0m_2^{3}+ 288 a_1^{4}m_0m_2^{3}\\&+24 \cos \left( \frac{1}{12} \sqrt {{ \frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_2^{ 2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) a_ {{1}}^{2}b_{{0}}c_{{2}}m_2^{2}\\&-24 b_{{0}}m_2^{2}a_{{1}}^{2}c_{{2}}-b_1^{2}c_2^{2} \end{aligned} \right), \end{aligned} \end{equation}$

(3.20)

$\begin{equation} { \begin{aligned} q_{16} = &\frac{1}{ 192m_2^{2}a_1^{2}c_{{2}}\left( \cos \left( \frac{1}{48}\sqrt {{\frac {576a_1^{4}m_0m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2}a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\left( \left( \cos \left( \frac{1}{48}\sqrt {{\frac {576a_1^{4}m_0m_2^{3} -b_1^{2}c_2^{2}}{m_2^{2}a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t + C \right) \right) \right) ^{2}-1 \right) }\\ &\times\left( \begin{aligned} &2304 \left( \cos \left( \frac{1}{48} \sqrt {{\frac {576 a_1^{4}m_{{0 }}m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4} }}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{4} a_1^{4}m_0 m_2^{3}\\&+192 \left( \cos \left( \frac{1}{48} \sqrt {{\frac {576 a_{{ 1}}^{4}m_0m_2^{3}-b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{4}a_{{1} }^{2}b_{{0}}c_{{2}}m_2^{2}\\&-2304 \left( \cos \left( \frac{1}{48} \sqrt {{\frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_ {{2}}^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2} a_1^{4}m_0m_2^{3}\\&-192 b_{{0}}m _{{2}}^{2} a_1^{2}c_{{2}} \left( \cos \left( \frac{1}{48} \sqrt {{ \frac {576 a_1^{4}m_0m_2^{3}-b_1^{2}c_2^{ 2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\&+576 a_1^{4}m_0m_2^{3}-b_1^{2}c_{ {2}}^{2} \end{aligned} \right), \end{aligned}} \end{equation}$

(3.21)

$\begin{equation} \begin{aligned} q_{17} = &b_0-12 \frac {m_2^{2} a_1^{2}}{c_2}\\ &\times\left( \begin{aligned} &\frac{\sqrt {- \left( -4 m_0m_2+{\frac {1}{144}} {\frac {b_1 ^{2}c_2^{2}}{m_2^{2} a_1^{4}}} \right) \left( p^{2 }-s^{2} \right) }}{2 m_2 \left( p\sin \left( \frac{1}{12} \sqrt {576 m_0m_2-{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) +s \right)}\\&-\frac{\frac{1}{12} p\sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}}\cos \left( \frac{1}{12} \sqrt {576 m_0m_{{ 2}}-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)}{2 m_2 \left( p\sin \left( \frac{1}{12} \sqrt {576 m_0m_2-{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) +s \right) }+\frac{1}{24} {\frac {b_{{1}}c_{{2}}}{m_2^{2} a_1^{2}}} \end{aligned} \right)^2 \\&+\left( \begin{aligned} &\frac{\sqrt {- \left( -4 m_0m_2+{\frac {1}{144}} {\frac {b_1 ^{2}c_2^{2}}{m_2^{2} a_1^{4}}} \right) \left( p^{2 }-s^{2} \right) }}{2 m_2 \left( p\sin \left( \frac{1}{12} \sqrt {576 m_0m_2-{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) +s \right)}\\&-\frac{\frac{1}{12} p\sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}}\cos \left( \frac{1}{12} \sqrt {576 m_0m_{{ 2}}-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)}{2 m_2 \left( p\sin \left( \frac{1}{12} \sqrt {576 m_0m_2-{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) +s \right) }+\frac{1}{24} {\frac {b_{{1}}c_{{2}}}{m_2^{2} a_1^{2}}} \end{aligned} \right)b_1, \end{aligned} \end{equation}$

(3.22)

$\begin{equation} \begin{aligned} q_{18} = &b_0-6912 m_0^{2} \left( \cos \left( \frac{1}{24} \sqrt {576 m_0m_{{2} }-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}m_2^{4} a_1^ {6} \Big/\\ &\left( \begin{aligned} &\sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_{{2} }^{2} a_1^{4}}}}\sin \left( \frac{1}{24} \sqrt {576 m_0m_2-{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}\\&-b_{{1}}c_{{2}} \cos \left( \frac{1}{24} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_{ {2}}^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \end{aligned} \right)^2c_2\\&-24 m_0\cos \left( \frac{1}{24} \sqrt {576 m_0m_2-{\frac {b_{{1 }}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}b_{{1}}\Big/\\ &\left( \begin{aligned} &\sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_{{2} }^{2} a_1^{4}}}}\sin \left( \frac{1}{24} \sqrt {576 m_0m_2-{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}\\&-b_{{1}}c_{{2}} \cos \left( \frac{1}{24} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_{ {2}}^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \end{aligned} \right), \end{aligned} \end{equation}$

(3.23)

$\begin{equation} \begin{aligned} q_{19} = &b_0-6912 m_0^{2} \left( \sin \left( \frac{1}{24} \sqrt {576 m_0m_{{2} }-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}m_2^{4} a_1^ {6} \Big/\\ &\left( \begin{aligned} &\sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_{{2} }^{2} a_1^{4}}}}\cos \left( \frac{1}{24} \sqrt {576 m_0m_2-{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}\\&+b_{{1}}c_{{2}} \sin \left( \frac{1}{24} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_{ {2}}^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \end{aligned} \right)^2c_2\\&+24 m_0\sin \left( \frac{1}{24} \sqrt {576 m_0m_2-{\frac {b_{{1 }}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}b_{{1}}\Big/\\ &\left( \begin{aligned} &\sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_{{2} }^{2} a_1^{4}}}}\cos \left( \frac{1}{24} \sqrt {576 m_0m_2-{ \frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) m_2 a_1^{2}\\&+b_{{1}}c_{{2}} \sin \left( \frac{1}{24} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_{ {2}}^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \end{aligned} \right), \end{aligned} \end{equation}$

(3.24)

$\begin{equation} \begin{aligned} q_{20} = &b_0-48 m_0^{2} \left( \cos \left( \frac{1}{12} \sqrt {576 m_0m_2- {\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}m_2^{2} a_1^ {2}\Big/\\ &\left( \begin{aligned} &\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}}\sin \left( \frac{1}{12} \sqrt {576 m_0m_{{2 }}-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \\&-\frac{\frac{1}{12} b_{{1}}c_{{2}}\cos \left( 1/ 12 \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_ {{2}}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)} {m_2^ {-1} a_1^{-2}}\\&+\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^ {2}c_2^{2}}{m_2^{2} a_1^{4}}}} \end{aligned} \right)^2c_2\\&-2 m_0\cos \left( \frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_{{1} }^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) b_{{1}}\Big/\\ &\left( \begin{aligned} &\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}}\sin \left( \frac{1}{12} \sqrt {576 m_0m_{{2 }}-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \\&-\frac{\frac{1}{12} b_{{1}}c_{{2}}\cos \left( 1/ 12 \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_ {{2}}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)} {m_2^ {-1} a_1^{-2}}\\&+\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^ {2}c_2^{2}}{m_2^{2} a_1^{4}}}} \end{aligned} \right), \end{aligned} \end{equation}$

(3.25)

$\begin{equation} \begin{aligned} q_{21} = &b_0-48 m_0^{2} \left( \sin \left( \frac{1}{12} \sqrt {576 m_0m_2- {\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}m_2^{2} a_1^ {2}\Big/\\ &\left( \begin{aligned} &\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}}\cos \left( \frac{1}{12} \sqrt {576 m_0m_{{2 }}-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \\&-\frac{\frac{1}{12} b_{{1}}c_{{2}}\sin \left( 1/ 12 \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_ {{2}}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)} {m_2^ {-1} a_1^{-2}}\\&+\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^ {2}c_2^{2}}{m_2^{2} a_1^{4}}}} \end{aligned} \right)^2c_2\\&-2 m_0\sin \left( \frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_{{1} }^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) b_{{1}}\Big/\\ &\left( \begin{aligned} &\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}}\cos \left( \frac{1}{12} \sqrt {576 m_0m_{{2 }}-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \\&-\frac{\frac{1}{12} b_{{1}}c_{{2}}\sin \left( 1/ 12 \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_ {{2}}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)} {m_2^ {-1} a_1^{-2}}\\&+\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^ {2}c_2^{2}}{m_2^{2} a_1^{4}}}} \end{aligned} \right), \end{aligned} \end{equation}$

(3.26)

$\begin{equation} { \begin{aligned} q_{22} = &b_0-192 m_0^{2} \left( \sin \left( \frac{1}{48} \sqrt {576 m_0m_2 -{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\&\times \left( \cos \left( \frac{1}{48} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_ {{2}}^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^ {2}m_2^{2} a_1^{2} \Big/\\ &\left( \begin{aligned} &\frac{1}{6} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m _{{2}}^{2} a_1^{4}}}} \left( \cos \left( \frac{1}{48} \sqrt {576 m_{{0 }}m_2-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{ 4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\& +\frac{b_{{1}}c_{{2}}\sin \left( \frac{1}{48} \sqrt {576 m_0m_2-{\frac {b_ {{1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \cos \left( \frac{1}{48} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)}{6 m_2 a_1^{2}}\\&-\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}} \end{aligned} \right)^2c_2\\& +4 m_0\sin \left( \frac{1}{48} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \cos \left( \frac{1}{48} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) b_{{1}}\Big/\\ &\left( \begin{aligned} &\frac{1}{6} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m _{{2}}^{2} a_1^{4}}}} \left( \cos \left( \frac{1}{48} \sqrt {576 m_{{0 }}m_2-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{ 4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \right) ^{2}\\& +\frac{b_{{1}}c_{{2}}\sin \left( \frac{1}{48} \sqrt {576 m_0m_2-{\frac {b_ {{1}}^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right) \cos \left( \frac{1}{48} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{m_2^{2} a_1^{4}}}} \left( a_1x+a_2y+a_3z+a_4 t +C \right) \right)}{6 m_2 a_1^{2}}\\&-\frac{1}{12} \sqrt {576 m_0m_2-{\frac {b_1^{2}c_2^{2}}{ m_2^{2} a_1^{4}}}} \end{aligned} \right). \end{aligned}} \end{equation}$

(3.27)

3.2. Solitary wave solutions using the GK method

This section will use the GK method to provide different solitary wave solutions of the 3DPTE in Eq (1.1). Now, balance $u^{(4)}$ with $\left(u^{\prime}\right)^2$ in Eq (3.2) to get $P = Q+2$ . If we let $Q = 1$ , then $P = 3$ , and from Eq (2.6), the solution takes the following form:

$\begin{equation} u(\xi) = \frac{b_0+b_1\Omega(\xi)+b_2\Omega^2(\xi)+b_3\Omega^3(\xi)}{f_0+f_1\Omega(\xi)}. \end{equation}$

(3.28)

If we substitute Eq (3.28) into Eq (3.2), using Eq (2.7) and equating the coefficients of $\Omega^i(\xi)$ to zero, then we obtain the following algebraic equations:

$\begin{eqnarray} \begin{aligned} \Omega(\xi):\quad& -a_1^{3}a_2b_0f_0^{3}f_1+a_1^{3}a_2b_1f_0^{4}-a_1^{2}b_0c_3f_0^{3}f_1+a_1^{2}b_1c_2f_0^{4}-a_1a_2b_0^{2}c_2f_0^{2}f_1+a_1a_2b_0b_1c_2f_0^{3}\\&-a_2a_4b_0c_1f_0^{3}f_1+a_2a_4b_1c_1f_0^{4}-a_3^{2}b_0c_4f_0^{3}f_1+a_3^{2}b_1c_4f_0^{4} = 0,\\ \Omega^2(\xi):\quad& 15 a_1^{3}a_2b_0f_0^{3}f_1+11 a_1^{3}a_2b_0f_0^{2}f_1^{2}-15 a_1^{3}a_2b_1f_0^{4}-11 a_1^{3}a_2b_1f_0^{3}f_1+16 a_1^{3}a_2b_2f_0^{4}+3 a_1^{2}b_0c_3f_0^{3}f_1\\&-a_1^{2}b_0c_3f_0^{2}f_1^{2}-3 a_1^{2}b_1c_3f_0^{4}+a_1^{2}b_1c_3f_0^{3}f_1+4 a_1^{2}b_2c_2f_0^{4}+3 a_1a_2b_0^{2}c_2f_0^{2}f_1+a_1a_2b_0^{2}c_2f_0f_1^{2}\\&-3 a_1a_2b_0b_1c_2f_0^{3}-3 a_1a_2b_0b_1c_2f_0^{2}f_1+4 a_1a_2b_0b_2c_2f_0^{3}+2 a_1a_2b_1^{2}c_2f_0^{3}+3 a_2a_4b_0c_1f_0^{3}f_1\\&-a_2a_4b_0c_1f_0 ^{2}f_1^{2}-3 a_2a_4b_1c_1f_0^{4}+a_2a_4b_1c_1f_0^{3}f_1+4 a_2a_4b_2c_1f_0^{4}+3 a_3^{2}b_0c_4f_0^{3}f_1-a_3^{2}b_0c_4f_0^{2}f_1^{2}\\&-3 a_3^{2}b_1c_4f_0^{4}+a_3^{2}b_1c_4f_0^{3}f_1+4 a_3^{2}b_2c_4f_0^{4} = 0,\\ \Omega^3(\xi):\quad& -50 a_1^{3}a_2b_0f_0^{3}f_1-55 a_1^{3}a_2b_0f_0^{2}f_1^{2}-11 a_1^{3}a_2b_0f_0f_1^{3}+50 a_1^{3}a_2b_1f_0^{4}+55 a_1^{3}a_2b_1f_0^{3}f_1\\&+11 a_1^{3}a_2b_1f_0^{2}f_1^{2}-130 a_1^{3}a_2b_2f_0^{4}-a_1^{3}a_2b_2f_0^{3}f_1+81 a_1^{3}a_2b_3f_0^{4}-2 a_1^{2}b_0c_3f_0^{3}f_1+5 a_1^{2}b_0c_3f_0^{2}f_1^{2}\\&+a_1^{2}b_0c_3f_0f_1^{3}+2 a_1^{2}b_1c_3f_0^{4}-5 a_1^{2}b_1c_3f_0^{3}f_1-a_1^{2}b_1c_3f_0^{2}f_1^{2}-10 a_1^{2}b_2c_3f_0^{4}+11 a_1^{2}b_2c_3f_0^{3}f_1\\&+9 a_1^{2}b_3c_3f_0^{4}-2 a_1a_2b_0^{2}c_2f_0^{2}f_1+2 a_1a_2b_0^{2}c_2f_1^{3}+2 a_1a_2b_0b_1c_2 f_0^{3}+5 a_1a_2b_0b_1c_2f_0^{2}f_1\\&-3 a_1a_2b_0b_1c_2f_0f_1^{2}-10 a_1a_2b_0b_2c_2f_0^{3}+2 a_1a_2b_0b_2c_2f_0^{2}f_1+9 a_1a_2b_0b_3c_2f_0^{3}-5 a_1a_2b_1^{2}c_2f_0^{3}\\&+a_1a_2b_1^{2}c_2f_0^{2}f_1+9 a_1a_2b_1b_2c_2f_0^{3}-2 a_2a_4b_0c_1f_0^{3}f_1+5 a_2a_4b_0c_1f_0^{2}f_1^{2}+a_2a_4b_0c_1f_0f_1^{3}\\&+2 a_2a_4b_1c_1f_0^{4}-5 a_2a_4b_1c_1f_0^{3}f_1-a_2a_4b_1c_1f_0^{2}f_1^{2}-10 a_2a_4b_2c_1f_0^{4}+11 a_2a_4b_2c_1f_0^{3}f_1\\&+9 a_2a_4b_3c_1f_0^{4}-2 a_3^{2}b_0c_4f_0^{3}f_1+5 a_3^{2}b_0c_4f_0^{2}f_1^{2}+a_3^{2}b_0c_4f_0f_1^{3}+2 a_3^{2}b_1c_4f_0^{4}\\&-5 a_3^{2}b_1c_4f_0^{3}f_1-a_3^{2}b_1c_4f_0^{2}f_1^{2}-10 a_3^{2}b_2c_4f_0^{4}+11 a_3^{2}b_2c_4f_0^{3}f_1+9 a_3^{2}b_3c_4f_0^{4} = 0,\\ \Omega^4(\xi):\quad&60 a_1^{3}a_2b_0f_0^{3}f_1+80 a_1^{3}a_2b_0f_0^{2}f_1^{2}+25 a_1^{3}a_2b_{{0} }f_0f_1^{3}+a_1^{3}a_2b_0f_1^{4}-60 a_1^{3}a_2b_1f_0^{4}-80 a_1^{3}a_2b_1f_0^{3}f_1\\&-25 a_1^{3}a_2b_1f_0^{2}f_1^{2}-a_1^{3}a_2b_1f_0f_1^{3}+330 a_1^{3}a_2b_2f_0^{4}-125 a_1^{3}a_2b_2f_0^{3}f_1+11 a_1^{3}a_2b_2f_0^{2}f_1^{2}\\&-525 a_1^{3}a_2b_3f_0^{4}+149 a_1^{3}a_2b_3f_0^{3}f_1-4 a_1^{2}b_0c_3f_0^{2}f_1^{2}+a_1^{2}b_0c_3f_0f_1^{3}+a_ {{1}}^{2}b_0c_3f_1^{4}\\&+4 a_1^{2}b_1c_3f_0^{3}f_1-a_1^{2}b_1c_3f_0^{2}f_1^{2}-a_1^{2}b_1c_3f_0f_1^{3}+6 a_1^{2}b_2c_3f_0^{4}-29 a_1^{2}b_2c_3f_0^{3}f_1+11 a_1^{2}b_2c_3f_0^{2}f_1^{2}\\ &-21 a_1^{2}b_3c_3f_0^{4}+29 a_1^{2}b_3c_3f_0^{3}f_1-a_1a_2b_0^{2}c_2f_0f_1^{2}-3 a_1a_2b_0^{2}c_2f_1^{3}-2 a_1a_2b_0b_1c_2f_0^{2}f_1\\&+7 a_1a_2b_0b_1c_2f_0f_1^{2}+a_1a_2b_0b_1c_2f_1^{3}+6 a_1a_2b_0b_2c_2f_0^{3}-8 a_1a_2b_0b_2c_2f_0^{2}f_1-2 a_1a_2b_0b_2c_2f_0f_1^{2}\\&-21 a_1a_2b_0 b_3c_2f_0^{3}+13 a_1a_2b_0b_3c_2f_0^{2}f_1+3 a_1a_2b_1^{2}c_2f_0^{3}-4 a_1a_2b_1^{2}c_2f_0^{2}f_1-a_1a_2b_1^{2}c_2f_0f_1^{2}\\ &-21 a_1a_2b_1b_2c_2f_0^{3}+13 a_1a_2b_1b_2c_2f_0^{2}f_1+16 a_1a_2b_1b_3c_2f_0^{3}+8 a_1a_2b_2^{2}c_2f_0^{3}-4 a_2a_4b_0c_1f_0^{2}f_1^{2}\\ &+a_2a_4b_0c_1f_0f_1^{3}+a_2a_4b_0c_1f_1^{4}+4 a_2a_4b_1c_1f_0^{3}f_1-a_2a_4b_1c_1f_0^{2}f_1^{2}-a_2a_4b_1c_1f_0f_1^{3}\\&+6 a_2a_4b_2c_1f_0^{4}-29 a_2a_4b_2c_1f_0^{3}f_1+11 a_2a_4b_2c_1f_0^{2}f_1^{2}-21 a_2a_4b_3c_1f_0^{4}+29 a_2a_4b_3c_1f_0^{3}f_1\\&-4 a_3^{2}b_0c_4f_0^{2}f_1^{2}+a_3^{2}b_0c_4f_0f_1^{3}+a_3^{2}b_0c_4f_1^{4}+4 a_3^{2}b_1c_4f_0^{3}f_1-a_3^{2}b_1c_4f_0^{2}f_1^{2}-a_3^{2}b_1c_4f_0f_1^{3}\\&+6 a_3^{2}b_2c_4f_0^{4}-29 a_3^{2}b_2c_4f_0^{3}f_1+11 a_3^{2}b_2c_4f_0^{2}f_1^{2}-21 a_3^{2}b_3c_4f_0^{4}+29 a_3^{2}b_3c_4f_0^{3}f_1 = 0, \end{aligned} \end{eqnarray}$

$\begin{eqnarray} \begin{aligned} \Omega^5(\xi):\quad& -24 a_1^{3}a_2b_0f_0^{3}f_1-36 a_1^{3}a_2b_0f_0^{2}f_1^{2}-14 a_1^{3}a_2b_0f_0f_1^{3}-a_1^{3}a_2b_0f_1^{4}+24 a_1^{3}a_2b_1f_0^{4}+36 a_1^{3}a_2b_1 f_0^{3}f_1\\&+14 a_1^{3}a_2b_1f_0^{2}f_1^{2}+a_1^{3}a_2b_1f_0f_1^{3}-336 a_1^{3}a_2b_2f_0^{4}+486 a_1^{3}a_2b_2f_0^{3}f_1-151 a_1^{3}a_2b_2f_0^{2}f_1^ {2}\\&+5 a_1^{3}a_2b_2f_0f_1^{3}+1164 a_1^{3}a_2b_3f_0^{4}-1149 a_1^{3}a_2b_3f_0^{3}f_1+155 a_1^{3}a_2b_3f_0^{2}f_1^{2}-2 a_1^{2}b_0c_3f_0f_1^{3}\\&-a_1^{2}b_ {{0}}c_3f_1^{4}+2 a_1^{2}b_1c_3f_0^{2}f_1^{2}+a_1^{2}b_1c_3f_0f_1^{3}+18 a_1^{2}b_2c_3f_0^{3}f_1-31 a_1^{2}b_2c_3f_0^{2}f_1^{2}+5 a_1^{2}b_2c_3f_0f_1^{3}\\&+12 a_1^{2}b_3c_3f_0^{4}-69 a_1^{2}b_3c_3f_0^{3}f_1+35 a_1^{2}b_3c_3 f_0^{2}f_1^{2}+a_1a_2b_0^{2}c_2f_1^{3}-4 a_1a_2b_0b_1c_2f_0f_1^{2}\\&-a_1a_2b_0b_1c_2f_1^{3}+6 a_1a_2b_0b_2c_2f_0^{2}f_1+2 a_1a_2b_0b_2c_2f_0f_1^{2}+12 a_1a_2b_0b_3c_2f_0^{3}-33 a_1a_2b_0b_3c_2f_0^{2}f_1\\&+5 a_1a_2b_0b_3c_2f_0f_1^{2}+3 a_1a_2 b_1^{2}c_2f_0^{2}f_1+a_1a_2b_1^{2}c_2f_0f_1^{2}+12 a_1a_2b_1b_2c_2f_0^{3}-33 a_1a_2b_1b_2c_2f_0^{2}f_1\\&+5 a_1a_2b_1b_2c_2f_0f_1^{2}-36 a_1a_2b_1b_3c_2f_0^{3}+30 a_1a_2b_1b_3c_2f_0^{2}f_1-18 a_1a_2b_2^{2}c_2f_0^{3}+15 a_1a_2b_2^{2}c_2f_0^{2}f_1\\ &+25 a_1a_2b_2b_3c_2f_0^{3}-2 a_2a_4b_0c_1f_0f_1^{3}-a_2a_4b_0c_1f_1^{4}+2 a_2a_4b_1c_1f_0^{2}f_1^{2}+a_2a_4b_1c_1f_0f_1^{3}\\&+18 a_2a_4b_2c_1f_0^{3}f_1-31 a_2a_4b_2c_1f_0^{2}f_1^{2}+5 a_2a_4b_2c_1f_0f_1^{3}+ 12 a_2a_4b_3c_1f_0^{4}-69 a_2a_4b_3c_1f_0^{3}f_1\\&+35 a_2a_4b_3c_1f_0^{2}f_1^{2}-2 a_3^{2}b_0c_4f_0f_1^{3}-a_3^{2}b_0c_4f_1^{4}+2 a_3^{2}b_1c_4f_0^{2}f_1^{2}+a_3^{2}b_1c_4f_0f_1^{3}+18 a_3^{2}b_2c_4f_0^{3}f_1\\&-31 a_3^{2}b_2c_4f_0^{2}f_1^{2}+5 a_3^{2}b_2c_4f_0f_1^{3}+12 a_3^{2}b_3c_4f_0^{4}-69 a_3^{2}b_3c_4f_0^{3}f_1+35 a_3^{2} b_3c_4f_0^{2}f_1^{2} = 0, \\ \Omega^6(\xi):\quad& 120 a_1^{3}a_2b_2f_0^{4}-600 a_1^{3}a_2b_2f_0^{3}f_1+500 a_1^{3}a_2b_2f_0 ^{2}f_1^{2}-75 a_1^{3}a_2b_2f_0f_1^{3}+a_1^{3}a_2b_2f_1^{4}-1080 a_1^{3}a_2b_{ {3}}f_0^{4}\\&+2800 a_1^{3}a_2b_3f_0^{3}f_1-1225 a_1^{3}a_2b_3f_0^{2}f_1^{2}+79 a_1^{3}a_2b_3f_0f_1^{3}+20 a_1^{2}b_2c_3f_0^{2}f_1^{2}-15 a_1^{2}b_2c_3f_0 f_1^{3}\\&+a_1^{2}b_2c_3f_1^{4}+40 a_1^{2}b_3c_3f_0^{3}f_1-85 a_1^{2}b_3c_3f_0^{2}f_1^{2}+19 a_1^{2}b_3c_3f_0f_1^{3}+20 a_1a_2b_0b_3c_2f_0^{2}f_1\\&-15 a_1a_2b_0b_3c_2f_0f_1^{2}+a_1a_2b_0b_3c_2f_1^{3}+20 a_1a_2b_1b_2c_2f_0^{2}f_1-15 a_1a_2b_1b_2c_2f_0f_1^{2}\\&+a_1a_2b_1b_2c_2f_1^{3}+20 a_1a_2b_1b_3c_2f_0^{3}-70 a_1a_2b_1b_3c_2f_0^{2}f_1+18 a_1a_2b_1b_3 c_2f_0f_1^{2}+10 a_1a_2b_2^{2}c_2f_0^{3}\\&-35 a_1a_2b_2^{2}c_2f_0^{2}f_1+9 a_1a_2b_2^{2}c_2f_0f_1^{2}-55 a_1a_2b_2b_3c_2f_0^{3}+53 a_1a_2b_2b_3c_2f_0^{2}f_1+18 a_1a_2b_3^{2}c_2f_0^{3} \\&+20 a_2a_4b_2c_1f_0^{2}f_1^{2}-15 a_2a_4b_2c_1f_0f_1^{3}+a_2a_4b_2c_1f_1^{4}+40 a_2a_4b_3c_1f_0^{3}f_1-85 a_2a_4b_3c_1f_0^{2}f_1^{2}\\&+19 a_2a_4b_3c_1f_0f_1^{3}+20 a_3^{2}b_2c_4f_0^{2}f_1^{2}-15 a_3^{2}b_2c_4 f_0f_1^{3}+a_3^{2}b_2c_4f_1^{4}+40 a_3^{2}b_3c_4f_0^{3}f_1\\&-85 a_3^{2}b_3c_4f_0^{2}f_1^{2}+19 a_3^{2}b_3c_4f_0 f_1^{3} = 0,\\ \Omega^7(\xi):\quad& 240 a_1^{3}a_2b_2f_0^{3}f_1-600 a_1^{3}a_2b_2f_0^{2}f_1^{2}+250 a_1^{3}a_2b_2f_0f_1^{3}-15 a_1^{3}a_2b_2f_1^{4}+ 360 a_1^{3}a_2b_3f_0^{4}\\&-2760 a_1^{3}a_2b_3f_0^{3}f_1+3050 a_1^{3}a_2b_3f_0^{2}f_1^{2}-635 a_1^{3}a_2b_3f_0f_1^{3}+16 a_1^{3}a_2b_3f_1^{4}+10 a_1^{2}b_2c_3f_0f_1^{3}\\&-3 a_1^{2}b_2c_3f_1^{4}+50 a_1^{2}b_3c_3f_0^{2}f_1^{2}-47 a_1^{2}b_3c_3f_0f_1^{3}+4 a_1^{2}b_3c_3f_1^{4}+10 a_1a_2b_0b_3c_2f_0f_1^{2}\\&-3 a_1a_2b_0b_3c_2f_1^{3}+10 a_1a_2b_1b_2c_2f_0f_1^{2}-3 a_1a_2b_1b_2c_2f_1^{3}+40 a_1a_2b_1b_3c_{{2} }f_0^{2}f_1-44 a_1a_2b_1b_3c_2f_0f_1^{2}\\&+4 a_1a_2b_1b_3c_2f_1^{3}+20 a_1a_2b_2^{2}c_2f_0^{2}f_1-22 a_1a_2b_2^{2}c_2f_0f_1^{2}+2 a_1a_2b_2^{2}c_2f_1^{3}+30 a_1a_2b_2b_3c_2f_0^{3}\\&-119 a_1a_2b_2b_3c_2f_0^{2}f_1+37 a_1a_2b_2b_3c_2f_0f_1^{2}-39 a_1a_2b_3^{2}c_2f_0^{3}+41 a_1a_2b_3^{2}c_2f_0^{2}f_1\\&+10 a_2a_4b_2c_1f_0f_1^{3}-3 a_2a_4b_2c_1f_1^{4}+50 a_2a_4b_3c_1f_0^{2}f_1^{2}-47 a_2a_4b_3c_1f_0f_1^{3}+4 a_2a_4b_3c_1f_1^ {4}\\&+10 a_3^{2}b_2c_4f_0f_1^{3}-3 a_3^{2}b_2c_4f_1^{4}+50 a_3^{2}b_3c_4f_0 ^{2}f_1^{2}-47 a_3^{2}b_3c_4f_0f_1^{3}+ 4 a_3^{2}b_3c_4f_1^{4} = 0,\\ \Omega^8(\xi):\quad& 240 a_1^{3}a_2b_2f_0^{2}f_1^{2}-300 a_1^{3}a_2b_2f_0f_1^{3}+50 a_1^{3}a_2b_{{ 2}}f_1^{4}+960 a_1^{3}a_2b_3f_0^{3}f_1-3060 a_1^{3}a_2b_3f_0^{2}f_1^{2}\\&+1600 a_1^{3}a_2b_3f_0f_1^{3}-130 a_1^{3}a_2b_3f_1^{4}+2 a_1^{2}b_2c_3f_1^{4}+28 a_1^{2}b_3c_3f_0f_1^{3}-10 a_1^{2}b_3c_3f_1^{4}+2 a_1a_2b_0b_3c_2f_1^{3}\\ &+2 a_1a_2b_1b_2c_2f_1^{3}+26 a_1a_2b_1b_3c_2f_0f_1^{2}-10 a_1a_2b_1 b_3c_2f_1^{3}+13 a_1a_2b_2^{2}c_2f_0f_1^{2}-5 a_1a_2b_2^{2}c_2f_1^{3}\\&+66 a_1a_2b_2b_3c_2f_0^{2}f_1-85 a_1a_2b_2b_3c_2f_0f_1^{2}+9 a_1a_2b_2b_3c_2f_1^{3}+21 a_1a_2b_3^{2}c_2f_0^{3}-90 a_1a_2b_3^{2}c_2f_0^{2}f_1 \\&+31 a_1a_2b_3^{2}c_2f_0f_1^{2}+2 a_2a_4b_2c_1f_1^{4}+28 a_2a_4b_3c_1f_{ {0}}f_1^{3}-10 a_2a_4b_3c_1f_1^{4}+2 a_3^{2}b_2c_4f_1^{4}\\&+28 a_3^{2}b_3c_4f_0f_1^{3}-10 a_3^{2}b_3c_4f_1^{4} = 0, \end{aligned} \end{eqnarray}$

$\begin{eqnarray} \begin{aligned} \Omega^9(\xi):\quad& 120 a_1^{3}a_2b_2f_0f_1^{3}-60 a_1^{3} a_2b_2f_1^{4}+1080 a_1^{3}a_2b_3f_0^{2}f_1^{2}-1620 a_1^{3}a_2b_3f_0f_1^{3}+330 a_1^{3}a_2b_3f_1^{4}+6 a_1^{2}b_3c_3f_1^{4}\\&+6 a_1a_2b_1b_3c_3f_1^ {3}+3 a_1a_2b_2^{2}c_2f_1^{3}+48 a_1a_2b_2b_3c_2f_0f_1^{2}-21 a_1a_2b_2 b_3c_2f_1^{3}+49 a_1a_2b_3^{2}c_2f_0^{2}f_1\\&-69 a_1a_2b_3^{2}c_2f_0f_1^{2}+8 a_1a_2b_3^{2}c_2f_1^{3}+6 a_2a_4b_3c_1f_1^{4}+6 a_3^{2}b_3c_4f_1^{4} = 0,\\ \Omega^{10}(\xi):\quad& 24 a_1^{3}a_2b_2f_1^{4}+576 a_1^{3}a_2 b_3f_0f_1^{3}-336 a_1^{3}a_2b_3f_1^{4}+12 a_1a_2b_2b_3c_2f_1^{3}+38 a_1a_2b_3^{2}c_2f_0f_1^{2}\\&-18 a_1a_2b_3^{2}c_2f_1^{3} = 0. \end{aligned} \end{eqnarray}$

Using a symbolic software package to solve the above equations, one gets the following sets of solutions:

Set 1.

$\begin{equation} \begin{aligned} &b_0 = {\frac {b_2 \left( a_1^{3}a_2+a_1^{2}c_3 +a_2a_4c_1+a_3^{2}c_{{4}} \right) }{12a_1^{3}a_{ {2}}}}, \quad b_1 = -b_2, \quad b_2 = b_2, \quad b_3 = 0, \quad f_0 = f_0,\\& f_1 = 0, \quad c_2 = - {\frac {12f_0a_1^{2}}{b_2}}. \end{aligned} \end{equation}$

(3.29)

Set 2.

$\begin{equation} \begin{aligned} &b_0 = {\frac {b_1f_0}{f_1}}, \quad b_1 = b_1, \quad b_2 = 0, \quad b_3 = 0, \quad f_0 = f_0, \quad f_1 = f_1, \quad c_2 = c_2. \end{aligned} \end{equation}$

(3.30)

Set 3.

$\begin{equation} \begin{aligned} &b_0 = 0,\quad b_1 = - {\frac {b_2 \left( a_1^{3}a_2+a_1^{2}c_{{3} }+a_2a_4c_1+a_3^{2}c_{{4}} \right) }{12a_1^{3}a_ {{2}}}},\quad b_2 = b_2, \quad b_3 = -b_2, \\&f_0 = 0, \quad f_1 = {\frac {b_2c_{{2}}}{12a_1^{2}}}, \quad c_2 = c_2. \end{aligned} \end{equation}$

(3.31)

Set 4.

$\begin{equation} \begin{aligned} &b_0 = -{\frac {f_0 \left( a_1^{3}a_2+a_1^{2}c_3+a_{{ 2}}a_4c_1+a_3^{2}c_{{4}} \right) }{a_{{1}}c_{{2}}a_2 }},\quad b_1 = -{\frac {-12 a_1^{3}a_2f_0+a_1^{3}a_2f_1+ a_1^{2}c_3f_1+a_2a_4c_1f_1+a_3^{2} c_{{4}}f_1}{a_{{1}}c_{{2}}a_2}},\\& b_2 = {\frac {12a_1^{2} \left( f_1-f_0 \right) }{c_2}}, \quad b_3 = - {\frac {12a_1^{2}f_1}{c_2}}, \quad f_0 = f_0, \quad f_1 = f_1, \quad c_2 = c_2. \end{aligned} \end{equation}$

(3.32)

Substitute the solutions obtained from Set 1 into Eq (3.28) to obtain the following solutions for Eq (1.1) as

$\begin{equation} q_{23} = \frac{\left( {\frac {b_2}{ \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right) ^{2}}}-{ \frac {b_2}{1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}}}}+ {\frac {b_2 \left( a_{{ 1}}^{3}a_2+a_1^{2}c_3+a_2a_4c_1+a_3^{ 2}c_{{4}} \right) }{12a_1^{3}a_2}} \right)} {{f_0}}. \end{equation}$

(3.33)

Similarly, substituting the solutions from Set 2 into Eq (3.28), we have

$\begin{equation} q_{24} = \frac{\left( {\frac {b_1}{1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}}}}+{\frac {b_1f_0}{f _{{1}}}} \right) \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right)} {\left( f_0{ {\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}}+f_0+f_1 \right)}. \end{equation}$

(3.34)

Again, substituting the solutions obtained from Set 3 into Eq (3.28), we get

$\begin{equation} q_{25} = \frac{12 \left( -{\frac {b_2}{ \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right) ^{3}}} +{\frac {b_2}{ \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right) ^{2}}}- { \frac {b_2 \left( a_1^{3}a_2+a_1^{2}c_3+a_{{2} }a_4c_1+a_3^{2}c_{{4}} \right) }{12 \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t) }} \right) a_2a_1^{3}}} \right) \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right) a_1^{2}}{{b_2}c_2}. \end{equation}$

(3.35)

Lastly, substituting the solutions obtained from Set 4 into Eq (3.28), we obtain

$\begin{equation} \begin{aligned} q_{26} = & \frac{\left( - {\frac {12a_1^{2}f_1}{ \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right) ^{3}c_{{2}}}}+ {\frac {12a_1^{2} \left( f_1-f_{{0} } \right) }{ \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right) ^{2}c_{{2}}}}-{\frac {- 12 a_1^{3}a_2f_0+a_1^{3}a_2f_1+a_1^ {2}c_3f_1+a_2a_4c_1f_1+a_3^{2}c_{{4}}f_{ {1}}}{ \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right) a_{{1}}c_{{2}}a_2}} \right) \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right)} {\left( f_0{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}}+f_0+f_1 \right)}\\&-\frac{\left({ \frac {f_0 \left( a_1^{3}a_2+a_1^{2}c_3+a_{{2} }a_4c_1+a_3^{2}c_{{4}} \right) }{a_{{1}}c_{{2}}a_2}} \right) \left( 1+{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}} \right)} {\left( f_0{{\rm e}^{ (a_1x+a_2y+a_3z+a_4 t)}}+f_0+f_1 \right)}. \end{aligned} \end{equation}$

(3.36)

4. Graphical results and discussion

This paper derives traveling wave solutions for the newly introduced 3DPTE in Eq (1.1) by using the IGRE and GK methods. We have obtained four different rational exponential function solutions for the considered equation using the GK method. These exponential rational function solutions are entirely different from three exponential function solutions reported in ^[22]. Hence, the exponential rational function solutions are new and have never been reported in previous studies. Using the IGRE method, we have obtained a total of twenty-two trigonometric and hyperbolic function solutions and mixed trigonometric and hyperbolic function solutions. These solutions are more succinct and general than those reported in ^{[17,18,19,20,21]}. Additionally, the majority of the derived solutions in this study are hyperbolic and trigonometric functions that may result in different periodic structures. Periodic soliton disturbances in optical fibers help us comprehend ultra-short pulse lasers and long-distance optical communication networks. Furthermore, trigonometric and hyperbolic functions, as well as complex structures, have a vital role in determining optical characteristics. Thus, the proposed solutions may have numerous potential uses in nano and optical fibers. Solutions with cotangent hyperbolic functions are specifically relevant to magnetic polarization since they may be found in the Langevin function. Tangent hyperbolic functions can be employed in special relativistic and magnetic moment computations. Hyperbolic secant solutions are known to be useful in laminar jets ^[46].

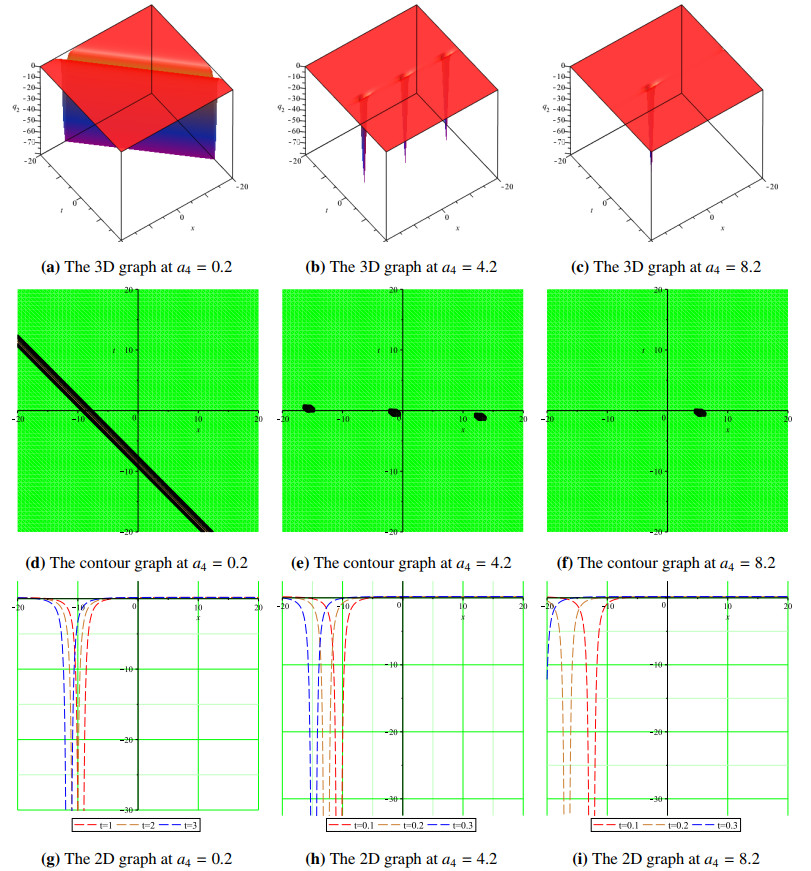
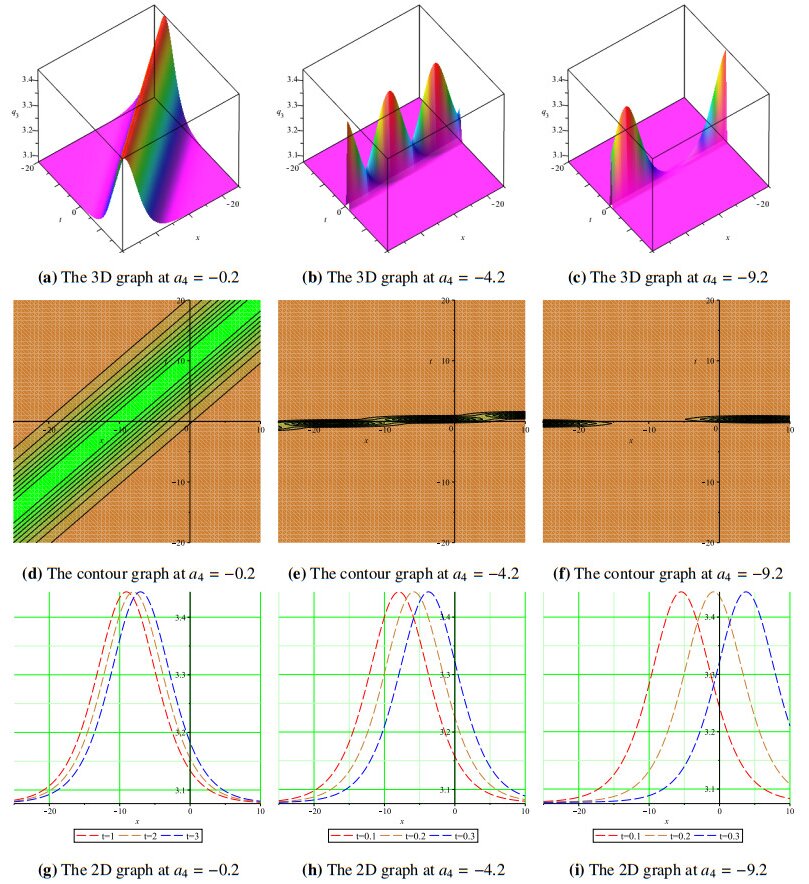
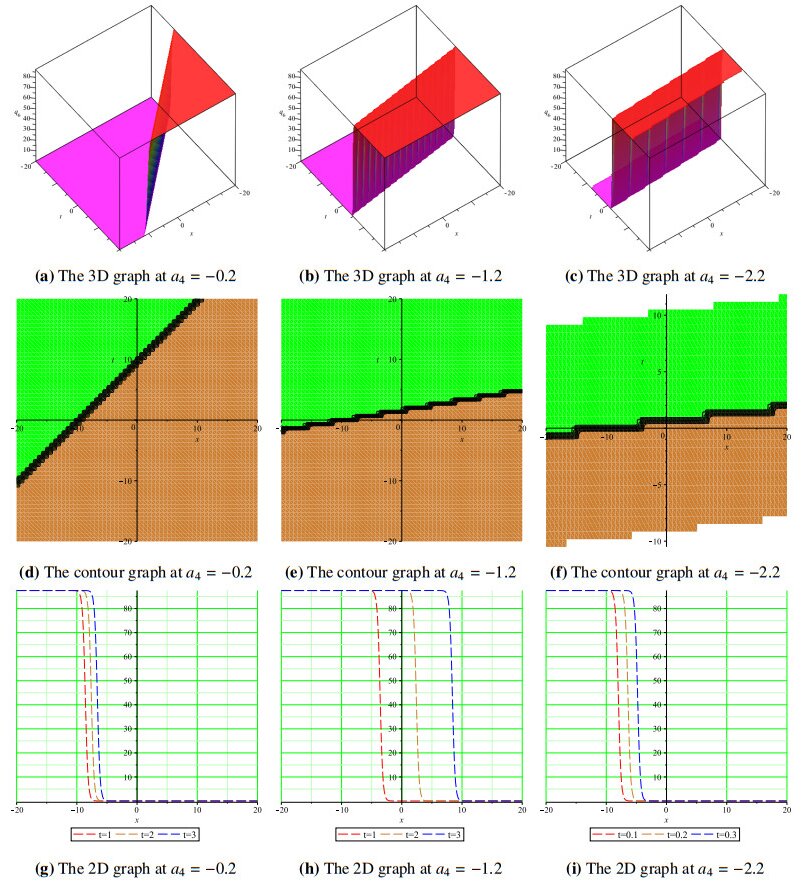
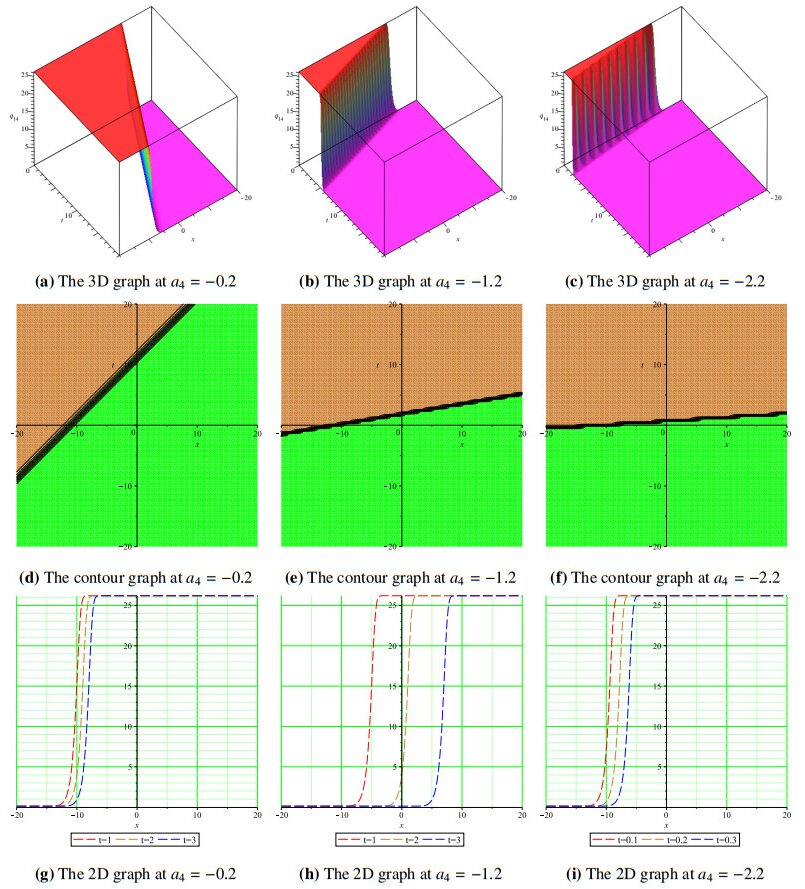
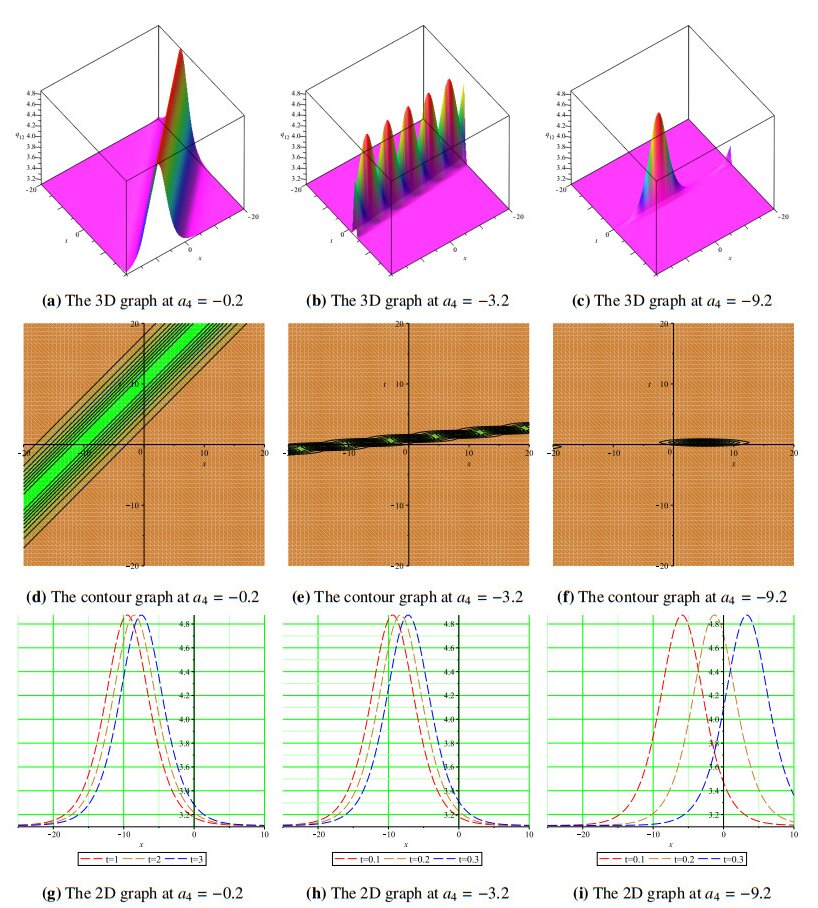
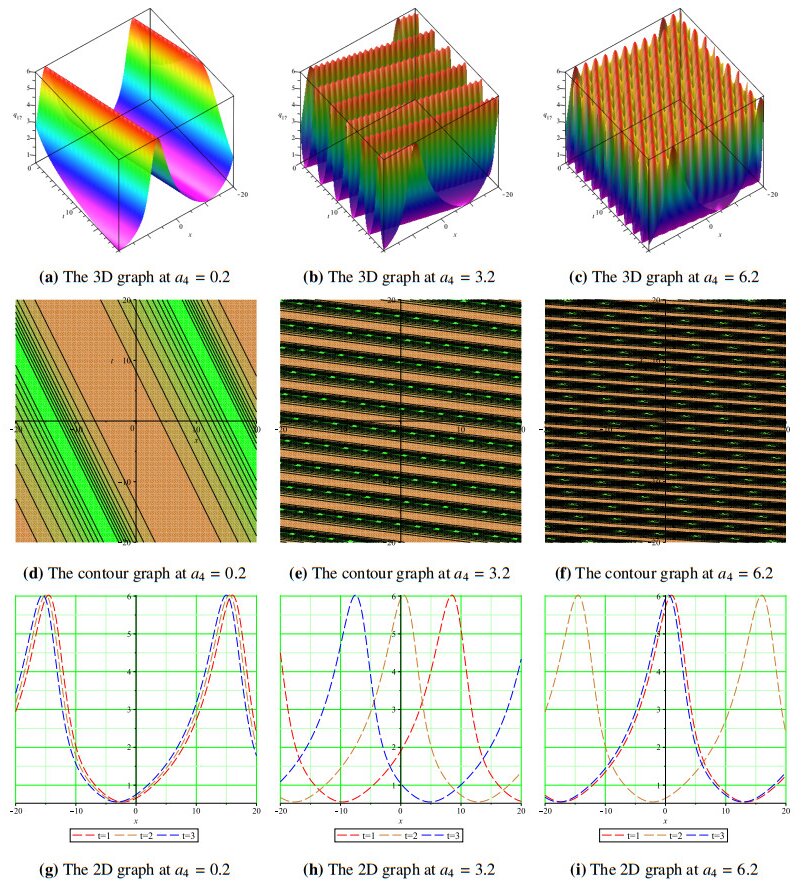
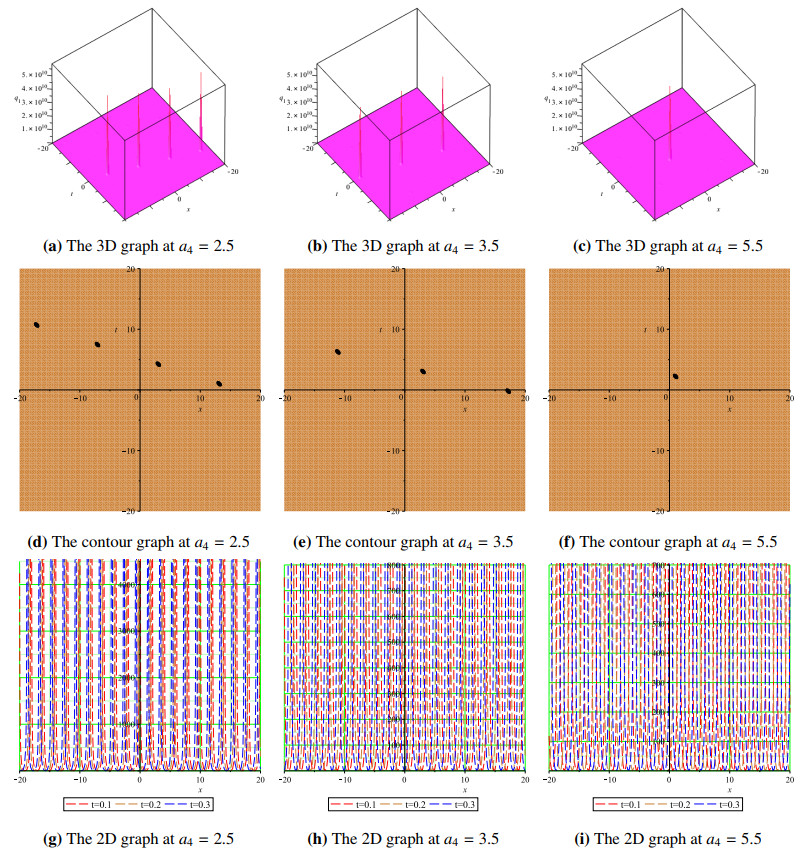
Moreover, using different $x, t$ domains, we have studied the wave propagation profiles of the proposed solutions as displayed in 3D, contour, and 2D plots at different time levels. Since rogue waves are space-time solitary waves with a large amplitude, we varied the wave amplitudes of the displayed solutions in our simulations to report 3D, contour and 2D graphs of some of a range of solutions. shows Kuztnetsov-Ma-like breathers at $a_4 = 2.5$ , $a_4 = 3.5$ , and shows a Peregrine-like soliton $a_4 = 5.5$ for the solutions $q_1$ . The same is demonstrated using contour plots in , while displays 2D plots of the solution $q_1$ at different time levels. demonstrates the dark wave propagation for solution $q_2$ , as the amplitude is increased from $a_4 = 0.2$ to $a_4 = 4.2$ and $a_4 = 8.2$ , and we obtain two different breather solitons in . The corresponding contour and 2D graphs are also shown in for the soliton solution $q_2$ . shows the bright-soliton wave profile at $a_4 = -0.2$ and at $a_4 = -4.2$ and $a_4 = -9.2$ , and we recovered Kuztnetsov-Ma-like breathers shown in . are the corresponding contour and 2D plots for the solution $q_3$ . and represent the kink soliton profiles for the solution $q_6$ in 3D, contour, and 2D plots at different amplitudes.

Figure 1. The evolution of breather solitons profile for

$q_1(x, y, z, t)$ by setting

$C = 1$ ,

$a_1 = 0.8$ ,

$a_3 = 0.2$ ,

$a_2 = 1$ ,

$c_2 = 0.3$ ,

$m_0 = 1.2$ ,

$m_2 = 3.2$ ,

$b_1 = 0.2$ ,

$b_0 = 0.2$ , and

$y = z = 1$ at

$a_4 = 2.5$ ,

$a_4 = 3.5$ , and

$a_4 = 5.5$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. The evolution of dark wave into breather-like soliton profiles for

$q_2(x, y, z, t)$ by setting

$C = 0.5$ ,

$a_1 = 0.2$ ,

$a_2 = 1$ ,

$a_3 = 0.2$ ,

$m_0 = -0.2$ ,

$m_2 = 0.3$ ,

$c_2 = 0.5$ ,

$b_0 = 0.2$ ,

$b_1 = 0.2$ , and

$y = z = 1$ at

$a_4 = 0.2$ ,

$a_4 = 4.2$ , and

$a_4 = 8.2$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. The evolution of bright-wave soliton profile into breather wave profiles for

$q_3(x, y, z, t)$ by setting

$C = 1$ ,

$a_1 = 0.2$ ,

$a_3 = 1$ ,

$a_2 = 0.001$ ,

$c_2 = 0.5$ ,

$m_0 = 0.4$ ,

$m_2 = 0.2$ ,

$b_1 = 0.2$ ,

$b_0 = 3$ , and

$y = z = 1$ at

$a_4 = -0.2$ ,

$a_4 = -4.2$ , and

$a_4 = -9.2$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. The evolution of kink soliton profile for

$q_6(x, y, z, t)$ by setting

$C = 1$ ,

$a_1 = 0.2$ ,

$a_3 = 0.01$ ,

$a_2 = 1$ ,

$c_2 = 10.5$ ,

$m_0 = 0.4$ ,

$m_2 = 0.2$ ,

$b_1 = 0.2$ ,

$b_0 = 3$ ,

$p = 0.8$ ,

$s = 2.18$ , and

$y = z = 1$ at

$a_4 = -0.2$ ,

$a_4 = -1.2$ , and

$a_4 = -2.2$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. The evolution kink soliton profile for

$q_{14}(x, y, z, t)$ by setting

$C = 1$ ,

$a_1 = 0.2$ ,

$a_3 = 0.1$ ,

$a_2 = 1$ ,

$c_2 = 0.5$ ,

$m_0 = 0.9$ ,

$m_2 = 0.2$ ,

$b_1 = 0.3$ ,

$b_0 = 3$ , and

$y = z = 1$ at

$a_4 = -0.2$ ,

$a_4 = -1.2$ , and

$a_4 = -2.2$ .

DownLoad: Full-Size Img PowerPoint

In addition, Figures 6 and represent the evolution of bright solitons to different forms of breather waves in 3D, 2D, and contour plots as the amplitudes are varied. shows the evolution of different periodic soliton patterns for the solution $q_{17}$ at $a_4 = 0.2$ , $a_4 = 3.2$ , and $a_4 = 6.2$ , This type of soliton perturbations help us to understand ultra-short pulse lasers and long-distance optical communication networks.

Figure 6. The evolution of bright soliton profile into breather wave profiles for

$q_{12}(x, y, z, t)$ by setting

$C = 1$ ,

$a_1 = 0.2$ ,

$a_3 = 0.1$ ,

$a_2 = 1$ ,

$c_2 = 0.4$ ,

$m_0 = 0.9$ ,

$m_2 = 0.1$ ,

$b_1 = -0.3$ ,

$b_0 = 3$ , and

$y = z = 1$ at

$a_4 = -0.2$ ,

$a_4 = -3.2$ , and

$a_4 = -9.2$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. The evolution of bright soliton profile to breather wave profiles for

$q_{25}(x, y, z, t)$ by setting

$C = 1$ ,

$a_2 = 1.8$ ,

$a_1 = 1$ ,

$a_3 = 3.2$ ,

$c_1 = 8$ ,

$c_2 = 4$ ,

$c_3 = 4$ ,

$c_4 = 3$ ,

$f_0 = 0.6$ ,

$f_1 = 0.5$ ,

$\delta_2 = 0.1,$ and

$y = z = 1$ at

$a_4 = 2$ ,

$a_4 = 9$ , and

$a_4 = 34$ .

DownLoad: Full-Size Img PowerPoint

Figure 8. The evolution of multiple-wave soliton profile for

$q_{17}(x, y, z, t)$ by setting

$C = 1$ ,

$a_1 = 0.4$ ,

$a_3 = 0.1$ ,

$a_2 = 1$ ,

$c_2 = 0.3$ ,

$m_0 = 0.4$ ,

$m_2 = 0.2$ ,

$b_1 = 0.3$ ,

$b_0 = 3$ ,

$p = 1.7$ ,

$q = 2.18$ , and

$y = z = 1$ at

$a_4 = 0.2$ ,

$a_4 = 3.2$ , and

$a_4 = 6.2$ .

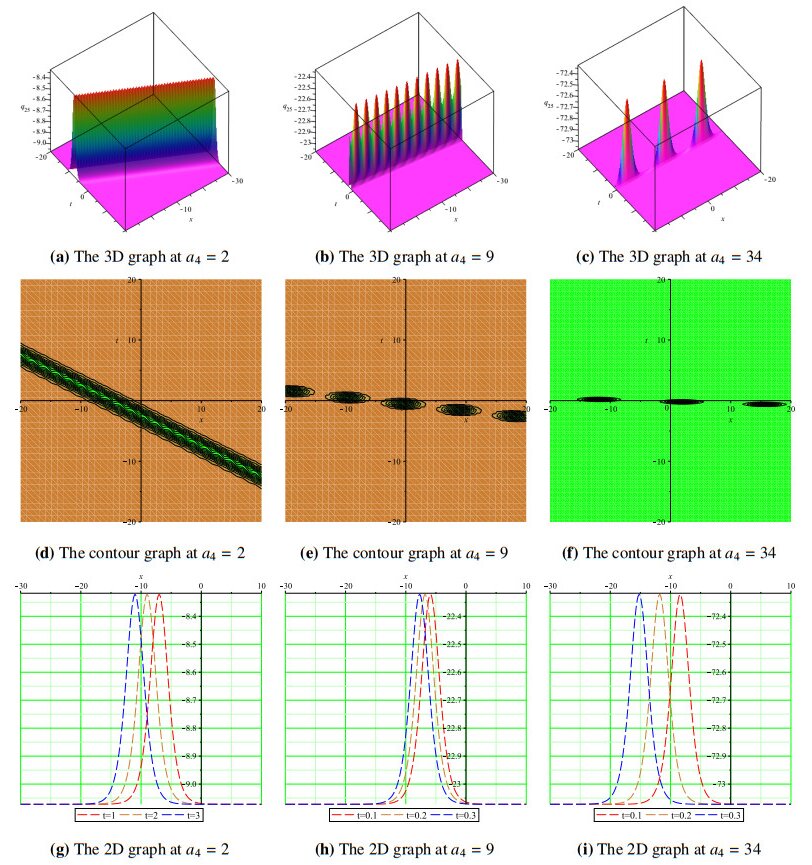
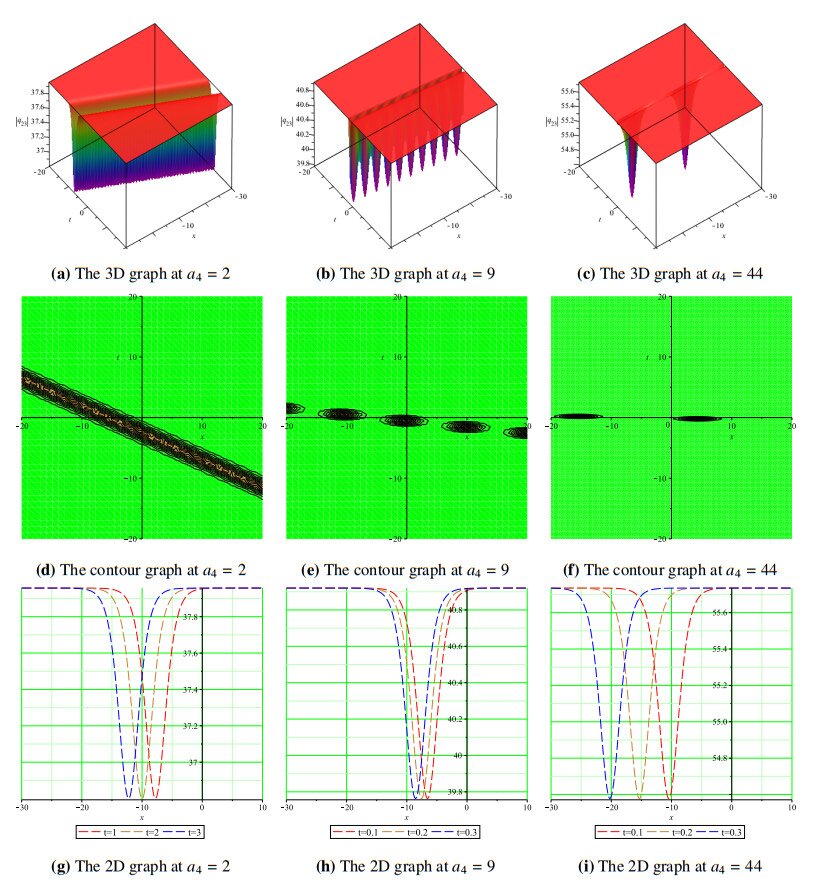
DownLoad: Full-Size Img PowerPoint

shows the evolution of dark wave solitons into breather waves at $a_4 = 2$ , $a_4 = 9$ , and $a_4 = 44$ for the solution $q_{23}$ . We also noticed that the solutions obtained using the GK method require larger amplitudes before they are transformed into different forms of rogue waves that include the Peregrine soliton and Kuztnetsov-Ma breather. All wave profiles presented in this study are based on assigning appropriate values to the free parameters listed in each figure's caption.

Figure 9. The evolution of dark soliton profile into breather wave profile for

$\left|q_{23}(x, y, z, t)\right|$ by setting

$C = 1$ ,

$a_2 = 1.8$ ,

$a_1 = 0.9$ ,

$a_3 = 3.2$ ,

$c_2 = 2.1$ ,

$c_1 = 0.8$ ,

$c_4 = 3$ ,

$c_3 = 2.1$ ,

$b_2 = 1$ ,

$b_3 = 6$ ,

$f_1 = 0.5$ ,

$\delta_2 = 0.1,$ and

$y = z = 1$ at

$a_4 = 2$ ,

$a_4 = 9$ , and

$a_4 = 44$ .

DownLoad: Full-Size Img PowerPoint

5. Conclusions

This study investigated diverse wave solutions for the newly introduced 3DPTE using the IGRE and GK methods. We derived various wave solutions for the 3DPTE based on wave transformation and the homogeneous balancing method. The solutions included rational exponential, trigonometric, and hyperbolic function solutions. The 3DPTE is considered to have various applications in soliton theory, nonlinear waves, and plasma physics including the evolution of plasma waves and instabilities. We studied the wave propagation phenomena in the derived solutions using 3D, 2D, and contour plots by assigning appropriate values to the real variables. We studied the wave instabilities of the recovered solutions by varying the value of the wave amplitude. We observed the transformation of dark and bright solitons into different forms of rogue waves that include Peregrine soliton and Kuztnetsov-Ma breather as we increased the value of the wave amplitude. Other intriguing wave patterns in this work include the kink and multi-wave profiles.

This research on the 3DPTE and recovered solutions should significantly advance wave instabilities in soliton theory. It can also be used in preventing coastal erosion and ensuring marine safety, maximizing wave energy extraction, developing efficient wave forecasting techniques, and many other important application areas for this equation. In addition, most of the derived solutions in this study are hyperbolic and trigonometric functions providing periodic structures. Ultra-short pulse lasers and long-distance optical communication networks are obtained by periodic soliton disturbances in optical fibers. Moreover, a vital role in determining optical properties can be found from trigonometric and hyperbolic functions and complex structures. Therefore, the proposed solutions can be potentially applied to nano and optical fibers. Cotangent hyperbolic function solutions are specifically relevant to magnetic polarization because they may be found in the Langevin function. Tangent hyperbolic function solutions can be utilized in special relativistic and magnetic moment computations. Applications in laminar jets can be studied using hyperbolic secant solutions. Finally, the used methods proved to be efficient techniques for investigating a wide range of traveling wave solutions for the 3DPTE.

Therefore, we strongly recommend these methods for the studies and beyond. Investigating the chaotic behavior and fractional aspects of the 3DPTE will be an intriguing future direction utilizing more efficient methods.

Author contributions

S. Sirisubtawee, S. Sungnul and M. Inc: Conceptualization, Methodology, Writing–review and editing; J. Sabi'u and S. Sirisubtawee: Formal analysis, Investigation, Writing–original draft. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This research was funded by King Mongkut's University of Technology North Bangkok with Contract no. KMUTNB-67-KNOW-18. In addition, the first author was financially supported by King Mongkut's University of Technology North Bangkok with contract no. KMUTNB-Post-67-05.

Conflict of interest

The authors declare that they have no conflicts of interest.

References

[1]	S. Raza, A. Rauf, J. Sabi'u, A. Shah, A numerical method for solution of incompressible Navier-Stokes equations in streamfunction-vorticity formulation, Comput. Math. Methods, 3 (2021), e1188. https://doi.org/10.1002/cmm4.1188 doi: 10.1002/cmm4.1188
[2]	D. J. Zhang, S. L. Zhao, Y. Y. Sun, J. Zhou, Solutions to the modified Korteweg-de Vries equation, Rev. Math. Phys., 26 (2014), 1430006. https://doi.org/10.1142/S0129055X14300064 doi: 10.1142/S0129055X14300064
[3]	V. Novikov, Generalizations of the Camassa-Holm equation, J. Phys. A Math. Theor., 42 (2009), 342002. https://doi.org/10.1088/1751-8113/42/34/342002 doi: 10.1088/1751-8113/42/34/342002
[4]	Z. Y. Yan, Abundant symmetries and exact compacton-like structures in the two-parameter family of the Estevez-Mansfield-Clarkson equations, Commun. Theor. Phys., 37 (2002), 27. https://doi.org/10.1088/0253-6102/37/1/27 doi: 10.1088/0253-6102/37/1/27
[5]	L. V. Bogdanov, V. E. Zakharov, The Boussinesq equation revisited, Phys. D, 165 (2002), 137–162. https://doi.org/10.1016/S0167-2789(02)00380-9 doi: 10.1016/S0167-2789(02)00380-9
[6]	J. Y. Yang, W. X. Ma, Abundant lump-type solutions of the Jimbo-Miwa equation in (3+1)-dimensions, Comput. Math. Appl., 73 (2017), 220–225. https://doi.org/10.1016/j.camwa.2016.11.007 doi: 10.1016/j.camwa.2016.11.007
[7]	M. P. Bonkile, A. Awasthi, C. Lakshmi, V. Mukundan, V. S. Aswin, A systematic literature review of Burgers' equation with recent advances, Pramana, 90 (2018), 1–21. https://doi.org/10.1007/s12043-018-1559-4 doi: 10.1007/s12043-018-1559-4
[8]	G. Biondini, D. Pelinovsky, Kadomtsev-Petviashvili equation, Scholarpedia, 3 (2008), 6539. https://doi.org/10.4249/scholarpedia.6539 doi: 10.4249/scholarpedia.6539
[9]	A. Hasegawa, Soliton-based optical communications: an overview, IEEE J. Sel. Top. Quantum Electron., 6 (2000), 1161–1172. https://doi.org/10.1109/2944.902164 doi: 10.1109/2944.902164
[10]	S. B. Wang, G. L. Ma, X. Zhang, D. Y. Zhu, Dynamic behavior of optical soliton interactions in optical communication systems, Chinese Phys. Lett., 39 (2022), 114202. https://doi.org/10.1088/0256-307X/39/11/114202 doi: 10.1088/0256-307X/39/11/114202
[11]	I. Nikolkina, I. Didenkulova, Rogue waves in 2006–2010, Nat. Hazards Earth Syst. Sci., 11 (2011), 2913–2924. https://doi.org/10.5194/nhess-11-2913-2011
[12]	S. Residori, M. Onorato, U. Bortolozzo, F. T. Arecchi, Rogue waves: a unique approach to multidisciplinary physics, Contemp. Phys., 58 (2017), 53–69. https://doi.org/10.1080/00107514.2016.1243351 doi: 10.1080/00107514.2016.1243351
[13]	X. Wang, L. Wang, C. Liu, B. W. Guo, J. Wei, Rogue waves, semirational rogue waves and W-shaped solitons in the three-level coupled Maxwell-Bloch equations, Commun. Nonlinear Sci. Numer. Simul., 107 (2022), 106172. https://doi.org/10.1016/j.cnsns.2021.106172 doi: 10.1016/j.cnsns.2021.106172
[14]	L. F. Li, Y. Y. Xie, Rogue wave solutions of the generalized (3+1)-dimensional Kadomtsev-Petviashvili equation, Chaos Soliton Fract., 147 (2021), 110935. https://doi.org/10.1016/j.chaos.2021.110935 doi: 10.1016/j.chaos.2021.110935
[15]	B. Mohan, S. Kumar, R. Kumar, Higher-order rogue waves and dispersive solitons of a novel P-type (3+1)-D evolution equation in soliton theory and nonlinear waves, Nonlinear Dyn., 111 (2023), 20275–20288. https://doi.org/10.1007/s11071-023-08938-1 doi: 10.1007/s11071-023-08938-1
[16]	D. Baldwin, W. Hereman, Symbolic software for the Painlevé test of nonlinear ordinary and partial differential equations, J. Nonlinear Math. Phys., 13 (2006), 90–110. https://doi.org/10.2991/jnmp.2006.13.1.8 doi: 10.2991/jnmp.2006.13.1.8
[17]	M. Şenol, M. Ö. Erol, New conformable P-type $(3+1)$ -dimensional evolution equation and its analytical and numerical solutions, J. New Theory, 2024, 71–88. https://doi.org/10.53570/jnt.1420224
[18]	S. Kumar, B. Mohan, A novel analysis of Cole-Hopf transformations in different dimensions, solitons, and rogue waves for a (2+1)-dimensional shallow water wave equation of ion-acoustic waves in plasmas, Phys. Fluids, 35 (2023), 127128. https://doi.org/10.1063/5.0185772 doi: 10.1063/5.0185772
[19]	S. K. Dhiman, S. Kumar, Analyzing specific waves and various dynamics of multi-peakons in (3+1)-dimensional p-type equation using a newly created methodology, Nonlinear Dyn., 112 (2024), 10277–10290. https://doi.org/10.1007/s11071-024-09588-7 doi: 10.1007/s11071-024-09588-7
[20]	U. K. Mandal, A. Das, W. X. Ma, Integrability, breather, rogue wave, lump, lump-multi-stripe, and lump-multi-soliton solutions of a (3+1)-dimensional nonlinear evolution equation, Phys. Fluids, 36 (2024), 037151. https://doi.org/10.1063/5.0195378 doi: 10.1063/5.0195378
[21]	S. Kumar, B. Mohan, Bilinearization and new center-controlled N-rogue solutions to a (3+1)-dimensional generalized KdV-type equation in plasmas via direct symbolic approach, Nonlinear Dyn., 112 (2024), 11373–11382. https://doi.org/10.1007/s11071-024-09626-4 doi: 10.1007/s11071-024-09626-4
[22]	M. N. Rafiq, H. B. Chen, Dynamics of three-wave solitons and other localized wave solutions to a new generalized (3+1)-dimensional P-type equation, Chaos Soliton Fract., 180 (2024), 114604. https://doi.org/10.1016/j.chaos.2024.114604 doi: 10.1016/j.chaos.2024.114604
[23]	A. Fahim, N. Touzi, X. Warin, A probabilistic numerical method for fully nonlinear parabolic PDEs, Ann. Appl. Probab., 21 (2011), 1322–1364. https://doi.org/10.1214/10-AAP723 doi: 10.1214/10-AAP723
[24]	J. Y. Wang, J. Cockayne, O. Chkrebtii, T. J. Sullivan, C. J. Oates, Bayesian numerical methods for nonlinear partial differential equations, Statist. Comput., 31 (2021), 1–20. https://doi.org/10.1007/s11222-021-10030-w doi: 10.1007/s11222-021-10030-w
[25]	S. N. Antontsev, J. I. Díaz, S. Shmarev, A. J. Kassab, Energy methods for free boundary problems: applications to nonlinear PDEs and fluid mechanics. Progress in nonlinear differential equations and their applications, Vol 48, Appl. Mech. Rev., 55 (2002), B74–B75. https://doi.org/10.1115/1.1483358 doi: 10.1115/1.1483358
[26]	G. M. Yao, C. S. Chen, H. Zheng, A modified method of approximate particular solutions for solving linear and nonlinear PDEs, Numer. Methods Partial Differ. Equ., 33 (2017), 1839–1858. https://doi.org/10.1002/num.22161 doi: 10.1002/num.22161
[27]	S. Garg, M. Pant, Meshfree methods: a comprehensive review of applications, Int. J. Comput. Methods, 15 (2018), 1830001. https://doi.org/10.1142/S0219876218300015 doi: 10.1142/S0219876218300015
[28]	J. A. Hernández, A. Giuliodori, E. Soudah, Empirical interscale finite element method (EIFEM) for modeling heterogeneous structures via localized hyperreduction, Comput. Methods Appl. Mech. Eng., 418 (2024), 116492. https://doi.org/10.1016/j.cma.2023.116492 doi: 10.1016/j.cma.2023.116492
[29]	H. Khalilzadeh, A. Habibzadeh-Sharif, M. Z. Bideskan, N. Anvarhaghighi, Design of a triple-band black phosphorus-based perfect absorber and full-wave analysis using the semi-analytical method of lines, Photonics Nanostruct., 53 (2023), 101112. https://doi.org/10.1016/j.photonics.2023.101112 doi: 10.1016/j.photonics.2023.101112
[30]	M. T. Hoang, M. Ehrhardt, A second-order nonstandard finite difference method for a general Rosenzweig-MacArthur predator-prey model, J. Comput. Appl. Math., 444 (2024), 115752. https://doi.org/10.1016/j.cam.2024.115752 doi: 10.1016/j.cam.2024.115752
[31]	A. J. M. Jawad, M. D. Petković, A. Biswas, Modified simple equation method for nonlinear evolution equations, Appl. Math. Comput., 217 (2010), 869–877. https://doi.org/10.1016/j.amc.2010.06.030 doi: 10.1016/j.amc.2010.06.030
[32]	W. X. Ma, J. H. Lee, A transformed rational function method and exact solutions to the 3+1 dimensional Jimbo-Miwa equation, Chaos Soliton Fract., 42 (2009), 1356–1363. https://doi.org/10.1016/j.chaos.2009.03.043 doi: 10.1016/j.chaos.2009.03.043
[33]	E. Yusufoğlu, New solitonary solutions for the MBBM equations using Exp-function method, Phys. Lett. A, 372 (2008), 442–446. https://doi.org/10.1016/j.physleta.2007.07.062 doi: 10.1016/j.physleta.2007.07.062
[34]	E. Fan, Extended tanh-function method and its applications to nonlinear equations, Phys. Lett. A, 277 (2000), 212–218. https://doi.org/10.1016/S0375-9601(00)00725-8 doi: 10.1016/S0375-9601(00)00725-8
[35]	Y. T. Gao, B. Tian, Generalized hyperbolic-function method with computerized symbolic computation to construct the solitonic solutions to nonlinear equations of mathematical physics, Comput. Phys. Commun., 133 (2001), 158–164. https://doi.org/10.1016/S0010-4655(00)00168-5 doi: 10.1016/S0010-4655(00)00168-5
[36]	M. Kaplan, A. Bekir, A. Akbulut, A generalized Kudryashov method to some nonlinear evolution equations in mathematical physics, Nonlinear Dyn., 85 (2016), 2843–2850. https://doi.org/10.1007/s11071-016-2867-1 doi: 10.1007/s11071-016-2867-1
[37]	L. Akinyemi, Two improved techniques for the perturbed nonlinear Biswas-Milovic equation and its optical solitons, Optik, 243 (2021), 167477. https://doi.org/10.1016/j.ijleo.2021.167477 doi: 10.1016/j.ijleo.2021.167477
[38]	U. A. Muhammad, J. Sabi'u, S. Salahshour, H. Rezazadeh, Soliton solutions of (2+1) complex modified Korteweg-de Vries system using improved Sardar method, Opt. Quantum Electron., 56 (2024), 802. https://doi.org/10.1007/s11082-024-06591-5 doi: 10.1007/s11082-024-06591-5
[39]	Sirendaoreji, S. Jiong, Auxiliary equation method for solving nonlinear partial differential equations, Phys. Lett. A, 309 (2003), 387–396. https://doi.org/10.1016/S0375-9601(03)00196-8 doi: 10.1016/S0375-9601(03)00196-8
[40]	I. S. Ibrahim, J. Sabi'u, Y. Y. Gambo, S. Rezapour, M. Inc, Dynamic soliton solutions for the modified complex Korteweg-de Vries system, Opt. Quantum Electron., 56 (2024), 954. https://doi.org/10.1007/s11082-024-06821-w doi: 10.1007/s11082-024-06821-w
[41]	M. I. Khan, S. Asghar, J. Sabi'u, Jacobi elliptic function expansion method for the improved modified Kortwedge-de Vries equation, Opt. Quantum Electron., 54 (2022), 734. https://doi.org/10.1007/s11082-022-04109-5 doi: 10.1007/s11082-022-04109-5
[42]	H. Rezazadeh, J. Sabi'u, R. M. Jena, S. Chakraverty, New optical soliton solutions for Triki-Biswas model by new extended direct algebraic method, Modern Phys. Lett. B, 34 (2020), 2150023. https://doi.org/10.1142/S0217984921500238 doi: 10.1142/S0217984921500238
[43]	J. Sabi'u, S. Sirisubtawee, M. Inc, Optical soliton solutions for the Chavy-Waddy-Kolokolnikov model for bacterial colonies using two improved methods, J. Appl. Math. Comput., 2024, 1–24. https://doi.org/10.1007/s12190-024-02169-2
[44]	S. T. Demiray, Y. Pandir, H. Bulut, Generalized Kudryashov method for time-fractional differential equations, Abstr. Appl. Anal., 2014 (2014), 901540. https://doi.org/10.1155/2014/901540
[45]	N. A. Kudryashov, Simplest equation method to look for exact solutions of nonlinear differential equations, Chaos Soliton Fract., 24 (2005), 1217–1231. https://doi.org/10.1016/j.chaos.2004.09.109 doi: 10.1016/j.chaos.2004.09.109
[46]	E. W. Weisstein, CRC concise encyclopedia of mathematics, New York: Chapman and Hall/CRC, 2002. https://doi.org/10.1201/9781420035223

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1245) PDF downloads(55) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(9)

AIMS Mathematics

Wave dynamics for the new generalized (3+1)-D Painlevé-type nonlinear evolution equation using efficient techniques

Related Papers:

Abstract

1. Introduction

2. Description of the IGRE and the GK methods

3. Applications of the IGRE and the GK methods

3.1. Solitary wave solutions using the IGRE method

3.2. Solitary wave solutions using the GK method

4. Graphical results and discussion

5. Conclusions

Author contributions

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Wave dynamics for the new generalized (3+1)-D Painlevé-type nonlinear evolution equation using efficient techniques

Related Papers:

Abstract

1. Introduction

2. Description of the IGRE and the GK methods

3. Applications of the IGRE and the GK methods

3.1. Solitary wave solutions using the IGRE method

3.2. Solitary wave solutions using the GK method

4. Graphical results and discussion

5. Conclusions

Author contributions

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog