Derivation of some solitary wave solutions for the (3+1)- dimensional pKP-BKP equation via the IME tanh function method

1.   Introduction

The nonlinear partial differential equations (NPDEs) have been used several scientific domains, such as earth sciences, engineering, physics, and other fields of technology ^[1,2,3,4,5]. The study of the nonlinear local waves is helpful to understand the dynamic behaviors of nonlinear waves ^[6,7,8]. Many researchers have focused on accurate and numerical solutions for NPDEs ^{[9,10,11,12,13]}. In particular, these studies have played an important role in the development of nonlinear optical materials and optical soliton propagation ^{[14,15,16,17]}. Several solutions, either solitary wave solutions or exact solutions, have been identified for NPDEs ^{[18,19,20,21]}. It is well known that nonlinear differential equations (NLDEs) with variable coefficients can better describe various nonlinear local waves than the ones with constant coefficients ^{[22,23,24,25]}. Therefore, it is important to find local wave solutions of NLDEs with variable coefficients. There are many classical methods for solving NLDEs, such as a lightweight method ^[26], account service network ^[27], quaternary ammonium salt surfactant ^[28], effect on electromagnetic vibration and optimized structure ^[29], and impedance matching ^[30]. In physics disciplines such as fluids, plasma theory, and nonlinear optics. Hosseini et al. ^[31,32] studied many novel models such as the generalized Kadomtsev-Petviashvili equation and the 3D generalized Korteweg-De Vries (KdV) equation in order to obtain newly created soliton solutions through different approaches. Li and Tian systematically solved the Cauchy problem of the general n-component nonlinear Schrödinger equations based on the Riemann-Hilbert method and N-soliton solutions. Moreover, they proposed a conjecture about the law of nonlinear wave propagation ^[33]. Yang, Tian, and Li successfully solved the soliton solutions of the focusing nonlinear Schrödinger equation with multiple high-order poles under nonzero boundary conditions for the first time ^[34]. In recent years, nonlinear local waves such as exact wave solutions and analytical methods have become a hot topic in nonlinear field and attracted the attention of many scholars. With respect to soliton resolution conjecture, Li, Tian, Yang, and Fan have done some interesting work in deriving the solutions of Wadati-Konno-Ichikawa equation, complex short pulse equation, and short pulse equation with the help of the Dbar-steepest descent method. They solved the long-time asymptotic behavior of the solutions of these equations, and proved the soliton resolution conjecture and the asymptotic stability of solutions of these equations. The potential Kadomtsev-Petviashvili (pKP) and the B-type Kadomtsev-Petviashvili (BKP) equations were combined to create the nonlinear pKP-BKP equation that offered a new integrable (3+1)-dimensional equation, having beneficial features ^{[35,36,37,38]}. Researchers ^[37] verified the integrability of these equations. Several unexpected outcomes may be produced due to the idea of combining two integrable systems with each other ^{[39,40,41,42]}. However, finding certain integrable systems is always an essential and difficult problem in theoretical physics. In ^[43], solitons were studied by Hirota due to the conjunction of Sawaka-Kotera and the Korteweg-de Vries (SK-KdV) equations. Wazwaz ^[44,45] obtained multi soliton solutions using the Caudrey-Dodd-Gibbon (KdV-CDG) equation in conjunction with the extended form of the Korteweg-de Vries equation. Wazwaz ^[46] obtained two reduced forms of (3+1)-dimensional pKP-BKP equation, which were built from the standard form, as well as retrieving a full spectrum of this used equation. As a result, for each of the three models that were under this investigation, a range of solutions, including kink, single, periodic, and exponential solutions, were determined. Almatrafi ^[47,48] studied many models to get solitary wave solutions to many fractional models using different approaches. Finding the so-called soliton molecules for an integrable nonlinear system has become a popular issue in recent years. In fact, integrating two integrable systems together frequently yields a wide range of surprising outcomes.

We plan to derive solutions of the following integrable (3+1)-dimensional pKP-BKP ^[46] with various exact traveling wave solutions as the result of the parameters' arbitrary values:

where $\alpha, \beta, \gamma, a, b,$ and $c$ act as arbitrary parameters having real values that will be calculated during this work. $\phi (x, y, z, t)$ represents a polynomial function in terms of $x, y, z$ that refer to the space variables also $t$ that denotes the time variation. This polynomial function appears with its partial derivatives to describe the breather wave profiles. This equation was examined as unanticipated unique waves having a significant amplitude that are maintained for a brief duration of time, satisfying localization in both the space and time domains ^[49,50,51]. The (3+1)-dimensional pKP-BKP equation is especially important for investigating complicated wave dynamics in systems like as fluids, plasmas, and optical media, as it represents the propagation of nonlinear waves in three spatial dimensions and one temporal dimension. By including wave interactions that take place both longitudinally and transversely, we expand the conventional KP equation and illustrate how perturbations in one direction can propagate over many spatial dimensions. Moreover, comprehension phenomena like shallow water waves, ion-acoustic waves in plasmas, and optical pulses in nonlinear media where the stability and development of the wave depend critically on the balance between nonlinearity and dispersion, requires a comprehension of this equation.

Our goal is to make maximum use of Eq (1.1) by involving its parameters to create more forms of analytical, exact solutions when employing a suitable, simple, easy method and with the aid of symbolic computations. A wide range of solitons and other exact wave solutions have been studied by many researchers using the IME tanh functional method ^[52,53]. We compute different solitons and other exact wave solutions using the IME tanh functional method for Eq (1.1). This combination is a newly created study and does not exist in others, where the used IME tanh function method gives the ability to yield precise analytical solutions to NPDE with efficiency, adaptability, and insights. This method yields a wide range of solutions, including Jacobi epsilon function, exponential, singular periodic, rational, singular soliton, and dark soliton solutions. Moreover, the recovered solutions validate both strength and usefulness for the implemented method.

The structure of this article is as follows: An overview of the suggested model and its theoretical underpinnings is given in Section 1. The major points of the IME tanh function method is presented in Section 2. In Section 3, we use the Wolfram Mathematica software to summarize the obtained results, carrying out symbolic computations. In Section 4, we use 3-D, contour, and 2-D simulations to graphically represent several dynamic wave patterns of various soliton solutions. In Section 5, we report the conclusions.

2.   Mathematical preliminaries of the IME tanh function method

We present the general framework of the IME tanh function method that will be applied in a later section. We begin by examining the NPDE that is displayed below ^[53,54]

where $\mathcal{Z}$ acts as a polynomial that is represented by $\varnothing(x, y, z, t)$ and some of its partial derivatives with respect to both time and space domains.

Step 1. By employing the wave transformation shown below

where $\mathcal{F}$ represents the solution function, $\mathit{k}, \ \aleph,$ and $\omega$ are few actual constants to be assessed afterwards.

Next, from inserting Eq (2.2) into Eq (2.1) and after rearranging, an obtained nonlinear ordinary differential equation (NLODE) can be constructed as:

Step 2. According to the applied method, the solution of Eq (2.3) takes the following form:

where $\mathfrak{L}_m$ and $\mathfrak{A}_m\; (m = 1, 2, ...)$ provide for constant values to be calculated, with the requirement that $\mathfrak{L}_{\mathbb{N}}$ and $\mathfrak{A}_{\mathbb{N}}$ cannot both be zero at the same time.

Step 3. Next, by performing the balancing between both of the nonlinearity and the dispersion of Eq (2.3) to determine the value of the number ${\mathbb{N}}$, besides $\mathfrak{W}(\zeta)$ having the following constraint:

where $\varepsilon = \pm 1$ and $r_i\; (0\leq i\leq 4)$ are constants of real values.

From the different possible values of $r_0$–$r_4$, we obtain from (2.5) the various kinds of fundamental solutions as follows:

Case 1. $r_0 = r_1 = r_3 = 0$,

Case 2. $r_1 = r_3 = 0$,

where $m$ is the modulus of the Jacobi elliptic functions.

Case 3. $r_0 = r_1 = r_2 = 0$,

Case 4. $r_3 = r_4 = 0$,

Case 5. $r_0 = r_1 = 0$, $r_4 > 0$,

Step 4. By inserting the presumably stated solutions in Eqs (2.4) and (2.5) into Eq (2.3), one can raise $\mathfrak{W}(\zeta)$ as a polynomial function. A series of algebraic non-linear equations resulting from the coefficients equalization of $\mathfrak{W}^i(\zeta)$, ($i = 0, \pm 1, \pm 2, ...$), to zero may be solved using a software such as Wolfram Mathematica. Then, for Eq (2.1), we obtain a variety of exact solutions.

The IME tanh function method is highly helpful for obtaining precise analytical solutions and gaining a deeper comprehension of soliton dynamics by comparing the proposed scheme with the other most current approaches. It can be challenging to control because to its complexity and sensitivity to initial conditions. Alternative methods offer increased adaptability and enhancement, although at the expense of increased complexity. The specific requirements of the issue, for example, the kind of the PDEs, determining the boundary constrains and the intended ratio of computational practicality to the analytical expertise, dictate which technique is applicable.

3.   Extraction of novel solutions

Using Eq (2.2), Eq (1.1) becomes the following NLODE:

After executing the integration step once with respect to $\zeta$ on Eq (3.1) and when we set the integration constant to zero, we get

It is possible to simplify Eq (3.2) to have:

such that $\mathfrak{H}(\zeta) = \mathcal{F}'(\zeta).$ Thus, by applying principle of balance that was mentioned in Section 2 to Eq (3.3), the exact solutions for Eq (3.3) can be constructed in the manner described as follows:

By placing the constraint in Eq (2.5), using Eqs (3.4) and (3.3), we obtain a polynomial in $\mathfrak{W}(\zeta)$. All terms having the same power are put together and seated to be equal zero, which generates an algebraic non-linear equations system. The coming scenarios of solutions are produced using the Wolfram Mathematica software program in order to solve these equations. It is stipulated that neither $\mathfrak{L}_2$ nor $\mathfrak{A}_2$ may be zero simultaneously.

Case-(1): If $r_0 = r_1 = r_3 = 0$, the sets of solutions listed below are resulted:

(1.1) $\mathfrak{L}_0 = \mathfrak{L}_1 = \mathfrak{A}_1 = \mathfrak{A}_2 = 0, \ \mathfrak{L}_2 = -2 r_4, \ a = -b \mathit{k}-c \aleph +\omega+\frac{\gamma ^2 \mathit{k}^2}{5 \alpha }-4 (\beta +\gamma \mathit{k}) r_2-16 \alpha r_2^2$.

(1.2) $\mathfrak{L}_0 = \mathfrak{L}_1 = \mathfrak{A}_1 = \mathfrak{A}_2 = 0, \ \mathfrak{L}_2 = -4 r _4, \ a = \frac{25 \alpha \omega +4 \beta ^2-25 \alpha b \mathit{k}-25 \alpha c \aleph +8 \beta \gamma \mathit{k} +9 \gamma ^2 \mathit{k}^2}{25 \alpha }.$

The following structures are the outcome of certain exact solutions to Eq (1.1), as per the set of solutions (1.1):

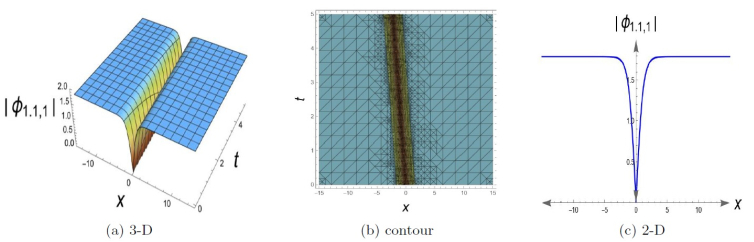
(1.1,1) If $r _2 > 0$ and $r _4 < 0$, we obtain the following dark soliton solution:

(1.1,2) If $r _2 < 0$ and $r _4 > 0$, we obtain the following singular periodic solution:

(1.1,3) If $r _2 = 0$ and $r _4 > 0$, we obtain the following rational solution such that $x +\mathit{k} y+\aleph z-\omega t\neq 0$:

While considering the set (1.2), the following solution can be constructed for Eq (1):

(1.2,1) If $r _2 > 0$ and $r _4 < 0$, we obtain the following dark soliton solution:

(1.2,2) If $r_2 < 0$ and $r_4 > 0$, we obtain the following singular periodic solution:

(1.2,3) If $r_2 = 0$ and $r_4 > 0$, we obtain the following rational solution such that $x +\mathit{k} y+\aleph z-\omega t\neq 0$:

Case-(2): If $r_1 = r_3 = 0$, the sets of solutions listed below are resulted:

(2.1) $\mathfrak{L}_0 = \mathfrak{L}_1 = \mathfrak{A}_1 = \mathfrak{A}_2 = 0, \ \mathfrak{L}_2 = -2 r_4, \ a = -b \mathit{k}-c \aleph +\omega+\frac{\gamma ^2 \mathit{k}^2}{5 \alpha }-12 \alpha r_0 r_4, \ r_2 = -\frac{\beta +\gamma \mathit{k}}{4 \alpha }$.

(2.2) $\mathfrak{L}_0 = \mathfrak{L}_1 = \mathfrak{A}_1 = 0, \ \mathfrak{L}_2 = -2 r _4, \ \mathfrak{A}_2 = -2 r_0, \ a = -b \mathit{k}-c \aleph+\omega +\frac{12 \beta \gamma \mathit{k}}{49 \alpha } +\frac{6 \beta ^2}{49 \alpha }+\frac{79 \gamma ^2 \mathit{k}^2}{245 \alpha }+48 \alpha r _0 r _4, \ r _2 = -\frac{\beta +\gamma \mathit{k}}{28 \alpha }.$

(2.3) $\mathfrak{L}_0 = \mathfrak{L}_1 = \mathfrak{L}_2 = \mathfrak{A}_1 = 0, \ \mathfrak{A}_2 = -2 r_0, \ a = -b \mathit{k}-c \aleph +\omega+\frac{\gamma ^2 \mathit{k}^2}{5 \alpha }-12 \alpha r_0 r_4, r_2 = -\frac{\beta +\gamma \mathit{k}}{4 \alpha }.$

The produced set of solutions (2.1) indicates that Eq (1.1) has exact solutions, which can be phrased as:

(2.1,1) If $r _0 = \frac{r_2^2}{4 r _4}$, $r _2 < 0,$ and $r _4 > 0$, we obtain the following dark soliton solution:

(2.1,2) If $r _0 = \frac{r_2^2}{4 r _4}$, $r _2 > 0,$ and $r _4 > 0$, we obtain the following singular periodic solution:

(2.1,3) If $r _0 = \frac{m^2 \left(1-m^2\right) r_2^2}{\left(2 m^2-1\right)^2 r _4}$, $r _2 > 0$, $r _4 < 0,$ and $\frac{1}{\sqrt{2}} < m\leq 1$, we obtain the following JEF solution:

where $\mathcal{E}$ is a Jacobi epsilon function.

Special case, when setting $m = 1$ in Eq (3.13), we obtain the following dark soliton solution:

(2.1,4) If $r _0 = \frac{\left(1-m^2\right) r_2^2}{\left(2-m^2\right)^2 r _4}$, $r _2 > 0$, $r _4 < 0$ and $0 < m\leq 1$, then we obtain the following JEF solution:

Special case, when setting $m = 1$ in Eq (3.15), we obtain the following dark soliton solution:

(2.1,5) If $r _0 = \frac{m^2 r_2^2}{\left(m^2+1\right)^2 r _4}$, $r _2 < 0$, $r _4 > 0,$ and $0 < m\leq 1$, we obtain the following JEF solution:

Special case, when setting $m = 1$ in Eq (3.17), we obtain the following dark soliton solution:

The mentioned set of solutions (2.2) indicates that Eq (1.1) has exact solutions, which can be phrased as:

(2.2,1) If $r _0 = \frac{r_2^2}{4 r _4}$, $r _2 < 0,$ and $r _4 > 0$, we obtain the following singular soliton solution:

(2.2,2) If $r _0 = \frac{r_2^2}{4 r _4}$, $r _2 > 0,$ and $r _4 > 0$, we obtain the following singular periodic solution:

The above set of solutions (2.3) indicates that Eq (1.1) has exact solutions, which can be phrased as:

(2.3,1) If $r _0 = \frac{r_2^2}{4 r _4}$, $r _2 < 0,$ and $r _4 > 0$, we obtain the following singular soliton solution:

(2.3,2) If $r _0 = \frac{r_2^2}{4 r _4}$, $r _2 > 0,$ and $r _4 > 0$, we obtain the following singular periodic solution:

Case-(3): If $r_0 = r_1 = r_2 = 0$, the resulted set of solutions is mentioned below:

The exact solutions to Eq (1.1) that arise from the gathered set of solutions, have the following displayed forms:

(3.1) If $r _4\neq 0$, $r _3\neq 0$ and $(x +\mathit{k} y+\aleph z-\omega t)^2r _3^2-4 r _4\neq 0$, the following rational solution is produced as:

(3.2) If $r _4 < 0$ and $r _3\neq 0$, the following exponential solution is produced as:

Case-(4): If $r_3 = r_4 = 0$, the raised set of solutions is generated as:

By using the acquired set of solutions with Eq (1.1), the below analytical solution is derived:

(4.1) If $r_0 = \frac{r _1^2}{4 r _2}$ and $r _2 > 0$, the following exponential solution is produced such that $r _1-2 r _2 e^{(x +\mathit{k} y+\aleph z-\omega t)\sqrt{r _2}} \neq 0$:

(4.2) If $r_0 > 0$, $r _1 = 0,$ and $r _2 < 0$, a singular periodic solution is produced on the following form:

(4.3) If $r_0 > 0$, $r _1 = 0,$ and $r _2 > 0$, an obtained singular soliton solution appears:

Case-(5): If $r_0 = r_1 = 0,$ and $r_4 > 0$, the sets of solutions listed below are resulted

(5.1) $\mathfrak{L}_0 = \mathfrak{A}_1 = \mathfrak{A}_2 = 0, \ \mathfrak{L}_1 = -r _3, \ \mathfrak{L}_2 = -2 r _4, \ a = -b \mathit{k}-c \aleph+\omega +\frac{\gamma ^2 \mathit{k}^2}{5 \alpha }-\frac{ (\beta +\gamma \mathit{k})r _3^2}{4 r _4} -\frac{\alpha r _3^4}{16 r _4^2}, \ r _2 = \frac{r_3^2}{4 r _4}.$

(5.2) $\mathfrak{L}_0 = \mathfrak{L}_1 = \mathfrak{A}_1 = \mathfrak{A}_2 = r_3 = 0, \ \mathfrak{L}_2 = -2 r _4, \ \omega = a+b \mathit{k}+c \aleph+ 4 (\beta +\gamma \mathit{k}) r _2-\frac{\gamma ^2 \mathit{k}^2}{5 \alpha }+16 \alpha r _2^2$.

By inserting the above parameters (5.1) for Eq (1.1), getting the following solution:

(5.1,1) If $r _2 > 0$ and $r _3 = 2 \sqrt{r _2 r _4}$, we obtain the following dark soliton solution:

Through the obtained set of solutions (5.2), the analytical solutions for Eq (1.1) can be obtained as follows:

(5.2,1) If $r _2 < 0$, we obtain the following singular periodic solution:

(5.2,2) If $r _2 > 0$ and $\ r _3\neq 2 \sqrt{r_2 r _4}$, we obtain the following singular soliton solution:

4.   Discussion and physical interpretations of the retrieved solutions

By manipulating the parameters in the model being studied, many sets of values were found for Eq (1.1) that had not been previously recorded or achieved. To shed light on the mathematical and physical characteristics of the recovered solutions, many formats of graphs are presented in this section like the contour plot, 3-D, and 2-D plots of a number of solutions. The dark soliton solution representation of Eq (3.5) is displayed in Figure 1, when selecting $r_ 2 = 0.8, \ \mathit{k} = 0.7, \ \aleph = 0.6, \ \omega = -0.45, \ y = z = 0, \ 0\leq t\leq 5$ and $-15\leq x\leq 15$. Dark solitons are localized regions of diminished amplitudes within a surrounding medium ^[55]. In fluid dynamics, they could be correlated with regions of decreased fluid density or pressure ^[56,57]. Figure 2 depicts the singular periodic solution of Eq (3.6) by setting $r_ 2 = -0.8, \ \mathit{k} = 0.7, \ \aleph = 0.6, \ \omega = 0.85, \ y = z = 0, \ 0\leq t\leq 5$ and $-15\leq x\leq 15$. In physical phenomena, a system can be described as a unique periodic solution when it displays periodic activity interspersed by sudden, discontinuous changes or extreme occurrences. Non-linearities, boundary conditions, or external stimuli might be the source of these singularities or discontinuities. Figure 3 displays the rational wave solution of Eq (3.7) when setting the parameters to be as $\mathit{k} = 0.9, \ \aleph = 0.8, \ \omega = -0.6, \ y = z = 0, \ 0\leq t\leq 5,$ and $-15\leq x\leq 15$. Rational solutions refer to solutions of partial differential equations (PDEs) that may be represented as a quotient of polynomials. Figure 4 depicts the singular soliton solution of Eq (3.27) with parameters $r_ 2 = 0.6$, $\mathit{k} = -1.9$, $\aleph = 0.6$, $a = 0.7$, $b = 0.8$, $c = 0.75$, $\alpha = -0.5$, $\gamma = 0.5$, $y = z = 0$, $0\leq t\leq 5$ and $-15\leq x\leq 15$. Singular solitons are solutions that behave singularly and are often characterized by a small area that includes an approaching infinity peak or trough. They may depict local phenomena symbolically. These are less common in physical systems because of their severity.

5.   Conclusions

The (3+1)-dimensional pKP-BKP equation, which was built from the combination of two different forms, were fully recovered in this article. For this model and after applying the suggested IME tanh function method, we obtained distinct breather wave solutions. For the integrable studied model, a range of solutions, including dark and singular solitons; singular periodic, JEF, rational, and exponential solutions, were determined. In terms of the soliton solutions that are found, solitons are self-reinforcing waves that are stable and hold their energy and form as they propagate. These solutions are crucial in understanding how energy or information can propagate without dispersion in a nonlinear medium. In addition, the periodic solutions represent standing waves or wave packets that repeatedly interact with a structured medium. Numerous solutions, including dark solitons, singular solitons, singular periodic solutions, Jacobi elliptic function solutions, and rational and exponential solutions, are provided by the IME tanh technique, which is based on the extended Riccati equation. In contrast to alternative methods, this strategy offers fresh approaches to this model's problems. We may hope that our achievements will serve and give valuable information to the field of nonlinear scientific community. Our findings may influence the evolution of integrated data transmission telecommunication systems. In the future, we may extend our study to examine soliton dynamics in 2D or 3D fiber arrays, as well as multi-dimensional connected systems. We may also look at the interactions between vector solitons in connected multi-component systems.

Author contributions

Abeer Khalifa: Formal analysis, Software, Methodology; Hamdy Ahmed: Validation, Methodology; Niveen Badra: Investigation, Writing-review & editing, Supervision; Jalil Manafian: Formal analysis, Writing-review & editing; Khaled H. Mahmoud: Resources, Writing-review & editing; Kottakkaran Nisar: Validation, Methodology; Wafaa Rabie: Software, Writing-review & editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-51).

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.