Wave solutions for the (3+1)-dimensional fractional Boussinesq-KP-type equation using the modified extended direct algebraic method

1.   Introduction

In several scientific fields, like quantum mechanics, chemical physics, mathematical physics, and optical fibers, nonlinear partial differential equations (NLPDEs) are utilized to mimic a wide range of physical phenomena, such as Kadomtsev–Petviashvili ^[1,2], Kudryashov's equation ^[3], generalization of Vakhnenko Equation ^[4], extended sixth-order Korteweg–de Vries ^[5], nonlinear Schrödinger equation ^[6] and others.

Acquiring the exact solution for NLPDEs is an extremely complex and usually challenging task due to the intrinsic complexity of nonlinear systems. Unlike LPDEs, which can be solved utilizing superposition principles and well-established methods such as the separation of variables, NLPDEs often require more advanced techniques. These may involve methods, for example, the modified extended mapping method ^[7], the modified Sardar sub-equation method ^[8], and the extended F-expansion method ^[9].

This study focuses on the integrable Boussinseq-Kadomtsev-Petviashvili (KP) equation, which merges the Boussinesq equation with the KP equation. The Boussinseq-KP equation is an important mathematical model used to describe various phenomena in fluid dynamics, nonlinear wave propagation, and mathematical physics. Many authors studied the Boussinseq-KP equation, for example, Ozisik et al. investigated the soliton waves with the (3+ 1)-dimensional Kadomtsev–Petviashvili–Boussinesq equation in water wave dynamics ^[10]. Akinyemi et al. established the novel soliton solutions of four sets of generalized (2+ 1)-dimensional Boussinesq–Kadomtsev–Petviashvili-like equations ^[11]. Liu and Zhang discussed the dynamics of localized waves and interaction solutions for the (3+ 1)-dimensional B-type Kadomtsev–Petviashvili–Boussinesq equation ^[12]. Ma et al. obtained the rational and semi-rational solution to the (3+ 1)-dimensional Kadomtsev-Petviashvili-Boussinesq-like equation ^[13]. Wang et al. studied the nonlinear dynamics of soliton molecules, hybrid interactions and other wave solutions for the (3+ 1)-dimensional generalized Kadomtsev–Petviashvili–Boussinesq ^[14]. Singh et al. discussed the localized nonlinear waves on spatio-temporally controllable backgrounds for a (3+ 1)-dimensional Kadomtsev-Petviashvili-Boussinesq model in water waves ^[15]. Manafian studied the multiple rogue wave solutions and the linear superposition principle for a (3+ 1)‐dimensional Kadomtsev–Petviashvili–Boussinesq‐like equation arising in energy ^[16]. Wang et al investigated the dynamics of kink solitary waves and lump waves with interaction phenomena in a generalized (3+ 1)-dimensional Kadomtsev–Petviashvili–Boussinesq equation ^[17]. Jia and Zuo established the properties of the hybrid solutions for a generalized (3+ 1)-dimensional KP equation ^[18]. Lu et al. introduced new analytical wave structures for the (3+ 1)-dimensional Kadomtsev-Petviashvili and the generalized Boussinesq models and their applications ^[19]. El-Shorbagy, et al. investigated the propagation of solitary wave solutions to (4+ 1)-dimensional Davey–Stewartson–Kadomtsev–Petviashvili equation arise in mathematical physics and stability analysis ^[20].

In this work, for the first time, we present the (3+1)-dimensional $\beta$-fractional Boussinseq-KP equation as follows ^[21]:

The beta derivative of $\mathcal{F} (x, y, z, t)$ of order $\beta$ is given by (see ^[22]):

where $\mathbb{C}, \sigma, \alpha, \rho, \gamma, \eta$, and $\mu$ are arbitrary real parameters to be calculated, and $\mathcal{F}(x, y, z, t)$ is a function of the spatial variables $x, y, z$ and the time variable $t$.

This study employs the modified extended direct algebraic method (MEDAM) to investigate the traveling wave solutions of Eq (1.1). This approach yields a variety of exact solutions, including dark and bright solitons, as well as, hyperbolic solutions, Weierstrass elliptic doubly periodic solutions, Jacobi elliptic function solutions, and rational and exponential solutions. We further elucidate these solutions through 2D and 3D graphical representations to validate our findings.

This paper is organized as follows: Section 2 outlines the proposed method, Section 3 details the results from applying this method, Section 4 employs 3D simulations and 2D plots to illustrate various dynamic wave patterns of different isolation solutions, and Section 5 concludes the work.

2.   Outline of the proposed technique

In this section, we present a comprehensive introduction to the modified extended direct algebraic method framework. This framework is designed specifically to be applied to the nonlinear fractional partial differential equation (NLFPDE) that will be elaborated upon in the paragraphs that follow. We aim to demonstrate how this innovative approach can effectively address the complexities associated with the equation under consideration ^[23,24]:

where $\mathcal{E}$ is a function represented by $\mathcal{F}(x, y, z, t)$ and its partial derivatives in both time and space domains.

Step 1: To solve Eq (2.1) effectively, we use the wave transformation method outlined below:

where $\mathcal{K}$, $\mathcal{V}$, and $\omega$ are constants to be determined later, while $\beta$ represents a fractional derivative of order $\beta \in (0, 1]$.

By substituting Eq (2.2) into Eq (2.1) and rearranging, we can derive the following nonlinear ordinary differential equation (NLODE):

Step 2: Based on the specific method that has been utilized, the resulting solution for the equation denoted as Eq (2.3) can be expressed in the following manner:

where $\mathcal{A}_i\;$ represent real constants to be determined later under constraint $\mathcal{A}_N^2+\mathcal{A}_{-N}^2\neq0\;$, and also $\mathcal{R}'(\zeta)$ must satisfy the following equation;

where $\epsilon = \pm$1 and $\tau_i\; (0, 1, 2, 3, 4, 6)$ are real-valued constants, while the value of ${\mathbb{N}}$ is determined by balancing both nonlinearity and equation dispersion.

Step 3: Equation (2.4) is combined with Eq (2.5) into Eq (2.3), yielding a polynomial in $\mathcal{R}$. Software tools such as Mathematica can be used to solve a series of nonlinear algebraic equations (NLAEs) that arise from setting the coefficients of the same powers to zero. Thus, Eq (2.1) can produce multiple exact solutions.

3.   Extract new solutions for the proposed system

To explore the analytical and precise solutions of Eq (1.1), the transformation indicated in Eq (2.2) is used, and therefore Eq (1.1) can be converted into a nonlinear ordinary differential equation (NLODE) as follows:

Now, we can apply the principle of balance in Section 2 to Eq (3.1), and thus we can create the exact solutions to Eq (3.1) in the manner shown below:

where $\mathcal{A}_j, (j = -2, -1, 0, 1, 2)$ are constants to be determined later by constraint $\mathcal{A}_2^2+\mathcal{A}_{-2}^2\neq0$.

We can now enter Eqs (3.2) and (2.5) into Eq (3.1), then the similar force coefficients are added and all set to zero, followed by the creation of a system of NLAEs, which can be solved with the help of Mathematica to obtain the results shown below:

Case-(1): If $\tau_0 = \tau_1 = \tau_3 = \tau_6 = 0$, the following solution combinations are obtained:

According to the above solution set, we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

(1.1) Bright soliton solution as follows:

where $\eta \neq 0, \ \tau _2 > 0$ and $\tau _4 < 0.$

Case-(2): If $\tau_1 = \tau_3 = \tau_6 = 0$ and $\tau_0 = \frac{\tau _2^2}{4 \ \tau _4},$ the following solution combinations are obtained:

(2.1) $\mathcal{A}_0 = \frac{-\alpha -\mathbb{C} \omega ^2-\mu \mathcal{K}^2 -\mathcal{K} \rho +\sigma \omega -4 \tau _2-\gamma \mathcal{V}}{2 \eta }, \; \; \; \; \; \; \mathcal{A}_1 = \mathcal{A}_{-1} = 0, \; \; \; \; \; \; \mathcal{A}_2 = -\frac{6 \tau _4}{\eta }, \; \; \; \; \; \; \mathcal{A}_{-2} = -\frac{3 \tau _2^2}{2 \eta \tau _4}$.

(2.2) $\mathcal{A}_0 = \frac{-\alpha -\mathbb{C} \omega ^2-\mu \mathcal{K}^2-\mathcal{K} \rho +\sigma \omega -4 \tau _2-\gamma \mathcal{V}}{2 \eta }, \; \; \; \; \; \; \mathcal{A}_1 = \mathcal{A}_{-1} = \mathcal{A}_{-2} = 0, \; \; \; \; \; \; \mathcal{A}_2 = -\frac{6 \tau _4}{\eta }$.

According to the solution set (2.1), we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

(2.1, 1) Hyperbolic solution as follows:

where $h(x, y, z, t) = \left[x+\mathcal{K} y+\mathcal{V} z-\frac{\omega}{\beta }\ \left(\frac{1}{\Gamma (\beta)}+t\right)^{\beta }\right]\ \sqrt{-2 \tau _2}$, while $\eta \neq 0, \ \tau _2 < 0$ and $\tau _4 > 0.$

According to the solution set (2.2), we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

(2.2, 1) Dark soliton solution as follows:

where $\eta \neq 0, \ \tau _2 < 0$ and $\tau _4 > 0.$

Case-(3): If $\tau_3 = \tau_4 = \tau_6 = 0$, the following solution combinations are obtained:

According to this solution set, we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

(3.1) Exponential solution as follows:

where $\eta \neq 0$ and $\tau _2 > 0.$

Case-(4): If $\tau_0 = \tau_1 = \tau_6 = 0$, the following solution combinations are obtained:

(4.1) $\mathcal{A}_0 = -\frac{\alpha +\mathbb{C} \omega ^2+\mathcal{K}^2 \mu +\mathcal{K} \rho -\sigma \omega +\tau _2+\gamma \mathcal{V}}{2 \eta }, \mathcal{A}_{-1} = \mathcal{A}_{-2} = 0, \mathcal{A}_{1} = \pm \frac{6 }{\eta }\sqrt{\tau _2 \tau _4}, \mathcal{A}_{2} = -\frac{6 \tau _4}{\eta }, \tau _3 = \mp 2\sqrt{\tau _2 \tau _4}$.

According to the solution set (4.1), we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

(4.1, 1) Hyperbolic solution as follows:

where $\eta \neq 0, \ \tau _3^2 = 4 \tau _2 \tau _4$ and $\tau _2 > 0.$

(4.1, 2) Hyperbolic solution as follows:

where $\eta \neq 0, \ \tau _3^2 = 4 \tau _2 \tau _4$ and $\tau _2 > 0.$

Case-(5): If $\tau_2 = \tau_4 = \tau_6 = 0$, the following solution combinations are obtained:

According to the above solution set, we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

Weierstrass elliptic doubly periodic solution as follows:

where $\eta \neq 0, \tau _2 > 0$ and $\tau _3 > 0.$

Case-(6): If $\tau_0 = \tau_1 = \tau_3 = 0$, the solution combinations obtained are listed below:

According to the above solution set, we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

(6.1) Hyperbolic solution as follows:

where $\eta \neq 0, \ \tau _4^2\neq 4 \tau _2 \tau _6$ and $\tau _2 > 0.$

(6.2) Periodic wave solution as follows:

where $\eta \neq 0, \ \tau _4^2\neq 4 \tau _2 \tau _6$ and $\tau _2 < 0.$

Case-(7): If $\tau_1 = \tau_3 = \tau_6 = 0$, the solution combinations obtained are listed below:

(7.1) $\mathcal{A}_0 = \frac{-\alpha -\mathbb{C} \omega ^2+\mathcal{K}^2 (-\mu)-\mathcal{K} \rho +\sigma \omega -4 \tau _2-\gamma \mathcal{V}}{2 \eta }, \; \; \; \; \; \; \mathcal{A}_1 = \mathcal{A}_{2} = \mathcal{A}_{-1} = 0, \; \; \; \; \; \; \mathcal{A}_{-2} = -\frac{6 \tau _0}{\eta }$.

(7.2) $\mathcal{A}_0 = \frac{-\alpha -\mathbb{C} \omega ^2+\mathcal{K}^2 (-\mu)-\mathcal{K} \rho +\sigma \omega -4 \tau _2-\gamma \mathcal{V}}{2 \eta }, \; \; \; \; \; \; \mathcal{A}_{-1} = \mathcal{A}_{1} = 0, \; \; \; \; \; \; \mathcal{A}_2 = -\frac{6 \tau _4}{\eta }, \; \; \; \; \; \; \mathcal{A}_{-2} = -\frac{6 \tau _0}{\eta }$.

(7.3) $\mathcal{A}_0 = \frac{-\alpha -\mathbb{C} \omega ^2+\mathcal{K}^2 (-\mu)-\mathcal{K} \rho +\sigma \omega -4 \tau _2-\gamma \mathcal{V}}{2 \eta }, \; \; \; \; \; \; \mathcal{A}_{-1} = \mathcal{A}_{1} = \mathcal{A}_{-2} = 0, \; \; \; \; \; \; \mathcal{A}_2 = -\frac{6 \tau _4}{\eta }$.

According to the solution set (7.1), we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

(7.1, 1) The Jacobian elliptic solutions (JESs) under constraints $\tau _0 = 1, \ \tau _2 = -m^2-1, \ \tau _4 = m^2, \ 0\leq m\leq 1$, and $\eta \neq 0$ are derived as follows:

or

where $Q(x, t) = x+\mathcal{K} y+\mathcal{V} z-\frac{\omega}{\beta }\ \left(\frac{1}{\Gamma (\beta)}+t\right)^{\beta }.$

(7.1, 2) The Jacobian elliptic solution (JES) under constraints $\tau _0 = m^2-1, \ \tau _2 = 2-m^2, \ \tau _4 = -1, \ 0\leq m < 1$, and $\eta \neq 0$ is derived as follows:

where $Q(x, t) = x+\mathcal{K} y+\mathcal{V} z-\frac{\omega}{\beta }\ \left(\frac{1}{\Gamma (\beta)}+t\right)^{\beta }.$

(7.1, 3) The JES under constraints $\tau _0 = -m^2, \ \tau _2 = 2m^2-1, \ \tau _4 = 1-m^2, \ 0 < m\leq1$, and $\eta \neq 0$ is derived as follows:

where $Q(x, t) = x+\mathcal{K} y+\mathcal{V} z-\frac{\omega}{\beta }\ \left(\frac{1}{\Gamma (\beta)}+t\right)^{\beta }.$

The bright soliton solution is derived by substituting $m = 1$ into Eq (3.15) as follows:

(7.1, 4) The JES under constraints $\tau _0 = -1, \ \tau _2 = 2-m^2, \ \tau _4 = m^2-1, \ 0\leq m\leq1$, and $\eta \neq 0$ is derived as follows:

where $Q(x, t) = x+\mathcal{K} y+\mathcal{V} z-\frac{\omega}{\beta }\ \left(\frac{1}{\Gamma (\beta)}+t\right)^{\beta }.$

The bright soliton solution is derived by substituting $m = 1$ into Eq (3.17) as follows:

(7.1, 5) The JES under constraints $\tau _0 = 1, \ \tau _2 = 2-4m^2, \ \tau _4 = 1, \ 0\leq m\leq1$, and $\eta \neq 0$ is derived as follows:

(7.1, 6) The JES under constraints $\tau _0 = m^4-2 m^3+m^2, \ \tau _2 = -\frac{4}{m}, \ \tau _4 = -m^2+ 6m-1, \ 0 < m\leq1$, and $\eta \neq 0$ is derived as follows:

The hyperbolic solution is obtained by substituting $m = 1$ into Eq (3.20) as follows:

(7.1, 7) The JESs under constraints $\tau _0 = \frac{1}{4}, \ \tau _2 = \frac{m^2-2}{2}, \ \tau _4 = \frac{m^4}{4}, \ 0\leq m\leq 1$, and $\eta \neq 0$ are derived as follows:

or

According to the solution set (7.2), we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

(7.2, 1) The JESs under constraints $\tau _0 = 1, \ \tau _2 = -m^2-1, \ \tau _4 = m^2, \ 0\leq m\leq 1$, and $\eta \neq 0$ are derived as follows:

or

The hyperbolic solution is obtained by substituting $m = 1$ into Eq (3.24) as follows:

(7.2, 2) The Jacobian elliptic solution (JES) under constraints $\tau _0 = m^2-1, \ \tau _2 = 2-m^2, \ \tau _4 = -1, \ 0\leq m\leq1$, and $\eta \neq 0$ is derived as follows:

The bright soliton solution is derived by substituting $m = 1$ into Eq (3.27) as follows:

(7.2, 3) The JES under constraints $\tau _0 = -m^2, \ \tau _2 = 2m^2-1, \ \tau _4 = 1-m^2, \ 0 < m\leq1$, and $\eta \neq 0$ is derived as follows:

The bright soliton solution is derived by substituting $m = 1$ into Eq (3.29) as follows:

(7.2, 4) The JES under constraints $\tau _0 = -1, \ \tau _2 = 2-m^2, \ \tau _4 = m^2-1, \ 0\leq m\leq1$, and $\eta \neq 0$ is derived as follows:

The bright soliton solution is derived by substituting $m = 1$ into Eq (3.31) as follows:

(7.2, 5) The JES under constraints $\tau _0 = m^4-2 m^3+m^2, \ \tau _2 = -\frac{4}{m}, \ \tau _4 = -m^2+ 6m-1, \ 0 < m\leq1$, and $\eta \neq 0$ is derived as follows:

The hyperbolic solution is obtained by substituting $m = 1$ into Eq (3.33) as follows:

According to the solution set (7.3), we can find explicit solutions of Eq (1.1) in different forms that can be formulated as follows:

(7.3, 1) The Jacobian elliptic solutions (JESs) under constraints $\tau _0 = 1, \ \tau _2 = -m^2-1, \ \tau _4 = m^2, \ 0\leq m\leq 1$, and $\eta \neq 0$ are derived as follows:

or

where $Q(x, t) = x+\mathcal{K} y+\mathcal{V} z-\frac{\omega}{\beta }\ \left(\frac{1}{\Gamma (\beta)}+t\right)^{\beta }.$

The bright soliton solution is derived by substituting m = 1 into Eq (3.35) as follows:

4.   Discussion and physical analysis of the obtained solutions

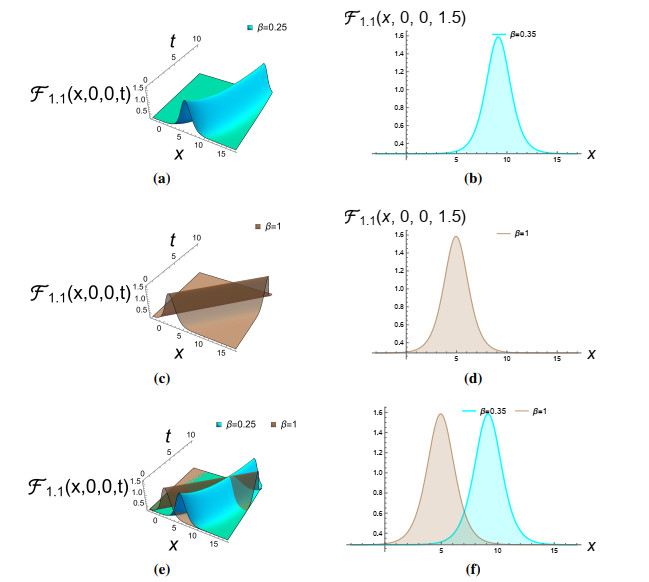
By adjusting the model parameters, numerous previously unrecorded value sets for Eq (1.1) were discovered. Adjusting the model parameters revealed many previously unrecorded value sets for Eq (1.1). This section illustrates the mathematical and physical properties of these solutions with various graph formats, including 3-D and 2-D plots, while explaining the effects of the fractional derivative. The visual representation of these soliton solutions typically involves 3D and 2D surface plots to illustrate the spatial and temporal evolution of the waves. Such graphical representations help in understanding the interaction patterns between solitons and their stability characteristics under various conditions. The bright soliton solution for Eq (3.3) is shown in Figure 1, with parameters $\alpha = 0.7, \ \mathcal{V} = 0.57$, $\gamma = 1.2, \ \mathcal{K} = 0.6, \ \mu = 0.72, \ \rho = 0.62$, $\sigma = 0.7, \ \mathbb{C} = 0.5, \ \omega = 1.98, \ \tau _2 = 0.39$, and $\eta = -1.8$. The bright soliton structures are characterized by localized peaks in the wave profile. The dark soliton solution for Eq (3.5) is shown in Figure 2, with parameters $\alpha = 0.87, \ \mathcal{V} = 0.75, \ \gamma = 1.24, \ \mathcal{K} = 0.8$, $\mu = 0.78, \ \rho = 0.76, \ \sigma = 0.95, \ \mathbb{C} = 0.75$, $\omega = 3.8, \ \tau _2 = -0.69$, and $\eta = -0.68$. Dark solitons represent localized waveforms characterized by a decrease in amplitude compared to the surrounding baseline. They are often seen as step-like or trough-like features in the wave profile.

5.   Conclusions

The conclusions drawn from this work highlight the importance of the analytical solutions obtained for the nonlinear wave propagation governed by the new (3+1)-dimensional $\beta$-fractional Boussinesq-KP equation. Using the MEDAM, the study successfully generated diverse wave solutions, such as soliton (dark, bright, and singular), hyperbolic, rational, exponential, singular periodic, Jacobi elliptic function, and Weierstrass elliptic doubly periodic solutions. It was observed that the fractional derivatives play a crucial role in influencing the amplitude, shape, and propagation patterns of the soliton solutions. The findings demonstrated that varying the fractional parameters significantly alters the characteristics and dynamics of these wave solutions. The graphical representations in this study have effectively shown how the fractional derivative affects the size and behavior of soliton waves. Changing the value of $\beta$ leads to noticeable variations in the amplitude, shape, and propagation dynamics of the soliton solutions. This highlights the significance of using fractional calculus in modeling these dispersive and nonlocal systems, as it provides a more precise depiction of the fundamental physical processes at play. Furthermore, a comparison with solutions obtained using traditional integer-order derivatives revealed significant differences ^[21]. The fractional-order solutions showed a higher degree of localization, faster propagation, and more intricate wave interactions. These observations underscore the value of fractional calculus in capturing more complex and realistic wave behaviors in nonlinear systems.

Author contributions

Wafaa B. Rabie: Formal analysis, Software; Hamdy M. Ahmed: Validation, Methodology; Taher A. Nofal: Resources, Writing–review & editing; Soliman Alkhatib: Software, Writing- review & editing. ll authors have read and agreed to the published version of the manuscript.

Acknowledgments

The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-46).

Funding

This research was funded by Taif University, Saudi Arabia, Project No. (TU-DSPP-2024-46).

Conflict of interest

All authors declare no conflicts of interest in this paper.