Event-triggered anti-windup strategy for time-delay systems subject to saturating actuators

1.   Introduction

In reality, almost all feedback control systems are affected by saturating actuators, and the existence of saturations could induce poor system performance, instability, and multiple equilibria ^[1]. In general, two typical approaches have been employed to tackle actuator saturations. The first approach is to directly design the feedback controller with consideration of actuator saturations ^[2,3,4,5], while the other approach is to first design a desirable controller satisfying some performance indices without taking saturations into account and afterwards synthesize an anti-windup (AW) compensator to alleviate saturation effects ^[6,7,8]. Under the AW strategy, one can perform the separation design, some standard techniques can be utilized to design the nominal controller. Moreover, compared to the direct design approach, the AW strategy has better application intuition and is thus more attractive for practicing engineers. When dealing with saturation nonlinearities, the polytopic models and the modified sector conditions (SCs) are two routine techniques ^[6,7,9,10]. In particular, using modified SCs, the AW synthesis criteria can be characterized by linear matrix inequalities (LMIs) ^[7].

Meanwhile, time delays are frequently unavoidable in a large number of control systems, which is another key factor resulting in system instability and performance degradation ^{[11,12,13,14,15]}. In the past two decades, abundant research has also been dedicated to the AW design for actuator-saturated control systems with time delays ^{[16,17,18,19,20]}. For example, in ^[16], delay-independent and delay-independent AW synthesis conditions have been established in the formwork of LMI by utilizing the Lyapunov-Krasovskii (L-K) approach and the modified SC. Moreover, in ^[17], delay-dependent SCs have been explored, and augmented L-K functionals as well as Wirtinger-based integral inequality have been employed to improve the previous results. In addition, dynamic AW compensators have been designed in ^[18,19] for linear control systems containing a state delay, and the AW synthesis problem has been studied in ^[20] for sampled-data time-delay systems.

Over the past several decades, communication networks have been embedded in many practical systems, and the resulting networked control systems (NCSs) have become a highly concerned research issue. However, the network bandwidth is definitely limited. Under the traditional time-triggered scenario, the embedding of a network in a control system could lead to the phenomenon of network congestion ^[21,22,23]. As a result, some imperfections will inevitably occur in NCSs, e.g., packet dropouts and disorders, and communication delays. To be able to mitigate network-induced phenomena, some scholars proposed the event-triggered mechanisms (ETMs) based on which certain redundant data are not allowed to be released by means of pre-designed triggering conditions ^[24,25,26]. So far, the state estimation and control for NCSs have been widely investigated under ETMs, and a great quantity of remarkable results have been acquired ^{[27,28,29,30,31]}.

In the past decade or so, the control synthesis has also been addressed for NCSs subject to saturating actuators under the ETMs ^{[32,33,34,35,36]}. For instance, dynamic output feedback control has been studied ^[32] for discrete LPV systems under two independent triggering conditions, and state feedback control has been discussed in ^[33] for continuous linear systems under a static ETM. In particular, the static AW design problem has been sufficiently considered in ^[37,38,39] under several ETMs, and the dynamic AW synthesis problem has been investigated in ^[40] under the dynamic ETM. However, it is observed that time delays have been ignored in the majority of existing references, possibly due to the complex mathematical deduction, which is the motivation for the present study.

This paper focuses on the event-triggered AW synthesis for linear systems subject to time-varying state delay and saturating actuators. Using the dynamic triggering condition, delay-dependent SCs, and augmented L-K functionals together with some less conservative inequalities, the delay-dependent AW synthesis criteria have been derived in light of the solvability of LMIs. Then, the maximization about the initial condition set (ICS) has been concretely discussed. Finally, a numerical example illustrates the availability of the obtained results and technique advantages of this paper. The main contributions of this study are highlighted as follows: 1) The delay-dependent AW synthesis criteria are established for the first time for linear time-delay systems under a dynamic ETM. 2) In order to abate the intrinsic conservatism, novel delay-dependent SCs containing double integral terms have been explored. Moreover, some less conservative inequalities are utilized to estimate the upper bound of the derivatives of L-K functionals as well as the lower bound of L-K functionals.

Notation. $\mathbb{R}^{n}$: $n$-dimensional Euclidean space; $\|\cdot\|_2$: $2$-norm of a vector; $\mathbb{C}^1[-\tau, 0]$: The space of continuously differentiable vector functions $\phi$ within $[-\tau, 0]$; $E^T$: The transposition of $E$; $R > 0\; (\geq 0)$: $R$ is a symmetric and positive definite (positive semi-definite) matrix; $\lambda_M(Q)$: The maximum eigenvalue of a matrix $Q$; $I$: The identity matrix; ${\rm Sym}(M)\triangleq M+M^{T}$.

2.   Problem formulation

Consider the linear system with time-varying delay and saturating actuators

where $x_p(t)\in\mathbb{R}^{n_{x}}$ is the system state, $y_p(t)\in\mathbb{R}^{n_{y}}$ is the system output, $u(t)\in\mathbb{R}^{n_{u}}$ is the control input, and $A_p$, $A_{pd}$, $B_p$, and $C_p$ are known matrices of appropriate dimensions. $\tau_t$ is a time-varying state delay satisfying $0 \leq \tau_t\leq \tau$ and $\mu_{1}\leq\dot{\tau}_t\leq \mu _{2}$. ${\rm sat}(u) = {\rm col}\{{\rm sat}(u_1), {\rm sat}(u_2), \ldots, {\rm sat}(u_m)\}$ is a vector saturation function representing saturating actuators, where ${\rm sat}(u_l) = \min \{\bar{u}_l, |u_l|\}{\rm sign}(u_l)$ with $\bar{u}_l > 0$ ($l = 1, 2\ldots n_{u}$) being the saturation levels.

To stabilize the system (1), we assume that an output feedback controller has been designed as

where $x_c(t)\in \mathbb{R}^{n_c}$ is the controller state, and $A_c$, $B_c$, $C_c$, and $D_c$ are dimension-compatible matrices.

To mitigate the adverse effects caused by saturating actuators, as in ^[6,7], one can add the anti-windup term to modify the controller (2) as

where $E_c$ is the AW gain matrix, and $\varphi (u(t))\triangleq{\rm sat}(u(t))-u(t)$.

Here, we assume that the output signals are transmitted over communication networks. More specifically, to save the communication resources, a dynamic ETM is adopted, and then the controller (2) can be further written as follows:

In (4), the triggering instants $t_k$ $(k = 0, 1, 2, \ldots)$ are determined by the updating algorithm as

where $e(t)\triangleq y_p(t_k)-y_p(t)$, $\theta > 0$, $0 < \delta_1 < 1$, $\delta_2 > 0$, $\zeta > 0$ are given scalars, and $\xi(t)$ is generated by

where $\xi(0) = \xi_0\geq 0$ and $\lambda > 0$.

Remark 1. From (5), we have the relation $\delta _1y^T_p(t)y_p(t)+\delta _2e^{-\zeta t}-e^T(t)e(t)\geq-\frac{1}{\theta}\xi(t)$, $t\in[t_k, \; t_{k+1})$. Then, one obtains from (6) that $\dot{\xi}(t)\geq-(\lambda+\frac{1}{\theta})\xi(t)$. Moreover, it follows that $\xi(t)\geq e^{-(\lambda+\frac{1}{\theta})t}\xi_0$. Noting $\xi_0\geq 0$, it is obvious that the dynamic variable $\xi(t)$ is non-negative, which means that the triggering interval could be enlarged. Therefore, the dynamic ETM has more potential to save communication resources compared to the static ETM without the introduction of dynamic variables. In (5) and (6), the term $\delta _2e^{-\zeta t}$ is used to avoid the Zeno behavior while ensuing the asymptotic stability of the overall systems ^[37]. On other hand, it is worth mentioning that there are other ETMs available in existing references, such as the sampled-data-based ETM ^[25], the memory-based ETMs ^[27], and the switching ETM ^[31]. Under such ETMs, the corresponding results can also be obtained, which is our further work.

Define $x(t)\triangleq{\rm col}\{x_p(t), x_c(t)\}\in \mathbb{R}^n$, where $\bar{n} = n_x+n_c$. Then, from (1) and (4), one has the system

where

The initial condition of (5) is denoted as $\phi (\theta) = {\rm col} \{\phi_p(\theta), \phi_c(\theta)\}$, which is supposed to belong to

For some $n_u\times \bar{n}$ matrices $U$, $V_1$, $V_2$, $V_3$, and $V_4$, one can define the vector as below:

Then, under the assumption that

we have the delay-dependent SC ^[1]

where $H > 0$ is any $n_{u}\times n_{u}$ diagonal matrix, and $\mathcal{K} = [D_cC_p\; \; C_c]$.

For the special case ($\tau_t\equiv \tau, \; t > 0$), one can simplify the vector $v(t)$ in (11) as

Remark 2. In ^[17], the modified delay-dependent SCs are developed to tackle the nonlinearity $\varphi(u(t))$. Compared to the SCs in ^[17], the double integral terms $V_{3}\int_{t-\tau_t}^{t}\int_{\theta}^{t} \frac{x(r)}{\tau_t} \mathrm{d}r\mathrm{d}\theta$ and $V_4\int_{t-\tau}^{t-\tau_t}\int_{\theta}^{t-\tau_t} \frac{x(r)}{\tau-\tau_t}\mathrm{d}r\mathrm{d}\theta$ are further incorporated in the sector condition (11) to decrease the conservatism except the term $D_ce(t)$ concerning the ETM.

Next, several inequalities are provided, which are crucial for the derivation of our main results.

Lemma 1. ^[11,12] Let the $n\times n$ matrix $Z > 0$, the continuously differentiable vector function $\psi(s):[\iota_1, \iota_2]\rightarrow \mathbb{R}^{n}$, and scalars $\iota_1$ and $\iota_2$ ($\iota_1 < \iota_2$) be given. The following integral inequalities hold:

where

Lemma 2. ^[13] For a given $n\times n$ matrix $S > 0$, two vectors $\vartheta_1\in \mathbb{R}^{n}$ and $\vartheta_2\in \mathbb{R}^{n}$, a scalar $\alpha\in(0, 1)$, as well as any $n\times n$ matrices $M_1$ and $M_2$, the following inequality is true:

where $\Omega(\alpha, S) = (1/\alpha)\vartheta^{T}_1S\vartheta_1+[1/(1-\alpha)]\vartheta^{T}_2S\vartheta_2$.

3.   Main results

For convenience of presentation, we first introduce some notations as follows:

For the analysis of the stability of the system (7), we select the augmented L-K functional

where $\sigma(t) = {\rm col}\{x(t), \tau_tw_{1t}, (\tau-\tau_t)w_{2t}, \tau_tw_{3t}, (\tau-\tau_t)w_{4t}\}$, $P$ is a symmetric matrix, and $Q_1 > 0$, $Q_2 > 0$, $Z > 0$ are some matrices.

Theorem 1. Let the scalars $\varepsilon\neq0$, $\delta_1 > 0$, $\delta_2 > 0$, $\zeta > 0$, and $\beta > 0$ be given. Suppose that there exists $5\bar{n}\times 5\bar{n}$ symmetric matrix $\bar{P}$, $\bar{n}\times\bar{n}$ matrices $\bar{Q}_1 > 0$, $\bar{Q}_2 > 0$, $\bar{Z} > 0$, $X$, $3\bar{n}\times 3\bar{n}$ matrices $\bar{S}_1$, $\bar{S}_2$, $n_u\times\bar{n}$ matrices $Y$, $G_1$, $G_2$, $G_3$, $G_4$, $n_c\times n_u$ matrix $W$, $n_u\times n_u$ diagonal matrix $\bar{H} > 0$, such that the LMIs as below are satisfied:

where

Then, the system (7) is asymptotically stable for all initial conditions $\xi_0$ and $\phi (\theta)\in\aleph_\rho$ satisfying $V(0)\leq \beta$ under the AW gain matrix $E_c = W\bar{H}^{-T}$.

Proof. Differentiating the L-K functional (13), and then combining (6), (11), one has

Using an auxiliary function-based inequality (i.e., the inequality (1) in Lemma 1) yields

Noting $\int_{t-\tau}^{t}(\cdot)\mathrm{d}r = \int_{t-\tau_t}^{t}(\cdot)\mathrm{d}r+\int_{t-\tau}^{t-\tau_t}(\cdot)\mathrm{d}r$ and using Lemma 2, we have from (18) and (19) that

where $\alpha\triangleq \tau_t/\tau$, and $S_1$ and $S_2$ are $3\bar{n}\times 3\bar{n}$ matrices.

For any given $\bar{n}\times \bar{n}$ matrices $T_1$, $T_2$, utilizing the system (7), the following equation is true

Let us add the left-hand side of (21) to (17) and use (20). Then, one can obtain

where

Clearly, if the matrix inequality as below is satisfied:

then, we can get from (22) that $\dot{V}(t) < 0$ is ensured.

Moreover, using the inequality (2) of Lemma 1 and the Jensen inequality ^[17], the lower bound of $V(t)$ can be given as

where

Denote $N_l\triangleq[U_l\; \; V_{1l}\; \; V_{2l}\; \; V_{3l}\; \; V_{4l}]$, $l = 1, 2, \ldots, n_u$, and suppose that the following inequalities hold:

Then, for all initial conditions $\xi_0$ and $\phi\in \aleph_{\rho}$ that satisfies $V(0)\leq \beta$, using (24) and (25), and noting that $\dot{V}(t) < 0$, we have

From (26), we can see that constraints in (10) are ensured. Meanwhile, it is seen from (25) that $V(t) > 0$ for any $x_t\triangleq x(t+s)\neq0$ ($s\in[-\tau, 0]$) under the conditions (25). Noting $\dot{V}(t) < 0$ again, we can conclude that the system (7) is asymptotically stable under the assumptions (23) and (25).

To design the AW gain matrix $E_c$ by means of LMIs, we set $T_2 = \varepsilon T_1$ $(\delta \neq 0)$, and then define

Pre- and post-multiplying (23) by ${\rm diag}\{X, X, X, X, X, X, X, \bar{H}, I, X\}$ and its transpose, and using (27) yields

where

with $\tilde{\Xi}_6 = \bar{\Xi}_6+{\rm diag}\{\delta_1X\mathcal{C}^T\mathcal{C}X^T, 0_{7\bar{n}+n_u+n_y}\}$.

Using the fact that $\tilde{\Pi}(\tau_t, \dot{\tau}_t)$ is convex about $\tau_t$ as well as $\dot{\tau}_t$, it follows that (28) can be ensured by

Noting that $\alpha = 0$ for the case $\tau_t = 0$, and applying Schur complement, it can be seen that (29) and (30) are equivalent to LMIs in (14) and (15), respectively. Pre- and post-multiplying (25) by ${\rm diag}\{X, X, X, X, X\}$ and its transpose, respectively, and meanwhile, employing (27) and Schur complement yields the LMIs (16). □

Remark 3. In obtaining Theorem 1, an augmented L-K functional (13) with double integral terms and the novel delay-dependent SC (11) are adopted to alleviate the conservatism. Moreover, an auxiliary function-based integral inequality is further utilized to estimate the upper bound $\dot{V}(t)$. In addition, the Wirtinger-based inequality (inequality (2) of Lemma 1) is employed to estimate the lower bounds of both integral terms $\int_{t-\tau_t}^{t} x^T(r)Q_1x(r) \mathrm{d}r$ and $\int_{t-\tau}^{t-\tau_t} x^T(r)Q_2x(r)\mathrm{d}r$.

For the constant delay case ($\tau_t = \tau$), we select the simplified L-K functional

where $\eta(t) = {\rm col}\big\{x(t), \int_{t-\tau}^{t} x(r)\mathrm{d}r, \frac{1}{\tau}\int_{t-\tau}^{t} \int_{\theta}^{t} x(r)\mathrm{d}r\mathrm{d}\theta\big\}$, $\tilde{P}$ is a symmetric matrix, and $Q > 0$, $Z > 0$.

Using the inequalities (2) and (3) in Lemma 1, we can estimate the $\tilde{V}(t)$ as

where

Moreover, we define the variables

Then, the AW design criterion for the constant delay case is stated as follows:

Corollary 1. Assume that there exist $3\bar{n}\times 3\bar{n}$ symmetric matrix $\check{P}$, $\bar{n}\times\bar{n}$ matrices $\bar{Q} > 0$, $\bar{Z} > 0$, $X$, $n_u\times\bar{n}$ matrices $Y$, $G_1$, $G_2$, $n_c\times n_u$ matrix $W$, $n_u\times n_u$ diagonal matrix $\bar{H} > 0$, such that the LMIs as below hold:

where

Then, the conclusion of Theorem 1 holds for the case $\tau_t = \tau$.

Remark 4. In deriving above Corollary 1, the lower bound of the integral term $\tau\int_{-\tau}^{0} \int_{t+\theta}^{t}\dot{x}^T(r)Z\dot{x}(r)\mathrm{d}r\mathrm{d}\theta$ is estimated based on an auxiliary function-based inequality (the inequality (3) of Lemma 1), which is different from the variable delay situation. Noting that, if the same technique is utilized in the variable delay situation, the resulting conditions are no longer LMIs. On the other hand, it is worth mentioning that, using the L-K functional (31), one can establish the corresponding result for the case that the time delay $\tau_t$ is not differentiate ^[14,41].

Next, we are concerned with the optimization of the ICS $\aleph_\rho$. To estimate $V(0)$, we set

Using Jensen integral inequalities ^[17] and noting that $\bar{P}\triangleq\hat{X}P\hat{X}^T$ yields

Similarly, we can set

Then, we get

Similar to ^[17], one can set $X^{-1}X^{-T}\leq xI$ ($x > 0$). The inequality is ensured by an LMI

Furthermore, one introduces the set of LMIs as follows:

Note that the admissible initial conditions satisfy the constraint $V(0)\leq \beta$. For given $\delta_2$, $\zeta$, $\xi_0$, and $\beta$, it can be seen from (37) and (39) that the small coefficients of $\rho_1$ and $\rho_2$ correspond to large $\rho_1$ and $\rho_2$. Then, the maximization of the ICS $\aleph_\rho$ can be achieved by minimizing the coefficients of $\rho_1$ and $\rho_2$. Correspondingly, the optimization of the ICS $\aleph_\rho$ involved in Theorem 1 as well as Corollary 1 can be, respectively, expressed as follows:

where

Once the optimization problem has the solution, then the AW gain matrix can be solved by $E_c = W\bar{H}^{-T}$. Also, two scalars $\rho_1$ and $\rho_2$ involved in ICS $\aleph_\rho$ can be characterized by the relation $\hat{V}_0\leq\beta$ or $\hat{\tilde{V}}_0\leq\beta$.

Remark 5. If the ETM is not introduced in measurement output $y(t)$, the corresponding optimization problems can be readily derived by removing some terms involving $e(t)$ in LMIs (14)–(15) and LMIs (34)–(35), which are respectively denoted as Prob.1' and Prob.2'. In fact, the AW synthesis has been considered in ^[17] for time-delay systems under continuous-time measurement. However, compared with the techniques used in ^[17], the double integral terms are further incorporated in L-K functionals and SCs. In addition, several more advanced inequalities are adopted to estimate the upper bounds of the derivatives of L-K functionals and the lower bounds of L-K functionals themselves.

4.   Numerical example

Example 1. Let us address the unstable system (1) and the controller (2) with the parameters

The parameters of the triggering conditions (5) and (6) are selected as:

Solving Prob.1 with $\beta = 1.35$, $\delta = 0.78$, and $\varrho = 5\times 10^3$, one can obtain the maximum scalars $\rho _1 = \rho _2 = 11.0493$ involved in ICS $\aleph_\rho$ defined in (8) and the AW gain $E_c = 0.8083$.

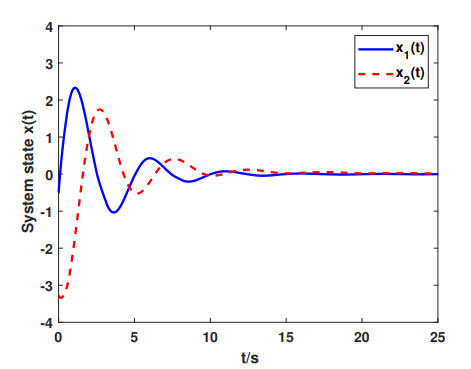
In Figures 1 and 2, we plot the state evolution of the closed-loop system and the saturated input, respectively. In Figure 3, we plot the event-triggering instants. In the simulation, we select $\tau_t\equiv0.4+0.1{\rm sint}$, $\phi_p(\theta) = [-0.5\; \; -3.28]$, $\phi_c(\theta) = 0$ ($\phi(\theta)\in\aleph_\rho$). From Figure 1, it is clear that the system state converges to zero, which verifies the availability of our obtained result. Figure 2 shows that the control input is saturated within the initial stage. In Figure 3, "1" denotes the triggering and "0" denotes no triggering, and the total number of event-triggering instances is 137 within $[0, 10]$. Noting that the sampling time is 0.01s, it is obvious that the ETM can save the communication resources effectively.

For the case without using the ETM, by solving Prob.2' with $\beta = 1$, the maximum scalars $\rho$ ($= \rho_1 = \rho_2$) related to the ICS $\aleph_\rho$ are easily obtained (see Table 1). In Table 1, we also list the upper bounds of $\rho$ obtained by the result in ^[20] and some special cases, where Cases I–III correspond to, respectively, $W = 0$ in LMIs (34), $\bar{\Phi}_1 = \check{P}+{\rm diag}\{0, \bar{Q}/\tau, 0\}$ and $\Phi_3 = 0$ in LMIs (35), and $G_2 = 0$ in LMIs (34) and (35).

From Table 1, we can see that Prob.2' provides the larger estimate of $\rho$ than the result in ^[17], which verifies that the proposed techniques in this paper have less conservatism. Noting that Case I is related to the controller without the AW term, it is illustrated that the AW strategy can enlarge the estimate of the ICS. Also, it is seen that Prob.2' can estimate a larger $\rho$ than Case II, which shows that our proposed technique dealing with the lower bound of the L-K functional is more effective. In addition, Prob.2' can give the larger $\rho$ than Case III, which demonstrates that the double integral term introduced in delay-dependent SCs can decrease the conservatism.

5.   Conclusions

In the paper, the AW synthesis has been investigated for linear control systems containing time-varying state delay and saturating actuators under a dynamic ETM. Using novel delay-dependent SCs and augmented L-K functionals together with several less conservative inequalities, delay-dependent AW design conditions have been obtained on the basis of the feasibility of a set of LMIs. Then, the optimization of ICSs has been concretely formulated. In the end, a simulation example has been provided to show the validity and advantages of our results. Here, it is worth mentioning that more effective results can be established by incorporating the switching AW design ^[8] and the dynamic AW technique ^[19], which is our further research. Moreover, by using the sampled-data-based ETM ^[25], the continuous supervision of the measurement is no longer required. In addition, the external disturbances might be unavoidable in actual control systems ^[18,19,42]. Using the similar analysis as in ^[18,19], it is easy to extend our results to control systems with external disturbances.

Author contributions

LiPing Luo: Writing-review & editing, Software; Yonggang Chen: Methodology, Writing-review & editing; Jishen Jia: Conceptualization, Revision-review & editing; Kaixin Zhao: Revision-review & editing; Jinze Jia: Revision-review & editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 62273132), the Natural Science Foundation of Henan Province of China (No. 242300421052), and the Major Science and Technology Projects of Xinxiang City of China (No. 22ZD004).

Conflict of interest

All authors declare no conflicts of interest in this paper.