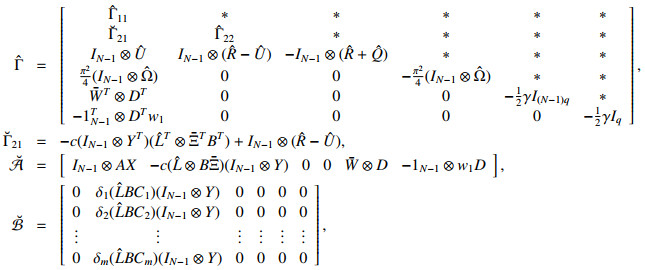H-infinity bipartite consensus of multi-agent systems with external disturbance and probabilistic actuator faults in signed networks

1.   Introduction

Recently, the distributed consensus control for multi-agent systems has received compelling attentions owing to its potential applications ^[1,2,3]. The main objective is to design distributed control protocol such that all agents can achieve an agreement. Generally speaking, the consensus problems can be divided into three types, leader-following consensus problem, which means a leader is designated and all the followers track the leader. Containment control is a consensus-like tracking problem with multiple leaders, the control target is to let the followers states finally converge to the convex hull spanned by the leaders. Leaderless consensus problem means all the agents can eventually converge to the weighted average value of all the agents. For the above three consensus problems, many fruitful results have been obtained for linear, nonlinear or stochastic multi-agent systems ^{[4,5,6,7,8,9,10]}, and so on.

It is noted that most of the existing results are focused on multi-agent systems with cooperative communication links, that is the elements of adjacency matrix are non-negative, however, the adjacency matrix with antagonistic links is very common in practical application to describe the competitive relationship among the agents ^[11,12]. Therefore, more and more attention has been paid to the signed networks with negative and positive elements ^{[13,14,15,16,17,18,19]} and the references therein. In ^[11], the concept of bipartite consensus is introduced for multi-agent systems with structurally balanced graph, all agents will reach a final state with opposite sign. The authors ^[13] have extended the concept of bipartite consensus to interval bipartite consensus, some interval bipartite consensus results are derived for structurally unbalanced networks. In ^[14], the distributed bipartite tracking consensus problem has studied for a class of linear multi-agent systems with a dynamic leader, where the leader's control inputs are allowed to be nonzero and unknown to each follower. In ^[15], a novel concept of node-to-node bipartite consensus is proposed, where the communication channels of the followers are assumed to be structurally balanced. For signed directed graphs, the reference ^[16] has designed two types of state feedback and dynamic output feedback control laws to achieve bipartite consensus, respectively. In ^[17], a pinning scheme is proposed for a class of coupled nonlinear systems with antagonistic interactions and switching topologies. Additionally, similar to bipartite consensus problem, the reverse group consensus is firstly studied in the cooperation-competition network ^[18], the results show that the couple group consensus can be achieved if the mirror graph is strongly connected, as an extension, the distributed stabilization problem is considered for multiple heterogeneous agents in the uncertain strong-weak completion network with exogenous disturbances ^[19].

In practical multi-agent systems, each agent is equipped with micro-processor, it can collect information from neighboring agents, therefore, it is desired to implement actuating the controller updates on a digital platform ^[20], the scheduling can be done in a time-triggered scheme and an event-triggered scheme, where time-triggered scheme with a fixed sampling period, which should be selected to guarantee a desired performance under worst conditions, this kind of triggered method will lead to send many unnecessary sampling data to neighboring agents. Considering the limited network resources, the event-triggered scheme is an effective method to improve the resources utilization while ensuring a satisfactory performance ^[21,22]. Event-triggered bipartite leader-following consensus problems have been studied in ^{[23,24,25,26]}, event-triggering condition is allowed to be intermittently examined at its own sampling instants in ^[23], a novel distributed protocol based on independent sampling period is presented. In ^[24], a novel event-triggered function is designed, where the continuous communication can be avoided and the Zeno-behavior can be excluded. In ^[25], the distributed static bipartite event-triggered controller and the fully distributed adaptive bipartite event-triggered controller are designed respectively, where the communication in both controller updating and triggered condition monitoring is intermittent, thus the communication resources can be greatly saved. In ^[26], by using pinning control strategies, a novel event-triggered controller is designed to achieve bipartite consensus. The refereances ^[27,28] discuss fully distributed bipartite output consensus of heterogeneous multi-agent systems, the fully distributed bipartite compensator and dynamic event-triggered mechanism are proposed in ^[27], where the proposed compensator is independent of any global information of the network topology. The reference ^[28] discusses the distributed bipartite finite-time event-triggered output consensus for heterogeneous linear multi-agent systems under directed signed communication topology, where a novel distributed bipartite compensator with intermittent communication mechanism is proposed in finite time. In ^[29], distributed event-triggered control strategy is proposed to guarantee the semi-global bipartite consensus. The reference ^[30] presents an even-triggered control framework to achieve bipartite consensus for networked Euler-Lagrange systems with external disturbance. In ^[31], event-triggered bipartite consensus is addressed under DoS attacks. Bipartite consensus of multi-agent systems with switching communication topologies is addressed in ^[32], where event-triggered conditions are piecewise functions depending on the variable couplings and topologies. However, the above schemes still exist some room for improvement. Inspired by ^[33,34,35], the next transmission instant is determined by $t_{k+1}h = t_{k}h+\min \{e^{T}(j_{k}h)\Phi e(j_{k}h) > \delta x^{T}(t_{k}h)\Phi x(t_{k}h)\}$, where $\Phi$ is a symmetric positive definite matrix, which can be replaced by $t_{k+1}h = t_{k}h+\min \{e^{T}(j_{k}h)\Phi_{1} e(j_{k}h) > \delta x^{T}(t_{k}h)\Phi_{2} x(t_{k}h)\}$, where $\Phi_{1}$ and $\Phi_{2}$ are two symmetric positive definite matrices, some comparisons are given in Section 4, it can be seen that our event-triggered scheme can lead to larger sampling period. The lower bound event interval is the sampling period $h$, which is strictly larger than zero, therefore, Zeno behavior is excluded in our proposed scheme.

Furthermore, it is well known that actuators often suffer from faults inevitably in practical applications, which may degrade the performance of even cause instability ^[36,37]. In response to requirements for the reliability of multi-agent systems, some considerable works have been done on designing control schemes to accommodate actuator faults ^{[38,39,40,41,42]}. The leader-following consensus problem for multi-agent systems with actuator faults ^[38,39], actuator faults are time-varying^[38], for two cases of the leader without control input and the leaders unknown bounded input, the distributed event-triggered fault-tolerant protocol is proposed to reach leader-following consensus. For a class of multi-agent systems against actuator faults and some perturbed factors as state-dependent uncertainties in ^[39], the distributed controllers is constructed to ensure leader-following consensus based on adaptive updates. In ^[40,41,42], the adaptive techniques are adopted to achieve the consensus of multi-agent systems with actuator faults. By the sliding mode control method, the reference ^[40] investigates the consensus tracking problem of second-order nonlinear multi-agent systems with disturbance. In ^[41], for a class of high-order nonlinear systems with intermittent actuator faults, a novel distributed adaptive controller is proposed to solve the output consensus tracking problem. In ^[42], for the actuator faults of partial loss of effectiveness fault and biased fault, a neural network-based adaptive consensus protocol is developed based on the Lyapunov analysis. In addition, the disturbance is inevitable and may degrade the performance in practical applications, H-infinity bipartite consensus problem is studied of nonlinear multi-agent systems with bounded disturbances in ^[43], where an performance criterion from bounded disturbances to the consensus error has been provided. In ^[44], the bipartite consensus controller is designed for cooperation-competition multi-agent systems with round-robin protocols such that the predetermined H-infinity bipartite consensus is satisfied over a given finite horizon. But in the above references, the event-triggered scheme and probabilistic actuator faults have not considered, to the best of the author's knowledge, no result has been reported for H-infinity bipartite consensus of multi-agent systems with event-triggered scheme and probabilistic actuator faults in signed networks, which motivates the present study.

Motivated by the aforementioned discussion, this paper is devoted to investigate H-infinity bipartite consensus for a class of linear multi-agent systems with external disturbance in signed networks. The main contributions can be summarized as follows: (1) A novel concept of H-infinity bipartite consensus is introduced to quantify against the exogenous disturbance. (2) The proposed event-triggered scheme can ensure the desired performance while further reducing the frequency of data transmission, Zeno behavior is excluded owing to the lower bound of inter event interval is the sampling period. (3) The generalized random variables are introduced to describe probabilistic actuator failures, which represent the case of complete measurement failure, partial failure and complete normal of the actuator, but also including the case of the measured value of the actuator bigger than the real value.

The remainder of this paper is organized as follows: In Section 2, some preliminaries are introduced. In Section 3, main results are presented for H-infinity bipartite consensus. A numerical simulation is provided to verify the theoretical results in Section 4. Some conclusions and future works are provided in Section 5.

Notation ${\mathbb R}^{n}$ denotes the $n$-dimensional Euclidean space and ${\mathbb R}^{n\times m}$ is a set of real $n\times m$ matrices. Notation $\|.\|$ is the Euclidean norms of vector and matrix. If $A$ is positive definite (or semi-definite), denote $A > 0$ (or $A\geq 0$). Suppose that matrix $M\in{\mathbb R}^{n\times n}$ is a real symmetric matrix, $\lambda_{max}(M)$ and $\lambda_{min}(M)$ denote the maximum and minimum eigenvalues of matrix $M$, respectively. The notation $\otimes$ means the Kronecker product. $diag\{\cdots\}$ stands for a block-diagonal matrix. The superscript $1_{n}(0_{n})$ indicates the $n$-dimensional column vector with each entry being $1(0)$. $sgn(\cdot)$ is the standard sign function. $E(\cdot)$ stands the mathematical expectation of random variable.

2.   Problem formulation and preliminaries

The communication topology can be described as a signed graph $g = (v, \varepsilon, A)$, where $v = (v_{1}, v_{2}, \ldots, v_{N})$ denotes a set of vertices, $\varepsilon \subseteq v\times v$ is a set of edges, $A = (a_{ij})_{N\times N}$ denotes a weighted adjacency matrix representing the communication topology, where the entry $a_{ij}$ of the matrix $A$ can be allowed to negative and positive, $a_{ij} > 0$ indicating node $i$ and node $j$ are cooperative relationship, if $a_{ij} < 0$ indicating node $i$ and node $j$ are competitive relationship, otherwise, $a_{ij} = 0$ means node $i$ and node $j$ have no information communication. The Laplacian matrix of the signed graph $g$ can be defined as $L = (l_{ij})_{N\times N}$, where $l_{ii} = \sum\limits_{k = 1, k\neq i}|a_{ik}|$, and $l_{ij} = -a_{ij}$ $(i\neq j)$. A signed graph $g$ is called structurally balance if the node set $v$ can be divided into two sub-networks $V_{1}$ and $V_{2}$, which satisfy $V_{1}\cup V_{2} = v$ and $V_{1}\cap V_{2} = \Phi$, $a_{ij}\geq 0$ holds for any $i, j\in V_{p}$, $p\in \{1, 2\}$ and $a_{ij} < 0$ holds for all $i\in V_{q}$, $j\in V_{r}$, where $q\neq r$, otherwise, the signed graph $g$ is called structurally unbalance.

Consider a group of $N$ identical agents with general linear dynamics, in which the dynamics of agent $i$ is described as follow:

where $x_{i}(t)\in \mathbb{R}^{n}$, $u_{i}(t)\in \mathbb{R}^{n}$ and $w_{i}(t)\in \mathbb{R}^{q}$ represent the system state, control input and external disturbance of the $i$th agent, respectively. $A\in \mathbb{R}^{n\times n}$, $B\in \mathbb{R}^{n\times m}$ and $D\in \mathbb{R}^{n\times q}$ are some known constant matrices with compatible dimensions.

In what follows, some key lemmas are summarized, which play the important roles to derive the main results.

Lemma 1. ^[11] Suppose that signed network $g$ is structurally balance, if and only if there is a gauge transformation $W$ such that $W^{T}AW = \bar{A}$ has all nonnegative entries, where a gauge transformation is a change of orthant order by $W = diag\{w_{1}, w_{2}, \ldots, w_{N}\}$ with $w_{i}\in \{1, -1\}$, $A = (a_{ij})_{N\times N}$ and $\bar{A} = (|a_{ij}|)_{N\times N}$ are the adjacency matrices of the signed and unsigned networks, respectively. In addition, $W$ provides a partition, that is $V_{1} = \{v_{i}|w_{i} = 1 \}$ and $V_{2} = \{v_{i}|w_{i} = -1 \}$.

Lemma 2. ^[45] If $x(t):(a, b)\rightarrow \mathbb{R}^{n}$ is absolutely continuous function satisfying $x(a) = 0$ and $M\in \mathbb{R}^{n\times n}$ is a positive definite matrix, then the following wirtinger's inequality holds:

Lemma 3. ^[46] It is assumed that there exists a positive definite matrix $M\in \mathbb{R}^{n\times n}$ and a vector function $x(t):(a, b)\rightarrow \mathbb{R}^{n}$, the following integrations are well defined, then

Lemma 4. ^[47] For any two real vector functions $y_{1}(t)\in \mathbb{R}^{n}$ and $y_{2}(t)\in \mathbb{R}^{n}$, a positive definite matrix $R\in \mathbb{R}^{n\times n}$ and any matrix $S\in \mathbb{R}^{n\times n}$, then

where $y(t) = \left[ \begin{array}{c} y_{1}(t) \\ y_{2}(t) \\ \end{array} \right]$, $\left[ \begin{array}{cc} R & S^{T} \\ S & R \\ \end{array} \right] > 0$ and $0 < \alpha < 1$.

Lemma 5. ^[48] The following linear matrix inequality

where $S_{11} = S_{11}^{T}$, $S_{12} = S_{21}^{T}$, $S_{22} = S_{22}^{T}$ are some constant matrices with appropriate dimensions, the following matrix inequalities hold:

For reducing the communication burden among the agents, and considering the unreliable channel from control to actuator, the sampled control algorithm is designed as follow:

where $c > 0$ is the coupling strength, $\Xi = diag\{\Xi_{1}, \Xi_{2}, \ldots, \Xi_{m}\}$ with $\Xi_{i}$ being $m$ unrelated random variables, taking on the interval $[0, \theta]$ with $\theta\geq 1$. $K\in \mathbb{R}^{m\times n}$ is the feedback matrix to be designed. $t_{k}h$ $(k = 0, 1, 2, \ldots)$ is the release times, $t_{0}h = 0$, $\{t_{0}, t_{1}, \ldots\}\subset \{0, 1, 2, \ldots\}$, the data will be updated until next event-triggered instant $t = t_{k+1}h$.

Remark 1. Inspired by some related literatures ^[49,50], the random variable $\Xi$ is used to describe the actuator fault. For the case of $\Xi = 0$, it means complete failure of the $i$th actuator. For $\Xi\in(0, 1)$, it means partial failure of the $i$th actuator. For the case of $\Xi = 1$, it means the $i$th actuator is in good working condition. For $\Xi > 1$, it means the data distortion with the measurement of the $i$th actuator.

Assumption 1. Supposed that mathematical expectation of $\Xi_{i}$ $(i = 1, 2, \ldots, m)$ is $\alpha_{i}$, the variance of $\Xi_{i}$ is $\delta_{i}^{2}$, denoted as $E(\Xi_{i}) = \alpha_{i}$ and $D(\Xi_{i}) = \delta_{i}^{2}$, respectively.

Substituting (2.5) into (2.1), one has

Based on the definition of Laplacian matrix, Eq (2.6) can be rewritten as

Considering limited bandwidth of the communication network, to further reduce the data transmission among the agents, the event-triggered communication scheme is proposed for system (2.1), which is utilized to determine whether or not the current sampled data should be transmitted to neighboring agents. Supposed that the latest transmitted data is $x(t_{k}h)$, then for $i = 2, 3, \ldots, N$, the next transmission instant $t_{k+1}h$ can be determined by

where the error $e_{i}(t) = w_{i}x_{i}(t)-w_{1}x_{1}(t)$, $\Phi_{i}^{(1)}$ and $\Phi_{i}^{(2)}$ are some positive definite event-triggered matrices to be designed, $\sigma_{i} > 0$ is event-triggered parameter, $t_{k+1}h-t_{k}h$ denotes the release period which corresponds to the sampling period given by the event-triggered scheme.

Remark 2. Noted that the sampled state $x(t_{k}h)$ satisfying the inequality (2.8) will be sent to the neighbour agents, some of the sampled states that violate (2.8) will not be transmitted. Obviously, the communication burden of the network is reduced, the corresponding transmission energy can also be saved.

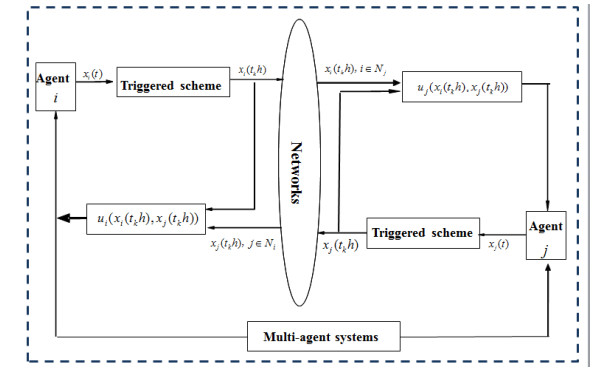
Remark 3. The above event-triggered communication scheme (2.8) includes the following special cases: (i) if $\Phi_{i}^{(1)} = \Phi_{i}^{(2)} = \Phi_{i}$ $(i = 2, 3, \ldots, N)$, the scheme shrinks to a discrete event-triggered transmission scheme. (ii) if $\sigma_{i} = 0$, one has $t_{k+1}h = t_{k}h+h$, then transmission scheme shrinks to a periodic transmission scheme. (iii) if $\Phi_{i}^{(1)} = \Phi_{i}^{(2)} = I_{n}$ $(i = 2, 3, \ldots, N)$, transmission scheme becomes a discrete absolute error-based transmission scheme. Hence the proposed event-triggered communication scheme includes some existing schemes. The framework of the event-triggered communication can be found in Figure 1.

Remark 4. The proposed transmission scheme (2.8) is different from a continuous absolute error-based needed to monitor the continuous measurement, where only the sampled-data is used, the lower bound event interval is the sampling period $h$, which is strictly larger than zero, therefore, Zeno behavior is excluded in our proposed scheme.

Let $\bar{x}_{i}(t) = w_{i}x_{i}(t)$ $(i = 1, 2, \ldots, N)$, here $w_{i} = 1$ $(i\in V_{1})$ and $w_{i} = -1$ $(i\in V_{2})$, it follows from (2.7) that

where $\bar{L} = (\bar{l}_{ij})_{N\times N}$ is the Laplacian matrix of unsigned graph with zero-row-sum, $\bar{l}_{ii} = \sum\limits_{k = 1, k\neq i}|a_{ik}|$, $\bar{l}_{ij} = w_{i}l_{ij}w_{j} = -|a_{ij}|$ $(i\neq j)$.

In views of (2.9) and $e_{i}(t) = \bar{x}_{i}(t)-\bar{x}_{1}(t)$ $(i = 2, 3, \ldots, N)$, one has

Inspired by ^[34,35], the interval $[t_{k}h, t_{k+1}h)$ can be expressed as the union of several subintervals as follow:

Define $\tau(t) = t-(t_{k}h+lh)$, for $t\in[t_{k}h+lh, t_{k}h+lh+h)$, it can be derived that $0\leq\tau(t) < h$, let $\bar{e}_{i}(t_{k}h+lh) = e_{i}(t_{k}h+lh)-e_{i}(t_{k}h)$ $(i = 2, 3, \ldots, N)$, we have

Applying (2.12) into (2.10), one has

Rewrite (2.13) in compact matrix form, we can get

where

Definition 1. For signed networks $g$, H-infinity bipartite consensus can be achieved for coupled linear system (2.1), if for given a weighting positive-definite matrix $S\in \mathbb{R}^{n\times n}$, a performance index $\gamma > 0$ and the initial disagreement vector $e(0)$, its solution satisfies

Definition 2. For given function $V: C_{F_{0}}^{b}([-\tau_{M}, 0], \mathbb{R}^{n})\times S$, its infinitesimal operator $\mathcal{L}$ is defined as

3.   Main result

In this section, H-infinity bipartite leaderless consensus problem is investigated under event-triggered scheme, supposed that the topology is directed signed graph and structurally balance.

Let $\bar{\Xi} = diag\{\alpha_{1}, \alpha_{2}, \ldots, \alpha_{m}\} = \sum\limits_{i = 1}^{m}\alpha_{i}C_{i}$, here $C_{i} = diag\{\underbrace{0, 0, \ldots, 0}_{i-1}, 1, \underbrace{0, \ldots, 0}_{m-i}\}$, then system (2.14) can be formulated as follow:

Combining (2.8) and (2.12), for $t\in[t_{k}h, t_{k+1}h)$, the event-triggered scheme can be rewritten as

From the above analysis, it can be known from (3.2) that the current sampled data $e_{i}(t_{k}h+lh)$ will not be sent, which will be employed in the following consensus analysis.

By using Kronecher product, it can be derived from (3.2) that

where

Theorem 1. Suppose that signed network is directed and structurally balance, for given sampled period $h > 0$, triggered parameters $\sigma_{i} > 0$ $(i = 2, 3, \ldots, N)$, coupled strength $c > 0$, feedback matrix $K\in \mathbb{R}^{n\times n}$, and a disturbance attenuation $\gamma > 0$, H-infinity bipartite consensus can be achieved in system (2.1) under the control algorithm (2.5) and event-triggered scheme (2.8), if there exist some $n\times n$ positive definite matrices $P > 0$, $Q > 0$, $R > 0$, $\Omega > 0$, $\Phi^{(1)} > 0$, $\Phi^{(2)} > 0$, and matrix $U\in \mathbb{R}^{n\times n}$, such that the following matrix inequalities hold:

where

Proof. Construct the following Lyapunov function candidate

where

where $P, Q, R, \Omega\in \mathbb{R}^{n\times n} > 0$.

Next, some necessary explanations are given to show the Lyapunov function $V_{4}(t)$ is valid. By using the Wirtinger's inequality in Lemma 2, one has

It can be easily derived that $V_{4}(t)\geq 0$ from (3.7), thus the Lyapunov function $V_{4}(t)$ is valid.

For convenient description, Eq (3.1) can be rewritten as the following concise form:

where

By using the fact $E\{\Xi-\bar{\Xi}\} = 0$, and infinitesimal operator (2.16) in Definition 2, taking the derivative of $V_{i}(t)$ $(i = 1, 2, 3, 4)$ along the trajectories (3.8), one gets

For any $\tau(t)\in [0, h)$, it follows from Jensen's inequality in Lemma 3 and the reciprocally convex approach in Lemma 4 that

It can be derived from (3.12) that

Recalling (3.8), (3.11) and (3.12), we can obtain

where $C_{j} = diag\{\underbrace{0, 0, \ldots, 0}_{j-1}, 1, \underbrace{0, \ldots, 0}_{m-j}\}$.

Combing Eqs (3.9–3.15), one gets

where

and the other elements can be found in Theorem 1.

By using Schur complement in Lemma 5 to (3.4), we can obtain (3.16), then

Next, integrating both sides of Eq (3.17) from $0$ to $\infty$, one has

where $\gamma = \frac{2}{\lambda_{min}(P)}$, which indicates H-infinity bipartite consensus is achieved by using Definition 1. This completes the proof.

Notice that if $\sigma_{i} = 0$ $(i = 2, 3, \ldots, N)$, then event-triggered scheme reduces to time-triggered scheme, from Theorem 1, we can obtain H-infinity bipartite consensus under sampled-data control.

Corollary 1. Suppose that signed network is directed and structurally balance, for given sampled period $h > 0$, coupled strength $c > 0$, feedback matrix $K\in \mathbb{R}^{n\times n}$, and a disturbance attenuation $\gamma > 0$, H-infinity bipartite consensus can be achieved in system (2.1) under the control algorithm (2.5), if there exist some $n\times n$ positive definite matrices $P > 0$, $Q > 0$, $R > 0$, $\Omega > 0$ and matrix $U\in \mathbb{R}^{n\times n}$, such that the following matrix inequalities hold:

where

Remark 5. When $\sigma_{i}\rightarrow 0^{+}$, it can be concluded that (3.3) can not be satisfied, the data of each sampling time will be transmitted to the neighbor agents, that is, event-triggered scheme reduces to time-triggered scheme, thus bipartite leaderless consensus can be derived based on the sampled control algorithm.

In the following, we will design the reliable protocol to achieve H-infinity bipartite consensus for multi-agent system (2.1) with probabilistic actuator faults.

Theorem 2. Suppose that signed network is directed and structurally balance, for given sampled period $h > 0$, triggered parameters $\sigma_{i} > 0$ $(i = 2, 3, \ldots, N)$, coupled strength $c > 0$, any a positive scalar $\varepsilon > 0$, and a disturbance attenuation $\gamma > 0$, H-infinity bipartite consensus can be achieved in system (2.1) under the control algorithm (2.5) and event-triggered scheme (3.3), if there exist some positive definite matrices $X > 0$, $\hat{Q} > 0$, $\hat{R} > 0$, $\hat{\Omega} > 0$, $\hat{\Phi}^{(1)} = diag\{X\hat{\Phi}_{2}^{(1)}X, X\hat{\Phi}_{3}^{(1)}X, \ldots, X\hat{\Phi}_{N}^{(1)}X\} > 0$, $\hat{\Phi}^{(2)} = diag\{X\hat{\Phi}_{2}^{(2)}X, X\hat{\Phi}_{3}^{(2)}X, \ldots, X\hat{\Phi}_{N}^{(2)}X\} > 0$, and matrix $\hat{U}\in \mathbb{R}^{n\times n}$, $Y\in \mathbb{R}^{m\times n}$, such that the following linear matrix inequalities hold:

where

then the feedback matrix $K = YX^{-1}$.

Proof. Denote $X = P^{-1}$, $\hat{Q} = XQX$, $\hat{R} = XRX$, $\hat{\Omega} = X\Omega X$, $\hat{U} = XUX$, $\hat{\Phi}^{(1)} = diag\{X\hat{\Phi}_{2}^{(1)}X, X\hat{\Phi}_{3}^{(1)}X, \ldots, X\hat{\Phi}_{N}^{(1)}X\}$, $\hat{\Phi}^{(2)} = diag\{X\hat{\Phi}_{2}^{(2)}X, X\hat{\Phi}_{3}^{(2)}X, \ldots, X\hat{\Phi}_{N}^{(2)}X\}$ and $Y = KX$, then pre-multiplying and post-multiplying Eq (3.4) with

Due to the fact

it can be derived from (3.23) that

then

Similar to Eq (3.25), we have

Replace the term $\tilde{R} = diag\{\underbrace{(I_{N-1}\otimes R)^{-1}, (I_{N-1}\otimes R)^{-1}, \ldots, (I_{N-1}\otimes R)^{-1}}_{m}\}$ by the following matrix

Replace the term $\tilde{\Omega} = diag\{\underbrace{(I_{N-1}\otimes \Omega)^{-1}, (I_{N-1}\otimes \Omega)^{-1}, \ldots, (I_{N-1}\otimes \Omega)^{-1}}_{m}\}$ by the following matrix

Combining (3.22–3.28), then Eqs (3.21) and (3.22) can be obtained. This completes the proof.

Corollary 2. Suppose that signed network is directed and structurally balance, for given sampled period $h > 0$, coupled strength $c > 0$, any a positive scalar $\varepsilon > 0$, and a disturbance attenuation $\gamma > 0$, H-infinity bipartite consensus can be achieved in system (2.1) under the control algorithm (2.5), if there exist some positive definite matrices $X > 0$, $\hat{Q} > 0$, $\hat{R} > 0$, $\hat{\Omega} > 0$, and matrix $\hat{U}\in \mathbb{R}^{n\times n}$, $Y\in \mathbb{R}^{m\times n}$, such that the following linear matrix inequalities hold:

where

then the feedback matrix $K = YX^{-1}$.

4.   A numerical example

Consider the following linear multi-agent systems consisting of seven agents

where

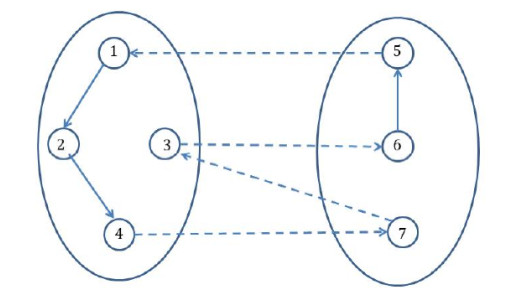
The network topology is structurally balance in Figure 2, which can be divided into two sub-networks $V_{1} = \{1, 2, 3, 4\}$ and $V_{2} = \{5, 6, 7\}$, the agents are cooperative relationship in $V_{1}$ or $V_{2}$, the agents are competitive relationship between $V_{1}$ and $V_{2}$, by using Lemma 1, we can obtain the gauge transformation $W = diag\{1, 1, 1, 1, -1, -1, -1\}$, then we have $w_{1} = 1$ and $\bar{W} = diag\{1, 1, 1, -1, -1, -1\}$.

Case 1: Event-triggered matrices $\Phi^{(1)}\neq \Phi^{(2)}$

Let the coupling strength $c = 1$, the sampling period $h = 0.01$, event-triggered parameter $\sigma_{i} = 0.01$ $(i = 2, 3, \ldots, 7)$, H-infinity performance index $\gamma = 0.001$, the positive scale $\varepsilon = 0.01$, the mathematical expectation $\bar{\Xi} = diag\{0.5, 0.1\}$, and the variance $\delta_{1} = 0.1$, $\delta_{2} = 0.2$, by using Theorem 2, the related matrices can be obtained, which means bipartite leaderless consensus can be achieved, the event-triggered matrices $\Phi_{i}^{(1)}$ and $\Phi_{i}^{(2)}$ $(i = 2, 3, \ldots, 7)$ is given as follows:

then the feedback gain can be obtained

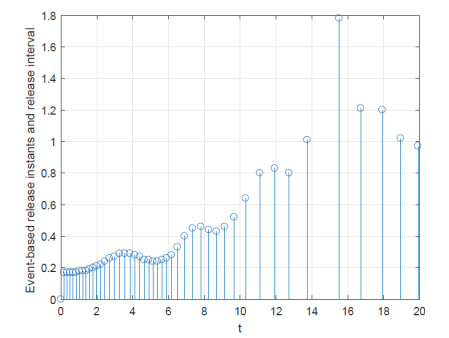
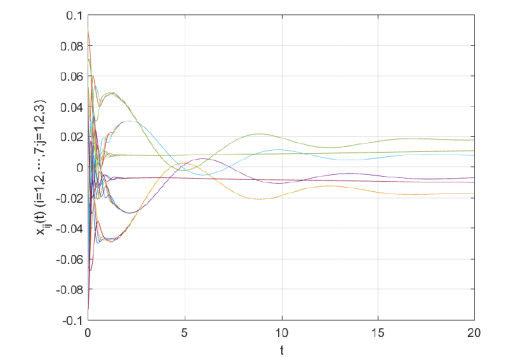
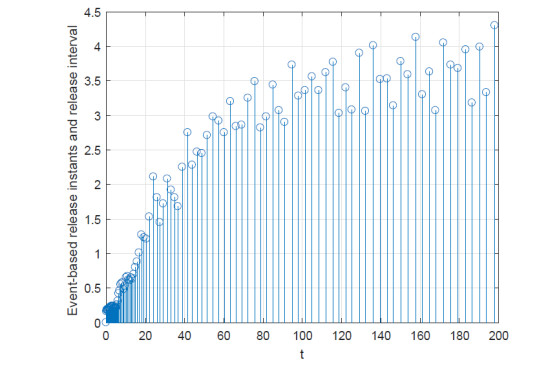
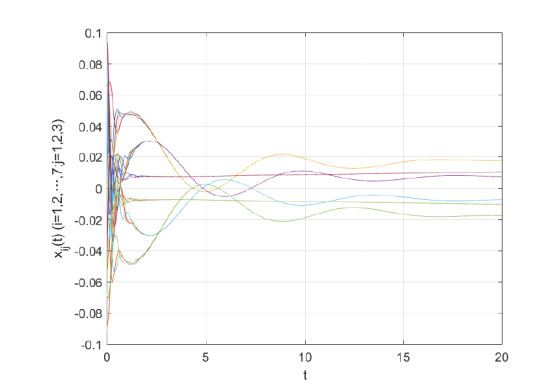
taking $t\in [0, 20)$, the simulation results show that only $38$ sampled data are sent out, which take $1.9\%$ of the sampled signals. It can be computed that the average sampling period is $0.5263$ by our proposed event-triggered scheme. The release instants and release intervals are illustrated in Figure 3. The curve of $x_{ij}(t)$ $(i = 1, 2, \ldots, 7, j = 1, 2, 3)$ are presented in Figure 4, it can be seen H-infinity bipartite consensus is achieved. In order to show the benefits of our proposed triggered scheme than ^[34,35], some comparisons are given in Table 1, it can be seen that our event-triggered scheme can lead to larger sampling period $h$.

Case 2: Event-triggered matrices $\Phi^{(1)} = \Phi^{(2)}$

Suppose that the dynamics of linear multi-agent systems and the related parameters are the same with Case 1. By using Theorem 2, the event-triggered matrix $\Phi_{i}$ $(i = 2, 3, \ldots, 7)$ can be obtained as follows:

then the feedback gain can be obtained

Taking $t\in [0, 20)$, the simulation results show that only $106$ sampled data are sent out, which take $5.3\%$ of the sampled signals. Moreover, it can be computed that our event-triggered scheme can obtain a average sampling period of $0.1887$, the release instants and release intervals are illustrated in Figure 5. The curve of $x_{ij}(t)$ $(i = 1, 2, \ldots, 7;j = 1, 2, 3)$ are presented in Figure 6, which can be seen $H_{\infty}$ bipartite consensus is achieved.

Remark 6. It can be shown from Case 1 that the sampled times are 38 for the event-triggered matrices $\Phi^{(1)}\neq \Phi^{(2)}$, for Case 2, the sampled times are 106 for the event-triggered matrices $\Phi^{(1)} = \Phi^{(2)}$, obviously, our event-triggered scheme can further reduce the sampled data transmission. From the perspective of average sampling period, in Case 1, the average sampling period is 0.4444, and the average sampling period is 0.1887 in Case 2, which can be seen from Figures 3 and 5, that is, our results are less conservative.

5.   Conclusions

In this paper, a novel event-triggered communication scheme has been proposed to study H-infinity bipartite consensus with external disturbance in the signed networks. Compared with some existing event-triggered results, the proposed event-triggered communication scheme has the advantage to achieve a better performance while saving the limited network resources. A more generalized random variable is introduced to describe probabilistic actuator failure. Some H-infinity bipartite consensus criteria can be derived, the feedback matrices and event-triggered matrices can be obtained by solving some linear matrix inequalities. Notice that the above results are based on the given event-triggered parameters, it would be interesting to further investigate adaptive event-triggered communication scheme, where the triggered parameters can be adjusted with respect to the dynamic errors. The related results can also be extended to the cases of nonlinear multi-agent systems and stochastic multi-agent systems and so on.

Conflict of interest

The author declares no conflict of interest in this paper.