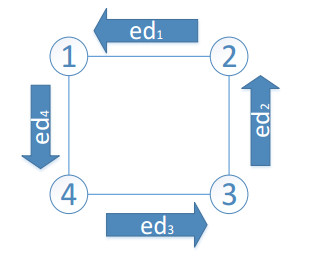
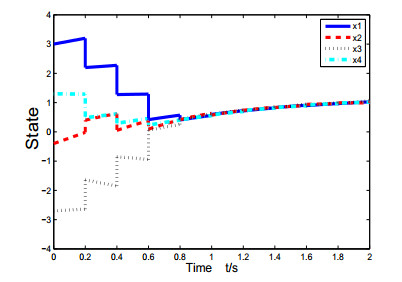
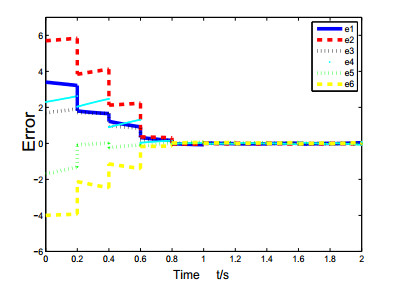
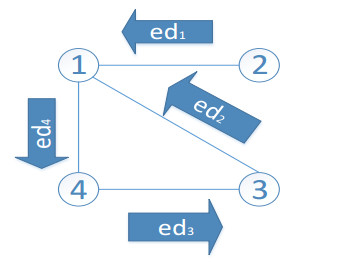
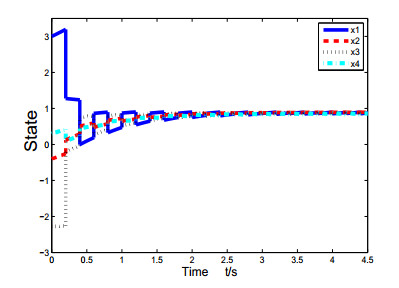
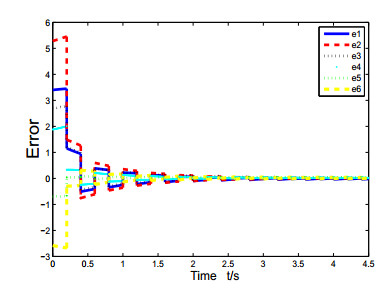
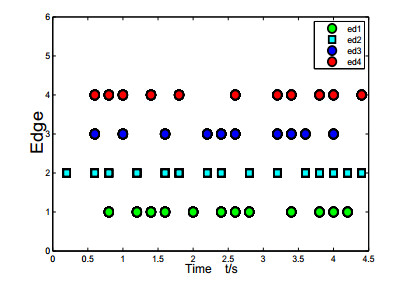
In the paper, some consensus problems of multi-agent system controlled by edge event-triggered strategy and state-constraint impulsive are taken into account. For the state-constraint impulsive protocol, two types of control protocols which contain input saturation and double actuator saturation are put forward. With regard to the edge event-triggered control, we propose the rule of it and let the time of the edge event-triggered be impulsive time to avoid the Zeno-behavior. Then, compared to the control method of others, we can greatly reduce the cost in the process of exchanging information. Next, some sufficient conditions of the system are required to reach consensus. In the end, a few examples are exploited for testing and checking the theoretical analyses.
1.
Introduction
In recent years, the development of science and technology has also driven the vigorous development of deep learning technology, especially the continuous introduction of powerful graphics processing unit (GPU) and central processing unit (CPU) devices. Directly promoting the continuous progress of the field of computer vision [1,2], deep learning has been widely applied in various fields of computer vision, such as image classification [3,4,5], object detection [6,7,8] and text-to-image (T2I) synthesis [9,10,11]. This technology can be applied in fields such as image restoration [12,13], image data amplification [14], image-text matching [15] and style conversion [16,17].
Goodfellow et al. [18] proposed the generalized adversarial network (GAN) in 2014. Once proposed, this method sparked a wave in the field of computer vision and achieved significant results in the field of image synthesis. This method can rely on the unsupervised synthesis of completely new virtual samples. This method has significant applications in multiple fields of computer vision, especially in the field of image data enhancement. For example, the new samples generated via simple image data enhancement methods (rotation, cropping, translation, etc.) are too similar to the original image and cannot generate images that differ significantly from the original image [19,20,21]. By using the GAN method, new samples with significant differences from the original image can be generated. By generating new samples with significant differences and incorporating model training, it can help to improve the performance and generalization ability of the model [22,23,24]. However, due to GAN's overly random strategy, there are shortcomings such as a lack of controllability. The conditional GAN (CGAN) method [25] was proposed to enhance the controllability of the model; it controls the output samples of the model by adding conditional special information features in the generator and discriminator. In subsequent work, researchers combined deep convolutional neural networks (CNNs) with a GAN to further improve the stability performance and image generation ability of the GAN model; they also proposed the deep convolutional GAN [26]. These basic GAN models are important prerequisites for subsequent GAN variants and provide a certain direction for future work.
T2I synthesis, as the name suggests, is a method of generating images through the use of natural language processing (NLP) technology [27], combined with image generation modeling technology. Models that can be used to generate images include the regression analysis model [28,29], variational autoencoder model [30,31] and GAN. The development of NLP technology [32,33] has indirectly promoted the development of T2I technology. In recent years, various NLP models have been continuously introduced, such as GPT-2 [34] and Bert [35,36,37]. Specifically, the model decodes the input from the NLP technology and generates virtual images that are consistent with or similar to the semantic descriptions based on the content depicted by the natural language. One of the important goals of T2I synthesis technology is to ensure that the generated images are as consistent as possible with the input textual information, and a large number of researchers have conducted extensive research on this. In 2016, Reed et al. [38] took the lead in applying conditional GANs for the generation of T2I images and achieved good results. In addition, in order to obtain better generated samples, optimization functions and evaluation indicators for promoting model iteration have been continuously proposed and applied to T2I tasks.
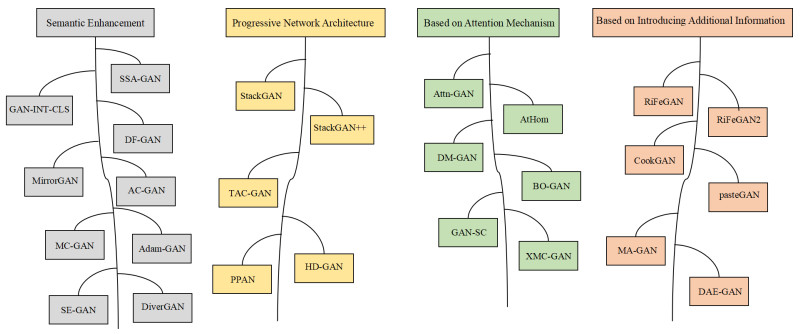
In order to provide a better introduction and summary of T2I generation methods, in this review, we classify the basic T2I methods into four categories. That is, a text-to-image synthesis method based on semantic enhancement, a T2I synthesis method based on progressive networks, a T2I synthesis method based on an attention mechanism and a T2I synthesis method based on additional signal generation. Figure 1 shows some classic and advanced methods from the four major categories of methods, which will be detailed in the following text. Compared to some review articles that only briefly summarize various methods, this article will try to analyze the starting points and advantages of these methods' improvements as much as possible. In addition, this article will try to explain and analyze the shortcomings of each method as much as possible.
GAN with interpretable and controllable latent space (GAN-INT-CLS), as an earlier model applied to T2I, adopts a semantic enhancement strategy. It has achieved certain results. However, the constituent modules in its architecture are relatively simple, so it can only generate some simple images (with low image resolution). However, its approximate network architecture has good reference value, and the approximate architectures of various subsequent methods are similar to it. To make the generated image more complex, the technique is to increase its sample complexity and diversity. As shown in Figure 1, multiple main improvement strategies have been proposed. The method of using semantic enhancement mainly enriches the scene and object information generated by improving or adding modules in the basic framework to enhance the expression of semantic information. For example, the description text can be increased from "a forest" to "a dense green forest" to increase its background complexity. Some strategies that adopt a progressive approach are aimed to increase the number of "generator discriminator" structures in the model. By continuously refining the resolution of the generated image layer by layer, the complexity of the generated image is enhanced. The methods that adopt attention mechanisms mostly focus on utilizing or introducing attention mechanisms so that some key information content in the input description information can be better captured by the model. This generates more diverse image samples. In addition, by introducing additional information content, the amount of information depicted in the text can also be better increased, thereby generating richer samples. There are many modules in the T2I basic architecture model. From the above information, we can find that improving the modules in the model or adding additional useful modules can improve the quality and complexity of the generated images in the model. However, this also increases the complexity of the model and the demand for computing device performance.
This article reviews some classic and recent work in the past, and the remaining parts of this review are arranged as follows. The T2I technology introduced in this article is mostly generated based on basic models such as GAN models and its variants. Therefore, in Section 2, some important basic GAN models for text generated images will be introduced in detail. In Section 3, the principles and characteristics of T2I synthesis methods based on semantic enhancement will be introduced. In Section 4, the principles and characteristics of T2I synthesis methods based on progressive networks will be introduced. Section 5 will provide a detailed explanation of the T2I synthesis method based on an attention mechanism. Section 6 will diacuss the T2I synthesis that introduces additional supervised information generation. In Section 7 of this review, we will summarize some advantages of the T2I model in terms of image generation and look forward to potential directions for improvement in the future. In the final section, a summary of the entire text is provided.
2.
Basic GAN architecture
Most of the T2I models in this review are generated based on a GAN. Therefore, in this section, we will provide a detailed introduction to some basic GANs and their excellent variant models. This serves as a foundation for some T2I models in the following text.
2.1. Basic GAN
The GAN [18] is shown in Figure 2, which mainly consists of a random vector generation module Z, a brand new image generator G and a generated image discriminator D. This framework can generate virtual images from unsupervised learning patterns. The general operation method entails first passing randomly sampled vectors from the Gaussian distribution to the generator to generate false samples. Afterward, the false samples are mixed with the real samples and transmitted to the discriminator, which then makes a one-to-one judgment on the incoming samples. The next step is to determine whether it is a virtual sample or a real sample. This process is essentially a game between the generator and the discriminator. The false samples generated by the generator at the beginning may be easily recognized by the discriminator. However, as the iterative process continues to progress, in the continuous game between the generator and the discriminator, the generator continuously improves and optimizes. The final generated samples can reach the point at which fake samples are confused with real ones, and even discriminators cannot recognize their authenticity. However, in order to identify false images that can be mistaken for real images, discriminators are constantly optimizing themselves. At this point, in the continuous game between the two, the generated images can gradually approach the real samples. In order to realize the purpose of the GAN model, it is necessary to apply its objective function, as shown below.
Among them, x represents the real sample, z represents the random noise vector, Ex represents the expected value of the distribution, and Px represents the real image distribution. GANs, as a very advanced network framework, can generate numerous realistic virtual samples. To a certain extent, it can help researchers to obtain richer image data. Moreover, the network framework is highly efficient in generating samples. However, this method also has some shortcomings. First, the process of generating false samples in this model is relatively random, making it difficult to generate samples in a targeted manner (i.e., lacking controllability). Second, the convergence performance of this method is poor in some cases. In order to improve some of its shortcomings, subsequent work has made some improvements to it.
2.2. CGAN
In the image generation of the original GAN model, the final generated image samples are random, making it difficult to predict the content of the final generated samples. The problem caused by this is also relatively obvious, that is, the model cannot be controlled to generate its expected images, and it lacks controllability. Mirza and Osindero [25] proposed the CGAN method to address this issue replace with a semicolon its general network framework is shown in Figure 3. The main improvement is to add condition y to the generator and discriminator based on the GAN. Specifically, in order to provide certain controllability for the generated image samples of the model, the CGAN adds additional conditional information y to the generator and discriminator. This improves the shortcomings of the original GAN model due to unconditional constraints. One can use this method to guide the image output of the model generator. Conditional informationy can be considered as different types of information content, such as the label category information of images, textual information, additional signals and other modal information. The main expression [25] is as follows.
From the above formula, we can see that its approximate information content is consistent with the objective function of a GAN, with a slight difference being the addition of conditional information y in the generator and discriminator. As shown in Figure 3, additional conditional information y can be added as additional information input to the discriminator and generator. CGANs transforms random unsupervised learning into supervised learning under certain conditions, enabling the model to better generate images. Although the CGAN has significant improvements relative to the GAN, there are also some shortcomings (such as insufficient resolution of generated images). However, this method also opens the door for a certain direction for subsequent work.
2.3. DCGAN
Although GANs have achieved certain results, there are also some obvious shortcomings. For example, the model has low stability during training and a certain probability of generating low-quality samples. In order to improve some of the shortcomings of the GAN model, Radford et al. [26] proposed the DCGAN method. The general network architecture of this method is shown in Figure 4. Compared to the GAN method, the biggest difference in the DCGAN method is that it is a combination of a CNN and GAN. In the generator and discriminator, the original fully connected network is replaced with a CNN to improve the overall performance of the model. Specifically, the DCGAN offers the following improvements.
1) First, there is a removal of the pooling layer from the generator and discriminator. In the generator, replace the convolution module is replaced with the deconvolution module. The CNN architecture in the discriminator is preserved.
2) Second, the batch normalization (BN) layer is applied to generators and discriminators. This improves the overall training iteration speed of the model and enhances the overall stability performance of the model. However, it is worth noting that the BN module is not added to the input layer of the generator and discriminator to prevent the possibility of BN causing oscillations and other issues in the generated model.
3) Afterward, the rectified liner uints (ReLU) function is applied as the activation function in the generator, but in the last layer of the module, tanh is selected as the activation function. The tanh activation function can alleviate the deficiency of gradient disappearance to a certain extent. Moreover, when the activation value is low, matrix vectors can be directly calculated to promote faster model training.
4) Furthermore, LeakyReLU is used as the activation function in the discriminator. Compared to the ReLU activation function, which discards information content, which discards x less than 0, this function can retain feature information where x less than 0. Replacing the activation function with LeakyReLU can improve the problem of gradient sparsity, thereby improving model performance to a certain extent.
5) Finally, the Adam optimizer is used in training, which is easy to use and can make the gradient decrease quickly.
2.4. Cycle-consistent GAN
The cycle-consistent GAN (CycleGAN) [39] is also a model that can generate virtual sample images without the need for supervised signals. This model includes two generators and two discriminators. To achieve strong correlation and consistency between the generated images from two datasets, this method uses cyclic consistency loss and adversarial loss as the loss function during image generation. The general architecture of the model is shown in Figure 5. Unlike most GAN models, the CycleGAN method can be trained without pairing between samples. In the forward loop of a CycleGAN, the first generator of this model can convert images from the original dataset into fake original target objects. The function of the second generator is to generate samples in the target dataset based on the false original images generated by the first generator. During the reverse loop, the second generator of the model first converts the image samples in the target dataset into false original images, which are then converted to generate image samples from the original dataset.
2.5. Progressively growing GAN
The initial GAN model can generate images with lower resolution. However, it is unable to generate high-resolution images, making it difficult to meet the needs of most tasks. The method of generating high-resolution images through the use of progressive methods has been widely studied. Through a progressive approach, it is possible to gradually generate high-resolution images from low-resolution images over multiple stages. The new samples generated in this way are more diverse and of higher quality. Currently, most network models are not suited to directly generate high-resolution images (such as 1024 × 1024 pixel resolution images). Because the image generated in this way is easily recognized by the discriminator as a fake image (which has many flaws), it is difficult to use as a normal image. For this reason, Karras et al. proposed the progressively growing GAN (PGGAN) [40], whose general model architecture is shown in Figure 6. The core idea is to generate images from low-resolution in a step-by-step manner 4 × 4 layers are multiplied layer by layer, and the final image resolution is synthesized to 1024 × 1024. During this process, the outputs of the generator and discriminator are also improved along with the incoming image resolution. At the same time, in order to improve the potential adverse effects of increasing network layers layer by layer on the original network, the PGGAN was designed to incorporate smoothing technology into the model. By integrating the lower level network into the upper layer, not only does it improve the stability of the model, it can also generate high-quality new samples.
2.6. Self-attention GAN
The convolutional blocks contained in CNNs can usually only learn from local or small areas in the image, establishing a small range of connections between them. However, it is difficult to capture the global and contextual information in the image effectively. Most GAN models that utilize CNNs inevitably encounter this problem. To alleviate this problem, Zhang et al. [41] introduced the self-attention mechanism into the GAN model and proposed the self-attention GAN (SAGAN). The general structure of the self-attention module included in this model is shown in Figure 7. It enhanced the model's ability to capture global and contextual information in images through the use of self-attention based contextual information capture. Specifically, the core idea of the SAGAN is to introduce a self-attention mechanism into the generator and discriminator of the model. By enhancing the generator's ability to understand images in this way, we can generate images that are closer to text descriptions. Introducing a self-attention mechanism can help the model to better calculate the global and local weight information of the image. By enabling the model to better capture contextual information, the performance of the model can be improved.
3.
T2I synthesis based on semantic enhancement
In the previous text, we introduced the classic GAN model and some variants of GANs as a foundation. In this section, we will introduce the T2I method based on the general GAN method. In order to improve the quality and diversity of images generated by T2I models, methods based on semantic enhancement have been widely studied. The performance of the model is enhanced by enhancing semantic expression in the text.
3.1. GAN-INT-CLS
GAN-INT-CLS [38] is the first model to incorporate textual descriptions (i.e., text statement-embedding vectors) as supervised conditional signals into GAN methods and generate image samples based on them. This model can also be referred to as a text based DCGAN model, which generates samples with a resolution of 64 × 64 pixels. As shown in Figure 8, the model passes textual description vectors and random noise vectors as inputs to the generator. The generated false samples will be mixed with real image samples and input to the discriminator, along with the vector information depicted in the text. It should be noted that the model includes two discriminators, namely GAN-CLS (GAN controllable latent space) and GAN-INT (GAN with interpretable) discriminators. GAN-INT-CLS, is an earlier model applied for T2I conversion, although its network framework is relatively simple. However, most of the subsequent work shares certain similarities with its general architecture, mostly regarding the improvement and innovation of some of its modules, or the addition of additional modules that can enhance the performance of the model.
1) In the GAN-CLS discriminator, the function of the discriminator is to identify whether the generated image sample matches the input text description. This will result in three matching results: (i) false images, correct textual descriptions; (ii) real images, correct textual descriptions; (iii) real images, incorrect textual descriptions. Obviously, unlike discriminators in mutual games, its goal is to minimize the probability of the second scenario and the other two scenarios as much as possible. For generators, it is necessary to maximize the first scenario in order to generate images that can deceive the discriminator. This allows the model generator to generate extremely realistic image samples. This is also the ideal generator.
2) The GAN-INT discriminator can perform interpolation-based learning. To increase the number of input text vectors, simple linear interpolation can be performed on the input samples. In addition, these additional vector text embeddings do not require additional labels to be obtained. Simply put, for example, there are now three marked text embedding vectors with (A) white butterflies, (B) red bird and (C) green leaves. Then, using linear difference representations (A) and (B), the text vector that can be generated is the (D) red butterfly and (E) white bird. We can find that the semantic mean of (D) and (E) is relatively close to that of (A) and (B). Through this example, it can also be found that randomly interpolating the input text vectors and concatenating them can result in the generation of image content with different styles. The T2I fusion formula is shown below.
Here, t1 and t2 represent text vector embeddings, and β represents a hyperparameters. However, upon careful observation, it can be observed that the continuity of the background in the samples generated via this method seems somewhat unsatisfactory, and there is still room for improvement. To this end, there are various methods to improve this by using different strategies in the future, as this will allow the model to generate more exquisite and realistic image samples.
3.2. Auxiliary classifier GAN
In 2018, Odena et al. [42] proposed improving the semantic perception ability of the model by introducing auxiliary classifiers into its training. This method is called the auxiliary classifier GAN (AC-GAN) method. Simply put, the samples generated by this model not only have separate labels about themselves, they are also assigned a class label. A class label can be a category of an image or a feature that is related to the target object in the image. By introducing class labels into generated images, not only can the generated image samples better reflect the content contained in their text, they also make the generated samples more diverse.
3.3. Multi conditional GAN
In order to better constrain the model, influence the style of the image generated by the model and meet the set conditions, Park et al. [43] proposed the multi conditional GAN method. The conditional encoder included in this method first converts the text description information and other information from the input generator into feature vectors. Afterward, it merges them together and inputs them into the generator. This method enhances the semantic expression ability of the text in this way. The experimental results indicate that this method has achieved good performance.
3.4. MirrorGAN
On the basis of CycleGAN, Qiao et al. [44] proposed the MirrorGAN method in 2019. In order to generate images with high consistency with the text and improve the semantic information of the text, global and local attention machines were introduced. This method can not only complete T2I tasks, but it can also perform T2I conversion. That means to use text to describe the generated image and regenerate text information to obtain better gradient information and improve the overall performance of the T2I model. The general framework of the MirrorGAN method is shown in Figure 9. This model is mainly composed of three modules, namely the semantic text embedding module (STEM), global local collaborative attention module (GLAM) and semantic text regeneration and alignment module (STREAM). The function of the STEM is to extract semantic information from the input text description vector and convert this into a semantic embedding vector input generator, where the network used for semantic information extraction is a recurrent neural network (RNN). Meanwhile, the image generator of this model adopts a multi-level cascading structure. The GLAM is mainly composed of global attention and local attention modules. Global attention mainly focuses on obtaining and capturing the global semantic information of images from a global perspective. Local attention, on the other hand, focuses on capturing the local feature information of the image, with a bias towards obtaining feature information about some local details in the image (such as local texture features, color features, and shape features). This module can help the model to coordinate, interact, and share information on the overall and local features, thereby establishing connections between different parts. The STREAM is a semantic regeneration and alignment module, its function is to realign the semantic content of the input model text information, thereby achieving the conversion of images to semantic text. Through this model, the generated images can be continuously adjusted by the model so that the final generated image samples are more and more in line with the initial input text description. Overall, the MirrorGAN achieved better performance in the final model by obtaining better gradient information and other means. Especially on the CUB dataset, the IS index reached 26.47, which is superior to various advanced methods during the same period. However, this model also has issues such as a complex structure, which leads to significant computational resource consumption and time expenditure. In addition, this method still has room for improvement in areas such as image diversity and some loca details.
3.5. Semantics enhanced GAN
In order to enhance the model's ability to obtain semantic information, Tan et al. [45] proposed the semantics enhanced GAN (SE-GAN). The general framework is shown in Figure 10. The main improvement of this model is the addition of the semantic consistency module (SCM) and attention competition module (ACM) to the image. Specifically, the SCM was designed to first be trained together with the network model. Afterward, Siamese networks and various semantic distance measurement methods were added to the network model to improve the coherence of the generated model. The ACM module can adaptively distinguish the importance of vocabulary vectors in the input text. By competing with each other, the model selectively selects the key vocabulary that it considers, and it synthesizes the final image. This makes the final generated image samples as accurate as possible. The experimental results and displayed images indicate that this method has strong performance and can generate more realistic image samples.
3.6. Deep fusion GAN
In most stacked T2I models, the image is converted from low pixels to high pixels. The transformation between different scales can cause entanglement interference between generators, which inevitably weakens the semantic consistency between "the text and image" to some extent. In order to improve or alleviate this deficiency, Tao et al. [46] proposed the deep fusion GAN (DF-GAN) model. The genaral network architecture is shown in Figure 11. To improve the entanglement problem that may arise when converting images of different scales in a stacked model, this model was designed to only use the primary backbone network to generate the final high-resolution image. In addition, in order to improve the acquisition of image and text semantic consistency information in the model without introducing additional networks. The authors proposed a target-aware discriminator (TAD) module for target perception discriminators. By introducing a target perception module into the discriminator, they enabled better supervision of the consistency between the final generated sample and the semantic description of the input. Finally, the DF-GAN included a deep text image fusion block (DFBlock) to achieve more effective fusion between different modes of the model (note: cross-mode refers to the fusion between different types of data, such as text and images). Multiple affine transformation components have been implemented in the DFBlock, which can help the model to better align text descriptions with images. This allows the model to generate better image samples.
3.7. Semantic-spatially aware GAN
Most T2I models tend to focus more on the encoding and decoding of text embedding vectors during the image generation process. Most people overlook the importance of matching semantic and spatial information between text vectors and generated images. Liao et al. [47] proposed the semantic-spatially aware GAN (SSA-GAN) method, which has the overall architecture shown in Figure 12. The core module in this method is the semantic spatially aware convolutional network (SSACN) module. This module predicts the mask mapping sketch and determines the addition of text information vectors in each region of the image by calculating the weights of each part. There is a semantic condition BN component in the SSACN module. This component can help the model to generate more diverse images. Simply put, this model can provide feedback and the synthesis of the semantic information obtained in various pixels of the generated image. The experimental results on some datasets indicate that this method has highly competitive performance, surpassing multiple methods. In addition, the pixels of the image samples generated via this method are relatively delicate. This serves to give it a better appearance.
3.8. Adam-GAN
GAN models often face shortcomings such as pattern collapse and mismatch between generated images and the semantic information depicted. In order to obtain better semantic information, the Adam-GAN [48] was constructed to include an attribute encoder. It encodes the local and global information of an image into feature vectors. The attribute encoder can better capture the semantic information in images and text, thereby containing more semantic information in the final samples generated by the model. In addition, the Adam GAN also includes a memory network structure. The model will select appropriate memory blocks in the network based on different tasks to guide the model in generating images. Through guidance, it is possible to promote the generation of new samples that match the text description as much as possible. This improves the final performance of the model.
3.9. DiverGAN
The DiverGAN [49] method is a method based on the single-stage generation of image samples. In order to enhance the model's ability to obtain important semantic information in text descriptions, two attention modules are utilized to capture important lexical information in the text. The channel attention module and pixel attention module can allocate more weight coefficients to important vocabulary in the text, allowing the model to give it more attention when generating images. Second, in order to make the training process of the model more stable, the model adopts conditional adaptive instance-layer normalization. The image samples generated via this method can be more consistent with their text description. This causes the final sample to be closer to the text description.
4.
T2I synthesis based on progressive network structure
The image resolution generated by common methods is generally low, making it difficult to generate high-resolution images. However, the application of a progressive network structure can yield low-resolution images. Afterward, the image resolution is gradually increased from low to high. While ensuring sufficient resolution, high-quality images can also be generated.
4.1. StackGAN
Although the GAN-INT-CLS has achieved good results, its generated image samples have a low-resolution of only 64 × 64 pixels. The image samples generated via other methods are generally 128 × 128 pixels, difficult to realize. For this reason, Zhang et al. [50] proposed a novel T2I generation method StackGAN, whose network framework is shown in Figure 13. This method generates image samples by introducing a stack, which contains two GAN models. It also generates images over two stages. In the first stage, this method generates a simple image with semantics that basically matches the description through the input text description vector, and it has a low-resolution of 64 × 64 pixels. In the second stage, the model utilizes the images from the first stage. And using the input text vector as guidance, it generates new samples with more detailed and realistic backgrounds. The resolution of the generated image samples can reach 256 × 256 pixels. Moreover, the images generated in the second stage can compensate for some shortcomings in the images generated in the first stage. In the two different stages of the GAN model training, different training methods are used. In the first stage, in order to obtain better discriminators and generators, it is necessary to minimize the differences between the generated brand new samples and the real samples. In the second stage, in order to improve the overall performance of the model as much as possible and generate high-quality samples, an additional loss function was introduced to evaluate the loss value during the GAN iterative process. This method has achieved good results on multiple indicators on the public dataset CUB and Oxford 102. However, this method also has some shortcomings. First, the StackGAN can generate samples with higher resolution. However, this is due to the relatively simple network model used for image generation and the low number of network layers used for generation. This may lead to issues such as blurring when generating complex images. Second, due to the use of two generators in the generation of images in the StackGAN, the generation time (i.e., computational efficiency) will be increased relative to the first stage's method. Therefore, more efficient network structures can also be used for image generation in subsequent research.
4.2. StackGAN++
On the basis of the StackGAN (also known as StackGAN-v1), Zhang's team [51] proposed the StackGAN++ (also known as StackGAN-v2). Compared to the StackGAN, the main advantages of the StackGAN++ are as follows. 1) First, although multi-stage gradual improvement of image resolution is still used, it is no longer like the StackGAN where the two stages are trained separately. 2) Second, the final generated image is generated in four stages. In order to keep the color and other feature information of images at different resolutions as consistent as possible, a new regularization method has been added to the model. 3) In cases in which the performance is superior to most methods, this model can not only generate images for conditional T2I tasks, it can also be used to achieve unsupervised virtual image generation. The general network framework of the StackGAN++ is shown in Figure 14. In the figure, it is evident that the model generates the final image in four stages. The first stage generates images with a resolution of 4 × 4 pixels. Winning in the second stage generates a resolution of 64 × 64 pixels. Afterward, images with resolutions of 128 × 128 pixels and 256 × 256 pixels were generated. However, the StackGAN++ also has some shortcomings. Moreover, the generation of multi-stage resolution images inevitably increases training time and computational resources. In addition, manual adjustments need to be made to various hyperparameters (i.e., generator, color consistency, etc.) to achieve better model performance.
4.3. Text conditioned AC-GAN
Based on the partial ideas of the AC-GAN and GAN-INT-CLS, the text conditioned AC-GAN (TAC-GAN) [52] was proposed by Dash et al. This method can not only generate the image content depicted in the depicted text, it can also satisfy the constraints on the target object by the image. Specifically, the model utilizes the generated images by importing spatial transformers and matrix masks. It can efficiently and accurately generate feature information such as the positions and shapes of the objects depicted in the text. This method can also enhance the controllability in image generation. Similar to many models, this model also includes two generators and two discriminators. The final image generation process of the TAC-GAN model is divided into two steps. In the first step, the random noise vector and text description are passed to the first generator to generate a relatively blurry image. In the second step, random noise vectors, text description information, and the blurred image generated in the first step will be re input. The final result is a clearer image with a resolution of 256 × 256 pixels, which is better than the 128 × 128 pixels of the AC-GAN. The function of the discriminator is to determine whether two images (initial blurred image and final clear image) are real images and calculate their loss values. The loss values of this model include the loss of textual information and the loss of image content information, respectively. This method has exhibited strong performance on some datasets. However, due to its complex training process, the difficulty and complexity of the model training process are also high. There may also be situations in which unreasonable images are generated.
4.4. Hierarchical-nested GAN
Zhang et al. proposed the hierarchical-nested GAN (HD-GAN) method [53], which is a progressive GAN (Figure 15). Its architecture is nested layer by layer. The generator and discriminator of this model optimize and evaluate the model according to images of different scales generated at each layer. By improving the resolution of the generated samples at multiple levels, the model can fully learn the information content in images of different resolutions. In addition, the HD-GAN method has better generalization performance and exhibits strong performance on tasks across different datasets.
4.5. Perceptual pyramid adversarial network
Gao et al. [54] proposed a perceptual pyramid adversarial network (PPAN) model for GANs based on perceptual pyramid modules. This module is a visual perception module. In order to better evaluate the generated and final synthesized images at each stage, the model evaluates the feature vector representations contained in the images at different scales. To determine the quality of the image synthesized by the text, the model continuously optimizes the balance between the generator and discriminator, improving the quality and diversity of the generated images. Finally, the final performance is enhanced through the adversarial training of multi-scale pyramid networks.
5.
T2I synthesis based on attention mechanism
How to more accurately obtain important information in textual descriptions determines the style and quality of image samples generated by the model. In order to obtain a more accurate representation of vocabulary in text, attention mechanisms have been widely studied. The attention mechanism can obtain the key areal information of input text and capture important contextual information in text and images. In this section, we will introduce some of its classic and advanced methods.
5.1. AttnGAN
The method adopted by the AttnGAN [55] utilizes fine-grained text information descriptions to generate images, which is essentially a GAN that utilizes attention. The model architecture is shown in Figure 16. This model mainly consists of two modules, one of which is the attention generation network that utilizes attention, and the other is the deep attention multimodal similarity model (DAMSM). The module is particularly important in the AttnGAN model. To understand how this module works, it is necessary to first understand its composition, which involves an "encoder decoder" structure. The input to the encoder is a feature vector depicted by the text. Then, the decoder will draw feature vectors of the input text and randomly generate noise vectors, which leads to the generation of different subregions accordingly. Finally, in order to allow the final generated image to more accurately present the details and contextual information in the text description, each decoding layer in the decoder is deployed with an attention module, which is used to explore the text description words with the highest correlation with each subregion. Then, it fuses the feature vectors related to words and fast region feature vectors of subgraphs. The DAMSM module is mainly used to calculate the distance between the input text description and the generated sample (i.e., where, similarity, if the distance is closer, there is higher similarity between the two). It mainly includes a bidirectional long short-term memory (LSTM) network and an Inception-v3 network. LSTM is used to obtain the feature information of the text, while Inception-v3 is used to obtain the feature information of the generated images. Finally, the distance function (using cosine similarity) is used to calculate the distance between the generated image and the input text. Through this strategy, the model can continuously enhance the semantic correlation between the generated images and input text, thereby improving the performance of the model. An experiment has shown that this method can significantly improve the performance of the benchmark method, especially on the COCO [56] dataset, where the model's IS [57] reached 25.89. Compared to methods such as the StackGAN and GAN-INT-CLS, the improvement is very significant. The AttnGAN method has low complexity and a low parameter count, but it can generate high-quality new sample images. However, this method has some shortcomings. When generating images, it may cause consistency bias and other issues, as it is a local-to-global generative scheme.
5.2. Dynamic memory GAN
In order to better obtain long dependency information from the text, the dynamic memory GAN (DM-GAN) [58] was developed. The architecture of the DM-GAN is shown in Figure 17, and its general structure is similar to that of most T2I models. A slight difference is that the generator and discriminator of the DM GAN both have dynamic memory mechanisms to generate better images by more precisely obtaining textual information. In addition, the model utilizes attention mechanisms in the generator to better encode the extracted vectors from the text descriptions. Finally, the vector is input into the RNN to enhance the model's ability to obtain important information from the text, as well as to improve the consistency between the final generated samples and the text description information. The dynamic memory mechanism can help the model to dynamically select the vocabulary information associated with the final sample, improving the quality of the generated samples. In addition, this algorithm can prevent direct connection of the samples and memory, but operate in an adaptive manner through the use of response gates.
5.3. Cross-modal contrast GAN
In order to make the content depicted in the text as consistent as possible with the generated image samples, Zhang et al. [59] added an attention mechanism to the generator and proposed the cross-modal contrast GAN (XMC-GAN) method. The general framework is shown in Figure 18. The images generated by typical GAN models may have shortcomings such as low image quality and mismatched new samples of text semantic information. Generators that utilize attention mechanisms can help them to better obtain information about the text. This is realized by matching the text description content with the key areas of the generated image one by one, followed by making the generated image as consistent as possible with the text description information. In short, the model improves its understanding of text description information by introducing attention, which improves the quality of sample generation and enhances the diversity of the images.
5.4. AtHom
Due to the inevitable issue of semantic information conversion bias between cross-modal models, Shi et al. [60] used two attention modules to extract important information from text description content, as well as an image attention module to improve the quality and robustness of image synthesis. In the AtHom model, homomorphic training is used for training. This is realized by adjusting the structure of the output data to be the same as that of the original data by changing the form of the input data. The two attention modules have respectively improved the ability to extract important vocabulary from input text and the ability to perceive important areas of the image. Through these strategies, the model performance has been improved, which thus improved the quality of generated samples. Experiments on multiple datasets have shown that this method outperforms most methods.
5.5. Background and object GAN
Chen et al. [61] utilized the Transformer self attention mechanism to contribute to the input of text vectors, which allowed them to more effectively obtain the contextual information of text description statements. Specifically, the text description information is passed to the Transformer module to obtain the important contextual information from the textual information and obtain important feature information such as background descriptions. Then, through techniques such as knowledge transfer, the object information related to the text is transferred to the new samples generated by the generator. Overall, some existing T2I methods have lacked attention to background content, resulting in the generated samples not being realistic enough. The background and object GAN method can generate images with realistic backgrounds ao as to reach the point at which what is fake is confused with what is real. In addition, in order to improve the performance of knowledge transfer in image sample generation, a normalization method called text-attached layout aware feature normalization has been incorporated into this model.
5.6. GAN based on semantic consistency
Unlike the strategies of most methods, the GAN based on semantic consistency (GAN-SC) [62] method first converts text description information into visual feature representation information. Afterward, guidance is provided on the generation of images. In short, the model first uses a module with an attention mechanism to convert key vocabulary in the input text description content into visual feature vectors. Vocabulary filtered through the attention mechanisms can contain important semantic information in the text. Afterwards, the feature information is passed to the generator to generate image samples. This model can retain important details and key information in the text through the attention mechanism, as well as give them greater weight. To generate image samples that are more in line with the text description. Experiments on multiple datasets have shown that this method has strong performance and can generate high-quality image samples.
6.
T2I synthesis based on introducing additional information
In addition to the above-mentioned methods, methods that introduce additional information into the model have also been proposed to improve the performance of the model. In this section, we will introduce some methods of incorporating additional supervisory information into the model.
6.1. PasteGAN
In addition to introducing auxiliary text statement information to assist the model in generating images, Li et al. [63] proposed introducing scene image information as auxiliary information and developed the PasteGAN method, whose general structure is shown in Figure 19. This method combines the advantages of CNN and Transformer methods, and it can capture important content in text description information. In addition, the model can integrate text description information and auxiliary information in scene images during the generator's image generation stage, train them and then it to a special space for representation. The model can adjust the optimization of model parameters by obtaining similarity scores so that the final generated samples can match the textual information and scene images. This strategy can allow the model to generate more diverse images.
6.2. CookGAN
Zhu and Ngo [64] proposed the CookGAN to improve the performance of T2I models; it incorporates causal chains into the model and trains them together with text description vector information. Generally speaking, recipes can provide guidance on the cooking of dishes at a textual level. In other words, the recipe guides many steps in the cooking process of a meal. Taking this as an inspiration, the CookGAN model not only focuses on the results of image generation, but it also focuses on some causal relationships in the process of generating various pixels in the image. Through step-by-step derivation and the introduction of additional causal information, the model can generate higher quality image samples.
6.3. Rich feature GAN
In order to further improve the performance of the model, Cheng et al. [65] proposed the rich feature GAN (RiFeGAN) method in 2020; its general network architecture is shown in Figure 20. Unlike other methods, this method utilizes a relatively new method to assist the model in generating samples. This method is essentially a method of generating adversarial networks based on conditions. However, the generator and discriminator of this method introduce relatively rich text feature information to help the model acquire a sufficient amount of information and important features in the text. Specifically, the RiFeGAN method first converts the input text description information into image feature vectors. Next, it converts all of the textual information into a textual knowledge base. When using textual information to generate images, the model introduces the text content with the highest similarity to the generated image as auxiliary text in the text knowledge base. Finally, it selects a module with an attention mechanism to participate in the generation of mixed images. By introducing additional information to participate in the generation of new samples, it will help to generate more realistic and informative image samples, which improves model performance.
6.4. RiFeGAN2
On the basis of the RiFeGAN, Cheng et al. [66] proposed the RiFeGAN2. Simply put, RiFeGAN2 has made improvements in the following three areas: the following three areas: 1) enhancement of feature mapping ability, 2) the introduction of rich feature generation and 3) constrained prior knowledge and improved training strategies. In order to improve the performance of the model and its generalization ability, prior knowledge with constraints has been introduced into the model. Simply put, to achieve this goal, prior knowledge was first introduced to assist the model in generating the final image samples. This prior knowledge can be guidance information for image labels or text content. This auxiliary information can help the model better relate text content and information between image samples more effectively.
6.5. Multi-sense auxiliary GAN
In order to obtain more accurate semantic text information, Yang et al. [67] proposed the multi-sense auxiliary GAN (MA-GAN). The general architecture is shown in Figure 21. This method synthesizes important information from multiple sentences and introduces it as auxiliary information into the training process of the model. By combining important information content from multiple sentences, the model can more thoroughly and comprehensively grasp the important information in text-type sentences. The attention mechanism in this network can more accurately obtain important semantic information. The samples generated via this method can more accurately generate images containing textual information content. Compared with various methods of the same period, this method generates higher quality images. At the same time, the performance of this method in terms of fine-grained classification also exceeds that of multiple methods.
6.6. Dynamic aspect-aware
In order to generate more accurate images and improve the performance of the model, Ruan et al. [68] proposed the dynamic aspect-aware (DAE-GAN) method, whose model architecture is shown in Figure 22. This method mainly enhances the model by introducing additional SMS information and using random fields. Specifically, this method first models the additional short sleeve information and adds it as input to the generator mapping space. The immediately formed text description vector about the image will contain input text description information and additional text message input; this is used to generate the image accordingly. Next, in order to better match the generated images with the information depicted in the text, the model can be optimized by using conditional random fields to enhance its performance. As a supplement, we provide an overview of the advantages and disadvantages of other T2I methods in Table 1.
7.
Dataset and evaluation indicators for T2I synthesis
In the previous section, we introduced four major categories of T2I models based on GAN methods. In the following section, we will provide a detailed introduction to the dataset and evaluation indicators used for performance verification and exploration of the T2I model.
7.1. Related datasets
In this section, we will provide a detailed introduction to the datasets commonly used in T2I tasks. Finally, the advantages and disadvantages of these datasets will be explained, as well as prospects for future datasets that may continue to be launched.
1) Oxford 102 [82]. The Oxford 102 dataset is a flower dataset released by researchers at the University of Oxford in 2008. This dataset contains a total of 102 categories of flowers, with varying numbers and sizes of images in each category. Among them, the validation set and test set each contain 1030 images (a total of 2060 images), while the training set contains 6129 images. The complete dataset contains 8189 image samples.
2) CUB [83]. The full name of the CUB dataset is CUB-200-2011, which is a bird dataset released by the California Institute of Technology in 2011. The total number of bird categories included in this dataset is 200. The total number of images in this dataset is 11, 788, of which 5994 are used for training and 5794 are used for testing. It is worth noting that the images in this dataset not only have category labels, but also boundary information, 15 part locations and 312 binary attributes for each image. Therefore, in the performance verification of most T2I models, this dataset is mostly used.
3) COCO [54]. The COCO dataset is a dataset sponsored by Microsoft in 2014. This dataset has a large scale and is widely used for tasks such as object detection and image segmentation. This dataset comes from some complex daily scenarios. The image has 91 categories, over 300, 000 images and 2.5 million target annotations.
4) SVHN [84]. The SVHN dataset was collected by Google Street View vehicles, with an image pixel size of 32 × 32 pixels. The number of images in the training set is 73, 257, while the number of images in the test set is 26, 032.
5) CIFAR-10 [85]. The CIFAR-10 dataset contains 10 categories of images, with a total of 60, 000 images. There are 50, 000 images in the training set and 10, 000 images in the test set. The image resolution in this dataset is 32 × 32 pixels.
6) CelebA-HQ [86]. CelebA-HQ is a large facial image dataset that contains 30, 000 images. This dataset, as a high-resolution image, can be applied for tasks such as facial detection and recognition.
In Figure 23, we present image samples from some datasets (Oxford 102 and CUB datasets).
In addition to the several datasets mentioned above, there are also datasets such as MNIST [87] and CIFAR-100 that can be used for T2I tasks. These datasets provide rich annotation information and a large number of target annotations. At the same time, they each also cover a large number of actual scenes and objects containing multiple categories and allow researchers to better evaluate the performance of the trained model. However, most datasets also have some shortcomings. First, these datasets tend not to contain enough scenes or categories of objects. Second, these datasets exhibit imbalances among certain categories and scenarios. Finally, with the increasing complexity of T2I models, the annotation information in traditional datasets is no longer sufficient to meet the training and evaluation needs of these complex tasks.
7.2. Related evaluation indicators
In this section, we will provide a detailed introduction to the evaluation indicators for the T2I task, which include the inception score (IS) [57], R-precision [55], the frechet inception distance (FID) [88], scene inception distance (SceneFID) [89], visual-semantic (VS) similarity [51], structural similarity index measurement (SSIM) [90], etc.
1) IS: First, calculate the average value of object confidence and diversity in the generated image of the model, and then evaluate the calculated values as indicators. Simply put, this section mainly relies on the pre trained Inception-V3 network model, which is used to calculate the kullback-leibler (KL) divergence between the conditional distribution and the edge distribution. The IS can be represented by using the following formula:
Among them, p(y|x) is the conditional distribution label of the pre trained model, and y is the output of Inception v3.
2) FID: The FID indicator is an indicator used to evaluate the quality and distribution differences between the images generated by the model and the real images. Specifically, this indicator calculates the similarity between the Frechet cumulative distribution function generated by the model and the real images. Similar to the IS metric, the FID also uses pre trained Inception-v3 networks as feature extraction networks. The shorter the value of the FID, the smaller the distance between the real image and the generated image, which also means that the model performance is better. The formula [88] is as follows:
Among them, Tr represents the trace of the matrix, μ denotes the mean, ∑r and ∑g represent covariance, r represents real images and g represents composite images.
3) SceneFID: SceneFID is an extended indicator of the FID, and compared to the FID, SceneFID is more comprehensive. This indicator not only takes into account the distribution of the objects in the newly generated samples, it also fully considers the structural content in the generated images.
4) VS: VS similarity is an indicator used to evaluate the similarity between generated images and depicted text. First, one should use appropriate models to generate feature vectors for the generated images and text description vectors, and then calculate the cosine similarity between them. The higher the VS value, the higher its similarity.
5) SSIM: SSIM is an indicator used in the T2I model to calculate the structural similarity between newly generated samples and actual image samples. The specific evaluation involves local structures such as texture, contrast and brightness. Its value ranges from 0 to 1, and the closer it is to 1, the higher its structural similarity. The SSIM can be represented by using the following formula:
Among them, l(x,y)α, c(x,y)β and s(x,y)γ represent the brightness factor, contrast factor, and structure factor.
6) R-Precision: R-Precision is an indicator used to evaluate the quality of the images generated by T2I models. Specifically, this indicator will first obtain the corresponding text description from the image. Subsequently, this metric calculates the cosine distance between the vector of the image and 100 candidate statements. Assuming that r results are in the first R obtained text, the R-Precision is r/R. Generally speaking, the higher the R-Precision value, the higher the matching between the sample generated by the generator and the text description.
In addition to the above indicators, there are also evaluation indicators such as the LPIPS metric [91], HE [92], SOA [93], CIDEr [94], etc.
In addition, in Table 2, we present various performance results for of classic and advanced T2I methods on COCO and CUB datasets. This enables a clearer understanding of the performance gaps between various methods.
8.
Current achievements and prospects for the future
In summary, up to now, the T2I generation technology based on GAN technology has achieved good results. We mainly reflect on the following aspects.
1) Diverse image generation. Most T2I models based on a CGAN can flexibly generate various images according to the different input condition vectors. Users and researchers can generate new samples that meet their needs by adjusting the semantic information content according to their own needs.
2) High quality image generation. Nowadays, T2I models can generate high-quality image samples. By providing text description information, the model can generate realistic image samples of backgrounds, objects, and target objects based on the information content. Users can fully indulge their imagination.
3) Applications in numerous fields. In many fields, there are also applications of T2I models. For example, on tasks lacking training data, the T2I model can be used to depict and generate the desired images based on the textual information that it receives. In addition, this method can also allow people to indulge their imagination in fields such as image editing and artistic creation.
In short, the T2I model based on the GAN method has indeed achieved significant results. However, there is still room for progress and many areas need to be optimized. Looking towards the future, we hereby summarize the outlook.
1) More accurate and detailed image generation control is needed. In order to achieve finer and more complex image generation, modules that can obtain more precise semantic and contextual information can be introduced.
2) More lightweight generative models are necessary. Currently, T2I models with high performance are mostly based on complex model architectures and significant computational resource consumption. Therefore, it is difficult to deploy effectively in practical application scenarios. In subsequent work, we can explore how to obtain a more lightweight model when the model performance approaches the desired model or slightly weakens (within an acceptable range). This also helps the T2I model to be deployed and implemented in practice.
3) More cross-modal interactions are necessary. At present, most of the methods based on GANs are T2I models, which convert textual data into image data. Other methods for generating images by using other modalities are relatively rare. In future work, we can explore embedding other modalities (such as voice and video data) into the model to enhance the diversity of image generation modeling methods.
4) In order to make the T2I model generate images with more complex backgrounds, the network architecture or modules in most methods have become increasingly complex. This also makes the model increasingly dependent on the performance and computational power of computing devices. In future work, we hope to explore T2I models that can satisfy the requirements of complex image generation on devices with low computational power.
5) In other fields, researchers have used fuzzy logic to process images [100]. Alternatively, fuzzy logic algorithms based on entropy calculation can be used to improve the quality of generated images [101], although these algorithms are applied to grayscale images. However, in future work, it may be extended to the T2I field to expand the way that images are generated.
6) More diverse model training methods are necessary. At present, when generating new samples in the T2I model, it is inevitable for the user to encounter certain issues such as information loss or for the generated samples to not match the semantic description of the text during the relevant transformation process. In future work, some methods from other fields may be introduced, e.g., introducing reinforcement learning methods to enhance the model's ability to make better decisions based on the current environment in different situations. In addition, it is possible to apply reinforcement processing to input text information. This will reduce issues such as text information loss by enabling more accurate text segmentation and other operations on textual information.
9.
Conclusions
The development of deep learning technology has also driven the development of NLP and GANs. In this review, we have provided a detailed review of classic GAN models and T2I synthesis techniques based on GAN methods. We have covered the introduction of GANs, to the addition of conditions to generate CGAN models with certain control over images, as well as the use of CNNs for DCGAN methods. T2I synthesis technology mainly utilizes cross-modal techniques to combine text data with image data. Thus, rich and colorful image samples can be directly generated through text description information. Additionally, this review provides a detailed introduction and review of some classic T2I methods, categorizing most of them into four main categories. These methods include GAN-INT-CLS methods based on semantic enhancement, as well as StackGAN and StackGAN++ methods based on a progressive network architecture. The T2I methods based on an attention mechanism include the AttnGAN method. The methods based on introducing additional signals include the RiFeGAN method. In addition, we also have provided a detailed introduction to the datasets commonly used in the training and validation of T2I models, such as COCO, CUB, Oxford 102, etc as well as evaluation indicators that are commonly used in model performance evaluation (such as the IS and FID). Finally, we summarized the advantages and shortcomings of the T2I method. This review can provide some reference for researchers and some readers interested in this field regarding the application of GAN models in the T2I field.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research was funded by the Natural Science Foundation of Fujian Province (2023J01348) and Fujian University of Engineering Science and Technology Project (GY-Z220205).
Conflict of interest
The authors declare there is no conflicts of interest.









 DownLoad:
DownLoad: