Figure 1.
Symptoms of PD [17].
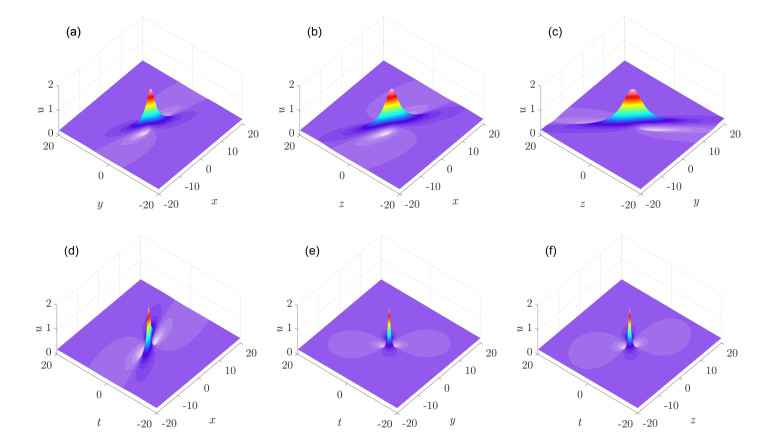
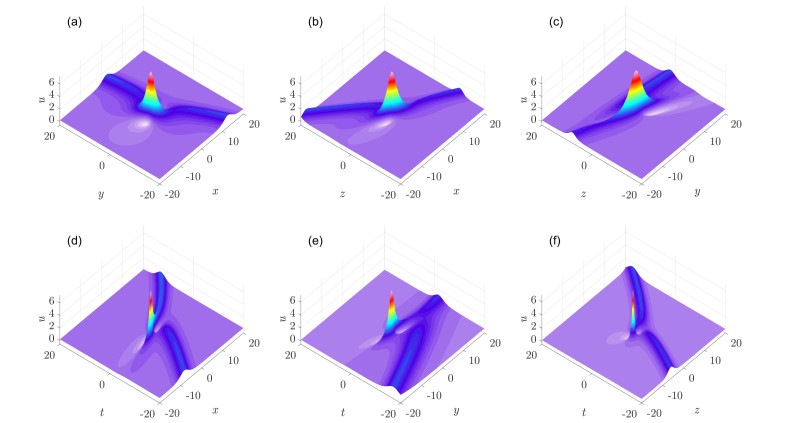
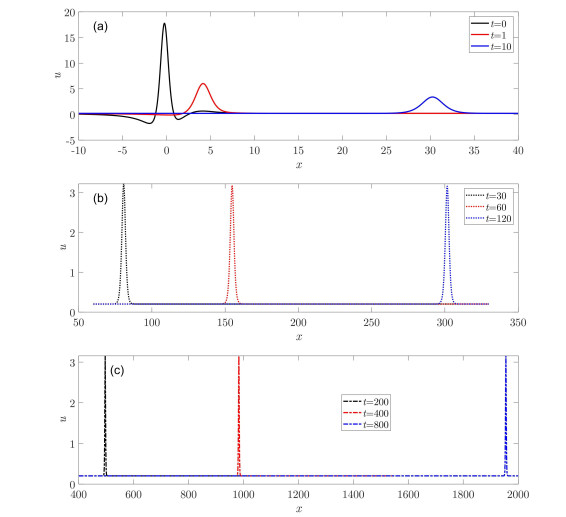
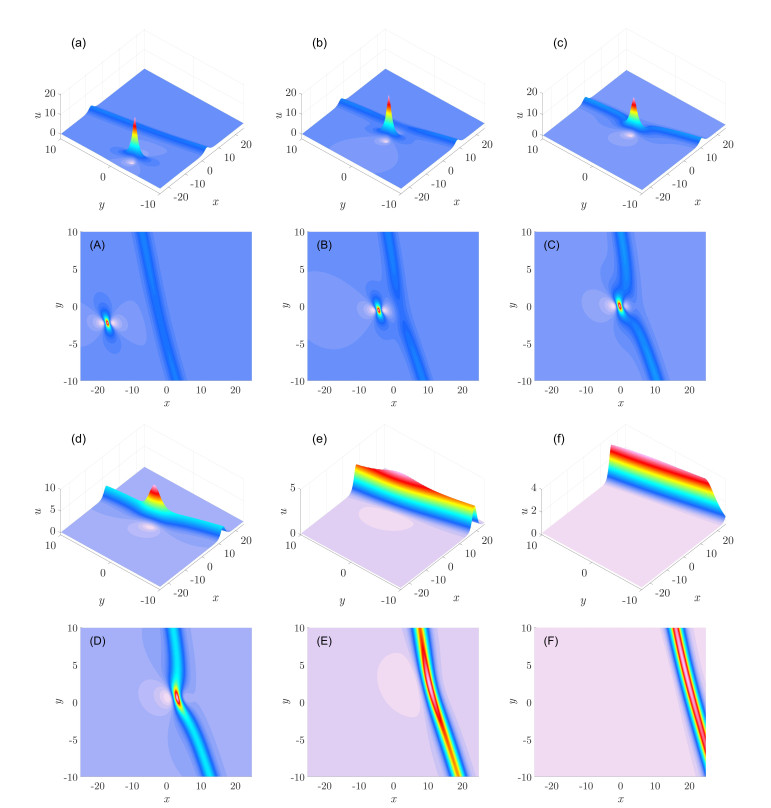
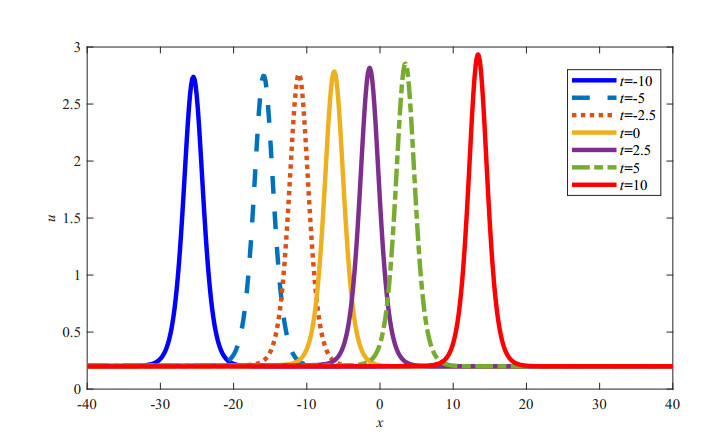
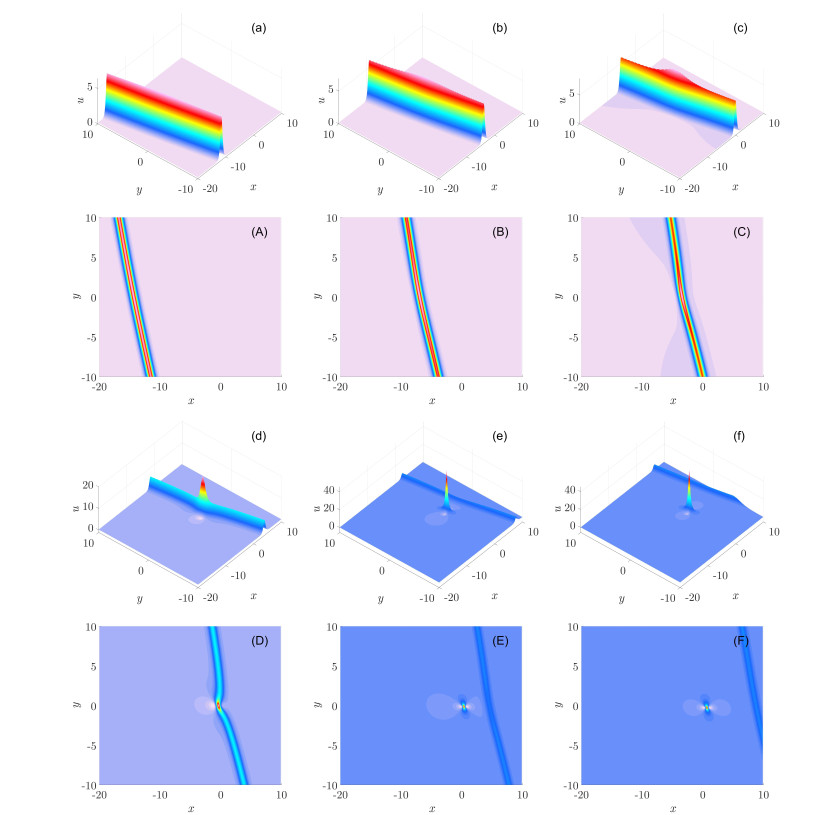
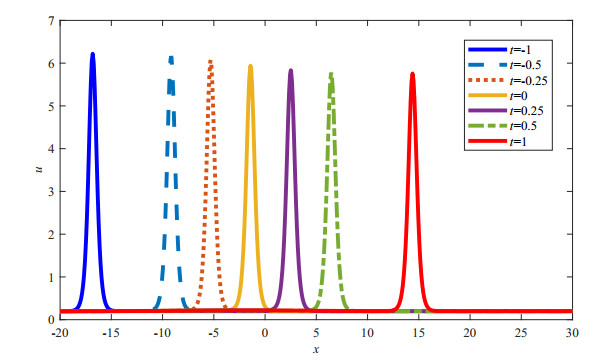
Citation: Yu-Lan Ma, Bang-Qing Li. Mixed lump and soliton solutions for a generalized (3+1)-dimensional Kadomtsev-Petviashvili equation[J]. AIMS Mathematics, 2020, 5(2): 1162-1176. doi: 10.3934/math.2020080
| [1] | Salman khan, Muhammad Naeem, Muhammad Qiyas . Deep intelligent predictive model for the identification of diabetes. AIMS Mathematics, 2023, 8(7): 16446-16462. doi: 10.3934/math.2023840 |
| [2] | Ghazanfar Latif, Jaafar Alghazo, Majid Ali Khan, Ghassen Ben Brahim, Khaled Fawagreh, Nazeeruddin Mohammad . Deep convolutional neural network (CNN) model optimization techniques—Review for medical imaging. AIMS Mathematics, 2024, 9(8): 20539-20571. doi: 10.3934/math.2024998 |
| [3] | Thavavel Vaiyapuri, Prasanalakshmi Balaji, S. Shridevi, Santhi Muttipoll Dharmarajlu, Nourah Ali AlAseem . An attention-based bidirectional long short-term memory based optimal deep learning technique for bone cancer detection and classifications. AIMS Mathematics, 2024, 9(6): 16704-16720. doi: 10.3934/math.2024810 |
| [4] | Alaa O. Khadidos . Advancements in remote sensing: Harnessing the power of artificial intelligence for scene image classification. AIMS Mathematics, 2024, 9(4): 10235-10254. doi: 10.3934/math.2024500 |
| [5] | Mesut GUVEN . Leveraging deep learning and image conversion of executable files for effective malware detection: A static malware analysis approach. AIMS Mathematics, 2024, 9(6): 15223-15245. doi: 10.3934/math.2024739 |
| [6] | Khaled Tarmissi, Hanan Abdullah Mengash, Noha Negm, Yahia Said, Ali M. Al-Sharafi . Explainable artificial intelligence with fusion-based transfer learning on adverse weather conditions detection using complex data for autonomous vehicles. AIMS Mathematics, 2024, 9(12): 35678-35701. doi: 10.3934/math.20241693 |
| [7] | Tamilvizhi Thanarajan, Youseef Alotaibi, Surendran Rajendran, Krishnaraj Nagappan . Improved wolf swarm optimization with deep-learning-based movement analysis and self-regulated human activity recognition. AIMS Mathematics, 2023, 8(5): 12520-12539. doi: 10.3934/math.2023629 |
| [8] | Karim Gasmi, Ahmed Kharrat, Lassaad Ben Ammar, Ibtihel Ben Ltaifa, Moez Krichen, Manel Mrabet, Hamoud Alshammari, Samia Yahyaoui, Kais Khaldi, Olfa Hrizi . Classification of MRI brain tumors based on registration preprocessing and deep belief networks. AIMS Mathematics, 2024, 9(2): 4604-4631. doi: 10.3934/math.2024222 |
| [9] | Nizar Alsharif, Mosleh Hmoud Al-Adhaileh, Mohammed Al-Yaari . Diagnosis of attention deficit hyperactivity disorder: A deep learning approach. AIMS Mathematics, 2024, 9(5): 10580-10608. doi: 10.3934/math.2024517 |
| [10] | Muhammad Ali Khan, Saleem Abdullah, Alaa O. Almagrabi . Analysis of deep learning technique using a complex spherical fuzzy rough decision support model. AIMS Mathematics, 2023, 8(10): 23372-23402. doi: 10.3934/math.20231188 |
Parkinson's disease (PD) is a neurodegenerative disorder that is defined by the progressive degeneration of the nervous system, which leads to the manifestation of symptoms such as tremors, stiffness, and bradykinesia [1]. The aforementioned condition is a neurodegenerative disorder characterized by the progressive deterioration of brain function. PD is associated with a range of consequences, including cognitive impairment, mood disturbances such as sadness, dysphagia, mastication difficulties, sleep disturbances or restlessness, and urinary and gastrointestinal dysfunction. PD significantly impacts an individual's everyday motor functions, particularly their automatic movements. This neurodegenerative disorder impairs one's capacity to execute involuntary actions, such as smiling or blinking. In addition, the impairment of bodily appendages has been documented in a variety of instances attributed to PD.
The likelihood of having PD is elevated amongst the elderly population. The fact that it affects 1% of the overall elderly population is a cause for concern [2]. Furthermore, PD poses a significant risk to the elderly population, making elder care facilities the most likely setting for encountering individuals affected by this condition.
According to a study conducted by the World Health Organization in 2019, over 8.5 million individuals were diagnosed with PD [3]. The incidence of this ailment is positively correlated with an advancing age, as shown by the fact that only 4% of affected individuals are below the age of 50. Globally, PD is of the most prevalent neurodegenerative diseases, comes in second after Alzheimer's disease, and impacts millions of individuals [4,5]. Now, physicians are limited in addressing the symptoms of this disorder due to the nascent stage of therapy [6]. The diagnosis of this ailment is not definitively established and is mostly dependent on the patient's medical history [3]. Due to the high costs and time requirements associated with an invasive diagnosis and therapy, it is imperative to develop a straightforward and dependable approach to diagnosing this illness [7,8].
In relation to nonmotor manifestations shown by individuals with PD, a diverse array of symptoms may be observed, including mood disorders and depressive states. These symptoms may be represented in the patient's facial expressions [9], such as language and other relevant factors [8,10]. The main primary objective of this research is to use handwriting modeling techniques, spirals, and waves to assess the impact of PD on both motor and nonmotor functions, while addressing the lack of research on the topic of employing both drawing spirals and waves while having PD.
The use of deep learning (DL) models has brought about a significant transformation within the domain of biomedical and medical image analyses [11]. DL models have been used in several fields, such as segmentation, detection, and disease classification [12]. DL models have a remarkable ability to extract high-level characteristics, thus resulting in an improved accuracy during disease classification. This may be largely attributed to their exceptional capacity for generalization. Furthermore, convolutional neural networks (CNNs) have played a vital role in facilitating the advancement of medical image processing. CNNs have shown significant achievements in several medical imaging applications [13,14,15].
Hence, it is essential to present a methodology that can extract the significant aspects that have a crucial impact on the detection of PD. PD is characterized by its progressive nature and is a condition that gradually advances over time. Early detection of the illness offers an opportunity for effective management with appropriate medicine, perhaps leading to its eradication [16,17]. Figure 1 displays the symptoms of PD.
This article presents a comprehensive account of the training and testing processes used for the DL models. Our primary objective was to construct a model capable of accurately diagnosing PD based on an analysis of spiral and wave drawings. This aspect is significant due to the propensity of older patients that experience rapid exhaustion, thus rendering it impractical to expect them to perform many sketching assignments within the confines of a primary care setting. Furthermore, from a clinical standpoint, it is noteworthy that we demonstrated the diagnostic potential of DL models in identifying PD. The DenseNet201 and VGG16 DL models have been notably efficacious in accurately differentiating persons with PD from healthy individuals by utilizing an analysis of spiral and wave drawing images. In this study, we conducted a comparative analysis between the outcomes of improved DL models and several current systems, as well as an open access code that used the same dataset. Our observations indicate that the proposed system exhibits a notable level of accuracy in the detection of PD when applied to two different drawings of images.
PD has been identified by several researchers using DL techniques. The use of voice analyses, brain scans, and artistic depictions using meander patterns, spirals, waves, and similar elements has been employed as a diagnostic system [18]. Due to its high level of accuracy, DL models are often used in the field of medical imaging for the early prediction of PD.
Rastegar et al. [19] introduced a novel model aimed at detecting PD. The methodology used involved the utilization of the random forest algorithm to analyze cytokine data. The examination of molecular data pertaining to cytokines provides significant insights into PD patients. The random forest approach was used alongside entropy and dataset data to diagnose Parkinson's illness. This system was evaluated using the root mean square error (RMSE).
Nilashi et al. [20] developed system based on the machine learning (ML) algorithm to predict PD using speech data. The University of California Irvine dataset was used to evaluate the system. The cluster technique was used to predict illnesses. The proposed model was evaluated using the RMSE metric, yielding a score of (RMSE = 0.537) at the test dataset.
The use of neural networks and decision trees was proposed in a study to enhance the diagnostic process of PD [21]. Sharma et al. [22] used speech data as a medium to identify PD, and the Unified PD Scale served as the foundation for their detection approach. The support vector machines (SVM) method was applied to detect PD. The efficacy of learning models is notably impacted by the quality of the data. The use of data preparation strategies can augment the efficacy of learning models. A regression analysis was performed on the preprocessed data using the SVM method. The performance of the model was assessed by computing its RMSE, which yielded a value of 0.24. Chen et al. [23] introduced a DL model to forecast PD using speech data obtained from individuals diagnosed with the condition. Nooritawati et al. [24] used gait movement as a prediction metric for PD. The proposed model was used to extract and statistically represent gait variables pertaining to the spatiotemporal, kinematic, and kinetic aspects. The data that was not cleansed underwent a preprocessing step, which included both intra-group and inter-group normalization. The aforementioned preprocessing approaches were used to extract gait information related to the spatiotemporal, kinematic, and kinetic components. Moreover, an artificial neural network model was used to detect PD [25], which used a linear SVM approach for clinically diagnosed with PD and proposed a cost-effective technique for the early detection of PD [26]. The use of a deep multivariate voice data analysis (DMVDA) has been employed to detect and diagnose disorders via the implementation of deep learning classifiers [27]. Maachi et al. [28] proposed the development of a CNN known as 1D-Convnet to predict PD. Moreover, several research have used transfer learning methodologies [29,30,31,32]. The usefulness of several machine learning models, such as deep neural networks, SVMs, and CNNs, to predict PD has been examined [33,34,35,36,37]. Pereira et al. [36] used a recurrent neural network (RNN) to enhance the monitoring of PD. The prediction of PD development was conducted using speech data via a hybrid model that incorporated CNNs and long short-term memory (LSTM). The aforementioned methodology was used in a research investigation carried out by [31]. Vasquez et al. [32] aimed to diagnose PD using DL techniques, feature-extraction methods, and dataset-balancing procedures.
Talitckii et al. [33] used several machine learning techniques, including random forest, logistic regression, SVM, light gradient boosting machine (GBM), and a stacked ensemble model to discern PD from other neurological conditions that exhibit motor discrepancies, thereby leveraging the data collected from wearable sensors. The highest level of accuracy, reaching 85%, was attained while using both feature sets. However, when just the tremor characteristics were utilized as the input for the machine learning models, the accuracy decreased to 80%.
Pereira et al. [34] developed a dataset named "HandPD" by using handwriting examinations con-ducted on a sample of 74 individuals diagnosed with PD and 18 control persons. The training phase of Naive Bayes, Optimum-Path Forest, and SVM models included using around 90% of the dataset. Moreover, the researchers devised a CNN structure to categorize the "HandPD" dataset into two distinct groups: PD and controls [35]. Additionally, meta-heuristic optimization methods were used to effectively adjust the hyperparameters. The researchers saw a notable increase in the classification accuracy, namely reaching 90%, when compared to their previous study [34]. Pereira et al. [36] proposed many CNN structures to categorize the handwriting dynamics acquired from a smart pen that was fitted with a set of sensors. The study used a sample of 224 individuals diagnosed with PD and 84 control participants. The CNN architectures were evaluated against the raw data categorized using baseline classification techniques.
Shaban et al. [37] investigated the use of a fine-tuned, pre-trained, VGG-19 model to distinguish between people diagnosed with PD and controls. The aforementioned discrimination was predicated upon the examination of datasets, including wave and spiral handwriting patterns. The model being evaluated showed a significant improvement in both the accuracy and sensitivity, exceeding 88% and 86%, respectively. Table 1 presents a complete overview of the latest breakthroughs in ML and DL approaches using different types of PD datasets.
| Authors, year | Types of datasets | Models | Object |
| Vanegas et al. [47], 2018 | EGG dataset | LR, DT, Extra tree | Biomarkers PD |
| Oh et al. [48], 2018 | EGG dataset | CNN | PD detection |
| Wagh et al. [49], 2020 | EGG dataset | CNN | PD detection |
| Shi et al. [50], 2019 | EGG dataset | CNN-RNN | PD detection |
| Zhang et al. [51], 2019 | MRI dataset | ResNext model | Detecting prodnormal PD |
| Ramirez et al. [52], 2020 | MRI dataset | Convolution auto encoder | Detecting de Novo PD |
| Prasuhn et al. [53], 2020 | MRI dataset | SVM, MKL | PD detection |
| Rasheed et al. [54], 2020 | Voice dataset | BPVAM | Detecting de Novo PD |
| Gunduz et al. [55], 2019 | Speech dataset | GB, | PD detection |
| Moon et al. [56], 2020 | Gait features dataset | ANN, SVM, KNN | Detecting ET versus PD |
| Zeng et al. [57], 2016 | Gait features dataset | RBF | PD detection |
| Pdisher et al. [58], 2020 | Sensory dataset | CNN | PD diagnosis |
| Taliki et al. [33], 2020 | Sensory dataset | RF | Detecting ET versus PD |
| Shaban et al. [37], 2020 | Handwriting dataset | VGG1-16 | PD detection |
| Robin [59], 2020 | Handwriting dataset (Same dataset) | RF, CNN, RestNet50 | PD detection |
| Stpete_ishii [60], 2023 | Handwriting dataset (Same dataset) | CNN | PD detection |
| Shaban et al. [61], 2020 | Handwriting dataset (Same dataset) | CNN | PD detection |
| Adrian [62], 2019 | Handwriting dataset (Same dataset) | CNN | PD detection |
DownLoad:
CSV
Wroge et al. [38] proposed a deep neural network-based approach to classify PD by utilizing the voices of patients. Dai et al. [39] designed U-net neural network algorithms to enhance the diagnosis of PD. Authors have applied various preprocessing approaches such as histogram equalization and gray level transformation to improve the U-net performance. The outcome data from preprocessing is processed using the U-net architecture. Rusz et al. [40] used a multilayer perceptron approach to detect several neurological illnesses, including PD. Haq et al. [41] designed a system to detect PD by analyzing the vocal characteristics of patients using preprocessing approaches to handle the missing and scaling of the data. The L1-norm SVM approach was used to extract the features from the voices of patients; the k-fold cross-validation method was used to evaluate their proposed system. The proposed system achieved a high accuracy of 99%. Prince et al. [42] introduced a wearable sensor to detect Parkinson's disease when placed on the patient's body. The sensors were used to monitor the actions and vital signs of the person being examined, without the need for physically inspecting the individual.
Zeng et al. [43] used a radial basis function (RBF) to detect PD using a dataset that contained 93 individuals with PD and 73 healthy controls. The suggested approach achieved an accuracy rate of 96.7%.
Muniz et al. [44] proposed logistic regression, probabilistic neural network, and SVM approaches to diagnose PD. The authors used a ground reaction force (GRF) as the input for the system. Pfister et al. [45] used a CNN to categorize PD into three classes: On, Off, and dyskinesia. The dataset was generated from wearable sensors and included a total of 30 patients. Drotar et al. [46] used feature selection and SVM techniques to distinguish between 37 patients with PD and 38 control individuals based on their handwriting motions. The calculated accuracies of the system for in-air trajectories was determined to be 84%, while it was 78% for on-surface movements.
Figure 2 presents the framework of the detection of PD. This work aims to propose the development of a system using artificial intelligence methods for the purpose of screening and staging PD, as well as identifying biomarkers of the condition via the analysis of handwriting examinations. The "HandPD" study demonstrated significant methods to detect PD at an early stage.
The dataset used in this study was developed by Adriano et al. [62] from the Innovation and Technology Assessment of the Federal University. The dataset was comprised of images that were pre-divided into a training set and a testing set. The training set included images of spirals and waves, as did the testing set. The study revealed that individuals diagnosed with PD had decreased drawing speeds and pen pressures, particularly among those in the more severe stages of the condition. The dataset consisted of a total of 204 images, including 102 images of spiral patterns and 102 images of waves. From this dataset, 70% of images were used for training purposes, while the remaining 30% of images were reserved for testing. The dataset consists of two distinct classes: individuals diagnosed with PD and healthy individuals. Figures 3 and 4 show a few samples of spiral and wave images.
A study by Zham et al. [63] revealed that individuals diagnosed with PD had reduced drawing speeds and decreased pen pressures, particularly among those with more severe forms of the condition. The visual characteristics of a hand-drawn spiral and wave may be directly impacted by the presence of tremors and muscle rigidity, which are two prominent manifestations of PD. This observation will be used in our analysis. The diversity in visual characteristics presents an opportunity to develop a computer vision and machine learning system capable of autonomously identifying PD. Figure 5 shows how patients draw a spiral.
The preprocessing method is a very important phase to enhance the DL models. The load_img function was used to load an image file. The function accepts the image file's path as its argument and outputs an object that represents the image. This process transformed the data into an array format. The function "img_to_array" was used to transform the imported image object into a NumPy array. During the process of converting the image into a NumPy array, a code proceeds the conversion to perform a division operation on the pixel values, dividing them by 244x244. Then, the pixel values are normalized to a range of 0 to 1. The process of normalizing the pixel values has been shown to enhance the convergence and performance of machine learning models.
CNNs are deep learning models that can analyze and process visual images. CNNs are applied in a number of the real-life applications, such as brain-computer interfaces and time series analyses.
Transfer learning refers to the process of retaining and using problem-solving expertise in the context of other issue domains. Transfer learning leverages preexisting information to develop models that exhibit accelerated learning and need a reduced amount of training data. Transfer learning is a prominent area of study in the field of artificial intelligence, which involves the use of knowledge gained by addressing a particular problem and applying it to address a similar problem [64,65,66].
The CNN architecture consists of an activation function alongside convolution and pooling operations. The process of convolution involves taking an image and a filter as the input to produce an output image. The dimensions of the image, namely its size (244×244), height, breadth, and number of channels have a significant impact on the performance of the neural network.
| C=∑i1∑j1IijFij. | (1) |
The symbol F represents a convolution kernel or filter, whereas Ij represents rows and columns. The operation involves the multiplication of the image by the kernel, therefore presenting both the input image and the filter. The process of convolution involves decomposing the image into perceptrons, which are then flattened along the y-axis and z-axis. Each layer is equipped with a set of x filters designed to detect and identify certain traits. Layer L produces feature maps of size X, which are then annotated as follows:
| CLi=BLi+∑x(L−1)j=1FLi,j∗C(L−1)j, | (2) |
where BLi represents the bias matrix and FLi,j denotes the value at position jth in the matrix F. The filter denoted as L serves as the connection between the jth feature map inside the layer. The CNN structure is presented in Figure 6.
DenseNet is a CNN that uses dense blocks to directly link all layers with matching feature map sizes. Each layer receives inputs from previous layers and provides feature maps to succeeding levels to maintain the feed-forwardness. Every layer of the DenseNet undergoes a forward propagation process. These modifications result in a reduction of parameters, the mitigation of the vanishing-gradient problem, the enhancement of feature propagation, and the facilitation of reuse.
The DenseNet architecture has transition layers and dense blocks. Dense blocks consist of convolutional layers that are connected. A connection is established by connecting the output of each layer to the input of the subsequent layer. Transition layers are used in dense blocks to decrease the size of feature maps, which facilitates the development of the network. Figure 7 displays the architecture of the DenseNet model.
DenseNet201 is a CNN characterized by its increased depth, which effectively mitigates the issue of gradient disappearance, improves the propagation and use of features, and reduces the number of network parameters involved. The DenseNet201 model establishes direct connections between all levels to optimize information transfer. The proposed model demonstrates the construction of the dense block and transition layer submodules of DenseNet201. As with other models, DenseNet201 is trained using ImageNet.
DenseNet201 is transfer learning method that trains a model to identify and classify PD by using handwriting images. The DenseNet201 architecture consists of three dense blocks and four transition layers that connect these blocks. Each convolution layer inside the dense block is interconnected. The feature map undergoes expansion with each dense block. Transition layers are responsible for down sampling. The DenseNet201 architecture utilizes average pooling for down sampling. DenseNet201, which consists of 201 layers, is a variant. The object under consideration has substantial dimensions and possesses distinct layers of varying composition. The process of down sampling feature maps is accomplished using transition layers inside dense blocks. A pretrained model is generated using the same architectural frameworks. The model uses average pooling with the parameter pooling = "avg" to produce feature maps using pre-trained ImageNet weights. The pretrained model is a dense layer consisting of 256 units, which is activated using the rectified linear unit (ReLU) activation function. The proposed architecture of the modified DenseNet201 is shown in Figure 8. The parameters of the DenseNet201 model are presented in Table 2.
| DenseNet 201 parameter setting | Details |
| Convolutional layer 1 | 256 |
| Kernel size | 5 |
| Convolutional layer 2 number of filters | 128 |
| Kernel size | 5 |
| MaxPooling layer with pool size | 5 |
| Activation function | Softmax function using two outputs |
| Optimizer | Adam RMSprop |
| Number of epochs | 60 |
| Batch size | 32 |
DownLoad:
CSV
The image resizing process in the DenseNet 201 model involved adjusting the dataset images to a shape of (224x 224) to ensure compatibility with the input shape of the pre-trained DenseNet 201 model. Then, transfer learning was performed up to the 5×5 global average pooling layer located above the 256 fully connected (FC) layer. Subsequently, an FC layer was added, with the number of neurons corresponding to the classes used in the dataset. This FC layer was equipped with a soft max activation layer. The final layer's weights were retrained using a learning rate of 0.001, the Adam optimizer, and a batch size of 256 for a total of 50 epochs. Prior to using the DenseNet 201 model, it is essential to perform normalization preprocessing on the dataset images. Figure 9 illustrates the flow chart of the experimental method that used the DenseNet 201 model.
VGGNet is a type of CNN that was collaboratively built by Google DeepMind and the Visual Geometry Group at the University of Oxford [57]. The VGG16 model is a CNN architecture consisting of 16 layers. The VGG16 model design prioritizes ConvNet layers with a kernel size of 3×3, as opposed to using several parameters. The minimum anticipated input image size for this model is 224x 224x 3 pixels, and it has three channels.
Optimization algorithms are often used in neural networks to assess the activation of individual neurons. This is achieved by calculating the weighted sum of the neuron's inputs. The use of a kernel function is motivated by the need to introduce nonlinearity into the output neuron. The neurons in a neural network are affected by weight, bias, and the associated training technique. The synaptic weights of the neurons are modified by the degree of discrepancy seen in the output. The inclusion of an input layer and the use of an activation function provide nonlinear characteristics that affect the input of artificial neural networks, and therefore enable them to acquire knowledge and successfully execute intricate tasks.
A pre-trained VGG16 model, specifically trained on the ImageNet dataset, is referred to in this study. The weights parameter is configured as "imagenet", thus suggesting the use of pre-trained weights. The process of immobilizing the layers in the base model is as follows. By assigning the value of "False" to the trainable attribute of each layer in the base_model, we effectively inhibit the modification of their weights throughout the training process. The global average pooling 2D function is a layer that applies global average pooling to decrease the spatial dimensions of feature maps. The dense layer, denoted as Dense (128, activation = "relu"), is a fully linked layer consisting of 256 units, which uses the rectified linear unit (ReLU) activation function. The output layer of the neural network is defined as Dense (two classes, activation = "softmax"). It consists of num_classes units and utilizes the softmax activation function to provide predicted class probabilities. The process of compiling the model is executed. The Adam optimizer was used with a learning rate of 0.0001. Figure 10 depicts the structure of the VGG16 model to detect PD. The VGG16 parameters are shown Table 3.
| VGG16 parameter settings | Values |
| Convolutional layer 1 | 256 |
| Kernel size | 5 |
| Convolutional layer 2 number of filters | 128 |
| Kernel Size | 5 |
| MaxPooling layer with pool size | 5 |
| Activation function | Relu |
| Optimizer | Adam |
| Number of epochs | 10 |
| Batch size | 32 |
DownLoad:
CSV
The VGG 16 model involved resizing the images in the dataset to a shape of (224x 224x 3) in order to align with the input shape required by the pre-trained VGG 16 model. Then, transfer learning was performed up to the 5×5 max pooling layer in the block. The output of the pooling layer was flattened, followed by the addition of a ReLU activation layer. Then, a dropout regularization layer with a rate of 0.5 was added. Finally, a FC layer with a number of neurons equal to the number of classes in the dataset was added, along with a softmax activation layer. The final layer weights were retrained using a learning rate of 0.001, the Adam optimizer, and a batch size of 32 for a total of 50 epochs. Figure 11 depicts the flowchart illustrating the experimental methodology used, which utilized the VGG 16 model.
The investigation of medical decision support systems that provide precise biomarkers to clinicians for the detection of PD is a significant field of study. Nevertheless, the use of novel methodologies with DL models has the potential to provide clinicians with a non-invasive, uninterrupted, and unbiased approach to assist the monitoring of patients. Emerging technologies have the potential to assist healthcare professionals and authorities in identifying PD in its early stages.
This study used a handwriting analysis to determine if individuals diagnosed with PD had distinctive characteristics in their handwriting that could serve as tools for a PD diagnosis. A proposed system using DL has achieved a high level of accuracy in discriminating between those with normal cognitive function and those with PD.
Evaluation metrics refer to quantitative measurements used to evaluate the performance of the DenseNet201 and VGG16 models. These metrics provide valuable insights into the performance of the model and facilitate the comparison of other models or algorithms.
| Accuracy=TP+TNTP+FP+FN+TN×100%, | (3) |
| Sensitivity=TPTP+FN×100%, | (4) |
| Precision=TPTP+FP×100%, | (5) |
| specificity=TNTN+FP×100%, | (6) |
| F1−score=2∗precision×Sensitivityprecision+Sensitivity×100%. | (7) |
The hardware and software requirements play a crucial role in the functioning of this particular system. The suggested system aims to identify PD by analyzing the handwriting of both those without PD and those diagnosed with PD. Subsequently, the system is used to detect PD from images. In the experiments, a GPU system with 16 GB (RAM) and Windows OS was employed during the training and testing development the PD system. The system was developed by employing the Python 3.9 programming language. Several DL and ML libraries were used to develop the PD system, such as TensorFlow 13.2.0, Keras, and scikit-learn.
The PD dataset was saved in a separate file, which was organized into two separate folders for training and testing. The total data was 204 images that consisted of spiral and wave patterns. The PD dataset was divided into a training set made up of 70% of the data and a testing set comprised of 30% of the data. Each directory of the dataset consisted of two subdirectories. One subdirectory included PD and healthy spiral images for the purposes of training and testing. The other subdirectory provided wave images of both PD and healthy individuals.
The ImageDataGenerator function provided a wide range of image augmentation techniques, such as rotation, shifting, shearing, zooming, flipping, and brightness adjustment. The implementation of these modifications augmented the diversity and uncertainty of the training dataset, thus resulting in enhancements in the efficacy and generalizability of the CNN model. This procedure involved the application of morphological transformations, such as rescaling, rotating within a range of 0 to 20 degrees, horizontal flipping, shifting the height within a range of 0 to 0.2, shearing within a range of 0 to 0.1, and zooming within a range of 0 to 0.2. Figure 12 shows the splitting of the spiral and wave datasets.
This section presents the outcome results of the use of DL techniques to identify and classify PD while utilizing the spiral and wave drawings of PD patients.
The DenseNet201 model was used to detect PD via the analysis of spiral and wave drawing images. The training procedure was conducted using a batch size of 32; each batch consisted of images with dimensions of 224×224. The training was carried out over a total of 60 epochs, and the early stopping technique was used based on the validation loss metric. Table 4 presents the outcomes obtained from the use of the DenseNet201 model to detect spiral images. Notably, the DenseNet201 model had a commendable accuracy rate of 94%. The DenseNet201 model achieved a high accuracy rate of 91% for identifying the normal class, as measured via a precision analysis. Additionally, it achieved a perfect recall and an F1-score of 95% for the same class.
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 91 | 100 | 95 | 94 |
| Parkinson's | 100 | 88 | 93 | |
| Weighted avg | 95 | 94 | 94 |
DownLoad:
CSV
The validation accuracy and loss were monitored throughout 60 epochs, and the training process was halted when the validation loss reached a value below the predetermined threshold of 0.5. At this point, the model achieved an accuracy of 94%, with a validation loss of 0.40. The accuracy of the DenseNet201 model is visualized in Figure 13, which depicts the convergence of the validation accuracy and loss and training loss over the training and validation processes, respectively.
The outcome results of the DenseNet201 model for identifying and classification PD using wave images is presented in Table 5. The DenseNet201 model had a relatively lower accuracy rate of 89%. The DenseNet201 model has shown a lower accuracy in identifying PD using wave classification. The DenseNet201 model achieved weighted average scores of 91%, 89%, and 89% for their respective assessment measures.
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 78 | 100 | 88 | 89 |
| Parkinson's | 100 | 82 | 90 | |
| Weighted avg | 91 | 89 | 89 |
DownLoad:
CSV
The model accuracy and loss of the DenseNet201 model for detecting the wave and spiral images for classifying PD is displayed in Figure 14. The validation accuracy exhibited fluctuations, with an initial value of 45% and a subsequent increase to over 89%. However, it stabilized at 55%, while the training accuracy reached 80%. The model's accuracy loss begins at a value of 1.8 and gradually decreases to 0.4.
The VGG16 model was used to identify PD via the examination of spiral and wave images. The training approach was executed with a batch size of 32, whereby each batch was comprised of images with a demension of 240×240×3. The training procedure had a duration of 10 epochs, during which the early stopping strategy was used, relying on the validation loss measure. The results of the VGG16 model for detecting PD using spiral images are shown in Table 6. The VGG16 model achieved an accuracy rate of 80%. The VGG16 model achieved a weighted average precision of 82%, a recall of 80%, and an F1-score of 80%.
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 74 | 93 | 82 | 80 |
| Parkinson's | 91 | 67 | 77 | |
| Weighted avg | 82 | 80 | 80 |
DownLoad:
CSV
Figure 15 presents the performance evaluation of the VGG16 model in identifying PD using spiral images. Starting from an initial accuracy 50% with 10 epochs, the training phase of VGG16 achieved an accuracy of 85%, while the testing procedure achieved an accuracy of 80%. The VGG16 loss begins with a value of 0.75 and then decreases to a final value of 0.42.
The outcomes of the VGG16 model in terms of the detection of PD utilizing wave images are shown in Table 7. The VGG16 model achieved a high accuracy rate of 91% in the wave detection. The accuracy, recall, and F1-score parameters for evolution were weighted averaged at 92%, 91%, and 91%, respectively. In conclusion, it was found that the VGG16 model exhibited a superior performance in recognizing wave images as opposed to spiral images.
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 83 | 100 | 91 | 91 |
| Parkinson's | 100 | 83 | 91 | |
| Weighted avg | 92 | 91 | 91 |
DownLoad:
CSV
Figure 16 illustrates the efficacy of VGG16 in identifying PD by the use of wave images. At the beginning of the VGG16 model testing phase, the accuracy was 45%, which improved to 91%. The VGG16 model indicated comparable loss values throughout both the training and testing phases, starting at 0.75 and converging to 0.40.
PD is a chronic and progressive condition that significantly impacts the quality of life of affected individuals. PPD remains incurable; hence, an early diagnosis offers the potential for an enhanced quality of life with appropriate medication, exercise, and therapeutic interventions. The first manifestation of this pathological condition is characterized by bradykinesia and tremors, which notably impact the motor skills involved in handwriting among affected individuals. There are several developed non-invasive methodologies for the diagnosis of PD by analyzing handwritten spirals produced by individuals affected by the condition.
PD is a neurodegenerative disorder characterized by the degeneration of cells within the nervous system. Initial indications include tremors or involuntary movements affecting the hands, arms, legs, and jaw. The artificial intelligence model has facilitated the development of applications that have the potential to assist in the diagnosis of PD without the need for clinical intervention. Handwriting irregularities are frequently identified in the majority of individuals afflicted with PD and are often described as one of the first manifestations of the condition. This study was conducted with a specific emphasis on the implications of handwriting on PD diagnosis.
In order to achieve the intended objective, a set of handwritten images was gathered from 204 people, including 102 individuals diagnosed with PD and 102 healthy individuals serving as the control. The dataset contained a collection of 204 spiral and wave images that served as training and testing data for a model designed to effectively categorize individuals with PD. Proposed transfer learning models, namely DenseNet201 and VGG16, were selected as the preferred approach DL models for detecting PD. In this study, many models of transfer learning were trained in order to determine the most suitable model. DenseNet201 had a 94% accuracy when detecting spiral images, whereas VGG16 achieved a high accuracy of 90% when detecting PD from wave images. This was found to be satisfactory, as shown by a testing accuracy of 94% and a testing accuracy of 90%.
The receiver operating characteristic (ROC) curve is a graphical representation that illustrates the classification model's performance across various categorization levels and represents the relationship between two variables. The ROC is calculated as follows:
| TRP=TPTP+FN | (8) |
| FPR=FPFP+TN | (9) |
where TRP is the true positive rate and FPR is the false positive rate.
The ROC curve of the DenseNet201 model is shown in Figure 17. The ROC metric is calculated based on the false positive rate (FPR) of the DenseNet201 model. When utilizing spiral images, the FPR is 1, whereas when using wave images, the FPR is 2. Therefore, the performance of the DenseNet201 model achieved a classification accuracy of 99% when trained on spiral images; however, it achieved a classification accuracy of only 95% when trained on wave images. The DenseNet201 model notably achieved a high accuracy when trained on spiral images.
Figure 18 presents the ROC curve of the VGG16 model in the context of identifying PD using spiral and wave images. The VGG16 model achieved a high accuracy rate by using wave images. The use of spiral images resulted in a reduced percentage of 90% or less for the ROC. The ROC was observed to be 80%.
We assessed the efficacy of our proposed model, which demonstrated a validation accuracy of the DenseNet201 and VGG16 models, as compared with various existing systems. Authors [41] used RF, CNN, and Resnet50 to detect PD using spiral and wave drawing images. The author used a similar dataset, where it was observed that the CNN and ResNet50 achieved 90%. The CNN used spiral images, while RestNet50 achieved 87% accuracy using wave images. Authors in [42] used the lightning CNN model and achieved an accuracy of 63.33%. Researchers in [52] used a CNN to identify PD based on spiral and wave images. The results indicated that the CNN model achieved an accuracy of 88% when recognizing PD from spiral images, and 89% when detecting PD from wave images. Approximately 80% of the models underwent training and validation processes. The SqueezeNet model obtained an accuracy of 72.53%, whereas AlexNet achieved an accuracy of 76.76% and MobileNet achieved an accuracy of 76.56%. The results are shown in Table 8. Figure 19 displays a graphical representation that compares the suggested systems using DL with the current systems.
| Ref. | Models | Dataset | Accuracy | ROC |
| Ref. [59] | RF | Same dataset 204 spiral and wave images | Wave images=80% | |
| CNN | Spiral image=67% | |||
| ResNet50 | Wave images=87% | |||
| Spiral image=90% | ||||
| Wave images=87% | ||||
| Spiral image=90% | ||||
| Ref. [60] | Lightning CNN | Same dataset used Spiral images | Spiral image=63.33% | |
| Ref. [61] | CNN | Same dataset 204 spiral and wave images | Wave images=88% | |
| Spiral image=89% | ||||
| Ref. [62] | CNN | Same dataset 204 spiral and wave images | Wave images=73% | |
| Spiral image=83% | ||||
| Our enhanced models | DenseNet201 | Same dataset 204 spiral and wave images | Spiral images=94% | 99% |
| VGG16 | Wave image=91% | 90% |
DownLoad:
CSV
Identification of PD poses significant challenges and necessitates the use of biomarkers in conjunction with symptomatic manifestations, such as tremors, bradykinesia, and stiffness, to enhance diagnostic precision.
The identification of PD would enable the formulation and implementation of targeted therapeutic approaches for those affected by this condition. PD completely affects the routine schedule life of patients. Detecting PD at its earliest stages helps physicians to treat patients better. To improve the detection of PD, DL models were presented in this research. This study showed that observations of spiral and wave drawings can help physicians distinguish between patients with PD and healthy patients. The proposed system used a standard dataset containing 204 spiral and wave drawings from Parkinson's patients. DL models such as DenseNet201 and VGG16 were applied to detect PD.
The objective of this study was to enhance the diagnostic process of PD using DL models. The primary goal was to discern between those without PD (healthy) and those diagnosed with PD. The emphasis of our methodology was the identification of anomalies in the locomotion patterns of patients via the use of drawing images. Furthermore, this study investigates the relative effectiveness of two drawing tasks, namely spiral and wave, in the discriminating process. The DenseNet201 classifier, which was trained using images of the spiral drawing task, was 94% accurate and had a ROC score of 99%. This suggests that it may serve as an effective and unbiased tool to distinguish individuals with PD from healthy individuals. The VGG16 model was used to discern between individuals with PD and healthy controls using wave images, achieving a notable accuracy rate of 91% and a ROC score of 90%. The use of DL techniques may be explored in future research to enhance the performance of the DenseNet201 and VGG16 models.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors extend their appreciation to the king Salman center for disability research for funding this work through research group No: KSGR-2023-236.
The authors declare no conflicts of interest.
Available from: https://www.kaggle.com/datasets/kmader/parkinsons-drawings/data (accessed on 2 August 2023).
| [1] | G. Whitham, Linear and nonlinear waves, Wiley, New York, 1974. |
| [2] | G. Eilenberger, Solitons, Springer-Verlag, Berlin, 1983. |
| [3] |
S. Burger, K. Bongs, S. Dettmer, et al. Dark solitons in Bose-Einstein condensates, Phys. Rev. Lett., 83 (1999), 5198-5201. doi: 10.1103/PhysRevLett.83.5198
|
| [4] |
K. E. Strecker, G. G. Partridge, A. G. Truscott, et al. Formation and propagation of matter-wave soliton trains, Nature, 417 (2002), 150-153. doi: 10.1038/nature747
|
| [5] | L. Khaykovich, F. Schreck, G. Ferrari, et al. Formation of a matter-wave bright soliton, Science, 296 (2002), 290-1293. |
| [6] |
B. Kibler, J. Fatome, C. Finot, et al. The Peregrine soliton in nonlinear fibre optics, Nat. Phys., 6 (2010), 790-795. doi: 10.1038/nphys1740
|
| [7] | B. Q. Li, Y. L. Ma, J. Z. Sun, The interaction processes of the N-soliton solutions for an extended generalization of Vakhnenko equation, Appl. Math. Comput., 216 (2010), 3522-3535. |
| [8] |
A. M. Wazwaz, Multiple soliton solutions and multiple complex soliton solutions for two distionct Boussinesq equations, Nonlinear Dyn., 85 (2016), 731-737. doi: 10.1007/s11071-016-2718-0
|
| [9] | L. Liu, B. Tian, H. P. Chai, et al. Certain bright soliton interactions of the Sasa-Satsuma equation in a monomode optical fiber, Phys. Rev. E, 95 (2017), 032202. |
| [10] |
Q. M. Huang, Y. T. Gao, S. L. Jia, et al. Bilinear Backlund transformation, soliton and periodic wave solutions for a (3+1)-dimensional variable-coefficient generalized shallow water wave equation, Nonlinear Dyn., 87 (2017), 2529-2540. doi: 10.1007/s11071-016-3209-z
|
| [11] | Y. L. Ma, Interaction and energy transition between the breather and rogue wave for a generalized nonlinear Schrödinger system with two higher-order dispersion operators in optical fibers, Nonlinear Dyn., 97 (2019), 95-105. |
| [12] |
B. Q. Li, Y. L. Ma, The wrinkle-like N-solitons for the thermophoretic motion equation through graphene sheets, Physica A, 494 (2018), 169-174. doi: 10.1016/j.physa.2017.12.014
|
| [13] | E. Pelinovsky, C. Kharif, Extreme Ocean Waves, Springer, Berlin, 2008. |
| [14] | A. R. Osborne, Nonlinear ocean waves, Academic Press, New York, 2009. |
| [15] | A. Chabchoub, N. Hoffmann, H. Branger, et al. Experiments on wind-perturbed rogue wave hydrodynamics using the Peregrine breather model, Phys. Fluids, 25 (2013), 101704. |
| [16] |
A. Lechuga, Rogue waves in a wave tank: experiments and modeling, Nat. Hazards Earth Sys. Sci., 13 (2013), 2951-2955. doi: 10.5194/nhess-13-2951-2013
|
| [17] | M. Närhi, B. Wetzel, C. Billet, et al. Real-time measurements of spontaneous breathers and rogue wave events in optical fibre modulation instability, Nat. Commun., 7 (2016), 13675. |
| [18] | D. R. Solli, C. Ropers, B. Jalali, Active control of rogue waves for stimulated supercontinuum generation, Phys. Rev. Lett., 101 (2008), 233902. |
| [19] | Y. V. Bludov, V. V. Konotop, N. Akhmediev, Matter rogue waves, Phys. Rev. A, 80 (2009), 033610. |
| [20] | Z. Y. Yan, V. V. Konotop, N. Akhmediev, Three-dimensional rogue waves in nonstationary parabolic potentials, Phys. Rev. E, 82 (2010), 036610. |
| [21] | A. Chabchoub, N. P. Hoffmann, N. Akhmediev, Rogue wave observation in a water wave tank, Phys. Rev. Lett., 106 (2011), 204502. |
| [22] | H. Bailung, S. K. Sharma, Y. Nakamura, Observation of peregrine solitons in a multicomponent plasma with negative ions, Phys. Rev. Lett., 107 (2011), 255005. |
| [23] | B. L. Guo, L. M. Ling, Rogue wave, breathers and bright-dark-rogue solutions for the coupled Schrödinger equations, Chin. Phys. Lett., 28 (2011), 110202. |
| [24] | B. L. Guo, L. M. Ling, Q. P. Liu, Nonlinear Schrödinger equation: Generalized Darboux transformation and rogue wave solutions, Phys. Rev. E, 85 (2012), 026607. |
| [25] | Y. Ohta, J. K. Yang, Dynamics of rogue waves in the Davey-Stewartson II equation, J. Phys. A, 46 (2013), 105202. |
| [26] | Z. Y. Ma, S. H. Ma, Analytical solutions and rogue waves in (3+1)-dimensional nonlinear Schrödinger equation, Chinese Phys. B, 21 (2012), 030507. |
| [27] | J. S. He, H. R. Zhang, L. H. Wang, et al. Generating mechanism for higher-order rogue waves, Phys. Rev. E, 87 (2013), 052914. |
| [28] | J. S. He, S. W. Xu, K. Porsezian, et al. Rogue wave triggered at a critical frequency of a nonlinear resonant medium, Phys. Rev. E, 93 (2016), 062201. |
| [29] |
Y. Zhang, H. H. Dong, X. E. Zhang, et al. Rational solutions and lump solutions to the generalized (3+1)-dimensional shallow water-like equation, Comput. Math. Appl., 73 (2017), 246-252. doi: 10.1016/j.camwa.2016.11.009
|
| [30] |
Y. H. Yin, W. X. Ma, J. G. Liu, et al. Diversity of exact solutions to a (3+1)-dimensional nonlinear evolution equation and its reduction, Comput. Math. Appl., 76 (2018), 1275-1283. doi: 10.1016/j.camwa.2018.06.020
|
| [31] | H. N. Xu, W. Y. Ruan, Y. Zhang, et al. Multi-exponential wave solutions to two extended Jimbo-Miwa equations and the resonance behavior, Appl. Math. Lett., 99 (2020), 105976. |
| [32] |
C. J. Wang, Spatiotemporal deformation of lump solution to (2+1)-dimensional KdV equation, Nonlinear Dyn., 84 (2016), 697-702. doi: 10.1007/s11071-015-2519-x
|
| [33] |
C. J. Wang, H. Fang, X. X. Tang, State transition of lump-type waves for the (2+1)-dimensional generalized KdV equation, Nonlinear Dyn., 95 (2019), 2943-2961. doi: 10.1007/s11071-018-04733-5
|
| [34] |
Z. L. Zhao, L. C. He, Multiple lump solutions of the (3+1)-dimensional potential Yu-Toda-Sasa-Fukuyama equation, Appl. Math. Lett., 95 (2019), 114-121. doi: 10.1016/j.aml.2019.03.031
|
| [35] | Z. L. Zhao, L. C. He, Y. B. Gao, Rogue wave and multiple lump solutions of the (2+1)-dimensional Benjamin-Ono equation in fluid mechanics, Complexity, 2019 (2019), 8249635. |
| [36] |
Z. L. Zhao, B. Han, Residual symmetry, Backlund transformation and CRE solvability of a (2+1)-dimensional nonlinear system, Nonlinear Dyn., 94 (2018), 461-474. doi: 10.1007/s11071-018-4371-2
|
| [37] |
Y. F. Hua, B. L. Guo, W. X. Ma, et al. Interaction behavior associated with a generalized (2+1)-dimensional Hirota bilinear equation for nonlinear waves, Appl. Math. Model., 74 (2019), 184-198. doi: 10.1016/j.apm.2019.04.044
|
| [38] |
C. J. Wang, Z. D. Dai, C. F. Liu, Interaction between kink solitary wave and rogue wave for (2+1)-dimensional Burgers equation, Mediterr. J. Math., 13 (2016), 1087-1098. doi: 10.1007/s00009-015-0528-0
|
| [39] |
J. C. Chen, Z. Y. Ma, Consistent Riccati expansion solvability and soliton-cnoidal wave interaction solution of a (2+1)-dimensional Korteweg-de Vries equation, Appl. Math. Lett., 64 (2017), 87-93. doi: 10.1016/j.aml.2016.08.016
|
| [40] |
B. Q. Li, Y. L. Ma, L. P. Mo, et al. The N-loop soliton solutions for (2+1)-dimensional Vakhnenko equation, Comput. Math. Appl., 74 (2017), 504-512. doi: 10.1016/j.camwa.2017.04.036
|
| [41] |
B. Q. Li, Y. L. Ma, T. M. Yang, The oscillating collisions between the three solitons for a dual-mode fiber coupler system, Superlattice Microst., 110 (2017), 126-132. doi: 10.1016/j.spmi.2017.08.054
|
| [42] | B. Q. Li, Y. L. Ma, Solitons resonant behavior for a waveguide directional coupler system in optical fibers, Opt. Quant. Electron., 50 (2018), 270. |
| [43] |
S. Wang, X. Y. Tang, S. Y. Lou, Soliton fission and fusion: Burgers equation and Sharma-Tasso-Olver equation, Chaos Solitons Fractals, 21 (2004), 231-239. doi: 10.1016/j.chaos.2003.10.014
|
| [44] | W. T. Zhu, S. H. Ma, J. P. Fang, et al. Fusion, fission, and annihilation of complex waves for the (2+1)-dimensional generalized Calogero-Bogoyavlenskii-Schiffsystem, Chinese Phys. B, 23 (2014), 060505. |
| [45] |
M. J. Ablowitz, H. Segur, On the evolution of packets of water waves, J. Fluid. Mech., 92 (1979), 691-715. doi: 10.1017/S0022112079000835
|
| [46] |
E. Infeld, G. Rowlands, 3 dimensional stability of Korteweg-de Vries waves and solitons, Acta Phys. Pol. A, 56 (1979), 329-332. doi: 10.1063/1.32091
|
| [47] | E. A. Kuznetsov, S. K. Turitsyn, Two- and three-dimensional solitons in weakly dispersive media, J. Exp. Theor. Phys., 55 (1982), 844-847. |
| [48] |
W. X. Ma, Comment on the 3+1 dimensional Kadomtsev-Petviashvili equations, Commun. Nonlinear Sci., 16 (2011), 2663-2666. doi: 10.1016/j.cnsns.2010.10.003
|
| [49] | C. Qian, J. G. Rao, Y. B. Liu, et al. Rogue waves in the three-dimensional Kadomtsev-Petviashvili equation, Chinese Phys. Lett., 33 (2016), 110201. |
| [50] |
M. Khalfallah, New exact traveling wave solutions of the (3+1) dimensional Kadomtsev-Petviashvili (KP) equation, Commun. Nonlinear Sci., 14 (2009), 1169-1175. doi: 10.1016/j.cnsns.2007.11.010
|
| [51] |
D. I. Sinelshchikov, Comment on: New exact traveling wave solutions of the (3 + 1)-dimensional Kadomtsev-Petviashvili (KP) equation, Commun. Nonlinear Sci., 15 (2010), 3235-3236. doi: 10.1016/j.cnsns.2009.11.028
|
| [52] |
W. X. Ma, Lump solutions to the Kadomtsev-Petviashvili equation, Phys. Lett. A, 379 (2015), 1975-1978. doi: 10.1016/j.physleta.2015.06.061
|
| [53] |
W. X. Ma, Z. Y. Qin, X. Lu, Lump solutions to dimensionally reduced -gKP and -gBKP equations, Nonlinear Dyn., 84 (2016), 923-931. doi: 10.1007/s11071-015-2539-6
|
| [54] |
X. Lu, W. X. Ma, Study of lump dynamics based on a dimensionally reduced Hirota bilinear equation, Nonlinear Dyn., 85 (2016), 1217-1222. doi: 10.1007/s11071-016-2755-8
|
| [55] |
W. X. Ma, Abundant lumps and their interaction solutions of (3+1)-dimensional linear PDEs, J. Geom. Phys., 133 (2018), 10-16. doi: 10.1016/j.geomphys.2018.07.003
|
| [56] |
H. Q. Sun, A. H. Chen, Lump and lump kink solutions of the (3+1)-dimensional Jimbo-Miwa and two extended Jimbo-Miwa equations, Appl. Math. Lett., 68 (2017), 55-61. doi: 10.1016/j.aml.2016.12.008
|
| [57] | R. Hirota, The direct method in soliton theory, Cambridge University Press, Cambridge, UK, 2004. |
| [58] |
D. S. Wang, B. L. Guo, X. L. Wang, Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions, J. Differ. Equations, 266 (2019), 5209-5253. doi: 10.1016/j.jde.2018.10.053
|
| [59] |
D. S. Wang, X. L. Wang, Long-time asymptotics and the bright N-soliton solutions of the Kundu-Eckhaus equation via the Riemann-Hilbert approach, Nonlinear Anal-Real, 41 (2018), 334-361. doi: 10.1016/j.nonrwa.2017.10.014
|
| 1. | Abdullah H. Al-Nefaie, Theyazn H. H. Aldhyani, Nesren Farhah, Deepika Koundal, Intelligent diagnosis system based on artificial intelligence models for predicting freezing of gait in Parkinson’s disease, 2024, 11, 2296-858X, 10.3389/fmed.2024.1418684 | |
| 2. | Yahya Dogan, An innovative approach for parkinson’s disease diagnosis using CNN, NCA, and SVM, 2024, 36, 0941-0643, 20089, 10.1007/s00521-024-10299-8 | |
| 3. | Hasan Alkahtani, Theyazn H. H. Aldhyani, Ahmed Abdullah Alqarni, Artificial Intelligence Models to Predict Disability for Mental Health Disorders, 2024, 3, 1658-9912, 10.57197/JDR-2024-0022 | |
| 4. | Marilena Ianculescu, Corina Petean, Virginia Sandulescu, Adriana Alexandru, Ana-Mihaela Vasilevschi, Early Detection of Parkinson’s Disease Using AI Techniques and Image Analysis, 2024, 14, 2075-4418, 2615, 10.3390/diagnostics14232615 |
Figures(7)
Yu-Lan Ma, Bang-Qing Li. Mixed lump and soliton solutions for a generalized (3+1)-dimensional Kadomtsev-Petviashvili equation[J]. AIMS Mathematics, 2020, 5(2): 1162-1176. doi: 10.3934/math.2020080
| Authors, year | Types of datasets | Models | Object |
| Vanegas et al. [47], 2018 | EGG dataset | LR, DT, Extra tree | Biomarkers PD |
| Oh et al. [48], 2018 | EGG dataset | CNN | PD detection |
| Wagh et al. [49], 2020 | EGG dataset | CNN | PD detection |
| Shi et al. [50], 2019 | EGG dataset | CNN-RNN | PD detection |
| Zhang et al. [51], 2019 | MRI dataset | ResNext model | Detecting prodnormal PD |
| Ramirez et al. [52], 2020 | MRI dataset | Convolution auto encoder | Detecting de Novo PD |
| Prasuhn et al. [53], 2020 | MRI dataset | SVM, MKL | PD detection |
| Rasheed et al. [54], 2020 | Voice dataset | BPVAM | Detecting de Novo PD |
| Gunduz et al. [55], 2019 | Speech dataset | GB, | PD detection |
| Moon et al. [56], 2020 | Gait features dataset | ANN, SVM, KNN | Detecting ET versus PD |
| Zeng et al. [57], 2016 | Gait features dataset | RBF | PD detection |
| Pdisher et al. [58], 2020 | Sensory dataset | CNN | PD diagnosis |
| Taliki et al. [33], 2020 | Sensory dataset | RF | Detecting ET versus PD |
| Shaban et al. [37], 2020 | Handwriting dataset | VGG1-16 | PD detection |
| Robin [59], 2020 | Handwriting dataset (Same dataset) | RF, CNN, RestNet50 | PD detection |
| Stpete_ishii [60], 2023 | Handwriting dataset (Same dataset) | CNN | PD detection |
| Shaban et al. [61], 2020 | Handwriting dataset (Same dataset) | CNN | PD detection |
| Adrian [62], 2019 | Handwriting dataset (Same dataset) | CNN | PD detection |
DownLoad:
CSV
| DenseNet 201 parameter setting | Details |
| Convolutional layer 1 | 256 |
| Kernel size | 5 |
| Convolutional layer 2 number of filters | 128 |
| Kernel size | 5 |
| MaxPooling layer with pool size | 5 |
| Activation function | Softmax function using two outputs |
| Optimizer | Adam RMSprop |
| Number of epochs | 60 |
| Batch size | 32 |
DownLoad:
CSV
| VGG16 parameter settings | Values |
| Convolutional layer 1 | 256 |
| Kernel size | 5 |
| Convolutional layer 2 number of filters | 128 |
| Kernel Size | 5 |
| MaxPooling layer with pool size | 5 |
| Activation function | Relu |
| Optimizer | Adam |
| Number of epochs | 10 |
| Batch size | 32 |
DownLoad:
CSV
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 91 | 100 | 95 | 94 |
| Parkinson's | 100 | 88 | 93 | |
| Weighted avg | 95 | 94 | 94 |
DownLoad:
CSV
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 78 | 100 | 88 | 89 |
| Parkinson's | 100 | 82 | 90 | |
| Weighted avg | 91 | 89 | 89 |
DownLoad:
CSV
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 74 | 93 | 82 | 80 |
| Parkinson's | 91 | 67 | 77 | |
| Weighted avg | 82 | 80 | 80 |
DownLoad:
CSV
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 83 | 100 | 91 | 91 |
| Parkinson's | 100 | 83 | 91 | |
| Weighted avg | 92 | 91 | 91 |
DownLoad:
CSV
| Ref. | Models | Dataset | Accuracy | ROC |
| Ref. [59] | RF | Same dataset 204 spiral and wave images | Wave images=80% | |
| CNN | Spiral image=67% | |||
| ResNet50 | Wave images=87% | |||
| Spiral image=90% | ||||
| Wave images=87% | ||||
| Spiral image=90% | ||||
| Ref. [60] | Lightning CNN | Same dataset used Spiral images | Spiral image=63.33% | |
| Ref. [61] | CNN | Same dataset 204 spiral and wave images | Wave images=88% | |
| Spiral image=89% | ||||
| Ref. [62] | CNN | Same dataset 204 spiral and wave images | Wave images=73% | |
| Spiral image=83% | ||||
| Our enhanced models | DenseNet201 | Same dataset 204 spiral and wave images | Spiral images=94% | 99% |
| VGG16 | Wave image=91% | 90% |
DownLoad:
CSV
| Authors, year | Types of datasets | Models | Object |
| Vanegas et al. [47], 2018 | EGG dataset | LR, DT, Extra tree | Biomarkers PD |
| Oh et al. [48], 2018 | EGG dataset | CNN | PD detection |
| Wagh et al. [49], 2020 | EGG dataset | CNN | PD detection |
| Shi et al. [50], 2019 | EGG dataset | CNN-RNN | PD detection |
| Zhang et al. [51], 2019 | MRI dataset | ResNext model | Detecting prodnormal PD |
| Ramirez et al. [52], 2020 | MRI dataset | Convolution auto encoder | Detecting de Novo PD |
| Prasuhn et al. [53], 2020 | MRI dataset | SVM, MKL | PD detection |
| Rasheed et al. [54], 2020 | Voice dataset | BPVAM | Detecting de Novo PD |
| Gunduz et al. [55], 2019 | Speech dataset | GB, | PD detection |
| Moon et al. [56], 2020 | Gait features dataset | ANN, SVM, KNN | Detecting ET versus PD |
| Zeng et al. [57], 2016 | Gait features dataset | RBF | PD detection |
| Pdisher et al. [58], 2020 | Sensory dataset | CNN | PD diagnosis |
| Taliki et al. [33], 2020 | Sensory dataset | RF | Detecting ET versus PD |
| Shaban et al. [37], 2020 | Handwriting dataset | VGG1-16 | PD detection |
| Robin [59], 2020 | Handwriting dataset (Same dataset) | RF, CNN, RestNet50 | PD detection |
| Stpete_ishii [60], 2023 | Handwriting dataset (Same dataset) | CNN | PD detection |
| Shaban et al. [61], 2020 | Handwriting dataset (Same dataset) | CNN | PD detection |
| Adrian [62], 2019 | Handwriting dataset (Same dataset) | CNN | PD detection |
| DenseNet 201 parameter setting | Details |
| Convolutional layer 1 | 256 |
| Kernel size | 5 |
| Convolutional layer 2 number of filters | 128 |
| Kernel size | 5 |
| MaxPooling layer with pool size | 5 |
| Activation function | Softmax function using two outputs |
| Optimizer | Adam RMSprop |
| Number of epochs | 60 |
| Batch size | 32 |
| VGG16 parameter settings | Values |
| Convolutional layer 1 | 256 |
| Kernel size | 5 |
| Convolutional layer 2 number of filters | 128 |
| Kernel Size | 5 |
| MaxPooling layer with pool size | 5 |
| Activation function | Relu |
| Optimizer | Adam |
| Number of epochs | 10 |
| Batch size | 32 |
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 91 | 100 | 95 | 94 |
| Parkinson's | 100 | 88 | 93 | |
| Weighted avg | 95 | 94 | 94 |
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 78 | 100 | 88 | 89 |
| Parkinson's | 100 | 82 | 90 | |
| Weighted avg | 91 | 89 | 89 |
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 74 | 93 | 82 | 80 |
| Parkinson's | 91 | 67 | 77 | |
| Weighted avg | 82 | 80 | 80 |
| Precision % | Recall % | F1-score % | Accuracy % | |
| Normal | 83 | 100 | 91 | 91 |
| Parkinson's | 100 | 83 | 91 | |
| Weighted avg | 92 | 91 | 91 |
| Ref. | Models | Dataset | Accuracy | ROC |
| Ref. [59] | RF | Same dataset 204 spiral and wave images | Wave images=80% | |
| CNN | Spiral image=67% | |||
| ResNet50 | Wave images=87% | |||
| Spiral image=90% | ||||
| Wave images=87% | ||||
| Spiral image=90% | ||||
| Ref. [60] | Lightning CNN | Same dataset used Spiral images | Spiral image=63.33% | |
| Ref. [61] | CNN | Same dataset 204 spiral and wave images | Wave images=88% | |
| Spiral image=89% | ||||
| Ref. [62] | CNN | Same dataset 204 spiral and wave images | Wave images=73% | |
| Spiral image=83% | ||||
| Our enhanced models | DenseNet201 | Same dataset 204 spiral and wave images | Spiral images=94% | 99% |
| VGG16 | Wave image=91% | 90% |
