Analytical subthreshold swing model of junctionless elliptic gate-all-around (GAA) FET

1.   Introduction

The study of non-Newtonian fluids such as the Walters fluid, Rivlin-Ericksen fluid, and pair stress fluid is critically necessary due to the expanding importance of these fluids in various domains such as industries and modern technologies. In convective problems, it is preferable to study fluid flow with free boundaries in the presence of a solute gradient due to the wide range of applications in the ionosphere, astrophysics, and atmospheric physics. Several liquid systems contain more than two components. As a result, the stability of multi-object systems must be considered. Few authors have looked into triple diffusive convection for fluid/porous media ^[1,2,3,4]. Heat generated by chemical reactions in the fluid brought on by radiation from an external medium might result in the development of an internal heat source (sink), which can help speed up or slow down convection. A perturbation approach was used by Raghunatha et al. ^[5] to study the three-component convection in a porous layer. Patil et al. ^[6,7] investigate triple diffusive boundary layer flow along an external flow velocity that is exponentially and vertically decreasing. The effects of the magnetic field and heat source on three-component convection in an Oldroyd-B liquid were investigated using the Galerkin method by Gayathri et al. ^[8]. Archana et al. ^[9] studied the triple diffusive flow in the presence of nanofluid. Heat transfer has been one of the top contenders to get involved in many applications, which has drawn the attention of many researchers to the study of porous media ^[10]. Eyring-Powell nanomaterials were examined from the triple diffusion perspective by Khan et al. ^[11]. The effects triple-diffusive mixed convection was studied numerically by Sushma et al. ^[12] for Casson fluid. Li et al. ^[13] studied the double diffusion for nanofluid with mixed convection in the presence of a heat source. They discovered that the viscoelastic parameter and Hartmann number cause the wall shear stress to rise. The triple-mass diffusion for nanoparticle mixes in Carreau-Yasuda material was explored by Sohail et al. ^[14]. In presence of chemical reaction and heat source, Sharma and Gandhi ^[15] examined the MHD on heat and mass transmission in a Darcy-Forchheimer porous medium. Using Oldroyd-B type model with heat source, Arshika et al. ^[16] explored the impact of sinusoidal and nonsinusoidal waveforms on triple diffusive-convection in viscoelastic liquids. Using lie-group transformation, Nagendramma et al. ^[17] look into the dynamics of triple diffusive convection. They found that the influence of heat and mass transfer rates decreased for both fluid flow scenarios as the Lewis number increased. In the presence of heat source/sink ^{[18,19,20,21]} and nanofluid ^{[22,23,24,25,26]} few authors have attempted to study the convective stability. The inverse problems in porous media have been studied extensively see ^[27,28].

Recently, for the composite layers, Manjunatha and Sumithra ^[29,30] examined the problem of triple component convection in a combined layer for three different temperature profiles with and without a magnetic field and obtained the corresponding thermal Marangoni numbers. The double-diffusive convection in the existence of a heat source and temperature profiles were studied by Manjunatha and Sumithra ^[31] and Manjunatha et al. ^[32]. They found that a linear model is unstable and an inverted parabolic model is more stable.

The current work examines the stability of the onset of triple-diffusive convective stability in a fluid and fluid-saturated porous layer in the presence of a constant heat source and uses an exact technique to investigate the effect of temperature gradients on the corresponding thermal Marangoni (surface-tension-driven) numbers. Furthermore, the investigation of non-uniform fundamental temperature gradients at the start is intriguing since it opens up new perspectives on how convective instability is managed. The discussion takes into account the following non-dimensional basic temperature gradients: linear, parabolic, and inverted parabolic temperature profiles. Over a wide range of controlling physical parameters, the eigenvalue problem is analytically resolved using the exact technique. Numerous applications in astronomy, engineering, geophysics, climatology, and crystal formation (see Rudolph et al. ^[33]) will surely benefit from this work.

2.   Materials and methods

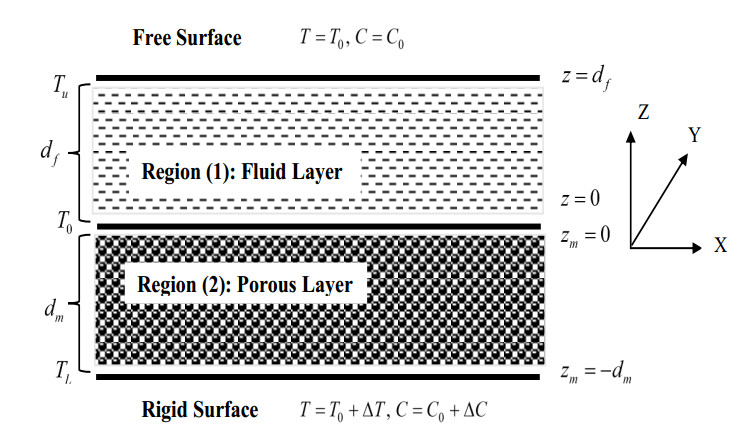
Consider horizontally infinite fluid and fluid-saturated porous layers of depth $d_{f}$ and $d_{m}$ respectively. The lower rigid surface $z_{m} = -d_{m}$ and upper free surface boundary $z = d_{f}$ are maintained at constant temperature and concentration $T = T_{0}$ and $C = C_{0}$. At the upper free region, surface tension ($\sigma_{t}$) force acts which varies linearly with temperature and concentration respectively in the form $\sigma_{t} = \sigma_{0}-\sigma_{T} \Delta T$ and $\sigma_{t} = \sigma_{0}-\sigma_{C} \Delta C$. Where $\sigma_{T} = \frac{-\partial \sigma_{t}}{\partial T}$, $\sigma_{C} = \frac{-\partial \sigma_{t}}{\partial C}$ and $\sigma_{0}$ is the unperturbed value. The fluid-saturated porous medium interface is located at position at $z = 0 = z_{m}$, and the temperature and concentration difference between the lower and higher bounds is denoted by $\Delta T$ and $\Delta C$. A coordinate system is used as shown in Figure 1. The relevant equations with Oberbeck-Boussinesq approximation for two regions as following Roberts ^[34], Char & Chiang ^[35], Del Rio & Whitaker ^[36], Othman ^[37] and Shivakumara et al. ^[38,39].

Region-1, Fluid layer:

Region-2, Porous layer:

where the subscript 'f' refers to the fluid layer (region-1) and the subscript 'm' refers to the porous medium (region-2), ${\vec q_f} = (u, v, w), {\vec q_m} = ({u_m}, {v_m}, {w_m})$ are the velocity vectors, ${\rho _0}$ is the reference fluid density, ${P_f}, {P_m}$ are the pressures, ${Q_f}, {Q_m}$ are the constant heat sources, ${\kappa _f}, {\kappa _m}$ are the thermal diffusivities, ${C_{f1}}, {C_{f2}}, {C_{m1}}, {C_{m2}}$ are the salinity field1 and salinity field2, $K$ is the permeability, $M$ is the ratio of heat capacities, $\phi$ is the porosity, ${\mu _f}, {\mu _m}$ are the fluid viscosities, and ${\kappa _{f1}}, {\kappa _{f2}}, {\kappa _{m1}}, {\kappa _{m2}}$ are the solute1diffusivities and solute2 diffusivities.

The basic state is quiescent in regions 1 and 2, respectively.

The basic state of $T_{f b}(z), T_{m b}\left(z_{m}\right)$, $C_{f i b}(z), C_{m i b}\left(z_{m}\right)$, for $i = 1, 2$, are

where the basic state is denoted by the subscript 'b', $T_{0} = \frac{\kappa_{f} d_{m} T_{u}+\kappa_{m} d_{f} T_{l}}{\kappa d_{m}+\kappa_{m} d_{f}}+\frac{d_{f} d_{m}\left(Q_{m} d_{m}+Q_{f} d_{f}\right)}{2\left(\kappa_{f} d_{m}+\kappa_{m} d_{f}\right)}$ is the interface temperature, $C_{i 0} = \frac{\kappa_{f {i}} d_{m} C_{i u}+\kappa_{m i} d_{f} C_{i l}}{\kappa_{fi} d_{m}+\kappa_{m {i}} d_{f}}$ is the interface concentrations for $i = 1, 2$. $\int\limits_{0}^{d_{f}} \chi_{f}(z) d z = \frac{\Delta T_{f}}{d_{f}}, \int\limits_{0}^{d_{m}} \chi_{m}\left(z_{m}\right)) d z_{m} = \frac{\Delta T_{m}}{d_{m}}$ are the temperature gradient in region-1 and region-2.

To examine the stability of the system, we perturb the system as

where the perturbed primed quantities are those that are very small in relation to the primed quantities of the fundamental state. After substituting Eqs (17) and (18) into Eqs (1–10), linearized in usual manner, eliminate the pressure term from the Eqs (2) and (7) by executing curl twice, and retain the vertical element, the governing stability equations were eventually determined.

Region-1:

Region-2:

here $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}$ is the Laplacian operator.

3.   Stability analysis and normal mode technique

Establish dimensionless values using standard linear stability analysis methods.

The normal mode approach for the fluid and fluid-saturated porous media respectively,

where $\alpha_{x}, \alpha_{y}$ and $\alpha_{x m}, \alpha_{y m}$ are wavenumbers in $x$ and $y$ direction respectively, and $\varpi, \varpi _{m}$ are growth rate (real or complex) in region-1 and region-2 respectively.

Nondimensionalized using (27) and (28), and introducing Eqs (29) and (30) into (19)–(26), the equations are becomes

Region-1: $0 \leq z_{f} \leq 1$

Region-1: $-1 \leq z_{ {m }} \leq 0$

where $P_r = \frac{v_f}{\kappa_f}$, $P_{r m} = \frac{\nu_{m}}{\kappa_{m}}$ are the Prandtl numbers and $\beta = \sqrt{\frac{K}{d_{m}^{2}}}$ is the square root of Darcy number.

For the current problem, the approach of linear stability analysis and the idea of stability exchange are appropriate and effective so take $\sigma = 0$ and $w_{m} = 0$. (Refer Manjunatha and Sumithra ^[30] and Shivakumara et al. ^[38]).The eigenvalue problem (31)–(38) takes the form.

Region-1: $0 \leq z_{f} \leq 1$

Region-1: $-1 \leq z_{m} \leq 0$

where, ${D_f} = \frac{d}{{dz}}, {D_m} = \frac{d}{{d{z_m}}}$ are the Differential operator, ${a_f} = \sqrt {{\alpha _x}^2 + {\alpha _y}^2}, {a_m} = \sqrt {{\alpha _{xm}}^2 + {\alpha _{ym}}^2}$ are the overall horizontal wave numbers, $R_a^* = \frac{{{R_{If}}}}{{2({T_0} - {T_u})}}, R_{am}^* = \frac{{{R_{Im}}}}{{2({T_l} - {T_0})}}$ are the corrected internal Rayleigh numbers, ${R_{If}} = \frac{{{Q_f}d_f^2}}{{{\kappa _f}}}, {R_{Im}} = \frac{{{Q_m}d_m^2}}{{{\kappa _m}}}$ are the internal Rayleigh numbers, ${W_f}(z), {W_m}({z_m})$ are the vertical component of velocities, ${\tau _{f1}} = \frac{{{\kappa _{f1}}}}{{{\kappa _f}}}, {\tau _{f2}} = \frac{{{\kappa _{f2}}}}{{{\kappa _f}}}$ are the diffusivity ratios, ${\tau _{m1}} = \frac{{{\kappa _{m1}}}}{{{\kappa _m}}}, {\tau _{m2}} = \frac{{{\kappa _{m2}}}}{{{\kappa _m}}}$ are the diffusivity ratios in porous region, ${\Sigma _{f1}}(z), {\Sigma _{f2}}(z)$ are the salinity distributions, ${\Sigma _{m1}}({z_m}), {\Sigma _{m2}}({z_m})$ are the salinity distributions on porous region, and ${\Theta _f}(z), {\Theta _m}({z_m})$ are the amplitude temperatures. For the composite system, the overall horizontal wave numbers must be ${a_m} = \hat d{\kern 1pt} {\kern 1pt} {\kern 1pt} {a_f}$, here $\hat d = \frac{{{d_m}}}{{{d_f}}}$ is the depth ratio.

4.   Boundary conditions

The bottom layer is a rigid surface, while the top border is a free surface, with temperature and concentration/salinity affecting surface tension. Prior to applying the normal mode technique, each boundary condition is nondimensionalized (see Sumithra ^[2]).

where $M_{t} = \sigma_{T} \frac{\Delta T d_{f}}{\mu_{f} \kappa_{f}}$ denotes the thermal Marangoni (surface-tension-driven) number (TMN), ${M_{Si}} = \frac{{{\sigma _C}\left({{C_{iu}} - {C_{i0}}} \right){d_f}}}{{{\mu _f}{\kappa _f}}}$ for $i = 1, 2$ denotes the solute Marangoni (surface-tension-driven) numbers (SMN's), $\beta$ is the porous parameter, ${\hat S_i} = \frac{{{C_{il}} - {C_{i0}}}}{{{C_{i0}} - {C_{iu}}}}$ for $i = 1, 2$ is the solute diffusivity ratio, $\widehat T$ is the thermal ratio, and $\hat{\mu} = \frac{\mu_{m}}{\mu_{f}}$ is the viscosity ratio.

5.   Exact method of solution

The eigenvalue problem with an eigenvalue of $M_{t}$ is formed by the boundary conditions of (48) and the Eqs (39)−(46). We address this problem using the exact technique procedure, which produces acceptable results when dealing with difficulties of this nature (see Manjunatha and Sumithra ^[29,30]).

5.1.   Velocity profiles

The velocity profiles are obtained from Eqs (39) and (43) as follows:

where $b_{i}^{\prime} s(i = 1, 2, 3, 4, 5)$ need to be calculated utilizing the suitable velocity conditions of (48) yields to ${b}_{1} = \frac{{a}_{m}{\mathit{cot}ha}_{m}}{2{a}_{f}^{3}{\beta }^{2}{\widehat{d}}^{3}}, {b}_{2} = -1-({b}_{1}+{b}_{3}){\mathit{tan}ha}_{f}, {b}_{3} = \frac{{a}_{m}^{2}\widehat{\mu }-{a}_{f}^{2}{\widehat{d}}^{2}}{{a}_{f}{\widehat{d}}^{2}}, {b}_{4} = \widehat{T}, {b}_{5} = \widehat{T}{\mathit{cot}ha}_{m}$.

5.2.   Salinity profiles

Using the solutal boundary conditions (48), the salinity profiles are obtained from Eqs (41), (42), (45) and (46) as follows

Where, ${g}_{2}\left(z\right) = \frac{-z}{4{a}_{f}^{2}{\tau }_{f1}}\left[\left(2{a}_{f}{b}_{1}-{b}_{2}+{a}_{f}{b}_{3}z\right){\mathit{cos}ha}_{f}z+\left(2{a}_{f}-{b}_{3}+{a}_{f}{b}_{2}z\right){\mathit{sin}ha}_{f}z\right]$, ${g_{2m}}({z_m}) = \frac{{ - {z_m}\cosh {a_m}{z_m}}}{{2{a_m}{\tau _{m1}}}}[({b_5} + {b_4}\tanh {a_m}{z_m})],$${b}_{18} = {\widehat{S}}_{1}{b}_{20}, {b}_{19} = \frac{1}{{a}_{f}}\left({b}_{21}{a}_{m}+{\mathbb{N}}_{1}-{\mathbb{N}}_{2}\right)$, ${b}_{20} = \frac{{\mathbb{N}}_{6}{a}_{m}{\mathit{cos}ha}_{m}-{\mathbb{N}}_{3}{\mathbb{N}}_{5}}{{a}_{m}{\mathit{sin}ha}_{m}\left({\mathbb{N}}_{5}+{\mathbb{N}}_{4}{\mathit{cot}ha}_{m}\right)},$ ${b}_{21} = \frac{{\mathbb{N}}_{3}{\mathbb{N}}_{4}+{\mathbb{N}}_{6}{a}_{m}{\mathit{sin}ha}_{m}}{{a}_{m}{\mathit{sin}ha}_{m}\left({\mathbb{N}}_{5}+{\mathbb{N}}_{4}{\mathit{cot}ha}_{m}\right)}$, ${g_3}(z) = \frac{{ - z}}{{4a_f^2{\tau _{f2}}}}\left[{\left({2{a_f}{b_1} - {b_2} + {a_f}{b_3}z} \right)\cosh {a_f}z + \left({2{a_f} - {b_3} + {a_f}{b_2}z} \right)\sinh {a_f}z} \right],$${g_{3m}}({z_m}) = \frac{{ - {z_m}\sinh {a_m}{z_m}}}{{2{a_m}{\tau _{m2}}}}[({b_5}\coth {a_m}{z_m} + {b_4})],$ ${b}_{22} = {\widehat{S}}_{2}{b}_{24}, {b}_{23} = \frac{1}{{a}_{f}}\left({b}_{25}{a}_{m}+{\mathbb{N}}_{8}-{\mathbb{N}}_{9}\right)$, ${b}_{24} = \frac{{\mathbb{N}}_{13}{a}_{m}{\mathit{cos}ha}_{m}-{\mathbb{N}}_{10}{\mathbb{N}}_{12}}{{a}_{m}{\mathit{sin}ha}_{m}({\mathbb{N}}_{12}+{\mathbb{N}}_{11}{\mathit{cot}ha}_{m})}, {b}_{25} = \frac{{\mathbb{N}}_{10}{\mathbb{N}}_{11}+{\mathbb{N}}_{13}{a}_{m}{\mathit{sin}ha}_{m}}{{a}_{m}{\mathit{sin}ha}_{m}({\mathbb{N}}_{12}+{\mathbb{N}}_{11}{\mathit{cot}ha}_{m})}.$

6.   Temperature gradient

We considered linear, parabolic and inverted parabolic profiles, these profiles have been discussed numerically and analytically by Shivakumara et al. ^[38,39,40] using the Galerkin procedure for porous layers in absence of heat source and in a linear case by Kaloni and Lou ^[41] by applying a compound matrix method for single layers. We have revisited these instances in order to determine the analytical reliability of the results for the two layers on the onset of triple-diffusive convection in a fluid and saturated porous layer.

6.1.   Model 1: Linear temperature profile: $\chi_{f}(z)=1$ and $\chi_m\left(z_m\right)=1$

Introducing model into (40) and (44), the linear profile takes the form

From (47), the thermal Marangoni (surface-tension-driven) number (TMN) for the linear model is

where $\Lambda_{1} = a_{f}^{2}\left(\cosh a_{f}+b_{1} \sinh a_{f}\right)+b_{2}\left(a_{f}^{2} \cosh a_{f}+2 a_{f} \sinh a_{f}\right)+b_{3}\left(a_{f}^{2} \sinh a_{f}+2 a_{f} \cosh a_{f}\right)$, $\Lambda_{2} = \left[b_{18} \cosh a_{f}+b_{18} \sinh a_{f}+g_{2}(1)\right]$, $\Lambda_{3} = \left[b_{25} \cosh a_{f}+b_{2 s} \sinh a_{f}+g_{3}(1)\right]$, $\Theta_{f}(1) = B_{1}\left[b_{6} \cosh a_{f}+b_{3} \sinh a_{f}+g_{1}(1)\right]$, $g_{1}(z) = B_{1}\left[\Delta_{1}-\Delta_{2}+\Delta_{3}-\Delta_{4}\right], g_{1 m}\left(z_{m}\right) = B_{1}\left[\Delta_{5}-\Delta_{6}\right]$.

6.2.   Model 2: Parabolic temperature profile: $\chi_{f}(z)=2 z$ and $\chi_m\left(z_m\right)=2 z_m$

Introducing model (Sparrow et al. ^[42]) into (40) and (44), the profile takes the form

From (47), the TMN for the model is

where $\Theta_{f}(1) = B_{1}\left[b_{10} \cosh a_{f}+b_{11} \text { sinh } a_{f}+g_{4}(1)\right]$,

$g_{4}(z) = B_{1}\left[\Delta_{17}-\Delta_{18}+\Delta_{10}-\Delta_{20}\right], g_{4 m}\left(z_{m}\right) = B_{1}\left[\Delta_{21}-\Delta_{22}\right]$.

6.3.   Model 3: Inverted Parabolic temperature profile: $\chi_{f}(z)=2(1-z)$ and $\chi_m\left(z_m\right)=2\left(1-z_m\right)$

When model is introduced into (40) and (44), the profile becomes

From (47), the TMN for the profile is

where $\Theta_{f}(1) = B_{1}\left[b_{4} \cosh a_{f}+b_{15} \sinh a_{f}+g_{5}(1)\right]$, $g_5(z) = B_1\left[\Delta_{31}-\Delta_{32}+\Delta_{33}-\Delta_{34}\right], g_{5 m}\left(z_m\right) = B_1\left[\Delta_{35}-\Delta_{36}\right]$ (See Appendix).

7.   Results and discussion

The present study aims at solving exactly the problem of Marangoni convection in presence of a heat source and temperature gradients. The exact method provides useful results and also general basic temperature profiles can be readily treated with minimum mathematical computations. The graphs are plotted using MATHEMATICA version 11. The TMNs $M_{t 1}$ for model 1 as linear, $M_{t2}$ model 2 as parabolic, and $M_{t3}$ model 3 as inverted parabolic temperature profiles have been investigated with the object of understanding the control of convection. The depth ratio $\hat{d}$ is used to draw the limits. The effects of the parameters $\beta, R_{a}^{*}$$R_{a m}^{*}, M_{s 1}, M_{s 2}$ and $\tau_{f 2}$ for linear, parabolic and inverted parabolic profiles on all three TMNs are depicted in Figures 2−7. The major finding is that for a given set of fixed parameter values, the inverted parabolic profile is the most stable, while the linear profile is the most unstable, as the corresponding TMNs are highest and lowest, respectively, for porous layer dominant systems, i.e., $M_{t 1} \prec M_{t 2} \prec M_{t 3}$.

Figure 2 depicts the fluctuations of the porous parameter $\beta$ on the three TMNs for linear, parabolic, and inverted temperature profiles for $\beta = 0.1, 0.5, 1, 5, 10$. The TMNs for all three profiles rise when the value of $\beta$, i.e., the permeability of the porous layer, increases. As a result, raising the porosity parameter can influence the onset of triple-diffusive convection, which is physically sensible because the fluid has more ways to travel. As a result, the system has reached a state of equilibrium. The effect of corrected internal Rayleigh numbers $R_{a}^{*}$ and ${R}_{a m}^{*}$ on the onset of triple-diffusive convection is explained in Figures 3 and 4 respectively, for all three profiles. Negative values of these parameters indicate heat sinks, while the positive values indicate heat sources. It is evident from the figures that these parameters are effective for larger values of depth ratio, i.e., for porous layer dominant composite layer systems and the effect of ${R}_{a m}^{*}$ is drastic when compared to that of $R_{a}^{*}$. For a given depth ratio, the thermal Marangoni number rises as the value of these parameters rises, indicating a delay in the commencement of the onset of triple-diffusive convection, which is particularly pronounced for ${R}_{a m}^{*}$. The effects of $M_{S 1}$ and $M_{S 2}$, the solute1, solute2 Marangoni numbers for $M_{S 1} = M_{S 2} = 1, 5, 10, 25, 50$ on the onset of triple-diffusive convection is displayed in Figures 5 and 6. The TMNs drop for each of the three temperature profiles as the solute1 Marangoni number values are raised. So, the onset of triple-diffusive convection can be postponed; hence, the system can be destabilized. The system easily stabilizes if more high-solute diffusivity salts are added. However, it is clear that the solute2 Marangoni number turns the process around. Therefore, by increasing the solute2 Marangoni number, the onset of triple-diffusive convection can be postponed, stabilizing the system and helping to determine its stability features. This demonstrates that there is a third diffusing component, at which point the onset of triple-diffusive convection influences the stability of the system.

Figure 7 displays the effects of $\tau_{f 2}$, the ratio of solute2 diffusivity to thermal diffusivity fluid in the fluid layer, which is the significance of the presence of a third diffusing component, for $M_{{t1}}, M_{t 2}$ and $M_{t3}$ respectively, for the values $\tau_{f 2} = 0.1, 0.3, 0.5, 0.7, 0.9$. Smaller depth ratio values, or fluid layer dominating composite layer systems, have no effect on the TMNs for any of the three profiles. In a composite layer system with a porous layer as the dominating layer, the system can become unstable as $\tau_{f 2}$ is increased because onset of triple-diffusive convection begins to develop more quickly. This is perfectly understandable because, in contrast to the energy stability theory, the linear stability theory specifies sufficient requirements for stability.

8.   Conclusions

The conclusions presented above provide a general framework for investigating the role of the porous parameter, corrected internal Rayleigh numbers, solutal Marangoni (surface-tension-driven) numbers, and fluid thermal diffusivity ratio on the onset of triple-diffusive convection in a fluid and fluid-saturated layer of the porous medium. For a variety of fundamental uniform and non-uniform temperature gradients in the presence of a constant heat source, the principle of exchange of stability is found to be valid, and the problem of eigenvalue is solved using the exact technique.

The investigation's findings are as follows:

The parameters in the study have a larger influence on the porous layer dominant composite layer systems than that on the fluid layer dominant composite systems.

The larger values of the porous parameter, corrected internal Rayleigh numbers and solute Marangoni (surface-tension-driven) number $M_{s2}$ and the lower values of $\tau_{f 2}$ and $M_{s1}$ are preferable for controlling the onset of triple-diffusive convection.

The system is stabilized by the porous parameter, corrected internal Rayleigh numbers, and the solute2 Marangoni (surface-tension-driven) number, while the system is destabilized by the solute1 Marangoni (surface-tension-driven) number and the ratio of the solute2 diffusivity to the thermal diffusivity of the fluid.

The inverted parabolic temperature (model 3) profile is the most stable and hence suitable for controlling the onset of triple-diffusive convection whereas the linear temperature (model 1) profile is the most unstable for augmenting the onset of triple-diffusive convection for the set of parameters chosen for this investigation.

The system is more stable for model 3 and less stable for model 1. i.e., $M_{t 1} \prec M_{t 2} \prec M_{t 3}$.

This work can be extended to temperature-dependent heat sources and Soret and Dupour effects to analyses the onset of triple-diffusive convection.

Acknowledgments

The authors are thankful for the support of Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R163), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

Authors are declaring no conflict of interest.

Supplementary (Appendix)