Evolving blocks by segmentation for neural architecture search

1.   Introduction

As stated in ^[1], a nervous system in the real world, synaptic transmission is a noisy process caused by random fluctuations in neurotransmitter release and other probabilistic factors. Therefore, it is necessary to consider stochastic neural networks (NNs) because random inputs may change the dynamics of the (NN) ^[2,3,4,5].

SICNNs, which were proposed in ^[6], have attracted the interest of many scholars since their introduction due to their special roles in psychophysics, robotics, adaptive pattern recognition, vision, and image processing. In the above applications, their dynamics play an important role. Thereupon, their various dynamics have been extensively studied (see ^{[7,8,9,10,11,12,13]} and references therein). However, there is limited research on the dynamics of stochastic SICNNs. Therefore, it is necessary to further study the dynamics of such NNs.

On the one hand, research on the dynamics of NNs that take values from a non commutative algebra, such as quaternion-valued NNs ^[14,15,16], octonion-valued NNs ^{[17,18,19,20]}, and Clifford-valued NNs ^[21,22,23], has gained the interest of many researchers because such neural networks can include typical real-valued NNs as their special cases, and they have superior multi-dimensional signal processing and data storage capabilities compared to real-valued NNs. It is worth mentioning that in recent years, many authors have conducted extensive research on various dynamics of Clifford-valued NNs, such as the existence, multiplicity and stability of equilibrium points, and the existence, multiplicity and stability of almost periodic solutions as well as the synchronization problems ^{[22,23,24,25,26,27,28,29,30]}. However, most of the existing results for the dynamics of Clifford-valued NNs has been obtained through decomposition methods ^{[24,25,26,27]}. However, the results obtained by decomposition methods are generally not convenient for direct application, and there is little research on Clifford-valued NNs using non decomposition methods ^[28,29,30]. Therefore, further exploration of using non decomposition methods to study the dynamics of Clifford-valued NNs has important theoretical significance and application value.

On the other hand, Bohr's almost periodicity is a special case of Stepanov's almost periodicity, but there is little research on the Stepanov periodic oscillations of NNs ^{[19,31,32,33]}, especially the results of Stepanov's almost periodic solutions of stochastic SICNNs with discrete and infinitely distributed delays have not been published yet.

Motivated by the discussion above, our purpose of this article is to establish the existence and global exponential stability of Stepanov almost periodic solutions in the distribution sense for a stochastic Clifford-valued SICNN with mixed delays via non decomposition methods.

The subsequent sections of this article are organized as follows. Section 2 introduces some concepts, notations, and basic lemmas and gives a model description. Section 3 discusses the existence and stability of Stepanov almost periodic solutions in the distribution sense of the NN under consideration. An example is provided in Section 4. Finally, Section 5 provides a brief conclusion.

2.   Preliminaries and model description

Let $\mathscr{A} = \big\{\sum_{\vartheta\in \mathbb{P}}x^\vartheta e_\vartheta, x^\vartheta\in \mathbb{R}\big\}$ be a real Clifford-algebra with $N$ generators $e_{\emptyset} = e_0 = 1$, and $e_h, h = 1, 2, \cdots, N$, where $\mathbb{P} = \{\emptyset, 0, 1, 2, \cdots, \vartheta, \cdots, 12\cdots N\}$, $e_i^2 = 1, i = 1, 2, \cdots, r, e_i^2 = -1, i = r+1, r+2, \cdots, m, e_ie_j+e_je_i = 0, i\neq j$ and $i, j = 1, 2, \cdots, N$. For $x = \sum_{\vartheta\in \mathbb{P}}x^\vartheta e_\vartheta \in \mathscr{A}$, we indicate $\| x \|_{\flat} = \max_{\vartheta\in \mathbb{P}}\{|x^\vartheta|\}, x^c = \sum_{\vartheta\neq\emptyset}x^\vartheta e_\vartheta, x^{0} = x-x^c$, and for $x = (x_{11}, x_{12}, \ldots, x_{1n}, x_{21}, x_{22}, \ldots, x_{2n}, \ldots, x_{mn})^T\in \mathscr{A}^{m\times n}$, we denote $\| x \|_{0} = \max\{\| x_{ij} \|_{\flat}, 1\leq i\leq m, 1\leq j\leq n\}$. The derivative of $x(t) = \sum_{\vartheta\in \mathbb{P}}x^\vartheta(t)e_\vartheta$ is defined by $\dot{x}(t) = \sum_{\vartheta\in \mathbb{P}}\dot{x}^\vartheta(t)e_\vartheta$ and the integral of $x(t) = \sum_{\vartheta\in \mathbb{P}}x^\vartheta(t)e_\vartheta$ over the interval $[a, b]$ is defined by $\int_{a}^{b}{x}(t)dt = \sum_{\vartheta\in \mathbb{P}}\big(\int_{a}^{b}{x}^\vartheta(t)dt\big) e_\vartheta$.

Let $(\mathbb Y, \rho)$ be a separable metric space and $\mathcal P(\mathbb Y)$ the collection of all probability measures defined on Borel $\sigma$-algebra of $\mathbb{Y}$. Denote by $C_b(\mathbb Y)$ the set of continuous functions $f:\mathbb Y\rightarrow \mathbb R$ with $\|g\|_\infty: = \sup_{x\in\mathbb Y}\{| g(x)|\} < \infty$.

For $g\in C_b(\mathbb Y)$, $\mu, \nu\in \mathcal{P}(\mathbb Y)$, let us define

According to ^[34], $(\mathbb{Y}, \rho_{BL}(\cdot, \cdot))$ is a Polish space.

Definition 2.1. ^[35] A continuous function $g:\mathbb{R}\rightarrow \mathbb{Y}$ is called almost periodic if for every $\varepsilon > 0$, there is an $\ell(\varepsilon) > 0$ such that each interval with length $\ell$ has a point $\tau$ meeting

We indicate by $AP(\mathbb{R}, \mathbb{Y})$ the set of all such functions.

Let $(\mathbb{X}, \|\cdot\|)$ signify a separable Banach space. Denote by $\mu(X): = P\circ X^{-1}$ and $E(X)$ the distribution and the expectation of $X:(\Omega, \mathcal{F}, P)\rightarrow \mathbb{X}$, respectively.

Let $\mathcal L^p(\Omega, \mathbb{X})$ indicate the family of all $\mathbb{X}$-valued random variables satisfying $E(\| X\|^p) = \int_{\Omega}\| X\|^pdP < \infty.$

Definition 2.2. ^[21] A process $Z:\mathbb R\rightarrow \mathcal L^p(\Omega, \mathbb{X})$ is called $\mathcal L^p$-continuous if for any $t_0\in \mathbb R$,

It is $\mathcal L^p$-bounded if $\sup\limits_{t\in \mathbb R}E\| Z(t)\|^p < \infty$.

For $1 < p < \infty$, we denote by $\mathcal{L}_{loc}^p(\mathbb{R}, \mathbb{X})$ the space of all functions from $\mathbb{R}$ to $\mathbb{X}$ which are locally $p$-integrable. For $g\in \mathcal{L}_{loc}^p(\mathbb{R}, \mathbb{X})$, we consider the following Stepanov norm:

Definition 2.3. ^[35] A function $g\in \mathcal{L}^p_{loc}(\mathbb R, \mathbb{X})$ is called $p$-th Stepanov almost periodic if for any $\varepsilon > 0$, it is possible to find a number $\ell > 0$ such that every interval with length $\ell$ has a number $\tau$ such that

Definition 2.4. ^[9] A stochastic process $Z\in \mathcal L_{loc }^p(\mathbb{R}, \mathcal{L}^p(\Omega, \mathbb{X}))$ is said to be $S^p$-bounded if

Definition 2.5. ^[9] A stochastic process $Z\in \mathcal{L}_{loc}(\mathbb R, \mathcal L^p(\Omega, \mathbb{H}))$ is called Stepanov almost periodic in $p$-th mean if for any $\varepsilon > 0$, it is possible to find a number $\ell > 0$ such that every interval with length $\ell$ has a number $\tau$ such that

Definition 2.6. ^[9] A stochastic process $Z:\mathbb R\rightarrow \mathcal L^p(\Omega, \mathbb{X}))$ is said to be $p$-th Stepanov almost periodic in the distribution sense if for each $\varepsilon > 0$, it is possible to find a number $\ell > 0$ such that any interval with length $\ell$ has a number $\tau$ such that

Lemma 2.1. ^[36] (Burkholder-Davis-Gundy inequality) If $f\in\mathcal L^2(J, \mathbb R)$, $p > 2$, $B(t)$ is Brownian motion, then

where $c_p = \Big(\frac{p^{p+1}}{2(p-1)^{p-1}} \Big)^{\frac{p}{2}}.$

The model that we consider in this paper is the following stochastic Clifford-valued SICNN with mixed delays:

where $i = 1, 2, \cdots, m, j = 1, 2, \cdots, n$, $C_{ij}(t)$ represents the cell at the $(i, j)$ position, the $h_1$-neighborhood $N_{h_1}(i, j)$ of $C_{ij}$ is given as:

$N_{h_2}(i, j), N_{h_3}(i, j)$ are similarly defined, $x_{ij}$ denotes the activity of the cell $C_{ij}$, $L_{ij}(t):\mathbb{R}\to \mathscr{A}$ corresponds to the external input to $C_{ij}$, the function $a_{ij}(t):\mathbb{R}\to \mathscr{A}$ represents the decay rate of the cell activity, $C_{ij}^{kl}(t):\mathbb{R}\to \mathscr{A}, B_{ij}^{kl}(t):\mathbb{R}\to \mathscr{A}$ and $E_{ij}^{kl}(t):\mathbb{R}\to \mathscr{A}$ signify the connection or coupling strength of postsynaptic activity of the cell transmitted to the cell $C_{ij}$, and the activity functions $f(\cdot):\mathscr{A}\to\mathscr{A}$, and $g(\cdot):\mathscr{A}\to\mathscr{A}$ are continuous functions representing the output or firing rate of the cell $C_{kl}$, and $\tau_{kl}(t), \sigma_{ij}(t):\mathbb{R}\to\mathbb{R}^+$ are the transmission delay, the kernel $K_{ij}(t):\mathbb{R}\to\mathbb{R}$ is an integrable function, $\omega_{ij}(t)$ represents the Brownian motion defined on a complete probability space, $\delta_{ij}(\cdot):\mathscr{A}\to \mathscr{A}$ is a Borel measurable function.

Let ($\Omega$, $\mathscr{F}$, $\{\mathscr{F}_t\}_{t\geqslant 0}$, $P$) be a complete probability space in which $\{\mathscr{F}_t\}_{t\geqslant 0}$ is a natural filtration meeting the usual conditions. Denote by $B_{\mathscr{F}_0}([-\theta, 0], \mathscr{A}^n)$ the family of bounded, $\mathscr{F}_0$-measurable and $\mathscr{A}^n$-valued random variables from $[-\theta, 0]\rightarrow \mathscr{A}^n$. The initial values of system (2.1) are depicted as

where $\phi_i\in B_{\mathscr{F}_0} ([-\theta, 0], \mathscr{A}), \theta = \max\limits_{1\leq i, j\leq n}\{ \sup\limits_{t\in \mathbb{R}}\tau_{ij}(t), \sup\limits_{t\in \mathbb{R}}\sigma_{ij}(t)\}$.

For convenience, we introduce the following notations:

Throughout this paper, we make the following assumptions:

$(A1)$ For $ij\in\Lambda$, $f, g, \delta_{ij}\in C(\mathscr{A}, \mathscr{A})$ satisfy the Lipschitz condition, and $f, g$ are bounded, that is, there exist constants $L_f > 0, L_g > 0, L_{ij}^{\delta} > 0, M_f > 0, M_g > 0$ such that for all $x, y\in \mathscr{A}$,

furthermore, $f(0) = g(0) = \delta_{ij}(0) = 0$.

$(A2)$ For $ij\in\Lambda$, ${a}_{ij}^0\in AP(\mathbb{R}, \mathbb{R}^+), {a}_{ij}^c\in AP(\mathbb{R}, \mathscr{A}), \tau_{ij}, \sigma_{ij}\in AP(\mathbb{R}, \mathbb{R}^+)\cap C^1(\mathbb{R}, \mathbb{R})$ satisfying $1-\dot{\tau}_{ij}^+, 1-\dot{\sigma}_{ij}^+ > 0$, $C_{ij}^{kl}, B_{ij}^{kl}, E_{ij}^{kl}\in AP(\mathbb{R}, \mathscr{A})$, $L = (L_{11}, L_{12}, \cdots, L_{mn})\in\mathscr{L}_{loc}^p(\mathbb{R}, L^p(\Omega, \mathscr{A}^{m\times n}))$ is almost periodic in the sense of Stepanov.

$(A3)$ For $p > 2, \frac{1}{p}+\frac{1}{q} = 1$,

and for $p = 2$,

$(A4)$ For $\frac{1}{p}+\frac{1}{q} = 1$,

$(A5)$ The kernel $K_{ij}$ is almost periodic and there exist constants $M > 0$ and $u > 0$ such that $|K_{ij}(t)|\leq Me^{-ut}$ for all $t\in \mathbb{R}$.

3.   Main results

Let $\mathbb{X}$ indicate the space of all $\mathcal{L}^p$-bounded and $\mathcal{L}^p$-uniformly continuous stochastic processes from $\mathbb{R}$ to $\mathcal{L}^p(\Omega, \mathscr{A}^{m\times n})$, then with the norm $\|\phi\|_{\mathbb{X}} = \sup\limits_{t\in\mathbb{R}}\big\{E\|\phi(t)\|_0^p\big\}^{\frac{1}{p}},$ where $\phi = (\phi_{11}, \phi_{12}, \ldots, \phi_{mn})\in \mathbb{X}$, it is a Banach space.

Set $\phi^0 = (\phi_{11}^0, \phi_{12}^0, \ldots, \phi_{mn}^0)^T$, where $\phi_{ij}^0(t) = \int_{-\infty}^te^{-\int_s^ta_{ij}^0(u)du}L_{ij}(s)ds, t\in\mathbb{R}, ij\in\Lambda$. Then, $\phi^0$ is well defined under assumption $(A2)$. Consequently, we can take a constant $\kappa$ such that $\kappa\geq \|\phi^0\|_{\mathbb{X}}$.

Definition 3.1. ^[37] An $\mathscr{F}_t$-progressively measurable stochastic process $x(t) = (x_{11}(t), x_{12}(t), \ldots, x_{mn}(t))^T$ is called a solution of system (2.1), if $x(t)$ solves the following integral equation:

In (3.1), let $t_0\rightarrow -\infty$, then one gets

It is easy to see that if $x(t)$ solves (3.2), then it also solves (2.1).

Theorem 3.1. Assume that $(A1)$–$(A4)$ hold. Then the system (2.1) has a unique $\mathcal{L}^p$-bounded and $\mathcal{L}^p$-uniformly continuous solution in $\mathbb{X}^* = \{\phi\in\mathbb{X}:\|\phi-\phi^0\|_{\mathbb{X}}\leq \kappa\}$, where $\kappa$ is a constant satisfying $\kappa\geq \|\phi^0\|_{\mathbb{X}}$.

Proof. Define an operator $\phi:\mathbb{X}^*\to \mathbb{X}$ as follows:

where $(\phi_{11}, \phi_{12}, \ldots, \phi_{mn})^T\in\mathbb{X}$, $t\in\mathbb{R}$ and

First of all, let us show that $E\|\Psi \phi(t)-\phi^0(t)\|_{0}^p\leq \kappa$ for all $\phi\in \mathbb{X}^*$.

Noticing that for any $\phi\in\mathbb{X}^*$, it holds

Then, we deduce that

By the Hölder inequality, we have

Similarly, one has

By the Burkolder-Davis-Gundy inequality and the Hölder inequality, when $p > 2$, we infer that

When $p = 2$, by the It$\rm \hat{o}$ isometry, it follows that

Putting (3.5)–(3.9) into (3.4), we obtain that

and

It follows from (3.10), (3.11) and $(A3)$ that $\|\Psi\phi-\phi^0\|_{\mathbb{X}} \leq \kappa$.

Then, using the same method as that in the proof of Theorem 3.2 in ^[21], we can show that $\Psi\phi$ is $\mathcal{L}^p$-uniformly continuous. Therefore, we have $\Psi({\mathbb{X}}^*) \subset \mathbb{X}^*$.

Last, we will show that $\Psi$ is a contraction mapping. Indeed, for any $\psi, \varphi \in \mathbb{X}^*$, when $p > 2$, we have

Similarly, for $p = 2$, we can get

From (3.12) and (3.13) it follows that

Hence, by virtue of $(A3)$, $\Psi$ is a contraction mapping. So, $\Psi$ has a unique fixed point $x$ in $\mathbb{X}^*$, i.e., (2.1) has a unique solution $x$ in $\mathbb{X}^*$. □

Theorem 3.2. Assume that $(A1)$–$(A5)$ hold. Then the system (2.1) has a unique $p$-th Stepanov-like almost periodic solution in the distribution sense in $\mathbb{X}^* = \{\phi\in\mathbb{X}:\|\phi-\phi^0\|_{\mathbb{X}}\leq \kappa\}$, where $\kappa$ is a constant satisfying $\kappa\geq \|\phi^0\|_{\mathbb{X}}$.

Proof. From Theorem 3.1, we know that (2.1) has a unique solution $x$ in $\mathbb{X}^*$. Now, let us show that $x$ is Stepanov-like almost periodic in distribution. Since $x\in \mathbb{X}^*$, it is $\mathcal{L}^p$-uniformly continuous and satisfies $\|x\|\leq 2\kappa$. So, for any $\varepsilon > 0$, there exists $\delta\in (0, \varepsilon)$, when $|h| < \delta$, we have $\sup_{t\in\mathbb{R}} E\| x(t+h)-x(t) \|_0^p < \varepsilon$. Hence, we derive that

For the $\delta$ above, according to $(A2)$, we have, for $ij\in\Lambda$,

As $|\tau_{ij}(t+\tau)-\tau_{ij}(t)| < \delta$, by (3.14), there holds

Based on (3.2), we can infer that

in which $ij\in\Lambda, \omega_{ij}(s+\tau)-\omega_{ij}(\tau)$ is a Brownian motion having the same distribution as $\omega_{ij}(s)$.

Let us consider the process

From (3.2) and (3.15), we deduce that

Employing the Hölder inequality, we can obtain

By a change of variables and Fubini's theorem, we infer that

where

Similarly, when $p > 2$, one can obtain

where

and when $p = 2$, we have

where

In the same way, we can get

Noting that

We can gain

when $p > 2$, we have

for $p = 2$, we get

Substituting (3.17)–(3.36) into (3.16), we have the following two cases:

Case 1. When $p > 2$, we have

where $\rho^1$ is the same as that in $(A3)$ and $H^1 = \bigtriangleup_{H_1} + \bigtriangleup_{H_2} +\bigtriangleup_{H_4} +\bigtriangleup_{H_6} +\bigtriangleup_{H_8} +\bigtriangleup_{H_9} +\bigtriangleup_{H_{10}} +\bigtriangleup_{H_{14}} +\bigtriangleup_{H_{16}} +\bigtriangleup_{H_{11}^1} +\bigtriangleup_{H_{12}^1} +\bigtriangleup_{H_{13}^1}.$

By $(A4)$, we know $\rho^1 < \frac{p\underline{a}^0}{q}$. Hence, we derive that

Case 2. When $p = 2$, we can obtain

where $\rho^2$ is defined in $(A4)$ and

Similar to the previous case, by $(A4)$, we know $\rho^2 < \underline{a}^0$ and hence, we can get that

Noting that

Hence, we have

Combining (3.37)–(3.39), we can conclude that $x(t)$ is $p$-th Stepanov almost periodic in the distribution sense. The proof is complete. □

Similar to the proof of Theorem 3.7 in ^[21], one can easily show that.

Theorem 3.3. Suppose that $(A1)$–$(A5)$ are fulfilled and let $x$ be the Stepanov almost periodic solution in the distribution sense of system (2.1) with initial value $\varphi$. Then there exist constants $\lambda > 0$ and $M > 0$ such that for an arbitrary solution $y$ with initial value $\psi$ satisfies

where $\| \varphi -\psi \|_1 = \sup_{a\in[-\theta, 0]} E\| \varphi(s) -\psi(s) \|_0^p$, i.e., the solution $x$ is globally exponentially stable.

4.   Numerical example

The purpose of this section is to demonstrate the effectiveness of the results obtained in this paper through a numerical example.

In neural network (2.1), choose $f(x) = \frac{1}{25} \sin x^0 e_0+\frac{1}{30} \sin (x^2+x^0) e_1+\frac{1}{35}\sin^2x^{12} e_2+\frac{1}{40}\tanh^2x^2 e_{12}$, $g(x) = \frac{1}{40} \sin x^0 e_0+\frac{1}{35} \sin (x^2+x^1) e_1+\frac{1}{30}\sin^2x^{12} e_2+\frac{1}{25}\tanh^2x^1 e_{12}$, $K_{ij}(t) = \frac{1}{e^{t}}$ and

and let $h_1 = h_2 = 1, h_3 = 0, m = n = 2$. Then we get

Take $\kappa = 1$, $p = \frac{21}{10}, q = \frac{21}{11}$, then we have

And when $p = 2$, we have

Thus, all assumptions in Theorems 3.2 and 3.3 are fulfilled. So we can conclude that the system (2.1) has a unique $S^p$-almost periodic solution in the distribution sense which is globally exponentially stable.

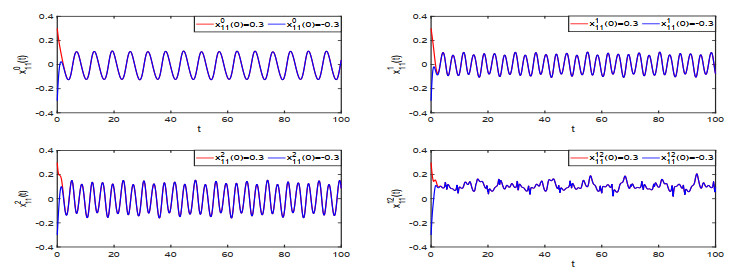
The results are also verified by the numerical simulations in Figures 1–4.

From these figures, we can observe that when the four primitive components of each solution of this system take different initial values, they eventually tend to stabilize. It can be seen that these solutions that meet the above conditions do exist and are exponentially stable.

5.   Conclusions

In this article, we establish the existence and global exponential stability of Stepanov almost periodic solutions in the distribution sense for a class of stochastic Clifford-valued SICNNs with mixed delays. Even when network (2.1) degenerates into a real-valued NN, the results of this paper are new. In fact, uncertainty, namely fuzziness, is also a problem that needs to be considered in real system modeling. However, we consider only the disturbance of random factors and do not consider the issue of fuzziness. In a NN, considering the effects of both random perturbations and fuzziness is our future direction of effort.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant No. 12261098.

Conflict of interest

The authors declare that they have no conflicts of interest.