Almost periodic solutions of fuzzy shunting inhibitory CNNs with delays

1.   Introduction

In 1993, a new class of cellular neural networks (CNNs) was introduced, called shunting inhibitory CNNs (SICNNs) ^[1]. SICNNs are based on shunting neural networks and CNNs, both of which were applied in different branches of engineering, described in ^[1]. Apart from applicability of neural networks, it is also interesting to investigate periodic and almost periodic solutions, as they are important for analyzing the stability of biological systems ^[2]. In this paper, we consider SICNNs which incorporate consequences of real-world applications, such as possible delay of system response ^[3] and uncertainties. Both of these effects are modeled using time-delays and fuzziness respectively, resulting in modified version of SICNNs, called fuzzy SICNNs (FSICNNs) with time-delays. We aim to study existence and stability of almost periodic solutions of FSICNNs, continuing the study initiated in ^[4].

Existence and stability of different types of periodic solutions were extensively studied for CNNs, fuzzy CNNs (FCNNs), SICNNs. For instance, sufficient conditions for existence and stability of periodic solutions were presented for delayed CNNs ^[5,6], CNNs with time-varying delays ^[7], discrete analogue of CNNs ^[8]. Similarly, almost periodic solutions were studied for CNNs with distributed delays ^[9], time-varying delays ^[10,11], time-varying delays in leakage terms ^[12]. Delayed CNNs with impulsive effects were studied for periodic solutions ^[13] and anti-periodic solutions ^[14]. Using Lyapunov functionals, existence and stability criteria of periodic solutions were shown for FCNNS with time-varying delay ^[15], with distributed delay ^[16]. Almost periodic solutions of FCNNs were also considered, with time-varying delays ^[17], multi-proportional delays ^[18]. Existence and stability of pseudo almost periodic solutions were studied for FCNNs with multi-proportional delays ^[19], time-varying delays ^[20] and for quaternion-valued version with delays ^[21]. Study about almost periodic solutions for SICNNs were initiated in ^[22]. Further, existence of stable almost periodic solutions were analyzed for SICNNs with time-varying delay ^[23,25], continuously distributed delays ^[24], impulse ^[26]. In addition, with no assumption of Lipshitz conditions for activation function, results about almost periodic solutions were further improved ^[27,28]. Anti-periodic solutions were presented for SICNNs with different types of delays ^{[29,30,31,32,33,34]}.

Existence of periodic solutions were also studied for FSICNNs with delays ^[4]. However, to the best of our knowledge, existence and stability analysis of almost periodic solutions for FSICNNs are not studied yet. Therefore, we aim to fill this gap by presenting the study of almost periodic solutions for FSICNNs with several delays. In particular, here we present sufficient conditions for existence and stability of almost periodic solutions, and importantly, numerical examples confirming theoretical findings are presented.

We will consider the description of the FSICNN in the following form.

where $C_{pq},$ $p = 1, 2, \ldots, m,$ $q = 1, 2, \ldots, n,$ denote the cell at the $(p, q)$ position of the lattice, the $r-$neighborhood of $C_{pq}$ is

$x_{pq}$ represents the activity of the cell $C_{pq}$ at time $t;$ the positive function $a_{pq}(t)$ is the passive decay rate of the cell activity; $U_{pq}(t)$ is the external input whereas $L_{pq}(t)$ is the external bias on the $(p, q)$th cell; the nonnegative functions $C_{pq}^{kl}(t)$, $D_{pq}^{kl}(t),$ $E_{pq}^{kl}(t),$ $T_{pq}^{kl}(t),$ and $H_{pq}^{kl}(t)$ are the connection or coupling strength of the postsynaptic activity, the fuzzy feedback MIN template, fuzzy feedback MAX template, fuzzy feed forward MIN template, and fuzzy feed forward MAX template of the cell $C_{kl}$ transmitted to the cell $C_{pq}$ at time $t,$ respectively; $\bigwedge$ is the fuzzy AND operation whereas $\bigvee$ is the fuzzy OR operation; the function $f(x_{kl})$ represents a measure of activation to the output or firing rate of the cell $C_{kl}$; and $\tau_{kl}$ corresponds to the transmission delay along the axon of the $(k, l)$th cell from the $(p, q)$th cell.

We consider the network (1.1) subject to initial data

where $\rho_{pq}(s)$ is the real-valued continuous function and $\tau = \max\limits_{\begin{smallmatrix}1\leq k\leq m\\1\leq l\leq n\end{smallmatrix}}\{\tau_{kl}\}$. Let us denote $\overline{g} = \underset{t \in R}{\sup}\ g(t)$ and $\underline{g} = \underset{t \in R}{\inf}\ g(t)$. In this paper, we use the maximum and supremum norms given by $||x|| = \max_{(p, q)}|x_{pq}|$, $x = \left\lbrace x_{pq} \right\rbrace \in \mathbb{R}^{m\times n}$, and $||x||_{\infty} = \sup_{t\in R}\|x(t)\|$, respectively. We use the following Bohr definition of almost periodic functions.

Definition 1.1. ^[35,36] A continuous function $\psi: \mathbb{R} \mapsto \mathbb{R}$ is almost periodic if for every $\epsilon > 0$, there exists a number $l > 0$ with the property that any interval of length $l$ of the real line contains at least one point $\omega$ for which

2.   Almost periodic solutions

In this section, we study the existence and uniqueness of almost periodic solutions to the network (1.1). For this purpose, we shall need the following conditions.

$\textbf{(A1)}$ The functions $a_{pq}(t), B_{pq}^{kl}(t), C_{pq}^{kl}(t), D_{pq}^{kl}(t), E_{pq}^{kl}(t),$ $H_{pq}^{kl}(t), T_{pq}^{kl}(t), L_{pq}(t)$ and $U_{pq}(t)$ are continuous almost-periodic functions for $p, k = \overline{1, m}, \, q, l = \overline{1, n}$.

$\textbf{(A2)}$ The function $f(\cdot)$ is Lipschitz continuous on $\mathbb{R}$ with Lipschitz constant $L^f$ such that $|f(x)-f(y)|\leq L^f|x-y|$.

$\textbf{(A3)}$ There exists a positive constant $M$ such that $|f(x)|\leq M$.

$\textbf{(A4)}$ $\sigma = \underset{p, q}{\min}\ \underline{a}_{pq} > 0$, where $\underline{a}_{pq} = \underset{t \in R}{\inf}\ {a}_{pq}(t)$.

$\textbf{(A5)}$ $M\rho < 1$ where

Set

and $P = \frac{\theta}{1-M\rho}.$

$\textbf{(A6)}$ $(M+PL^f)\rho < 1.$

Define

and

From (A6), it follows that $u_{pq} > v_{pq} > 0$. Moreover, the following auxiliary lemmas will be useful in obtaining the main results. The original version of the first lemma was proven for discontinuous functions with discontinuities at $t = t_i$ which can easily be generalized to a continuous case.

Lemma 2.1. ^[37] Let $M(t)$ be a $m\times n$ almost periodic matrix function and suppose (A1) holds true. Then, there exists $\delta > 0$ such that

● $|| M(t+\omega) - M(t) || < \delta$;

● $|a_{pq}(t+\omega)-a_{pq}(t)| < \delta$;

● $|B_{pq}^{kl}(t+\omega)-B_{pq}^{kl}(t)| < \delta$;

● $|C_{pq}^{kl}(t+\omega)-C_{pq}^{kl}(t)| < \delta$;

● $|D_{pq}^{kl}(t+\omega)-D_{pq}^{kl}(t)| < \delta$;

● $|E_{pq}^{kl}(t+\omega)-E_{pq}^{kl}(t)| < \delta$;

● $|H_{pq}^{kl}(t+\omega)-H_{pq}^{kl}(t)| < \delta$;

● $|I_{pq}^{kl}(t+\omega)-I_{pq}^{kl}(t)| < \delta$;

● $|L_{pq}^{kl}(t+\omega)-L_{pq}^{kl}(t)| < \delta$;

● $|U_{pq}^{kl}(t+\omega)-U_{pq}^{kl}(t)| < \delta$

for all $p, k = \overline{1, m}, \, q, l = \overline{1, n}$.

In other words, Lemma 2.1 asserts that it is possible to choose a common almost period to several almost periodic functions.

Lemma 2.2. ^[37] Let $\Phi(t, s)$ be a fundamental matrix of a linear system $\dot{x} = A(t)x$, where $A(t)$ is a $n\times n$ almost periodic matrix. Assume that there exist $K\ge1$ and $\beta > 0$ such that

Then, for any $\delta > 0$ there exists a relatively dense set of almost periods $\omega$ of $A(t)$ such that

where $\Lambda$ does not depend on $t$ and $s$. Lemma 2.2 states that $\Phi(t, s)$ is diagonally almost periodic. It is easy to check that $\Phi_{pq}(t, s) = e^{-\int_{s}^{t}a_{pq}(u)du}$ is a fundamental matrix of the linear equation $\dot{x}_{pq}(t) = -a_{pq}(t)x_{pq}(t)$, the linear part of the network (1.1). One can show that $\Phi_{pq}(t, s)$ meets the condition (2.1) with $K = 1$ and $\beta = \underline{a}_{pq}$. Thus, for each $i$ and $j$ we have

Theorem 2.1. If the conditions (A1)–(A6) hold true, then the network (1.1) has a unique almost periodic solution.

Proof. One can easily prove that $\phi_{pq}$ is a unique and bounded solution of (1.1) if and only if it satisfies the following integral equation

Let us define $\mathfrak{S}$ to be set of almost periodic functions $\phi(t) = \{\phi_{pq}(t)\}, \, p = 1, \cdots, m, q = 1, \cdots, n$ such that $||\phi||_{\infty} \leq P$ and a nonlinear operator on $\mathfrak{S}$ by

Denote

Let's check that $\mathfrak{T}(\mathfrak{S}) \subseteq \mathfrak{S}$. For any $\phi \in \mathfrak{S}$, it suffices to prove that $||\mathfrak{T}\phi||_{\infty}\leq P$. Indeed,

which implies $\|\mathfrak{T}\phi\|_{\infty} \le P$. Therefore, $\mathfrak{T}(\mathfrak{S}) \subseteq \mathfrak{S}$. Next, we show that $\mathfrak{T}\phi(t)$ is almost periodic. To this end, given arbitrary $\epsilon > 0$ consider the numbers $\omega$ and $\delta > 0$ as in Lemma 2.1 such that $\|\phi(t+\omega)-\phi(t)\| < \delta$, $|a_{pq}(t+\omega)-a_{pq}(t)| < \delta$, $|B_{pq}^{kl}(t+\omega)-B_{pq}^{kl}(t)| < \delta$, $|C_{pq}^{kl}(t+\omega)-C_{pq}^{kl}(t)| < \delta$, $|D_{pq}^{kl}(t+\omega)-D_{pq}^{kl}(t)| < \delta$, $|E_{pq}^{kl}(t+\omega)-E_{pq}^{kl}(t)| < \delta$, $|H_{pq}^{kl}(t+\omega)-H_{pq}^{kl}(t)| < \delta$, $|I_{pq}^{kl}(t+\omega)-I_{pq}^{kl}(t)| < \delta$, $|L_{pq}^{kl}(t+\omega)-L_{pq}^{kl}(t)| < \delta$ and $|U_{pq}^{kl}(t+\omega)-U_{pq}^{kl}(t)| < \delta$ for all $p, k = \overline{1, m}, \, q, l = \overline{1, n}$ and $t\in \mathbb{R}$. It is easy to see that

Thus, by means of the condition (2.3) one can show that

where

Hence, $\Lambda_0(\delta)$ is a bounded function of $\delta$. Now, let us choose $\epsilon$ so that $\delta\Lambda_0(\delta) < \epsilon$. Thus, we have $\|\mathfrak{T}\phi(t+\omega)-\mathfrak{T}\phi(t)\| < \epsilon$ for all $t\in \mathbb{R}$, which yields that $\mathfrak{T}\phi(t)$ is almost periodic.

Finally, for $\phi$, $\psi \in \mathfrak{S}$ one can verify that

Hence, we have $\|\mathfrak{T}\phi(t)-\mathfrak{T}\psi(t)\|_{\infty}\le (M+PL^f)\rho||\phi-\psi||_{\infty}$. Due to the condition (A6), we conclude that $\mathfrak{T}$ is contraction from $\mathfrak{S}$ to $\mathfrak{S}$. Thus, the network (1.1) admits a unique almost periodic solution.

3.   Stability

Before starting the proof of global exponential stability of almost periodic solutions, we need the following result: according to Huang's paper ^[38], the equation below has a unique positive solution $\alpha$

where $u > v > 0$.

Theorem 3.1. Suppose that the conditions (A1)–(A6) are fulfilled. Then, a unique almost periodic solution of the network (1.1) is globally exponentially stable, with convergence rate $\alpha$, satisfying the Eq (3.1).

Proof. In the previous section, we have shown that the network (1.1) has a unique almost-periodic solution. Let us define the following norm $\|x(t)-y(t)\| = \max\limits_{(p, q)}|x_{pq}(t)-y_{pq}(t)|$, and for simplicity, we denote as $\|x(t)-y(t)\| = |x_{pq}(t)-y_{pq}(t)|$. Theorem 2.1 can similarly be proven using such norm. Consider arbitrary two solutions of the network (1.1): $x(t) = (x_{11}(t), \ldots, x_{1n}(t), \ldots, x_{m1}(t) \ldots, x_{mn}(t))$ and $y(t) = (y_{11}(t), \ldots, y_{1n}(t), \ldots, y_{m1}(t) \ldots, y_{mn}(t))$ with the initial conditions $x(s) = \rho(s), \, s\in [-\tau, 0],$ and $y(s) = \kappa(s), \, s\in [-\tau, 0],$ respectively.

Above inequality is of the form

where

and

Since $u > v > 0$, according to Halanay's inequality, solution $y(t)$ converges exponentially to almost periodic solution $x(t)$. In addition, convergence rate $\alpha$ is a unique solution of the following equation

4.   Examples

4.1.   Example 1: 3x3 lattice

We consider FSICNN, where $m = 3, n = 3$ and the functions $a_{pq}(t),$ $C_{pq}(t),$ $L_{pq}(t),$ $B_{pq}(t),$ $U_{pq}(t),$ $D_{pq}(t),$ $E_{pq}(t),$ $T_{pq}(t),$ and $H_{pq}(t)$ are given by

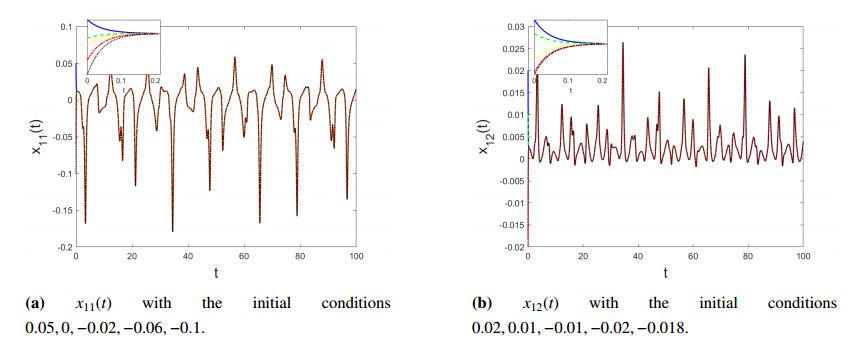
In this example, we consider an activation function $f_{pq}(x) = 0.05\tanh(x)$, and delays $\tau_{11} = 0.5$, $\tau_{12} = \pi$, $\tau_{13} = \pi/2$, $\tau_{21} = \pi/3$, $\tau_{22} = 0.3$, $\tau_{23} = \pi/6$, $\tau_{31} = \pi/8$, $\tau_{32} = \pi$, $\tau_{33} = \pi/2$. Definition of coefficients above implies that condition (A1) is satisfied. Conditions (A2) and (A3) are also satisfied with $L^{f} = M = 0.05$. Conditions (A4)–(A6) are satisfied with $\sigma = 17.2$, $M\rho = 0.3$ and $(M+PL^{f})\rho = 0.8$ respectively. Hence, Theorems 2.1 and 3.1 hold true for this example, and this system should have globally unique and stable almost periodic solutions. Figures 1–3 present numerical simulation of this example, confirming theoretical results. We see that all solutions converge to each other until $T = 0.2\; s$, and these solutions are indeed almost periodic until $T = 100\; s$. And lastly, thanks to approach using Halanay's inequality, convergence rates can also be computed. As an example, solutions for (1, 2, 4, 5) sets of initial conditions converge the $3^{\rm{rd}}$ with convergence rates $\alpha = 0.8042, 0.8042, 0.6863, 0.878$ respectively.

4.2.   Example 2: 2x2 lattice

We consider FSICNN, where $m = 2, n = 2$ and the functions $a_{pq}(t),$ $C_{pq}(t),$ $L_{pq}(t),$ $B_{pq}(t),$ $U_{pq}(t),$ $D_{pq}(t),$ $E_{pq}(t),$ $T_{pq}(t),$ and $H_{pq}(t)$ are given by

In this example, we consider the same activation function and delays. Similar to analysis in previous example, Theorem 2.1 and 3.1 hold true with $\sigma = 0.8$, $M\rho = 0.03$ and $(M+PL^{f})\rho = 0.07$. Figure 4 present numerical simulation of this example, confirming theoretical results. We see that all solutions converge to each other until $T = 3.5\; s$, and these solutions are indeed almost periodic until $T = 100\; s$.

5.   Conclusions

In this paper, we analyzed FSICNNs for uniqueness and stability of almost periodic solutions which was not studied thoroughly before. To prove existence, uniqueness and stability of these solutions, 6 sufficient conditions are presented. Existence of unique almost periodic solutions was proven using Banach fixed-point theorem. Stability part was proven using Halanay inequality approach. One of the advantages of using Halanay inequality is that it provided a way to compute how fast solutions converge to each other. Lastly, numerical example was presented, where 5 sets of initial conditions were considered, resulting in the converging and stable solutions which confirmed our theoretical findings.

Acknowledgments

This research is funded by the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan Grant OR11466188 ("Dynamical Analysis and Synchronization of Complex Neural Networks with Its Applications") and Nazarbayev University under Collaborative Research Program Grant No. 11022021CRP1509.

Conflict of interest

The authors declare no conflicts of interest.