Nonlinear robust control of trajectory-following for autonomous ground electric vehicles with active front steering system

Xianjian Jin; Qikang Wang; Zeyuan Yan; Hang Yang; Xianjian Jin; Qikang Wang; Zeyuan Yan; Hang Yang

doi:10.3934/math.2023565

AIMS Mathematics

2023, Volume 8, Issue 5: 11151-11179. doi: 10.3934/math.2023565

Previous Article Next Article

Research article Special Issues

Nonlinear robust control of trajectory-following for autonomous ground electric vehicles with active front steering system

1.
School of Mechatronic Engineering and Automation, Shanghai Key Laboratory of Intelligent Manufacturing and Robotics, Shanghai University, Shanghai 200072, China
2.
State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130025, China

Received: 03 January 2023 Revised: 18 February 2023 Accepted: 26 February 2023 Published: 09 March 2023
MSC : 93B52, 93C95, 93D05

This paper presents a nonlinear robust H-infinity control strategy for improving trajectory following performance of autonomous ground electric vehicles (AGEV) with active front steering system. Since vehicle trajectory dynamics inherently influenced by various driving maneuvers and road conditions, the main objective is to deal with the trajectory following control challenges of parametric uncertainties, system nonlinearities, and external disturbance. The AGEV system dynamics and its uncertain vehicle trajectory following system are first modeled and constructed, in which parameter uncertainties related to the physical limits of tire are considered and handled, then the control-oriented vehicle trajectory following augmented system with dynamic error is developed. The resulting nonlinear robust H-infinity state-feedback controller (NHC) of vehicle trajectory-following system is finally designed by H-infinity performance index and nonlinear compensation under AGEV system requirements, and solved utilizing a set of linear matrix inequalities derived from quadratic H-infinity performance and Lyapunov stability. Simulations for double lane change and serpentine scenes are carried out to verify the effectiveness of the proposed controller with a high-fidelity, CarSim^®, full-vehicle model. It is found from the results that the proposed NHC provides improved vehicle trajectory following performance compared with the linear quadratic regulator (LQR) controller and robust H-infinity state-feedback controller (RHC).

Keywords:

Citation: Xianjian Jin, Qikang Wang, Zeyuan Yan, Hang Yang. Nonlinear robust control of trajectory-following for autonomous ground electric vehicles with active front steering system[J]. AIMS Mathematics, 2023, 8(5): 11151-11179. doi: 10.3934/math.2023565

Related Papers:

[1]	Zigui Kang, Tao Li, Xiaofei Fan . Delay-dependent anti-disturbance control of electric vehicle based on collective observers. AIMS Mathematics, 2023, 8(6): 14684-14703. doi: 10.3934/math.2023751
[2]	Xing Zhang, Lei Liu, Yan-Jun Liu . Adaptive NN control based on Butterworth low-pass filter for quarter active suspension systems with actuator failure. AIMS Mathematics, 2021, 6(1): 754-771. doi: 10.3934/math.2021046
[3]	Hany Bauomy . Control and optimization mechanism of an electromagnetic transducer model with nonlinear magnetic coupling. AIMS Mathematics, 2025, 10(2): 2891-2929. doi: 10.3934/math.2025135
[4]	Sultanah M. Alshammari, Nofe A. Alganmi, Mohammed H. Ba-Aoum, Sami Saeed Binyamin, Abdullah AL-Malaise AL-Ghamdi, Mahmoud Ragab . Hybrid arithmetic optimization algorithm with deep learning model for secure Unmanned Aerial Vehicle networks. AIMS Mathematics, 2024, 9(3): 7131-7151. doi: 10.3934/math.2024348
[5]	Xia Song, Lihua Shen, Fuyang Chen . Adaptive backstepping position tracking control of quadrotor unmanned aerial vehicle system. AIMS Mathematics, 2023, 8(7): 16191-16207. doi: 10.3934/math.2023828
[6]	Xiaoling Liang, Chen Xu, Duansong Wang . Adaptive neural network control for marine surface vehicles platoon with input saturation and output constraints. AIMS Mathematics, 2020, 5(1): 587-602. doi: 10.3934/math.2020039
[7]	Fang Zhu, Pengtong Li . Adaptive fuzzy consensus tracking control of multi-agent systems with predefined time. AIMS Mathematics, 2025, 10(3): 5307-5331. doi: 10.3934/math.2025245
[8]	Simone Fiori . Coordinate-free Lie-group-based modeling and simulation of a submersible vehicle. AIMS Mathematics, 2024, 9(4): 10157-10184. doi: 10.3934/math.2024497
[9]	Guijun Xing, Huatao Chen, Zahra S. Aghayan, Jingfei Jiang, Juan L. G. Guirao . Tracking control for a class of fractional order uncertain systems with time-delay based on composite nonlinear feedback control. AIMS Mathematics, 2024, 9(5): 13058-13076. doi: 10.3934/math.2024637
[10]	Wajdi Kallel, Noura Allugmani . Finite-time stabilization of stochastic systems with varying parameters. AIMS Mathematics, 2023, 8(8): 17687-17701. doi: 10.3934/math.2023903

Abstract

1. Introduction

The emergence of AGEV attracted academia research interest and attention due to it has great advantages in reducing road congestion, environmental pollution and improving traffic safety in recent years ^[1,2,3,4]. As the new technology of chassis active control for AGEV steer system, active front steering (AFS) is used to improve lateral stability and active safety by applying variable steering gear ratio in different speed scenarios. AGEV equipped with AFS systems can bring strong guarantees of driver safety and handling flexibility through quick input response and efficient steering execution, it has been widely applied and developed in trajectory-following control system for autonomous vehicles ^[5,6,7]. In view of the advantages of fast response and accurate execution, AFS system has excellent abilities to enhance the active safety of vehicle and the following performance of target trajectory for AGEV ^{[8,9,10,11,12,13]}.

The trajectory-following for AGEV with AFS system has been explored in many literatures ^[14,15]. The feedforward and feedback controller of the multi-rate Kalman filter with compensation ability is designed by considering the difference between the control period of the AGEV motor and the sampling time of the ordinary camera, and its AFS is used to realize the trajectory-following successfully ^[16]. Aiming at the mutual interference and control distribution problems of AFS system and electronic stability control system for AGEV, a novel integrated stability model predictive control (MPC) controller is proposed in ^[17], and the control of steering and braking based on tire force is reassigned to follow the target trajectory. In order to improve the handling stability and the steering comfort for AGEV, the work in ^[18] proposed a variable steering ratio AFS controller by constructing the mapping of steering wheel angle and longitudinal vehicle speed. Trajectory-following control in ^[19] is based on successive online linearization of the vehicle model of autonomous vehicles, and its controller computed the front steering angle of AFS to follow the trajectory on slippery roads. In addition, due to the advanced steering technology of the AFS system, it also plays a non-negligible role in other related application fields of trajectory-following control ^[20,21,22].

Although the aforementioned efforts of trajectory following were successful, there are still some challenges such as uncertain model parameters, system nonlinearity and external disturbances ^[23,24]. To address above challenges, nonlinear model predictive control (NMPC) is used to transform the nonlinear system into a parameter-dependent adjustment problem, its sufficient conditions for the feasibility and convergence are given in ^[25]. In order to reduce the influence of external disturbances on trajectory-following, a combination of super twisting second-order sliding mode (SOSM) and nonlinear disturbance observer technique is used to estimate the environmental disturbances and modeling errors, and system's robustness and security is gained through hardware-in-the-loop experiments ^[26]. A novel adaptive sliding mode control (SMC) frame is presented to solve the safety problems caused by actuator failures and external attacks of Markov jump cyber-physical systems, a new linear-type switching surface is established by state estimator, and the stability criterion of system with uncertainty is also deduced, and then the effectiveness of proposed control strategy is final tested in tunnel diode circuit experiments ^[27]. To accurately track the motion trajectory of the uncertain industrial robotic arm system, a SMC framework with switching neural networks is proposed in ^[28], and the adaptive algorithm technology and radial basis function are used to provide real-time feedback for the multi-modal system with control gain so that the robustness of the trajectory following control system can be enhanced. A novel composite adaptive fuzzy controller (FC) is proposed to solve the nonlinear problem of the system following model in ^[29], its strict stability analysis is carried out by Lyapunov method, and the performance of the proposed controller is also verified. Some extensions of FC can be found here ^[30,31]. The active disturbance rejection control (ADRC) is also used to estimate and compensate the unmodeled dynamics and unknown external disturbances of the system in real time to improve the robustness of vehicle trajectory-following ^[32]. An optimal preview controller is designed to improve the dynamic trajectory following performance and high-speed motion stability for the articulated vehicle through the compound lateral position deviation, and the vehicle following performance and motion stability are verified in experiments ^[33]. An MPC strategy for optimal speed is presented to achieve fast and accurate trajectory tracking in ^[34], and the appropriate front wheel steering angle is calculated to obtain a satisfactory trajectory following effect, experimental results verify the effectiveness of the proposed strategy. An optimal control strategy with nonlinear time delay differential equation is used to suppress the chatter of the milling system in ^[35], and the optimal control rate is obtained with the extreme value change algorithm to optimize the chatter performance index of the system. The work ^[36] presented an adaptive multi-model switching control method to solve the parameter jump problem of complex nonlinear systems, and some key lemmas and extended recursive least squares algorithms are used in the design of adaptive control law. To deal with unstructured disturbances of nonlinear systems, a new nonlinear optimal control technique is proposed by iterative techniques in ^[37], and the conditions for asymptotic stability of the system and the corresponding H-infinity control law are given. The study ^[38] designed a new global adaptive control based on output feedback to deal with nonlinear and unknown parameters of the system, the proposed system feedback controller can ensure the convergence of the system state, boundedness of other signals by scaling technology and backstepping method. Meanwhile, robust control has been utilized in the field of trajectory-following control for its advantages in dealing with system nonlinearity ^[39], linear variation of parameters ^[40] and external disturbance of the system ^[41].

Therefore, this paper proposes nonlinear robust control strategy of AGEV with AFS to deal with the trajectory following control challenges of parametric uncertainties, system nonlinearities, and external disturbance. The AGEV system dynamics and its uncertain vehicle trajectory following system is first established. Then, under the requirements of H-infinity performance index, system nonlinear compensation and trajectory-following target, the nonlinear robust state feedback controller for AGEV of trajectory-following is designed. Finally, the effective of the proposed controller is verified with double lane change and serpentine scenes in Simulink/Carsim. The rest of paper structure is as follows: problem description and trajectory-following modeling are presented in Section 2. Section 3 provides the design process of nonlinear robust controller. Simulation results are analyzed and discussed in Section 4, and the conclusions are offered in Section 5.

2. Problem description and trajectory following model

2.1. Vehicle dynamics system model

The paper mainly studies the trajectory following of AGEV problem, we assume that the suspension is a rigid structure, the vehicle tire slip angle tends to be small under normal driving conditions. In order to facilitate the study of vehicle motion, the vehicle dynamics bicycle model is selected as:

$m({\dot v_x} - {v_y}\dot \varphi ) = {F_{fy}}\sin {\delta _f} + {F_{fx}}\cos {\delta _f} + {F_{rx}} ,$

(2.1)

$m(\ddot y + {v_x}\dot \varphi ) = {F_{fy}}\cos {\delta _f} + {F_{fx}}\sin {\delta _f} + {F_{ry}} - {F_{af}} ,$

(2.2)

${F_{af}} = {F_a} + {F_f} .$

(2.3)

where m is mass, φ is yaw angle. Lateral and longitudinal velocity are v_x, v_y. F_iy (I = f, r) and F_ix (I = f, r) are the lateral and longitudinal tire forces. δ_f is front wheel steering angle, the air resistance F_a is proportional to V_l, F_f is the rolling resistance, they can be expressed as:

${F_a} = \frac{1}{2}C\rho AV_l^2 ,$

(2.4)

${F_f} = ({\mu _0} + {\mu _1}v_{wx}^2)mg ,$

(2.5)

where ρ, C, and A are the density parameter, air resistance coefficient and windward area. μ₀, μ₁ are nominal and variable value of resistance coefficient respectively, and v_wx is the longitudinal velocity of the tire.

${I_z}\ddot \varphi = {l_f}({F_{fy}}\cos {\delta _f} + {F_{fx}}\sin {\delta _f}) - {l_r}{F_{ry}} ,$

(2.6)

where I_z is moment of inertia, l_f and l_r are the distance from the front and rear axles to the center of vehicle. The longitudinal driving force F_y of the tire can be expressed as:

${F_y} = {f_y}(\alpha , {F_z}, s, \mu ) .$

(2.7)

Tire slip angle α is calculated by v_wx and v_wy:

$\alpha = {\tan ^{ - 1}}(\frac{{{v_{wx}}}}{{{v_{wy}}}}) ,$

(2.8)

where v_wx is the longitudinal velocity of the tire, v_wy is the lateral velocity of the tire. They can be represented:

$\left\{ \begin{gathered} {v_{wfx}} = {v_x}\cos \delta + ({v_y} + a\dot \varphi )\sin \delta \hfill \\ {v_{wrx}} = {v_x}\cos \delta + ({v_y} - b\dot \varphi )\sin \delta \hfill \\ \end{gathered} \right. ,$

(2.9)

$\left\{ {\begin{array}{*{20}{l}} {{v_{wfy}} = {v_x}\cos \delta - ({v_y} + a\dot \varphi )\sin \delta } \\ {{v_{wry}} = {v_x}\cos \delta - ({v_y} - b\dot \varphi )\sin \delta } \end{array}} \right. .$

(2.10)

Due to the difference between wheel speed and actual speed during the actual vehicle movement, the desired slip rate s_r is as follows:

${s_r} = \left\{ {\begin{array}{*{20}{l}} {1 - \frac{{{v_{wx}}}}{{r{w_w}}}(r{w_w} \ne 0, r{w_w} > {v_{wx}})} \\ {\frac{{r{w_w}}}{{{v_{wx}}}} - 1({v_{wx}} \ne 0, r{w_w} < {v_{wx}})} \end{array}} \right.$

(2.11)

where r and w_w are the radius and angular velocity of the tire.

The vertical load on the front and rear tires of the vehicle can be expressed as the following equation:

$\left\{ \begin{gathered} {F_{Zfl, Zfr}} = \frac{{{l_r}mg}}{{2({l_r} + {l_f})}} \mp \Delta {F_1} + \Delta {F_2} \hfill \\ {F_{Zrl, Zrr}} = \frac{{{l_f}mg}}{{2({l_r} + {l_f})}} + \Delta {F_1} \mp \Delta {F_2} \hfill \\ \end{gathered} \right.$

(2.12)

where ΔF₁, ΔF₂ denote the longitudinal and lateral transfer loads of vehicles, respectively, and the specific equations are as follows:

$\left\{ {\begin{array}{*{20}{l}} {\Delta {F_1} = \frac{{m({{\dot v}_x} - {v_y}w){h_{cog}}}}{{2({l_r} + {l_f})}}{\text{ }}} \\ {\Delta {F_2} = \frac{{m({{\dot v}_x} - {v_y}w){h_{cog}}}}{{2{L_h}}} + \frac{{g{m_s}{h_s}}}{{2{L_h}}}(\frac{{{h_{cog}}\xi }}{g} - \sin \xi )} \end{array}} \right.$

(2.13)

where h_cog is the height between the center of mass and the ground, L_h is half of wheel base, and h_s is the suspension height of vehicle body. ξ is slip angle of wheel.

Based on the assumption that the tire slip angle tends to be small under normal driving conditions, the tire slip force F_fy, F_ry are simplified as:

$\left\{ {\begin{array}{*{20}{l}} {{F_{fy}} = {N_{\alpha f}}{\alpha _f}} \\ {{F_{ry}} = {N_{\alpha r}}{\alpha _r}} \end{array}} \right.$

(2.14)

where N_αf and N_αr are the cornering stiffness. From vehicle kinematics model, it can be gained that the front wheel angle α_f and rear wheel angle α_r:

$\left\{ {\begin{array}{*{20}{l}} {{\alpha _f} = {\delta _f} - \frac{{{v_y} + {l_f}\dot \varphi }}{{{v_x}}}} \\ {{\alpha _r} = - \frac{{{v_y} + {l_f}\dot \varphi }}{{{v_x}}}{\text{ }}} \end{array}} \right. .$

(2.15)

Considering the small front wheel angle, cosδ ≈ 1 and sinδ ≈ 0. At the same time, we suppose the AGEV only moves in a plane coordinate system, and the aerodynamics and rolling effect of the motion process is not considered in order to study. Therefore, according to Eqs (2.14) and (2.15), the Eqs (2.2) and (2.6) are rewritten as:

$\ddot y = - \frac{{{N_{\alpha f}} + {N_{\alpha f}}}}{{m{v_x}}}\dot y - (\frac{{{l_f}{N_{\alpha f}} - {l_r}{N_{\alpha f}}}}{{m{v_x}}} + {v_x})\dot \varphi + {w_{\text{2}}} ,$

(2.16)

$\ddot \varphi = - \frac{{{l_f}{N_{\alpha f}} - {l_r}{N_{\alpha f}}}}{{{I_z}{v_x}}}\dot y - \frac{{l_f^2{N_{\alpha f}} + l_r^2{N_{\alpha f}}}}{{{I_z}{v_x}}}\dot \varphi + {w_4}$

(2.17)

where w₂ and w₄ represent the error of the lateral and yaw angular acceleration.

2.2. Vehicle trajectory following formulation

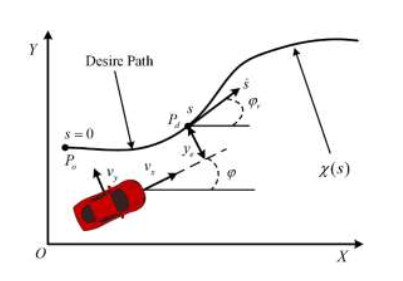
When the AGEV is following the desired trajectory, the current and expected position and heading information of the AGEV are what we need to care about. Figure 1 shows diagram of AGEV trajectory following process, φ, φ_r are the current yaw angles and expected yaw angles, and the first derivatives of lateral error y_e and yaw angle error φ_e can be written as:

${\dot y_e} = {v_y} - {v_x}{\varphi _e} ,$

(2.18)

${\dot \varphi _e} = \dot \varphi - {\dot \varphi _r} = \dot \varphi - \chi \dot s$

(2.19)

Figure 1. Vehicle trajectory following process.

DownLoad: Full-Size Img PowerPoint

where s, χ are the actual trajectory and the curvature of the road. The first and second derivatives of s can be described as:

$\dot s = {v_x} + {v_y}{\varphi _e} ,$

(2.20)

$\ddot s = {\dot v_x} + {\dot v_y}{\varphi _e} + {v_y}{\dot \varphi _e} .$

(2.21)

From the Eqs (2.18) to (2.21), and the second derivatives of y_e and φ_e can be converted to the Eqs (2.22) and (2.23).

${\ddot y_e} = {\dot v_y} - {\dot v_x}{\varphi _e} - {v_x}{\dot \varphi _e} ,$

(2.22)

${\ddot \varphi _e} = \dot \zeta - \dot \chi \dot s - \chi \ddot s .$

(2.23)

2.3. Uncertain vehicle trajectory following model

According to a series of formula derivations and equation transformations, the above vehicle dynamics equation is rewritten as a state space expression:

$\dot x = Ax + {B_u}u + {B_w}w$

(2.24)

where w, B_w are model disturbances and coefficient matrix to state space, u = δ_f is the control input. The expressions for system matrices x, A, B_u, w and B_w are as follows:

$x = \left[ {\begin{array}{*{20}{l}} {{y_e}} \\ {{{\dot y}_e}} \\ {{\varphi _e}} \\ {{{\dot \varphi }_e}} \end{array}} \right], A = \left[ {\begin{array}{*{20}{l}} 0&1&0&0 \\ 0&{ - \frac{{{N_{\alpha f}} + {N_{\alpha r}}}}{{m{v_x}}}}&{\frac{{{N_{\alpha f}} + {N_{\alpha r}}}}{m}}&{ - \frac{{{l_f}{N_{\alpha f}} - {l_r}{N_{\alpha r}}}}{{m{v_x}}}} \\ 0&0&0&1 \\ 0&{ - \frac{{{l_f}{N_{\alpha f}} - {l_r}{N_{\alpha r}}}}{{{I_z}{v_x}}}}&{\frac{{{l_f}{N_{\alpha f}} - {l_r}{N_{\alpha r}}}}{{{I_z}}}}&{ - \frac{{l_f^2{N_{\alpha f}} + l_r^2{N_{\alpha r}}}}{{{I_z}{v_x}}}} \end{array}} \right]$

${B_u} = {\left[ {\begin{array}{*{20}{l}} 0&{\frac{{{N_{\alpha f}}}}{m}}&0&{\frac{{{l_f}{N_{\alpha f}}}}{{{I_z}}}} \end{array}} \right]^T}, {B_w} = \left[ {\begin{array}{*{20}{l}} 0&1&0&1 \end{array}} \right]$

The relationship between the steering wheel angle and the front wheel angle of the steering system can be described by the following formula:

${\delta _a} = \tau {\delta _f}$

(2.25)

where τ is the transmission ratio of the steering system.

When vehicles travel on complex and changeable roads, due to changes in steering angles and road surface roughness, the value of tire cornering stiffness N_i (I = αf, αr) is constantly changing and bounded. It can be handled as follows:

$\left\{ {\begin{array}{*{20}{l}} {{N_{\alpha f}} = {{\bar N}_{\alpha f}} + {n_{\alpha f}}{{\tilde N}_{\alpha f}}} \\ {{N_{\alpha r}} = {{\bar N}_{\alpha r}} + {n_{\alpha r}}{{\tilde N}_{\alpha r}}{\text{ }}} \end{array}} \right., \left| {{n_i}} \right| < 1(i = \alpha f, \alpha r) ,$

(2.26)

${\bar N_{\alpha j}} = \frac{{{N_{\alpha j\min }} + {N_{\alpha j\max }}}}{2}(j = f, r) ,$

(2.27)

${\tilde N_{\alpha j}} = \frac{{{N_{\alpha j\max }} - {N_{\alpha j\min }}}}{2}(j = f, r)$

(2.28)

where N_imax, N_imin are the maximal and minimal values of N_i (i = αf, αr). The system's n_i time varying parameters meet |n_i| ≤ 1(i = αf, αr).

It is possible to change the vehicle system model (2.24) of the as follows:

$\dot x = {A_d}x + {B_{ud}}u + {B_w}w$

(2.29)

where the arguments have the following meaning:

${A_d} = {\bar A_d} + \Delta A, {B_{ud}} = {\bar B_{ud}} + \Delta {B_u}, \left[ {\begin{array}{*{20}{l}} {\Delta A}&{\Delta {B_u}} \end{array}} \right] = {H_d}{F_d}\left[ {\begin{array}{*{20}{l}} {{E_A}}&{{E_B}} \end{array}} \right], \left| {{F_d}} \right| \leqslant 1 ,$

${\bar A_d} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0 \\ 0&{ - \frac{{{{\bar N}_{\alpha f}} + {{\bar N}_{\alpha r}}}}{{m{v_x}}}}&{\frac{{{{\bar N}_{\alpha f}} + {{\bar N}_{\alpha r}}}}{m}}&{ - \frac{{{l_f}{{\bar N}_{\alpha f}} - {l_r}{{\bar N}_{\alpha r}}}}{{{I_z}}}} \\ 0&0&0&1 \\ 0&{ - \frac{{{l_f}{{\bar N}_{\alpha f}} - {l_r}{{\bar N}_{\alpha r}}}}{{{I_z}{v_x}}}}&{\frac{{{l_f}{{\bar N}_{\alpha f}} - {l_r}{{\bar N}_{\alpha r}}}}{{{I_z}}}}&{ - \frac{{l_f^2{{\bar N}_{\alpha f}} + l_r^2{{\bar N}_{\alpha r}}}}{{{I_z}{v_x}}}} \end{array}} \right], {\bar B_{ud}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {\frac{{{{\bar N}_{\alpha f}}}}{m}} \\ 0 \\ {\frac{{{l_f}{{\bar N}_{\alpha f}}}}{{{I_z}}}} \end{array}} \right] ,$

${E_A} = \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{{m{v_x}}}}&{\frac{1}{m}}&{ - \frac{{{l_f}}}{{m{v_x}}}} \\ 0&{ - \frac{1}{{m{v_x}}}}&{\frac{1}{m}}&{\frac{{{l_r}}}{{m{v_x}}}} \\ 0&{ - \frac{{{l_f}}}{{{I_z}{v_x}}}}&{\frac{{{l_f}}}{{{I_z}}}}&{ - \frac{{l_f^2}}{{{I_z}{v_x}}}} \\ 0&{\frac{{{l_r}}}{{{I_z}{v_x}}}}&{ - \frac{{{l_r}}}{{{I_z}}}}&{ - \frac{{l_r^2}}{{{I_z}{v_x}}}} \end{array}} \right], {H_d} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0 \\ {{{\tilde N}_{\alpha f}}}&{{{\tilde N}_{\alpha r}}}&0&0 \\ 0&0&0&0 \\ 0&0&{{{\tilde N}_{\alpha f}}}&{{{\tilde N}_{\alpha r}}} \end{array}} \right], {E_B} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{m}} \\ 0 \\ {\frac{{{l_f}}}{{{I_z}}}} \\ 0 \end{array}} \right] .$

3. Nonlinear robust controller design

3.1. Design of robust feedback control

The trajectory-following system takes into account a number of objectives, including as lateral error, yaw error and vehicle workload. In order to track the target, we define the error function and design of robust linear feedback gain as:

${J_s} = \int_0^\infty {{q_1}y_e^2} + {q_2}\dot y_e^2 + {q_3}\varphi _e^2 + {q_4}\dot \varphi _e^2 + {q_4}{\delta ^2}dt{\text{ }}$

(3.1)

where the meaning of the letter symbol is as follows:

${y_e} = {y_a} - {y_d}, {\dot y_e} = {v_y} - {v_x}{\varphi _e}, {\varphi _e} = \varphi - {\varphi _r}, {\dot \varphi _e} = \dot \varphi - \chi \dot s .$

The above equation can be written as:

$\begin{gathered} J = \int_0^\infty {{\text{[(}}{{\bar C}_1}x + {{\bar D}_{11}}w{{\text{)}}^T}U{\text{(}}{{\bar C}_1}x + {{\bar D}_{11}}w{\text{)}}} + {u^T}Vu{\text{]}}dt \hfill \\ {\text{ }} = \int_0^\infty {{\text{[(}}{U^{\frac{1}{2}}}{{\bar C}_1}x + {U^{\frac{1}{2}}}{{\bar D}_{11}}w{{\text{)}}^T}{\text{(}}{U^{\frac{1}{2}}}{{\bar C}_1}x + {U^{\frac{1}{2}}}{{\bar D}_{11}}w{\text{)}}} + \int_0^\infty {{{{\text{(}}{V^{\frac{1}{2}}}u{\text{)}}}^T}{\text{(}}{V^{\frac{1}{2}}}u{\text{)}}} dt \hfill \\ \end{gathered}$

(3.2)

where the arguments have the following meaning:

${\bar C_1} = \left[ {\begin{array}{*{20}{l}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right], {\bar D_{11}} = 1, U = \left[ {\begin{array}{*{20}{l}} {{q_1}}&0&0&0 \\ 0&{{q_2}}&0&0 \\ 0&0&{{q_3}}&0 \\ 0&0&0&{{q_4}} \end{array}} \right]0, V = {q_5}$

The control output of the model can be defined as:

$z = {C_1}x + {D_{11}}w + {D_{12}}u$

(3.3)

where

${C}_{1} = \left[\begin{array}{c}{U}^{\frac{1}{2}}{\stackrel{̄}{C}}_{1}\\ 0\end{array}\right], {D}_{11} = \left[\begin{array}{c}{U}^{\frac{1}{2}}{\stackrel{̄}{D}}_{11}\\ 0\end{array}\right], {D}_{12} = \left[\begin{array}{c}0\\ {V}^{\frac{1}{2}}\end{array}\right] .$

The optimization of the error performance function J can be translated into the optimization of the control output z in order to facilitate the design of the trajectory tracking controller. The error cost function J has the following relationship with the control output z:

$J = \left\| z \right\|_2^2 .$

(3.4)

Based on the above system model of vehicle dynamics (2.29) and the control output of the system (3.3), vehicle trajectory following with parameter uncertainties can be transformed into a standard H-infinity control problem.

$\left\{ \begin{gathered} \dot x = {A_d}x + {B_w}w + {B_{ud}}u \hfill \\ z = {C_1}x + {D_{11}}w + {D_{12}}u \hfill \\ \end{gathered} \right. .$

(3.5)

According to H_∞ control theory, the purpose of this system model is to design a control gain K and state feedback controller u_L = Kx to meet the vehicle trajectory following requirements.

From Eq (3.5) and u_L = Kx, the following closed-loop system of vehicle trajectory following can be obtained.

$\left\{ {\begin{array}{*{20}{l}} {\dot x = {A_s}x + {B_s}w} \\ {z = {C_s}x + {D_s}w} \end{array}} \right.$

(3.6)

where:

${A_s} = {\bar A_d} + {\bar B_{ud}}K + {H_d}{F_d}({E_A} + {E_B}K){\text{ }}, {\text{ }}{B_s} = {B_w}, {C_s} = {C_1} + {D_{12}}K{\text{ }}, {\text{ }}{D_s} = {D_{11}} .$

The sufficient and necessary conditions for vehicle trajectory tracking system to be stable are that A_s and B_s are stable, and A_s and C_s are detectable. In this paper, we regard the system model error w as the external perturbation of the system. Considering the system (3.6), its transfer function is:

$T{\text{(}}s{\text{) = }}{C_s}{\text{(}}sI - {A_s}{\text{)}}{B_s} + {D_s} .$

(3.7)

The input signal w(t) and output signal energy z(t) are respectively defined as:

$\left\| \Xi \right\|_2^2 = \int_0^{ + \infty } {{\Xi ^T}{\text{(}}t{\text{)}}} \Xi {\text{(}}t{\text{)}}dt, \Xi = w, z .$

(3.8)

The H_∞ norm of T(s) is defined as:

${\left\| {T{\text{(}}s{\text{)}}} \right\|_\infty } = \mathop {sup}\limits_{w \ne 0} \frac{{{{\left\| z \right\|}_2}}}{{{{\left\| w \right\|}_2}}} .$

(3.9)

The equality (3.9) can be changed to:

${\left\| {T{\text{(}}s{\text{)}}} \right\|_\infty } = \mathop {sup}\limits_w \sqrt {\frac{{E{\text{(}}{z^T}{\text{(}}t{\text{)}}z{\text{(}}t{\text{))}}}}{{E{\text{(}}{w^T}{\text{(}}t{\text{)}}w{\text{(}}t{\text{))}}}}}$

(3.10)

where E(·) is mathematical expectation.

That is, the peak value of the maximum singular value of the system's frequency response. In fact, the design of H-infinity state feedback controller is to find the optimal K meet the performance of tracking system, and the influence of perturbation on the output performance is controlled under a certain level. Therefore, the following H_∞ performance index is selected:

$\int_0^\infty {{z^T}{\text{(}}t{\text{)}}z{\text{(}}t{\text{)}}dt} < {\gamma ^2}\int_0^\infty {{w^T}{\text{(}}t{\text{)}}w{\text{(}}t{\text{)}}dt} .$

(3.11)

The above inequality has the following equivalence relation.

${\left\| {G{\text{(}}s{\text{)}}} \right\|_\infty } < \gamma \Leftrightarrow {\sigma _{\max }}{\text{[}}G{\text{(}}jw{\text{)] < }}\gamma \Leftrightarrow {\text{ }}{\gamma ^2}I > G{{\text{(}}jw{\text{)}}^T}G{\text{(}}jw{\text{)}} .$

(3.12)

To prove the closed-loop system of path following (3.6) is stable and meets H_∞ performance, some lemmas will be introduced.

Lemma 1. Given matrix $L = \left[ {\begin{array}{*{20}{l}} {{L_{11}}}&{{L_{12}}} \\ {{L_{21}}}&{{L_{22}}} \end{array}} \right]$ , the dimension of L₁₁ is r×r, where L = L^T, the following three equivalent conditions can be obtained:

${\text{ }}L < 0 ,$

(3.13)

${L_{11}} < 0, {L_{22}} - L_{12}^TL_{_{11}}^{ - 1}{L_{12}} < 0 ,$

(3.14)

${L_{22}} < 0, {L_{11}} - {L_{12}}L_{_{22}}^{ - 1}L_{12}^T < 0 .$

(3.15)

Lemma 2. Given an appropriate dimension matrix Q = Q^T, B and J are symmetric matrices, B and J are real matrices, and F^TF ≤ 1. Then there is the following inequation:

$Q + BFJ + {J^T}{F^T}{B^T} < {\text{0}} .$

(3.16)

The sufficient and necessary condition is that there exists a positive value ε > 0 satisfy following inequation:

$Q + \varepsilon B{B^T} + {\varepsilon ^{ - 1}}{J^T}J < 0 .$

(3.17)

For the above closed-loop system (3.6) for vehicle path tracking, the H_∞ control gain K can be solved by the developed Theorem 1.

Theorem 1. The stability of path following system is considered, the conditions for a closed-loop system (3.6) to satisfy the H_∞ performance are that there are symmetric matrices X > 0, V > 0, and positive numbers γ, ε, satisfy the following inequation (3.18), and there exists a control gain K of H_∞ in the system such that:

$\left[ {\begin{array}{*{20}{c}} {syms({{\bar A}_d}X + {{\bar B}_{ud}}V)}&{{B_w}}&{{\Upsilon _1}}&{\varepsilon {H_d}}&{{\Upsilon _2}} \\ *&{ - \gamma I}&{D_{11}^T}&0&0 \\ *&*&{ - \gamma I}&0&0 \\ *&*&*&{ - \varepsilon I}&0 \\ *&*&*&*&{ - \varepsilon I} \end{array}} \right] < 0$

(3.18)

where

$syms( * ) = * + { * ^T}, {\Upsilon _1} = XC_1^T + {V^T}D_{12}^T, {\Upsilon _2} = XE_A^T + {V^T}E_B^T .$

Proof. According to Lyapunov stability theory. For the closed-loop system (3.6), if there is a symmetric positive definite matrix P satisfies that the inequality (3.19) holds for all uncertain parameters δ ∈ ∆.

$A_s^T(\delta )P + P{A_s}(\delta ) < 0 .$

(3.19)

That is, there exist appropriate positive definite n-order matrices P > 0 and scalars β > 0 such that:

${x^T}(t)[A_s^TP + P{A_s}]x(t) + 2x(t)\Delta A_s^T(t)Px(t) \leqslant - \beta {\left\| {x(t)} \right\|^2} .$

(3.20)

Define the Lyapunov function:

$V(x(t)) = x{(t)^T}Px(t) .$

(3.21)

And assuming that:

$\left\{ {\begin{array}{*{20}{l}} {{e_1} = {\sigma _{\min }}(P)} \\ {{e_2} = {\sigma _{\max }}(P)} \end{array}} \right. .$

(3.22)

There are:

${e_1}{\left\| {x(t)} \right\|^2} \leqslant V(x(t)) \leqslant {e_2}{\left\| {x(t)} \right\|^2} ,$

(3.23)

$\frac{{dV(x(t))}}{{dt}} = {x^T}(t)[P{A_s} + A_s^TP]x(t) + 2x(t)\Delta A_s^T(t)Px(t) \leqslant - \alpha {\left\| {x(t)} \right\|^2} .$

(3.24)

Stability of closed-loop systems means that for any ΔA(t) is exponentially stable, and for any initial state x(0), there is:

${\left\| {x(t)} \right\|^2} \leqslant \frac{{{\sigma _{\max }}(P)}}{{{\sigma _{\min }}(P)}}{\left\| {x(0)} \right\|^2}\exp [ - \frac{\beta }{{{\sigma _{\min }}(P)}}t] .$

(3.25)

According to the Raccati theory, there being a positive definite matrix P > 0 such that:

$P{A_0} + A_0^TP + P{H_d}H_d^TP + {E^T}E < 0 .$

(3.26)

Among them:

${A_0} = {\bar A_d} + {\bar B_{ud}}K , E = {E_A} + {E_B}K .$

(3.27)

Assume:

$Q = - (A_0^TP + P{A_0} + P{H_d}H_d^TP + {E^T}E) > 0 .$

(3.28)

Define V(x) = x^TPx, then there is the following relationship:

$\begin{gathered} \frac{{dV(x(t))}}{{dt}} = {x^T}(A_0^TP + P{A_0})x + 2x\Delta A_0^TPx \hfill \\ {\text{ }} = {x^T}( - Q - P{H_d}H_d^TP - {E^T}E)x + 2{x^T}{E^T}F_d^T{E^T}Px \hfill \\ {\text{ }} \leqslant - {x^T}Qx - {x^T}P{H_d}H_d^TPx - {x^T}{E^T}F_d^T{F_d}Ex + 2x{E^T}F_d^T{E^T}Px \hfill \\ {\text{ }} = - {x^T}Qx - {x^T}(P{H_d} - {E^T}F_d^T)(H_d^TP - {F_d}E)x \hfill \\ {\text{ }} \leqslant - \beta {\left\| x \right\|^2} \hfill \\ \end{gathered}$

(3.29)

where α > 0 satisfies:

$\alpha \leqslant {\sigma _{\min }}(Q) .$

(3.30)

Thus, sufficiency of the closed-loop system (3.6) stability is proved.

Next, it is proved whether the concerned H_∞ performance condition is satisfied in the presence of road disturbance.

The conditions for the system (3.6) to be asymptotically and satisfies H_∞ performance condition (3.11) is that there exists a symmetric positive definite matrix P > 0 and scale γ that satisfies the following matrix inequation:

$\left[ {\begin{array}{*{20}{c}} {P{A_s} + A_s^TP}&{P{B_s}}&{C_s^T} \\ {\text{*}}&{ - \gamma I}&{D_s^T} \\ {\text{*}}&{\text{*}}&{ - \gamma I} \end{array}} \right] < 0 .$

(3.31)

According to closed-loop system (3.6), inequation (3.31) can be written as the following conditions:

$\left[ {\begin{array}{*{20}{c}} {syms(P({{\bar A}_d} + {{\bar B}_{ud}}K) + P{H_d}{F_d}({E_A} + {E_B}K))}&{P{B_w}}&{{{({C_1} + {D_{12}}K)}^T}} \\ *&{ - \gamma I}&{{D_{11}}T} \\ *&*&{ - \gamma I} \end{array}} \right] < 0 .$

(3.32)

Inequation (3.32) can be written as the following conditions.

$\left[ {\begin{array}{*{20}{c}} {syms(P({{\bar A}_d} + {{\bar B}_{ud}}K))}&{P{B_w}}&{C_s^T} \\ *&{ - \gamma I}&{D_{11}^T} \\ *&*&{ - \gamma I} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {syms(P{H_d}{F_d}({E_A} + {E_B}K))}&0&0 \\ *&0&0 \\ *&*&0 \end{array}} \right] < 0 .$

(3.33)

Inequation (3.33) is equivalent to the following:

$\begin{gathered} \left[ {\begin{array}{*{20}{c}} {syms(P({{\bar A}_d} + {{\bar B}_{ud}}K))}&{P{B_w}}&{C_s^T} \\ *&{ - \gamma I}&{D_{11}^T} \\ *&*&{ - \gamma I} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {P{H_d}} \\ 0 \\ 0 \end{array}} \right]{F_d}\left[ {\begin{array}{*{20}{c}} {({E_A} + {E_B}K)}&0&0 \end{array}} \right] \hfill \\ {\text{ }} + \left[ {\begin{array}{*{20}{c}} {({E_A} + {E_B}K)} \\ 0 \\ 0 \end{array}} \right]F_d^T\left[ {\begin{array}{*{20}{c}} {P{H_d}}&0&0 \end{array}} \right] < 0 \hfill \\ \end{gathered} .$

(3.34)

Let

${\stackrel{̄}{H}}_{d} = {\left[\begin{array}{ccc}P{H}_{d}& 0& 0\end{array}\right]}^{T}, {\stackrel{̄}{F}}_{d} = {F}_{d}, {\stackrel{̄}{E}}_{AB} = \left[\begin{array}{ccc}({E}_{A}+{E}_{B}K)& 0& 0\end{array}\right], \varpi = \left[\begin{array}{ccc}{\Gamma }_{1}& P{B}_{w}& {C}_{cl}^{T}\\ *& -\gamma I& {D}_{11}T\\ *& *& -\gamma I\end{array}\right] .$

Inequation (3.34) can be written as the following conditions:

$\varpi + {\bar H_d}{\bar F_d}{\bar E_{AB}} + \bar E_{AB}^T\bar F_d^T\bar H_d^T < 0 .$

(3.35)

According to Lemma 2, there exists a positive value ε₁ > 0 satisfy following inequation:

$\varpi + {\varepsilon _1}{\bar H_d}\bar H_d^T + \varepsilon _1^{ - 1}{\bar E_{AB}}\bar E_{AB}^T < 0 .$

(3.36)

According to Lemma 1, the following inequation can be gained.

$\left[ {\begin{array}{*{20}{c}} \varpi &{{{\bar H}_d}}&{\bar E_{AB}^T} \\ {}&{ - \varepsilon _1^{ - 1}I}&0 \\ {}&{}&{{\varepsilon _1}I} \end{array}} \right] < 0 .$

(3.37)

Expand the above inequality (3.37):

$\left[ {\begin{array}{*{20}{c}} {syms(P({{\bar A}_d} + {{\bar B}_{ud}}K))}&{P{B_w}}&{{{({C_1} + {D_{12}}K)}^T}}&{P{H_d}}&{{{({E_A} + {E_B}K)}^T}} \\ *&{ - \gamma I}&{D_{11}^T}&0&0 \\ *&*&{ - \gamma I}&0&0 \\ *&*&*&{\varepsilon _1^{ - 1}I}&0 \\ *&*&*&*&{{\varepsilon _1}I} \end{array}} \right] < 0 .$

(3.38)

The diagonal matrix diag{P^-1, I, I, ε₁, I} is multiplied to the left and right of the above formula respectively, and the following inequation (3.39) is obtained.

$\left[ {\begin{array}{*{20}{c}} {syms(({{\bar A}_d} + {{\bar B}_{ud}}K){P^{ - 1}})}&{{B_w}}&{{P^{ - 1}}{{({C_1} + {D_{12}}K)}^T}}&{{\varepsilon _1}{H_d}}&{{P^{ - 1}}{{({E_A} + {E_B}K)}^T}} \\ *&{ - \gamma I}&{D_{11}^T}&0&0 \\ *&*&{ - \gamma I}&0&0 \\ *&*&*&{{\varepsilon _1}I}&0 \\ *&*&*&*&{{\varepsilon _1}I} \end{array}} \right] < 0 .$

(3.39)

Let X = P^-1, the following inequation (3.40) is obtained.

$\left[ {\begin{array}{*{20}{c}} {syms(({{\bar A}_d} + {{\bar B}_{ud}}K)X))}&{{B_w}}&{X{{({C_1} + {D_{12}}K)}^T}}&{{\varepsilon _1}{H_d}}&{X{{({E_A} + {E_B}K)}^T}} \\ *&{ - \gamma I}&{D_{11}^T}&0&0 \\ *&*&{ - \gamma I}&0&0 \\ *&*&*&{{\varepsilon _1}I}&0 \\ *&*&*&*&{{\varepsilon _1}I} \end{array}} \right] < 0 .$

(3.40)

Then let KX = V, by the fundamental transformation of the inequality, the Theorem 1 can be obtained.

3.2. Nonlinear robust control feedback design

Next, so as to improve the system's fast response, transient response performance and reduce overshoot, the nonlinear compensation feedback control rate will be designed as:

${u_{nonlinear}} = \varphi (r, h){B^T}Px$

(3.41)

where φ(r, h) is nonlinear compensation function, xis error state, r, h are output reference value and actual value respectively. The matrix P is the only positive definite matrix of the following Lyapunov equation, and the asymptotic stability of A_s also guarantees the existence of matrix P.

$A_s^TP + P{A_s} + W = 0$

(3.42)

where W ∈ R^n×n is positive definite weighted diagonal matrix. The selection of W can determine stability closed-loop poles of the system. The principle of matrix selection is to make the closed-loop pole have greater damping when the system reaches the set goal. Thus, the system overshoot near the given reference signal is suppressed, the adjustment time of the system is shortened, and the transient performance of the system is improved.

$W = {10^\vartheta } \cdot I$

(3.43)

whereϑ is an adjustable parameter, I is the corresponding dimension of the unit matrix.

The selection of nonlinear function φ(r, h) is very crucial, and its selection needs to satisfy the following two basic properties: (1) In the early stage of control, when the error is relatively large, the value of the nonlinear function φ(r, h) needs to become smaller, so the nonlinear feedback compensation has no obvious effect on the system. At this time, the linear feedback controller plays a leading role and gives priority to meeting the needs of the control system's rapidity. (2) When the control is close to the steady state, the error is relatively small, and the value of the nonlinear function should become larger and occupy a dominant position. By continuously increasing the system damping, it will meet demand for fast response speed and low overshoot.

From the above analysis, the form of nonlinear compensation function selected in this paper is as follows:

$\varphi (r, h) = - \beta \frac{1}{{1 - {e^{ - 1}}}}({e^{ - \alpha \left| {1 - \frac{{h - {h_0}}}{{r - {h_0}}}} \right|}} - {e^{ - 1}})$

(3.44)

where r and h are reference outputs and control outputs respectively, h₀ is the initial value of the control output. α and β are non-negative adjustable parameters, e is natural number.

Combining the linear feedback and the nonlinear compensation function, the output of the actuator is finally formed in the following form (3.45). The linear gain feedback can bring a faster response to the trajectory following system, at the same time, the nonlinear compensation function can obtain a stable output and reduce the overshoot of the system.

${u_{final}} = Kx + \varphi (r, h)B_{ud}^TPx .$

(3.45)

According to the design of the above nonlinear compensation function and considering that the output of the actuator of the system will be saturated, the following form of nonlinear robust control system model can be rewritten:

$\left\{ \begin{gathered} \dot x = {A_d}x + {B_w}w + {B_{ud}}sat{\text{(}}{u_{final}}{\text{)}} \hfill \\ z = {C_1}x + {D_{11}}w + {D_{12}}sat{\text{(}}{u_{final}}{\text{)}} \hfill \\ \end{gathered} \right.$

(3.46)

where sat(∗) represents the saturation function of the system, sat(u_final) can be expressed as:

$sat{\text{(}}{u_{final}}{\text{)}} = \left\{ {\begin{array}{*{20}{l}} {{u_{\max }}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {u_{final}} > {u_{\max }}} \\ {Kx + \varphi {\text{(}}r, h{\text{)}}B_{ud}^TPx, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left| {{u_{final}}} \right| < {u_{\max }}} \\ { - {u_{\max }}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {u_{final}} < - {u_{\max }}} \end{array}} \right. .$

(3.47)

Considering that the front wheel angle will be saturated, the actual nonlinear compensation can be expressed as:

${u_{nla}} = sat(u) - Kx .$

(3.48)

According to the above conditions, u_nla can be written as

$0 < \left| {{u_{nla}}} \right| < \varphi (r, h)B_{ud}^TPx .$

(3.49)

Next, the influence of nonlinear compensation function on the stability and H-infinity performance of the system will be proved.

Proof. The Lyapunov functional is first defined as

$V = {x^T}Px .$

(3.50)

Take the derivative of the Lyapunov functional:

$\begin{gathered} \dot V = {{\dot x}^T}Px + {x^T}P\dot x \hfill \\ {\text{ }} = {(\bar Ax + \bar Rx + {B_w}w)^T}Px + {x^T}P(\bar Ax + \bar Rx + {B_w}w) \hfill \\ {\text{ }} = {x^T}{{\bar A}^T}Px + {x^T}{{\bar R}^T}Px{\text{ + }}{w^T}B_w^TPx + {x^T}P\bar Ax + {x^T}P\bar Rx + {x^T}P{B_w}w \hfill \\ {\text{ }} = {x^T}({{\bar A}^T}P + P\bar A)x + {x^T}({{\bar R}^T}P + P\bar R)x + {w^T}B_w^TPx + {x^T}P{B_w}w \hfill \\ \end{gathered}$

(3.51)

where

$\bar A = {A_d} + {B_{ud}}K, \bar R = {B_{ud}}{u_{nla}} .$

When there is no disturbance outside the system, it is assumed that w = 0, and the Lyapunov functional can be expressed as:

$\dot V = {x^T}({\bar A^T}P + P\bar A)x + {x^T}({\bar R^T}P + P\bar R)x .$

(3.52)

Assuming that

${V_1} = {x^T}({\bar A^T}P + P\bar A)x .$

(3.53)

It is known from the matrix inequality that V₁ is less than zero.

Assuming that

${V_{\text{2}}} = {x^T}({\bar R^T}P + P\bar R)x = 2{x^T}P{B_{ud}}(sat(Kx + \varphi B_{ud}^TPx) - Kx) = 2i(sat(j + \varphi i) - j)$

(3.54)

where i = x^TPB_ud, j = Kx.

V₂ will be discussed in two cases.

(1) When the input is not saturated, it satisfies:

$\left| {sat(j + \varphi i)} \right| < {u_{\max }} .$

(3.55)

Then there is the following inequality:

${V_{\text{2}}} = 2i(sat(j + \varphi i) - j) = 2\varphi {i^2} < = 0 .$

(3.56)

Therefore:

$\dot V = {V_1} + {V_2} = {x^T}({\bar A^T}P + P\bar A)x + 2i(sat(j + \varphi i) - j) < = {x^T}({\bar A^T}P + P\bar A)x < 0 .$

(3.57)

(2) When the input is saturated, it means:

$\left| {sat(j + \varphi i)} \right| \geqslant {u_{\max }} .$

(3.58)

Consider that when j is also saturated, when φi = 0, there is only linear feedback at this time, and the system is asymptotically stable.

When j is unsaturated, the output has the following two forms:

$\left\{ {\begin{array}{*{20}{c}} {i < 0, sat(j + \varphi i) - j \geqslant 0, {\text{ }}When{\text{ }}j + \varphi i \geqslant {u_{\max }}{\text{ }}and{\text{ }}j > 0{\text{ }}} \\ {i > 0, sat(j + \varphi i) - j \leqslant 0, {\text{ }}When{\text{ }}j + \varphi i \leqslant - {u_{\max }}{\text{ }}and{\text{ }}j < 0{\text{ }}} \end{array}} \right. .$

(3.59)

It can be seen from the condition of inequality (3.59) that when saturation occurs, the signs of i and sat (j + φi) - j are opposite, that is:

${V_{\text{2}}} = 2i(sat(j + \varphi i) - j) < = 0 .$

(3.60)

Thus:

$\dot V = {V_1} + {V_2} = {x^T}({\bar A^T}P + P\bar A)x + 2i(sat(j + \varphi i) - j) < = {x^T}({\bar A^T}P + P\bar A)x < 0 .$

(3.61)

Therefore, the system is also closed-loop stable with the introduction of nonlinear compensation function and without external interference.

Next, it will be proved that the system with nonlinear compensation function is closed-loop stable when subjected to external interference and satisfies the H_∞ performance index. First let's define a cost function J_c:

${J_c} = \dot V + {z^T}z - {\gamma ^2}{w^T}w .$

(3.62)

Since the system is asymptotically stable, then if the H_∞ norm has the following inequality:

${\left\| z \right\|^2} < {\gamma ^2}{\left\| w \right\|^2} .$

(3.63)

In other words, the following inequality exists:

${J_c} = \dot V + {z^T}z - {\gamma ^2}{w^T}w < 0 .$

(3.64)

According to the above conditions:

$\begin{gathered} \dot V = {{\dot x}^T}Px + {x^T}P\dot x \hfill \\ {\text{ }} = {x^T}{{\bar A}^T}Px + {x^T}{{\bar R}^T}Px{\text{ + }}{w^T}B_w^TPx + {x^T}P\bar Ax + {x^T}P\bar Rx + {x^T}P{B_w}w \hfill \\ {\text{ = }}{x^T}({{\bar A}^T}P + P\bar A + 2P\bar R)x + {w^T}B_w^TPx + {x^T}P{B_w}w \hfill \\ \end{gathered} .$

(3.65)

It could also be written:

$\dot V = {\left[ {\begin{array}{*{20}{c}} x \\ w \end{array}} \right]^T}\left[ {\begin{array}{*{20}{c}} {{{\bar A}^T}P + P\bar A + 2P\bar R}&{P{B_w}} \\ {B_w^TP}&{\text{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x \\ w \end{array}} \right] .$

(3.66)

In the same way:

${z^T}z = {(Cx + Dw)^T}(Cx + Dw) = {x^T}{C^T}Cx + {x^T}{C^T}Dw + {w^T}{D^T}CxDw .$

(3.67)

The above equation can be further rewritten:

${z^T}z = {\left[ {\begin{array}{*{20}{c}} x \\ w \end{array}} \right]^T}\left[ {\begin{array}{*{20}{c}} {{C^T}C}&{{C^T}D} \\ {{D^T}C}&{{D^T}D} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x \\ w \end{array}} \right] ,$

(3.68)

${J_c} = {\left[ {\begin{array}{*{20}{c}} x \\ w \end{array}} \right]^T}\left( {\left[ {\begin{array}{*{20}{c}} {{{\bar A}^T}P + P\bar A + 2P\bar R}&{P{B_w}} \\ {B_w^TP}&{\text{0}} \end{array}} \right]{\text{ + }}\left[ {\begin{array}{*{20}{c}} {{C^T}C}&{{C^T}D} \\ {{D^T}C}&{{D^T}D} \end{array}} \right]{\text{ + }}\left[ {\begin{array}{*{20}{c}} {\text{0}}&{\text{0}} \\ {\text{0}}&{{\gamma ^{\text{2}}}} \end{array}} \right]} \right)\left[ {\begin{array}{*{20}{c}} x \\ w \end{array}} \right] .$

(3.69)

According to the properties of quadratic form and inequality (3.62), the following inequality holds:

$\Psi {\text{ = }}\left[ {\begin{array}{*{20}{c}} {{{\bar A}^T}P + P\bar A + 2P\bar R}&{P{B_w}} \\ {B_w^TP}&{\text{0}} \end{array}} \right]{\text{ + }}\left[ {\begin{array}{*{20}{c}} {{C^T}C}&{{C^T}D} \\ {{D^T}C}&{{D^T}D} \end{array}} \right]{\text{ + }}\left[ {\begin{array}{*{20}{c}} {\text{0}}&{\text{0}} \\ {\text{0}}&{{\gamma ^{\text{2}}}} \end{array}} \right] < 0 .$

(3.70)

Rewrite the above inequation:

$\Psi = \left[\begin{array}{cc}{\stackrel{̄}{A}}^{T}P+P\stackrel{̄}{A}+2P\stackrel{̄}{R}& P{B}_{w}\\ {B}_{w}^{T}P& 0\end{array}\right]+\left[\begin{array}{cc}{C}^{T}C& {C}^{T}D\\ {D}^{T}C& {D}^{T}D\end{array}\right] = \left[\begin{array}{cc}{\stackrel{̄}{A}}^{T}P+P\stackrel{̄}{A}+2P\stackrel{̄}{R}& P{B}_{w}\\ {B}_{w}^{T}P& {\gamma }^{2}I\end{array}\right]+\left[\begin{array}{c}{C}^{T}\\ {D}^{T}\end{array}\right]\left[\begin{array}{cc}C& D\end{array}\right] .$

(3.71)

Let π = [C D], the above inequality has the following relation:

$\Psi {\text{ = }}\left[ {\begin{array}{*{20}{c}} {{{\bar A}^T}P + P\bar A + 2P\bar R}&{P{B_w}} \\ {B_w^TP}&{{\gamma ^{\text{2}}}I} \end{array}} \right] + {\pi ^{\text{T}}}\pi .$

(3.72)

According to Lemma 1:

$\Psi {\text{ = }}\left[ {\begin{array}{*{20}{c}} {{{\bar A}^T}P + P\bar A + 2P\bar R}&{P{B_w}}&{{C^T}} \\ {B_w^TP}&{{\gamma ^{\text{2}}}I}&{{D^T}} \\ C&D&{ - I} \end{array}} \right] .$

(3.73)

According to Theorem 1 and inequalities (3.54), (3.56) and (3.60), the above equation is less than 0. Thus, the theorem of robust state feedback control with nonlinear compensation function is proved.

Remark 1. Note that, in this study, the nonlinear robust control proposed in this paper includes linear feedback gain and nonlinear feedback gain parts, which can combine the advantages of linear feedback control and nonlinear feedback control. Since the direct design of fully nonlinear robust controller is complex and challenged for vehicle trajectory-following system, the main advantage of the proposed controller is in allowing application of powerful linear synthesis concepts to nonlinear vehicle dynamics system. In addition, compared with optimal control such as model predictive control, perhaps the proposed nonlinear robust control method is not better than optimal control in terms of optimal performance and implementation ^{[11,12,23,24,25,26]}, whereas the proposed controller excels at robust stability and robust performance for the trajectory following system of AGEV where parameter uncertainties, system nonlinearity and external disturbances can be effectively dealt with using the proposed technique.

4. Simulation and analysis

In this section, the nonlinear robust H-infinity state-feedback controller (NRC) law designed above is simulated and verified on the Simulink-Carsim^® joint platform. Simulink provides the overall framework environment, and the high-fidelity CarSim^® software provides the dynamics model of AGEV trajectory following. The specific flowchart of system simulation framework is shown in Figure 2, the main parameters of AGEV are defined in Table 1. During the movement of the vehicle, system parameter uncertainty is mainly considered that the tire cornering stiffness of the N_αf, N_αr will changes due to factors such as vehicle steering, ground roughness and environmental disturbances. Note that the tire cornering stiffness is variable and bounded, and the range of tire cornering stiffness in the system simulation: N_αf ∈ [79351,96985] N/rad, N_αr ∈ [97996,119772] N/rad. Since the vehicle will inevitably encounter interference from the external environment during the movement, the interference often affects the change of vehicle state parameters, so that there is a certain difference between the measured signal and the actual signal. This paper assumes that the system interference w = [0.01sin(t), 0, 0.01sin(t), 0]. The simulated road conditions are set to double lane change (DLC) and serpentine curve scenes, and the forward speed is 72 km/h. The reference trajectory of DLC and serpentine curve are generated by a quintic polynomial technique, it is composed of a series of time-related vehicle state trajectory points, which contains information on vehicle position, heading angle, velocity, acceleration and radius of curvature. The reference trajectory we planned has already satisfied the obstacle avoidance function, because our work is not focused on trajectory planning of AGEV, here we assume that the reference trajectory we planned has already satisfied the obstacle avoidance function. For the dynamic trajectory planning, interested readers can refer to our previous and other related works ^[42,43]. In order to reflect the strong tracking ability and good steady-state response performance of the proposed controller, the linear quadratic regulator (LQR) controller and robust H-infinity state-feedback controller (RHC) are also researched and compared.

Figure 2. Specific flowchart of system simulation framework.

DownLoad: Full-Size Img PowerPoint

Table 1. Definition of key parameters of the vehicle.

Parameters	Explanation	Value(unit)
m	Vehicle mass	1413(kg)
I_z	The moment of inertia around the $z$ -axis	1536.7(kg·m²)
l_f	Distance from center of mass to front axle	1.015(m)
l_r	Distance from center of mass to rear axle	1.895(m)
N_αf	Cornering stiffness of front wheels	88168(N/rad)
N_αr	Cornering stiffness of vehicle rear wheels	108884(N/rad)
l_z	Height of centroid to ground	0.54(m)
r	Wheel radius	0.325(m)

| Show Table

DownLoad: CSV

4.1. Double lane change condition

The simulation results of DLC including the global trajectories and lateral errors, curvature of road and the front wheel angle, yaw error, the lateral error and nonlinear compensation are shown in Figures 3–6. Figure 3 shows the global trajectories and lateral errors of different controllers under double lane change working conditions, among which the three controllers all have good tracking effects. The maximum lateral error of the LQR and RHC controller are about 0.4 m and 0.2 m respectively. The maximum lateral error of NRC is less than the other two controls, it indicates that the tracking performance of NRC is better than LQR and NRC. In addition, it can be seen from Figure 3, global X is between 56 and 65 meters, NRC also possesses outstanding system response when tracking DLC, which shows that proposed controller can improve the transient performance of the closed-loop system.

Figure 3. The global trajectories and lateral errors under DLC condition.

DownLoad: Full-Size Img PowerPoint

Figure 4. curvature of road and the front wheel angle under DLC condition.

DownLoad: Full-Size Img PowerPoint

Figure 5. Yaw error under DLC condition.

DownLoad: Full-Size Img PowerPoint

Figure 6. The lateral error and nonlinear compensation under DLC condition.

DownLoad: Full-Size Img PowerPoint

Figure 4 shows the curvature of road and the front wheel angle of AGEV during tracking DLC. It can be seen from Figure 4 that the value of front wheel angle of NRC is always between LQR and RHC, which is because too small front wheel angle will lead to a small response speed of the system, while too large front wheel angle will lead to a large overshot. However, the NRC has linear gain part to accelerate the system response, while the nonlinear compensation part can reduce large overshoot that results in excellent trajectory-following capability.

In Figure 5, it can be seen that NRC has smaller yaw error and stronger following ability compared with LQR and NRC. Figure 6 shows the magnitude of the lateral error and nonlinear compensation of NRC. It can see that when the lateral error is small, the nonlinear compensation part of NRC is large, and when the lateral error is increased, the nonlinear compensation part of NRC will become smaller, which indicates that the nonlinear compensation part meets the original intention of our NRC design, specifically the system has a fast response speed in the case of increasing error, and the system has a small overshoot under the condition of small error.

4.2. Serpentine condition

The simulation results of serpentine condition including the global trajectories and lateral errors, curvature of road and the front wheel angle, yaw error, the lateral error and nonlinear compensation are shown in Figures 7–10. Figure 7 shows the global trajectories and lateral errors of following in serpentine condition. The maximum lateral errors of NRC are smaller than those of LQR and RHC, and its response speed and transient performance are also higher than those of the other two controllers, it indicating that NRC has better tracking performance on serpentine roads than LQR and NRC.

Figure 7. The global trajectories and lateral errors under serpentine condition.

DownLoad: Full-Size Img PowerPoint

Figure 8. curvature of road and the front wheel angle under serpentine condition.

DownLoad: Full-Size Img PowerPoint

Figure 9. Yaw error under serpentine condition.

DownLoad: Full-Size Img PowerPoint

Figure 10. Lateral error and nonlinear compensation under serpentine condition.

DownLoad: Full-Size Img PowerPoint

Figure 8 shows the curvature and the front wheel angle of AGEV during tracking serpentine road. The maximum curvature of the serpentine road is 0.004. Similar to DLC condition, the value of front wheel angle of NRC is larger than LQR and smaller than RHC in serpentine working condition. Under the compensation of nonlinear part, NRC also has stable trajectory following ability.

In Figure 9, it can be seen that when AGEV follows a trajectory with large curvature, NRC can respond quickly with small yaw error, which brings low yaw error to the system and has stable tracking ability. Figure 10 displays the lateral error and nonlinear compensation under the serpentine condition, the maximum lateral error is 0.1 m. When the error changes, the nonlinear compensation part changes correspondingly, and it has the characteristics of fast response and small overshoot, and meets the requirements of trajectory following.

For quantitative analysis of the tracking performance of the proposed controller, the maximum error (ME), the mean absolute error (MAE) and the root mean square error (RMSE) of the vehicle lateral displacement are used as the metrics for analysis, and the LQR and RHC are used as comparative experiments. The ME, MAE and RMSE are calculated as follows:

$ME = Max\{ \left| {{Y_{ai}} - {Y_{di}}} \right|, i = 1, 2 \cdots N\} ,$

(4.1)

$MAE = \frac{{\sum\limits_{i = 1}^N {\left| {{Y_{ai}} - {Y_{di}}} \right|} }}{N} ,$

(4.2)

$RMSE = \frac{{\sqrt {\sum\limits_{i = 1}^N {{{({Y_{ai}} - {Y_{di}})}^2}} } }}{N}$

(4.3)

where Y_ai and Y_di represent actual and ideal values, N is the number of samples.

Table 2 shows ME, MAE, RMSE, Reduction I and Reduction II under the lateral displacement of DLC and serpentine conditions. It can be seen from the data in Table 2 that NRC have smaller the ME, MAE and RMS than LQR and RHC in the two scenarios. From the point of view of working conditions, the error of DLC is greater than that of serpentine condition, which is due to the large lateral displacement of DLC, which leads to a larger error in trajectory following. In DLC condition, the overall improvement degree of NRC compared with LQR is more than 40%, and in serpentine condition, the degree of improvement of NRC compared with LQR is more than 50%. The ME of NRC is 10% higher than RHC under DLC condition, it indicating that NRC has a faster response speed than RHC in trajectory following with large errors. At the same time, the MAE of NRC is about 7% higher than that of RHC under DLC scenario, which shows that NRC has a smaller overshoot in trajectory following with small errors than RHC. On the whole, compared with LQR and RHC, the proposed controller has the advantages of fast response speed and small overshoot.

Table 2. Index analysis of lateral error under DLC and serpentine conditions.

Condition	Index(m)	LQR	RHC	NRC	Reduction I	Reduction II
DLC	ME	0.3977	0.2414	0.2146	46.04%	11.10%
	MAE	0.1538	0.0921	0.0859	44.15%	6.73%
	RMSE	0.1987	0.1248	0.1136	42.83%	8.97%
Serpentine	ME	0.2160	0.1211	0.1077	50.14%	11.07%
	MAE	0.1173	0.0629	0.0580	50.55%	7.79%
	RMSE	0.1372	0.0744	0.0684	50.15%	8.06%
Notes: Reduction I = (LQR - NRC)/ LQR, Reduction II = (RHC - NRC)/ RHC.

| Show Table

DownLoad: CSV

5. Conclusions

To improve the tracking accuracy, response speed and the overshoot suppression of the trajectory following control system, the nonlinear robust H_∞ state-feedback controller strategy of AGEV with AFS system is proposed. Firstly, the AGEV system dynamics and its control-oriented vehicle trajectory following system with dynamic error is developed. According to Lyapunov stability theory, the nonlinear robust H_∞ state-feedback controller of AGEV trajectory-following system is finally designed, solved by applying a set of linear matrix inequalities. Simulation including double lane change and serpentine conditions is implemented to verify the effectiveness of the proposed controller by using Matlab/Simulink-Carsim^®. The simulation shows that the designed controller possesses effectual trajectory following performance of AGEV with AFS system. In addition, because we have compared the proposed method with LQR control and robust control in simulations, also the main purpose of this paper is to solve the engineering application problem of AGEV trajectory following control rather than pure control theory development. Therefore, we did not provide more robust optimal control and adaptive control as comparison. In the future, we will investigate and compare advanced robust optimal control and adaptive optimal control techniques such as SMC for trajectory following control for AGEV.

Acknowledgments

This work was supported by NNSF of China (Grant No. 51905329), Foundation for State Key Laboratory of Automotive Simulation and Control (Grant No. 20181112).

Conflict of interest

The authors declare that there are no conflict of interests.

References

[1]	G. Demesure, M. Defoort, A. Bekrar, D. Trentesaux, M. Djemaï , Decentralized motion planning and scheduling of AGVs in an FMS, IEEE Trans. Ind. Informat., 14 (2018), 1744–1752. https://doi.org/10.1109/TII.2017.2749520 doi: 10.1109/TII.2017.2749520
[2]	S. Riazi, K. Bengtsson, B. Lennartson, Energy optimization of large-scale AGV systems, IEEE Trans. Autom. Sci. Eng., 18 (2021), 638–649. https://doi.org/10.1109/TASE.2019.2963285 doi: 10.1109/TASE.2019.2963285
[3]	V. Digani, L. Sabattini, C. Secchi, C. Fantuzzi, Ensemble coordination approach in multi-AGV systems applied to industrial warehouses, IEEE Trans. Autom. Sci. Eng., 12 (2015), 922–934. https://doi.org/10.1109/TASE.2015.2446614 doi: 10.1109/TASE.2015.2446614
[4]	T. Wang, Y. Xu, S. Ahipasaoglu, C. Courcoubetis, Ex-post max-min fairness of generalized AGV mechanisms, IEEE Trans. Autom. Control, 62 (2017), 5275–5281. https://doi.org/10.1109/TAC.2016.2632424 doi: 10.1109/TAC.2016.2632424
[5]	S. Hoshino, J. Ota, A. Shinozaki, H. Hashimoto, Hybrid design methodology and cost-effectiveness evaluation of AGV transportation systems, IEEE Trans. Autom. Sci. Eng., 4 (2007), 360–372. https://doi.org/10.1109/TASE.2006.887162 doi: 10.1109/TASE.2006.887162
[6]	S. Lu, C. Xu, R. Zhong, An active RFID tag-enabled locating approach with multipath effect elimination in AGV, IEEE Trans. Autom. Sci. Eng., 13 (2016), 1333–1342. https://doi.org/10.1109/TASE.2016.2573595 doi: 10.1109/TASE.2016.2573595
[7]	H. Gao, J. Zhu, X. Li, Y. Kang, J. Li, H. Su, Automatic parking control of unmanned vehicle based on switching control algorithm and backstepping, IEEE /ASME Trans. Mech., 27 (2022), 1233–1243. https://doi.org/10.1109/TMECH.2020.3037215 doi: 10.1109/TMECH.2020.3037215
[8]	M. Graf Plessen, D. Bernardini, H. Esen, A. Bemporad, Spatial-based predictive control and geometric corridor planning for adaptive cruise control coupled with obstacle avoidance, IEEE Trans. Control. Syst. Technol., 26 (2018), 38–50. https://doi.org/10.1109/TCST.2017.2664722 doi: 10.1109/TCST.2017.2664722
[9]	R. Utriainen, M. Pöllänen, H. Liimatainen, The safety potential of lane keeping assistance and possible actions to improve the potential, IEEE Trans. Intell. Veh., 5 (2020), 556–564. https://doi.org/10.1109/TIV.2020.2991962 doi: 10.1109/TIV.2020.2991962
[10]	W. Li, Q. Li, S. Li, R. Li, Y. Ren, W. Wang, Indirect shared control through non-zero sum differential game for cooperative automated driving, IEEE Trans. Intell. Transp. Syst., 23 (2022), 15980–15992. https://doi.org/10.1109/TITS.2022.3146895 doi: 10.1109/TITS.2022.3146895
[11]	X. Jin, J. Wang, X. He, Z. Yan, L. Xu, C. Wei, et al., Improving vibration performance of electric vehicles based on in-wheel motor-active suspension system via robust finite frequency control, IEEE Trans. Intell. Transp. Syst., 24 (2023), 1631–1643. https://doi.org/10.1109/TITS.2022.3224609 doi: 10.1109/TITS.2022.3224609
[12]	X. Jin, J. Wang, Z. Yan, L. Xu, G. Yin, N. Chen, Robust vibration control for active suspension system of in-wheel-motor-driven electric vehicle via μ-synthesis methodology, ASME J. Dyn. Sys. Meas. Control, 144 (2022), 051007. https://doi.org/10.1115/1.4053661 doi: 10.1115/1.4053661
[13]	X. Jin, Q. Wang, Z. Yan, H. Yang, J. Wang, G. Yin, A learning-based evaluation for lane departure warning system considering driving characteristics, Proc. Inst. Mech. Eng. D-J. Aut., 2022. https://doi.org/10.1177/09544070221140973 doi: 10.1177/09544070221140973
[14]	K. Nam, H. Fujimoto, Y. Hori, Advanced motion control of electric vehicles based on robust lateral tire force control via active front steering, IEEE/ASME Trans. Mech., 19 (2014), 289–299. https://doi.org/10.1109/TMECH.2012.2233210 doi: 10.1109/TMECH.2012.2233210
[15]	H. Wang, Y. Tian, H. Xu, Neural adaptive command filtered control for cooperative path following of multiple underactuated autonomous underwater vehicles along one path, IEEE Trans. Syst, Man, Cybern. Syst., 52 (2022), 2966–2978. https://doi.org/10.1109/TSMC.2021.3062077 doi: 10.1109/TSMC.2021.3062077
[16]	Y. Wang, B. Nguyen, H. Fujimoto, Y. Hori, Multirate estimation and control of body slip angle for electric vehicles based on onboard vision system, IEEE Trans. Ind. Electron., 61 (2014), 1133–1143. https://doi.org//10.1109/TIE.2013.2271596 doi: 10.1109/TIE.2013.2271596
[17]	G. Wang, Y. Liu, S. Li, Y. Tian, N. Zhang, G. Cui, New integrated vehicle stability control of active front steering and electronic stability control considering tire force reserve capability, IEEE Trans. Veh. Technol., 70 (2021), 2181–2195. https://doi.org//10.1109/TVT.2021.3056560 doi: 10.1109/TVT.2021.3056560
[18]	J. Cho, K. Huh, Active front steering for driver's steering comfort and vehicle driving stability, Int. J. Automt. Technol., 20 (2019), 589–596. https://doi.org/10.1007/s12239-019-0056-1 doi: 10.1007/s12239-019-0056-1
[19]	P. Falcone, F. Borrelli, J. Asgari, H. Tseng, D. Hrovat, Predictive active steering control for autonomous vehicle systems. IEEE Trans. Control Syst. Technol., 15 (2007), 566–580. https://doi.org/10.1109/TCST.2007.894653 doi: 10.1109/TCST.2007.894653
[20]	T. Faulwasser, R. Findeisen, Nonlinear model predictive control for constrained output path following, IEEE Trans. Autom. Control, 61 (2016), 1026–1039. https://doi.org/10.1109/TAC.2015.2466911 doi: 10.1109/TAC.2015.2466911
[21]	P. Liljeback, I. Haugstuen, K. Pettersen, Path following control of planar snake robots using a cascaded approach, IEEE Trans. Control Syst. Technol., 20 (2012), 111–126. https://doi.org/10.1109/TCST.2011.2107516 doi: 10.1109/TCST.2011.2107516
[22]	A. Hladio, C. Nielsen, D. Wang, Path following for a class of mechanical systems, IEEE Trans. Control Syst. Technol., 21 (2013), 2380–2390. https://doi.org/10.1109/TCST.2012.2223470 doi: 10.1109/TCST.2012.2223470
[23]	S. Mobayen, Robust tracking controller for multivariable delayed systems with input saturation via composite nonlinear feedback, Nonlinear. Dyn., 76 (2014), 827–838. https://doi.org/10.1007/s11071-013-1172-5 doi: 10.1007/s11071-013-1172-5
[24]	V. Ghaffari, Optimal tuning of composite nonlinear feedback control in time-delay nonlinear systems, J. Franklin Inst., 357 (2020), 1331–1356. https://doi.org/10.1016/j.jfranklin.2019.12.024 doi: 10.1016/j.jfranklin.2019.12.024
[25]	S. Yu, X. Li, H. Chen, F. Allgöwer, Nonlinear model predictive control for path following problems, Int. J. Robust Nonlinear Control, 25 (2015), 1168–1182. https://doi.org/10.1002/rnc.3133 doi: 10.1002/rnc.3133
[26]	J. Chen, Z. Shuai, H. Zhang, W. Zhao, Path following control of autonomous four-wheel-independent-drive electric vehicles via second-order sliding mode and nonlinear disturbance observer techniques, IEEE Trans. Ind. Electron., 68 (2021), 2460–2469. https://doi.org/10.1109/TIE.2020.2973879 doi: 10.1109/TIE.2020.2973879
[27]	Z. Liu, X. Chen, Adaptive sliding mode security control for stochastic Markov jump cyber-physical nonlinear systems subject to actuator failures and randomly occurring injection attacks, IEEE Trans. Ind. Informat., 2022. https://doi.org/10.1109/TII.2022.3181274 doi: 10.1109/TII.2022.3181274
[28]	X. Zhao, Z. Liu, B. Jiang, C. Gao, Switched controller design for robotic manipulator via neural network-based sliding mode approach, IEEE Trans. Circuits Syst. II: Exp. Briefs, 70 (2022), 561–565. https://doi.org/10.1109/TCSII.2022.3169475 doi: 10.1109/TCSII.2022.3169475
[29]	B. Xu, F. Sun, Y. Pan, B. Chen, Disturbance observer based composite learning fuzzy control of nonlinear systems with unknown dead zone, IEEE Trans. Syst. Man. Cybern. Syst., 47 (2017), 1854–1862. https://doi.org/10.1109/TSMC.2016.2562502 doi: 10.1109/TSMC.2016.2562502
[30]	H. A. Hagras, A hierarchical type-2 fuzzy logic control architecture for autonomous mobile robots, IEEE Trans. Fuzzy. Syst., 12 (2004), 524–539. https://doi.org/10.1109/TFUZZ.2004.832538 doi: 10.1109/TFUZZ.2004.832538
[31]	J. Cervantes, W. Yu, S. Salazar, I. Chairez, Takagi-Sugeno dynamic neuro-fuzzy controller of uncertain nonlinear systems, IEEE Trans. Fuzzy. Syst., 25 (2017), 1601–1615. https://doi.org/10.1109/TFUZZ.2016.2612697 doi: 10.1109/TFUZZ.2016.2612697
[32]	Y. Wu, L. Wang, J. Zhang, F. Li, Path following control of autonomous ground vehicle based on nonsingular terminal sliding mode and active disturbance rejection control, IEEE Trans. Veh. Technol., 68 (2019), 6379–6390. https://doi.org/10.1109/TVT.2019.2916982 doi: 10.1109/TVT.2019.2916982
[33]	M. Islam, Y. He, An optimal preview controller for active trailer steering systems of articulated heavy vehicles, SAE Tech. Pap., 2011, 1–14. https://doi.org/10.4271/2011-01-0983
[34]	T. Ding, Y. Zhang, G. Ma, Z. Cao, X. Zhao, B. Tao, Trajectory tracking of redundantly actuated mobile robot by MPC velocity control under steering strategy constraint, Mechatronics, 84 (2022), 102779. https://doi.org/10.1016/j.mechatronics.2022.102779 doi: 10.1016/j.mechatronics.2022.102779
[35]	H. Moradi, G. Vossoughi, M. R. Movahhedy, H. Salarieh, Suppression of nonlinear regenerative chatter in milling process via robust optimal control, J. Process Control, 23 (2013), 631–648. https://doi.org/10.1016/j.jprocont.2013.02.006 doi: 10.1016/j.jprocont.2013.02.006
[36]	Y. Fu, B. Li, J. Fu, Multi-model adaptive switching control of a nonlinear system and its applications in a smelting process of fused magnesia, J. Process Control, 115 (2022), 67–76. https://doi.org/10.1016/j.jprocont.2022.04.009 doi: 10.1016/j.jprocont.2022.04.009
[37]	S. Fahmy, S. Banks, Robust H_∞ control of uncertain nonlinear dynamical systems via linear time-varying approximations, Nonlinear Anal., 63 (2005), 2315–2327. https://doi.org/10.1016/j.na.2005.03.030 doi: 10.1016/j.na.2005.03.030
[38]	G. Ju, Y. Wu, W. Sun, Adaptive output feedback asymptotic stabilization of nonholonomic systems with uncertainties, Nonlinear Anal., 71 (2009), 5106–5117. https://doi.org/10.1016/j.na.2009.03.088 doi: 10.1016/j.na.2009.03.088
[39]	E. Jafari, T. Binazadeh, Observer-based improved composite nonlinear feedback control for output tracking of time-varying references in descriptor systems with actuator saturation, ISA Trans., 91 (2019), 1–10. https://doi.org/10.1016/j.isatra.2019.01.035 doi: 10.1016/j.isatra.2019.01.035
[40]	S. Mobayen, An LMI-based robust tracker for uncertain linear systems with multiple time-varying delays using optimal composite nonlinear feedback technique, Nonlinear Dyn., 80 (2015), 917–927. https://doi.org/10.1007/s11071-015-1916-5 doi: 10.1007/s11071-015-1916-5
[41]	V. Ghaffari, S. Mobayen, D. Ud, T. Rojsiraphisal, M. T. Vu, Robust tracking composite nonlinear feedback controller design for time-delay uncertain systems in the presence of input saturation, ISA Trans., 129 (2022), 88–99. https://doi.org/10.1016/j.isatra.2022.02.029 doi: 10.1016/j.isatra.2022.02.029
[42]	X. Jin, Z. Yan, G. Yin, S. Li, C. Wei, An adaptive motion planning technique for on-road autonomous driving, IEEE Access, 9(2020), 2655–2664. https://doi.org/10.1109/ACCESS.2020.3047385 doi: 10.1109/ACCESS.2020.3047385
[43]	B. Paden, M. Čáp, S. Yong, D. Yershov, E. Frazzoli, A survey of motion planning and control techniques for self-driving urban vehicles, IEEE Trans. Intell. Veh., 1 (2016), 33–55. https://doi.org/10.1109/TIV.2016.2578706 doi: 10.1109/TIV.2016.2578706

This article has been cited by:

1.	Xianjian Jin, Chongfeng Wei, Chao Huang, Chuan Hu, Guodong Yin, Mohammed Chadli, Advanced Modeling, Analysis and Control for Electrified Vehicles, 2023, 11, 2075-1702, 866, 10.3390/machines11090866
2.	Ali Ajmi, Saber Krim, Anissa Hosseyni, Majdi Mansouri, Mohamed Faouzi Mimouni, Robust Variable Structure Control Approach of Two Series-Connected Five-Phase PMSMs Under Healthy and Faulty Operation Modes, 2023, 11, 2169-3536, 96401, 10.1109/ACCESS.2023.3311029
3.	Ying Li, Particle swarm optimization based neural network automatic controller for stability steering control of four-wheel drive electric vehicle, 2024, 10, 2297-3079, 10.3389/fmech.2024.1378175
4.	Xianjian Jin, Qikang Wang, Zeyuan Yan, Hang Yang, Guodong Yin, Integrated robust control of path following and lateral stability for autonomous in-wheel-motor-driven electric vehicles, 2024, 0954-4070, 10.1177/09544070241227266
5.	Kunhee Ryu, Bumsu Kim, Jehwi Yoo, Jinsung Kim, Jae Sung Bang, Juhoon Back, Robust Torque Vectoring With Desired Cornering Stiffness for In-Wheel Motor Vehicles, 2023, 11, 2169-3536, 133021, 10.1109/ACCESS.2023.3336681
6.	Dimitrios Papagiannis, Evangelos Tsioumas, Nikolaos Jabbour, Christos Mademlis, A Cost-Effective and Highly Accurate Observer for the Real-Time Estimation of the Vehicle Velocity and the Road Inclination and Bank Angles, 2023, 11, 2169-3536, 107867, 10.1109/ACCESS.2023.3320280
7.	Giseo Park, Sooyoung Kim, Hyeongmuk Kang, Optimal Driving Control for Autonomous Electric Vehicles Based on In-Wheel Motors Using an Artificial Potential Field, 2024, 12, 2169-3536, 113799, 10.1109/ACCESS.2024.3443869
8.	Hun Hwangbo, Jaeun Ryu, Sangwon Han, Kunsoo Huh, Robust Sliding Mode Control With Optimal Path Following for Lateral Motion of Autonomous Bus, 2023, 11, 2169-3536, 71981, 10.1109/ACCESS.2023.3294965
9.	Xianjian Jin, Hang Yang, Xiongkui He, Guohua Liu, Zeyuan Yan, Qikang Wang, Robust LiDAR-Based Vehicle Detection for On-Road Autonomous Driving, 2023, 15, 2072-4292, 3160, 10.3390/rs15123160
10.	Xiaojing Wu, Zhenan Guo, Xinyue Liu, Tian Xie, Fault-Tolerant Time-Varying Formation Tracking Control for Multi-Agent Systems With Actuator Faults and Switching Topologies, 2023, 11, 2169-3536, 131140, 10.1109/ACCESS.2023.3333660
11.	Hao Wen, Zaixin Song, Senyi Liu, Zhiping Dong, Chunhua Liu, A Hybrid LiDAR-Based Mapping Framework for Efficient Path Planning of AGVs in a Massive Indoor Environment, 2024, 10, 2332-7782, 3504, 10.1109/TTE.2023.3280738
12.	Chuanwei Zhang, Peng Gao, Jianlong Wang, Meng Dang, Xinyue Yang, Yansong Feng, Research on Active Rear-Wheel Steering Control Method With Sliding Mode Control Optimized by Model Predictive, 2023, 11, 2169-3536, 57228, 10.1109/ACCESS.2023.3283330
13.	Ara Jo, Woojin Kwon, Kyongsu Yi, Motion Planning for Urban Autonomous Bus Considering Localization Uncertainty Using Offset-Free MPC, 2024, 12, 2169-3536, 11743, 10.1109/ACCESS.2024.3355205
14.	Xianjian Jin, Zhaoran Wang, Junpeng Yang, Liwei Xu, Guodong Yin, Novel Payload Parameter Sensitivity Analysis on Observation Accuracy of Lightweight Electric Vehicles, 2023, 24, 1229-9138, 1313, 10.1007/s12239-023-0106-6
15.	Xianjian Jin, Huaizhen Lv, Zhihui He, Zhiwei Li, Zhaoran Wang, Nonsly Valerienne Opinat Ikiela, Design of Active Disturbance Rejection Controller for Trajectory-Following of Autonomous Ground Electric Vehicles, 2023, 15, 2073-8994, 1786, 10.3390/sym15091786
16.	Akram Hashim Hameed, Shibly Ahmed Al-Samarraie, Amjad Jaleel Humaidi, Nagham Saeed, Backstepping-Based Quasi-Sliding Mode Control and Observation for Electric Vehicle Systems: A Solution to Unmatched Load and Road Perturbations, 2024, 15, 2032-6653, 419, 10.3390/wevj15090419

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(2304) PDF downloads(192) Cited by(16)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(10) / Tables(2)

AIMS Mathematics

Nonlinear robust control of trajectory-following for autonomous ground electric vehicles with active front steering system

Related Papers:

Abstract

1. Introduction

2. Problem description and trajectory following model

2.1. Vehicle dynamics system model

2.2. Vehicle trajectory following formulation

2.3. Uncertain vehicle trajectory following model

3. Nonlinear robust controller design

3.1. Design of robust feedback control

3.2. Nonlinear robust control feedback design

4. Simulation and analysis

4.1. Double lane change condition

4.2. Serpentine condition

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Nonlinear robust control of trajectory-following for autonomous ground electric vehicles with active front steering system

Related Papers:

Abstract

1. Introduction

2. Problem description and trajectory following model

2.1. Vehicle dynamics system model

2.2. Vehicle trajectory following formulation

2.3. Uncertain vehicle trajectory following model

3. Nonlinear robust controller design

3.1. Design of robust feedback control

3.2. Nonlinear robust control feedback design

4. Simulation and analysis

4.1. Double lane change condition

4.2. Serpentine condition

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog