Hybrid arithmetic optimization algorithm with deep learning model for secure Unmanned Aerial Vehicle networks

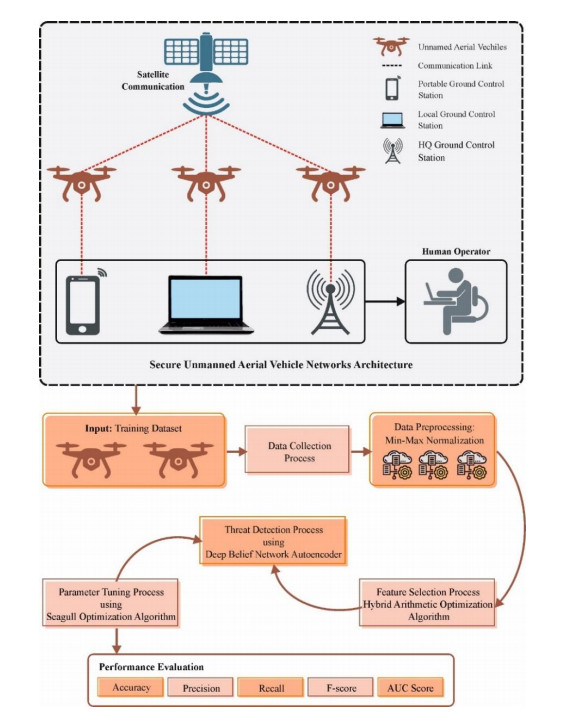
1.   Introduction

We can identify two types of graph invariants which are currently being studied in chemical graph theory. Namely,

and

Here, $uv$ denotes the edge of the graph $G = (V(G), E(G))$ connecting the vertices $u$ and $v$, $d_u$ is the degree of the vertex $u$, and $F_V(x)$ and $F_E(x, y)$ are appropriately defined functions (see e.g., ^[1]). Since $X_\Sigma(G)$ and $X_\Pi(G)$ are usually known as topological indices in the literature, here we will refer to $X_\Pi(G)$ as multiplicative topological indices (MTIs) to make a clear difference between both types of indices.

Among the vast amount of topological indices of the form $X_\Sigma(G)$, the first and second Zagreb indices ^[2] stand out, and they are defined as

and

respectively. Also, the Randić connectivity index ^[3]

the harmonic index ^[4]

the sum-connectivity index ^[5]

and the inverse degree index ^[4]

The topological indices mentioned above and many others of the form $X_\Sigma(G)$ have been widely studied during recent decades.

More recently, MTIs have attracted a lot of attention, see e.g., ^{[6,7,8,9,10,11,12]}. Indeed, several MTIs have already been deeply analyzed in the literature (see e.g., the work of V. R. Kulli). Among the most relevant ones, the Narumi-Katayama index ^[13] should be mentioned:

Additionally, multiplicative versions of the Zagreb indices ^[14]

and

In addition to the MTIs of Eqs (1.9)–(1.12), in this work we also consider multiplicative versions of the indices in Eqs (1.5)–(1.8): the multiplicative Randić connectivity index

the multiplicative harmonic index

the multiplicative sum-connectivity index

and the multiplicative inverse degree index

Therefore, motivated by their potential applications, in this work we perform an analytical as well as computational study of MTIs. Specifically, the purpose of this work is threefold:

First, we follow an analytical viewpoint to find several new inequalities that relate two MTIs indices between them as well as to their additive versions in Section 2. Note that the search for inequalities between different indices is a classical topic in the study of topological indices. See e.g., ^{[6,7,8,9,10,11,12]} for previous results relating MTIs.

Second, we want to establish the statistical analysis of MTIs as a generic tool for the study of average properties of random networks in Section 3. For some previous works dealing with the statistical analysis of (non-multiplicative) topological indices, see, e.g., ^{[15,16,17,18,19]}.

Finally, in this paper we perform for the first time (to our knowledge) a scaling study of MTIs on random networks which let us state a scaling law that relates different random graph models in Section 4.

2.   Inequalities involving multiplicative topological indices

There are many works studying particular MTIs; see, e.g., ^[20,21] and the references therein. However, in this section we obtain several analytical inequalities involving the general MTIs $X_{\Pi, F_V}(G)$ and $X_{\Pi, F_E}(G)$.

The following equalities are direct:

Since the geometric mean is at most the arithmetic mean (by Jensen's inequality), we have the following inequalities.

Proposition 2.1. Let $G$ be a graph with $n$ vertices and $m$ edges. Then,

This general result has as a particular consequence the following known inequality, see [9, Theorem 2.1].

Corollary 2.1. Let $G$ be a graph with $n$ vertices and $m$ edges. Then,

Proof. If we take $F_V(d_u) = d_u$, then

and Proposition 2.1 gives

which implies the desired inequality. □

Proposition 2.1 has several consequences:

Proposition 2.2. Let $G$ be a graph with $n$ vertices and $m$ edges.

$(1)$ If $F_E(d_u, d_v) = h(d_u) + h(d_v)$ and $F_V(d_u) = d_u h(d_u)$ for some function $h$, then

$(2)$ If $F_E(d_u, d_v) = h(d_u)h(d_v)$ and $F_V(d_u) = h(d_u)^{d_u}$ for some function $h$, then

Proof. Let $G$ be a graph with $n$ vertices and $m$ edges.

If $F_E(d_u, d_v) = h(d_u) + h(d_v)$ and $F_V(d_u) = d_u h(d_u)$ for some function $h$, then

Consequently, Proposition 2.1 implies

If $F_E(d_u, d_v) = h(d_u)h(d_v)$ and $F_V(d_u) = h(d_u)^{d_u}$ for some function $h$, then

Hence, Proposition 2.1 gives

□

Theorem 2.1. Let $G$ be a graph with $m$ edges. Assume that $F_1(d_u, d_v) = h(d_u) + h(d_v)$ and $F_2(d_u, d_v) = h(d_u) h(d_v)$ for some function $h$. Then,

Proof. Since the (weighted) geometric mean is at most the (weighted) arithmetic mean (by Jensen's inequality), the following inequality holds for every $x_i, w_i > 0$:

If we take $x_i = h(d_u)$ and $w_i = d_u$, then we get

□

This general result has as a particular consequence the following known inequality, see [9, Theorem 3.1].

Corollary 2.2. Let $G$ be a graph with $m$ edges. Then,

Proof. If we take $h(x) = x$, then $F_1(d_u, d_v) = d_u + d_v$, $F_2(d_u, d_v) = d_u d_v$, $X_{\Pi, F_2}(G) = \Pi_2(G)$, $X_{\Sigma, F_1}(G) = M_{1}(G)$, and Theorem 2.1 gives the desired inequality. □

In ^[22] appears the following Jensen-type inequality.

Theorem 2.2. Let $\mu$ be a probability measure on the space $X$ and $a \le b$ be real constants. If $f: X \rightarrow [a, b]$ is a measurable function and $\varphi$ is a convex function on $[a, b]$, then $f$ and $\varphi \circ f$ are $\mu$-integrable functions, and

Theorem 2.2 allows one to find the following converse of Proposition 2.1, if we consider the normalized counting measure as $\mu$.

Theorem 2.3. Let $G$ be a graph with $n$ vertices and $m$ edges, $a_V \le b_V$, $a_E \le b_E$ be real constants, and $F_V$, $F_E$ be functions satisfying

Then,

Proof. Since $\varphi(x) = e^x$ is a convex function on $\mathbb{R}$, Theorem 2.2 gives

In a similar way,

□

Theorem 2.3 provides the following new lower bounds of $\Pi_1$ and $\Pi_1^*$.

Corollary 2.3. Let $G$ be a graph with $n$ vertices and $m$ edges, minimum degree $\delta$, and maximum degree $\Delta$. Then,

Proof. Since $\delta^2 \le d_u^2 \le \Delta^2$ and $2 \delta \le d_u+d_v \le 2 \Delta$, Theorem 2.3 implies

□

The following Kober's inequalities in ^[23] (see also [24, Lemma 1]) are useful.

Lemma 2.1. If $a_j > 0$ for $1\le j \le k$, then

Lemma 2.1 has the following consequence.

Theorem 2.4. Let $G$ be a graph with $n$ vertices and $m$ edges. Then,

Proof. Lemma 2.1 gives

and

In a similar way, replacing $F_V(d_u)$ and $n$ with $F_E(d_u, d_v)$ and $m$, respectively, we obtain

and

□

Let us recall the following known Petrović inequality ^[25].

Theorem 2.5. Let $\varphi$ be a convex function on $[0, a]$, and $w_1, \dots, w_n \ge 0$. If $t_1, \dots, t_n \in [0, a]$ satisfy $\sum_{k = 1}^n t_kw_k \in (0, a]$, and

then

Theorem 2.5 has the following consequence.

Proposition 2.3. Let $\varphi$ be a convex function on $[0, a]$. If $t_1, \dots, t_n \in [0, a]$ satisfy $\sum_{k = 1}^n t_k \in (0, a]$, then

Proposition 2.3 allows for the proof of the following inequalities.

Theorem 2.6. Let $G$ be a graph with $n$ vertices and $m$ edges. Then,

Proof. Let us consider the convex function $\varphi(x) = e^x$. Proposition 2.3 gives

In a similar way,

□

Theorem 2.7. Let $G$ be a graph. Then,

Proof. The equality $e^x \ge x+1$ holds for every $x \in \mathbb{R}$. This inequality gives

The same argument gives the second inequality. □

In ^[26], the Gutman-Milovanović index is defined as

which is a natural generalization of Zagreb indices.

Next, we present an inequality relating some multiplicative indices and the Gutman-Milovanović index.

Theorem 2.8. Let $G$ be a graph with $m$ edges, and $\alpha, \beta \in \mathbb{R}$. Then,

The equality is attained for any $\alpha, \beta$ if $G$ is regular.

Proof. Since the geometric mean is at most the arithmetic mean, we get

Thus,

If the graph is $\delta$-regular, then $M_{ \alpha, \beta}(G) = 2^ \beta \delta^{2 \alpha+ \beta}m$, $\Pi_2(G)^{ \alpha/m} = (\delta^{2m})^{ \alpha/m} = \delta^{2 \alpha}$, $\Pi_1^*(G)^{ \beta/m} = ((2 \delta)^{m})^{ \beta/m} = 2^ \beta \delta^{ \beta}$, and the equality holds. □

We have some direct formulas for some multiplicative indices, e.g.,

for every graph $G$ with $m$ edges.

Let us show some inequalities relating different multiplicative indices.

Theorem 2.9. Let $G$ be a graph with $m$ edges, maximum degree $\Delta$ and minimum degree $\delta$. Then,

Furthermore, the equality in each inequality is attained for every regular graph.

Proof. First of all, note that if

for every $\delta \le x, y \le \Delta$, then we have for every $uv \in E(G)$,

for every graph $G$ with $m$ edges, maximum degree $\Delta$, and minimum degree $\delta$.

Since

we have

Since

we have

Since

we have

Let us consider the function

where

Since

$f$ is decreasing on $(0, 1]$ and increasing on $[1, \infty)$. Since $f(1) = 2$, we conclude

Hence,

Let $G$ be a $\delta$-regular graph. Hence,

Therefore, the equality in each inequality is attained for every regular graph. □

Recall that a biregular graph is a bipartite graph for which any vertex in one side of the given bipartition has degree $\Delta$ and any vertex in the other side of the bipartition has degree $\delta$. We say that a graph is $(\Delta, \delta)$-biregular if we want to write explicitly the maximum and minimum degrees.

Theorem 2.10. If $G$ is a graph with $m$ edges, minimum degree $\delta$, and maximum degree $\Delta$, then

The equality in the lower bound is attained if and only if each connected component of $G$ is a regular graph. The equality in the upper bound is attained if and only if $G$ is a regular or biregular graph.

Proof. Define

for $x, y \in [ \delta, \Delta]$. Note that, in order to find the bounds of $A$, it suffices to consider the case $y \ge x$. We have

for every $y \in (x, \Delta]$. Hence, $A(x, x) \le A(x, y) \le A(x, \Delta)$. Note that $A(x, x) = 8$.

Define

for $x \in [ \delta, \Delta]$. We get

for every $x \in [ \delta, \Delta)$. Therefore,

for $x \in [ \delta, \Delta]$. Hence,

and so,

The previous argument gives that the equality in the lower bound is attained if and only if $d_u = d_v$ for every $uv \in E(G)$, and this happens if and only if each connected component of $G$ is a regular graph.

Also, the equality in the upper bound is attained if and only if $\{d_u, d_v\} = \{ \Delta, \delta\}$ for every $uv \in E(G)$, and this happens if and only if $G$ is a regular (if $\Delta = \delta$) or $(\Delta, \delta)$-biregular (if $\Delta \neq \delta$) graph. □

3.   Statistical properties of multiplicative topological indices on random networks

The statistical properties of topological indices in random networks have been intensively studied, see, e.g., ^[27,28]. Within this statistical approach, it has been recently shown that the average values of indices of the type $X_\Sigma(G)$, normalized to the order of the network $n$, scale with the average degree $\left < d \right >$, see, e.g., ^{[15,16,17,18]}. That is, $\left < X_\Sigma(G) \right > /n$ is a function of $\left < d \right >$ only. Moreover, it was also found that $\left < X_\Sigma(G) \right >$, for indices like $R(G)$ and $H(G)$, is highly correlated with the Shannon entropy of the eigenvectors of the adjacency matrix of random networks ^[19]. This is a notable result because it puts forward the application of topological indices beyond mathematical chemistry. Specifically, given the equivalence of the Hamiltonian of a tight-binding network (in the proper setup) and the corresponding network adjacency matrix, either $\left < R(G) \right >$ or $\left < H(G) \right >$ could be used to determine the eigenvector localization and delocalization regimes which in turn determine the insulator and metallic regimes of quantum transport.

Below, for the first time to our knowledge, we apply the MTIs of Eqs (1.9)–(1.16) on three models of random networks: Erdös-Rényi (ER) networks, random geometric (RG) graphs, and bipartite random (BR) networks.

ER networks ^[29,30,31] $G_{\mbox{ER}}(n, p)$ are formed by $n$ vertices connected independently with probability $p \in [0, 1]$. While RG graphs ^[32,33] $G_{\mbox{RG}}(n, r)$ consist of $n$ vertices uniformly and independently distributed on the unit square, where two vertices are connected by an edge if their Euclidean distance is less than or equal to the connection radius $r \in [0, \sqrt{2}]$. In addition, we examine BR networks $G_{\mbox{BR}}(n_1, n_2, p)$ composed of two disjoint sets, set 1 and set 2, with $n_1$ and $n_2$ vertices each such that there are no adjacent vertices within the same set, being $n = n_1+n_2$ the total number of vertices in the bipartite network. The vertices of the two sets are connected randomly with probability $p \in [0, 1]$.

3.1.   Multiplicative topological indices on Erdös-Rényi random networks

Before computing MTIs on ER random networks, we note that in the dense limit, i.e., when $\left < d \right > \gg 1$, we can approximate $d_u \approx d_v \approx \left < d \right >$ in Eqs (1.9)–(1.16), with

Thus, for example, when $np\gg 1$, we can approximate $NK_\Pi(G_{\mbox{ER}})$ as

which leads us to

or

A similar approximation gives

Also, for $\Pi_2(G_{\mbox{ER}})$, we have that

where we have used $\mid E(G_{\mbox{ER}}) \mid = n\left < d \right > /2$. Therefore,

or

Following this procedure, for the rest of the MTIs of Eqs (1.12)–(1.16) we get:

and

From the approximate expressions above we note that the logarithm of the MTIs on ER random networks, normalized to the network size $n$, does not depend on $n$. That is, in the dense limit, we expect $\ln X_\Pi(G_{\mbox{ER}})/n$ to depend on $\left < d \right >$ only; here, $X_\Pi$ represents all the MTIs of Eqs (1.9)–(1.16).

With Eqs (3.2)–(3.9) as a guide, in what follows we compute the average values of the logarithm of the MTIs listed in Eqs (1.9)–(1.16). All averages are computed over ensembles of $10^7/n$ ER networks characterized by the parameter pair $(n, p)$.

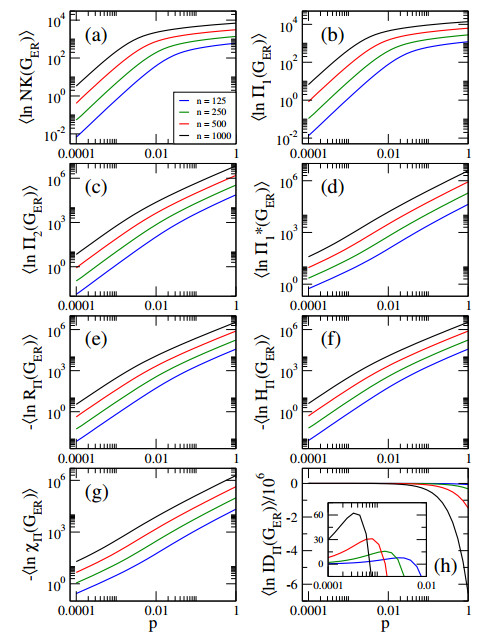
In Figure 1 we present the average logarithm of the eight MTIs of Eqs (1.9)–(1.16) as a function of the probability $p$ of ER networks of sizes $n = \{125,250,500, 1000\}$. Since $\left < \ln X_\Pi(G_{\mbox{ER}}) \right > < 0$, for $R_\Pi$, $H_\Pi$, and $\chi_\Pi$ we conveniently plotted $-\left < \ln X_\Pi(G_{\mbox{ER}}) \right >$ in log scale to have a detailed view of the data for small $p$, see Figure 1(e–g). Thus, we observe that $\left < \ln X_\Pi(G_{\mbox{ER}}) \right >$ for $NK$, $\Pi_{1, 2}$, and $\Pi_1^*$ [for $R_\Pi$, $H_\Pi$, and $\chi_\Pi$] is a monotonically increasing [monotonically decreasing] function of $p$. In contrast, $\left < \ln ID_\Pi(G_{\mbox{ER}}) \right >$ is a nonmonotonic function of $p$, see Figure 1(h).

Then, following Eqs (3.2)–(3.9), in Figure 2 we show again the average logarithm of the MTIs, but now normalized to the network size, $\left < \ln X_\Pi(G_{\mbox{ER}}) \right > /n$, as a function of $\left < d \right >$. As can be clearly observed in this figure, the curves $\left < \ln X_\Pi(G_{\mbox{ER}}) \right > /n$ versus $\left < d \right >$ fall one on top of the other for different network sizes; so, these indices are properly scaled where $\left < d \right >$ works as the scaling parameter. That is, $\left < d \right >$ is the parameter that fixes the average values of the normalized MTIs on ER networks. It is remarkable that the scaling of $\left < \ln X_\Pi(G_{\mbox{ER}}) \right > /n$ with $\left < d \right >$, expected for $\left < d \right > \gg 1$ according to Eqs (3.2)–(3.9), works perfectly well for all values of $\left < d \right >$; even for $\left < d \right > \ll 1$. Since the topological properties of random graphs and networks, when characterized by indices of the form $X_\Sigma(G)$, have been shown to scale with $\left < d \right >$ for all values of $\left < d \right >$ (see e.g., ^{[15,16,17,18,19]}), we should expect other topological measures to also scale with $\left < d \right >$, such as the MTIs studied here. Also, in Figure 2, we show that Eqs (3.2)–(3.9) (orange-dashed lines) indeed describe well the data (thick full curves) for $\left < d \right > \ge 10$, which can be regarded as the dense limit of the ER model.

3.2.   Multiplicative topological indices on random geometric graphs

As in the previous Subsection, here we start by exploring the dense limit. Indeed, for RG graphs in the dense limit, i.e., when $\left < d \right > \gg 1$, we can approximate $d_u \approx d_v \approx \left < d \right >$, where

and ^[34]

Thus, we obtain

and

Remarkably, the approximate Eqs (3.12)–(3.19) for RG graphs are exactly the same as the corresponding equations for ER graphs, see Eqs (3.2)–(3.9); however, note that the definition of $\left < d \right >$ is different for both models, i.e., compare Eqs (3.1), (3.10), and (3.11).

Then, in Figure 3 we present the average logarithm of the eight MTIs of Eqs (1.9)–(1.16) as a function of the connection radius $r$ of RG graphs of sizes $n = \{125,250,500, 1000\}$. All averages are computed over ensembles of $10^7/n$ random graphs, and each ensemble is characterized by a fixed parameter pair $(n, r)$.

For comparison purposes, Figure 1 for ER networks and Figure 3 for RG graphs have the same format and contents. In fact, all the observations made in the previous Subsection for ER networks are also valid for RG graphs by replacing $G_{\mbox{ER}}\to G_{\mbox{RG}}$ and $p\to g(r)$. Therefore, in Figure 4 we plot $\left < \ln X_\Pi(G_{\mbox{RG}}) \right > /n$ as a function of $\left < d \right >$ showing that all curves are properly scaled; that is, curves for different graph sizes fall on top of each other. Also, in Figure 4 we show that Eqs (3.12)–(3.19) (orange-dashed lines) indeed describe the data well (thick full curves) for $\left < d \right > \ge 10$, which can be regarded as the dense limit of RG graphs.

3.3.   Multiplicative topological indices on bipartite random networks

We start by writing approximate expressions for the MTIs on BR networks in the dense limit. Moreover, since edges in a bipartite network join vertices of different sets, and we are labeling here the sets as set 1 and set 2, we replace $d_u$ by $d_1$ and $d_v$ by $d_2$ in the expression for the MTIs. Thus, when $n_1p\gg 1$ and $n_2p\gg 1$, we can approximate $d_u = d_1 \approx \left < d_1 \right >$ and $d_v = d_2 \approx \left < d_2 \right >$ in Eqs (1.9)–(1.16), with

Therefore, in the dense limit, the MTIs of Eqs (1.11)–(1.16) on BR networks are well approximated by

and

Above we used $\mid E(G_{\mbox{BR}}) \mid = n_1n_2p = n_{1, 2}\left < d_{1, 2} \right >$. We note that we are not providing approximate expressions for neither $NK(G_{\mbox{BR}})$ nor $\Pi_1(G_{\mbox{BR}})$.

Now we compute MTIs on ensembles of $10^7/n$ BR networks. In contrast to ER and RG networks, now the BR network ensembles are characterized by three parameters: $n_1$, $n_2$, and $p$. For simplicity, but without lost of generality, in our numerical calculations we consider $n_1 = n_2$. It is remarkable to notice that, in the case of $n_1 = n_2 = n/2$, where $\left < d_1 \right > = \left < d_2 \right > = \left < d \right > = np/2$, Eqs (3.21)–(3.26) reproduce Eqs (3.4)–(3.9).

Then, in Figure 5 we present the average logarithm of the eight MTIs of Eqs (1.9)–(1.16) as a function of the probability $p$ of BR networks of sizes $n_1 = n_2 = \{125,250,500, 1000\}$. Therefore, by plotting $\left < \ln X_\Pi(G_{\mbox{BR}}) \right > /n$ as a function of $\left < d \right >$ (see Figure 6), we confirm that the curves of the MTIs on BR networks are properly scaled, as predicted by Eqs (3.21)–(3.26); see the orange dashed lines in Figure 6 (c–h). Here, we can also say that $\left < d \right > \ge 10$ can be regarded as de dense limit of BR networks. We have verified (not shown here) that we arrive at equivalent conclusions when $n_1\neq n_2$.

Note that in panels (a, b) of Figure 6 we included Eqs (3.2) and (3.3) as orange dashed lines. Those equations were obtained for ER networks, however they reproduce perfectly well both $NK(G_{\mbox{BR}})$ and $\Pi_1(G_{\mbox{BR}})$ when $\left < d \right > \ge 10$ since we are considering $n_1 = n_2 = n/2$.

4.   Discussion and conclusions

In this work we have performed a thorough analytical and statistical study of multiplicative topological indices (MTIs) $X_\Pi$.

From an analytical viewpoint, we found several inequalities that relate MTIs among themselves as well as to their additive versions $X_\Sigma$. To find inequalities between different indices is a classical topic in the study of topological indices.

Within a statistical approach we computed MTIs on random networks. Some previous works deal with the statistical analysis of (non-multiplicative) topological indices. As models of random networks we have used Erdös-Rényi (ER) networks, random geometric (RG) graphs, and bipartite random (BR) networks. We showed that the average logarithm of the MTIs, $\left < \ln X_\Pi(G) \right >$, normalized to the order of the network, scale with the network average degree $\left < d \right >$. Thus, we conclude that $\left < d \right >$ is the parameter that fixes the average values of the logarithm of the MTIs on random networks. Moreover, the equivalence among Eqs (3.2)–(3.9) for ER networks, Eqs (3.12)–(3.19) for RG graphs, and Eqs (3.21)–(3.26) for BR networks (when the subsets are equal in size) allows us to state a scaling law that connects the three graph models. That is, given the MTI $X_\Pi$, the average of its logarithm divided by the network size is the same function of the average degree regardless the network model:

To validate Eq (4.1), without loss of generality we choose three MTIs: the Narumi-Katayama index, the multiplicative sum-connectivity index, and the multiplicative inverse degree index. We apply these indices to ER networks, RG graphs, and BR networks and plot $\left < \ln NK_\Pi(G) \right > /n$, $-\left < \ln \chi_\Pi(G) \right > /n$ and $\left < \ln ID_\Pi(G) \right > /n$ in Figure 7. There, for each index, we can clearly see that the curves corresponding to the three network models fall one on top of the other, thus validating Eq (4.1). Also, notice that we are using networks of different sizes to stress the scaling law in Eq (4.1). We observe the same scaling behavior in all the other MTIs of Eqs (1.10)–(1.14) (not shown here).

Finally, it is fair to mention that we found that the multiplicative version of the geometric-arithmetic index $GA_\Pi(G)$ on random networks does not scale with the average degree. This situation is quite unexpected for us since all other MTIs we study here scale with $\left < d \right >$. In addition, our previous statistical and theoretical studies of topological indices of the form $X_\Sigma(G)$ (see Eq (1.1)), showed that the normalized geometric-arithmetic index $GA_\Sigma(G)$ scales with $\left < d \right >$ ^[16]. Thus, we believe that the multiplicative index $GA_\Pi(G)$ on random graphs requires further analysis.

Augmented Reality (AR) algorithms have shown rapid development in recent years when applied to the study of different networks, such as neural and communication networks (see e.g., ^[35,36]). Therefore, it would be interesting to apply AR techniques in the analysis of random networks.

We hope that our work may motivate further analytical and computational studies of MTIs.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This publication is part of the grant PID2019-106433GB-I00 funded by Agencia Estatal de Investigación MCIN/AEI/ 10.13039/501100011033. J.A.M.-B. thanks support from CONACyT (Grant No. 286633), CONACyT-Fronteras (Grant No. 425854), and VIEP-BUAP (Grant No. 100405811-VIEP2023), Mexico. J.M.R. was supported by the Madrid Government (Comunidad de Madrid-Spain) under the Multiannual Agreement with UC3M in the line of Excellence of University Professors (EPUC3M23), and in the context of the V PRICIT (Regional Programme of Research and Technological Innovation).

We would like to thank the referees for their comments which have improved the presentation of the paper.

Conflict of interest

Prof. Jose M. Rodriguez is the Guest Editor of special issue "Graph theory and its applications" for AIMS Mathematics. Prof. Jose M. Rodriguez was not involved in the editorial review and the decision to publish this article.

All authors declare no conflicts of interest in this paper.