Newly defined fuzzy Misbalance Prodeg Index with application in multi-criteria decision-making

1.   Introduction

Graph theory originated with Euler's 1736 study on the Seven Bridges of Königsberg issue. To answer this difficulty, Euler created the concept of a graph, and his book "Solution of a Problem Related to the Geometry of Position" is recognised as the fundamental work in graph theory. The development of fuzzy notions in graphs involves expanding classical graph theory to enable the representation of imprecision via fuzzy logic. Fuzzy graph theory is an area of graph theory that addresses uncertainty or imprecision in the representation of connections among objects or entities. Traditional graph theory defines graphs as nodes (vertices) connected by edges (links) that express specific relationships between them. However, in many real-world settings, object relationships may be ambiguous or imprecise. Fuzzy graph theory presents the concept of fuzzy sets, which indicate the degree of membership or resemblance between nodes and edges. Various fundamental research and examples of applications of fuzzy graph theory in diverse disciplines, proving its adaptability in handling uncertainty and ambiguity in real-world circumstances, are described in ^[1,2,3] The notion of the fuzzy set was established in ^[4] to describe the concept of vagueness in a classical set. This served as the inspiration for Rosenfeld ^[5], who proposed the fuzziness for graphs in 1975 and gave them the name fuzzy graph (FG). Topological indices (TIs) are molecular descriptors that are determined on the molecular graph of a chemical compound in the areas of mathematical chemistry known as chemical graph theory, molecular topology, and molecular topology. These molecular descriptors are numerical quantities that characterize a graph's topology. The first topological descriptor, named as Wiener index (WI), which is deployed to find the BP(Boiling Point) of alkane(Paraffin), was initially examined in 1947 ^[6]. In order to determine the special types of energy namely $\pi$-electron energy of hydrocarbons, the Zagreb index (ZI) was developed in ^[7]. Following the definition of this molecular descriptive, authors investigated the forgotten topological index (F-index), another index based on the degree of vertices in ^[8]. Mondal et al. discuss a few neighborhood degree-based topological indices ^[9,10]. Topological indices are important in fields such as molecular chemistry, chemical graph theory, spectral graph theory, and network theory. Numerous scholars are investigating the concept of topological indices (TIs) in fuzzy graphs as well, owing to the extensive applicability of TIs in crisp graphs across various domains. Uzma et al. discussed the algebraic perspective of TIs using the automorphism of group action ^[11]. Extremal values of benzenoid structures have been discussed via degree-based topological indices ^[12,13]. Distance degree-based indices have been in ^[14]. For the study on the general Randic index, one can see in ^[15,16]. Researchers initially concentrated on extending standard topological indices, such as the Wiener, Randić, and Zagreb indices, to fuzzy graphs. These ´ additions involved generating suitable fuzzy versions of distance, degree, and associated concepts. Aside from enhancing classical indices, researchers created totally new fuzzy topological indices specifically designed to capture the unique characteristics of fuzzy graphs. These indices frequently entail aggregating the fuzzy memberships of vertices and edges in a graph to obtain a scalar value that represents a specific topological attribute. For fuzzy graphs, Kalathian et al. ^[17] defined the first degree-based topological indices.

Islam and Pal ^[18] examine the first Zagreb index and prove several related results for several fuzzy graphs, including fuzzy path graph, Fuzzy cycle graph, Fuzzy star graph, and fuzzy subgraphs. Additionally, a method for multi-criteria decision-making (MCDM) is presented, which identifies the competent employee in a company by utilizing the fuzzy graph's first Zagreb index. It has been observed that authors found certain bounds along with numerous of its properties and by the use of the Randic index, Akram et al. presented the fuzzy graphs using bipolar concept. They also described an expression for the Randic index of bipolar fuzzy cycles and fuzzy graphs.

Since 1972, several degree-based topological indices have been introduced and examined in Chemical Graph Theory ^[19,20]. Gutman ^[21] invented the Sombor index, a degree-based index. The motivation behind this study is that topological indices (TIs) for crisp graphs have many uses in a variety of contexts, therefore it makes sense to investigate the concept of TIs for fuzzy graphs as well. For fuzzy graphs, the group of Zagreb indices and Wiener indices are the main topics of the literature currently available on topological indices in fuzzy graph theory. This paper introduces a new fuzzy topological index, the fuzzy Misbalance Prodeg Index (FMPI), as a result of the widespread use and importance of topological indices in fuzzy graphs. We defined this novel index and investigated its features and applications in the area of multi-criteria decision-making, particularly with fuzzy graphs. Numerous research publications have contributed to our understanding of how graphs can be used to improve decision-making processes. Comparing and discussing the outcomes of this line of research is critical for various reasons. Researchers can validate particular study findings by comparing them to other studies, assuring consistency and reliability. Assessing several studies assists in detecting common trends and patterns, which can lead to the creation of best practices and standard techniques for graph-driven decision-making. Comparing studies might sometimes reveal differences or contradicting results, requiring additional research to determine the underlying causes and strengthen decision-making models. Discussing multiple findings allows for a more comprehensive grasp of the subject, combining many perspectives and ways to graph-driven decision-making. For example, the study cited in ^[22] provides detailed insights into graph-driven decision-making. By comparing this study to others in the field, researchers can examine the robustness of the methodologies utilised, the application of the results in diverse contexts, and the overall contribution to the body of knowledge. In the study of fuzzy graphs, the fuzzy Misbalance Prodeg Index (FMPI) is an important addition to topological indices, opening up new paths for research and real-world applications. This paper is arranged in the following manner: in Section 2 some basic elements of fuzzy graphs are given which are necessary part for the better understanding of this study. In Section 3, some topological indices along with the Misbalance Prodeg index are defined for fuzzy graphs. Some bounds of these two indices for fuzzy graphs are discussed in section 4. Section 5 explains an algorithm to evaluate these indices for fuzzy graphs. In Section 6, applications in multi-criteria decision-making problems for Misbalance Prodeg indices are considered. Finally, a comparison of related indices on the application's outcome is given, demonstrating the worth of our approach in Section 7, and in Section 8 we have given our conclusion.

2.   Preliminaries

A graph is an ordered pair $\Re = (\eta, \tau)$ with vertex set $\eta(\Re)$ and edge set $\tau (\Re)$. The vertex set $\eta(\Re)$ is always non-empty whereas the edge set $\tau (\Re)$ may or may not be an empty set. There are two types of graphs we are dealing with in this research such as crisp graphs and fuzzy graphs. This paper aims to study fuzzy graphs. All the definitions in this section are taken from ^[23].

Let $A(\neq\emptyset)$ be given a finite set. Let Fuzzy graph (FG) is $\Re = (\eta, \tau)$, where $\eta$ is fuzzy subset $(FSS)$ of $A$ and $\tau$ is FSS of $A\times A$ with $\tau (\varpi, \varrho)\leq \wedge\{\eta(\varpi), \eta(\varrho)\}$, where $\wedge$ shows the minimum, $\eta(\varpi)$ is weight of the vertex $\varpi$, and $\tau (\varpi, \varrho)$ is the weight of the edge $\varpi\varrho$. We write $\Re^\ast = (\eta^\ast, \tau^\ast)$, where $\eta^\ast = \{\varpi\in A :\eta(\varpi)\neq \emptyset \}$ and $\tau^\ast = \{ (\varpi, \varrho) \in A \times A : \tau (\varpi, \varrho) \neq 0\}$. Here $\eta^\ast$ and $\tau^\ast$ are called the vertex and edge set of the FG, respectively. The membership value of all the vertices and edges are taken from the closed interval $0$ and $1$. If all the membership values are the same and equal to 1, then the fuzzy graph becomes a crisp graph. There are three possibilities for the vertices in a fuzzy graph, the membership value of the vertex in a fuzzy graph is either $0$, between $0$ and $1$, or $1$. If the membership value is equal to $0$, it means no vertex exists. if the membership value is equal to 1, this shows that the vertex certainly exists in the graph but if the membership value lies between $0$ and $1$, it indicates that the vertex exists in the graph with some possibilities.

The degree or the valency of a vertex $\varpi$ is the sum of the membership values of edges joining to vertex $\varpi$ and denoted by $Deg_{\Re}(\varpi) = \sum_{\varpi\neq\varrho} \tau (\varpi, \varrho).$ The minimum degree denoted by $\delta(\Re)$ and is defined as $\delta(\Re) = \wedge\{Deg_{\Re}(\varpi): \varpi\in\eta^\ast\}$. The maximum degree denoted by $\Delta(\Re)$ and is defined as $\Delta(\Re) = \vee \{Deg_{\Re}(\varpi): \varpi\in\eta^\ast\}$, where $\wedge$ shows the minimum and $\vee$ shows the maximum. Let $\Re = (\eta, \tau)$ be a fuzzy graph. The order of fuzzy graph $\Re$ is represented by $O(\Re)$ is the sum of all membership values of all vertices and is denoted by $O(\Re) = \sum_{\varpi\in\eta^\ast} \eta (\varpi)$. The size of a fuzzy graph $\Re$ is denoted by $S(\Re)$ is the sum of all membership values of all edges and is denoted by $S(\Re) = \sum_{(\varpi, \varrho)\in\eta^\ast\times\eta^\ast} \tau (\varpi, \varrho)$. A path graph is a graph in which a sequence of vertices are connected in such a way that all vertices are connected except the first and last vertex. A path graph is called a cycle graph if the first and last vertex is also connected. A regular fuzzy graph is a graph if the $Deg_{\Re}(\varpi) = l$, for all $\varpi\in\eta^\ast$, where $l$ is a real number and it is also called $l-$ regular fuzzy graphs. A fuzzy graph is called an irregular fuzzy graph if two adjacent vertices have different degrees.

3.   Fuzzy topological indices

In this section, we discuss the fuzzy topological indices with their uses. We define a new fuzzy topological index Fuzzy Misbalance Prodeg Index and also find some bounds of different classes of graphs such as path graph, cycle graph, wheel graph, complete graph, and complete bipartite graph. We also give a real-life application of multi-criteria decision-making (MCDM) give an analysis and show on the basis of our analysis that our index is more useful than other existing indices. The list of some fuzzy topological indices with their definitions is given below:

Fuzzy first Zagreb Index

Kalathian discovered the first fuzzy Zagreb Index (FZI) for fuzzy graphs and was denoted by

here, $\eta(\varpi)$ and $d(\varpi)$ are the node weight and the degree of the vertex $\varpi$, respectively.

Fuzzy modified first Zagreb Index

Islam and Pal modified the first Zagreb Index for fuzzy graphs in 2021. Suppose $\Re = (\eta, \tau)$ is a fuzzy graph, then first fuzzy Zagreb index (FZI) of the Fuzzy graph ($\Re$) is represented by $ZF_1(\Re)$ and is expressed as:

Fuzzy second Zagreb Index

Kalathian et al. presented the second Zagreb index for fuzzy graphs in 2020 Let $\Re = (\eta, \tau)$, be an FG, then the second fuzzy Zagreb Index (SZI) of the Fuzzy graph ($\Re$) is represented by $ZF_2(\Re)$ and is expressed as:

Fuzzy randic index

S. Kalathian established the fuzzy Randic Index(FRI)

Fuzzy $F$-index

Islam explained the $F$-Index for fuzzy graphs in 2021. Let $\Re = (\eta, \tau)$ is a fuzzy graph, then $F$-index of the Fuzzy graph is represented by $FF(\Re)$ and is defined as:

Let $\Re^\ast$ be a finite, connected graph, and simple graph with the vertex set $V(\Re^\ast)$ and edge set $E(\Re^\ast)$ Numerous vertex degree-based topological descriptors have been proposed and thoroughly investigated in Chemical Science ^[24,25].

Sum Connectivity Index

Another index namely Sum Connectivity Index ^[26] is described as

Sombor index

The Sombor Index was discovered by Ivan Gutman in ^[27] and defined as

Some other types of Sombor indices were recently investigated. Das et al. discussed the Sombor index in ^[28]. In ^[29], Kulli along with Gutman defined the Revan Sombor index. Kulli another invention, Status Sombor index was established in ^[30]. Some properties of Somber indices were investigated in ^[31].

Misbalance Prodeg Index

In ^[32] introduced Misbalance Prodeg Index for $\Re^\ast$ as:

4.   Main results

In this section, we introduce our main results on the Fuzzy Misbalance Prodeg index. We have generated some bounds for certain classes of graphs such as path graph, cycle graph, complete graph, complete bipartite graph, and star graph.

Fuzzy Misbalance Prodeg Index

Let $\Re = (\eta, \tau)$ be a fuzzy graph, then the Misbalance Prodeg Index of the Fuzzy graph is represented by $FMPI(\Re)$ and is demonstrated as:

where, $\eta(\varpi)$ and $\eta(\varrho)$ is the weight of vertices $\varpi$ and $\varrho$ and $d(\varpi)$ and $d(\varrho)$ is the degree of the vertex $\varpi$ and $\varrho$, respectively.

Example 1

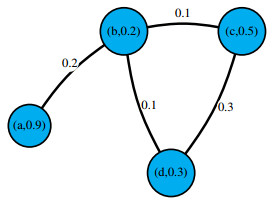
Suppose $\Re$ be a fuzzy graph (FG) shown in Figure 1 such that $V(\Re) = \{a, b, c, d\}$ be the end nodes with $\eta(a) = 0.9$, $\eta(b) = 0.2$, $\eta(c) = 0.5$, and $\eta(d) = 0.3$. The edge set contains $\tau(a, b) = 0.2$, $\tau(b, c) = 0.1$, $\tau(c, d) = 0.3$, $\tau(b, d) = 0.1$. Where $d(a) = 0.2$, $d(b) = 0.4$, $d(c) = 0.4$ and $d(d) = 0.4$ are all the degrees of vertices $a$, $b$, $c$, and $d$, respectively. Fuzzy Misbalance Prodeg index $FMPI(\Re)$ is given as

After substituting the values of the vertex weights and the degree of each vertex, we have

Theorem 1. Let $\Re = (\eta^\ast, \tau^\ast)$ be a FG and $\eta^\ast$ be the set of vertices with order $\ddot{N}$ and $\tau^\ast$ be the edge set with size $\ddot{M}$, then the Fuzzy Misbalance Prodeg index $FMPI(\Re)$ is given as

where $\varpi, \varrho\in\eta^\ast$. Also, $\eta(\varpi)$ and $\eta(\varrho)$ are the weights of the vertices $\varpi$ and $\varrho$, respectively.

Proof. For fuzzy graph $\Re = (\eta^\ast, \tau^\ast)$ the degree of vertex $\varpi\in\eta^\ast$ is denoted $d_{\Re}(\varpi)$ and evaluated as $d_{\Re}(\varpi) = \sum_{\varpi \neq \varrho}\tau^\ast(\varpi, \varrho)$ then,

$\eta(\varpi) > 0$ be the weight of the vertex $\varpi$. Multiplying with $\eta(\varpi)$ both side of the equation

Taking square root on both sides, we have

Similarly, for vertex $\varrho$

Summing the square root inequalities over all edges $\varpi\varrho\in\tau^\ast(\Re)$

Hence, the Fuzzy Misbalance Prodeg Index $FMPI(\Re)$ is given as

□

Theorem 2. Let $P_{z} = (\eta^\ast, \tau^\ast)$ be a fuzzy path graph with $\eta^\ast = \{\varpi_1, \varpi_2..., \varpi_z\}$ as vertex set and $\tau^\ast = \{\varpi_1\varpi_2, \varpi_2\varpi_3, ..., \varpi_{z-2}\varpi_{z-1}, \varpi_{z-1}\varpi_{z} \}$ as edge set.The order of fuzzy path graph $P_{z}$ is $z$ with size $z-1$, then

Proof. As $P_{z} = (\eta^\ast, \tau^\ast)$ be a fuzzy path graph, then:

$d_{P_{z}}(\varpi_1) = \tau_1$, $d_{P_{z}}(\varpi_2) = \tau_1+\tau_2$, ...$d_{P_{z}}(\varpi_{z-1}) = \tau_{z-2}+\tau_{z-1}$ and $d_{P_{z}}(\varpi_z) = \tau_{z-1}$ for $i = 2, 3, ...z$ therefore

As $\eta_z\leq1$ and $\tau_z\leq1$, $\eta(\varpi_i)$ is the vertex weight of a fuzzy graph and $d_{P_{z}}(\varpi)$ be degree of vertex $\varpi$. In the path graph, there will be two types of partitions: The first partition contains the first and last vertex and the second partition contains from second vertex to the second and last vertex. This formula reflects the contributions of every vertex over the path graph. Since each vertex weight and edge weight has a maximum value equal to 1. The following inequality obtained gets the following result.

□

Theorem 3. Let $C_{z} = (\eta^\ast, \tau^\ast)$ is a fuzzy cycle graph with vertex set $\eta^\ast = \{\varpi_1, \varpi_2, ..., \varpi_z \}$ and order $z$ where $z\geq 3$. $\tau^\ast = \{\varpi_1\varpi_2, \varpi_2\varpi_3, ..., \varpi_{z-1}\varpi_{z}, \varpi_{z}\varpi_{1}\}$ be an edge set with size $z$, then

Proof. As $C_{z} = (\eta^\ast, \tau^\ast)$ be a fuzzy cycle graph then $d_{C_{z}}(\varpi_1) = \tau_1+\tau_z$, $d_{C_{z}}(\varpi_2) = \tau_1+\tau_2$ $d_{C_{z}}(\varpi_{z-1}) = \tau_{z-2}+\tau_{z-1}$ and $d_{C_{z}}(\varpi_z) = \tau_{z-1}+\tau_{z}$, then the fuzzy Misbalance Prodeg index is as follows:

Since $\eta_z\leq1$ and $\tau_z\leq1$, the fuzzy Misbalance Prodeg index is bounded and after simple calculation, we obtain the following result.

□

Theorem 4. Let $K_N = (\eta^\ast, \tau^\ast)$ be a complete graph with $N$ vertices in which every $\varpi_{i}\in\eta^\ast$ is connected to all other vertices $\varpi_{j}$ where $i\neq j$, then fuzzy Misbalance Prodeg Index (FMPI) for $K_N$ is given as:

Proof. Since in a complete graph $K_N$, every vertex $\varpi_i$ is linked with all other vertices, having degree $d(\varpi_i) = N-1$. The fuzzy Misbalance Prodeg Index (FMPI) for $K_N$ takes into account the pairwise connections between each vertex. For every pair of vertices $(\varpi_i, \varpi_j)$, the FMPI role is stated as $\sqrt{\eta(\varpi_i)d_\Re(\varpi_i)}+\sqrt{\eta(\varpi_j)d_\Re(\varpi_j)}$. Summing this over all pairs of vertices in the complete graph yields:

Considering that $\varpi_i\leq1$, the complete graph $K_N$ contains $\frac{N(N-1)}{2}$ edges. Then the upper bound for $K_N$ is evaluated as:

The next theorem is about the wheel graph, which has a central hub connected to a peripheral cycle, and is the subject of the following theorem, which looks at its Fuzzy Misbalance Prodeg Index to reflect its distinct topological structure. □

Theorem 5. For a wheel graph, $W_N$, with $N$ end nodes $(N\geq4)$, the Fuzzy Misbalance Prodeg Index is given as:

Proof. Let $W_N$ be a wheel graph, then the Fuzzy Misbalance Prodeg Index is given as:

where $\varpi_h$ is the hub vertex, $\varpi_i$ and $\varpi_{i+1}$ are the adjacent vertices on the rim. Since $d(\varpi_h) = N-1$ and $\eta(\varpi_h)\leq1$, since there are $N-1$ such edges so for hub vertex the FMPI is to be $(N-1)[\sqrt{N-1}+\sqrt{3}]$. Where the rim forms a cycle $C_N$ with $N-1$ vertices and edges as well. Let the maximum membership value for $\eta(\varpi_i)$ is $1$ and $d(\varpi_i) = 3$, then for $N-1$ edges of rim we have FMPI as $(N-1)[\sqrt{3}+\sqrt{3}]$. From the above discussion, we conclude fuzzy Misbalance Prodeg Index() for $W_N$ as:

□

Theorem 6. Let $S_N = (\eta^\ast, \tau^\ast)$ be a star graph with $\eta^\ast = \{ \varpi_{1}, \varpi_{2}, ..., \varpi_{N}\}$ vertex set having $N$ vertices, and $\tau^\ast = \{\varpi_{1}\varpi_{s}, \varpi_{2}\varpi_{s}, ..., \varpi_{n-1}\varpi_{s}\}$ as an edge set then fuzzy Misbalance Prodeg Index for $S_N$ is explained as:

Proof. In a star graph, each vertex $\varpi_i$ where $1\leq i\leq N-1$, is connected to one central vertex $\varpi_s$. Here degree of $\varpi_s$ is $N-1$ where degree of each $\varpi_i$ is $1$, and defined as $d_{S_{N}}(\varpi_{s}) = \sum_{i = 1}^{N-1}\tau(\varpi_{s}, \varpi_{i})$ with $d_{S_{N}}(\varpi_{i}) = \tau(\varpi_{i}, \varpi_{s})$. $(\varpi_s, \varpi_i)$ is the pair of connections between the vertices of the star graph. As there are total $N-1$ edges in $S_N$, so fuzzy Misbalance Prodeg Index for $S_N$ is described as $\sqrt{\eta(\varpi_s)d(\varpi_s)}+\sqrt{\eta(\varpi_i)d(\varpi_i)}$. Since $\eta(\varpi_s)$ and $\eta(\varpi_i)$ are bounded by $1$, then For $N-1$ edges we get the following result as:

□

Theorem 7. For two sets of vertices $U$ and $V$ in complete bipartite graph $K_{x, y}$, we have $|U| = x$ and $|V| = y$, then the bounds of fuzzy Misbalance Prodeg Index for $K_{x, y}$ is given as:

Proof. In complete bipartite graph $K_{x, y}$, each vertex in set $U$ has a degree of $x$, where $y$ is the degree of every vertex contained in $V$. The FMPI index for $K_{x, y}$ examines the pairwise relationships between the vertices in various sets. For an edge connecting a vertex $\varpi_i\in U$ and vertex $\varrho_j\in V$, the contribution to fuzzy Misbalance Prodeg Index is $\sqrt{\eta (\varpi_i)x}+\sqrt{\eta (\varrho_j)y}$. As there are $xy$ edges in $K_{x, y}$, joining a vertex in $U$ to the vertex in $V$. Since the membership value of $\eta(\varpi_i)$ and $\eta(\varpi_j)$ is bounded by $1$, so the total fuzzy Misbalance Prodeg Index for $xy$ edges is described as:

□

5.   FMPI Algorithm

Here we present an algorithm to compute the Misbalance Prodeg Index for FG. The pseudo-code is presented below in Table 1. Clearly, the complexity of the fuzzy Misbalance Prodeg Index is dominated by the calculation of $FMPI(\Re)$, which is of the order $O(\Re)^2$.

6.   Proposed model for MCDM problem using Misbalance Prodeg Index

Multi-criteria decision-making (MCDM) problems involving fuzzy graphs are complex situation where decision-makers need to consider multiple criteria while dealing with uncertainty represented by fuzzy information. Fuzzy graphs extend traditional graph theory to handle imprecise and vague information. Here's a general framework for addressing multi-criteria decision-making problems with fuzzy graphs:

Let $X = \{X_1, X_2, ..., X_a\}$ be the set of alternatives and $Y = \{Y_1, Y_2, ..., Y_b\}$ be the set of attributes, $K = \{K_1, K_2, ..., K_c\}$ be the weight vector of attributes $Y_i$, where $K_i$ characterize the degree of importance of $Y_r$, fulfilling $K_i\in [0, 1]$ and $\sum_{i = 1}^{c} K_i = 1$. Our current goal is to identify the most suitable alternative. For each attribute, we first construct FGs with a vertex set of alternatives in order to determine which alternative is best. Edges are the influencing factors and connections between the available options. The Fuzzy graph $\beta_{Y_j}$ related to the attribute $Y_j$ having vertex set as a set of alternatives $X$, for each $i = 1, 2, ..., c.$

7.   Real-life application using multi-criteria decision-making

Consider a manufacturing company that needs to select suppliers for critical components used in their production process. The decision-makers are faced with the challenge of evaluating potential suppliers based on various criteria while dealing with uncertainties and imprecise information. Let us consider five suppliers namely $A, B, C, D,$ and $E$ and we choose three attributes such as $Y_1 =$ cost, $Y_2 =$ Quality, and $Y_3 =$ lead time. Not all suppliers must use the same set of specifications. However, each measure is significant in assessing their performance. In every fuzzy graph for each attribute, Nodes represent potential suppliers. Where edges between nodes denote the fuzzy relationships among suppliers, considering factors like historical performance, collaboration, and shared resources. As $Y_1$, $Y_2$ and $Y_3$ are the attributes and just English words their characteristics may get some membership values. The membership value for these parameters are taken as $K_1 = 0.3$, $K_2 = 0.4$, and $K_3 = 0.3$ and the rank value of each supplier is displayed in Table 2.

Now, we construct different fuzzy graphs $\beta_{Y_j}$ related to every attribute. In these fuzzy graph constructions, suppliers are the vertex set and edges are the influence relation between the suppliers, and display their Rank table and associated score table figure along with its detailed explanation. First of all, we construct a fuzzy graph $\beta_{Y_1}$ as shown in Figure 2.

All the information about the influence relation among the suppliers is displayed in Table 3. In the first step, we will evaluate the fuzzy Misbalance Prodeg Index for $\beta_{Y_1}$ by using the FMPI algorithm, we get the value

In the second step, we construct subgraphs for each vertex by deleting that vertex and the edges associated with it. Now, we pick vertex $A$ from Figure 2 and delete that vertex $A$ and all its associated edges. The related fuzzy subgraph $\beta_{{Y}_{1}}(A)$ by deleting vertex $A$ and all its related edges is obtained and shown in Figure 3.

For criteria $Y_1$ the fuzzy Misbalance Prodeg Index of the supplier $A$, first we calculate $FMPI(\beta_{{Y}_{1}}(A))$:

then fuzzy Misbalance Prodeg Index for supplier $A$ is calculated by using the following formula:

by substituting the value of $FMPI(\beta_{Y_1})$ and $FMPI(\beta_{{Y}_{1}}(A))$ in the above equation, we have:

Now, we pick vertex $B$ from Figure 2 and delete that vertex $B$ and all its associated edges. The related fuzzy subgraph $\beta_{{Y}_{1}}(B)$ by deleting vertex $B$ and all its related edges is obtained and shown in Figure 4.

For criteria $Y_1$ the fuzzy Misbalance Prodeg Index of the supplier $B$, first we calculate $FMPI(\beta_{{Y}_{1}}(B))$:

then fuzzy Misbalance Prodeg Index for supplier $B$ is calculated by using the following formula:

by substituting the value of $FMPI(\beta_{Y_1})$ and $FMPI(\beta_{{Y}_{1}}(B))$ in the above equation, we have:

Now, we pick vertex $C$ from Figure 2 and delete that vertex $C$ and all its associated edges. The related fuzzy subgraph $\beta_{{Y}_{1}}(C)$ by deleting vertex $C$ and all its related edges is obtained and shown in Figure 5.

For criteria $Y_1$ the fuzzy Misbalance Prodeg Index of the supplier $C$, first we calculate $FMPI(\beta_{{Y}_{1}}(C))$:

then fuzzy Misbalance Prodeg Index for supplier $C$ is calculated by using the following formula:

by substituting the value of $FMPI(\beta_{Y_1})$ and $FMPI(\beta_{{Y}_{1}}(C))$ in the above equation, we have:

Now, we pick vertex $D$ from Figure 2 and delete that vertex $D$ and all its associated edges. The related fuzzy subgraph $\beta_{{Y}_{1}}(D)$ by deleting vertex $D$ and all its related edges is obtained and shown in Figure 6.

For criteria $Y_1$ the fuzzy Misbalance Prodeg Index of the supplier $D$, first we calculate $FMPI(\beta_{{Y}_{1}}(D))$:

then fuzzy Misbalance Prodeg Index for supplier $D$ is calculated by using the following formula:

by substituting the value of $FMPI(\beta_{Y_1})$ and $FMPI(\beta_{{Y}_{1}}(D))$ in the above equation, we have:

Now, we pick vertex $E$ from Figure 2 and delete that vertex $E$ and all its associated edges. The related fuzzy subgraph $\beta_{{Y}_{1}}(E)$ by deleting vertex $E$ and all its related edges is obtained and shown in Figure 7.

For criteria $Y_1$ the fuzzy Misbalance Prodeg Index of the supplier $E$, first we calculate $FMPI(\beta_{{Y}_{1}}(E))$:

then fuzzy Misbalance Prodeg Index for supplier $E$ is calculated by using the following formula:

by substituting the value of $FMPI(\beta_{Y_1})$ and $FMPI(\beta_{{Y}_{1}}(E))$ in the above equation, we have:

Similarly, we have used the same process for attributes $Y_{2}$ and $Y_{3}$. The fuzzy graphs $\beta_{Y_2}$ and $\beta_{Y_3}$ shown in Figures 8 and 9 are related to the attributes $Y_{2}$ and $Y_{3}$, respectively.

The influence relation between the attributes is given in the matrix in Table 4.

The influence relation between the attributes is given in the matrix in Table 5.

Now, in Table 6, we display all the fuzzy Misbalance Prodeg Index values of all the suppliers with respect to given attributes $Y_1$ = Time, $Y_2\; = \;$ Quality, $Y_3\; = \;$ lead time.

Following that, the next method is used to choose the most suitable alternatives. The steps are as follows:

Input: The Fuzzy graph $\beta_{Y_j}$ related to the attribute $Y_j$ having vertex set as a set of alternatives $X$ and the influence relation between the vertices represented by an edge, for each $j = 1, 2, ..., c$ and $K_j$ be the weight of criteria.

Output: Best Alternative

Step 1: compute fuzzy Misbalance Prodeg Index as described in the FMPI algorithm.

Step 2: Evaluate rank of each vertex by using the formula

$(X_j) = \sum_{j = 1}^{c}K_j FMPI(X_j; \beta_{Y_j})$.

Step 3: Evaluate the normalized rank of each vertex by using the following formula, $NS(X_j) = \frac{S(X_j)}{R(X_i) = \sum_{j = 1}^{c}K_j FMPI(\beta)}$

Step 4: Compare all alternatives $X_j$ with respect to the normalised rank. If $NS(X_p) > NS(X_j)$ of each alternative, then, $X_p\succ X_j$ and we say $X_p$ is better than $X_j$.

By following steps 1 to 3, we have found the rank of each supplier shown in Table 7, and the graphical analysis is shown in Figure 10.

After following steps 4 and 5, we have found the Normalized rank of each supplier shown in Table 8, and the graphical analysis is shown in Figure 11.

8.   Designing the most interactive bus stop

Imagine that a city transportation department aims to design the most interactive bus stop to enhance passenger experience and encourage public transportation usage. The goal is to identify a location and design a bus stop that offers the highest level of interactivity based on multiple criteria. Suppose $C = \{C_{1}, C_{2}, C_{3}, C_{4}\}$ are the criteria which include Accessibility(e.g., ramps, tactile markers for visually impaired), Passenger Engagement (interactive touchscreens, QR code information), Passenger Comfort (e.g., seating, shelter, lighting) and Information Availability (e.g., real-time bus schedules, route maps). Assign fuzzy membership values to each criterion to represent the degree to which a potential bus stop location satisfies that criterion.Here we consider it as weight of the criteria as $W = \{W_{1}, W_{2}, W_{3}, W_{4}\}$. Now consider there are four possible locations for the bus stop $L = \{L_{1}, L_{2}, L_{3}, L_{4}\}$. Represent potential bus stop locations as nodes in the fuzzy graph. Assign fuzzy values to each node based on each of the criteria. Define edge weights to represent the connectivity or accessibility between different bus stop locations. These edge weights can also have fuzzy values, reflecting the ease of reaching one location from another. Here, we consider $0.25, 0.25, 0.25, 0.25$ as the weight value for each characteristic. Now, we construct fuzzy graphs $G_{C_{i}}$ for each criteria.For every $G_{C_{i}}$ each vertex represents locations $L_{j}$ in Figures 12, 13, 14 and 15.

All the score values of locations are shown in Table 9.

All the score values for the relation between locations in $G_{C_1}$ in Table 10.

All the score values for the relation between locations in $G_{C_2}$ in Table 11.

All the score values for the relation between locations in $G_{C_3}$ in Table 12.

All the score values for the relation between locations in $G_{C_4}$ in Table 13.

All the Modified Fuzzy Misbalance Prodeg Index of the Locations for $G_{{C}_{i}}$ in Table 14.

Now, the grade of each location is evaluated by using the following formula given in Table 15:

9.   Comparative analysis

In this section, the comparative analysis of location grades given in Table 16 and graphical analysis in Figure 16. The normalized grades of all locations are shown in Table 17 and graphical analysis in Figure 17.

10.   Conclusions

In this paper, we have defined a new topological index named fuzzy Misbalance Prodeg Index and also we have found some bounds of this index. By using this bound, we have defined bounds for certain classes of graphs. We have presented an algorithm for multi-criteria decision-making in daily life and applied this algorithm to a manufacturing company that needs to select suppliers for critical components used in their production process. The decision-makers are faced with the challenge of evaluating potential suppliers based on various criteria while dealing with uncertainties and imprecise information. By using the algorithm displayed in Sections 5 and 6, the fuzzy Misbalance prodeg index of every supplier with respect to all attributes is displayed in Table 6. The comparative analysis of fuzzy Misbalance Prodeg Index with Misbalance Prodeg Index, second Zagreb Index, and fuzzy second Zagreb Index is displayed in Table 7 and the graphical analysis of fuzzy Misbalance Prodeg Index with Misbalance Prodeg Index, second Zagreb Index, and fuzzy second Zagreb Index are displayed in Figure 10. The normalized rank of each supplier is computed and given in Table 8 and its graphical analysis is shown in Figure 11. Now, we display the order of the alternatives as $A\succ E\succ B\succ D \succ C$. Hence, $A$ is the most suitable supplier. The same algorithm is applied in identifying the Most Interactive Bus Stop. The goal is to identify a location and design a bus stop that offers the highest level of interactivity based on multiple criteria. All the values are displayed in Tables from 9 to 15 and the comparative analysis shown in Tables 16 and 17 with graphical representation in Figures 16 and 17. So the modified fuzzy Misbalance Prodeg Index has great importance in multi-criteria decision-making analysis. In future, we will use the same idea for intuitionistic fuzzy graphs, bipolar fuzzy graphs, and Pythagorean fuzzy graphs and investigate other topological indices.

Author contributions

Shama Liaqat: Conceptualization, Methodology, Validation, Formal Analysis; Zeeshan Saleem Mufti:Conceptualization, Investigation, writing---review and editing; Yilun Shang; Methodology, Validation, Writing - Original Draft, Writing - Review & Editing. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The author declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The author declare that they have no conflict of interest.