Generalized Buchdahl equations as Lie–Hamilton systems from the "book" and oscillator algebras: quantum deformations and their general solution

Rutwig Campoamor-Stursberg; Eduardo Fernández-Saiz; Francisco J. Herranz; Rutwig Campoamor-Stursberg; Eduardo Fernández-Saiz; Francisco J. Herranz

doi:10.3934/math.2025315

AIMS Mathematics

2025, Volume 10, Issue 3: 6873-6909. doi: 10.3934/math.2025315

Previous Article Next Article

Research article Special Issues

Generalized Buchdahl equations as Lie–Hamilton systems from the "book" and oscillator algebras: quantum deformations and their general solution

1.
Instituto de Matemática Interdisciplinar, Universidad Complutense de Madrid, Madrid 28040, Spain
2.
Departamento de Álgebra, Geometría y Topología, Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, Plaza de Ciencias 3, Madrid 28040, Spain
3.
Department of Mathematics, CUNEF Universidad, Leonardo Prieto Castro 2, Madrid 28040, Spain
4.
Departamento de Física, Universidad de Burgos, Burgos 09001, Spain

Received: 09 December 2024 Revised: 10 March 2025 Accepted: 17 March 2025 Published: 26 March 2025
MSC : 16T05, 17B66, 34A26, 34A34

We revisit the nonlinear second-order differential equations $\ddot{x}(t) = a (x)\dot{x}(t)^2+b(t)\dot{x}(t),$ where $a(x)$ and $b(t)$ are arbitrary functions on their argument from the perspective of Lie–Hamilton systems. For the particular choice $a(x) = 3/x$ and $b(t) = 1/t$ , these equations reduce to the Buchdahl equation considered in the context of general relativity. It is shown that these equations are associated with the "book" Lie algebra $\mathfrak{b}_2$ by determining a Lie–Hamilton system for which the corresponding $t$ -dependent Hamiltonian and the general solution of the equations are given. The procedure is illustrated considering several particular cases. We also make use of the quantum deformation of $\mathfrak{b}_2$ with the quantum deformation parameter $z$ (where $q = {{{\rm{e}}}}^z$ ), leading to a deformed generalized Buchdahl equation. Applying the formalism of Poisson–Hopf deformations of Lie–Hamilton systems, we derive the corresponding deformed $t$ -dependent Hamiltonian, as well as its general solution. The generalized Buchdahl equation is further extended to the oscillator Lie–Hamilton algebra $\mathfrak{h}_4\supset \mathfrak{b}_2$ , together with its quantum deformation, and the corresponding (deformed) equations are also analyzed for their exact solutions. The presence of the quantum deformation parameter $z$ is interpreted as the introduction of an integrable perturbation of the (initial) generalized Buchdahl equation, which is described in detail in its linear approximation. Finally, it is also shown that, under quantum deformations, the higher-dimensional deformed generalized Buchdahl equations from either the book or the oscillator algebras do not reduce to a sum of copies of the initial system but to intrinsic coupled systems governed by $z$ .

Keywords:

Citation: Rutwig Campoamor-Stursberg, Eduardo Fernández-Saiz, Francisco J. Herranz. Generalized Buchdahl equations as Lie–Hamilton systems from the 'book' and oscillator algebras: quantum deformations and their general solution[J]. AIMS Mathematics, 2025, 10(3): 6873-6909. doi: 10.3934/math.2025315

Related Papers:

[1]	Rutwig Campoamor-Stursberg, Eduardo Fernández-Saiz, Francisco J. Herranz . Exact solutions and superposition rules for Hamiltonian systems generalizing time-dependent SIS epidemic models with stochastic fluctuations. AIMS Mathematics, 2023, 8(10): 24025-24052. doi: 10.3934/math.20231225
[2]	Nouf Almutiben, Ryad Ghanam, G. Thompson, Edward L. Boone . Symmetry analysis of the canonical connection on Lie groups: six-dimensional case with abelian nilradical and one-dimensional center. AIMS Mathematics, 2024, 9(6): 14504-14524. doi: 10.3934/math.2024705
[3]	Junyuan Huang, Xueqing Chen, Zhiqi Chen, Ming Ding . On a conjecture on transposed Poisson $n$ -Lie algebras. AIMS Mathematics, 2024, 9(3): 6709-6733. doi: 10.3934/math.2024327
[4]	Nouf Almutiben, Edward L. Boone, Ryad Ghanam, G. Thompson . Classification of the symmetry Lie algebras for six-dimensional co-dimension two Abelian nilradical Lie algebras. AIMS Mathematics, 2024, 9(1): 1969-1996. doi: 10.3934/math.2024098
[5]	Wen Teng, Jiulin Jin, Yu Zhang . Cohomology of nonabelian embedding tensors on Hom-Lie algebras. AIMS Mathematics, 2023, 8(9): 21176-21190. doi: 10.3934/math.20231079
[6]	Baiying He, Siyu Gao . The nonisospectral integrable hierarchies of three generalized Lie algebras. AIMS Mathematics, 2024, 9(10): 27361-27387. doi: 10.3934/math.20241329
[7]	Huizhang Yang, Wei Liu, Yunmei Zhao . Lie symmetry reductions and exact solutions to a generalized two-component Hunter-Saxton system. AIMS Mathematics, 2021, 6(2): 1087-1100. doi: 10.3934/math.2021065
[8]	Muhammad Asad Iqbal, Abid Ali, Ibtesam Alshammari, Cenap Ozel . Construction of new Lie group and its geometric properties. AIMS Mathematics, 2024, 9(3): 6088-6108. doi: 10.3934/math.2024298
[9]	He Yuan, Zhuo Liu . Lie $n$ -centralizers of generalized matrix algebras. AIMS Mathematics, 2023, 8(6): 14609-14622. doi: 10.3934/math.2023747
[10]	Xinfeng Liang, Mengya Zhang . Triangular algebras with nonlinear higher Lie n-derivation by local actions. AIMS Mathematics, 2024, 9(2): 2549-2583. doi: 10.3934/math.2024126

Abstract

1. Introduction

In a seminal paper in 1964, Buchdahl considered ^[1] a class of metrics on a (3+1)-dimensional spherically symmetric static spacetime in a general relativity framework ^[2]. In terms of the so-called isotropic coordinates $(t, r, \theta, \phi)$ , this family of metrics is given by

$\begin{equation} {{{\rm{d}}}} s^2 = \frac{\bigl(1-f(r)\bigr)^2}{\bigl(1+f(r)\bigr)^2} \, {{{\rm{d}}}} t^2 - (1+f(r))^4\left[{{{\rm{d}}}} r^2 +r^2 \bigl({{{\rm{d}}}}\theta^2 +\sin^2\theta {{{\rm{d}}}} \phi^2 \bigr) \right] , \end{equation}$

(1.1)

where the function $f(r)$ had to be determined and units are chosen such that the speed of light is normalized to $c = 1$ . This equation was shown to correspond to a relativistic fluid sphere. Under some additional requirements, the field equations gave rise to the following scalar second-order nonlinear ordinary differential equation (ODE):

$\begin{equation} \frac{{{{\rm{d}}}}^2 f}{{{{\rm{d}}}} r^2}-\frac 3 f \left(\frac{{{{\rm{d}}}} f}{{{{\rm{d}}}} r}\right)^2-\frac 1r \, \frac{{{{\rm{d}}}} f}{{{{\rm{d}}}} r} = 0, \end{equation}$

(1.2)

which admits the exact solution (see ^[1])

$\begin{equation} f(r) = \frac{\pm 1}{ k_1\sqrt{1+k_2 r^2} } , \end{equation}$

(1.3)

where $k_1$ , $k_2$ are the two integration constants. Note that Eq (1.2) can be written alternatively in terms of total derivatives as

$\begin{equation} \frac{{{{\rm{d}}}} }{{{{\rm{d}}}} r}\left(\frac 1r\, \frac{{{{\rm{d}}}} }{{{{\rm{d}}}} r}\left( \frac1{f^2} \right) \right) = 0 . \label{a3} \nonumber \end{equation}$

The Buchdahl equation (1.1) has also been considered in a different context, namely that of nonlinear ODEs with time- and position-dependent coefficients, by replacing the radial function $f(r)$ by $x(t)$ and interpreting $t$ as the time ^[3,4,5,6], leading to the modified Buchdahl equation

$\begin{equation} \frac{{{{\rm{d}}}}^2 x}{{{{\rm{d}}}} t^2} = \frac 3 x \left(\frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}\right)^2+\frac 1t \, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} . \end{equation}$

(1.4)

In this form, the equation has been studied in the aforementioned works using several different methods in [3, Example 2], [5, Example 1], and [6, Example 3.6].

In the general context of nonlinear ODEs, Eq (1.4) is nothing but a special case of the generic equation

$\begin{equation} \frac{{{{\rm{d}}}}^2 x}{{{{\rm{d}}}} t^2} = a(x)\left(\frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}\right)^2+b(t)\, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} , \end{equation}$

(1.5)

where $a(x)$ and $b(t)$ are arbitrary functions of their arguments. This generalization can also be regarded as the equation of the motion of a dynamical system with variable coefficients $a(x)$ and $b(t)$ , depending on the velocity/momentum terms. It is not difficult to see that, by dividing by

$\dot{x} = \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t},$

the equation^* can be rewritten as

^*In other terms, the equation admits an integrating factor.

$\begin{equation} \frac{{{{\rm{d}}}} }{{{{\rm{d}}}} t} \ln |\dot{x}| = \frac{{{{\rm{d}}}} }{{{{\rm{d}}}} t}\left(\int^{x} a(\xi) {{{\rm{d}}}} \xi\right) +\frac{{{{\rm{d}}}} }{{{{\rm{d}}}} t}\left( \int^{t} b(\tau){{{\rm{d}}}} \tau \right), \end{equation}$

(1.6)

showing that (1.5) is an exact equation, the solution of which is recovered from the expression

$\begin{equation} \ln |\dot{x}| = \int^{x} a(\xi) {{{\rm{d}}}} \xi +\int^{t} b(\tau){{{\rm{d}}}} \tau +k_1 \end{equation}$

(1.7)

using quadratures, where $k_1$ is a constant of integration ^[7,8,9]. It can be further shown that for any choices of $a(x)$ and $b(t)$ , Eq (1.5) is linearizable by a point transformation, i.e., it admits a maximal Lie algebra of point symmetries isomorphic to $\mathfrak{sl}(3, \mathbb{R})$ ^[10]^†. However, as the point transformation is not canonical, it may change the physical meaning of the dependent and independent variables, and thus this does not constitute the most appropriate strategy for some applications. On the other hand, the first-order equation (1.7) may not always be explicitly integrable, in the sense that $x$ can be expressed in terms of the elementary functions of the independent variable $t$ .

^†In Appendix, the symmetry generators are explicitly given.

As already mentioned, in various physical applications, the use of (1.6) may not be computationally satisfactory, and an alternative approach to derive exact solutions (whenever possible) is required. In this context, it was observed in ^[11,12] that the Eq (1.4), when interpreted as a first-order system of ODEs, possesses the supplementary structure of a Lie–Hamilton (LH) system associated with the so-called "book algebra" $\mathfrak{b}_2$ (see ^[12,13,14] and references therein). It was further shown in ^[14] that any LH system based on this Lie algebra can be integrated by quadratures, a property that also holds, under certain constraints, for its quantum deformation ^[15].

The structure of the paper is as follows. In Section 2, we reconsider the generalized Buchdahl equation (1.5) from the point of view of LH systems, determining the general solution by means of the associated book Lie algebra $\mathfrak{b}_2$ , following the general ansatz proposed in ^[14]. The procedure is illustrated through some special types of the generalized Buchdahl equations in Section 3. In particular, it is shown that no further extension of the generalized Buchdahl equation as an LH system based on $\mathfrak{b}_2$ is possible. In Section 4, we study the Poisson–Hopf deformation of the generalized Buchdahl equations associated with the quantum book algebra ^[15], showing that the corresponding equations can also be solved exactly, and then apply such results in Section 5 to the special cases considered before in Section 3, with special emphasis on the first-order approximation in the quantum deformation parameter $z$ . It is shown that these equations can also be solved exactly. In Section 6, we extrapolate the results thus obtained to the oscillator algebra $\mathfrak{h}_4$ extending $\mathfrak{b}_2$ , finding that the corresponding systems can still be solved exactly. The procedure is illustrated by considering the extension of the special cases studied in Section 3. In Section 7, their Poisson–Hopf deformation, based on the "nonstandard" quantum deformation of $\mathfrak{h}_4$ , is analyzed, also obtaining its general solution, which is a completely novel result. In addition, it is applied to the systems in Section 5, arriving at their extended version. In Section 8, the physical and mathematical significance of the quantum deformation parameter $z$ is considered in more detail. Specifically, it is shown that for higher-dimensional deformations, the corresponding Hamiltonian equations exhibit interaction terms that are intrinsic to the deformation, meaning that the equations of the motion are no longer copies of the original one-dimensional system. Finally, in a concluding section, we summarize the results obtained concerning the (deformed) generalized Buchdahl equations based on $\mathfrak{b}_2$ and $\mathfrak{h}_4$ , also highlighting how these systems are related by a limiting process. Moreover, the existence of a Lagrangian formalism for any (quantum deformed) equation obtained from (1.4) is indicated. Some conclusions are drawn, and possible future developments of the method in connection with the embedding of the book algebra into either the simple Lie algebra $\mathfrak{sl}(2, \mathbb{R})\supset \mathfrak{b}_2$ or the two-photon algebra $\mathfrak{h}_6\supset\mathfrak{h}_4\supset \mathfrak{b}_2$ are briefly discussed.

2. The generalized Buchdahl equation as an LH system

We call (1.5) the generalized Buchdahl equation, as considered in ^[6]. For the special choice

$a(x) = 3/x \; \; \; \text{and}\; \; \; b(t) = 1/t,$

the classical Buchdahl equation is recovered. As shown in ^[6], Eq (1.5) admits both a standard and reciprocal Lagrangian description for arbitrary choices of the parameter functions. The generalized equation, besides its applications in the context of general relativity, can also be interpreted as the equation of the motion for nonlinear systems with variable coefficients.

We first reinterpret the generalized Buchdahl equation in the context of the LH system framework, deriving its general solution in appropriate coordinates after a canonical transformation, and we analyze some relevant particular cases in Section 3. Although this approach does not supply essential new information (the equation is solved by (1.6)), it is relevant for the study of perturbations or quantum deformations of the equation, which are, in general, no longer exact and linearizable by a point transformation, and where the application of the traditional direct integration methods may be too cumbersome.

Considering the variable

$y\equiv \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t },$

Equation (1.5) is equivalent to the first-order nonlinear system of ODEs

$\begin{equation} \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} = y, \qquad \frac{{{{\rm{d}}}} y}{{{{\rm{d}}}} t} = a(x)y^2+b(t)y . \end{equation}$

(2.1)

This system can further be expressed in terms of the $t$ -dependent vector field

$\begin{equation} {\bf{X}}_t = {\bf{X}}_1+b(t){\bf{X}}_2, \end{equation}$

(2.2)

where the vector fields ${\bf{X}}_1$ and ${\bf{X}}_2$ are explicitly given by

$\begin{equation} {\bf{X}}_1 = y\frac{\partial }{\partial x}+a(x)y^2\frac{\partial}{\partial y} , \qquad {\bf{X}}_{2} = y\dfrac{\partial}{\partial y} . \end{equation}$

(2.3)

These vector fields satisfy the Lie bracket

$\begin{equation} [{\bf{X}}_2, {\bf{X}}_1] = {\bf{X}}_1; \end{equation}$

(2.4)

hence they span a Lie algebra isomorphic to the book algebra $\mathfrak{b}_2$ ^‡. The generator ${\bf{X}}_2$ can be seen as a dilation, while ${\bf{X}}_1$ corresponds to a translation. Formally, (2.1) and (2.2) define a Lie system ^[16,17,18] with a noninvariance Lie algebra (called Vessiot–Guldberg Lie algebra) isomorphic to the "book" Lie algebra $\mathfrak{b}_2$ . It can actually be shown (see e.g., ^[9]) that the ODE (1.5) is the most general second-order scalar equation that admits $\mathfrak{b}_2$ as a Vessiot–Guldberg algebra. However, the generalized Buchdahl equation is more than a mere Lie system, as it admits a symplectic form $\omega$ such that the vector fields ${\bf{X}}_i$ are Hamiltonian vector fields with respect to the appropriate Hamiltonian functions $h_i$ $(i = 1, 2)$ . The compatibility conditions

^‡This is the same as the affine algebra in two dimensions.

$\begin{equation} \mathcal{L}_{{\bf{X}}_i}\omega = 0, \qquad \iota_{{\bf X}_i}\omega = {\rm d}h_i , \end{equation}$

(2.5)

with $\iota$ denoting the contraction or inner product of $\omega$ , determine the structure of an LH system (see ^[13] and the references therein)^§.

^§According to the classification of LH systems on $\mathbb R^2$ ^[11,12], the book Lie algebra $\mathfrak{b}_2$ is locally diffeomorphic to the imprimitive class ${\rm I}_{14A}$ with $r = 1$ and $\eta_1(x) = {\rm e}^x$ .

In this case, the symplectic form is given by

$\begin{equation} \omega = \dfrac{\exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right)}{y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y . \end{equation}$

(2.6)

Hereafter, it will be assumed that $y\ne 0$ . The Hamiltonian functions associated with the Hamiltonian vector fields ${\bf{X}}_i$ are

$\begin{equation} h_1 = y\exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right), \qquad h_2 = -\int^x\exp\left(-\int^\xi a( \xi'){{{\rm{d}}}} \xi'\right){{{\rm{d}}}} \xi , \end{equation}$

(2.7)

which satisfy the following Poisson bracket with respect to $\omega$ (see (2.4)):

$\begin{equation} \{h_{2}, h_{1}\}_\omega = -h_{1}. \nonumber \end{equation}$

Hence, the LH system (2.2) has a $t$ -dependent Hamiltonian given by

$\begin{equation} h_t = h_{1}+b(t) h_{2}, \end{equation}$

(2.8)

whose Hamilton equations with respect to the noncanonical symplectic form $\omega$ (2.6) give rise to Eq (2.1)

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t}& = \{x, h_t\}_\omega = \frac{y}{\exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right)}\, \frac{\partial h_t}{\partial y} , \\ \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t}& = \{y, h_t\}_\omega = -\frac{y}{\exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right)}\, \frac{\partial h_t}{\partial x} . \end{split} \nonumber \end{equation}$

We observe that all the structures above are properly defined on $\mathbb R^2_{y\neq 0}$ .

2.1. The general solution as an LH system

LH systems related to the book algebra were generically studied in ^[11], with nonlinear superposition rules being given in ^[12], using an appropriate embedding of $\mathfrak{b}_2$ into a higher-dimensional LH algebra. The generalized Buchdahl equation is one particular case of an ample class of $\mathfrak{b}_2$ -LH systems that comprise, among others, complex Bernoulli differential equations (with $t$ -dependent real coefficients) ^[14], some Lotka–Volterra systems, and various types of time-dependent epidemic models with stochastic fluctuations ^[19], for which an exact solution can be found using an explicit diffeomorphism (corresponding to an appropriate change of variables) that leads to a canonical realization of the LH algebra (see ^[14,19] for further details).

As a shorthand notation, we define the function

$\begin{equation} {\Xi}(x): = \exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right) , \nonumber \end{equation}$

so that the expressions (2.6) and (2.7) read

$\begin{equation} \omega = \dfrac{{\Xi}(x)}{y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y , \qquad h_1 = y\, {\Xi}(x), \qquad h_2 = -\int^x {\Xi}(\xi) {{{\rm{d}}}} \xi \, . \end{equation}$

(2.9)

Now, under the change of variables

$\begin{equation} q = -y\, {\Xi}(x), \qquad p = \frac 1 y \, { {\Xi}(x)^{-1} {\int^x {\Xi}(\xi) {{{\rm{d}}}} \xi}}\, , \end{equation}$

(2.10)

the Buchdahl equation, as presented above, can be reformulated in terms of the $\mathfrak{b}_2$ -LH algebra in the canonical form introduced in ^[20] (see also ^[14,19])), which differs considerably from that given in the works ^[11,12], although both are (locally) diffeomorphic. In this context, the coordinates $(q, p)$ are canonical, and the symplectic form (2.6) and Hamiltonian functions (2.7) become

$\begin{equation} \omega\equiv {{\omega_{{\rm{can}}}}} = {{{\rm{d}}}} q\wedge {{{\rm{d}}}} p, \end{equation}$

(2.11)

$\begin{equation} h_1 = - q , \quad h_2 = qp, \quad \{ h_2, h_1\}_{{\omega_{{\rm{can}}}}} = - h_1 , \end{equation}$

(2.12)

while the $t$ -dependent Hamiltonian (2.8) reduces to

$\begin{equation} h_t = h_1 + b(t) h_2 = - q+ b(t) qp. \end{equation}$

(2.13)

The corresponding equations of the motion are given by

$\begin{equation} \frac{{{{\rm{d}}}} q}{{{{\rm{d}}}} t} = \{q, h_t\}_{{\omega_{{\rm{can}}}}} = b(t) q , \qquad \frac{{{{\rm{d}}}} p}{{{{\rm{d}}}} t} = \{p, h_t\}_{{\omega_{{\rm{can}}}}} = 1-b(t) p , \end{equation}$

(2.14)

which is a linear, uncoupled system. We observe that $a(x)$ does not appear explicitly in (2.14) (compare this with (2.1)), as it is "hidden" within the transformation (2.10) through ${\Xi}(x)$ . The Hamiltonian vector fields (2.3), when expressed in the canonical variables, are

$\begin{equation} {\bf{X}}_1 = \frac{\partial}{\partial p} , \qquad {\bf{X}}_2 = q\, \frac{\partial}{\partial q}- p\, \frac{\partial}{\partial p} , \end{equation}$

(2.15)

which satisfy the Lie commutator (2.4) and provide the same LH system (2.14). As follows from (2.14), the generalized Buchdahl LH system (2.1) is separable in the coordinates $(q, p)$ , and can be easily solved by quadratures as follows:

$\begin{equation} \begin{split} q(t)& = c_1 {{{\rm{e}}}}^{{\gamma}(t)}, \quad {\gamma}(t): = \int^t b(\tau){{{\rm{d}}}} \tau , \\[4pt] p(t)& = \left( c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau )} {{{\rm{d}}}} \tau\right) {{{\rm{e}}}}^{-{\gamma}(t)}, \end{split} \end{equation}$

(2.16)

where $c_1$ and $c_2$ are the two constants of integration determined by the initial conditions. These results are summarized in the following statement.

Proposition 2.1. The general solution of the generalized second-order Buchdahl equation (1.5) and its associated first-order system of ODEs (2.1) is given by

$\begin{equation} \begin{split} \int^x {\Xi}(\xi){{{\rm{d}}}} \xi & = - c_1 \left( c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau\right) , \qquad {\Xi}(x): = \exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right), \\[2pt] y(t)& = \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} = -c_1 \, \frac{{{{\rm{e}}}}^{{\gamma}(t)} }{ {\Xi}(x)}, \, \quad\quad\, \ \ \qquad {\gamma}(t): = \int^t b(\tau){{{\rm{d}}}} \tau , \end{split} \end{equation}$

(2.17)

where $c_1$ and $c_2$ are the two constants of integration determined by the initial conditions.

Observe, in particular, that the first equation of (2.17) can also be expressed as

$\begin{equation} \frac{{{{\rm{d}}}} }{{{{\rm{d}}}} t}\left( {{{\rm{e}}}}^{-{\gamma}(t)}\frac{{{{\rm{d}}}} }{{{{\rm{d}}}} t} \int^x {\Xi}(\xi){{{\rm{d}}}} \xi \right) = 0 \ \equiv \ \frac{{{{\rm{d}}}} }{{{{\rm{d}}}} t}\left( {{{\rm{e}}}}^{-{\gamma}(t)} \, {\Xi}(x) \, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} \right) = 0, \label{c10a} \nonumber \end{equation}$

which, taking into account that

$\begin{equation} \frac{{{{\rm{d}}}} }{{{{\rm{d}}}} t} \, {{{\rm{e}}}}^{-{\gamma}(t)} = -{{{\rm{e}}}}^{-{\gamma}(t)} b(t) , \qquad \frac{{{{\rm{d}}}} }{{{{\rm{d}}}} x}\, {\Xi}(x) = - {\Xi}(x)a(x) , \qquad \frac{{{{\rm{d}}}} }{{{{\rm{d}}}} t}\, {\Xi}(x) = - {\Xi}(x)a(x)\, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} , \label{c10b} \nonumber \end{equation}$

reproduces the initial generalized second-order Buchdahl equation (1.5).

In the context of nonlinear dynamical systems with variable coefficients, the previous result can be applied directly by means of appropriate choices for the parameter functions $a(x)$ and $b(t)$ . In this situation, the functions ${\Xi}$ and ${\gamma}$ are obtained from (2.17), reducing the problem to the integration of $x(t)$ , while $y(t)$ follows directly by insertion of $x(t)$ into the second equation, providing the solution of system (2.1).

3. Applications to particular generalized Buchdahl equations

We illustrate the procedure in terms of LH systems by studying some particular cases corresponding to explicit choices for the parameter functions $a(x)$ and $b(t)$ .

3.1. The classical Buchdahl equation

The equation arises from the specific choices

$\begin{equation} a(x) = \frac 3 x , \qquad b(t) = \frac 1 t , \qquad x\in \mathbb R^\ast, \qquad t\in \mathbb R^\ast \end{equation}$

(3.1)

in (2.1), so that the functions ${\Xi}(x)$ and ${\gamma}(t)$ in (2.17) are given by

$\begin{equation} {\Xi}(x) = x^{-3} , \qquad {\gamma}(t ) = \ln t . \nonumber \end{equation}$

Note that

${{{\rm{e}}}}^{{\gamma}(t)} = t,$

which in (2.17), is therefore always well-defined. It follows that the symplectic form and Hamiltonian functions (2.9) are given by

$\begin{equation} \omega = \dfrac{ 1}{x^3y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y , \qquad h_1 = \frac{y}{x^3} , \qquad h_2 = \frac{1}{2x^2} . \nonumber \end{equation}$

Substituting these expressions into the first equation of (2.17), we find that

$\begin{equation} \frac{1}{x^2(t)} = 2 c_1c_2+ c_1 {t^2}, \nonumber \end{equation}$

from which the general solution

$\begin{equation} x(t) = \frac{\pm 1}{ \sqrt{2 c_1c_2 +c_1 t^2} }\, , \qquad y(t) = \frac{\mp c_1 t}{ \bigl(2 c_1c_2 +c_1 t^2\bigr)^{3/2} }\, \end{equation}$

(3.2)

is obtained, recovering the expression (1.3) of the Buchdahl equation (1.4) with

$c_1 = k_1^2k_2, \; \; \; c_2 = \frac{1}{2 k_2}\; \; \; \text{and}\; \; \; f(r)\equiv x(t).$

3.2. Case with $a(x)=1/x$ and an arbitrary ${b(t)}$

As a first natural generalization in (2.1), we consider the function

$a(x) = x^{-1}$

and an arbitrary $b(t)$ . It follows that

$\begin{equation} {\Xi}(x) = x^{-1} , \qquad x > 0, \nonumber \end{equation}$

with ${\gamma}(t)$ as given in (2.17). The symplectic form and Hamiltonian functions (2.9) read

$\begin{equation} \omega = \dfrac{ 1}{xy}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y , \qquad h_1 = \frac{y}{x}\, , \qquad h_2 = -\ln x . \nonumber \end{equation}$

The first equation in (2.17) provides

$\begin{equation} \ln x(t) = - c_1 \left( c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau\right), \nonumber \end{equation}$

which can be easily solved, leading to the exact solution

$\begin{equation} \begin{split} x(t) = \exp\left(- c_1c_2 -c_1 \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau \right) , \quad y(t) = -c_1\, {{{\rm{e}}}}^{{\gamma}(t) }\exp\left(- c_1c_2 -c_1 \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau \right). \end{split} \nonumber \end{equation}$

For instance, choosing $b(t) = 1/t$ with $t\in \mathbb R^\ast$ (i.e., ${{{\rm{e}}}}^{{\gamma}(t)} = t$ ), we find that

$\begin{equation} x(t) = \exp\left(- c_1c_2 -c_1 \frac{t^2}2\right) , \qquad y(t) = -c_1 t\exp\left(- c_1c_2 -c_1 \frac{t^2}2\right), \end{equation}$

(3.3)

which can be compared with (3.2).

3.3. Case with $a(x)={\alpha}/x$ $({\alpha}\ne 1)$ and an arbitrary $b(t)$

We now choose

$a(x) = {\alpha} x^{-1}$

with ${\alpha}\in \mathbb R^\ast$ and ${\alpha}\ne 1$ , keeping $b(t)$ arbitrary, so that

$\begin{equation} {\Xi}(x) = x^{-{\alpha}}, \qquad x\in \mathbb R^\ast . \nonumber \end{equation}$

Hence the expression (2.9) gives rise to

$\begin{equation} \omega = \dfrac{ 1}{x^{\alpha} y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y , \qquad h_1 = \frac{y}{x^{\alpha}}\, , \qquad h_2 = -\frac{x^{1-{\alpha}}}{1-{\alpha}}\, , \qquad {\alpha}\ne 1. \nonumber \end{equation}$

The first equation in (2.17) reads

$\begin{equation} \frac{x^{1-{\alpha}}(t)}{1-{\alpha}} = - c_1 \left( c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau\right) , \nonumber \end{equation}$

providing the following exact solution:

$\begin{equation} \begin{split} x(t)& = \left( ({\alpha}-1) c_1\left( c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau \right) \right)^{\frac{1}{1-{\alpha}} } , \\ y(t)& = -c_1\, {{{\rm{e}}}}^{{\gamma}(t) } \left( ({\alpha}-1) c_1\left( c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau \right) \right)^{\frac{{\alpha}}{1-{\alpha}} }. \end{split} \nonumber \end{equation}$

As a particular case, taking $b(t) = 1/t$ with $t\in \mathbb R^\ast$ , we find that

$\begin{equation} x(t) = \left( ({\alpha}-1)c_1 \left( c_2 +\frac{t^2}2\right) \right)^{\frac{1}{1-{\alpha}} } , \qquad y(t) = - c_1 t\left( ({\alpha}-1)c_1 \left( c_2 +\frac{t^2}2\right) \right)^{\frac{{\alpha}}{1-{\alpha}} } , \nonumber \end{equation}$

which, as expected, reduces for ${\alpha} = 3$ to the solution (3.2) of the classical Buchdahl equation.

3.4. Case with $a(x)={\alpha} x^{r}$ $({r}\ne -1)$ and an arbitrary $b(t)$

Despite the previous particular cases determined by Proposition 2.1, for which exact solutions have been presented in an explicit form, it is worth observing that, in general, the first equation in (2.17) does not provide an explicit expression for $x(t)$ , as it may not be expressible in terms of the usual elementary functions.

The simplest choice for which this pattern is observed corresponds to polynomial choices of $a(x)$ ; more precisely

$\begin{equation} a(x) = {\alpha} x^{r} , \qquad x\in \mathbb R^\ast, \qquad {\alpha}\in \mathbb R^\ast, \qquad {r}\in\mathbb R^\ast, \qquad {r}\ne -1 . \nonumber \end{equation}$

Then we find that

$\begin{equation} {\Xi}(x) = \exp\left(-{\alpha}\, \frac{x^{{r}+1}}{{r}+1} \right) \nonumber \end{equation}$

along with

$\begin{equation} \begin{split} \omega& = \dfrac{ 1}{ y}\, \exp\left(-{\alpha}\, \frac{x^{{r}+1}}{{r}+1} \right) {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y , \qquad h_1 = {y} \exp\left(-{\alpha}\, \frac{x^{{r}+1}}{{r}+1} \right)\, , \\[4pt] h_2& = \frac{1}{{r}+1} \left( \frac{{\alpha}}{{r}+1} \right)^{-\frac{1}{{r}+1} } \Gamma\left(\frac{1}{{r}+1} , {\alpha}\, \frac{x^{{r}+1}}{{r}+1} \right), \qquad {r}\ne -1, \end{split} \nonumber \end{equation}$

where $\Gamma(u, v)$ denotes the incomplete Gamma function ^[21]. The first equation in (2.17), which provides the general solution $x(t)$ , adopts the cumbersome implicit form

$\begin{equation} \frac{1}{{r}+1} \left( \frac{{\alpha}}{{r}+1} \right)^{-\frac{1}{{r}+1} } \Gamma\left(\frac{1}{{r}+1} , {\alpha}\, \frac{x^{{r}+1}}{{r}+1} \right) = c_1 \left( c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau\right) . \nonumber \end{equation}$

For general values of $\alpha$ , this expression cannot be solved explicitly with respect to $x(t)$ , and alternative methods, like the Lie series ^[22], have to be applied to determine the solution of the system.

3.5. Nonexistence of $\mathfrak{b}_2$ -based extensions of the generalized Buchdahl equation

Taking into account the $\mathfrak{b}_2$ -LH algebra's symmetry (see (2.1)–(2.8)) of the generalized Buchdahl system, it is rather natural to analyze whether it is possible to extend the system adding a second $t$ -dependent arbitrary function, i.e., to consider two coefficient functions $b_1(t)$ and $b_2(t)$ . We start with the first-order ODE system

$\begin{equation} \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} = b_1(t) y, \qquad \frac{{{{\rm{d}}}} y}{{{{\rm{d}}}} t} = b_1(t)a(x)y^2+b_2(t)y , \end{equation}$

(3.4)

such that $b_1(t)$ and $b_2(t)$ are arbitrary. These equations determine a Lie system with the $t$ -dependent vector field

${\bf{X}}_t = b_1(t){\bf{X}}_1+b_2(t){\bf{X}}_2,$

where the $t$ -independent vector fields ${\bf{X}}_i$ are defined as in (2.3). It is straightforward to verify that (3.4) also determines a $\mathfrak{b}_2$ -LH system with the Hamiltonian

$h_t = b_1(t) h_{1}+b_2(t) h_{2}$

and the same Hamiltonian functions (2.7) and symplectic form (2.6).

Assuming that $b_1(t)\neq 0$ , we consider the following change in the coordinate $y$ :

$\begin{equation} \tilde y(t) = b_1(t) y(t). \nonumber \end{equation}$

It follows that

$\begin{equation} \frac{{{{\rm{d}}}} \tilde y}{{{{\rm{d}}}} t} = b_1\, \frac{{{{\rm{d}}}} y}{{{{\rm{d}}}} t}+ \frac{{{{\rm{d}}}} b_1}{{{{\rm{d}}}} t}\, y = b_1^2 a(x) y^2 + b_1b_2 y + \frac{{{{\rm{d}}}} b_1}{{{{\rm{d}}}} t}\, y = a(x) \tilde y^2+ b(t)\tilde y, \nonumber \end{equation}$

where

$\begin{equation} b(t) = b_2(t)+\frac 1{b_1(t)} \frac{{{{\rm{d}}}} b_1}{{{{\rm{d}}}} t}. \nonumber \end{equation}$

In this case, the system (3.4) is equivalent to (2.1), showing that the latter cannot be generalized as an LH system based on the LH algebra $\mathfrak{b}_2$ , consistent with the results derived in ^[9].

4. Deformed generalized Buchdahl equation from the quantum book algebra

Starting from the quantum deformation of the book algebra, which is briefly recalled, in this section, we obtain the deformed counterpart of the generalized Buchdahl system (2.1), together with its corresponding general solution, thus extending Proposition 2.1 to an arbitrary quantum deformation parameter $z$ , while keeping the parameter functions $b(t)$ and $a(x)$ arbitrary.

4.1. Quantum book algebra and deformed book LH systems

The quantum algebra deformation (see ^[23,24] for details) of the book Lie algebra $\mathfrak{b}_2$ is denoted by

$U_{ z}(\mathfrak{b}_2)\equiv \mathfrak{b}_{z, 2 },$

where $z$ is the quantum deformation real parameter (usually $q = {{{\rm{e}}}}^z$ ). Its Hopf structure is defined by the following deformed coproduct map $\Delta_z$ and compatible commutation relation in an "abstract" basis $(v_1, v_2)$ :

$\begin{equation} \begin{split} \Delta_z(v_1)& = v_1\otimes 1 + 1 \otimes v_1 , \\ \Delta_z(v_2)& = v_2\otimes {{{\rm{e}}}}^{-z v_1}+1\otimes v_2 , \\ [v_2, v_1]_z& = - \frac{1-{{{\rm{e}}}}^{-z v_1}}{z} , \end{split} \end{equation}$

(4.1)

such that $\Delta_z$ is an algebra homomorphism and satisfies the coassociativity condition

$\begin{equation} ({\rm Id}\otimes\Delta_z)\Delta_z = (\Delta_z\otimes {\rm Id})\Delta_z . \nonumber \end{equation}$

The pair $(\mathfrak{b}_{z, 2 }, \Delta_z)$ thus defines a coalgebra structure (see ^[14,15] and references therein for more details). In the following, we apply to $\mathfrak{b}_2$ the formalism of Poisson–Hopf deformations of LH systems introduced in ^[20,25], from which a deformation of the generalized Buchdahl system (2.1) will be derived.

A deformed symplectic representation $D_z$ of $\mathfrak b_{z, 2}$ (4.1) in terms of the canonical variables $(q, p)$ of Section 2.1 and the canonical symplectic form (2.11) is given by

$\begin{equation} h_{z, 1}: = D_z(v_1) = -q , \qquad h_{z, 2}: = D_z(v_2) = \left( \frac{ {{{\rm{e}}}}^{z q} -1}{z}\right) p, \end{equation}$

(4.2)

where the corresponding deformed Poisson bracket with respect to ${{\omega_{{\rm{can}}}}}$ is

$\begin{equation} \{h_{z, 2}, h_{z, 1}\}_{{\omega_{{\rm{can}}}}} = \frac{{{{\rm{e}}}}^{-z h_{z, 1}} -1}{z}\, . \nonumber \end{equation}$

From the relation

$\iota_{{\bf X}_{z, i}}{{\omega_{{\rm{can}}}}} = {\rm d}h_{z, i},$

we compute the corresponding deformation of the vector fields (2.15)

$\begin{equation} {\bf{X}}_{z, 1} = \frac{\partial}{\partial p} , \qquad {\bf{X}}_{z, 2} = \left( \frac{ {{{\rm{e}}}}^{z q}-1}{z} \right)\frac{\partial}{\partial q}- {{{\rm{e}}}}^{z q} p \, \frac{\partial}{\partial p} , \nonumber \end{equation}$

which span a smooth distribution in the sense of Stefan–Sussmann ^[26,27,28] through the commutator

$\begin{equation} [{\bf X}_{z, 2}, {\bf X}_{z, 1}] = {{{\rm{e}}}}^{z q} \, {\bf X}_{z, 1}. \nonumber \end{equation}$

The invariance condition of ${{\omega_{{\rm{can}}}}}$ in (2.11) under the Lie derivative (2.5) is trivially satisfied.

This leads to the deformed $t$ -dependent Hamiltonian and $t$ -dependent vector field (compare this with Eq (2.13))

$\begin{equation} \begin{split} h_{z, t}& = h_{z, 1} + b(t) h_{z, 2} = - q + b(t) \left( \frac{ {{{\rm{e}}}}^{z q} -1}{z}\right) p , \\[2pt] {\bf{X}}_{z, t}& = {\bf{X}}_{z, 1} + b(t) {\bf{X}}_{z, 2} = \frac{\partial}{\partial p}+ b(t) \left( \left( \frac{ {{{\rm{e}}}}^{z q}-1}{z} \right)\frac{\partial}{\partial q}- {{{\rm{e}}}}^{z q}p \, \frac{\partial}{\partial p} \right) , \end{split} \nonumber \end{equation}$

where $b(t)$ is an arbitrary real parameter function. The associated first-order system of nonautonomous nonlinear and coupled ODEs on $\mathbb R^2$ is given by

$\begin{equation} \begin{split} \frac{{{{\rm{d}}}} q}{{{{\rm{d}}}} t}& = b(t) \left( \frac{ {{{\rm{e}}}}^{z q}-1}{z} \right) , \\[2pt] \frac{{{{\rm{d}}}} p}{{{{\rm{d}}}} t}& = 1 - b(t) {{{\rm{e}}}}^{z q} p . \end{split} \end{equation}$

(4.3)

For the limit $z\rightarrow 0$ , the system (2.14) is recovered^¶. As the first of the equations above is separable, it can be easily solved, and substitution into the second equation yields, after a quadrature, the general solution (see ^[14,15])

^¶All the deformed expressions above reduce to (2.12)–(2.16) concerning the classical $\mathfrak{b}_2$ -LH algebra.

$\begin{equation} \begin{split} q(t)& = -\frac{\ln \left(1- z c_1 {{{\rm{e}}}}^{{\gamma}(t)} \right)}z , \qquad {\gamma}(t): = \int^t b(\tau){{{\rm{d}}}} \tau , \\[4pt] p(t)& = \left( {{{\rm{e}}}}^{-{\gamma}(t)} -z c_1 \right) \left( c_2 + \int^t \frac{1}{{{{\rm{e}}}}^{-{\gamma}(\tau)}-z c_1 } \, {{{\rm{d}}}} \tau \right) , \end{split} \end{equation}$

(4.4)

where $c_1$ and $c_2$ are the two constants of integration determined by the initial conditions. Observe that the first equation in (4.4) can be expressed alternatively as

$\begin{equation} \frac{1- {{{\rm{e}}}}^{-zq(t)} }{z} = c_1 \, {{{\rm{e}}}}^{{\gamma}(t)}. \nonumber \end{equation}$

It is worth observing that the presence of the quantum deformation parameter $z$ can be regarded as the introduction of a perturbation in the classical $\mathfrak{b}_2$ -LH system (2.14), in such a manner that a nonlinear interaction or coupling between the variables $(q, p)$ in the deformed $\mathfrak{b}_2$ -LH system (4.3) arises through the term ${{{\rm{e}}}}^{z q} p$ . This fact can be clearly appreciated by taking a power series expansion in $z$ of (4.3) and truncating at the first order, leading to the system

$\begin{equation} \begin{split} \frac{{{{\rm{d}}}} q}{{{{\rm{d}}}} t}& = b(t) \bigl( q +\tfrac 12 z q^2 \bigr) +o[z^2] , \\[2pt] \frac{{{{\rm{d}}}} p}{{{{\rm{d}}}} t}& = 1 - b(t) \bigl( p +z qp \bigr)+o[z^2] , \end{split} \end{equation}$

(4.5)

which hold for a small value of $z$ . In this approximation, we find that $z$ introduces a quadratic term $q^2$ in the first equation of (4.5), leading to a real Bernoulli equation, while the second equation is linear in $p$ , once the value of $q$ has been obtained. This enables us to integrate the system by quadratures, allowing us to obtain the general solution.

4.2. Deformed generalized Buchdahl equation and its general solution

By introducing the change of variables (2.10) into the expressions of (4.2) to (4.3) with the initial canonical variables $(q, p)$ , we directly obtain the deformation of the generalized Buchdahl equation presented in Section 2 in the appropriate coordinates $(x, y)$ . This result is summarized as follows.

Proposition 4.1. (i) The deformation of the $t$ -dependent generalized Buchdahl Hamiltonian (2.8) in terms of the variables $(x, y)$ is defined by

$\begin{equation} \begin{split} h_{z, t}& = h_{z, 1} + b(t) h_{z, 2} , \\[2pt] h_{z, 1} & = y\, {\Xi}(x) , \qquad {\Xi}(x): = \exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right) , \\[2pt] h_{z, 2} & = \frac{\exp\bigl(-z y\, {\Xi}(x)\bigr) -1}{z y\, {\Xi}(x)}\int^x {\Xi}(\xi) {{{\rm{d}}}} \xi , \end{split} \end{equation}$

(4.6)

such that

$\begin{equation} \{h_{z, 2}, h_{z, 1}\}_\omega = \frac{ {{{\rm{e}}}}^{-z h_{z, 1}} -1} {z} \nonumber \end{equation}$

with respect to the noncanonical symplectic form $\omega$ (2.9).

(ii) The deformation of the generalized Buchdahl system (2.1) is given by

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t} = &\{x, h_{z, t}\}_\omega = y + b(t) \left( \frac{\exp\bigl(z y\, {\Xi}(x)\bigr) -1 -z y\, {\Xi}(x) }{z y\, {\Xi}^2(x)}\right) \exp\bigl(-z y\, {\Xi}(x)\bigr) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi , \\[2pt] \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t} = &\{y, h_{z, t}\}_\omega = a(x) y^2 + b(t) \exp\bigl(-z y\, {\Xi}(x)\bigr) \\[2pt] & \times \left( \frac{\exp\bigl(z y\, {\Xi}(x)\bigr) -1}{z \, {\Xi}(x)} + \frac{ \exp\bigl(z y\, {\Xi}(x)\bigr) -1 -z y\, {\Xi}(x) }{z \, {\Xi}^2(x)}\, a(x) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi \right) , \end{split} \end{equation}$

(4.7)

for any arbitrary $a(x)$ , $b(t)$ , and $z$ .

It follows that the introduction of the Poisson–Hopf deformation of the book algebra leads to the appearance of strong nonlinear interaction terms in the initial generalized Buchdahl system (2.1) determined by the quantum deformation parameter $z$ . In this sense, note that the first equation in (4.7) is no longer equal to

$\frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} = y,$

and additional functions depending on $(x, y)$ and $z$ , as well as the coefficient $b(t)$ itself, enter into the deformation. At the first-order approximation in $z$ , the system (4.7) reduces to

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t}& = y + \frac 12 z y \, b(t) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi +o[z^2] , \\[2pt] \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t}& = a(x) y^2 + b(t) y \left( 1- \frac 12 z y \left( {\Xi}(x)- a(x) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi \right) \right) +o[z^2] , \end{split} \end{equation}$

(4.8)

which nontrivially couples the coordinate functions.

The deformed vector fields corresponding to the Hamiltonian (4.6) are given by

$\begin{equation} \begin{split} {\bf{X}}_{z, t}& = {\bf{X}}_{z, 1}+b(t){\bf{X}}_{z, 2} , \qquad {\bf{X}}_{z, 1} = y\frac{\partial }{\partial x}+a(x)y^2\frac{\partial}{\partial y}\, , \\[2pt] {\bf{X}}_{z, 2}& = \left( \frac{\exp\bigl(z y\, {\Xi}(x)\bigr) -1 -z y\, {\Xi}(x) }{z y\, {\Xi}^2(x)}\right) \exp\bigl(-z y\, {\Xi}(x)\bigr) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi \, \dfrac{\partial}{\partial x}\\[2pt] &\quad + \exp\bigl(-z y\, {\Xi}(x)\bigr) \left( \frac{\exp\bigl(z y\, {\Xi}(x)\bigr) -1}{z \, {\Xi}(x)} + \frac{ \exp\bigl(z y\, {\Xi}(x)\bigr) -1 -z y\, {\Xi}(x) }{z \, {\Xi}^2(x)}\, a(x) \int^x {\Xi}(\xi){{{\rm{d}}}} \xi \right)\dfrac{\partial}{\partial y} , \end{split} \nonumber \end{equation}$

which fulfill the relation (2.5) with respect to $\omega$ in (2.6) and provide the same deformed generalized Buchdahl system (4.7). These vector fields span a distribution with the commutator

$\begin{equation} [{\bf X}_{z, 2}, {\bf X}_{z, 1}] = \exp\bigl(-z y\, {\Xi}(x)\bigr) {\bf X}_{z, 1}. \nonumber \end{equation}$

Despite the complicated expressions of the deformed generalized Buchdahl system (4.7), we emphasize that a general solution can be derived from the exact solution for deformed book LH systems (4.4) with canonical variables and the change of coordinates (2.10). This is achieved as follows.

Proposition 4.2. The general solution of the first-order system of deformed generalized Buchdahl equations (4.7) is given by

$\begin{equation} \begin{split} \int^x {\Xi}(\xi){{{\rm{d}}}} \xi & = \frac{\ln \left(1- z c_1 {{{\rm{e}}}}^{{\gamma}(t)} \right)}z \left( {{{\rm{e}}}}^{-{\gamma}(t)} -z c_1 \right) \left( c_2 + \int^t \frac{1}{{{{\rm{e}}}}^{-{\gamma}(\tau)}-z c_1 } \, {{{\rm{d}}}} \tau \right) , \\[4pt] y(t)& = \frac{\ln \left(1- z c_1 {{{\rm{e}}}}^{{\gamma}(t)} \right)}{z\, {\Xi}(x)} , \qquad {\Xi}(x): = \exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right) , \qquad {\gamma}(t): = \int^t b(\tau){{{\rm{d}}}} \tau , \end{split} \end{equation}$

(4.9)

where $c_1$ and $c_2$ are the two integration constants determined by the initial conditions.

Notice that, in contrast to Proposition 2.1, now $y\ne {{{\rm{d}}}} x/{{{\rm{d}}}} t$ (see (4.7)). As expected, under the limit $z\to 0$ , we recover the undeformed/classical solution presented in Proposition 2.1. As in the classical case, one has to choose explicit expressions for $a(x)$ and $b(t)$ in the first equation of (4.9) and try to derive the solution $x(t)$ . The solution $y(t)$ can be deduced from the second equation. As already mentioned, despite the algorithmic procedure, an explicit integration differs from being a trivial task in the general case.

5. Applications to particular deformed Buchdahl equations

We illustrate the results established in Propositions 4.1 and 4.2 by constructing the deformed counterpart of the particular generalized Buchdahl equations described in Sections 3.1–3.3.

5.1. Deformation of the proper Buchdahl equations

We choose the functions

$a(x) = 3x^{-1} \ \ (x\in \mathbb R^\ast)$

and

$b(t) = t^{-1} \ \ (t\in \mathbb R^\ast)$

as in (3.1), giving rise to

${\Xi}(x) = x^{-3}$

and

${\gamma}(t) = \ln t .$

Thus the symplectic form and the deformed Hamiltonian vector fields (4.6) read

$\begin{equation} \omega = \dfrac{ 1}{x^3y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y , \qquad h_{z, 1} = \frac{y}{x^3} , \qquad h_{z, 2} = x\, \frac{1-\exp\left(-\frac{zy}{x^3}\right)}{2zy} . \nonumber \end{equation}$

The deformed system of Buchdahl equation (4.7) is given by

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t}& = y + \frac 1{2t} \left( x \exp\left(-\frac{zy}{x^3}\right)- x^4\, \frac{1-\exp\left(-\frac{zy}{x^3}\right)}{zy} \right) , \\[2pt] \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t} & = \frac 3x\, y^2 +\frac 1{2 t}\left( 3 y \exp\left(-\frac{zy}{x^3}\right)- x^3\, \frac{1-\exp\left(-\frac{zy}{x^3}\right)}{z}\right) .\end{split} \end{equation}$

(5.1)

The corresponding exact solution is obtained by the application of Proposition 4.2. In particular, the first equation of (4.9) directly yields the exact solution for $x(t)$ , namely

$\begin{equation} \frac{1}{x^2(t)} = \frac{2(z c_1 t-1)\ln\bigl(1-z c_1 t \bigr)}{zt} \left( c_2 - \frac{z c_1 t+\ln\bigl(1-z c_1 t \bigr)}{z^2 c^2_1} \right). \end{equation}$

(5.2)

The second equation gives the following solution $y(t)$ in terms of the result above:

$\begin{equation} y(t) = x^3(t)\, \frac{\ln\bigl(1-z c_1 t \bigr)}{z } . \nonumber \end{equation}$

The exact solution (3.2) of the proper Buchdahl equation is recovered under the undeformed limit $z\to 0$ ; the limit of the first factor in (5.2) leads to $2 c_1$ , while the second factor gives $c_2+t^2/2$ .

Furthermore, we stress that the quantum deformation parameter $z$ can be regarded as a small integrable perturbation parameter, similarly to (4.8). Under such a first-order approximation in $z$ , the system (5.1) reduces to

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t}& \simeq y -z\, \frac{y}{4 t x^2} , \\[2pt] \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t} & \simeq\frac 3x\, y^2 + \frac y t- z\, \frac{5y^2}{4 t x^3} , \end{split} \end{equation}$

(5.3)

where, for simplicity, we omit the term $o[z^2]$ for such approximations. From (5.3), and taking into account that only terms that are at most linear in $z$ are considered, it follows that the first-order deformation of the Buchdahl equation (1.4) adopts the form

$\begin{equation} \frac{{{{\rm{d}}}}^2 x}{{{{\rm{d}}}} t^2}\simeq\frac 3 x \left(\frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}\right)^2+\frac 1t \, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} + z\, \frac{1}{4 t^2 x^2}\, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} . \end{equation}$

(5.4)

In contrast to the nondeformed equation, Eq (5.4) only admits one Lie point symmetry

$\begin{equation*} {\bf Y} = t\frac{\partial}{\partial t}-\frac{x}{2}\frac{\partial}{\partial x}, \end{equation*}$

showing that the maximal symmetry has been broken, i.e., the equation is no longer linearizable ^[10]. According to the previous discussion, the solution of (5.3) and (5.4) is given by

$\begin{equation} \begin{split} x(t)&\simeq \frac{\pm 1}{ \sqrt{2 c_1c_2 +c_1 t^2} } \left( 1+ z\, \frac{c_1 t \bigl(6 c_2 -t^2 \bigr) } { 12\bigl(2 c_2 + t^2 \bigr)} \right) , \\[2pt] y(t) & \simeq \frac{\mp c_1 t}{ \bigl(2 c_1c_2 +c_1 t^2\bigr)^{3/2} } \left( 1+ z\, \frac{c_1 t \bigl(10 c_2 +t^2\bigr) } { 4\bigl(2 c_2 + t^2\bigr)} \right) , \end{split} \end{equation}$

(5.5)

which can be compared with Eq (3.2).

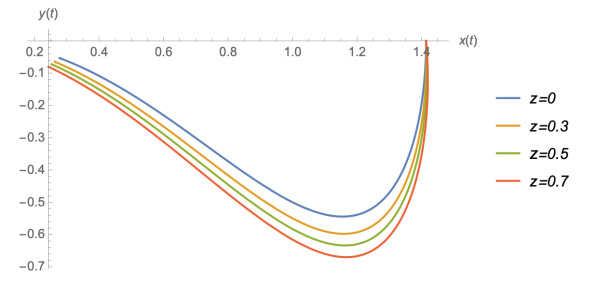
To illustrate the effect of the real deformation parameter, in , we plot several solutions (5.5) for positive values of $z$ , whereas Figure 2 shows the corresponding negative values.

Figure 1. First-order solutions (5.5) of Eq (5.4), for a positive

$x(t)$ and negative

$y(t)$ , with the choices of the integration constants

$c_1 = c_2 = 0.5$ and positive values of the deformation parameter

$z$ . The case

$z = 0$ is the solution (3.2) of the proper Buchdahl equation (1.4).

DownLoad: Full-Size Img PowerPoint

Figure 2. First-order solutions (5.5) of Eq (5.4), as in Figure 1, but with negative values of the deformation parameter

$z$ .

DownLoad: Full-Size Img PowerPoint

5.2. Deformed case with $a(x)=1/x$ and an arbitrary ${b(t)}$

$a(x) = x^{-1},$

then

${\Xi}(x) = x^{-1}\ \ ( x > 0) .$

From (4.6) we find that

$\begin{equation} \omega = \dfrac{ 1}{xy}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y , \quad h_{z, 1} = \frac{y}{x}\, , \quad h_{z, 2} = x\ln x\, \frac{\exp\left(-\frac{zy}{x}\right)-1}{zy}\, . \nonumber \end{equation}$

Proposition 4.1 leads to the corresponding deformed system of Buchdahl equations for any $b(t)$ , namely

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t}& = y + b(t)\, x \ln x\left( x \, \frac{\exp\left(\frac{zy}{x}\right)-1}{zy} -1\right) \exp\biggl(-\frac{zy}{x}\biggr), \\[2pt] \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t} & = \frac {y^2}x + b(t)\left( x \, \frac{1-\exp\left(-\frac{zy}{x}\right)}{z} \, (1+\ln x) - y \exp\biggl(-\frac{zy}{x}\biggr) \ln x\right) .\end{split} \end{equation}$

(5.6)

Its exact solution, provided by Proposition 4.2, reads as

$\begin{equation} \begin{split} \ln x(t) & = \frac{\ln \left(1- z c_1 {{{\rm{e}}}}^{{\gamma}(t)} \right)}z \left( {{{\rm{e}}}}^{-{\gamma}(t)} -z c_1 \right) \left( c_2 + \int^t \frac{1}{{{{\rm{e}}}}^{-{\gamma}(\tau)}-z c_1 } \, {{{\rm{d}}}} \tau \right), \\[4pt] y(t)& = x(t)\, \frac{\ln \left(1- z c_1 {{{\rm{e}}}}^{{\gamma}(t)} \right)}{z } . \end{split} \end{equation}$

(5.7)

This yields a family of deformed Buchdahl-type systems, together with their exact solution, depending on the function $b(t)$ . Once the latter is fixed, it is possible to study the first-order approximation in $z$ , analogous to the discussion in Section 5.1.

Let us choose, for example,

$b(t) = 1/t$

with $t\in \mathbb R^\ast$ (so ${{{\rm{e}}}}^{{\gamma}(t)} = t$ ), as in Section 3.2. The exact solution (5.7) for Eq (5.6) reduces to

$\begin{equation} \begin{split} \ln x(t) & = \frac{ (1-z c_1 t)\ln\bigl(1-z c_1 t \bigr)}{zt} \left( c_2 - \frac{z c_1 t+\ln\bigl(1-z c_1 t \bigr)}{z^2 c^2_1} \right), \\[4pt] y(t)& = x(t)\, \frac{\ln \left(1- z c_1 t\right)}{z } . \end{split} \nonumber\nonumber \end{equation}$

At the first-order in $z$ , the system (5.6) becomes

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t}& \simeq y + z\, \frac{ y\ln x}{2t} , \\[2pt] \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t} & \simeq \frac {y^2}x + \frac y t+ z\, \frac{ y^2(\ln x-1)}{2tx} .\end{split} \end{equation}$

(5.8)

After some algebraic manipulation, we arrive at the approximation of the deformed second-order generalized Buchdahl equation (1.5) in the form

$\begin{equation} \frac{{{{\rm{d}}}}^2 x}{{{{\rm{d}}}} t^2}\simeq\frac 1 x \left(\frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}\right)^2+\frac 1t \, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} - z\, \frac{\ln x}{2 t^2 }\, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} . \end{equation}$

(5.9)

As expected, the deformed equation only admits one Lie point symmetry

${\bf Y} = t\frac{\partial}{\partial t}+x\ln x\, \frac{\partial}{\partial x},$

and the solution of (5.8) and (5.9) turns out to be

$\begin{equation} \begin{split} x(t)&\simeq \exp\left(- c_1c_2 -c_1 \frac{t^2}2\right) \left(1+z\, \frac {c_1^2 t}{2} \left( c_2-\frac {t^2}{6} \right) \right) , \\[2pt] y(t) &\simeq -c_1 t \exp\left(- c_1c_2 -c_1 \frac{t^2}2\right) \left(1+z\, \frac {c_1 t}{2} \left(1+ c_1 c_2-\frac {c_1t^2}{6} \right) \right), \end{split} \nonumber \end{equation}$

which can be compared with the nondeformed Eq (3.3).

5.3. Deformed case with $a(x)={\alpha}/x$ $({\alpha}\ne 1)$ and an arbitrary $b(t)$

As a final example, we consider the function

${\Xi}(x) = x^{-{\alpha}}\ \ (x\in \mathbb R^\ast)$

with ${\alpha}\ne 1$ . The expression (4.6) yields

$\begin{equation} \omega = \dfrac{ 1}{x^{\alpha} y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y , \qquad h_{z, 1} = \frac{y}{x^{\alpha}} , \qquad h_{z, 2} = x\, \frac{\exp\bigl(- {zy x^{-{\alpha}}} \bigr)-1}{zy(1-{\alpha})} , \qquad {\alpha}\ne 1, \nonumber \end{equation}$

in such a manner that the deformed system of the Buchdahl equation (4.7) is now given by

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t}& = y + b(t)\, \frac{x}{1-{\alpha}} \left( x^{\alpha} \, \frac{\exp\bigl({zy x^{-{\alpha}}} \bigr)-1}{zy } -1\right) \exp\bigl(- {zy x^{-{\alpha}}} \bigr), \\[2pt] \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t} & = {\alpha}\, \frac {y^2}x + b(t)\, \frac{1}{1-{\alpha}} \left( x^{\alpha} \, \frac{\exp\bigl({zy x^{-{\alpha}}} \bigr)-1}{z } -{\alpha} y\right) \exp\bigl(- {zy x^{-{\alpha}}} \bigr) . \end{split} \end{equation}$

(5.10)

The corresponding exact solution, obtained by the previous prescription, turns out to be

$\begin{equation} \begin{split} x^{1-{\alpha}}(t) & = (1-{\alpha}) \, \frac{\ln \left(1- z c_1 {{{\rm{e}}}}^{{\gamma}(t)} \right)}z \left( {{{\rm{e}}}}^{-{\gamma}(t)} -z c_1 \right) \left( c_2 + \int^t \frac{1}{{{{\rm{e}}}}^{-{\gamma}(\tau)}-z c_1 } \, {{{\rm{d}}}} \tau \right), \\[4pt] y(t)& = x^{\alpha}(t)\, \frac{\ln \left(1- z c_1 {{{\rm{e}}}}^{{\gamma}(t)} \right)}{z } . \end{split} \end{equation}$

(5.11)

As in the preceding cases, we can obtain an approximation of the deformed system at the first order in $z$ , once an explicit function $b(t)$ has been chosen. To compare these with the previous results, we again set

$b(t) = 1/t\ \ (t\in \mathbb R^\ast).$

Under such an approximation, Eq (5.10) reads

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t}& \simeq y + z\, \frac{ y\, x^{1-{\alpha}}}{2(1-{\alpha})t} , \\[2pt] \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t} & \simeq {\alpha}\, \frac {y^2}x + \frac y t- z\, \frac{ y^2 x^{-{\alpha}}(1-2{\alpha})}{2(1-{\alpha})t} , \end{split} \end{equation}$

(5.12)

which leads to the following deformed second-order Buchdahl equation

$\begin{equation} \frac{{{{\rm{d}}}}^2 x}{{{{\rm{d}}}} t^2}\simeq\frac {\alpha} x \left(\frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}\right)^2+\frac 1t \, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} + z\, \frac{x^{1-{\alpha}}}{2({\alpha}-1) t^2 }\, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} . \end{equation}$

(5.13)

This ODE again only possesses one Lie point symmetry

${\bf Y} = (1-\alpha)t\frac{\partial}{\partial t}+x\frac{\partial}{\partial x},$

showing that it is not linearizable by point transformations ^[10]. A solution of (5.12) and (5.13) can, however, be deduced from (5.11), showing that

$\begin{equation} \begin{split} x(t)&\simeq \left( ({\alpha}-1)c_1 \left( c_2 +\frac{t^2}2\right) \right)^{\frac{1}{1-{\alpha}} } +\frac{z}{12}\, c_1^2 t\bigl(6c_2-t^2\bigr) \left( ({\alpha}-1)c_1 \left( c_2 +\frac{t^2}2\right) \right)^{\frac{{\alpha}}{1-{\alpha}} } , \\[2pt] y(t) &\simeq - \frac{z}{12}\, c_1^3 t^2 \left(6c_2(2{\alpha}-1)+t^2(2{\alpha} -3)\right) \left( ({\alpha}-1)c_1 \left( c_2 +\frac{t^2}2\right) \right)^{\frac{2{\alpha}-1}{1-{\alpha}} } \\[2pt] &\qquad - c_1 t\left( ({\alpha}-1)c_1 \left( c_2 +\frac{t^2}2\right) \right)^{\frac{{\alpha}}{1-{\alpha}} }. \end{split} \nonumber \end{equation}$

Many other particular equations and their solutions can be analyzed by applying the general results described in Propositions 4.1 and 4.2.

6. Extending the generalized Buchdahl equation from the oscillator algebra

So far, we have obtained (deformed) generalized Buchdahl equations from the (quantum) book algebra $\mathfrak{b}_2$ in terms of the arbitrary functions $a(x)$ and $b(t)$ . Moreover, we have proven, in Section 3.5, that there is no possible extension of the generalized Buchdahl equation (2.1) from $\mathfrak{b}_2$ , i.e., from this underlying symmetry, no additional $t$ -dependent coefficient can be considered in a nontrivial way.

Nevertheless, as $\mathfrak{b}_2$ has arisen as a subalgebra of other higher-dimensional Lie algebras, it is natural to extend the method of exact solutions to other LH systems (and their corresponding Poisson–Hopf deformations) that keep $\mathfrak{b}_2$ as an LH subalgebra. From the classification of LH systems on the plane (see ^[11,12]), it follows that the relevant candidates are the oscillator $\mathfrak{h}_4$ , $\mathfrak{sl}(2, \mathbb{R})$ and the so-called two-photon $\mathfrak{h}_6$ LH algebras.

Taking into account the canonical representation (2.12), we find that the simplest extension is provided by the oscillator LH algebra, corresponding to the imprimitive class ${\rm I}_{8}$ in ^[11,12], which entails the introduction of an additional nontrivial arbitrary $t$ -dependent coefficient. Furthermore, the corresponding exact solution is straightforward, allowing us to apply this result to the framework of Buchdahl equations, which we develop in what follows. We recall that the embedding $\mathfrak{b}_2\subset \mathfrak{h}_4$ has already been used in the context of $t$ -dependent epidemic models in ^[19]. However, we stress that an exact solution can also be deduced for the deformed counterpart from a quantum oscillator algebra, which, to best of our knowledge, has been lacking but will be addressed in the next section.

Thus, we start with the oscillator $\mathfrak{h}_4$ -LH algebra with Hamiltonian functions, expressed in canonical coordinates $(q, p)$ as ^[11,12]

$\begin{equation} h_1 = - q , \quad h_2 = qp, \quad h_3 = p, \quad h_0 = 1, \end{equation}$

(6.1)

obeying the commutation relations

$\begin{equation} \{ h_2, h_1\}_{{\omega_{{\rm{can}}}}} = - h_1 , \quad\{ h_2, h_3\}_{{\omega_{{\rm{can}}}}} = h_3 , \quad\{ h_3, h_1\}_{{\omega_{{\rm{can}}}}} = h_0 , \quad \{ h_0, \, \cdot\, \}_{{\omega_{{\rm{can}}}}} = 0 , \end{equation}$

(6.2)

with respect to the canonical symplectic form (2.11). Hence, $h_2$ can be regarded as the number generator, $h_1$ , $h_3$ as lowering/raising generators, and $h_0$ as the central element (which is necessary to close the brackets). The extension of the $t$ -dependent Hamiltonian (2.13) in terms of two arbitrary $t$ -dependent functions

$b_1(t)\equiv b(t)$

and $b_2(t)$ yields

$\begin{equation} h_t = h_1 + b_1(t) h_2 + b_2(t) h_3 = - q+ b_1(t) qp + b_2(t) p, \end{equation}$

(6.3)

giving rise to the Hamilton equations

$\begin{equation} \frac{{{{\rm{d}}}} q}{{{{\rm{d}}}} t} = \{q, h_t\}_{{\omega_{{\rm{can}}}}} = b_1(t) q +b_2(t), \qquad \frac{{{{\rm{d}}}} p}{{{{\rm{d}}}} t} = \{p, h_t\}_{{\omega_{{\rm{can}}}}} = 1-b_1(t) p , \end{equation}$

(6.4)

which again form a linear and uncoupled system.

The associated Hamiltonian vector fields are obtained from (6.1) through the relation (2.5) and read as

$\begin{equation} {\bf{X}}_1 = \frac{\partial}{\partial p}\, , \qquad {\bf{X}}_2 = q\, \frac{\partial}{\partial q}- p\, \frac{\partial}{\partial p}\, , \qquad {\bf{X}}_3 = \frac{\partial}{\partial q}\, , \end{equation}$

(6.5)

which satisfy the Lie commutators

$\begin{equation} [{\bf{X}}_2, {\bf{X}}_1] = {\bf{X}}_1, \qquad [{\bf{X}}_2, {\bf{X}}_3] = -{\bf{X}}_3, \qquad [{\bf{X}}_1, {\bf{X}}_3] = 0. \end{equation}$

(6.6)

Therefore, the Vessiot–Guldberg Lie algebra is isomorphic to the (1+1)-dimensional Poincaré algebra on a light-cone basis, with ${\bf{X}}_2$ playing the role of the boost generator, and ${\bf{X}}_1$ , ${\bf{X}}_3$ as translations. In fact, if $(q, p)$ are identified with the light-like coordinates $(x_+, x_-)$ , the vector fields (6.5) are just the Killing vector fields of the metric

${{{\rm{d}}}} s^2 = {{{\rm{d}}}} x_+{{{\rm{d}}}} x_-$

in Minkowskian spacetime.

The oscillator LH system (6.4) can then be solved directly, leading to the following exact solution in terms of the two integration constants $c_1$ and $c_2$ :

$\begin{equation} \begin{split} q(t)& = \left( c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau )}b_2(\tau) {{{\rm{d}}}} \tau\right) {{{\rm{e}}}}^{{\gamma}(t)} , \qquad {\gamma}(t): = \int^t b_1(\tau){{{\rm{d}}}} \tau , \\[1pt] p(t)& = \left( c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau )} {{{\rm{d}}}} \tau\right) {{{\rm{e}}}}^{-{\gamma}(t)}. \end{split} \end{equation}$

(6.7)

The results above can be applied in a straightforward manner to the generalized Buchdahl equations by applying the change of coordinates (2.10). The Hamiltonian function (6.1) and the vector fields (6.5) turn out to be

$\begin{equation} h_1 = y \, \Xi(x), \quad h_2 = -\int^x \Xi(\xi){{{\rm{d}}}} \xi, \quad h_3 = \frac{1}{y\, \Xi(x) }\int^x \Xi(\xi){{{\rm{d}}}} \xi, \quad h_0 = 1, \end{equation}$

(6.8)

and

$\begin{equation} \begin{split} & {\bf{X}}_1 = y\frac{\partial }{\partial x}+a(x)y^2\frac{\partial}{\partial y}, \quad {\bf{X}}_{2} = y\dfrac{\partial}{\partial y} , \\[1pt] &{\bf{X}}_3 = - \frac{1}{y\, \Xi^2(x) }\int^x \Xi(\xi){{{\rm{d}}}} \xi \, \frac{\partial }{\partial x}-\frac{1}{\Xi^2(x) }\left(\Xi(x) +a(x)\int^x \Xi(\xi){{{\rm{d}}}} \xi \right)\frac{\partial}{\partial y}, \end{split} \end{equation}$

(6.9)

with $\Xi(x)$ as given in (2.17). They fulfill the same commutation rules (6.2) and (6.6) (the former is with respect to the symplectic form (2.6)). Observe that, as a byproduct, the $t$ -independent vector fields ${\bf{X}}_i$ in (6.9) are Killing vector fields of the Minkowskian metric, now reading as

$\begin{equation} \begin{split} {{{\rm{d}}}} s^2 = &a(x)\left(\Xi(x)+a(x)\int^x \Xi(\xi){{{\rm{d}}}} \xi \right){{{\rm{d}}}} x^2+\frac 1{y^2}\int^x \Xi(\xi){{{\rm{d}}}} \xi \, {{{\rm{d}}}} y^2\\[1pt] & -\frac 1 y \left(\Xi(x) + 2 a(x) \int^x \Xi(\xi){{{\rm{d}}}} \xi \right){{{\rm{d}}}} x\, {{{\rm{d}}}} y. \end{split} \nonumber \end{equation}$

From $h_t$ (6.3) or

${\bf{X}}_t = {\bf{X}}_1 + b_1(t) {\bf{X}}_2 + b_2(t) {\bf{X}}_3,$

we arrive at the extended generalized Buchdahl equations as the first-order nonlinear system of ODEs given by

$\begin{equation} \begin{split} & \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} = y - b_2(t) \, \frac{1}{y\, \Xi^2(x) }\int^x \Xi(\xi){{{\rm{d}}}} \xi, \\ & \frac{{{{\rm{d}}}} y}{{{{\rm{d}}}} t} = a(x)y^2+b_1(t)y -b_2(t)\, \frac{1}{\Xi^2(x) }\left(\Xi(x) +a(x)\int^x \Xi(\xi){{{\rm{d}}}} \xi \right), \end{split} \end{equation}$

(6.10)

(compare this with the system (2.1)). In this respect, it should be observed that consideration of the $\mathfrak{h}_4$ -LH algebra implies the introduction of a "naïve" term $b_2(t)p$ in the Hamiltonian $h_t$ (6.3), whose effect becomes quite strong in the context of the Buchdahl equations above. In particular, the coefficient $b_2(t)$ introduces complicated terms in both equations with

$\frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}\ne y.$

Their corresponding exact solution is provided by (6.7) and is characterized by the following "extended" version of Proposition 2.1.

Proposition 6.1. The general solution of the extended generalized Buchdahl equations (6.10), determined by the oscillator $\mathfrak{h}_4$ -LH algebra, is given by

$\begin{equation} \begin{split} \int^x {\Xi}(\xi){{{\rm{d}}}} \xi & = - \left( c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau )}b_2(\tau) {{{\rm{d}}}} \tau\right) \left( c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau\right) , \\[2pt] y(t)& = - \frac{ {{{\rm{e}}}}^{{\gamma}(t)}}{\Xi(x) }\left( c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau )}b_2(\tau) {{{\rm{d}}}} \tau\right) , \\[2pt] {\Xi}(x)&: = \exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right), \quad {\gamma}(t): = \int^t b_1(\tau){{{\rm{d}}}} \tau , \end{split} \end{equation}$

(6.11)

where $c_1$ and $c_2$ are the two constants of integration determined by the initial conditions.

Once the coefficients $b_1(t)$ , $b_2(t)$ , and $a(x)$ have been chosen, the procedure used to obtain the solution $(x(t), y(t))$ from Proposition 6.1 consists of calculating ${\Xi}(x)$ and ${\gamma}(t)$ , introducing them in the first equation trying to compute $x(t)$ , and substituting it into the second equation, finding $y(t)$ .

We point out that the particular case with the constant

$b_2(t) = b_0,$

covered by Proposition 6.1, is also endowed with the $\mathfrak{h}_4$ -LH algebra. Although $h_t$ (6.3) is thus composed of only two Hamiltonian functions, a third function is needed to close the Poisson brackets, leading to an LH algebra isomorphic to $\mathfrak{h}_4$ . Explicitly, if we define

$h_\pm : = h_1\pm b_0 h_3,$

then the commutation rules (6.2) are transformed into

$\begin{equation} \{ h_2, h_\pm\}_\omega = - h_\mp , \quad\{ h_+, h_-\}_\omega = 2 b_0 h_0 , \quad \{ h_0, \, \cdot\, \}_\omega = 0 , \nonumber \end{equation}$

with respect to the symplectic form (2.6), and

$h_t = h_+ +b_1(t)h_2.$

Likewise, this particular system comes from the $t$ -dependent vector field

${\bf{X}}_t = {\bf{X}}_+ + b_1(t) {\bf{X}}_2 ,$

where

${\bf{X}}_\pm: = {\bf{X}}_1\pm b_0 {\bf{X}}_3,$

such that

$[{\bf{X}}_2, {\bf{X}}_\pm] = {\bf{X}}_\mp$

and

$[{\bf{X}}_+, {\bf{X}}_-] = 0,$

which is isomorphic to the Poincaré Lie algebra.

We illustrate the $\mathfrak{h}_4$ -LH systems (6.10) together with their general solution (6.11) by constructing the extensions of the particular generalized Buchdahl equations studied previously in Sections 3.1–3.3, the final results of which are summarized in Table 1.

Table 1. Extensions of the particular generalized Buchdahl equations of Sections 3.1–3.3 from the oscillator LH algebra.

● Case Ⅰ Extended Buchdahl equation $a(x)= 3 x^{-1}$ $b_1(t)= t^{-1}$ ${\Xi}(x)= {x^{-3}}$ ${\gamma}(t)=\ln t$
${\quad \omega=\dfrac{ 1}{x^3y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y \qquad h_1=\frac{y}{x^3} \qquad h_2=\frac{1}{2x^2}\qquad h_3=-\frac{x}{2y} }$
${\quad \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}=y + b_2(t)\frac{x^4}{2y} \qquad \frac{{{{\rm{d}}}} y}{{{{\rm{d}}}} t}=\frac{3y^2}{x} +\frac{y}{t}+b_2(t) \frac{x^3}{2} }$
${\quad x(t)=\pm\left\{ \left(c_1+\int^t\frac{b_2(\tau)}{\tau}\, {{{\rm{d}}}}\tau \right)\left(2 c_2+t^2 \right) \right\}^{-1/2} }$
${\quad y(t)=\mp\, t \left(c_1+\int^t\frac{b_2(\tau)}{\tau}\, {{{\rm{d}}}}\tau \right)^{-1/2} \left(2 c_2+t^2 \right)^{-3/2} }$
● Case Ⅱ $a(x)= x^{-1}$ arbitrary $b_1(t)$ ${\Xi}(x)=\ {x^{-1}}$
${\quad \omega=\dfrac{ 1}{x y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y \qquad h_1=\frac{y}{x } \qquad h_2=- \ln x\qquad h_3= \frac{x\ln x}{y} }$
${\quad \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}=y - b_2(t)\frac{x^2\ln x}{y} \qquad \frac{{{{\rm{d}}}} y}{{{{\rm{d}}}} t}=\frac{y^2}{x} +b_1(t) {y} -b_2(t) x \bigl(1+\ln x\bigr) }$
${\quad x(t)= \exp\left\{ - \left(c_1+\int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}{b_2(\tau)}{{{\rm{d}}}}\tau \right) \left(c_2+\int^t {{{\rm{e}}}}^{{\gamma}(\tau)}{{{\rm{d}}}}\tau \right) \right\} }$
${\quad y(t)=-{{{\rm{e}}}}^{{\gamma}(t)}\left(c_1+\int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}{b_2(\tau)}{{{\rm{d}}}}\tau \right) \exp\left\{ - \left(c_1+\int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}{b_2(\tau)}{{{\rm{d}}}}\tau \right) \left(c_2+\int^t {{{\rm{e}}}}^{{\gamma}(\tau)}{{{\rm{d}}}}\tau \right) \right\} }$
Subcase Ⅱ $a(x)= x^{-1}$ $b_1(t)=t^{-1}$ ${\Xi}(x)=\ {x^{-1}}$ ${\gamma}(t)=\ln t$
${\quad x(t)= \exp\left\{ - \left(c_1+\int^t \frac{b_2(\tau)}{\tau}\, {{{\rm{d}}}}\tau \right) \left(c_2+ \frac{t^2}2 \right) \right\} }$
${\quad y(t)=- t\left(c_1+\int^t \frac{b_2(\tau)}{\tau}\, {{{\rm{d}}}}\tau \right) \exp\left\{ - \left(c_1+\int^t \frac{b_2(\tau)}{\tau}\, {{{\rm{d}}}}\tau\right) \left(c_2+ \frac{t^2}2\right) \right\} }$
● Case Ⅲ $a(x)= \alpha\, x^{-1}\ (\alpha\ne 1)$ arbitrary $b_1(t)$ ${\Xi}(x)=\ {x^{-\alpha}}$
${\quad \omega=\dfrac{ 1}{x^\alpha y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y \qquad h_1=\frac{y}{x^\alpha } \qquad h_2=- \frac{x^{1-\alpha}}{1-\alpha} \qquad h_3= \frac{x }{y(1-\alpha)} }$
${\quad \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}=y - b_2(t)\frac{x^{1+\alpha}}{(1-\alpha)y} \qquad \frac{{{{\rm{d}}}} y}{{{{\rm{d}}}} t}=\frac{\alpha\, y^2}{x} +b_1(t) {y} -b_2(t) \frac{x^\alpha}{1-\alpha} }$
${\quad x(t)= \left\{ ({\alpha}-1) \left(c_1+\int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}{b_2(\tau)}{{{\rm{d}}}}\tau \right) \left(c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau \right) \right\}^{\frac{1}{1-{\alpha}} } }$
${\quad y(t)=-{{{\rm{e}}}}^{{\gamma}(t)}\left(c_1+\int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}{b_2(\tau)}{{{\rm{d}}}}\tau \right) \left\{ ({\alpha}-1) \left(c_1+\int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}{b_2(\tau)}{{{\rm{d}}}}\tau \right) \left(c_2 + \int^t {{{\rm{e}}}}^{{\gamma}(\tau)} {{{\rm{d}}}} \tau \right) \right\}^{\frac{{\alpha}}{1-{\alpha}} } }$
Subcase Ⅲ $a(x)= \alpha\, x^{-1}\ (\alpha\ne 1)$ $b_1(t)=t^{-1}$ ${\Xi}(x)=\ {x^{-\alpha}}$ ${\gamma}(t)=\ln t$
${\quad x(t)= \left\{ ({\alpha}-1) \left(c_1+\int^t \frac{b_2(\tau)}{\tau}\, {{{\rm{d}}}}\tau \right) \left(c_2 + \frac{t^2}2 \right) \right\}^{\frac{1}{1-{\alpha}} } }$
${\quad y(t)=- t\left(c_1+\int^t \frac{b_2(\tau)}{\tau}\, {{{\rm{d}}}}\tau\right) \left\{ ({\alpha}-1) \left(c_1+\int^t \frac{b_2(\tau)}{\tau}\, {{{\rm{d}}}}\tau \right) \left(c_2 + \frac{t^2}2\right) \right\}^{\frac{{\alpha}}{1-{\alpha}} } }$
$^*$ Note: For each case, we indicate the choice of the coefficients $a(x)$ and $b_1(t)$ for an arbitrary $b_2(t)$ , the symplectic form (2.6), the functions $\Xi(x)$ and ${\gamma}(t)$ , the Hamiltonian functions (6.8), the system (6.10), and its corresponding general solution (6.11).

| Show Table

DownLoad: CSV

7. Deformed generalized Buchdahl equation from the quantum oscillator algebra

Among all possible quantum deformations of the oscillator Lie algebra $\mathfrak{h}_4$ ^[29], only the so-called nonstandard deformation, namely

$U_{z}(\mathfrak{h}_4)\equiv \mathfrak{h}_{z, 4 },$

enables the Hopf algebra embedding

$\mathfrak{b}_{z, 2}\subset \mathfrak{h}_{z, 4 }.$

In fact, $\mathfrak{h}_{z, 4 }$ is a central extension of the nonstandard quantum (1+1) Poincaré algebra ^[30,31] on the light-cone basis (6.6). In what follows, we first recall the role of $\mathfrak{h}_{z, 4 }$ in the framework of LH systems and then apply these results to the context of Buchdahl equations, arriving at the extension of the deformed generalized equations obtained in Sections 4 and 5.

7.1. Quantum oscillator algebra and deformed oscillator LH systems

The Hopf structure of $\mathfrak{h}_{z, 4 }$ is determined by the following coproduct map and compatible commutation relations in a basis $(v_1, v_2, v_3, v_0)$ ^[29]:

$\begin{equation} \begin{split} \Delta_z(v_1)& = v_1\otimes 1 + 1 \otimes v_1 , \qquad \Delta_z(v_2) = v_2\otimes {{{\rm{e}}}}^{-z v_1}+1\otimes v_2, \\ \Delta_z(v_3)& = v_3\otimes {{{\rm{e}}}}^{-z v_1}+1\otimes v_3 + z v_2 \otimes {{{\rm{e}}}}^{-z v_1} v_0 , \qquad \Delta_z(v_0) = v_0\otimes 1 + 1 \otimes v_0 , \\[1pt] [v_2, v_1]_z& = \frac{{{{\rm{e}}}}^{-z v_1}-1}{z}, \quad [v_2, v_3]_z = v_3 , \quad [v_3, v_1]_z = {{{\rm{e}}}}^{-z v_1}v_0, \quad [v_0, \, \cdot\, ]_z = 0. \end{split} \end{equation}$

(7.1)

In canonical variables $(q, p)$ , a deformed symplectic representation $D_z$ of $\mathfrak{h}_{z, 4 }$ turns out to be ^[31]

$\begin{equation} \begin{split} h_{z, 1}:& = D_z(v_1) = -q , \qquad\ \, h_{z, 2}: = D_z(v_2) = \left( \frac{ {{{\rm{e}}}}^{z q} -1}{z}\right) p, \\ h_{z, 3}:& = D_z(v_3) = {{{\rm{e}}}}^{z q} p, \qquad h_{z, 0}: = D_z(v_0) = 1, \end{split} \end{equation}$

(7.2)

which fulfill the deformed Poisson brackets given by

$\begin{equation} \begin{split} \{h_{z, 2}, h_{z, 1}\}_{{\omega_{{\rm{can}}}}}& = \frac{{{{\rm{e}}}}^{-z h_{z, 1}} -1}{z}, \qquad \{h_{z, 2}, h_{z, 3}\}_{{\omega_{{\rm{can}}}}} = h_{z, 3}, \\[2pt] \{h_{z, 3}, h_{z, 1}\}_{{\omega_{{\rm{can}}}}}& = {{{\rm{e}}}}^{-z h_{z, 1}}h_{z, 0}, \qquad\quad\ \, \{h_{z, 0}, \, \cdot\, \}_{{\omega_{{\rm{can}}}}} = 0, \end{split} \end{equation}$

(7.3)

with respect to the canonical symplectic form (2.11).

The relation

$\iota_{{\bf X}_{z, i}}{{\omega_{{\rm{can}}}}} = {\rm d}h_{z, i}$

leads to the associated deformed Hamiltonian vector fields

$\begin{align*} {\bf{X}}_{z, 1} = \frac{\partial}{\partial p} , \quad {\bf{X}}_{z, 2} = \left( \frac{ {{{\rm{e}}}}^{z q}-1}{z} \right)\frac{\partial}{\partial q}- {{{\rm{e}}}}^{z q} p \, \frac{\partial}{\partial p} , \quad {\bf{X}}_{z, 3} = {{{\rm{e}}}}^{z q} \frac{\partial}{\partial q} -z {{{\rm{e}}}}^{z q} p \, \frac{\partial}{\partial p} , \end{align*}$

which do not close on the nonstandard quantum Poincaré algebra ^[30] but on a smooth Stefan–Sussmann distribution ^[26,27,28] given by the commutation relations ^[20]

$\begin{equation} \begin{split} [{\bf X}_{z, 2}, {\bf X}_{z, 1}]& = {{{\rm{e}}}}^{-z h_{z, 1}} \, {\bf X}_{z, 1}, \\ [{\bf X}_{z, 2}, {\bf X}_{z, 3}]& = - {\bf X}_{z, 3}, \\ [{\bf X}_{z, 3}, {\bf X}_{z, 1}]& = z\, {{{\rm{e}}}}^{-z h_{z, 1}}h_{z, 0} \, {\bf X}_{z, 1}. \end{split} \end{equation}$

(7.4)

Thus, we obtain a deformed $t$ -dependent Hamiltonian and a vector field in terms of two coefficients

$b_1(t)\equiv b(t)$

and $b_2(t)$ as follows

$\begin{equation} \begin{split} h_{z, t}& = h_{z, 1} + b_1(t) h_{z, 2} + b_2(t) h_{z, 3} = - q + b_1(t) \left( \frac{ {{{\rm{e}}}}^{z q} -1}{z}\right) p + b_2(t) {{{\rm{e}}}}^{z q} p, \\ {\bf{X}}_{z, t}& = {\bf{X}}_{z, 1} + b_1(t) {\bf{X}}_{z, 2} + b_2(t) {\bf{X}}_{z, 3} \\[2pt] & = \frac{\partial}{\partial p}+ b_1(t) \left( \left( \frac{ {{{\rm{e}}}}^{z q}-1}{z} \right)\frac{\partial}{\partial q}- {{{\rm{e}}}}^{z q}p \, \frac{\partial}{\partial p} \right) +b_2(t) \left( {{{\rm{e}}}}^{z q} \frac{\partial}{\partial q} -z {{{\rm{e}}}}^{z q} p \, \frac{\partial}{\partial p} \right) , \end{split} \end{equation}$

(7.5)

yielding the first-order system of nonlinear and coupled ODEs on $\mathbb R^2$ given by

$\begin{equation} \begin{split} \frac{{{{\rm{d}}}} q}{{{{\rm{d}}}} t}& = b_1(t) \left( \frac{ {{{\rm{e}}}}^{z q}-1}{z} \right) +b_2(t) {{{\rm{e}}}}^{z q }, \\ \frac{{{{\rm{d}}}} p}{{{{\rm{d}}}} t}& = 1 - b_1(t) {{{\rm{e}}}}^{z q} p - z b_2(t) {{{\rm{e}}}}^{z q} p . \end{split} \end{equation}$

(7.6)

The first equation can be solved directly, and by substituting into the second one, we obtain the general solution

$\begin{equation} \begin{split} q(t) = &-\frac 1 z \, {\ln \left\{ 1- z {{{\rm{e}}}}^{{\gamma}(t)} \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}b_2(\tau) {{{\rm{d}}}} \tau\right)\right\}} , \\ {\gamma}(t): = &\int^t b_1(\tau){{{\rm{d}}}} \tau , \\ p(t) = & \left\{ {{{\rm{e}}}}^{-{\gamma}(t)} -z \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}b_2(\tau) {{{\rm{d}}}} \tau\right) \right\}\\ & \times \left\{ c_2 + \int^t \left({{{\rm{e}}}}^{-{\gamma}(\tau)}-z \left(c_1 + \int^\tau {{{\rm{e}}}}^{-{\gamma}(\tau')}b_2(\tau') {{{\rm{d}}}} \tau'\right) \right)^{-1} {{{\rm{d}}}} \tau \right\} , \end{split} \end{equation}$

(7.7)

where $c_1$ and $c_2$ are the two integration constants. We note that, to best of our knowledge, this exact solution has not yet been considered in the framework of LH systems. On the contrary, the usual approach is to deduce "deformed" superposition rules from $t$ -independent constants of the motion ^[20]. Note also that, as expected, the expressions (6.1)–(6.7) are recovered from (7.2)–(7.7) under the limit $z\to 0$ .

The first-order of the power series expansion in $z$ of (7.6) yields

$\begin{equation} \begin{split} \frac{{{{\rm{d}}}} q}{{{{\rm{d}}}} t}& = b_2(t) + b_1(t)q+z\left( b_2(t) q +\frac 12 b_1(t) q^2 \right) +o[z^2] , \\ \frac{{{{\rm{d}}}} p}{{{{\rm{d}}}} t}& = 1 - b_1(t) p-z \bigl( b_2(t) p + b_1(t) qp \bigr) +o[z^2] , \end{split} \nonumber \end{equation}$

which can be compared with (4.5).

7.2. Deformed extended generalized Buchdahl equation and its general solution

Similarly to Section 4.2, we apply the change of variables (2.10) to the expressions (7.2) and (7.6), obtaining the deformation of the extended generalized Buchdahl equation in Section 6 from the quantum oscillator algebra $\mathfrak{h}_{z, 4 }$ .

Proposition 7.1. (i) The deformation of the $t$ -dependent extended generalized Buchdahl Hamiltonian (6.3) is defined, in terms of the variables $(x, y)$ , by the Hamiltonian functions

$\begin{equation} \begin{split} h_{z, t}& = h_{z, 1} + b_1(t) h_{z, 2} + b_2(t) h_{z, 3} , \\ h_{z, 1} & = y\, {\Xi}(x) , \\ h_{z, 2} & = \frac{\exp\bigl(-z y\, {\Xi}(x)\bigr) -1}{z y\, {\Xi}(x)}\int^x {\Xi}(\xi) {{{\rm{d}}}} \xi , \\ h_{z, 3} & = \frac{\exp\bigl(-z y\, {\Xi}(x)\bigr) }{y\, {\Xi}(x)}\int^x {\Xi}(\xi) {{{\rm{d}}}} \xi , \\ {\Xi}(x)&: = \exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right) , \end{split} \end{equation}$

(7.8)

which, together with

$h_{z, 0} = 1,$

verify the same deformed Poisson brackets (7.3), now with respect to the (noncanonical) symplectic form $\omega$ (2.9).

(ii) The Poisson–Hopf deformation of the extended generalized Buchdahl system (6.10) reads as

$\begin{equation} \begin{split} \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t} = &\{x, h_{z, t}\}_\omega\\ = & y + b_1(t) \left( \frac{\exp\bigl(z y\, {\Xi}(x)\bigr) -1 -z y\, {\Xi}(x) }{z y\, {\Xi}^2(x)}\right) \exp\bigl(-z y\, {\Xi}(x)\bigr) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi \\[2pt] & - b_2(t) \left( \frac{ 1+ z y\, {\Xi}(x)}{ y\, {\Xi}^2(x)}\right) \exp\bigl(-z y\, {\Xi}(x)\bigr) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi , \\ \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t} = &\{y, h_{z, t}\}_\omega\\ = & a(x) y^2 + b_1(t) \exp\bigl(-z y\, {\Xi}(x)\bigr) \\ & \times \left( \frac{\exp\bigl(z y\, {\Xi}(x)\bigr) -1}{z \, {\Xi}(x)} + \frac{ \exp\bigl(z y\, {\Xi}(x)\bigr) -1 -z y\, {\Xi}(x) }{z \, {\Xi}^2(x)}\, a(x) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi \right) \\[2pt] & - b_2(t) \, \frac{\exp\bigl(-z y\, {\Xi}(x)\bigr) }{ {\Xi}^2(x)} \left( {\Xi}(x)+\bigl(1+ z y \, {\Xi}(\xi)\bigr) a(x) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi\right) , \end{split} \end{equation}$

(7.9)

for any arbitrary $a(x)$ , $b_1(t)$ , $b_2(t)$ , and $z$ .

The deformed vector fields associated with the Hamiltonian functions (7.8) turn out to be

$\begin{equation} { \begin{split} {\bf{X}}_{z, t} = &{\bf{X}}_{z, 1}+b_1(t){\bf{X}}_{z, 2} +b_2(t){\bf{X}}_{z, 3} , \\ {\bf{X}}_{z, 1} = &y\frac{\partial }{\partial x}+a(x)y^2\frac{\partial}{\partial y}\, , \\ {\bf{X}}_{z, 2} = &\left( \frac{\exp\bigl(z y\, {\Xi}(x)\bigr) -1 -z y\, {\Xi}(x) }{z y\, {\Xi}^2(x)}\right) \exp\bigl(-z y\, {\Xi}(x)\bigr) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi \, \dfrac{\partial}{\partial x}\\[2pt] & + \exp\bigl(-z y\, {\Xi}(x)\bigr) \left( \frac{\exp\bigl(z y\, {\Xi}(x)\bigr) -1}{z \, {\Xi}(x)} + \frac{ \exp\bigl(z y\, {\Xi}(x)\bigr) -1 -z y\, {\Xi}(x) }{z \, {\Xi}^2(x)}\, a(x) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi \right)\dfrac{\partial}{\partial y}\, , \\[2pt] {\bf{X}}_{z, 3} = &-\left( \frac{ 1+ z y\, {\Xi}(x)}{ y\, {\Xi}^2(x)}\right) \exp\bigl(-z y\, {\Xi}(x)\bigr) \int^x {\Xi}(\xi) {{{\rm{d}}}} \xi \, \dfrac{\partial}{\partial x}\\[2pt] & - \frac{\exp\bigl(-z y\, {\Xi}(x)\bigr) }{ {\Xi}^2(x)} \left( {\Xi}(x)+\bigl(1+ z y \, {\Xi}(\xi)\bigr) a(x) \int^x {\Xi}(\xi){{{\rm{d}}}} \xi\right), \end{split} \nonumber } \end{equation}$

that span a distribution with the same commutation rules given by (7.4).

From the general solution of the deformed extended generalized Buchdahl equations in canonical variables (7.7), we arrive at the one corresponding to the deformed system in Proposition 7.1.

Proposition 7.2. The general solution of the first-order system of deformed extended generalized Buchdahl equation (7.9) is given by

$\begin{equation} \begin{split} \int^x {\Xi}(\xi){{{\rm{d}}}} \xi = & \frac 1 z \, {\ln \left\{ 1- z {{{\rm{e}}}}^{{\gamma}(t)} \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}b_2(\tau) {{{\rm{d}}}} \tau\right)\right\}} \left\{ {{{\rm{e}}}}^{-{\gamma}(t)} -z \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}b_2(\tau) {{{\rm{d}}}} \tau\right) \right\} \\[2pt] & \times \left\{ c_2 + \int^t \left({{{\rm{e}}}}^{-{\gamma}(\tau)}-z \left(c_1 + \int^\tau {{{\rm{e}}}}^{-{\gamma}(\tau')}b_2(\tau') {{{\rm{d}}}} \tau'\right) \right)^{-1} {{{\rm{d}}}} \tau \right\} , \\[2pt] y(t) = & \frac 1{z\, {\Xi}(x)}\, {\ln \left\{ 1- z {{{\rm{e}}}}^{{\gamma}(t)} \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)}b_2(\tau) {{{\rm{d}}}} \tau\right)\right\}} , \\[2pt] {\Xi}(x): = &\exp\left(-\int^x a(\xi){{{\rm{d}}}} \xi\right) , \\ {\gamma}(t): = & \int^t b(\tau){{{\rm{d}}}} \tau , \end{split} \end{equation}$

(7.10)

where $c_1$ and $c_2$ are the two integration constants provided by the initial conditions.

Propositions 7.1 and 7.2 state the most general results of this work, covering all the previous systems obtained so far. They can be applied to particular cases, along the same lines as in Section 5, by selecting precise functions $a(x)$ , $b_1(t)$ , and $b_2(t)$ . The main results concerning the extensions of the systems in Sections 5.1–5.3 are presented in , which correspond to the deformation of the $\mathfrak{h}_4$ -LH systems shown in , which are recovered when $z\to 0$ . It is clear that a further analysis of the perturbations at the first order in $z$ can be performed in a similar way to that in Section 5.

Table 2. Extensions of the particular deformed generalized Buchdahl equations of Sections 5.1–5.3 from the deformed oscillator LH algebra.

● Case Ⅰ Deformed extended Buchdahl equation $a(x)= 3 x^{-1}$ $b_1(t)= t^{-1}$ ${\Xi}(x)= {x^{-3}}$ ${\gamma}(t)=\ln t$
${\quad \omega=\dfrac{ 1}{x^3y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y \qquad h_{z, 1}=\frac{y}{x^3} \qquad h_{z, 2}=x\, \frac{1-\exp\bigl(-\frac{zy}{x^3}\bigr)}{2zy} \qquad h_{z, 3}=-\frac{x}{2y} \exp\biggl(-\frac{zy}{x^3}\biggr)}$
${\quad \frac {{{{\rm{d}}}} x}{{{{\rm{d}}}} t} = y + \frac 1{2t} \left(x \exp\biggl(-\frac{zy}{x^3}\biggr)- x^4\, \frac{1-\exp\bigl(-\frac{zy}{x^3}\bigr)}{zy} \right) +b_2(t)\, \frac{x^4+z x y }{2 y} \exp\biggl(-\frac{zy}{x^3}\biggr) }$
${\quad \frac {{{{\rm{d}}}} y}{{{{\rm{d}}}} t} =\frac {3y^2}x +\frac 1{2 t}\left(3 y \exp\biggl(-\frac{zy}{x^3}\biggr)- x^3\, \frac{1-\exp\bigl(-\frac{zy}{x^3}\bigr)}{z}\right) +\frac 12 b_2(t) \bigl(x^3+ 3 z y \bigr) \exp\biggl(-\frac{zy}{x^3}\biggr)}$
${\quad \frac{1}{x^2(t)} = \frac{2}{zt} \left(z t \left(c_1 + \int^t \frac {b_2(\tau)}{\tau}\, {{{\rm{d}}}} \tau\right) -1\right) {\ln \left\{ 1- z t \left(c_1 + \int^t \frac {b_2(\tau)}{\tau}\, {{{\rm{d}}}} \tau\right)\right\} } }$
${\ \qquad \qquad \times \left(c_2 + \int^t t \left(1-z t \left(c_1 + \int^\tau \frac{b_2(\tau') }{\tau'}\, {{{\rm{d}}}} \tau'\right) \right)^{-1} {{{\rm{d}}}} \tau\right)}$
${\quad y(t)=x^3(t)\, \frac 1 z \, {\ln \left\{ 1- z t \left(c_1 + \int^t \frac {b_2(\tau)}{\tau}\, {{{\rm{d}}}} \tau\right)\right\} } }$
● Case Ⅱ $a(x)= x^{-1}$ arbitrary $b_1(t)$ ${\Xi}(x)=\ {x^{-1}}$
${\quad \omega=\dfrac{ 1}{x y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y \qquad h_{z, 1}=\frac{y}{x}\qquad h_{z, 2}=x\ln x\, \frac{\exp\bigl(-\frac{zy}{x}\bigr)-1}{zy} \qquad h_{z, 3}= \frac{x\ln x}{y}\exp\biggl(-\frac{zy}{x}\biggr) }$
${\quad \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}=y + b_1(t)\, x \ln x\left(x \, \frac{\exp\bigl(\frac{zy}{x}\bigr)-1}{zy} -1\right) \exp\biggl(-\frac{zy}{x}\biggr) - b_2(t)\, \frac{\bigl(x^2+ z x y\bigr)\ln x}{y} \exp\biggl(-\frac{zy}{x}\biggr) }$
${\quad \frac{{{{\rm{d}}}} y}{{{{\rm{d}}}} t}=\frac {y^2}x + b_1(t)\left(x \, \frac{1-\exp\bigl(-\frac{zy}{x}\bigr)}{z} \, (1+\ln x) - y \exp\biggl(-\frac{zy}{x}\biggr) \ln x\right)- b_2(t)\bigl(x+(x + zy)\ln x \bigr) \exp\biggl(-\frac{zy}{x}\biggr) }$
${\quad \ln x(t)= \frac 1 z \, {\ln \left\{ 1- z {{{\rm{e}}}}^{{\gamma}(t)} \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)} {b_2(\tau)} {{{\rm{d}}}} \tau\right)\right\} } \left({{{\rm{e}}}}^{-{\gamma}(t)} -z \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)} {b_2(\tau)} {{{\rm{d}}}} \tau\right) \right) }$
${\ \ \ \qquad \qquad \times \left\{ c_2 + \int^t \left({{{\rm{e}}}}^{-{\gamma}(\tau)}-z \left(c_1 + \int^\tau {{{\rm{e}}}}^{-{\gamma}(\tau')}b_2(\tau') {{{\rm{d}}}} \tau'\right) \right)^{-1} {{{\rm{d}}}} \tau \right\}}$
${\quad y(t) =x(t)\, \frac 1 z \, {\ln \left(1- z {{{\rm{e}}}}^{{\gamma}(t)} \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)} {b_2(\tau)} {{{\rm{d}}}} \tau\right)\right) } }$
● Case Ⅲ $a(x)= \alpha\, x^{-1}\ (\alpha\ne 1)$ arbitrary $b_1(t)$ ${\Xi}(x)=\ {x^{-\alpha}}$
${\quad \omega=\dfrac{ 1}{x^\alpha y}\, {{{\rm{d}}}} x\wedge {{{\rm{d}}}} y \qquad h_{z, 1}=\frac{y}{x^{\alpha}} \qquad h_{z, 2}=x\, \frac{\exp\bigl(- {zy x^{-{\alpha}}} \bigr)-1}{zy(1-{\alpha})} \qquad h_{z, 3}= \frac{x }{y(1-\alpha)}\, \exp\bigl(- {zy x^{-{\alpha}}} \bigr) }$
${\quad \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}=y + b_1(t)\, \frac{x}{1-{\alpha}} \left(x^{\alpha} \, \frac{\exp\bigl({zy x^{-{\alpha}}} \bigr)-1}{zy } -1\right) \exp\bigl(- {zy x^{-{\alpha}}} \bigr) - b_2(t)\, \frac{x^{1+\alpha}+ z x y}{(1-\alpha)y}\, \exp\bigl(- {zy x^{-{\alpha}}} \bigr) }$
${\quad \frac{{{{\rm{d}}}} y}{{{{\rm{d}}}} t}=\frac {{\alpha}\, y^2}x + b_1(t)\, \frac{1}{1-{\alpha}} \left(x^{\alpha} \, \frac{\exp\bigl({zy x^{-{\alpha}}} \bigr)-1}{z } -{\alpha} y\right) \exp\bigl(- {zy x^{-{\alpha}}} \bigr) - b_2(t)\, \frac{x^{\alpha}+ z \alpha y}{1-\alpha }\, \exp\bigl(- {zy x^{-{\alpha}}} \bigr) }$
${\quad x^{1-\alpha}(t)=(1-\alpha) \frac 1 z \, {\ln \left\{ 1- z {{{\rm{e}}}}^{{\gamma}(t)} \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)} {b_2(\tau)} {{{\rm{d}}}} \tau\right)\right\} } \left({{{\rm{e}}}}^{-{\gamma}(t)} -z \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)} {b_2(\tau)} {{{\rm{d}}}} \tau\right) \right) }$
${\ \ \ \ \qquad \qquad \times \left\{ c_2 + \int^t \left({{{\rm{e}}}}^{-{\gamma}(\tau)}-z \left(c_1 + \int^\tau {{{\rm{e}}}}^{-{\gamma}(\tau')}b_2(\tau') {{{\rm{d}}}} \tau'\right) \right)^{-1} {{{\rm{d}}}} \tau \right\}}$
${\quad y(t) =x^\alpha(t)\, \frac 1 z \, {\ln \left(1- z {{{\rm{e}}}}^{{\gamma}(t)} \left(c_1 + \int^t {{{\rm{e}}}}^{-{\gamma}(\tau)} {b_2(\tau)} {{{\rm{d}}}} \tau\right)\right) } }$
$^*$ Note: For each case we show the coefficients $a(x)$ and $b_1(t)$ , always with an arbitrary $b_2(t)$ , the symplectic form (2.6), the functions $\Xi(x)$ and ${\gamma}(t)$ , the Hamiltonian functions (7.8), the system (7.9), and its general solution (7.10).

| Show Table

DownLoad: CSV

8. Higher-dimensional deformed generalized Buchdahl equations

As a final stage, it seems pertinent to discuss the mathematical and physical roles played by the quantum deformation parameter $z$ in more detail.

In general, given a system, considering a quantum deformation induced by introducing $z$ (or $q = {{{\rm{e}}}}^z$ ) implies dealing with an additional degree of freedom which, in turn, can be regarded as a modification of the initial system. One approach is to interpret this presence as a (integrable) perturbation of the initial system, as we have considered here, but, in addition, it also allows the construction of analytical models from experimental results. In other words, in some cases, it would be possible to fix a certain value of $z$ in some quantum algebra that matches with the data for some model, arriving at an underlying quantum group symmetry and, therefore, analytical expressions. For instance, this was exactly the procedure used in ^[32] to determine the spectrum in quantum optical models and in ^[33] to describe fermion–boson interactions in a nuclear physics context.

Furthermore, the introduction of $z$ usually leads to a coupling of the differential equations of the initial system, as shown by the explicit expressions in Sections 5 and 7; this has consequences with respect to linearization and maximal symmetry which are broken.

Beyond these comments, a quantum deformation, i.e., a Poisson–Hopf deformation of LH systems in our framework, has profound implications when constructing higher-dimensional systems. In particular, let us address this point by taking the oscillator $\mathfrak{h}_4$ -LH algebra of Section 6 and its quantum deformation $\mathfrak{h}_{z, 4}$ from Section 7 in canonical variables $(q, p)$ , as they give rise to the most general systems of this work.

The tool which enables one to obtain higher-dimensional systems is the coproduct map, which, for any LH algebra, is always (trivial) primitive and denoted $\Delta$ . Let $(v_1, v_2, v_3, v_0)$ be a basis of $\mathfrak{h}_4$ , fulfilling the Lie brackets

$\begin{equation} [v_2, v_1] = - v_1 , \quad [v_2, v_3] = v_3 , \quad [ v_3, v_1] = v_0 , \quad [ v_0, \, \cdot\, ] = 0 , \nonumber \end{equation}$

and thus they are formally similar to (6.2).

The Hopf structure is determined by the coproduct $(i = 0, 1, 2, 3)$

$\begin{equation} \Delta(v_i) = v_i\otimes 1 + 1 \otimes v_i . \nonumber \end{equation}$

If we denote the "one-particle" symplectic representation of $\mathfrak{h}_4$ (6.1) as

$D( v_i) = h_{i}(q_1, p_1): = h_{i}^{(1)} ,$

then the "two-particle" representation is obtained as ^[12]

$\begin{equation} \begin{split} (D\otimes D)(\Delta( v_1))& = h_1(q_1, p_1)+h_1(q_2, p_2) = - q_1 - q_2: = h_{1}^{(2)}, \\[2pt] (D\otimes D)(\Delta( v_2))& = h_2(q_1, p_1)+h_2(q_2, p_2) = q_1p_1+q_2p_2: = h_{2}^{(2)}, \\[2pt] (D\otimes D)(\Delta( v_3))& = h_3(q_1, p_1)+h_3(q_2, p_2) = p_1+ p_2: = h_{3}^{(2)}, \\[2pt] (D\otimes D)(\Delta( v_0))& = h_0(q_1, p_1)+h_0(q_2, p_2) = 1+1: = h_{0}^{(2)}. \end{split} \nonumber \end{equation}$

These Hamiltonian functions satisfy the same commutation relations (6.2) with respect to the canonical symplectic form

$\omega^{(2)}_{\rm can} = {{{\rm{d}}}} q_1\wedge {{{\rm{d}}}} p_1+ {{{\rm{d}}}} q_2\wedge {{{\rm{d}}}} p_2.$

In the same way, one can construct higher-dimensional representations. The relevant point is that any system with $\mathfrak{h}_4$ -LH algebra symmetry in any dimension is equivalent to considering several copies of the initial system, which is a well-known property in Lie systems; in other words, they can trivially be reduced to the initial "one-particle" one. In our case, the two-particle version of the $t$ -dependent Hamiltonian $h_t$ (6.3) reads as

$\begin{equation} \begin{split} h_t^{(2)}& = h^{(2)}_1 + b_1(t) h^{(2)}_2 + b_2(t) h^{(2)}_3 = h_t(q_1, p_1)+h_t(q_2, p_2) \\[2pt] & = \bigl( - q_1+ b_1(t) q_1p_1 + b_2(t) p_1\bigr)+\bigl( - q_2+ b_1(t) q_2p_2 + b_2(t) p_2\bigr). \end{split} \nonumber \end{equation}$

This situation changes drastically when a Poisson–Hopf deformation is introduced, since the deformed coproduct $\Delta_z$ naturally entails a coupling of the representation ^[20,25]. From the deformed coproduct $\Delta_z$ (7.1) and representation $D_z$ (7.2) of $\mathfrak{h}_{z, 4}$ , we obtain its "two-particle" representation in the form

$\begin{equation} \begin{split} (D_z\otimes D_z)(\Delta_z( v_1)) = & h_{z, 1}(q_1, p_1)+h_{z, 1}(q_2, p_2) = - q_1 - q_2: = h_{z, 1}^{(2)}, \\[2pt] (D_z\otimes D_z)(\Delta_z( v_2)) = &h_{z, 2}(q_1, p_1){{{\rm{e}}}}^{-z h_{z, 1}(q_2, p_2)}+h_{z, 2}(q_2, p_2) \\[2pt] = & \left( \frac{ {{{\rm{e}}}}^{z q_1} -1}{z}\right) p_1 {{{\rm{e}}}}^{z q_2 }+ \left( \frac{ {{{\rm{e}}}}^{z q_2} -1}{z}\right) p_2: = h_{z, 2}^{(2)}, \\[2pt] (D_z\otimes D_z)(\Delta_z( v_3)) = &h_{z, 3}(q_1, p_1){{{\rm{e}}}}^{-z h_{z, 1}(q_2, p_2)}+h_{z, 3}(q_2, p_2)\\[2pt] & +z h_{z, 2}(q_1, p_1){{{\rm{e}}}}^{-z h_{z, 1}(q_2, p_2)} h_{z, 0}(q_2, p_2) \\[2pt] = & {{{\rm{e}}}}^{z q_1} p_1 {{{\rm{e}}}}^{z q_2 } + {{{\rm{e}}}}^{z q_2} p_2+ z \left( \frac{ {{{\rm{e}}}}^{z q_1} -1}{z}\right) p_1 {{{\rm{e}}}}^{z q_2} : = h_{z, 3}^{(2)}, \\[2pt] (D_z\otimes D_z)(\Delta_z( v_0)) = & h_{z, 0}(q_1, p_1)+h_{z, 0}(q_2, p_2) = 1+1: = h_{z, 0}^{(2)}. \end{split} \nonumber \end{equation}$

They fulfill the deformed commutation relations (7.3) with respect to $\omega^{(2)}_{\rm can}$ . The "two-particle" version of the Hamiltonian $h_{z, t}$ (7.5) turns out to be

$\begin{equation} h^{(2)}_{z, t} = h^{(2)}_{z, 1} + b_1(t) h^{(2)}_{z, 2} + b_2(t) h^{(2)}_{z, 3}, \nonumber \end{equation}$

and, consequently, is no longer the sum of two copies of (7.5) as $h_{z, t}(q_1, p_1)+h_{z, t}(q_2, p_2)$ . The corresponding Hamilton equations are given by

$\begin{equation} \begin{split} \frac{{{{\rm{d}}}} q_1}{{{{\rm{d}}}} t}& = b_1(t) \biggl( \frac{ {{{\rm{e}}}}^{z q_1}-1}{z} \biggr) {{{\rm{e}}}}^{z q_2 } +b_2(t) \bigl( 2\, {{{\rm{e}}}}^{z q_1} -1\bigr){{{\rm{e}}}}^{z q_2}, \\[2pt] \frac{{{{\rm{d}}}} p_1}{{{{\rm{d}}}} t}& = 1 - b_1(t) {{{\rm{e}}}}^{z q_1} {{{\rm{e}}}}^{z q_2} p_1 - 2 z b_2(t) {{{\rm{e}}}}^{z q_1} {{{\rm{e}}}}^{z q_2} p_1 , \\[2pt] \frac{{{{\rm{d}}}} q_2}{{{{\rm{d}}}} t}& = b_1(t) \biggl( \frac{ {{{\rm{e}}}}^{z q_2}-1}{z} \biggr) +b_2(t) {{{\rm{e}}}}^{z q_2}, \\[2pt] \frac{{{{\rm{d}}}} p_2}{{{{\rm{d}}}} t}& = 1 - b_1(t){{{\rm{e}}}}^{z q_2} \bigl( \bigl({{{\rm{e}}}}^{z q_1} -1\bigr) p_1 +p_2 \bigr)- z b_2(t) {{{\rm{e}}}}^{z q_2} \bigl( \bigl(2{{{\rm{e}}}}^{z q_1} -1\bigr) p_1 +p_2 \bigr) , \end{split} \nonumber \end{equation}$

showing that there are coupling terms and that the resulting system is intrinsic in the sense that it is completely different from the initial one (7.6), and hence finding that the corresponding solutions should be seen as a new problem.

9. Concluding remarks

In this work, using the general approach proposed in ^[14], the generalized Buchdahl equation has been revisited from the perspective of LH systems. Although the Buchdahl equation can be solved directly by means of integrating factors (and is further linearizable by point transformations), its reformulation in terms of a book $\frak{b}_2$ -LH system is of interest, as the solution method can be extended to Poisson–Hopf deformations from the quantum algebra $\frak{b}_{z, 2}$ , providing a systematic procedure to determine the general solution of differential equations that, in general, do not admit more than one Lie point symmetry and are not related to exact equations. Further, truncation of the series expansion in the quantum deformation parameter $z$ provides perturbations of the equation of an arbitrary order, which under certain circumstances, can also be solved explicitly. Certain special cases of the generalized Buchdahl equation and their quantum deformations have been analyzed, as well as the first-order approximations in the deformation parameter $z$ . The next natural step, namely extending the underlying Lie algebra to the oscillator algebra $\mathfrak{h}_4\supset \frak{b}_2$ , provides additional generalizations of the Buchdahl equation that still preserve the property of allowing an explicit solution, including the quantum deformations $\mathfrak{h}_{z, 4}\supset \frak{b}_{z, 2}$ . An interesting question in this context is whether equivalence criteria for the first-order approximation of the deformed equations can be obtained, eventually making possible the obtainment of canonical forms of such perturbations and simplifying the computation of exact solutions.

To summarize the results obtained in this paper, the most general cases have been presented in Propositions 7.1 and 7.2, by considering the deformed oscillator algebra $\mathfrak{h}_{z, 4}$ . From them, the different generalized systems of Buchdahl equations can be recovered through the nondeformed limit $z\to 0$ or by setting the additional $t$ -dependent coefficient $b_2(t) = 0$ , as shown in Figure 3:

Figure 3. The different generalized systems of Buchdahl equations.

DownLoad: Full-Size Img PowerPoint

As a general remark, it is worth observing that any perturbation at an arbitrary order in $z$ of the generalized Buchdahl equation (in particular, (5.13)) always admits a Lagrangian formulation, as actually happens with any scalar second-order ODE ^[34]. For example, restricting it to the case of perturbations of the type

$\begin{equation} \frac{{{{\rm{d}}}}^2 x}{{{{\rm{d}}}} t^2}\simeq\frac 3 x \left(\frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}\right)^2+\frac 1t \, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} + \phi_z(t, x)\, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t} , \end{equation}$

(9.1)

such that

$\lim\limits_{z\rightarrow 0}\phi_z(t, x) = 0,$

setting

$u = \frac{\partial \mathcal{L}}{\partial \dot{x}^2},$

a (nonstandard) Lagrangian $\mathcal{L}$ can be obtained as a solution of the first-order linear partial differential equation

$\begin{equation} \frac{\partial u}{\partial t}+\dot{x}\, \frac{\partial u}{\partial x}+\left(\frac{3}{x}\, \dot{x}^2+\left(\frac{1}{t}+\phi_z(t, x)\right)\dot{x}\right)\frac{\partial u}{\partial \dot{x}}+\left(\frac{6}{x}\, \dot{x}+\frac{1}{t}+\phi_z(t, x)\right)u = 0, \end{equation}$

(9.2)

which is deeply connected with the Jacobi multipliers ^[35]. Clearly, an admissible solution must satisfy the constraint that

$\mathcal{L}_0 = \lim\limits_{z\rightarrow 0}\mathcal{L}(z, t, x, \dot{x})$

provides a (nonstandard) Lagrangian for the undeformed Buchdahl equation (1.4). It can be easily verified that the Lagrangian

$\mathcal{L}_0 = t^3x^6\dot{x}^{-2}$

given in ^[6] is a particular solution of (9.2) for

$\phi_z(t, x) = 0,$

as well as the alternative Lagrangian

$\mathcal{L}_1 = \frac{ t^3x^6}{\dot{x}^{2}+kt^2x^6},$

where $k$ is an arbitrary nonzero constant^||.

^||In this context, we observe that the second Lagrangian $L_2 = \bigl(k \dot{x}^2t^3x^6+t \bigr)^{-1}$ given in ^[6] does not provide Eq (1.4) but the equation $\frac{{{{\rm{d}}}}^2 x}{{{{\rm{d}}}} t^2} = -\left(\frac 3 x \left(\frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}\right)^2+\frac 1t \, \frac{{{{\rm{d}}}} x}{{{{\rm{d}}}} t}\right)$ .

The solution procedure is valid for other types of scalar ordinary differential equations that can be expressed as LH systems based on the book algebra $\mathfrak{b}_2$ , encompassing, among others, complex Bernoulli equations with real parameter functions, some types of Lotka–Volterra systems and various oscillator systems, as well as their corresponding quantum deformations ^[14,15]. The same holds for equations leading to LH systems governed by the oscillator algebra $\mathfrak{h}_4$ . In this context, a physically relevant class of differential equations that deserves a deeper analysis in connection with the LH formalism is given by the three-dimensional Hamiltonians associated with metric tensors in (3+1) dimensions, in the specific context of integrable cosmological models ^[36].

Finally, concerning the extension of the method of exact solutions to other LH systems (and their corresponding quantum deformations) based on Lie algebras that contains $\mathfrak{b}_2$ as a subalgebra, let us mention that the remaining possibilities in the classification of ^[11,12] are the simple Lie algebra $\mathfrak{sl}(2, \mathbb{R})$ and the two-photon one $\mathfrak{h}_6\supset \mathfrak{h}_4\supset \mathfrak{b}_2$ . However, no exact solution is yet known to be obtainable for such LH systems, so that the LH approach considered here merely provides $t$ -independent constants of the motion and superposition rules ^[12,20,25], from which, eventually, the generic solution can be derived once a sufficient number of particular solutions has been determined. A detailed analysis of these further generalizations is currently in progress.

Author contributions

Rutwig Campoamor-Stursberg: conceptualization, methodology, investigation, and writing; Eduardo Fernández-Saiz: conceptualization, methodology, investigation, writing–review and editing; Francisco J. Herranz: methodology, investigation, software, and writing. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Rutwig Campoamor-Stursberg and Francisco J. Herranz have been partially supported by Agencia Estatal de Investigación (Spain) under the grant PID2023-148373NB-I00 funded by MCIN/AEI/10.13039/501100011033/FEDER, UE. Francisco J. Herranz acknowledges support by the Q-CAYLE Project funded by the Regional Government of Castilla y León (Junta de Castilla y León, Spain) and by the Spanish Ministry of Science and Innovation (MCIN) through the European Union funds NextGenerationEU (PRTR C17.I1). The authors also acknowledge the contribution of RED2022-134301-T funded by MCIN/AEI/10.13039/501100011033 (Spain).

Conflict of interest

Rutwig Campoamor-Stursberg and Francisco J. Herranz are the Guest Editors of the special issue "Applications of Lie group analysis to integrability and superintegrability" for AIMS Mathematics. Rutwig Campoamor-Stursberg and Francisco J. Herranz were not involved in the editorial review and the decision to publish this article. All authors declare no conflicts of interest in this paper.

Appendix

Symmetry generators of Eq (1.5)

The Lie point symmetries of the generalized Buchdahl equations are obtained using the standard Lie symmetry method ^[37].

Let us write

$A(x) = \int^x a(\xi) {\rm d}\xi$

and

$B(t) = \int^t b(\tau) {\rm d}\tau.$

The Lie symmetry generators are given by

$\begin{equation*} \begin{split} Y_1& = {\rm e}^{A(x)}\frac{\partial}{\partial x}, \qquad Y_2 = {\rm e}^{A(x)}\left(\int {\rm e}^{-A(x)}{\rm d}x\right)\frac{\partial}{\partial x}, \\[2pt] Y_3& = {\rm e}^{-B(t)}\frac{\partial}{\partial t}, \qquad Y_4 = {\rm e}^{-B(t)}\left(\int {\rm e}^{B(t)}{\rm d}t\right)\frac{\partial}{\partial t}, \\[2pt] Y_5 & = {\rm e}^{A(x)}\left(\int {\rm e}^{B(t)}{\rm d}t\right)\frac{\partial}{\partial x}, \qquad Y_6 = {\rm e}^{-B(t)}\left(\int {\rm e}^{-A(x)}{\rm d}x\right)\frac{\partial}{\partial t}, \\[2pt] Y_7& = {\rm e}^{-B(t)} \left( \int {\rm e}^{-A(x)}{\rm d}x \right)\left(\int {\rm e}^{B(t)}{\rm d}t\right)\frac{\partial}{\partial t}+ {\rm e}^{A(x)} \left(\int {\rm e}^{-A(x)}{\rm d}x\right)^2 \frac{\partial}{\partial x}, \\[2pt] Y_8& = {\rm e}^{-B(t)}\left(\int {\rm e}^{B(t)}{\rm d}t\right)^2\frac{\partial}{\partial t}+{\rm e}^{A(x)}\left( \int {\rm e}^{-A(x)}{\rm d}x \right)\left(\int {\rm e}^{B(t)}{\rm d}t\right)\frac{\partial}{\partial x}. \end{split} \end{equation*}$

The corresponding nontrivial commutators are

$\begin{equation*} \begin{split} \left[Y_1, Y_2\right]& = Y_1, \qquad \left[Y_1, Y_6\right] = Y_3, \qquad \left[Y_1, Y_7\right] = Y_4+2Y_2, \qquad \left[Y_1, Y_8\right] = Y_5, \\[2pt] \left[Y_2, Y_5\right]& = -Y_5, \quad\, \left[Y_2, Y_6\right] = Y_6, \qquad \left[Y_2, Y_7\right] = Y_7, \qquad \left[Y_3, Y_4\right] = Y_3, \qquad \left[Y_3, Y_5\right] = Y_1, \\[2pt] \left[Y_3, Y_7\right]& = Y_6, \qquad \left[Y_3, Y_8\right] = 2Y_4+Y_2, \qquad \left[Y_4, Y_5\right] = Y_5, \qquad \left[Y_4, Y_6\right] = -Y_6, \\[2pt] \left[Y_4, Y_8\right]& = Y_8, \qquad \left[Y_5, Y_6\right] = Y_4-Y_2, \qquad \ \, \left[Y_5, Y_7\right] = Y_8, \qquad \left[Y_6, Y_8\right] = Y_7, \end{split} \end{equation*}$

which are easily seen to generate a Lie algebra isomorphic to $\mathfrak{sl}(3, \mathbb{R})$ , implying that the equation is linearizable via a point transformation ^[10,37]. We further observe that two-dimensional Lie point symmetry algebras of the canonical types $L_{2, 1}^{\rm I}$ , $L_{2, 1}^{\rm II}$ , $L_{2, 2}^{\rm I}$ , and $L_{2, 2}^{\rm II}$ (see ^[10] for details) that also imply linearization are, respectively, generated by the following vector fields:

$\begin{equation*} \begin{split} L_{2, 1}^{\rm I}\!: & \quad Y_1, \ Y_3, \quad \left[Y_1, Y_3\right] = 0, \quad\ \delta = -{\rm e}^{A(t)}{\rm e}^{-B(t)}\neq 0 , \\[2pt] L_{2, 1}^{\rm II}\!: & \quad Y_1, \ Y_5, \quad \left[Y_1, Y_5\right] = 0, \quad\ \delta = 0, \\ L_{2, 2}^{\rm I}\!: & \quad Y_2, \ Y_6, \quad \left[Y_2, Y_6\right] = Y_6, \quad \delta = -{\rm e}^{A(x)}{\rm e}^{-B(t)}\left(\int {\rm e}^{-A(x)}{\rm d}x\right)^2\neq 0 , \\[2pt] L_{2, 2}^{\rm II}\!: & \quad Y_1, \ Y_2, \quad \left[Y_1, Y_2\right] = Y_1, \quad \delta = 0 , \end{split} \end{equation*}$

where

$\delta = \det \left(\begin{array}[c]{cc} \xi_1 & \eta_1\\ \xi_2 & \eta_2 \end{array}\right)$

and

$Z_i = \xi_i \frac{\partial}{\partial t}+ \eta_i \frac{\partial}{\partial x}$

are the infinitesimal symmetry generators for $i = 1, 2$ .

The point symmetries of Eqs (5.4), (5.9), and (5.13) are computed similarly. On the other hand, equations of the type in (9.1) admit point symmetries of the type

$Z = \beta_1 \frac{\partial}{\partial t}+\left(\frac{\alpha_1}{ x^3}+\alpha_2x \right) \frac{\partial}{\partial x}$

for perturbation terms of the form

$\begin{equation*} \phi_z(t, x) = \frac{1}{t}\Phi\!\left(z, \frac{1}{\alpha_2}\, t^{\frac{-4\alpha_2}{\beta_1}}\bigl(\alpha_2x^4+\alpha_1 \bigr)\right). \end{equation*}$

References

[1]	H. A. Buchdahl, A relativistic fluid sphere resembling the Emden polytrope of index 5, Astrophys. J., 140 (1964), 1512–1516. https://doi.org/10.1086/148055 doi: 10.1086/148055
[2]	H. Stephani, D. Kramer, M. Maccallum, C. Hoenselears, E. Herldt, Exact solutions to Einstein's fields equations, Cambridge University Press, 1995.
[3]	L. G. S. Duarte, S. E. S. Duarte, L. A. C. P. da Mota, J. E. F. Skea, Solving second-order ordinary differential equations by extending the Prelle-Singer method, J. Phys. A, 34 (2001), 3015–3024. https://doi.org/10.1088/0305-4470/34/14/308 doi: 10.1088/0305-4470/34/14/308
[4]	L. G. S. Duarte, L. A. C. P. da Mota, Finding elementary first integrals for rational second order ordinary differential equations, J. Math. Phys., 50 (2009), 013514. https://doi.org/10.1063/1.3050281 doi: 10.1063/1.3050281
[5]	V. K. Chandrasekar, M. Senthilvelan, M. Lakshmanan, On the complete integrability and linearization of certain second-order nonlinear ordinary differential equations, Proc. R. Soc. A, 461 (2005), 2451–2477. https://doi.org/10.1098/rspa.2005.1465 doi: 10.1098/rspa.2005.1465
[6]	J. L. Cieśliński, T. Nikiciuk, A direct approach to the construction of standard and non-standard Lagrangians for dissipative-like dynamical systems with variable coefficients, J. Phys. A, 43 (2010), 175205. https://doi.org/10.1088/1751-8113/43/17/175205 doi: 10.1088/1751-8113/43/17/175205
[7]	E. L. Ince, Integration of ordinary differential equations, Oliver and Boyd, 1939.
[8]	E. Kamke. Differentialgleichungen–Lösungsmethoden und Methoden. Band 1, Geest und Portig, 1959.
[9]	R. Campoamor-Stursberg, Low dimensional Vessiot-Guldberg-Lie algebras of second-order ordinary differential equations, Symmetry, 8 (2016), 15. https://doi.org/10.3390/sym8030015 doi: 10.3390/sym8030015
[10]	F. M. Mahomed, Symmetry group classification of ordinary differential equations: survey of some results, Math. Meth. Appl. Sci., 30 (2007), 1995–2012. https://doi.org/10.1002/mma.934 doi: 10.1002/mma.934
[11]	A. Ballesteros, A. Blasco, F. J. Herranz, J. de Lucas, C. Sardón, Lie–Hamilton systems on the plane: properties, classification and applications, J. Differ. Equations, 258 (2015), 2873–2907. https://doi.org/10.1016/j.jde.2014.12.031 doi: 10.1016/j.jde.2014.12.031
[12]	A. Blasco, F. J. Herranz, J. de Lucas, C. Sardón, Lie–Hamilton systems on the plane: applications and superposition rules, J. Phys. A, 48 (2015), 345202. https://doi.org/10.1088/1751-8113/48/34/345202 doi: 10.1088/1751-8113/48/34/345202
[13]	J. de Lucas, C. Sardón, A guide to Lie systems with compatible geometric structures, World Scientific, 2020. https://doi.org/10.1142/q0208
[14]	R. Campoamor-Stursberg, E. Fernández-Saiz, F. J. Herranz, Solutions by quadratures of complex Bernoulli differential equations and their quantum deformation, Axioms, 13 (2024), 26. https://doi.org/10.3390/axioms13010026 doi: 10.3390/axioms13010026
[15]	E. Fernández-Saiz, R. Campoamor-Stursberg, F. J. Herranz. Generalized time-dependent SIS Hamiltonian models: exact solutions and quantum deformations, J. Phys., 2667 (2023), 012083. https://doi.org/10.1088/1742-6596/2667/1/012083 doi: 10.1088/1742-6596/2667/1/012083
[16]	S. Lie, G. Scheffers. Vorlesungen über continuierliche Gruppen mit geometrischen und anderen Anwendungen, Teubner, 1883.
[17]	P. Winternitz, Lie groups and solutions of nonlinear differential equations, In: K. B. Wolf, Nonlinear phenomena, Springer, 1983,263–305. https://doi.org/10.1007/3-540-12730-5_12
[18]	J. F. Cariñena, J. Grabowski, G. Marmo, Lie–Scheffers systems: a geometric approach, Bibliopolis, 2000.
[19]	R. Campoamor-Stursberg, E. Fernández-Saiz, F. J. Herranz, Exact solutions and superposition rules for Hamiltonian systems generalizing time-dependent SIS epidemic models with stochastic fluctuations, AIMS Math., 8 (2023), 24025–24052. https://doi.org/10.3934/math.20231225 doi: 10.3934/math.20231225
[20]	A. Ballesteros, R. Campoamor-Stursberg, E. Fernández-Saiz, F. J. Herranz, J. de Lucas, Poisson–Hopf deformations of Lie-Hamilton systems revisited: deformed superposition rules and applications to the oscillator algebra, J. Phys. A, 54 (2021), 205202. https://doi.org/10.1088/1751-8121/abf1db doi: 10.1088/1751-8121/abf1db
[21]	M. Abramowitz, I. A. Stegun, Handbook of mathematical functions with formulas, graphs and mathematical tables, Department of Commerce, 1964.
[22]	W. Gröbner, H. Knapp, Contributions to the method of Lie series, Bibliographisches Institut, 1967.
[23]	V. Chari, A. Pressley, A guide to quantum groups, Cambridge University Press, 1994.
[24]	E. Abe, Hopf algebras, Cambridge University Press, 2004.
[25]	A. Ballesteros, R. Campoamor-Stursberg, E. Fernández-Saiz, F. J. Herranz, J. de Lucas, Poisson–Hopf algebra deformations of Lie-Hamilton systems, J. Phys. A, 51 (2018), 065202. https://doi.org/10.1088/1751-8121/aaa090 doi: 10.1088/1751-8121/aaa090
[26]	I. Vaisman, Lectures on the geometry of Poisson manifolds, Birkhäuser Verlag, 1994.
[27]	R. S. Palais, A global formulation of the Lie theory of transformation groups, Memoirs Amer. Math. Soc., 1957. https://doi.org/10.1090/memo/0022 doi: 10.1090/memo/0022
[28]	H. J. Sussmann, Orbits of families of vector fields and integrability of distributions, Trans. Amer. Math. Soc., 180 (1973), 171–188. https://doi.org/10.2307/1996660 doi: 10.2307/1996660
[29]	A. Ballesteros, F. J. Herranz, Lie bialgebra quantizations of the oscillator algebra and their universal $R$ -matrices, J. Phys. A, 29 (1996), 4307–4320. https://doi.org/10.1088/0305-4470/29/15/006 doi: 10.1088/0305-4470/29/15/006
[30]	A. Ballesteros, F. J. Herranz, M. A. del Olmo, C. M. Pereña, M. Santander, Non-standard quantum (1+1) Poincaré group: a $T$ -matrix approach, J. Phys. A, 28 (1995), 7113–7125. https://doi.org/10.1088/0305-4470/28/24/012 doi: 10.1088/0305-4470/28/24/012
[31]	A. Ballesteros, F. J. Herranz, J. Negro, Boson representations, non-standard quantum algebras and contractions, J. Phys. A, 30 (1997), 6797–6809. https://doi.org/10.1088/0305-4470/30/19/018 doi: 10.1088/0305-4470/30/19/018
[32]	A. Ballesteros, S. M. Chumakov, On the spectrum of a Hamiltonian defined on $su_q(2)$ and quantum optical models, J. Phys. A, 32 (1999), 6261–6269. https://doi.org/10.1088/0305-4470/32/35/305 doi: 10.1088/0305-4470/32/35/305
[33]	A. Ballesteros, O. Civitarese, F. J. Herranz, M. Reboiro, Fermion-boson interactions and quantum algebras, Phys. Rev. C, 66 (2002), 064317. https://doi.org/10.1103/PhysRevC.66.064317 doi: 10.1103/PhysRevC.66.064317
[34]	R. M. Santilli, Foundations of theoretical mechanics I. The inverse problem in Newtonian mechanics, Springer, 1978.
[35]	M. C. Nucci, P. G. L. Leach, Jacobi's last multiplier and Lagrangians for multidimensional systems, J. Math. Phys., 49 (2008), 073517. https://doi.org/10.1063/1.2956486 doi: 10.1063/1.2956486
[36]	K. Rosquist, C. Uggla, Killing tensors in two-dimensional space-times with applications to cosmology, J. Math. Phys., 32 (1991), 3412–3422. https://doi.org/10.1063/1.529455 doi: 10.1063/1.529455
[37]	P. J. Olver, Applications of Lie groups to differential equations, Springer, 1986.

Reader Comments

Your name:*

Email:*
© 2025 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(95) PDF downloads(23) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(3) / Tables(2)

AIMS Mathematics

Generalized Buchdahl equations as Lie–Hamilton systems from the "book" and oscillator algebras: quantum deformations and their general solution

Related Papers:

Abstract

1. Introduction

2. The generalized Buchdahl equation as an LH system

2.1. The general solution as an LH system

3. Applications to particular generalized Buchdahl equations

3.1. The classical Buchdahl equation

3.2. Case with $a(x)=1/x$ and an arbitrary ${b(t)}$

3.3. Case with $a(x)={\alpha}/x$ $({\alpha}\ne 1)$ and an arbitrary $b(t)$

3.4. Case with $a(x)={\alpha} x^{r}$ $({r}\ne -1)$ and an arbitrary $b(t)$

3.5. Nonexistence of $\mathfrak{b}_2$ -based extensions of the generalized Buchdahl equation

4. Deformed generalized Buchdahl equation from the quantum book algebra

4.1. Quantum book algebra and deformed book LH systems

4.2. Deformed generalized Buchdahl equation and its general solution

5. Applications to particular deformed Buchdahl equations

5.1. Deformation of the proper Buchdahl equations

5.2. Deformed case with $a(x)=1/x$ and an arbitrary ${b(t)}$

5.3. Deformed case with $a(x)={\alpha}/x$ $({\alpha}\ne 1)$ and an arbitrary $b(t)$

6. Extending the generalized Buchdahl equation from the oscillator algebra

7. Deformed generalized Buchdahl equation from the quantum oscillator algebra

7.1. Quantum oscillator algebra and deformed oscillator LH systems

7.2. Deformed extended generalized Buchdahl equation and its general solution

8. Higher-dimensional deformed generalized Buchdahl equations

9. Concluding remarks

Author contributions

Use of Generative-AI tools declaration

Acknowledgments

Conflict of interest

Appendix

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Generalized Buchdahl equations as Lie–Hamilton systems from the "book" and oscillator algebras: quantum deformations and their general solution

Related Papers:

Abstract

1. Introduction

2. The generalized Buchdahl equation as an LH system

2.1. The general solution as an LH system

3. Applications to particular generalized Buchdahl equations

3.1. The classical Buchdahl equation

3.2. Case with a(x)=1/x a(x)=1/x and an arbitrary b(t) {b(t)}

3.3. Case with a(x)=α/x a(x)={\alpha}/x (α≠1) ({\alpha}\ne 1) and an arbitrary b(t) b(t)

3.4. Case with a(x)=αxr a(x)={\alpha} x^{r} (r≠−1) ({r}\ne -1) and an arbitrary b(t) b(t)

3.5. Nonexistence of b2 \mathfrak{b}_2 -based extensions of the generalized Buchdahl equation

4. Deformed generalized Buchdahl equation from the quantum book algebra

4.1. Quantum book algebra and deformed book LH systems

4.2. Deformed generalized Buchdahl equation and its general solution

5. Applications to particular deformed Buchdahl equations

5.1. Deformation of the proper Buchdahl equations

5.2. Deformed case with a(x)=1/x a(x)=1/x and an arbitrary b(t) {b(t)}

5.3. Deformed case with a(x)=α/x a(x)={\alpha}/x (α≠1) ({\alpha}\ne 1) and an arbitrary b(t) b(t)

6. Extending the generalized Buchdahl equation from the oscillator algebra

7. Deformed generalized Buchdahl equation from the quantum oscillator algebra

7.1. Quantum oscillator algebra and deformed oscillator LH systems

7.2. Deformed extended generalized Buchdahl equation and its general solution

8. Higher-dimensional deformed generalized Buchdahl equations

9. Concluding remarks

Author contributions

Use of Generative-AI tools declaration

Acknowledgments

Conflict of interest

Appendix

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

3.2. Case with $a(x)=1/x$ and an arbitrary ${b(t)}$

3.3. Case with $a(x)={\alpha}/x$ $({\alpha}\ne 1)$ and an arbitrary $b(t)$

3.4. Case with $a(x)={\alpha} x^{r}$ $({r}\ne -1)$ and an arbitrary $b(t)$

3.5. Nonexistence of $\mathfrak{b}_2$ -based extensions of the generalized Buchdahl equation

5.2. Deformed case with $a(x)=1/x$ and an arbitrary ${b(t)}$

5.3. Deformed case with $a(x)={\alpha}/x$ $({\alpha}\ne 1)$ and an arbitrary $b(t)$