1.
Introduction
Goncharov was the first to find relations between the Grassmannian complex of projective configurations and Bloch-Suslin complex for weight n=2, and to the Goncharov's motivic complex for weight n=3 (see [3]). This idea leads to the remarkable proof of Zagier's conjecture for weights n=2,3 (see [4]). On the other hand, Cathelineau introduced the tangent form of the Bloch-Suslin complex and provided some suggestions about the tangent form of Goncharov's complex (see [1]).
The main idea of this article is to view geometric features of tangent groups, TB2(F) and TB3(F), where TB2(F) is the tangent form of Bloch group B2(F) (see [1]), and TB3(F) is the tangent form of Goncharov's group B3(F) (see §3.2) for any field F. To accomplish this task, we define morphisms τ20,ε, τ21,ε, (between the Grassamannian complex of geometric configurations and tangent to the Bloch-Suslin complex) and τ30,ε, τ31,ε, τ32,ε (between the Grassamannian complex of geometric configurations and tangent to the Goncharov's complex) for weights n=2,3. Due to these morphisms, we get diagrams which are shown to be commutative (main result Theorem 3.7). The major techniques for showing our main result, are to invoke combinatorics in the symmetric group S6 and to rewrite triple ratios in the product of two projected cross-ratios. Here, we use permutations of symmetric group S6 in the alternation sums. The alternation sum Alt6 in our map τ32,ε has 6! terms, but due to inversion and cyclic symmetry, it reduces to 6!/(3!)=120 terms.
The cross ratio identity over a field F was first defined by Siegel (see [6]). To view the geometry of configurations in tangent groups, it is required to introduce an analogue to the Siegel cross-ratio identity for the determinants of matrices of order 2×2 (see Lemma 2.1) that can also be extended to 3×3 determinants of matrices. These analogues and Lemma 2.1 enabled us to produce the analogues of cross-ratios and triple ratios.
On the basis of these analogues, we find morphisms between the Grassmannian subcomplex C∗(AnF[ε]2,d) and tangent to the Bloch-Suslin and to Goncharov complexes (see §3.1 and §3.2). The proof of the main result requires projected five term relation in TB2(F). To serve this purpose, we prove the existence of the projected five term relation in TB2(F) (see Lemma 3.4). This relation is also an analogue of Goncharov's projected five term relation in B2(F).
In §3.2, we define the tangent group TB3(F) which was first hypothetically defined in §9 of [1]. On the basis of our definition, we mimic construction of TB3(F) with the F-vector space βD3(F) ([5]) and reproduce Cathelineau's 22-term functional equation for TB3(F).
2.
Materials and method
Let F be a field of characteristic 0. For ν≥1, we denote the νth truncated polynomial ring over F by F[ε]ν:=F[ε]/εν. Further define Cm(AnF[ε]ν) as a free abelian group generated by m generic points in AnF[ε]ν (an n dimensional affine space over F[ε]ν). Here, we are not considering degenerate points and are also assuming that no two points coincide and no three points lie on a line. Now for n=2 and ν=2, any ηi=(aibi)∈A2F∖{(00)} and ηi,ε:=(ai,εbi,ε)∈A2F, we put η∗i=(ai+ai,εεbi+bi,εε)=(aibi)+(ai,εbi,ε)ε=ηi+ηi,εε and define a boundary map
Let ω∈V∗2 be a volume element formed in V2:=A2F and Δ(ηi,ηj)=⟨ω,ηi∧ηj⟩, where ηi,ηj∈A2F. Here we define
where
More generally for ν=n+1, we have
and we get
where
Consider the Siegel cross-ratio identity for the 2×2 determinants of four vectors in C4(A2F) (see [3], [6])
With the above notation, an analogue to the Siegel cross-ratio identity turns out to be true for A2F[ε]n+1, and we can extract further results which are essential for the proof of our main results. Throughout this section we will assume that Δ(ηi,ηj)≠0 for i≠j.
Lemma 2.1. For (η∗0,η∗1,η∗2,η∗3)∈C4(A2F[ε]n+1), we have
where
for
Proof. For r=0,…,n, we can write η∗=(∑r≥0ηrεr∑r≥0η′rεr) and m∗=(∑r≥0mrεr∑r≥0m′rεr).
Now we have
Hence
and similarly for Δ(η∗0,η∗2)Δ(η∗1,η∗3) and Δ(η∗0,η∗3)Δ(η∗1,η∗2). Hence we use the validity of (2.1) to deduce the analogue for Δ(η∗i,η∗j)'s in place of Δ(ηi,ηj) passing from the ring F[[ε]] of power series to a truncated polynomial ring, say to F[ε]n+1.
For the special cases; we find the identity (2.1) for n=0, while for n=1 we have the following identity which will be used extensively below:
if we write
then (2.3) can be more concisely written as
2.1. Cross-ratio in F[ε]ν
Now we have enough tools to find the cross-ratios of four points over the truncated polynomial ring F[ε]ν. The identity (2.2) of Lemma 2.1 enables us to compute this ratio in F[ε]ν for ν=n+1. First we define the cross-ratio of four points (η∗0,…,η∗3)∈C4(A2F[ε]n+1) as
We also expand r(η∗0,…,η∗3) as a truncated polynomial over F[ε]n+1
After truncating this for n=0, one gets
If we truncate (2.4) for n=1 then the coefficient of ε0 will remain the same as for n=0, thus we only need to compute the coefficient of ε in the following way:
After considering (η∗0,…,η∗3)∈C4(A2F[ε]2) in a generic position, we get
If a≠0∈F then 1a+bε=1a−ba2ε∈F[ε]2 (this is the same as the inversion relation in TB2(F) discussed later in §3.3).
Let us simplify the above obtained result by multiplying the inverses of denominators and separate the coefficients of ε0 and ε. The coefficient of ε becomes
Let us trancate it for n=2, i.e., (η∗0,…,η∗3)∈C4(A2F[ε]3). To make computations easy, we write (ηi,ηj) instead of Δ(ηi,ηj)
simplify and then separate the coefficients of ε0, ε1 and ε2. The coefficients of ε0 and ε1 are the same as we computed in (2.5) and (2.6) respectively, and the coefficient of ε2 is
Remark 2.2. The computation of coefficient of εn, which is rεn(η∗0,…,η∗3), in the truncated polynomial (2.4) will give us the following:
where Δ(ηi,ηj)≠0 for i≠j and (η∗0,…,η∗3)∈C4(A2F[ε]n+1).
2.2. Triple-ratio in F[ε]ν
First, we define a triple-ratio r3:C6(A3F)→F as (see [4])
where C6(A3F) is a free abelian group generated by the configurations of six points in A3F and A3F is a three dimensional affine space over a field F. Here, we will discuss triple-ratio (generalized cross-ratio) of 6 points, i.e., (η∗0,…,η∗5)∈C6(A3F[ε]ν) for ν=n+1. The calculations in triple-ratio are similar to the cross-ratio of 4 points (η∗0,…,η∗3)∈C4(A2F[ε]ν). Let's consider ν=2 since the other cases are not required.
We take (η∗0,…,η∗5)∈C6(A3F[ε]2), for any η∗i∈(η∗0,…,η∗5)
where Δ(ηi,ηj,ηk) is a 3×3-determinant,
and
As we can expand, we also get the equalities.
for Δ(ηi,ηj,ηj)≠0, the multiplicative inverse of Δ(η∗i,η∗j,η∗k) is −1Δ(ηi,ηj,ηj)−Δ(η∗i,η∗j,η∗k)εΔ(ηi,ηj,ηj)2ε and from now on, If simplify the previous equalities, we may use (η∗iη∗jη∗k) instead of Δ(η∗i,η∗j,η∗k) unless specified.
Simplifying the above and separating the coefficients of ε0 and ε1, we see that the coefficient of ε0 is the triple-ratio of six points (η0,…,η5)∈C6(A3F) and the coefficient of ε is the following:
2.3. Tangent to Bloch group([1])
Let F be an algebraically closed field of characteristic 0. Let F[ε]2=F[ε]/ε2 be the truncated polynomial ring (or a ring of dual numbers) for an arbitrary field F. We can define an F×-action in F[ε]2 as follows. For λ∈F×,
we denote this action by ⋆, so we use λ⋆(ϕ+ϕ′ε)=ϕ+λϕ′ε.
The tangent group TB2(F) is defined as a Z-module generated by the combinations [ϕ+ϕ′ε]−[ϕ]∈Z[F[ε]2],(ϕ,ϕ′∈F): For which we put shorthand ⟨ϕ;ϕ′]:=[ϕ+ϕ′ε]−[ϕ] and quotient by the subetaoup generated by the following relation
where
and
Remark 2.3. See [1] for a discussion of TB2(F), where the definition of TB2(F) was justified using Lemma 3.1 of [1]
We give a list of relations in TB2(F) from [1].
(1) The two-term relation:
(2) The inversion relation:
(3) Four-term relation:
If we use ϕ′=ϕ(1−ϕ) and ψ′=ψ(1−ψ) then (2.9) becomes four-term relation (see [1]).
where ϕ,ψ≠0,1,ϕ≠ψ.
The following map is an infinitesimal analogue of δ (defined in [4]) and ∂ (defined in [1] and [5]), Cathelineau called it the tangential map.
with
First term of the complex is in degree one and ∂ε has a degree +1.
Note that we get the direct sum of two spaces on the right side.
3.
Main results and discussion
3.1. Dilogarithmic bicomplexes
In this section, we will connect the Grassmannian bicomplex to the tangent to the Bloch-Suslin complex.
We will use the following notations throughout this section
and we will assume that Δ(ηi,ηj)≠0 (as we often want to divide by such determinants).
Let Cm(A2F[ε]2) be the free abelian group generated by the configuration of m points in A2F[ε]2, where A2F[ε]2 is defined as an affine space over F[ε]2. The configurations of m points in A2F[ε]2 are 2-tuples of vectors over F[ε]2 modulo GL2(F[ε]2). In this case, one can write the Grassmannian complex as follows:
where η∗i=(ϕi+ϕi,εεψi+ψi,εε)=(ϕiψi)+(ϕi,εψi,ε)ε=ηi+ηi,εε and ϕi,ψi,ϕi,ε,ψi,ε∈F, (ϕiψi)≠(00).
The diagram below gives the relation between Grassmannian complex and tangent to the Bloch-Suslin complex.
where
τ20,ε can be written as a sum of two morphisms
and
where
and
Furthermore, we put
where r(η0,…,η3) and rε(η∗0,…,η∗3) are the coefficients of ε0 and ε1 respectively.
Our maps τ20,ε and τ21,ε are based on ratios of determinants and cross-ratios respectively, so there is enough evidence that they are well-defined. This independence can be seen directly through the definition of maps.
We will also use shorthand (ηiηj) instead of Δ(ηi,ηj) wherever we find less space to accommodate long expressions.
Now we calculate,
where
Remark 3.1. The F×-action of TB2(F) lifts to an F×-action on C4(A2F[ε]2) in the obvious way:
The F×-action is defined above for F[ε]2 induces an F×-action in A2F[ε]2 diagonally as
Lemma 3.2. The diagram (4.2a) is commutative.
Proof. The proof follows directly from calculation.
In the remainder of this section we prove that the following diagram is a bicomplex.
To prove that the above diagram is bicomplex, we will give the next results.
Proposition 3.3. The map C4(A3F[ε]2)d′→C3(A2F[ε]2)τ20,ε→(F⊗F×)⊕(⋀2F) is zero.
Proof. Let ω∈detV∗3 be the volume form in three-dimensional vector space V3, i.e., Δ(ηi,ηj,ηk)=⟨ω,ηi∧ηj∧ηk⟩. Then Δ(ηi,⋅,⋅) is a volume form in V3/⟨ηi⟩. Use
where
We can directly compute τ20,ε∘d′ which gives zero.
The following result is very important for proving Theorem 3.7. Through this result we are able to see the projected-five term relation for TB2(F).
Lemma 3.4. Let x∗0,…,x∗4∈P2F[ε]2 be 5 points in generic position. Then
where x∗i=xi+x′iε and xi,x′i∈P2F
Proof. Consider five points y0,…,y4∈P1F in generic position. We can write the five-term relation in terms of cross-ratios in B2(F) as (see Proposition 4.5 (2)b in [2]):
These five points depend on 2 parameters modulo the action of PGL2(F), whose action on P1F is 3-fold transitive. So we can express these five points with two variables modulo this action as, we can put
Then we can get the five-term relation in two variables (by using inversion relation in the last two terms).
Now we consider five points y∗0,…,y∗4∈P1F[ε]2, in generic position, where y∗i=yi+y′iε for yi,y′i∈P1F. A generic 2×2 matrix in PGL2(F[ε]2) depends on 6=2(2×2)−2(1) parameters, while each point in P1F[ε]2 depends on 2 parameters, so these five points in P1F[ε]2 modulo the action of PGL2(F[ε]2) have 4 parameters. Now we can express them by using four variables we choose:
We calculate all possible determinants which are the following:
For y∗0,…,y∗4∈P1F[ε]2, we can write the following expression in TB2(F)
If we expand the above expression and substitute all the determinants in it, we will get the following expression in two variables.
From (3.2) it is clear that the above is the LHS of the five-term relation in TB2(F). We first show underneath, that this claim is valid, then later we reduce it to the five-term relation.
Consider x0,…,x4∈P2F in generic position. These five points also depend on 2 parameters modulo the action of PGL2(F), so we can express these five points in terms of two variables by the following choice:
We compute all possible 3×3 determinants of the above and put them in the expansion of the following:
we get the following expression in two variables
clearly the above is the LHS of one version of five-term relation in B2(F).
Since by assumption x∗0,…,x∗4∈P2F[ε]2 are 5 points in generic position, we can express them as modulo the action of PGL3(F[ε]2) into 4 parameters, then we can choose these points in terms of four variables in the following way:
We compute all possible 3×3 determinants and substitute them in an expansion of the following:
we get
which is the five-term expression in TB2(F) up to invoking the inversion relation for the last two terms, which also holds in TB2(F).
Lemma 3.4 indicates that we now have the projected five-term relation for TB2(F) and this relation will help us to prove the commutative diagram for weight n=3 in the tangential case.
Proposition 3.5. The map C5(A3F[ε]2)d′→C4(A2F[ε]2)τ21,ε→TB2(F) is zero.
Proof. We can directly calculate τ21ε∘d′.
The above is the projected five term relation in TB2(F) by Lemma 3.4.
Theorem 3.2 shows that the diagram (4.2a) is commutative and Propositions 3.3 and 3.5 shows that we have formed a bicomplex between the Grassmannian complex and Cathelineau's tangent complex.
3.2. Trilogarithmic complexes
We have already discussed the tangent group (or Z-module) TB2(F) over F[ε]2 in §3.1. In this section we will discuss group TB3(F) and its functional equations and will connect Grassmannian complex and tangential complex to Goncharov complex.
3.2.1. The Abelian group TB3(F)
The Z-module TB3(F) over F[ε]2 is defined as the group generated by:
and quotient by the kernel of the following map
Now we say that ⟨a;b]3∈TB3(F)⊂Z[F[ε]2]/ker∂ε,3.
We have the following relations which are satisfied in TB3(F).
(1) The three-term relation.
(2) The inversion relation
(3) The Cathelineau 22-term relation ([2])
This relation J(a,b,c) for the indeterminates a,b,c can be written in this way:
where
while τ(a,b) is defined via five term relation and ⋆-action. We take ⟨xi;xi,ε]3 with coefficient 11−xi which is handled by ⋆-action.
and
Then we can calculate Cathelineau's 22-term expression by substituting all values in (3.4).
For the special condition aε=a(1−a), bε=b(1−b) and cε=c(1−c), this 22-term expression becomes zero in TB3(F).
One can write the following complex for TB3(F).
3.2.2. Morphisms between Grassmannian and tangent to Goncharov's complex in weight 3
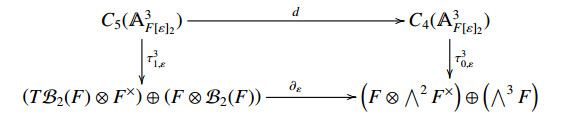
In this section, we will introduce morphisms between the Grassmannian complex and the tangent to Goncharov's complex for weight n=3. Consider the following diagram
Here we define the projected cross-ratio
which can be further simplifed to
where
where the morphisms between the two complexes are defined as follows:
and
where
and
the map ∂ε is defined as
and
Theorem 3.6. Diagram (4.3a), i.e.,
is commutative, i.e., τ30,ε∘d=∂ε∘τ31,ε
Proof. First we divide the map τ30,ε=τ(1)+τ(2) then calculate τ(1)∘d(η∗0,…,η∗4)
Now, we expand the inner sum that contains 12 terms and pass them through the this alternation to the inner sum, gives us 60 different terms overall. We collect terms involving the same Δ(η∗i,η∗j,η∗k)Δ(ηi,ηj,ηk)⊗⋯ together for calculation purposes. On the other hand the second part of the map is:
The other side of the proof requires tedious computations. For the calculation of ∂ε∘τ31,ε we will use the short hand (η∗iη∗jη∗k)ε for Δ(η∗i,η∗j,η∗k)ε and (ηiηjηk) for Δ((ηi,ηj,ηk). First we write ∂ε∘τ31,ε(η∗0,…,η∗4) by using the definitions above.
then we divide ∂ε=∂(1)+∂(2). The first part ∂(1)∘τ31,ε(η∗0,…,η∗4) is
The second part ∂(2)∘τ31,ε(η∗0,…,η∗4) is
then we calculate bεa and bε1−a. i.e., all the values of the form rε(η∗0|η∗1,η∗2,η∗3,η∗4)r(η0|η1,η2,η3,η4) and rε(η∗0|η∗1,η∗2,η∗3,η∗4)1−r(η0|η1,η2,η3,η4). By using formula (2.6) we get
Similarly, we can find this ratio for each value of i=0,…,4. Now use formula (2.6) with the identities (2.1) and (2.3);
After calculating all these values, expand the sums (3.9) and (3.10) and put all values that we have calculated above. For instance, let us calculate (3.9). In this sum we have a large number of terms, so we group them in a suitable way. First collect all the terms involving (η∗0η∗1η∗2)ε(η0η1η2)⊗⋯, we find that there are 6 different terms with coefficient -3 involving (η∗0η∗1η∗2)ε(η0η1η2)⊗⋯
There are exactly 10 possible terms of (η∗iη∗jη∗k)ε(ηiηjηk). Compute all of them individually. We will see that each will have the coefficient −3 that will be cancelled by −13 in (3.9) and then combine 60 different terms with 6 in a group of the same (η∗iη∗jη∗k)ε(ηiηjηk), write in the sum form then we will note that it will be the same as (3.7).
Computation for the second part is relatively easy and direct. We need to put all values of the form rε(η∗0|η∗1,η∗2,η∗3,η∗4)r(η0|η1,η2,η3,η4) and rε(η∗0|η∗1,η∗2,η∗3,η∗4)1−r(η0|η1,η2,η3,η4) in (3.10), expand the sums, use a∧a=0 modulo 2 torsion. Here we will have simplified result which can be recombined in the sum notation which will be the same as (3.8).
Theorem 3.7. The following diagram (4.3a), i.e.,
is commutative i.e., τ32,ε∘∂ε=d∘τ31,ε
Proof. The map τ32,ε gives 720 terms and due to symmetry (cyclic and inverse) we find 120 different ones (up to the inverse). By definition, we have
For convenience, and similar to our previous conventions, we will abbreviate our notation by dropping Δ and commas.
We need to compute the value of r3,ε(η∗0…η∗5)r3(η0…η5) which is
Formula (3.11) can also be written as
We will consider here only the first part of the above relation.
Further,
We use the even cycle (η0η1η2)(η3η4η5) (or (η∗0η∗1η∗2)(η∗3η∗4η∗5)) to obtain
We can also use here the symmetry
since
and similar for the others as well so that (3.12) will be
If we apply the odd permutation (η3η4) (or (η∗3η∗4)), then we have
Again apply the odd permutation (η0η3) (or (η∗0η∗3))
but up to 2-torsion, which we ignore here, we have (η0η1η3)=(η3η1η0) and then the above will become
Recall from the triple-ratio
can be expressed as the ratio of two projected cross-ratios.
We will see here that r3,ε(η∗0η∗1η∗2η∗3η∗4η∗5) can also be converted into the ratio of two first order cross-ratios.
Let a and b be two projected cross-ratios whose ratio is the triple-ratio
then r3,ε(η∗0η∗1η∗2η∗3η∗4η∗5) will be written as (a∗b∗)ε. Since we can also write as
or
we get
Now it is clear that r3,ε(η∗0η∗1η∗2η∗3η∗4η∗5) can also be written as the ratio or product of two projected cross-ratios. There are exactly three ways to write it (projected by (η∗0 and η∗1), (η∗1 and η∗2) and (η∗0 and η∗2)) but we will use here η∗1 and η∗2. The last expression can be written as
and (3.13) can be written as
Applying five-term relations in TB2(F) which are analogous to the one in (2.9).
For each individual determinant, e.g., (η0η1η3) will have three terms. First consider the third term of (3.14)
We need a subetaoup in S6 which fixes (η0η1η3) as a determinant i.e., (η0η1η3)∼(η3η1η0)∼(η3η0η1)⋯
Here in this case S3 permuting {η0,η1,η3} and another one permuting {η2,η4,η5} i.e., S3×S3. Now consider
By using the odd permutation (η2η5) the above becomes zero.
then (3.14) becomes
Consider the first term now,
The permutation (η0η2η3) does not have any role because the ratio is projected by 2. So, it will be reduced to S3.
Write all possible inner alternation, then
Now we can use projected five-term relation in TB2(F) here,
The second term of the relation (3.15) can also be written as
(3.16) can be combined with the above so we get
Use the permutation (η0η1η3)(η2η4η5) to get
The Bloch group B2(F) also holds the five-term relation, thus we write the following:
Now go to the other side. Map τ31,ε can also be written in the alternation sum form
Compute τ31,ε∘d(η∗0…η∗5) and apply cycle (η0η1η2η3η4η5) for d and then expand Alt5 from the definition of τ31,ε;
Use the odd permutation (η2η3), then
Finally use the two-term relation in TB2(F) and the Bloch group B2(F) to get the required sign. The final answer will be the same as (3.18)
There are some more related results.
Proposition 3.18. The map C5(A4F[ε]2)d′→C4(A3F[ε]2)τ30,ε→(F⊗⋀2F×)⊕(⋀3F) is zero.
Proof. The proof of this is obtained directly by calculation. Let (η∗0,…,η∗4)∈C5(A4F[ε]2) where
Let ω be the volume formed in four-dimensional vector space, and Δ(ηi,⋅,⋅,⋅) be the volume form in V4/⟨ηi⟩.
First, we expand inner sum that gives us 12 different terms after simplification. By applying alternation sum, we get 60 terms and there is direct cancellation which leads to zero. Now consider the second coordinate, which gives us
Again if we expand the inner sum, then we get only four different terms, but after the application of alternation we get zero.
As an analogy of Proposition 3.8 in higher weight, we present the following result.
Proposition 3.9. The map Cn+2(An+1F[ε]2)d′→Cn+1(AnF[ε]2)τn0,ε→(F⊗⋀n−1F×)⊕(⋀nF) is zero, where
Proof. Let (η∗0,…,η∗n+1)∈Cn+2(An+1F[ε]2). We have
Now use the definition of alternation to represent this sum then we have
Expanding the inner sum gives us n+1 number of terms. Expand again by using the properties of wedge that gives n(n+1) terms. Applying the alternation sum on that, gives us n(n+1)(n+2) terms, so there are n+2 sets each consisting n(n+1) terms and each term in n(n+1) term has n+1 sets of n terms which cancel off set by set.
Now expand the inner sum in the second term of (3.20) that gives n+1 terms and then apply the alternation sum which gives n+2 sets of n+1 terms, we now find cancellation in the expansion of sum accordingly, which gives a zero as well.
4.
Conclusion
Many studies have been done on Scissor's congruence and Bloch's groups. Bringing geometry of configurations in Bloch's and Goncharov's groups plays a vital role in proving Zagier's conjucutre for weights n=2,3. In this article, we introduced the tangent to Goncharov's complex and view them by means of geometric configurations. This leads to the idea at the higher orders of tangent groups.
Theorem 3.6 proves the commutativity of the right hand side square of the diagram (4.3a) and Theorem 3.7 shows the commutativity of the left hand square of the diagram (4.3a).
Acknowledgments
This article consists on major part of the author's Doctoral thesis completed at University of Durham, UK. The author would like to thank to his advisor Dr. Herbert Gangl. The author would also like to thank to Spencer Bloch for his valuable suggestions.
Conflict of interest
The author declares no conflict of interest in this paper.









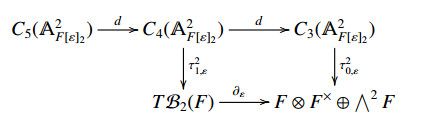

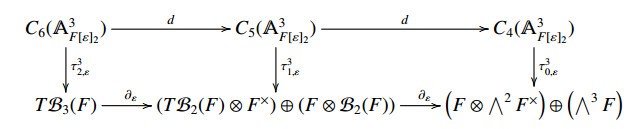
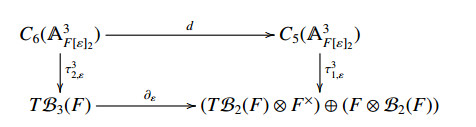




 DownLoad:
DownLoad: