Infinitesimal and tangent to polylogarithmic complexes for higher weight

1.   Introduction and motivation

One of the main challenges faced by financial companies is to evaluate market risks in a set of changes of the basic variables such as stock prices, interest rates or exchange rates. In this regard the Value-at-Risk ($\text{VaR}$) introduced by J. P. Morgan in the mid 1990s has become a standard risk measure of financial market risk. Despite its extensive use, the $\text{VaR}$ is not a coherent risk measure because it fails to satisfy subadditivity property (see ^[1]). The $\text{VaR}$ can not determine the expected loss of portfolio in $q$ worst case, but it defines the minimum loss. Furthermore, the computation of the $\text{VaR}$ is based on the assumption that financial data returns follow the normal distribution. However, as shown in the literatures, the underlying distributions of many financial data exhibit skewness, non-symmetric, heavy tails and excess kurtosis (see ^[10]). They suggest in particular that large losses occur with much higher probability than the normal distribution would suggest.

The tail conditional expectation (TCE) risk measure shares properties that are considered desirable in all cases. For instance, due to the additivity of expectations, $\text{TCE}$ allows venture capital to decompose naturally among its various components.

Consider $X$ to be a loss random variable whose cumulative distribution function (cdf) is denoted by $F_X(x)$. The $\text{TCE}$ is defined as

where $x_p =$inf${\{x\in \Bbb{R}\; :\; F_X(x)\geq p\}} = \text{VaR}_p(X)$. The $\text{TCE}$ has been discussed in many literatures (see e.g., ^{[11,12,15,17]}).

The tail conditional expectation risk measure shares properties that are considered desirable in a variety of situations. For instance, due to the additivity of expectations, $\text{TCE}$ allows for a natural decomposition of risk capital among its various constituents. The conception of capital allocation principle has long been introduced, in which the capital allocated to each risk unit can be expressed as its contribution to the tail conditional expectation of total risk. Risk allocation can not only help to evaluate and compare the performance of individual risk units, but also help to understand the risk contribution of each unit towards the total risk of the portfolio. Landsman and Valdez ^[17] derived the portfolio risk decomposition with $\text{TCE}$ for the multivariate elliptical distribution. In ^[18], authors derived the portfolio risk decomposition with $\text{TCE}$ for the exponential dispersion model, and Kim ^[14] for the exponential family class. The allocation for the class of exponential marginal was developed in ^[]. The portfolio risk decomposition with $\text{TCE}$ was further considered in ^[19] for the skew-normal distribution. Furman and Landsman ^[16] for the multivariate Gamma distribution. Cai and Li ^[2] for the phase-type distribution. Goovaerts et al. ^[9] and Chiragiev and Landsman ^[4] have provided the $\text{TCE}$-capital allocation for the multivariate Pareto distribution while Cossette et al. ^[5] have considered multivariate compound distribution. Ignatieva and Landsman ^[12] for generalized hyperbolic distribution. Recently, Kim and Kim ^[15] and Ignatieva and Landsman ^[12] investigated the $\text{TCE}$ allocation for the family of multivariate normal mean-variance mixture distributions and skewed generalized hyperbolic, respectively. The univariate $\text{TCE}$ and risk allocation formula for the generalized hyper-elliptical class were available in ^[13].

Furman and Landsman ^[8] observed that in many cases the $\text{TCE}$ does not provide adequate information about the risks on the right tail. This point can be confirmed by the fact that the $\text{TCE}$ does not include the information that the risk deviates from the upper tail expectation. Furman and Landsman ^[8] introduced the tail variance measure. The tail variance is defined as

and it has been discussed in many literatures (see e.g., ^[8,15]).

In this paper we consider a class of multivariate location-scale mixtures of elliptical ($\text{LSME}$) distributions which is known to be extremely flexible and contains many special cases as its members. Examples include the generalized hyper-elliptical distribution and generalized hyperbolic distribution.

The rest of the paper is organized as follows. Section 2 reviews the definition and properties of the multivariate $\text{LSME}$ class, and introduces the generalized hyper-elliptical distribution as a representative subclass. Section 3 presents a theorem and proves the proposed $\text{TCE}$ formula for the $\text{LSME}$ and in Section 4, the development is extended to the portfolio risk decomposition with $\text{TCE}$ for the multivariate $\text{LSME}$. In Section 5, we develop $\text{TV}$ formula for univariate $\text{LSME}$. Section 6 deals with the special case of generalized hyperbolic distribution. Numercial illustration is presented in Section 7. Finally, concluding remarks are presented in Section 8.

2.   Mixture of elliptical distributions

In this section, we introduce the class of location-scale mixtures of elliptical distributions and some of its properties.

Let $\boldsymbol{\Psi}_n$ be a class of functions $\psi(t): [0, \infty)\rightarrow \Bbb{R}$ such that function $\psi(\sum_{i = 1}^{n}t_{i}^{2})$ is an $n$-dimensional characteristic function.

A random vector $\boldsymbol{Y}$ is said to have a multivariate elliptical distribution, denoted by $\boldsymbol{Y}\sim \text{E}_n(\boldsymbol{\mu}, \boldsymbol{\Sigma}, \psi)$, if its characteristic function can be expressed as

for column-vector vector $\boldsymbol{\mu}$, $n\times n$ positive definite scale matrix $\boldsymbol{\Sigma}$, and for function $\psi(t)\in \boldsymbol{\Psi}_n$, which is called the characteristic generator.

In general, a multivariate elliptical distribution may not have a probability density function (pdf), but if its pdf exists then the form will be

for function $g_n(\cdot)$, which is called the density generator. The condition

guarantees $g_n(u)$ to be the density generator (^[7]). In addition, the normalizing constant $c_n$ is

Similarly, the elliptical distribution can also be introduced by the density generator and then written $\boldsymbol{Y}\sim \text{E}_n(\boldsymbol{\mu}, \boldsymbol{\Sigma}, g_n)$.

From (2.1), it follows that, if $\boldsymbol{Y}\sim \text{E}_n(\boldsymbol{\mu}, \boldsymbol{\Sigma}, g_n)$ and $A$ is $m\times n$ matrix of rank $m\leq n$ and $\boldsymbol{b}$ is $m$-dimensional column-vector, then

The following condition:

guarantees the existence of the mean. If, in addition, $|\psi'(0)| < \infty$, the covariance matrix exists and is equal to

(see ^[3]).

From (2.2) and (2.3), $g_{1}(x)$ can be a density generator of univariate elliptical distribution of the random variable $Y\sim \text{E}_{1}(\mu, \sigma^2, g_{1})$ whose $\text{pdf}$ can be expressed as

where $c$ is the normalizing constant. In this paper, we assume

where $Z = \frac{Y-\mu}{\sigma}$ is the spherical random variable. The $\text{cdf}$ of the random variable $Z$ can be written as the following integration form:

We can obtain the mean and variance of $Z$:

and

Landsman and Valdez ^[17] showed that

is the density of another spherical random variable $Z^{*}$ associated with $Z$, where

The random vector $\boldsymbol X\sim$ LSME $_n(\boldsymbol{\mu}, \boldsymbol{\Sigma}, \boldsymbol{\gamma}, g_n;\Pi)$ has an $n$-dimensional $\text{LSME}$ distribution with location parameter $\boldsymbol{\mu}$, positive definite scale matrix $\boldsymbol{\Sigma}$, if

in distribution, where

(1) $\boldsymbol Y \sim \text{E}_n(\boldsymbol0, \boldsymbol I_n, g_n)$, the $n$-dimensional multivariate elliptical variable;

(2) Non-negative scalar random variable $\Theta$ is independent of $\boldsymbol{Y}$, whose $\text{pdf}$ and $\text{cdf}$ are $\pi(\theta)$ and $\Pi(\theta)$ respectively;

(3) $\boldsymbol {m}(\Theta) = \boldsymbol {\mu}+\Theta \boldsymbol {\gamma}$, where $\boldsymbol {\mu} = (\mu_{1}, \ldots, \mu_n)^{T} \; \text{and} \; \boldsymbol {\gamma} = (\gamma_{1}, \ldots, \gamma_n)^{T}$ are constant vectors in $\Bbb R^{n}$.

The pdf of the $\text{LSME}$ can be written as the following integration form:

We find that the conditional distribution of $\boldsymbol{X}|\theta$ is elliptical, that is

We can obtain the mean and covariance of $\boldsymbol{X}$:

and

The characteristic function of $\boldsymbol{X}|\Theta = \theta$ exists and equals to

Then the characteristic function of the $\text{LSME}$-distributed random vector $\boldsymbol{X}$ can be written as

Under the condition (2.2) and from (2.5), we can conclude $\overline{G}(z)$ is the density generator of the associated elliptical variable $Z^*$, then

is said to have a univariate $\text{LSME}$ distributions, denoted by $X^{*}\sim \text{LSME}_{1}(\mu, \sigma^{2}, \gamma, \Theta, \overline{G}; \Pi)$.

Proposition 1. If $\boldsymbol X\sim \text{LSME}_n(\boldsymbol{\mu}, \boldsymbol{\Sigma}, \boldsymbol{\gamma}, g_n; \Pi)$ and $\boldsymbol{Y} = B\boldsymbol{X}+\boldsymbol{b}$ where $B$ is $m\times n$ ($m\leq n$) matrix and $\boldsymbol{b}$ is $m$-dimensional column-vector, then it holds that $\boldsymbol Y\sim \text{LSME}_m(B\boldsymbol{\mu}+\boldsymbol{b}, B\boldsymbol{\Sigma}B^T, B\boldsymbol{\gamma}, g_m; \Pi).$

Proof. Using the characteristic function (2.8), we write

i.e., $\boldsymbol Y\sim \text{LSME}_m(B\boldsymbol{\mu}+\boldsymbol{b}, B\boldsymbol{\Sigma}B^T, B\boldsymbol{\gamma}, g_m; \Pi).$

$\bf{Example\; 2.1}$ (Generalized hyper-elliptical distribution). The $\text{GHE}$ distribution is constructed by mixing a generalized inverse Gaussian distribution with elliptical distribution. A positive random variable $\Theta$ is said to have a generalized inverse Gaussian distribution, denoted by $\Theta \sim \text{GIG}(\lambda, a, b)$, if its pdf is given by

where parameters follow

and $K_{\lambda}(\cdot)$ denotes the modified Bessel function of the second kind with index $\lambda\in\Bbb{R}$. A random vector $\boldsymbol{X}\sim \text{GHE}_n(\boldsymbol{\mu}, \boldsymbol{\Sigma}, \boldsymbol{\gamma}, g_{n}, \lambda, a, b)$ has an $n$-dimensional $\text{GHE}$ distribution, if there exists a random vector $\boldsymbol{Y}$ follows (2.6) such that

where $\Theta\sim \text{GIG}(\lambda, a, b)$.

3.   Tail conditional expectation for univariate case

The univariate $\text{LSME}$ variable is given by $n = 1$ in the multivariate definition. That is, the univariate $\text{LSME}$ variable $X\sim \text{LSME}_1(\mu, \sigma^2, \gamma, g_1;\Pi)$ satisfies

where $Z\sim \text{E}_1(0, 1, g_1)$ is the standard elliptical variable, and non-negative scalar random variable $\Theta$ with pdf $\pi(\theta)$ is independent of $Z$. From (2.7), we have

Assuming that both the conditional distribution and the mixed distribution are continuous, the $\text{pdf}$ of $X$ produced by the mixed distribution can be written as

where $f(x|\theta)$ is the $\text{pdf}$ of $X|\theta$ and $\Omega_{\theta}$ is the support of $\pi(\theta)$. Now let $x_p$ be the quantile of the LSME variable $X$. Then the TCE of $X$ can be expressed as

The $\text{TCE}$ formula for a univariate elliptical distribution is introduced by ^[17], and equals to

where

We now give a general $\text{TCE}$ formula for the univariate $\text{LSME}$ distributions.

Theorem 1. Let $X\sim \text{LSME}_1(\mu, \sigma^2, \gamma, g_1;\Pi)$ and $\pi'(\theta) = (c')^{-1}\theta \pi(\theta)$ be a mixing $\text{pdf}$ with $c' = \text{E}(\Theta) < \infty$. Then the $\text{TCE}$ of $X$ can be computed by:

where $\Pi'$ is the $\text{cdf}$ corresponding to the $\text{pdf}$ $\pi'$.

Proof. From (3.3) and (3.4), we have

From the definition of $\text{LSME}$ distributions and (3.2), we have

As a result, (3.6) can be further simplified

Corollary 1. Let $X\sim \text{GHE}_1(\mu, \sigma^2, \gamma, g_1, \lambda, a, b)$. Assume the conditions in Theorem 1 are satisfied, then the $\text{TCE}$ of $\text{GHE}$ can be computed by:

Proof. From the GIG density in (2.11), we conclude

by setting

then

which also is the GIG density. Using (3.5) we can directly obtain (3.7).

4.   Portfolio risk decomposition with ${TCE}$ for multivariate ${LSME}$

Consider a risk vector $\boldsymbol Y = (Y_1, \ldots, Y_n)^{T}$ and $S = Y_1 +\ldots+Y_n$. We denote $s_p$ as the $p$-quantile of $S$, then

where $\text{E}(Y_i|S > s_p)$ is the contribution of the $i$-th risk to the aggregated risks.

Let $\boldsymbol Y = (Y_1, \ldots, Y_n)\sim \text{E}_n(\boldsymbol{\mu}, \boldsymbol{\Sigma}, g_n)$ and $S = Y_1 +\ldots+Y_n$, then (^[6])

The contribution of risk $Y_i, \; 1\leq i \leq n,$ to the total $\text{TCE}$ can be expressed as

We now exploit this formulation to the multivariate $\text{LSME}$ to obtain its portfolio risk decomposition with $\text{TCE}$.

Let us assume $\boldsymbol{X} = (X_1, \ldots, X_n)^{T}\sim \text{LSME}_{n}(\boldsymbol{\mu}, \boldsymbol{\Sigma}, \boldsymbol{\gamma}, g_{n}; \Pi)$. Denote the $(i, j)$ element of $\boldsymbol{\Sigma}$ by $\sigma_{ij}$, define

Then, $\text{E}(X_i|S = s)$ can be further expanded by conditioning on $\theta$ as follows:

To deal with the inner integral, we define a matrix $B_{i}$ of size $2\times n$:

The first row vector has 1 in the $i$th position. If we keep the general form

we have

here $(X_i, S|\theta)^{T}$ stands for a random column vector of size $2\times 1$, with each element being $X_i|\theta$ and $S|\theta$, respectively. Thus, the joint distribution of $(X_i, S)$ under the condition of $\Theta = \theta$ is a bivariate elliptical distribution

where the mean vector and convariance matrix of $(X_i, S|\theta)$ are given by

where

Therefore, if we impose another condition on $S$, we see that $f(x_i|s, \theta)$ is an elliptical density. In particular

Consequently

Eventually

This expression, though complex, can produce a closed-form quantity to properly select $\pi{(\theta)}$ and $m_j(\theta)$.

The portfolio risk decomposition with $\text{TCE}$ is additive, that is, the sum of all portfolio risk decomposition must amount to the $\text{TCE}$ for $S$. We can verify this

as required. Now the general portfolio risk decomposition with $\text{TCE}$ formula for the multivariate $\text{LSME}$ distributions class in presented is a more concrete and compact manner when $\boldsymbol m{(\theta)}$ is linear in $\theta$.

Theorem 2. Let $\boldsymbol{X} = (X_{1}, X_{2}, \cdots, X_{n})^{T}\sim \text{LSME}_n(\boldsymbol{\mu}, \boldsymbol{\Sigma}, \boldsymbol{\gamma}, g_n; \Pi)$ and denote the $\text{pdf}$ of $S = \boldsymbol{1}^{T}\boldsymbol{X}$ by $f_S(s)$. Let $\pi'(\theta) = (c')^{-1}\theta \pi(\theta)$ be a mixing $\text{pdf}$ with $c' = \text{E}(\Theta) < \infty$.

Then the portfolio risk decomposition with $\text{TCE}$ for the $i$-$\text{th}$ marginal variable is given by

where $\Pi'$ is the $\text{cdf}$ corresponding to the $\text{pdf}$ $\pi'$, the coefficients $b_{0, i}, \; b_{1, i}$, and $b_{2, i}$ are defined as

and $s_p$ is the $p$-quantile of $S$.

Proof. Let $m_i(\theta) = \mu_i+\theta \gamma_i$, and from (4.3) we have

By inserting this into the portfolio risk decomposition with $\text{TCE}$ formulation (4.4), we complete the proof as

Notice that $\sum_{i = 1}^{n}b_{0, i} = 0, \; \sum_{i = 1}^{n}b_{1, i} = 1$, and $\sum_{i = 1}^{n}b_{2, i} = 0$, which can be used to verify that the sum of these portfolio risk decomposition amounts to $\text{E}(S|S > s_p)$.

Corollary 2. Let $\boldsymbol{X} = (X_{1}, X_{2}, \cdots, X_{n})^{T}\sim \text{GHE}_{n}(\boldsymbol{\mu}, \boldsymbol{\Sigma}, \boldsymbol{\gamma}, g_n, \lambda, a, b)$. The portfolio risk decomposition with $\text{TCE}$ for the $i$-$\text{th}$ marginal variable is given by

Proof. We can know $S\sim \text{GHE}_{1} (s_{p}; \boldsymbol{1}^{T}\boldsymbol{\mu}, \boldsymbol{1}^{T}\boldsymbol{\Sigma}\boldsymbol{1}, \boldsymbol{1}^{T}\boldsymbol{\gamma}, g_{1}, \lambda+1, a, b)$ by using Proposition 1. Using (4.5), we see that $\text{TCE}$ of $S$ is given by

Therefore

5.   Tail variance for univariate case

The $\text{TV}$ of the univariate elliptical distribution is introduced by ^[8]. From (3.1), We can write the $\text{TV}$ for $X|\theta$ as

where $\kappa(x; \theta)$ is the same as in (3.4),

is the distorted ratio function, and

is the distorted hazard function.

$\text{TV}$ can be rewritten as:

Consequently, we need to derive the second order conditional tail moment $\text{E}(X^2|X > x_p)$. We now provide its analytic expression in the following result.

Proposition 2. Assume a random variable $X\sim \text{LSME}_1(\mu, \sigma^2, \gamma, g_1;\Pi)$. Let $\pi'(\theta) = (c')^{-1}\theta \pi(\theta)$ and $\pi''(\theta) = (c'')^{-1}\theta^2 \pi(\theta)$ be two different mixing $\text{pdf}$s with $c' = \text{E}(\Theta) < \infty$ and $c'' = \text{E}(\Theta^2) < \infty$ respectively. Then

where $\Pi'$ and $\Pi''$ are two $\text{cdf}$s corresponding to the two different $\text{pdf}$s $\pi'$ and $\pi''$, respectively.

Proof. From observing

To deal with the second order conditional tail moment in the integration, we write it as

From ^[17], we know

taking $\text{Var}(X|\theta) = \theta \sigma^2 \sigma_{Z}^{2}$ into consideration, then (5.3) becomes

As a result

Theorem 3. Under assumptions of Proposition 2, the $\text{TV}$ of $X$ is given by

where $\Pi'$ and $\Pi''$ are two $\text{cdf}$s corresponding to the two different $\text{pdf}$s $\pi'$ and $\pi''$, respectively.

Proof. From the Theorem 1, the $\text{TCE}$ formula is

Hence, the result can be derived by using Proposition 2 and (5.1).

Corollary 3. Let $X\sim \text{GHE}_1(\mu, \sigma^2, \gamma, g_1, \lambda, a, b)$. Assume the conditions in Theorem 3 are satisfied, then the $\text{TV}$ for $\text{GHE}$ can be computed by:

Proof. From the GIG density in (2.11), we conclude

and

By setting

the two $\text{pdf}$s can be presented as

and

which also are two GIG $\text{pdf}$s. Using (5.4) we can directly obtain (5.5).

6.   Examples

$\bf{Example\; 6.1}$ (Generalized hyperbolic distribution). If $\boldsymbol{\mu} = \boldsymbol{0}$, $\boldsymbol{\Sigma} = \boldsymbol{I_n}$ and density generator $g(u) = e^{-u}$ in (2.2), then the elliptical vector $\boldsymbol{Y}$ is said to have a multivariate normal distribution, denoted by $\boldsymbol{Y}\sim \text{N}_n(\boldsymbol{0}, \boldsymbol{I_n})$. Letting $\boldsymbol{Y}\sim \text{N}_n(\boldsymbol{0}, \boldsymbol{I_n})$ in (2.6), then the random vector $\boldsymbol{X}\sim \text{GH}_n(\boldsymbol{\mu}, \boldsymbol{\Sigma}, \boldsymbol{\gamma}, \lambda, a, b)$ is an $n$-dimensional generalized hyperbolic ($\text{GH}$) distribution. Therefore, the pdf of the $\text{GH}$ distribution is (see ^[15])

where the normalizing constant is

From Corollary 1, $\text{TCE}$ of $\text{GH}$ distribution is given by

From Corollary 2, portfolio risk decomposition with $\text{TCE}$ for the $i$-th marginal of $\text{GH}$ distribution is given by

From Corollary 3, $\text{TV}$ of $\text{GH}$ distribution is given by

7.   Numerical illustration

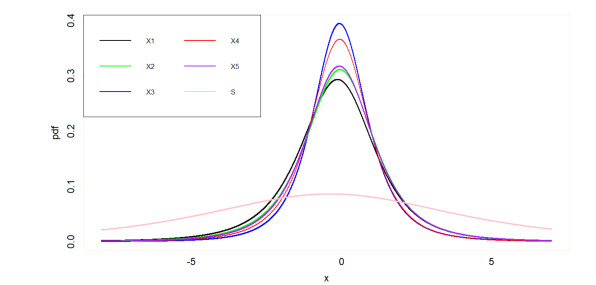
In this section we discuss the $\text{TV}$ of five stocks (Amazon, Goldman Sachs, IBM, Google, and Apple) and aggregate portfolio covering a time frame from the 1st of January 2015 to the 1st of January 2017. Ignatieva and Landsman ^[12] fitted a $\text{GH}$ model to five stocks and aggregate portfolio, and obtained the following parameter set based on the maximum likelihood technique.

For the risk analysis, we denote five stocks as $X_{1}, \cdots, X_{5}$. We also consider aggregate portfolio $S$ where each stock has equal weight for simplicity, so that the aggregate portfolio is defined as $S = X_{1}+\cdots+X_{5}$. Figure 1 shows the densities for five stocks $X_{i}, i = 1, \cdots, 5$ and aggregate portfolio $S$. The $\text{pdf}$ of $S$ has the largest variance, and Amazon has the largest dispersion among five stocks. IBM has the smallest dispersion. Figure 2 presents the $\text{TV}$ for five stocks $X_{i}, i = 1, \cdots, 5$ and aggregate portfolio $S$. All the risk measures increase over the quantile with the $\text{TV}$. Also Figure 2 shows the differences in the $\text{TV}$ measure along with five stocks and aggregate portfolio. For the same quantile, the $\text{TV}$ of Apple is the largest one and the $\text{TV}$ of IBM is the smallest one among the five stocks.

8.   Conclusions

In this paper we generalize the tail risk measure and portfolio risk decomposition with $\text{TCE}$ formula derived by ^[15] for the class of multivariate normal mean-variance mixture distributions to the larger class of multivariate elliptical location-scale mixtures distributions. A prominent member in the normal mean-variance mixture class is the generalized hyperbolic ($\text{GH}$) distribution, which itself can construct a L$\acute{e}$vy process. The $\text{GH}$ is a special case of normal mean-variance mixture random variable with $\boldsymbol{X}\sim \text{N}_n{(\boldsymbol{0}, \boldsymbol{I_n})}$ and the distribution of $\Theta$ given by a generalized inverse Gaussian (GIG) distribution with three parameters (see ^[12,15] for details). Prominent member in the elliptical location-scale mixtures class is the generalized hyper-elliptical ($\text{GHE}$) distribution. The $\text{GHE}$ distribution provides excellent fit to univariate and multivariate data, allowing to capture a long right tail in the distribution of losses even more effectively than the $\text{GH}$ distribution considered in ^[12]. And $\text{GHE}$ is a special case of elliptical location-scale mixtures random variable with $\boldsymbol{X}\sim \text{N}_n{(\boldsymbol{0}, \boldsymbol{I_n})}$ and the distribution of $\Theta$ given by a generalized inverse Gaussian (GIG) distribution with three parameters. Although the univariate $\text{TCE}$ and portfolio risk decomposition with $\text{TCE}$ formula for the $\text{GHE}$ class was available in ^[13], it can be derived more efficiently and seen as a special case of $\text{TCE}$ for the unified location-scale mixtures of elliptical distributions and risk allocation formula in Theorems 1 and 2, respectively. And the univariate $\text{TV}$ formula for the $\text{GHE}$ class can be derived efficiently and seen as a special case of $\text{TV}$ for the unified location-scale mixtures of elliptical distributions in Theorem 3.

Acknowledgments

The research was supported by the National Natural Science Foundation of China (No. 12071251).

Conflict of interest

The authors declare no conflict of interest.