Enhancing curve smoothness with whale optimization algorithm in positivity and monotonicity-preserving interpolation

1.   Introduction

In the classical formulation of Stefan's problem, certain assumptions are made about the physical factors involved in the phase change process to simplify the model description. One of these assumptions is that the thermal conductivity $k$, the specific heat $c$, the latent heat $\ell$, and the density of the material $\rho$ are considered positive constants. However, various arguments from thermodynamics motivate the solution of Stefan's problems with variable thermal coefficients.

In engineering calculations, it is common to measure thermal coefficients phenomenologically, but for some materials, the values obtained in tables are not adequate to predict those thermal coefficients with satisfactory precision since they depend on other factors.

In the last years, several studies have shown that modeling thermal parameters as functions of temperature can describe phase change processes with greater precision and realism and can be more useful for physical and industrial applications. For instance, in [1], a Stefan type problem that models the glaciation of the outer surface of a cylindrical gas pipeline in seawater was studied, considering that the latent heat and the thermal diffusivity depend on the radial distance. Approximate solutions to one-phase Stefan-like problems with space-dependent latent heat were obtained in [2].

In [3], explicit solutions of similarity-type were obtained for a model conduction heat transfer with phase change into a semi-infinite slab, where the thermal conductivities and specific heats of both phases are a linear function of the temperature. A similar analysis for the nonclassical Stefan problem was carried out in [4]. In [5], the existence and uniqueness of approximate solutions of a nonlinear boundary value problem arising from a two-phase Stefan problem, where the thermal conductivities and specific heats of both phases were assumed to be a linear function of the temperature, was proved.

Some generalizations considering power-type thermal coefficients are available in the literature. For example, in [6] a one-dimensional Stefan problem for a semi-infinite material with temperature-dependent thermal coefficients was considered, and the existence and uniqueness of solutions were obtained imposing a Dirichlet, a Neumann, or a Robin type condition at fixed face. In [7], the p-generalized modified error function was defined as the solution to a second order nonlinear ordinary differential equation with a Robin type boundary condition at the fixed face which arises from a one-phase Stefan problem. In [8], an exact solution for a nonclassical one-phase Stefan problem with two different heat source terms were examined. Furthermore, a nonclassical Stefan problem with nonlinear thermal parameters of general order and heat source term was presented in [9]. Approximate solutions using the shifted Chebyshev Tau method for a one-dimensional Stefan problem considering different power-type temperature dependent specific heat and thermal conductivity were studied assuming a Robin and a Dirichlet boundary condition at the fixed face in [10] and [11], respectively.

Other references that deal with free boundary problems with variable thermal coefficients can be found in the following references. In [12], a thermal conductivity that depends not only on the temperature but also on time was considered. [13] addresses Stefan problems for the diffusion–convection equation with temperature-dependent thermal coefficients. In [14], a model for the contact melting of a block of phase change material on a flat, heated surface was introduced where the block and melt have linear temperature-dependent thermal conductivity and viscosity. [15] discussed a Stefan problem that includes a moving phase change material and a size-dependent thermal conductivity. Additionally, [16] considered a mathematical model of an initial stage of electrical contact closure involving a metallic vaporization after instantaneous exploding of contact due to arc ignition where the temperature field in the liquid region of such kind of material was modeled by a Stefan problem for the generalized heat equation. Similarly, in [17] the existence and uniqueness of a one-phase spherical Stefan problem with nonlinear thermal coefficients and heat flux condition was studied.

The following previous works motivate the idea of taking a variable thermal conductivity. In [18], a two-phase phase Stefan problem with a linear temperature-dependent thermal conductivity and a Dirichlet boundary condition at the fixed face was studied. The one-phase Stefan problem with a Robin boundary condition at the fixed face was considered in [19], assuming that the thermal conductivity varies linearly with temperature. Recently, in [10,11], approximate solutions by the Tau method for a one-phase Stefan problem were obtained considering a power-type temperature-dependent thermal conductivity and specific heat. In [6], existence and uniqueness of solutions to the same problem for the particular case taking the same power was proved.

Based on the bibliography mentioned above, it is quite natural from a mathematical point of view to define a one-dimensional two-phase Stefan problem with a power type temperature-dependent thermal conductivity. The problem models the melting of a semi-infinite material $x \geq 0$ imposing a Dirichlet type condition $T_0 > 0$ at the fixed face $x = 0$, which is initially at temperature $-T_r < 0$ with a null phase-change temperature. This free boundary problem consists of finding the temperature $T_1 = T_1(x, t)$ of the liquid region $i = 1$, the temperature $T_2 = T_2(x, t)$ of the solid region $i = 2$, and the position of the interface $x = s(t)$, $t \geq 0$. This problem can be formulated mathematically in the following way:

where $\ell > 0$ is the latent heat of fusion by unit of mass, $\rho > 0$ is the mass density, and $c_i > 0$ is the specific heat of each region $i = 1, 2$. The thermal conductivity coefficients depend on temperature by the expressions:

with $\delta_i \geq 0$ and $p_i\geq 1$, where $k_{i}^0 > 0$ is the reference thermal conductivity for $i = 1, 2$. We denote by

for $i = 1, 2$, being $a_i$ the square root of the thermal diffusivity at the liquid phase and solid phase, respectively.

In Section 2, we prove existence of a solution to problem (1.1)–(1.7). First, we obtain an equivalence between the Stefan problem and two coupled ordinary differential problems through a suitable convenient change of variables. Second, we show that these problems are equivalent to finding the fixed point of certain contracting operators.

Since the Stefan's problems are characterized as nonlinear, finding an exact solution to them presents formidable mathematical difficulties. We will focus on the heat balance integral method introduced by Goodman [20]. This method consists of the transformation of the heat equation into an ordinary differential equation in time assuming a quadratic temperature profile in the spatial variable.

One of the mechanisms of heat conduction is diffusion, the excitation at the fixed boundary $x = 0$, for example, a temperature condition does not immediately propagate to the entire material $x > 0$ but rather its effect is perceived in a limited interval $\left(0, \delta(t)\right)$, for each time $t > 0$, outside of which the temperature remains equal to the initial temperature. The integral balance method postulates the existence of a function $\delta = \delta(t)$ that measures the thermal layer, that is, the distance to which heat penetrates. In phase change problems, this thermal layer is assumed to be the free boundary, that is, $\delta(t) = s(t)$.

For one phase Stefan's problems, a variant of the heat balance integral method, known as the modified integral balance, was introduced by Wood [21]. It simply involves integrating the heat equation, leaving the other conditions of the problem the same. In Section 3, we will generalize this method to a two-phase Stefan's problem, proposing two quadratic temperature profiles for each of the phases.

Although the integral balance method may not always be as accurate as other solution approximation techniques such as numerical methods, perturbation solutions, etc., it remains a popular choice due to its simplicity and the fact that it produces analytical solutions for a wide range of problems and parameter values. That is why for several decades, articles have been published that have used this approximation method and variants of it have emerged and been applied to a wide variety of thermal and free boundary problems, assuming different temperature profiles. Some references assuming a quadratic temperature profile can be found in [22], where approximate solutions to a one-phase Stefan problem with nonlinear temperature-dependent thermal conductivity was developed. Moreover, two different Stefan problems for a semi-infinite material for a nonclassical heat equation with a source that depends on the heat flux at the fixed face were approximated in [23]. Heat balance integral methods applied to a one-phase Stefan problem with a convective boundary condition at the fixed face were discussed in [24]. Furthermore, the determination of one or two unknown thermal coefficients in a one phase Stefan problem using the heat balance integral method was explored in [25]. Variants of the heat balance integral method were studied in [26] for a one-phase Stefan problem with time-dependent boundary conditions and in [27] for heat conduction problems with absorption. In [28,29], a cubic temperature profile was chosen, while an exponential temperature profile was considered in [30]. Generalizations with a parabolic temperature profile with an unspecified exponent were studied in [31]. The reference [32] implemented the idea of an entropy generation approach in optimal profile determination as a measure of approximation error to solutions through the heat balance integral method with the specific parabolic profile in question. For a nonlinear diffusion model of wood impregnation by methacrylatea, approximate integral-balance solutions were developed in [33]. The combined integral method was applied to a simple one-dimensional ablation problem in [34] and a nonclassical two-phase Stefan problem with delayed onset of phase change in [35]. The study in [36] examined approximate solutions through a heat balance integral method to a one-dimensional Stefan problem describing the sorption of a finite amount of swelling solvent in a glassy polymer. An improvement to the heat balance integral method was applied to thermal problems with time-dependent boundary conditions in [37]. The employment of the heat balance integral method to solve various thermal and phase change problems in a multitude of industrial contexts can be found in [38]. Similar analyses were discussed in [39] for a free boundary problem involving the sorption of a finite amount of solvent into a glassy polymer.

In Section 4, we test the accuracy of this heat balance integral method for the two-phase Stefan problem with constant thermal conductivity and we obtain a good accuracy with respect to the explicit solution given in paragraph 4.1 for small times. Moreover, we present numerical results when power-type temperature-dependent thermal conductivities are given. Finally, in Section 5, we provide some conclusions.

2.   Existence of solution to the two-phase free boundary problem with a Dirichlet type condition

In this section we will prove the existence of the solution of similarity type to the two-phase free boundary problem with a Dirichlet type condition defined by (1.1)–(1.7) using a the Banach fixed point theorem.

The temperatures $T_1 = T_1(x, t)$ and $T_2 = T_2(x, t)$ depend on the similarity variable given by

where $a_1$ is defined by (1.10). Through the following change of variables:

the phase front moves as

where $\lambda > 0$ must be determined, and, thus, we have the following result:

Theorem 1. Let $p_i \geq 1$, $\delta_i \geq 0$ for $i = 1, 2$. The Stefan problem (1.1)–(1.7) has a similarity solution $(T_1, T_2, s)$ given by:

if, and only if, the functions $y_1 = y_1(\eta) \in C^2(0, \lambda)$, $y_2 = y_2(\eta) \in C^2(\lambda, +\infty)$ and the parameter $\lambda > 0$ satisfy the following ordinary differential problems:

and

coupled through the following condition:

where $\mathrm{Ste}_1 = \frac{c_1T_0}{\ell} > 0$, $\mathrm{Ste}_2 = \frac{c_2T_r}{\ell} > 0$ are the Stefan numbers.

Proof. It follows by simple computations, recalling that the similarity variable $\eta$ is given by (2.1).

□

First, we will analyze for a fixed $\lambda > 0$ the existence and uniqueness of the solution to the ordinary differential problems (2.7)–(2.9) and (2.10)–(2.12). For this purpose, we will show that solving these problems is equivalent to finding the fixed point of certain operators that will be defined later in the following theorems.

Theorem 2. Let us assume $\delta_1\geq 0$ and $p_1\geq 1$.

a) For each $\lambda > 0$, the function $y_1\in K_1$ is a solution to the problem (2.7)–(2.9) if, and only if, $y_1$ is a fixed point of the operator $F_1: K_1 \rightarrow K_1$ given by:

where

b) For each $\lambda > 0$, $y_1, \overline{y}_1\in K_1$, we have that

where $\varepsilon_1(\lambda)$ is given by

with

and we define $\left\Vert \cdot \right\Vert_*$ by the following expression:

c) For each $\lambda > 0$, if we assume

then there exists a unique fixed point $\widehat{y}_1 \in K_1$ of the operator $F_1$ defined by (2.14).

Proof.

a) Notice that for each $y_1 \in K_1$, we have that

then

that is, $0\leq F_1(y_1)(\eta)\leq 1$ for every $0\leq \eta\leq \lambda$. Moreover, it is clear that $F_1(y_1)(0) = 1$ and $F_1(y_1)(\lambda) = 0$. Therefore, $F_1(y_1)\in K_1$.

If we define $v_1 = y'_1$, taking into account that $\Psi_{y_1}$ is given by (2.18), the ordinary differential equation (2.7) becomes

which is equivalent to

We integrate the previous equation:

with $c_0 \in \mathbb{R}$. From $v_1 = y'_1$ and taking into account (2.8), we get that

Then, from (2.9) it follows that:

Therefore,

Therefore, if $y_1\in K_1$ is a solution to the problem (2.7)–(2.9), then $y_1$ is a fixed point of the operator $F_1: K_1 \rightarrow K_1$, i.e.,

Reciprocally, if $y_1 = y_1(\eta)$ given by (2.24) is a fixed point of the operator $F_1$, we immediately obtain that conditions (2.8) and (2.9) hold. In addition, if we derive (2.24) with respect to $\eta$, (2.7) holds, and then $y_1 = y_1(\eta)$ is a solution to the ordinary differential problem (2.7)–(2.9).

b) Let us consider $y_1, \overline{y}_1\in K_1$. Notice that for each $w\in[0, \lambda]$:

then

Applying the mean value theorem, we deduce the following inequality:

where $\widetilde{y}_1$ is a function between $\overline{y}_1$ and $y_1$. As a consequence, $\widetilde{y}_1\in K_1$ and, therefore,

Moreover, if we apply the mean value theorem again, and taking into account (2.25) and (2.27), we have that

In addition, inequalities (2.25), (2.27), and (2.28) yield to

where $H$ is given by (2.21).

Therefore, from (2.26) and (2.47), we have that

where $\varepsilon_1(\lambda)$ is given by (2.20).

c) First, notice that $K_1$ is a closed subset of the Banach space of the continuous functions $C^0\left[0, \lambda\right]$ endowed with the supremum norm $\left\Vert \cdot \right\Vert_{*}$.

In addition, from [40], $H$ given by (2.21) is a decreasing function that satisfies $H(0) = \frac{\sqrt{\pi}}{2}$ and $H(+\infty) = 0$. Then, $\varepsilon_1(\lambda)$ defined by (2.20) is an increasing function that satisfies

and

Assuming (2.22) yields to $\varepsilon_1(+\infty) < 1$, the operator $F_1$ becomes a contraction. The fixed point Banach theorem assures the existence and uniqueness of a fixed point $\widehat{y}_1\in K_1$ of $F_1$ for each $\lambda > 0$.

□

Theorem 3. Let us assume $\delta_2\geq 0$ and $p_2\geq 1$.

a) For each $\lambda > 0$, the function $y_2\in K_2$ is a solution to the problem (2.10)–(2.12) if, and only if, $y_2$ is a fixed point of the operator $F_2: K_2 \rightarrow K_2$ given by:

where

b) For each $\lambda > 0$, $y_2, \overline{y}_2\in K_2$, we have that

where $\varepsilon_2(\lambda)$ is given by

with

and we define $|| \cdot ||_{**}$ by the following expression:

c) For each $0 < \lambda < L$, with

if we assume

then there exists a unique fixed point $\widehat{y}_2 \in K_2$ of the operator $F_2$ defined by (2.31).

Proof.

a) First of all, notice that for each $w\in[\lambda, +\infty)$ and $y_2\in K_2$, the following inequalities hold:

then

As a consequence,

In addition, from (2.31) and (2.33), we can easily check that $F_2(y_2)\in K_2$, i.e.,

and by (2.43), we can conclude that $F_2(y_2)$ is well-defined.

If we define $v_2 = y'_2$, taking into account that $\Phi_{y_2}$ is given by (2.35), the ordinary differential equation (2.7) becomes

By a similar argument to the Theorem 2, we obtain that

As a consequence, if $y_2\in K_2$ is a solution to the problem (2.10)–(2.12), then $y_2$ is a fixed point to the operator $F_2: K_2\to K_2$, i.e.,

Reciprocally, if $y_2 = y_2(\eta)$ given by (2.44) is a fixed point of the operator $F_2$, we immediately obtain that conditions (2.11) and (2.12) hold. In addition, if we derive (2.44) with respect to $\eta$, (2.10) holds, and then $y_2 = y_2(\eta)$ is a solution to the ordinary differential problem (2.10)–(2.12).

b) Let us consider $y_2, \overline{y}_2\in K_2$. If we apply the mean value theorem, we deduce the following inequality:

where $\widetilde{y}_2$ is a function between $\overline{y}_2$ and $y_2$. As a consequence,

Moreover, if we apply the mean value theorem again, we have that

where $\widetilde{h}_2$ is a function between $-2\tfrac{a_1^2}{a_2^2}\int_\lambda^w\tfrac{\xi}{\Phi_{y_2}(\xi)}d\xi$ and $-2\tfrac{a_1^2}{a_2^2}\int_\lambda^w\tfrac{\xi}{\Phi_{ \overline{y}_2}(\xi)}d\xi$.

From (2.41), we obtain that

Then, using (2.45), it results that

In addition, inequalities (2.41), (2.45), and (2.46) yield to

Therefore, from (2.42)–(2.46), we have that

where $\varepsilon_2(\lambda)$ is given by (2.37) and $G$ is defined by (2.38).

c) First, notice that $K_2$ is a closed subset of the Banach space of the continuous and bounded functions on $[\lambda, +\infty)$ given by $C_b[\lambda, +\infty)$ endowed with the supremum norm $\Vert \cdot \Vert_{**}$ (see [41,42,43]). In addition, from [40] we know that $G$ is an increasing function that satisfies $G(0) = 1$ and $G(+\infty) = +\infty$. Then, it is clear that $\varepsilon_2(\lambda)$ given by (2.37) is an increasing function that satisfies

and

The assumption (2.40) implies that $\varepsilon_2(0) < 1$, therefore there exists a unique $L = \varepsilon_2^{-1}(1)$ such that $\varepsilon_2(\lambda) < 1$ for all $0 < \lambda < L$. As a consequence, the operator $F_2$ becomes a contraction, and applying the fixed point Banach theorem, we conclude the existence and uniqueness of a fixed point $\widehat{y}_2 \in K_2$ of $F_2$ for each $0 < \lambda < L$.

□

The following result is a direct consequence of the Theorems 2 and 3.

Corollary 4. Suppose that (2.22) and (2.40) hold, then for each $0 < \lambda < L$ there exists a unique solution $\widehat{y}_1 \in K_1$, $\widehat{y}_2\in K_2$ to the ordinary differential problems (2.7)–(2.9) and (2.10)–(2.12), respectively, where $L$ is given by (2.39), $K_1$ by (2.15), and $K_2$ is defined by (2.32).

Now, we will provide the existence of the solution to the ordinary differential problems (2.7)–(2.9) and (2.10)–(2.12) coupled with (2.13). Taking into account Corollary 4, it remains to analyze the existence of the solution to Eq (2.13), which can be rewritten as

where

Lemma 5. Suppose that (2.22) and (2.40) hold. For each $0 < \lambda < L$, where $L$ is given by (2.39), the following inequalities hold:

where

with $G$ given by (2.38).

Proof. The proof is straightforward. □

Remark 6. Notice that the functions $\mathcal{V}_1$ and $\mathcal{V}_2$ do not depend on $\widehat{y}_1$, $\widehat{y}_2$.

Lemma 7. If we assume (2.22), (2.40), and

where $L$ is given by (2.39) and $G$ is defined by (2.38), then there exists at least one solution $\widehat{\lambda} \in (0, L)$ to the Eq (2.49).

Proof. Let us define $\mathcal{W}(\lambda) = \mathcal{V}(\lambda)-2\lambda$, $\lambda\in(0, L)$ where $\mathcal{V}$ is defined by (2.50). According to Lemma 5, we have that

and

where $\mathcal{V}_1$ and $\mathcal{V}_2$ are given by (2.52) and (2.53), respectively.

Notice that assumption (2.54) implies $\mathcal{W}(L) < 0$. Then, there exists at least one root $\widehat{\lambda} \in (0, L)$ of the function $\mathcal{W}$, i.e., $\widehat{\lambda}$ is a solution to Eq (2.49). □

From Corollary 4 and Lemma 7, we can conclude the following main result:

Theorem 8. If (2.22), (2.40), and (2.54) hold, then there exists at least one solution $\widehat{y}_1 \in K_1$, $\widehat{y}_2 \in K_2$, and $\widehat{\lambda} \in \left(0, L\right)$ to the ordinary differential problems (2.7)–(2.9) and (2.10)–(2.12) coupled with (2.13), where $L$ is given by (2.39), $K_1$ by (2.15), and $K_2$ is defined by (2.32), and $\widehat{\lambda}$ is one solution to Eq (2.49).

As a consequence, taking into account Theorem 1, we obtain the existence of solution to the Stefan problem.

Theorem 9. If (2.22), (2.40), and (2.54) hold, then there exists at least one solution to the two-phase Stefan problem (1.1)–(1.7) given by

where $\widehat{y}_1$, $\widehat{y}_2$, and $\widehat{\lambda}$ are defined in Theorem 8.

3.   Approximate solution to the two-phase Stefan problem applying a balance integral method

In this section, we are going to obtain an approximate solution to the two-phase Stefan problem (1.1)–(1.7), applying a heat balance integral method described in the introduction.

In the liquid phase, taking an average of Eq (1.1) leads to the following equality:

which, from condition (1.4), can be rewritten as

In the solid phase, for practical purposes, the method assumes the existence of a heat penetration depth $r(t) > s(t)$, called the thermal layer, beyond which there is no heat transfer. This is equivalent to assume that for each $x > r(t)$, the slab is at an equilibrium temperature, and so

therefore, condition (1.5) is replaced by condition

If we integrate Eq (1.2) in the domain $(s(t), r(t))$, it results that

which, according to conditions (1.4), (3.3), and (3.4), it is equivalent to

The heat balance integral method suggests solving an approximate problem that involves Eqs (3.2) and (3.6), making the heat equations (1.1) and (1.2) be satisfied only on the average. In addition, it requires to choose approximate functions for each phase. In our problem, we settle an approximate function $\widetilde{T}_1$ for the liquid phase, which adopts a quadratic profile in space given by

where $A_1$, $B_1$, and $C_1$ are unknown constants. In the same manner, an approximate quadratic function in space $\widetilde{T}_2$ is taken for the solid phase given by

Therefore, this heat balance integral method consists of solving an approximate problem $\widetilde{P}$ that can be stated as follows:

Find $\widetilde{T}_1$ of the form (3.7), $\widetilde{T}_2$ of the form (3.8), and $\widetilde{s} = \widetilde{s}(t)$ and $r = r(t)$ that satisfy the average heat equations (3.2), (3.6), and all the rest of the conditions of the two-phase Stefan problem. That is to say: The Dirichlet boundary condition at $x = 0$ given by (1.3), the boundary condition at the free boundary (1.4), the Stefan condition (1.6), the initial condition for the free boundary (1.7), and conditions (3.3) and (3.4) on $r(t)$.

Theorem 10. There exists a unique solution to the problem $\widetilde{P}$ given by

where

and $\widetilde{\lambda}$ is the unique solution to the equation

with

Proof. If $\widetilde{T}_1$ is given by (3.7), from conditions (1.3) and (1.4), we get that

Therefore, $\widetilde{T}_1$ is given by (3.9).

In the same manner, taking into account that $\widetilde{T}_2$ is given by (3.8), by conditions (1.4), (3.3), and (3.4), it follows that

Then, $\widetilde{T}_2$ adopts the form (3.10).

Substituting the profile for the liquid phase (3.9) into Eq (3.2) leads to the following ordinary differential equation for $\widetilde{s}$:

which together with the initial condition $\widetilde{s}(0) = 0$ allow us to deduce that $\widetilde{s}$ is given by (3.11) with $\widetilde{\lambda} > 0$ being an unknown constant to be determined. Therefore, from (3.19), we obtain that $A_1$ is given by (3.13).

According to (3.9) and (3.10), the Stefan condition becomes equivalent to

from where we deduce that $r$ is given by (3.12) and $\mu$ is an unknown coefficient to be determined. As a consequence, we obtain that (3.20) implies that $\mu$ is given by (3.14).

Notice that, according to the statement of the problem, we need $\mu > \widetilde{\lambda}$. This means that $R(\widetilde{\lambda}) > 0$, or, equivalently, $\mathrm{Ste}_1 A_1-2\widetilde{\lambda}^2 > 0$. Taking into account that $A_1$ is given by (3.13), this restriction can be rewritten as $p(\widetilde{\lambda}) > 0$ with $p$ defined by

Then, it is clear that there exists a unique $\widetilde{L} = p^{-1}(0)$ given by (3.17) that satisfies $p(\widetilde{\lambda}) > 0$ for all $0 < \widetilde{\lambda} < \widetilde{L}$. Therefore, the restriction $\mu > \widetilde{\lambda}$ is satisfied if, and only if, $0 < \widetilde{\lambda} < \widetilde{L}$.

Finally, taking into account that the profile for $\widetilde{T}_2$ is given by (3.10), and from formulas (3.11) and (3.12) for $\widetilde{s}$ and $r$, respectively, the Eq (3.6) transforms into

which implies that $\widetilde{\lambda}$ must be a solution to the Eq (3.15) in the interval $(0, \widetilde{L})$.

Defining the right hand side of Eq (3.15) by $g$, we immediately get that $g(0) = 0$ and $g(\widetilde{L}) = +\infty$. Taking into account that $A_1$ is a decreasing function on $\widetilde{\lambda}$, it follows that $R$ is an increasing function and so it is the function $g$. Therefore, there exists a unique solution $\widetilde{\lambda}$ in the interval $(0, \widetilde{L})$ to the Eq (3.15).

□

Corollary 11. For constant thermal coefficients, i.e., $\delta_1 = \delta_2 = 0$, there exists a unique solution to the problem $\widetilde{P}$ given by (3.9)–(3.12) where

$\mu$ is given by (3.14), and $\widetilde{\lambda}$ is the unique solution to Eq (3.15) in $(0, \widetilde{L})$ with

4.   Numerical results

4.1.   Constant thermal conductivity

First, we are going to test the accuracy of the heat balance integral method for the particular case of constant thermal conductivity, taking into account that the exact solution to the classical two-phase Stefan problem is available in the literature.

The exact solution to the two-phase Stefan problem (1.1)–(1.7) for $k_1 = k_1^0$, $k_2 = k_2^0$, i.e., $\delta_1 = \delta_2 = 0$, is given by

where $\lambda > 0$ is the unique solution to the following equation:

where $\mathrm{Ste}_1 = \frac{c_1T_0}{\ell} > 0$ and $\mathrm{Ste}_2 = \frac{c_2T_r}{\ell} > 0$ are the Stefan numbers in each phase.

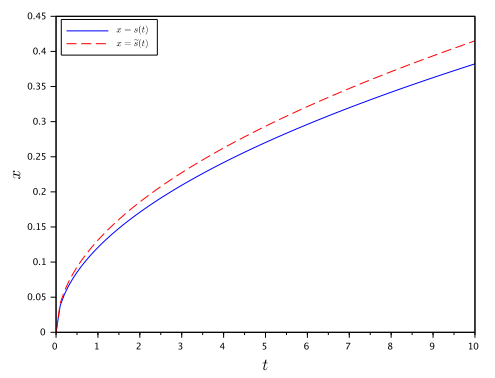
In Figures 1 and 2, we compare the exact and the approximate solutions to the classical two-phase Stefan problem when $\text{Ste}_1 = 0.1$, $\text{Ste}_2 = 0.9$, $\tfrac{a_2}{a_1} = 1.1$, $T_0 = 3 ^\circ C$, and $T_r = 1 ^\circ C$. Figure 1 shows the approximate free boundary $x = \widetilde{s}(t)$ given by (3.11) and the exact free boundary $x = s(t)$ obtained in (4.3) for $t \in (0, 10)$. Figure 2 gives the approximate temperature $\widetilde{T}$ given by (3.9) and (3.10) and the exact temperature $T$ given by (4.1) and (4.2) at $t = 10$s for $x \in (0, 10)$. As it was expected, the exact and the approximate temperatures have a discontinuous heat flux at their free boundaries.

4.2.   Variable thermal conductivity

Notice first that from Theorem 9 for the existence of at least one solution to the two-phase Stefan problem (1.1)–(1.7), we will need the following assumptions: (2.22), (2.40), and (2.54). However, note that, from Theorem 10, we do not have any requirements to prove that there exists a unique solution to the approximate two-phase Stefan problem $\widetilde{P}$ that arises when we apply a heat balance integral method.

In this way, taking into account that the case $\delta_i = 0$ was presented in the previous subsection, we focus now on the case $\delta_i > 0$ ($i = 1, 2$). Notice from Theorem 10 that the approximate solution to the two-phase Stefan problem does not depend on the coefficients that characterize the thermal conductivity of the solid region, that is, $p_2$ and $\delta_2$. Bearing in mind (2.22) and (2.40), we choose $p_1, \delta_1$ that guarantee the assumption:

and $\text{Ste}_1 > 0$ such as (2.54) holds.

In Figures 3 and 4, we set $p_1 = 1$, $\text{Ste}_1 = 0.1$, $\text{Ste}_2 = 0.9$, $\frac{a_2}{a_1} = 1.1$, $T_0 = 3^{\circ}C$, and $T_r = 1^\circ C$. Figure 3 shows the approximate free boundary $x = \widetilde{s}(t)$ defined by (3.11) for $t\in(0, 6)$ varying $\delta_1$. Figure 4 displays the approximate temperature $\widetilde{T}$ given by (3.7) and (3.8) for $x\in(0, 2)$ when $t = 5 s$, $\delta_1 = 0.1$, and $\delta_1 = 0.2$.

5.   Conclusions

A one-dimensional two-phase Stefan problem for the melting of a semi-infinite material with a power-type temperature-dependent thermal conductivity imposing a Dirichlet condition at the fixed face was considered. An equivalent ordinary differential problem was obtained through a similarity transformation. Then, an integral problem was deduced and the existence of at least one analytical solution was proved by using the Banach fixed point theorem. Moreover, approximate solutions applying a heat balance integral method assuming a quadratic temperature profile in space were found. The accuracy of this method was verified using the exact solution for the particular case with constant thermal conductivity. Some numerical simulations were provided. Future works will involve a deeper analysis with a more realistic boundary condition at the fixed face, specifically, a Robin type condition. Additionally, other numerical methods can be developed in order to discuss the accuracy of the heat balance integral method.

Author contributions

Julieta Bollati: Conceptualization, methodology, software, validation, writing—original and editing; María F. Natale: Conceptualization, methodology, validation, writing—original and editing; José A. Semitiel: Conceptualization, methodology, software, validation, writing—original and editing; Domingo A. Tarzia: Conceptualization, methodology, validation, writing-review and editing, supervision, formal analysis, resources. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The present work has been partially sponsored by the European Union's Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie grant agreement 823731 CONMECH and the Projects O06-24CI1901 and O06-24CI1903 from Universidad Austral, Rosario, Argentina.

Conflict of interest

The authors declare no potential conflict of interest.