Triangular algebras with nonlinear higher Lie n-derivation by local actions

1.   Introduction

The real-time solution to the Moore-Penrose inverse (MP-inverse or pseudoinverse) ^[1,2], that frequently arises in robotics ^[3,4,5], game theory ^[6], nonlinear systems ^[7] and other technical and scientific disciplines ^[8,9,10], has attracted a lot of interest in recent times. Quaternions, on the other hand, are crucial in a wide range of domains, such as computer graphics ^[11,12,13], robotics ^[14,15], navigation ^[16], quantum mechanics ^[17], electromagnetism ^[18] and mathematical physics ^[19,20]. Let $\mathbb{H}^{m\times n}$ present the set of all $m\times n$ matrices on the quaternion skew field $\mathbb{H} = \{\delta_1 + \delta_2\imath + \delta_3\jmath+ \delta_4k\ |\ \imath^2 = \jmath^2 = k^2 = \imath\jmath k = -1, \delta_1, \delta_2, \delta_3, \delta_4\in\mathbb{R}\}$. Considering that $\tilde{A}\in\mathbb{H}^{m\times n}$, its conjugate transpose is denoted by $\tilde{A}^*$, and its rank by $\mathrm{rank}({{\tilde{A}}})$. The generalization of the inverse matrix $\tilde{A}^{-1}$ is the MP-inverse $\tilde{A}^\dagger$, whereas $\tilde{A}^\dagger$ is just one solution $\tilde{X}$ that satisfies the next Penrose equations ^[21,22]:

Recently, research has begun to focus on time-varying quaternion (TVQ) problems involving matrices, such as inversion of TVQ matrices ^[23], solving the dynamic TVQ Sylvester matrix equation ^[24], addressing the TVQ constrained matrix least-squares problem ^[25] and solving the TVQ linear matrix equation for square matrices ^[26]. Furthermore, real-world applications involving TVQ matrices are employed in kinematically redundant manipulator of robotic joints ^[15,27], chaotic systems synchronization ^[25], mobile manipulator control ^[23,28] and image restoration ^[26,29]. All these studies have one thing in common: they all use the zeroing neural network (ZNN) approach to derive the solution.

ZNNs are a subset of recurrent neural networks that are especially good at parallel processing and are used to address time-varying issues. They were initially developed by Zhang et al. ^[30] to handle the problem of time-varying matrix inversion, but their subsequent iterations were dynamic models for computing the time-varying MP-inverse of full-row/column rank matrices ^{[31,32,33,34]} in the real and complex domain. Today, their use has expanded to include the resolution of generalized inversion issues ^{[35,36,37,38,39,40]}, linear and quadratic programming tasks ^[41,42,43], certain types of matrix equation ^[44,45], systems of nonlinear equations ^[46,47], systems of linear equations ^[48,49,50] and systems of equations with noise ^[51]. The TVQ MP-inverse (TVQ-MPI) problem for any TVQ matrix will be addressed in this paper using the ZNN approach. Of greater significance, we will determine whether a direct solution in the quaternion domain or an indirect solution through representation in the complex and real domains is more efficient. To do this, we will create three ZNN models, one for each domain, and rigorously validate them on four numerical simulations and a real-world application involving robotic motion tracking. By doing theoretical analysis and analyzing the computational complexity of all presented models, this research strengthens the existing body of literature.

The rest of the article is divided into the following sections. Section 2 presents introductory information and the TVQ-MPI problem formulation. Section 3 introduces the three ZNN models, while their theoretical analysis is presented in Section 4. Numerical simulations and applications are explored in Section 5 and, finally, Section 6 provides concluding thoughts and comments.

2.   Introductory information and problem formulation

This part outlines some introductory information about TVQ matrices, the TVQ-MPI problem, ZNNs and the notation that will be used throughout the remainder of the study as well as the primary findings that will be covered.

A division algebra or skew-field over the field of real numbers makes up a quaternion. As a result, the set of quaternions $\mathbb{H}$ is not commutative under the operation of multiplication, which causes complexity to rise quickly in real-world applications ^[52]. On the other hand, a real $4\times 4$ matrix or a complex $2\times 2$ matrix can both be used to easily express a scalar quaternion ^[53]. The dimensions of the representation matrices scale suitably, and this fact also applies to matrices of quaternions. In order to tackle quaternion-based problems, it is now customary to first solve an analogous issue in the real or complex domain before converting the result back to quaternion form. This method, which is undeniably effective even in a static setting, excels at solving issues with time-varying characteristics.

Let $\tilde{A}(t) = A_1(t)+A_2(t)\imath+A_3(t)\jmath+A_4(t)k\in\mathbb H^{m\times n}$, with $A_i(t)\in\mathbb{R}^{m\times n}$ for $i = 1, 2, 3, 4$, be a TVQ matrix and $t\in[0, t_f)\subseteq[0, +\infty)$ be the time. The conjugate transpose of a TVQ matrix $\tilde{A}(t)$ is the following ^[52,53]:

where the operator $()^ {\mathrm T}$ denotes transposition. The product of the two TVQ matrices $\tilde{A}(t)$ and $\tilde{B}(t) = B_1(t)+B_2(t)\imath+B_3(t)\jmath+B_4(t)k\in\mathbb H^{n\times g}$, with $B_i(t)\in\mathbb{R}^{n\times g}$ for $i = 1, \cdots, 4$, is:

where

with $Y_i(t)\in\mathbb{R}^{m\times g}$ for $i = 1, \cdots, 4$. Additionally, one complex representation of the TVQ matrix $\tilde{A}(t)$ is the following ^[24,54]:

and one real representation of the TVQ matrix $\tilde{A}(t)$ is the following ^[26]:

In this paper, the following TVQ matrix equations problem is taken into consideration for computing the TVQ-MPI of any $\tilde{A}(t)\in\mathbb{H}^{m\times n}$ ^[21,22]:

where the TVQ matrix $\tilde{X}(t) = X_1(t)+X_2(t)\imath+X_3(t)\jmath+X_4(t)k\in\mathbb{H}^{n\times m}$, with $X_i(t)\in\mathbb{R}^{n\times m}$ for $i = 1, 2, 3, 4$, is the TVQ matrix of interest. Additionally, we consider that $\tilde{A}(t)$ is a smoothly time-varying matrix and its time derivative is either given or can be accurately estimated. It is important to note that (2.6) is the TVQ-MPI problem and it is satisfied only for $\tilde{X}(t) = \tilde{A}^\dagger(t)$.

On the one hand, taking into account that the complex representation of the TVQ matrix acquired by multiplying two TVQ matrices is similar to the TVQ matrix acquired by multiplying the complex representations of two TVQ matrices [24, Theorem 1], solving (2.6) is equivalent to solving the real matrix equation:

where $\hat{X}(t)\in\mathbb{C}^{2n\times 2m}$. On the other hand, taking into account that the real representation of the TVQ matrix acquired by multiplying two TVQ matrices is similar to the TVQ matrix acquired by multiplying the real representations of two TVQ matrices [26, Corollary 1], solving (2.6) is equivalent to solving the real matrix equation:

where $X(t)\in\mathbb{R}^{4n\times 4m}$.

Three novel ZNN models are introduced for solving the TVQ-MPI problem of (2.6) in this research. One model, dubbed as ZNNQ, is created for directly resolving the TVQ-MPI problem of (2.6). The two additional models, dubbed as ZNNQC and ZNNQR, are created to indirectly solve the TVQ-MPI problem of (2.6) through (2.7) in the complex domain and (2.8) in the real domain, respectively. The creation of a ZNN model typically involves two fundamental steps. First, one defines an error matrix equation (ERME) function $E(t)$. Second, the next ZNN dynamical system under the linear activation function must be used:

where the operator $\left({ }^{\cdot}\right)$ denotes the time derivative. Additionally, the design parameter $\lambda > 0$ is a positive real number, though one may adjust the convergence rate of the model. For instance, a higher value for $\lambda$ will result in the model converging even faster ^[55,56,57]. It is important to point out that continual learning is defined as learning continually from non-stationary data, while transferring and preserving prior knowledge. It is true that as time evolves, the ZNN's architecture relies around driving each entry of the error function $E(t)$ to 0. The continuous-time learning rule, which is the consequence of the definition of the ERME function (2.9), is used to do this. Therefore, it is possible to think of the error function as a tool for tracking the learning of ZNN models.

The key conclusions of the paper are listed next:

(1) For the first time, the TVQ-MPI problem is addressed through the ZNN approach.

(2) With the purpose of addressing the TVQ-MPI problem, three novel ZNN models are provided.

(3) Matrices of any dimension can be used with the proposed ZNN models.

(4) The models are subjected to a theoretical analysis that validates them.

(5) Numerical simulations and applications are carried out to complement the theoretical concepts.

The following notations are employed in the remainder of this article: $I_u$ refers to the identity $u\times u$ matrix; $\mathbf{0}_{u}$ and $\mathbf{0}_{m\times n}$, respectively, refer to the zero $u\times u$ and $m\times n$ matrices; $\left\lVert{\cdot}\right\rVert_ {\mathrm F}$ denotes the matrix Frobenius norm; $\mathrm{vec}(\cdot)$ denotes the vectorization process; $\odot$ denotes the elementwise multiplication; $\otimes$ denotes the Kronecker product.

3.   ZNN models in solving the TVQ-MPI

Three ZNN models, each working in a distinct domain, will be developed in this section. Further, we assume that $\tilde{A}(t)\in\mathbb{H}^{m\times n}$ is a differentiable TVQ matrix, and $\tilde{X}(t)\in\mathbb{H}^{n\times m}$ is the unknown MP-inverse matrix of $\tilde{A}(t)$ to be found.

3.1.   The ZNNQ model

To develop the ZNNQ model, the TVQ-MPI of (2.6) is considered. According to (2.1) and (2.2), we set $\tilde{A}^*(t)\tilde{A}(t) = \tilde{U}(t) = U_1(t)+U_2(t)\imath+U_3(t)\jmath+U_4(t)k$, where

with $U_i(t)\in\mathbb{R}^{n\times n}$ for $i = 1, \cdots, 4$, and $\tilde{A}(t)\tilde{A}^*(t) = \tilde{V}(t) = V_1(t)+V_2(t)\imath+V_3(t)\jmath+V_4(t)k$, where

with $V_i(t)\in\mathbb{R}^{m\times m}$ for $i = 1, \cdots, 4$. Taking into account (3.1) and (3.2), the TVQ-MPI (2.6) can be rewritten as below:

or equivalent,

where

with $C_i(t)\in\mathbb{R}^{n\times m}$ for $i = 1, \cdots, 4$, and

with $C_i(t)\in\mathbb{R}^{n\times m}$ for $i = 1, \cdots, 4$. Then, setting

where $Z_1(t)\in\mathbb R^{4m\times 4n}$, $Z_2(t)\in\mathbb R^{4n\times 4m}$, $Y_1(t), W_1(t)\in\mathbb R^{4n\times m}$ and $Y_2(t), W_2(t)\in\mathbb R^{n\times 4m}$, the following ERME is considered:

where $E_1(t)\in\mathbb R^{4n\times m}$ and $E_2(t)\in\mathbb R^{n\times 4m}$. The first time derivative of (3.8) is as follows:

When $E_Q(t)$ of (3.8) and $\dot{E}_Q(t)$ of (3.9) are replaced in (2.9) and solving in terms of $\dot{Y}_1(t)$ and $\dot{Y}_2(t)$, we have the next result:

Then, with the aid of the Kronecker product and the vectorization process, the dynamic model of (3.10) may be simplified:

and after setting:

the next ZNNQ model is derived for solving the TVQ-MPI of (2.6):

where $\dot{\mathbf{y}}(t), \mathbf{y}(t), L(t)\in\mathbb R^{4mn}$, $K(t)\in\mathbb R^{4mn\times 4mn}$ is a nonsingular mass matrix and $\gamma\geq0$ is the regularization parameter.

Given that we perform $4mn$ additions/subtractions and $(4mn)^2$ multiplications in each iteration of (3.13), the complexity of solving (3.13) is $\mathcal{O}((4mn)^2)$ operations. In addition, the complexity of solving (3.13) through use of an implicit ${\tt ode}$ MATLAB solver is $\mathcal{O}((4mn)^3$ as it involves a $(4mn)\times (4mn)$ matrix. As a consequence, the computational complexity of the ZNNQ model of (3.13) is $\mathcal{O}((4mn)^3)$.

3.2.   The ZNNQC model

To develop the ZNNQC model, the TVQ-MPI of (2.7) is considered. Let $\hat{A}(t)\in\mathbb C^{2m\times 2n}$ and $\hat{X}(t)\in\mathbb C^{2n\times 2m}$, we set the following ERME:

where $E_1(t), E_2(t)\in\mathbb C^{2n\times 2m}$. The first time derivative of (3.14) is as follows:

When $E_C(t)$ of (3.14) and $\dot{E}_C(t)$ of (3.15) are replaced in (2.9) and solving in terms of $\dot{\hat{X}}(t)$, we have the next result:

Then, with the aid of the Kronecker product and the vectorization process, the dynamic model of (3.16) may be simplified:

and after setting:

the ZNNQC model is derived for solving the TVQ-MPI of (2.6):

where $\dot{\hat{\mathbf{x}}}(t), \hat{\mathbf{x}}(t), H(t)\in\mathbb C^{4mn}$, $W(t)\in\mathbb C^{4mn\times 4mn}$ is a nonsingular mass matrix and $\gamma\geq0$ is the regularization parameter.

In terms of computational complexity, it is important to note that multiplying two complex numbers results in the calculation $(c+d\imath)(k+h\imath) = ck-dh+ch\imath+dk\imath$, which calls for a total of 4 multiplications and 2 addition/subtraction operations. Taking this into account, the complexity of computing (3.19) is $\mathcal{O}(4(4mn)^2) = \mathcal{O}((8mn)^2)$ as each iteration of (3.19) has $4(4mn)^2$ multiplication and $2(4mn)$ addition/subtraction operations. In addition, the complexity of solving (3.19) through use of an implicit ${\tt ode}$ MATLAB solver is $\mathcal{O}((8mn)^3)$ as it involves a $(4mn)\times (4mn)$ matrix in the complex domain. As a consequence, the computational complexity of the ZNNQC model of (3.19) is $\mathcal{O}((8mn)^3)$.

3.3.   The ZNNQR model

To develop the ZNNQR model, the TVQ-MPI of (2.8) is considered. Let $A(t)\in\mathbb C^{4m\times 4n}$ and $X(t)\in\mathbb R^{4n\times 4m}$, we set the following ERME:

where $E_1(t), E_2(t)\in\mathbb R^{4n\times 4m}$. The first time derivative of (3.20) is as follows:

When $E_R(t)$ of (3.20) and $\dot{E}_R(t)$ of (3.21) are replaced in (2.9) and solving in terms of $X(t)$, we have the next result:

Then, with the aid of the Kronecker product and the vectorization process, the dynamic model of (3.22) may be simplified:

and after setting:

the ZNNQR model is derived for solving the TVQ-MPI of (2.6):

where $\dot{\mathbf{x}}(t), \mathbf{x}(t), P(t)\in\mathbb R^{16mn}$, $M(t)\in\mathbb R^{16mn\times 16mn}$ is a nonsingular mass matrix and $\gamma\geq0$ is the regularization parameter.

Given that we perform $16mn$ additions/subtractions and $(16mn)^2$ multiplications in each iteration of (3.25), the complexity of solving (3.25) is $\mathcal{O}((16mn)^2)$ operations. In addition, the complexity of solving (3.25) through use of an implicit ${\tt ode}$ MATLAB solver is $\mathcal{O}((16mn)^3$ as it involves a $(16mn)\times (16mn)$ matrix. As a consequence, the computational complexity of the ZNNQR model of (3.25) is $\mathcal{O}((16mn)^3)$.

4.   Stability and convergence analysis

This section examines the convergence and stability of the ZNNQ (3.13), ZNNQC (3.19), and ZNNQR (3.25) models.

Theorem 4.1. Assuming that $Z_1(t)\in\mathbb R^{4m\times 4n}$, $Z_2(t)\in\mathbb R^{4n\times 4m}$, $Y_1(t), W_1(t)\in\mathbb R^{4n\times m}$ and $Y_2(t), W_2(t)\in\mathbb R^{n\times 4m}$, and $Z_1(t), Z_2(t), W_1(t)$ and $W_2(t)$ are differentiable, the dynamical system (3.10) converges to $\tilde{A}^\dagger(t)$, which is the theoretical solution (THSO) of the TVQ-MPI (2.6). The solution is then stable, based on Lyapunov.

Proof. The substitution $\bar{Y}_i(t): = \check{Y}_i(t)-Y_i(t), i = 1, 2,$ implies $Y_i(t) = \check{Y}_i(t)-\bar{Y}_i(t)$, where $\check{Y}_i(t)$ is a THSO. The time derivative of $Y_i(t), i = 1, 2,$ is $\dot{Y}_i(t) = \dot{\check{Y}}_i(t)-\dot{\bar{Y}}_i(t)$. Notice that

and its first derivative

As a result, following the substitution of $Y_i(t) = \check{Y}_i(t)-\bar{Y}_i(t), i = 1, 2,$ into (3.8), one can verify

Further, the implicit dynamics (2.9) imply

We then determine the candidate Lyapunov function so as to confirm convergence:

Then, the next identities can be verified:

Consequently, it holds

With $\bar{Y}(t) = \left\{ \begin{array}{ll} \bar{Y}_1(t), &m\geq n\\ \bar{Y}_2(t), &m < n \end{array} \right.$ being the equilibrium point of the system (4.4) and $E_Q(0) = 0$, we have that:

By the Lyapunov stability theory, we infer that the equilibrium state:

is stable. Thus, $Y_i(t)\rightarrow \check{Y}_i(t), i = 1, 2,$ as $t\rightarrow \infty$. □

Theorem 4.2. Let $\tilde{A}(t) \in \mathbb H^{m\times n}$ be differentiable. For any initial value $\mathbf{y}(0)$ that one may consider, the ZNNQ model (3.13) converges exponentially to the THSO $\check{\mathbf{y}}(t)$ at each time $t$.

Proof. First, the ERME of (3.8) is declared so as to determine the THSO of the TVQ-MPI. Second, the model (3.10) is developed utilizing the ZNN's architecture (2.9) for zeroing (3.8). So, when $t\rightarrow \infty$, $Y(t)\rightarrow \check{Y}(t)$ for any initial value, according to Theorem 4.1. Third, with the aid of the Kronecker product and the vectorization process, the dynamic model of (3.10) is simplified into the ZNNQ model (3.13). Therefore, the ZNNQ model (3.13) converges to the THSO $\check{\mathbf{y}}(t)$ for any initial value $\mathbf{y}(0)$ when $t\rightarrow \infty$, as it is simply an alternative version of (3.10). The proof is thus completed. □

Theorem 4.3. Assuming that $\hat{A}(t) \in \mathbb C^{2m\times 2n}$ is differentiable, the dynamical system (3.16) converges to $\hat{A}^\dagger(t)$, which is the THSO of the TVQ-MPI (2.7). The solution is then stable, based on Lyapunov.

Proof. Given that the proof mirrors the proof of Theorem 4.1, it is omitted. □

Theorem 4.4. Let $\hat{A}(t) \in \mathbb C^{2m\times 2n}$ be differentiable. For any initial value $\hat{\mathbf{x}}(0)$ that one may consider, the ZNNQC model (3.19) converges exponentially to the THSO $\check{\hat{\mathbf{x}}}(t)$ at each time $t$.

Proof. Given that the proof mirrors the proof of Theorem 4.2 once we replace Theorem 4.1 with Theorem 4.3, it is omitted. □

Theorem 4.5. Assuming that $A(t) \in \mathbb R^{4m\times 4n}$ is differentiable, the dynamical system (3.22) converges to $A^\dagger(t)$, which is the THSO of the TVQ-MPI (2.8). The solution is then stable, based on Lyapunov.

Proof. Given that the proof mirrors the proof of Theorem 4.1, it is omitted. □

Theorem 4.6. Let $A(t) \in \mathbb R^{4m\times 4n}$ be differentiable. For any initial value $\mathbf{x}(0)$ that one may consider, the ZNNQR model (3.25) converges exponentially to the THSO $\check{\mathbf{x}}(t)$ at each time $t$.

Proof. Given that the proof mirrors the proof of Theorem 4.2 once we replace Theorem 4.1 with Theorem 4.5, it is omitted. □

5.   Experiments

In this section, four numerical simulations (NSs) and a real-world application involving robotic motion tracking are presented. The essential clarifications that have been used across all NSs and application are shown below. The ZNN design parameter $\lambda$ is used with values of 10 and 100 in NSs and 10 in application, while the initial values of the ZNNQ, ZNNQC and ZNNQR models have been set to $\mathbf{y}(0) = \mathbf{0}_{4mn}$, $\hat{\mathbf{x}}(0) = \mathbf{0}_{4mn}$ and $\mathbf{x}(0) = \mathbf{0}_{16mn}$, respectively. Additionally, we have set $\alpha(t) = \sin(t)$ and $\beta(t) = \cos(t)$ and we will refer to the four Penrose equations in (1.1) as (P-i), (P-ii), (P-iii) and (P-iv) for convenience. The notation QMP (i.e. quartenion MP) in the figures legend refers to the MP-inverse of the input TVQ matrix $\tilde{A}(t)$, i.e. $\tilde{A}^\dagger(t)$. Finally, the NSs have used the MATLAB ${\tt ode15s}$ solver in the time interval $[0, 10]$ using the default double precision arithmetic ($eps = 2.22\cdot 10^{-16}$), whereas the application has used the solver in the time interval $[0, 20]$. As a consequence, the minimum value in all of the figures of this section are mostly of order $10^{-5}$.

5.1.   Numerical simulations

Example 5.1. Considering the next coefficients:

the input matrix $\tilde{A}(t)\in\mathbb{H}^{3\times 3}$ is a singular TVQ matrix with $\mathrm{rank}({{\tilde{A}(t)}}) = 2$. As a consequence, we set $\gamma = 10^{-8}$ in the ZNNQ, ZNNQC and ZNNQR models. The performance of the ZNN models is shown in Figures 1, 2 and 3.

Example 5.2. Utilizing the next coefficients:

the input matrix $\tilde{A}(t)\in\mathbb{H}^{4\times 2}$ is a full rank TVQ matrix with $\mathrm{rank}({{\tilde{A}(t)}}) = 2$. As a consequence, we set $\gamma = 0$ in the ZNNQ, ZNNQC and ZNNQR models. The performance of the ZNN models is shown in Figures 1, 2 and 3.

Example 5.3. Using the following coefficients:

the input matrix $\tilde{A}(t)\in\mathbb{H}^{3\times 6}$ is a rank deficient TVQ matrix with $\mathrm{rank}({{\tilde{A}(t)}}) = 2$. As a consequence, we set $\gamma = 10^{-8}$ in the ZNNQ, ZNNQC and ZNNQR models. The performance of the ZNN models is shown in Figures 1, 2 and 3.

Example 5.4. Considering the following matrix

the coefficients of the input matrix $\tilde{A}(t)$ have been set to

As a consequence, $\tilde{A}(t)\in\mathbb{H}^{12\times 4}$ is a rank deficient TVQ matrix with $\mathrm{rank}({{\tilde{A}(t)}}) = 3$ and, thus, we set $\gamma = 10^{-8}$ in the ZNNQ, ZNNQC and ZNNQR models. The performance of the ZNN models is shown in Figures 1, 2 and 3.

5.2.   Application to robotic motion tracking

The applicability of the ZNNQ, ZNNQC and ZNNQR models is validated in this experiment using a 3-link planar manipulator (PM), as shown in Figure 4a. It is important to mention that the 3-link PM's kinematics equations at the position level $r(t)\in \mathbb{R}^{m}$ and the velocity level $\dot{r}(t)\in \mathbb{R}^{m}$ are expressed as follows:

where $\theta\in \mathbb{R}^{n}$ is the angle of the 3-link PM, $f(\cdot)$ is a smooth nonlinear mapping function, $r(t)$ is the end-effector's position, and $J(\theta) = \partial f(\theta)/\partial\theta \in \mathbb{R}^{m\times n}$.

To comprehend how this 3-link PM tracked motion, the inverse kinematic equation is solved. The equation of velocity can be thought of as a system of linear equations when the end-effector motion tracking task is assigned with $\dot{r}(t)$ known and $\dot{\theta}(t)$ unknown. To put it another way, by setting $\tilde{A}(t) = J(\theta)$, we find $\tilde{X}(t) = A^\dagger(t)$ to solve $\dot{\theta}(t) = \tilde{X}(t)\dot{r}(t)$. Therefore, we may track control of the 3-link PM by using the ZNN models to resolve the underlying linear equation system.

The 3-link PM's end-effector is anticipated to follow a "M"-shaped path in the simulation experiment; ^[58] contains the X and Y-axis velocity functions of this path along with the specifications of 3-link PM. The task duration $4T$ is $20$ seconds (i.e., $T = 5$ seconds) in these functions, and the design parameter is $s = 6$ cm. Additionally, the link length is $\alpha = [1, 2/3, 5/4]^ {\mathrm T}$ and the initial value of the joints is $\theta(0) = [\pi/4, \pi/4, \pi/4]^ {\mathrm T}$. The performance of the ZNN models is shown in Figure 4.

5.3.   Numerical simulations discussion

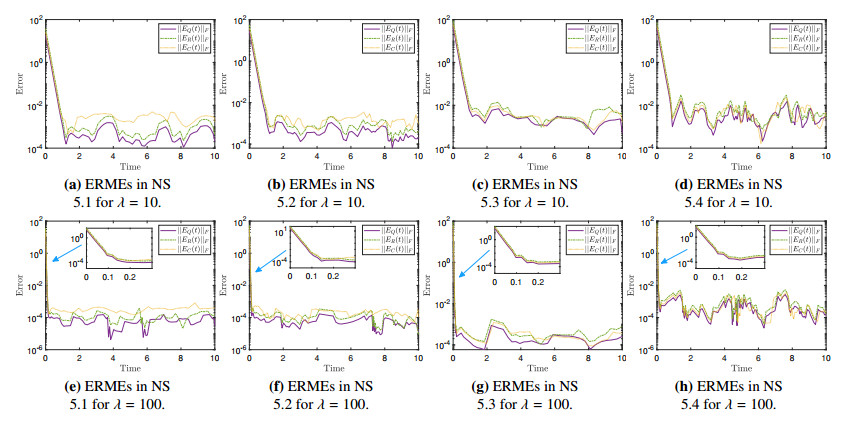
The performance of the ZNNQ (3.13), ZNNQC (3.19) and ZNNQR (3.10) models for solving the TVQ-MPI (2.6) is investigated throughout the NSs 5.1–5.4. While the input TVQ matrices $\tilde{A}(t)$ used have varied dimensions and rank conditions, each NS solves the TVQ-MPI problem. Particularly, NS 5.1 has a singular TVQ matrix of dimensions $3\times 3$, NS 5.2 has a full rank TVQ matrix of dimensions $4\times 2$, NS 5.3 has a rank deficient TVQ matrix of dimensions $3\times 6$, while NS 5.4 has a rank deficient TVQ matrix of dimensions $12\times 4$, which is much larger than the other NSs.

Figsure 1a–1d and Figure 1e–1h show the ERME's Frobenius norms of the ZNNQ, ZNNQC and ZNNQR models for $\lambda$ values of 10 and 100 in NSs 5.1–5.4, respectively. In the case of $\lambda = 10$ in Figure 1a–1d, it can be observed that the error values in all NSs start from a high error value at $t = 0$ and, by the time-mark of $t\approx 1$, they experience a steep decline that brings them to the range $[10^{-4}, 10^{-2}]$. Notice that a higher value for $\lambda$ will typically cause the ZNN models to converge even more quickly. This is demonstrated in the case of $\lambda = 100$ in Figures 1e–1h, where we observe that the error values in all NSs start from a high error value at $t = 0$ and, by the time-mark of $t\approx 0.1$, they experience a steep decline that brings them to the range $[10^{-4}, 10^{-3}]$. Also, all ZNN models exhibit the same convergence speed, but the ZNNQC has the highest overall error in the region $[0, 10]$ while the ZNNQ has the lowest. In other words, the ZNNQ model shows better performance than the ZNNQC and ZNNQR models.

The fact that all three models successfully converged is further highlighted in Figure 2, which contrasts the THSO's real and imaginary parts trajectories with the corresponding $\tilde{X}(t)$ trajectories produced by the three models. Particularly, Figure 2a depicts the real part and Figure 2b–2d depict the imaginary parts in NS 5.1, Figure 2e depicts the real part and Figure 2f–2h depict the imaginary parts in NS 5.2, Figure 2i depicts the real part and Figure 2j–2l depict the imaginary parts in NS 5.3, and Figure 2m depicts the real part and Figure 2n–2p depict the imaginary parts in NS 5.4. In these figures, it can be observed that the three models' $\tilde{X}(t)$ trajectories coincide with the corresponding THSO's trajectories, whereas their convergence speed follows the convergence tendency of the ZNNQ, ZNNQC and ZNNQR models' ERMEs shown in Figure 1. It is important to note that the convergence and stability theorems of Section 4 are validated in all of the figures in this section by the convergence tendency of the ERME's Frobenius norms alongside the solution trajectories that match the THSO's trajectories. That is, the ZNNQ, ZNNQC and ZNNQR models of Section 3 converge exponentially to the QMP, i.e. $\tilde{A}^\dagger(t)$, for any initial value when $t\rightarrow \infty$.

By assessing the error of Penrose equations (1.1), the three models' performance is examined in order to further validate them. Particularly, Figure 3a, 3e, 3i and 3m depict the error of (P-i) in NSs 5.1–5.4, respectively, Figure 3b, 3f, 3j and 3n depict the error of (P-ii) in NSs 5.1–5.4, respectively, Figure 3c, 3g, 3k and 3o depict the error of (P-iii) in NSs 5.1–5.4, respectively, and Figure 3d, 3h, 3l and 3p depict the error of (P-iv) in NSs 5.1–5.4, respectively. In these figures, it can be observed that convergence speed of the error produced by the three models follows the convergence tendency of the ZNNQ, ZNNQC and ZNNQR models' ERMEs shown in Figure 1. In NSs 5.1 and 5.2, the ZNNQ and ZNNQR have identical performance. Additionally, the ZNNQC has the highest overall error in the region $[0, 10]$ while the ZNNQ and ZNNQR have has the lowest. In NSs 5.3 and 5.4, all models produces almost identical overall error values.

Additionally, the applicability of the ZNNQ, ZNNQC and ZNNQR models is validated in the experiment of Section 5.2 using a 3-link PM. Particularly, Figure 4b shows the ERME's Frobenius norms of the ZNN models. It can be observed that the error values start from a high error value at $t = 0$ and, by the time-mark of $t\approx 1$, they experience a steep decline that brings them to the range $[10^{-5}, 10^{-4}]$. The error values fall more gradually after $t\approx 1$ until $t = 20$, when they drop to a range of $[10^{-13}, 10^{-11}]$. All ZNN models exhibit the same convergence speed and very similar overall error in the region $[0, 20]$, but the ZNNQR has the highest overall error while the ZNNQ has the lowest. Figsure 4c–4f depict the error of (P-i)-(P-iv), respectively. In these figures, it can be observed that convergence speed of the error produced by the three models follows the convergence tendency of the ZNNQ, ZNNQC and ZNNQR models' ERMEs shown in Figure 4b. In other words, the ZNNQ model shows better performance than the ZNNQC and ZNNQR models. Figure 4g and 4h depict the trajectories of the velocity and the "M"-shaped path tracking. As seen in these figures, all ZNN model solutions match the actual velocity $\dot{\theta}(t)$, and the 3-link PM successfully completes the "M"-shaped path tracking task, where $\dot{r}(t)$ is the actual "M"-shaped path.

Not to mention, once we take into account the complexity of each model, the results above can be placed into better context. Because the dimensions of the associated real valued matrix $A(t)$ are 2 times larger than those of the complex valued matrix $\hat{A}(t)$ and 4 times larger than those of the quaternion valued matrix $\tilde{A}(t)$, the ZNNQR is, by far, the most complex model. Because of this, choosing to solve the TVQ-MPI problem in the real domain has a significant memory penalty, with RAM fast being a limiting factor as $\tilde{A}(t)$ grows in size. When everything is taken into account, all three ZNN models can solve the TVQ-MPI problem, although the ZNNQ appears to have the most potential.

6.   Conclusions

Three models, namely ZNNQ, ZNNQC and ZNNQR, have been presented in order to address the TVQ-MPI problem for TVQ matrices of arbitrary dimension. The creation of those models has been aided by theoretical research and an examination of their computing complexity, in addition to simulated examples and the real-world application involving robotic motion tracking. The TVQ-MPI problem has been successfully solved both directly in the quaternion domain and indirectly, through representation in the complex and real domains. Of the three methods, the direct method, implemented by the ZNNQ model, has been suggested as the most effective and efficient. In light of this, the established findings pave the path for more engaging research projects. The following considerations ought to be taken into account:

● Using the predefined-time ZNN architecture to TVQ-based problems is something that can be looked into.

● Solving nonlinear TVQ-based matrix equations is another task that could be taken into consideration.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by a Mega Grant from the Government of the Russian Federation within the framework of federal project No. 075-15-2021-584.

Conflict of interest

Vasilios N. Katsikis is an editorial board member for AIMS Mathematics and was not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.