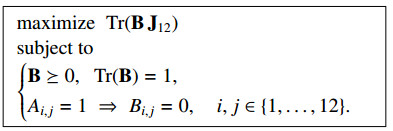1.
Introduction
The concept of the graph capacity, as introduced in Shannon's seminal 1956 paper on zero-error communication [1], plays a key role for understanding the synergy and interaction between the fields of information theory and graph theory. This importance is highlighted in various survey papers [2,3,4,5].
The behavior of the Shannon capacity of a graph, along with its convergence, is quite erratic as is demonstrated by various studies [6,7,8]. The Shannon capacity of a graph and the zero-error capacity of a discrete memoryless channel are generally difficult to compute or even approximate, and notions of their computability have been explored [8,9,10]. Despite these studies, some computability aspects of the capacities in question remain unresolved. Using computationally feasible upper bounds on the Shannon capacity of a graph therefore provides valuable insights [11,12,13,14,15,16,17,18]. These bounds, including the easily computable Lovász ϑ-function [11,12] and others that may be more challenging to compute, offer informative results. In some cases, these bounds also prove to be tight.
The concept of the asymptotic spectrum of graphs, introduced by Zuiddam [19], delineates a space of graph parameters that remain invariant under graph isomorphisms. This space is characterized by the following unique properties: Additivity under disjoint union of graphs, multiplicativity under strong product of graphs, normalization for a simple graph with a single vertex, and monotonicity under graph complement homomorphisms. Building upon Strassen's theory of the asymptotic spectra [20], a novel dual characterization of the Shannon capacity of a graph is derived in [19], expressed as the minimum over the elements of its asymptotic spectrum. By confirming that various graph invariants, including the Lovász ϑ-function [11] and the fractional Haemers bound [14], are elements of the asymptotic spectrum of a graph (spectral points), it can be deduced that these elements indeed serve as upper bounds on the Shannon capacity of a graph. For further exploration, the comprehensive paper by Wigderson and Zuiddam [21] provides a survey on Strassen's theory of the asymptotic spectra and its application areas, including the Shannon capacity of graphs.
The Lovász ϑ-function of a graph, introduced in [11], has important and fascinating properties. It serves as an upper bound on the independence number, and even on the Shannon capacity of a graph, while concurrently functioning as a lower bound on the chromatic number and even on the fractional chromatic number of the complement graph. It found many other applications in graph theory, such as providing a novel lower bound on the max-cut of the complement graph [22]. Remarkably, the Lovász ϑ-function, which is a combinatorial characteristic of graphs, reveals intriguing connections with probabilistic properties, particularly in lower bounding the decoding error probability in classical and quantum information theory, as explored in [23,24]. Additionally, this function was independently extended in [25,26] within the framework of zero-error communication via general quantum channels.
The Lovász ϑ-function of a graph is efficiently computable by the numerical solution of semidefinite optimization problems [11,12,27,28,29]. Its computational efficiency is notable, particularly in light of the NP-hard complexity inherent in computing other graph invariants, such as the independence, clique, and chromatic numbers of a graph, as well as their fractional counterparts [27,30].
This paper explores three research directions, using the properties of the Lovász ϑ-function of a graph. Its main results and structure are outlined as follows.
● Section 2 presents introductory content and notation. Additionally, every subsequent section (Sections 3 to 5) is equipped with specialized preliminaries tailored to its unique focus, offered at the outset of each respective section.
● Section 3 relies on the Lovász ϑ-function for the derivation of new results on the Shannon capacity of graphs (Theorems 3.26–3.29). This includes the calculation of the Shannon capacity for two infinite subclasses of strongly regular graphs, along with extensions of previously established findings. The subsequent discussions and illustrative examples further elucidate these results.
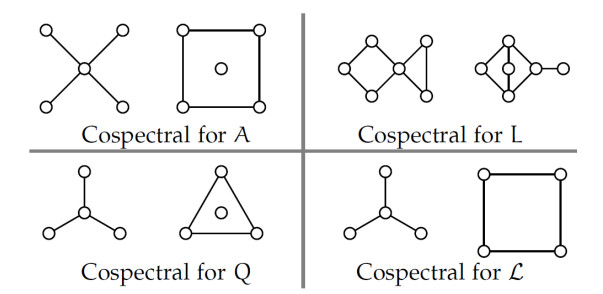
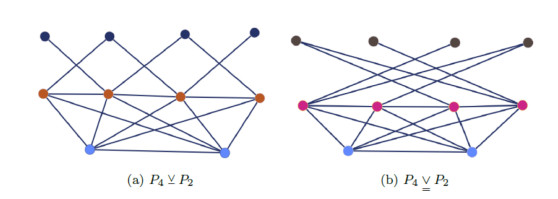
● Section 4 presents new results on cospectral and nonisomorphic irregular graphs. For every even integer n≥14, it offers a construction of connected, irregular, cospectral, and nonisomorphic graphs on n vertices, sharing identical independence, clique, and chromatic numbers, but being distinguished by their Lovász ϑ-functions (Theorem 4.19). The result relies in part on [31,32], and the constructed graphs have identical spectra with respect to each of the following matrices: the adjacency, Laplacian, signless Laplacian, and normalized Laplacian matrices. This section further provides exact expressions or bounds on graph invariants such as the independence number, clique number, chromatic number, Shannon capacity, and the Lovász ϑ-function for the two types of joins of graphs introduced in [32,33] (see Theorems 4.20 and 4.24 in this paper). Section 4 concludes with discussions and numerical experiments elaborating on these results.
● Section 5 relies on the properties of the Lovász ϑ-function for the derivation of bounds on graph invariants. The tightness of these bounds is then compared to existing ones. In light of the analysis presented in [34], closed-form bounds on graph invariants for strongly regular graphs are provided in Corollary 5.8. This section also presents spectral upper and lower bounds on the vector and strict vector chromatic numbers of regular graphs, along with sufficient conditions for their attainability, as stated in Theorem 5.9. Further, exact closed-form expressions for the vector and strict vector chromatic numbers are derived in Theorems 5.12 and 5.14, covering all strongly regular graphs and all graphs that are both vertex- and edge-transitive. This establishes that these two types of chromatic numbers coincide for all such regular graphs. The fractional chromatic number of a graph is known to be lower-bounded by the Lovász ϑ-function of the complement graph. That lower bound on the fractional chromatic number is studied in the context of perfect graphs (Theorem 5.17), and triangle-free graphs. For triangle-free graphs on n vertices, a lower bound on the Lovász ϑ-function is provided in Theorem 5.18, serving as a counterpart to an upper bound for a subfamily of regular and triangle-free graphs in [35]. These bounds match up to a constant scaling factor and scale proportionally to n23. Theorem 5.20 further provides lower bounds on the independence and clique numbers of a graph, derived from the Lovász ϑ-function of the graph or its complement. Additionally, a counterexample demonstrates that, in contrast to the Lovász ϑ-function, which provides an upper bound on the Shannon capacity of a graph, the variant of the ϑ-function by Schrijver does not possess that property (Example 5.24). This resolves a query regarding the variant of the ϑ-function proposed by Schrijver and the identical function presented by McEliece et al. (1978) [36,37], which was also posed as an open question in [16]. Throughout, the presented results in Section 5 are substantiated by numerical findings and are discussed in connection with other existing bounds.
● Section 6 furnishes a concise overview and delineates related open problems.
2.
Preliminaries
2.1. Graphs and matrices
Essential terms and standard notation are presented as follows.
2.1.1. General terminology and notation
Let G=(V,E) be a graph.
● V=V(G) is the vertex set of G, and E=E(G) is the edge set of G.
● An undirected graph is a graph whose edges are undirected.
● A self-loop is an edge that connects a vertex to itself.
● A simple graph is a graph having no self-loops and no multiple edges between any pair of vertices.
● A finite graph is a graph with a finite number of vertices.
● The order of a finite graph is the number of its vertices, |V(G)|=n.
● The size of a finite graph is the number of its edges, |E(G)|=m.
● Vertices i,j∈V(G) are adjacent if they are the endpoints of an edge in G; it is denoted by {i,j}∈E(G) or i∼j.
● An empty graph is a graph without edges, so its size is equal to zero.
● The degree of a vertex v in G is the number of adjacent vertices to v in G, denoted by dv=dv(G).
● A graph is regular if all its vertices have an identical degree.
● A d-regular graph is a regular graph whose all vertices have a fixed degree d.
● A walk in a graph G is a sequence of vertices in G, where every two consecutive vertices in the sequence are adjacent in G.
● A trail in a graph is a walk with no repeated edges.
● A path in a graph is a walk with no repeated vertices; consequently, a path has no repeated edges, so every path is a trail but a trail is not necessarily a path.
● A cycle C in a graph G is obtained by adding an edge to a path P such that it gives a closed walk.
● The length of a path or a cycle is equal to its number of edges. A triangle is a cycle of length 3.
● The length of a shortest cycle in a graph G is called the girth of G.
● A connected graph is a graph where every two distinct vertices are connected by a path.
● A tree is a connected graph that has no cycles (i.e., it is a connected and acyclic graph).
● An r-partite graph is a graph whose vertex set is a disjoint union of r subsets such that no two vertices in the same subset are adjacent. If r=2, then G is a bipartite graph.
● A complete graph on n vertices, denoted by Kn, is a graph whose all n distinct vertices are pairwise adjacent. Hence, Kn is an (n−1)-regular graph of order n.
● A path graph on n vertices is denoted by Pn, and its size is equal to n−1.
● A cycle graph on n vertices is called an n-cycle, and it is denoted by Cn with an integer n≥3. The order and size of Cn are equal to n, and Cn is a bipartite graph if and only if n≥4 is even.
● A complete r-partite graph, denoted by Kn1,…,nr with n1,…nr∈N, is an r-partite graph whose vertex set is partitioned into r disjoint subsets of cardinalities n1,…,nr, such that every two vertices in the same subset are not adjacent, and every two vertices in distinct subsets are adjacent.
● The line graph of G, denoted by ℓ(G), is a graph whose vertices are the edges in G, and two vertices are adjacent in ℓ(G) if the corresponding edges are incident in G.
● The Mycielskian graph of a simple graph G, denoted by M(G), is defined on the vertex set V(M(G))≜{V(G)×{0,1}}∪{zM(G)}, with the edge set
Throughout this paper, the graphs under consideration are finite, simple, and undirected. The standard notation [n]≜{1,…,n}, for every n∈N, is also used.
Definition 2.1 (Subgraphs and graph connectivity). A graph F is a subgraph of a graph G, and it is denoted by F⊆G, if V(F)⊆V(G) and E(F)⊆E(G).
● A spanning subgraph of G is obtained by edge deletions from G, while its vertex set is left unchanged. A spanning tree in G is a spanning subgraph of G that forms a tree.
● An induced subgraph is obtained by removing vertices from the original graph, followed by the deletion of their incident edges.
● A component of G is a maximal connected induced subgraph of G; it is G if connected.
● A connected graph is said to be k-connected, with k∈N, if the induced subgraph resulting from the deletion of any subset of k−1 vertices remains connected.
Definition 2.2 (Maximum-cut problem). Let G be a finite, simple, and undirected graph. Then,
● A maximum cut of G is a partition of the vertex set V(G) into two disjoint subsets S and T that maximizes the number of edges between S and T. The max-cut of G, denoted by mc(G), is the maximum number of edges between S and T for any such partition of V(G). In other words, mc(G) is the maximum number of edges among all bipartite spanning subgraphs of G.
● A simple greedy algorithm shows that mc(G)≥12|E(G)| holds for every graph G.
● The surplus of a graph G, denoted by sp(G), is given by sp(G)≜mc(G)−12|E(G)|≥0.
Definition 2.3 (Isomorphic graphs). Graphs G and H are isomorphic if there exists a bijection f:V(G)→V(H) (i.e., a one-to-one and onto mapping) such that {i,j}∈E(G) if and only if {f(i),f(j)}∈E(H). It is denoted by G≅H, and f is said to be an isomorphism from G to H.
Definition 2.4 (Complement and self-complementary graphs). The complement of a graph G, denoted by ¯G, is a graph whose vertex set is V(G), and its edge set is the complement set ¯E(G). Every vertex in V(G) is nonadjacent to itself in G and ¯G, so {i,j}∈E(¯G) if and only if {i,j}∉E(G) with i≠j. A graph G is self-complementary if G≅¯G (i.e., G is isomorphic to ¯G).
Example 2.5. It can be verified that P4 and C5 are self-complementary graphs.
Definition 2.6 (Disjoint union of graphs). Let G1,…,Gk be graphs. If the vertex sets in these graphs are not pairwise disjoint, let G′2,…,G′k be isomorphic copies of G2,…,Gk, respectively, such that none of the graphs G1,G′2,…G′k have a vertex in common. The disjoint union of these graphs, denoted by G=G1+…+Gk, is a graph whose vertex and edge sets are equal to the disjoint unions of the vertex and edge sets of G1,G′2,…,G′k [G is defined up to an isomorphism].
2.1.2. Graph invariants under isomorphism
Definition 2.7 (Independent sets and independence number). An independent set in a graph G is a subset of its vertices such that no two vertices in that subset are adjacent in G (i.e., it is an induced empty subgraph of G). The largest number of vertices in an independent set of G is called the independence number of G, and it is denoted by α(G).
Definition 2.8 (Cliques and clique number). A clique in a graph G is a subset of its vertices such that every two vertices in that subset are adjacent in G (i.e., it is an induced complete subgraph of G). The largest number of vertices in a clique of G is called the clique number of G, and it is denoted by ω(G). Consequently, every independent set in G is a clique in the complement ¯G, and every clique in G is an independent set in ¯G; in particular, it follows that α(G)=ω(¯G).
Definition 2.9 (Chromatic number). A proper vertex coloring in a graph G is an assignment of colors to its vertices such that no two adjacent vertices get the same color. The smallest number of colors required for such a vertex coloring is called the chromatic number of G, denoted by χ(G).
The chromatic number of a graph G is equal to the smallest number of independent sets in G that partition the vertex set V(G). Indeed, this holds since all vertices in an independent set can be assigned the same color. Consequently, for every graph G,
Proposition 2.10 (Graph invariants). If G≅H, then α(G)=α(H), ω(G)=ω(H), χ(G)=χ(H).
Fractional graph theory converts integer-based definitions of graph invariants as above into their fractional analogues, which are shown to be useful in solving theoretical and practical problems [38]. Essential definitions and results on fractional graph theory are next provided.
Definition 2.11 (Fractional graph coloring). A fractional graph coloring assigns a set of colors to each vertex in a graph such that adjacent vertices have no colors in common. The following terms are used:
(1) A b-fold coloring of a graph is an assignment of a set of b colors to each vertex such that adjacent vertices have no colors in common.
(2) An a:b-coloring is a b-fold coloring out of a available colors. It is a homomorphism to the Kneser graph K(a,b) since its vertices are in one-to-one correspondence with all the b-element subsets of the given a colors, and two vertices are adjacent if their corresponding sets of colors are disjoint.
(3) The b-fold chromatic number of G, denoted by χb(G), is the smallest natural number a such that an a:b-coloring of G exists (by Definition 2.9, χ1(G)=χ(G)).
(4) The fractional chromatic number of G, denoted by χf(G), is defined as
where (2.3) holds since {χb(G)}∞b=1 is a subadditive sequence, i.e.,
and, by Fekete's lemma, if {xk}k≥1 is a nonnegative sequence such that xm+n≤xm+xn for all m,n∈N, then the equality limn→∞xnn=infn∈Nxnn holds.
Theorem 2.12 (The fractional chromatic number of a graph). Let G be a graph, and let I(G) and Imax(G) denote, respectively, the sets of all the independent sets and maximal independent sets in G. Then, the fractional chromatic number of G is the solution of the linear programming (LP) problem
Furthermore,
(1) The solution of the LP problem (2.5) is not affected by restricting I(G) to Imax(G), which requires that only maximal independent sets in G can get positive weights.
(2) The fractional chromatic number of G is a rational number, i.e., χf(G)∈Q.
(3) The following inequality holds by [39]:
The LP problem (2.5) serves as a relaxation of the linear integer-programming problem aimed at determining the chromatic number χ(G). The chromatic number represents the smallest number of (maximal) independent sets required to partition the vertex set of graph G. This relaxation is justified by the observation that all vertices belonging to an independent set in G can be assigned identical colors. Consequently, the optimization variables {xI} in (2.5), corresponding to each independent set I∈I(G), are relaxed to lie within the interval [0,1] rather than being binary variables. This relaxation defines the fractional chromatic number χf(G). Notably, the minimization in the LP problem (2.5) is achieved by constraining the independent sets in G to be maximal. The computational complexity of determining the fractional chromatic number of a graph is NP-hard, as demonstrated in Section 7 of [27]. Additionally, it is noteworthy that the number of maximal independent sets in a graph of fixed order n grows exponentially with n. Specifically, Theorem 1 in [40] bounds this number between 3⌊n/3⌋ and 2⋅3⌊n/3⌋.
The dual LP of (2.5) is a maximization of the sum of the nonnegative weights that are assigned to the vertices in G such that the total weight of the vertices in every maximal independent set in G is at most 1. It is given by the LP problem
The dual LP problem (2.7) forms a relaxation of the integer programming problem for the clique number ω(G). It is defined to be the fractional clique number of the graph G, denoted by ωf(G). By the strong duality in linear programming, which states that the optimal values of the primal and dual LP problems are identical provided that these LP problems are feasible, it follows that
Definition 2.13 (Fractional independence number). The fractional independence number of a graph G is defined to be the fractional clique number of the complement ¯G, i.e.,
Corollary 2.14. The fractional independence, clique, and chromatic numbers of every graph G are rational numbers. These are graph invariants, i.e., if G≅H, then
2.1.3. Matrices associated with graphs
Spectral graph theory delves into relations between the structure of a graph and the eigenvalues of matrices that are associated with the graph. This field constitutes significant aspects of algebraic graph theory, as studied in textbooks such as [29,41,42,43,44,45,46,47]. Next, we provide essential background in spectral graph theory for this paper. The interested reader is further referred to a recent survey paper [48], which presents twenty open problems in spectral graph theory, along with accompanying historical notes.
Definition 2.15 (Adjacency matrix). Let G be a simple undirected graph on n vertices. The adjacency matrix of G, denoted by A=A(G), is an n×n symmetric matrix A=(Ai,j) where Ai,j=1 if {i,j}∈E(G), and Ai,j=0 otherwise (so, the entries in the principal diagonal of A are zeros).
Let di denote, for i∈[n], the degree of the vertex i∈V(G), and let D=D(G) be the diagonal matrix with the diagonal entries d1,…,dn (hence, for a d-regular graph on n vertices, D=dIn).
Definition 2.16 (Laplacian and signless Laplacian matrices). Let G be a simple undirected graph on n vertices with an adjacency matrix A and degree matrix D. Then, the Laplacian and signless Laplacian matrices of G are the symmetric matrices that are, respectively, given by
Definition 2.17 (Normalized Laplacian matrix). The normalized Laplacian matrix L=L(G) of a simple undirected graph G on n vertices, with the adjacency and degree matrices A and D, respectively, is defined to be
The entries of the normalized Laplacian matrix L=(Li,j) are given by
with the convention that if i∈V(G) is an isolated vertex in G (i.e., di=0), then d−12i=0.
The next theorems show that the spectra of a graph with respect to the above four matrices (i.e., the sets of eigenvalues of these matrices) give information about the structure of the graph.
Theorem 2.18 (Number of walks of a given length). Let G=(V,E) be a finite, simple, and undirected graph with an adjacency matrix A=A(G), let i,j∈V, and let ℓ∈N. Then, the number of walks of length ℓ in G, with the fixed endpoints i and j, is equal to (Aℓ)i,j.
Corollary 2.19 (Number of closed walks of a given length). Let G=(V,E) be a simple undirected graph on n vertices with an adjacency matrix A=A(G), and let its spectrum (with respect to A) be given by {λj}nj=1. Then, for all ℓ∈N, the number of closed walks of length ℓ in G is equal to ∑nj=1λℓj.
A graph G is bipartite if and only if it does not include odd cycles. In light of Corollary 2.19, a graph G is bipartite if and only if its spectrum {λj}nj=1 is symmetric around zero.
Corollary 2.20 (Number of edges and triangles in a graph). Let G be a simple undirected graph with n=|V(G)| vertices, e=|E(G)| edges, and t3 triangles. Let A=A(G) be the adjacency matrix of G, and let {λj}nj=1 be its spectrum. Then,
Theorem 2.21 (On the Laplacian matrix). Let G be a finite, simple, and undirected graph, and let L be the Laplacian matrix of G. Then,
(1) The matrix L is a positive semidefinite matrix.
(2) The smallest eigenvalue of L is equal to zero, and its multiplicity is equal to the number of components in G.
(3) The size of G, |E(G)|, is equal to one-half the sum of the eigenvalues of L (with multiplicities).
Theorem 2.22 (On the signless Laplacian matrix). Let G be a finite, simple, and undirected graph, and let Q be the signless Laplacian matrix of G. Then,
(1) The matrix Q is a positive semidefinite matrix.
(2) The least eigenvalue of the matrix Q is equal to zero if and only if G is a bipartite graph.
(3) The multiplicity of 0 as an eigenvalue of Q is equal to the number of bipartite components in G.
(4) The size of G is equal to one-half the sum of the eigenvalues of Q (with multiplicities).
Theorem 2.23 (On the normalized Laplacian matrix). Let G be a finite, simple, and undirected graph, and let L be the normalized Laplacian matrix of G. Then,
(1) The eigenvalues of L lie in the interval [0,2].
(2) The number of components in G is equal to the multiplicity of 0 as an eigenvalue of L.
(3) The number of the bipartite components in G is equal to the multiplicity of 2 as an eigenvalue of L.
Definition 2.24 (Characteristic polynomial). The characteristic polynomial of an n×n matrix M is given by fM(x)≜det(xIn−M), where In denotes the identity matrix of order n. Additionally,
(1) fX(⋅) denotes the X-characteristic polynomial of a graph G, with X∈{A,L,Q,L}.
(2) The zeros of the X-characteristic polynomial of a graph G are the X-eigenvalues of G.
(3) The collection of X-eigenvalues of G, including multiplicities, is the X-spectrum of G.
Let G be a graph on n vertices, and let
be, respectively, the {A,L,Q,L}-eigenvalues of G (including multiplicities). Then,
with equality in (2.26) if and only if G contains a bipartite component. The multiplicity of 2 as an eigenvalue of the normalized Laplacian matrix is equal to the number of bipartite components of G (see Item 3 of Theorem 2.23).
Theorem 2.25 (The number of spanning trees). The number of spanning trees in a graph G on n vertices is determined by the eigenvalues of the Laplacian matrix, and it is equal to 1nn∏ℓ=2μℓ(G).
Remark 2.26 (The number of spanning trees). There are no spanning trees in a disconnected graph, which is consistent with Theorem 2.25 and the fact that if G is disconnected, then the multiplicity of 0 as the smallest eigenvalue of the Laplacian matrix of G is at least 2 (by Item 2 of Theorem 2.21). Moreover, Cayley's formula, which states that the number of trees on n vertices is equal to nn−2 (see, e.g., proofs of this renowned formula in Chapter 33 of [92]), can be derived from Theorem 2.25. This is facilitated by the fact that μ1(Kn)=0 and μ2(Kn)=…=μn(Kn)=n.
The primary focus in spectral graph theory revolves around examining the spectra of graphs with respect to their adjacency and Laplacian matrices. Furthermore, [49,50] provide surveys on the properties of the spectra of finite graphs with respect to their normalized Laplacian and signless Laplacian matrices, respectively. An intriguing connection is next given between the A-eigenvalues of a graph's line graph and the Q-eigenvalues of the original graph, as presented in Proposition 1.4.1 of [41].
Theorem 2.27 (A-eigenvalues of a line graph). Let G be a graph with n vertices and m edges, and let ℓ(G) be the line graph of G. The A-eigenvalues of ℓ(G) satisfy the following properties:
(1) If m≥n, then λi(ℓ(G))=νi(G)−2 for all i∈[n], and λi(ℓ(G))=−2 for all i∈{n+1,…,m}.
(2) Otherwise, if n>m, then it is needed to remove n−m numbers of (−2) from the numbers listed first to get the A-spectrum of ℓ(G).
Remark 2.28 (Size of a graph). In contrast to the A-spectrum, L-spectrum, and Q-spectrum of a graph G, the L-spectrum of G does not determine the size of G (see (2.16), Item 3 in Theorem 2.21, and Item 4 in Theorem 2.22 for the first three spectra).
Unless explicitly specified, the spectrum refers to the A-spectrum of a graph (2.18).
2.1.4. Vertex- and edge-transitive graphs
Vertex- and edge-transitivity, defined as follows, play an important role in characterizing graphs.
Definition 2.29 (Automorphism). An automorphism of a graph G is an isomorphism from G to itself.
Definition 2.30 (Vertex-transitivity). A graph G is said to be vertex-transitive if, for every two vertices i,j∈V(G), there is an automorphism f:V(G)→V(G) such that f(i)=j.
Definition 2.31 (Edge-transitivity). A graph G is edge-transitive if, for every two edges e1,e2∈E(G), there is an automorphism f:V(G)→V(G) that maps the endpoints of e1 to the endpoints of e2.
Example 2.32. A vertex-transitive graph is necessarily regular, but the converse is false. For example, the Frucht graph is a 3-regular graph on 12 vertices that lacks vertex-transitivity (and it also lacks edge-transitivity) [51]. In contrast, an edge-transitive graph is not necessarily regular. As an example, consider a star graph on any number n≥3 of vertices, which is an irregular and edge-transitive graph.
2.1.5. Strongly regular graphs
Strongly regular graphs form an important subfamily of the class of regular graphs [52]. Essential definitions and properties of these graphs are next given.
Definition 2.33 (Strongly regular graphs). A regular graph G that is neither complete nor empty is called a strongly regular graph, with parameters srg(n,d,λ,μ) where λ and μ are nonnegative integers, if the following conditions hold:
(1) G is a d-regular graph on n vertices.
(2) Every two adjacent vertices in G have exactly λ common neighbors.
(3) Every two distinct and nonadjacent vertices in G have exactly μ common neighbors.
Definition 2.34 (Primitive and imprimitive strongly regular graphs). A strongly regular graph G is called primitive if G and its complement ¯G are connected graphs. Otherwise, it is called an imprimitive strongly regular graph.
Theorem 2.35 (On the imprimitive strongly regular graphs). Let G be a strongly regular graph with parameters srg(n,d,λ,μ). Then, the following conditions are equivalent:
(1) G is a disconnected graph;
(2) μ=0;
(3) λ=d−1;
(4) G is isomorphic to m disjoint copies of Kd+1 for some m≥2.
Theorem 2.36 (On the parameters of strongly regular graphs). The four parameters of strongly regular graphs satisfy the following properties:
(1) The complement of a strongly regular graph with parameters srg(n,d,λ,μ) is a strongly regular graph with parameters srg(nc,dc,λc,μc) where
(2) The four parameters of a strongly regular graph srg(n,d,λ,μ) satisfy the equality
Theorem 2.37 (The eigenvalues of strongly regular graphs). The following spectral properties are satisfied by the family of strongly regular graphs:
(1) A strongly regular graph has three distinct eigenvalues.
(2) Let G be a connected strongly regular graph, and let its parameters be srg(n,d,λ,μ). Then, the largest eigenvalue of its adjacency matrix is λ1(G)=d with multiplicity 1, and the other two distinct eigenvalues of its adjacency matrix are given by
with the respective multiplicities
(3) A connected regular graph with exactly three distinct eigenvalues is strongly regular.
Definition 2.38 (Conference graphs). A conference graph on n vertices is a strongly regular graph with the parameters srg(n,12(n−1),14(n−5),14(n−1)) (with n≥5).
By Item 1 of Theorem 2.36, if G is a conference graph on n vertices, then so is its complement ¯G; it is, however, not necessarily self-complementary. By Theorem 2.37, the distinct eigenvalues of the adjacency matrix of G are given by 12(n−1), 12(√n−1), and −12(√n+1) with multiplicities 1,12(n−1), and 12(n−1), respectively. A conference graph is a primitive strongly regular graph.
2.2. The Shannon capacity of graphs
The concept of the Shannon capacity of a graph G was introduced in [1] to consider the largest information rate that can be achieved with zero-error communication. A discrete memoryless channel consists of a finite input set X, a finite or a countably infinite output set Y, and a nonempty fan-out set Sx⊆Y, for every input x∈X. The set Sx is the set of all possible output symbols that can be received at the channel output with positive probability, in each channel use, if the transmitted symbol is x∈X. The study of the maximum amount (rate) of information that a channel can communicate without error is of great interest, and it turns to be a problem in graph theory. To that end, the channel is represented by a confusion graph G whose set of vertices V(G) represents the elements of the input set X, and its set of edges E(G) is constructed such that any two distinct vertices in G are adjacent if and only if the two input symbols are not distinguishable by the channel, so
(Two distinct input symbols are not distinguishable by the channel if and only if they can result in the same output symbol with some positive probability). The largest number of input symbols that a channel can communicate without error in a single use is α(G) (the independence number of the graph G). It is obtained as follows: The sender and the receiver agree in advance on an independent set I of a maximum size α(G), the sender transmits only input symbols in I, and every received output is in the fan-out set of exactly one input symbol in I, so the receiver can correctly determine the transmitted input symbol. Before we proceed, it is required to define the notion of a strong product of graphs.
Definition 2.39 (Strong product of graphs). Let G and H be graphs. The strong product G⊠H is a graph with a vertex set V(G⊠H)=V(G)×V(H) (the Cartesian product), and distinct vertices (g,h) and (g′,h′) are adjacent in G⊠H if and only if one of the following three conditions hold:
(1) g=g′ and {h,h′}∈E(H), (2) {g,g′}∈E(G) and h=h′, (3) {g,g′}∈E(G) and {h,h′}∈E(H). Strong products are therefore commutative and associative up to graph isomorphisms.
Consider the transmission of k-length strings over a channel that is used k≥1 times. The sender transmits a sequence x1…xk, and the receiver gets a sequence y1…yk, where yi∈Sxi for all i∈[k]. The k channel uses are viewed as a single use of an extended channel whose input set is Xk, its output set is Yk, and the fan-out set of (x1,…,xk)∈Xk is the Cartesian product Sx1×…×Sxk. The k-th confusion graph, which refers to the confusion graph of the extended channel, is the k-fold strong power of G that is given by G⊠k≜G⊠…⊠G. The largest number of k-length input strings that are distinguishable by the channel is then equal to α(G⊠k). Using distinguishable strings asserts error-free communication, so the largest achievable information rate per symbol is given by
Under the assumption that the length k of the input strings can be made arbitrarily large, the largest information rate per symbol is given by the supremum of the right-hand side of (2.35) over all k∈N. The resulting amount is defined to be the (logarithm of the) Shannon capacity of the graph G or also the zero-error Shannon capacity of the channel. By supremizing the exponent of the right-hand side of (2.35) over all k∈N, the Shannon capacity of a graph G is given by
where (2.37) holds by Fekete's lemma. Indeed, since α(G⊠H)≥α(G)α(H) holds for every two graphs G and H, it follows that the inequality α(G⊠(k1+k2))≥α(G⊠k1)α(G⊠k2) holds for every graph G and for all k1,k2∈N. This validates the application of Fekete's lemma in (2.37). The supremum on the right-hand side of (2.36) is not necessarily achieved by a finite k∈N [7,53], and the convergence to the Shannon capacity on the right-hand side of (2.37) exhibits erratic behavior [8]. Moreover, several notions of computability of the Shannon capacity of a graph and the zero-error capacity of discrete memoryless channels, known for their computational difficulty, have been addressed in [8,9,10], yet certain aspects of their computability remain unresolved. Except for specific graphs, the Shannon capacity of a graph remains undetermined, even for graphs with a very simple structure. For instance, the Shannon capacity of the cycle graph Cn or its complement, with odd n≥7, remains unresolved, with only bounds and an asymptotic limit theorem currently available [11,54,55,56,57,58,59,60,61,62] (for other graph analogues of odd-cycle graphs, see [63]). Specifically, the Shannon capacity of the 7-cycle graph C7 is bounded as follows [11,60]:
The Shannon capacity of disjoint unions, strong products of graphs, and the complement of the categorical (tensor) product of graphs is studied in [1,6,21,64,65,66].
2.3. Orthonormal representations of graphs
In [11], Lovász introduced the concept of orthonormal representations of graphs to derive an upper bound on the Shannon capacity of graphs in information theory. Orthonormal representations of graphs are related to several fundamental graph properties. That concept is defined and exemplified as follows.
Definition 2.40 (Orthogonal and orthonormal representations of a graph). Let G be a finite, simple, and undirected graph, and let d∈N.
● An orthogonal representation of the graph G in the d-dimensional Euclidean space Rd assigns to each vertex i∈V(G) a nonzero vector ui∈Rd such that uTiuj=0 for every {i,j}∉E(G) with i≠j. In other words, for every two distinct and nonadjacent vertices in the graph, their assigned nonzero vectors should be orthogonal in Rd.
● An orthonormal representation of G is additionally represented by unit vectors, i.e., ‖ for all i \in \mathsf{V}({\mathsf{{G}}}) .
● In an orthogonal (orthonormal) representation of \mathsf{{G}} , nonadjacent vertices in \mathsf{{G}} are mapped into orthogonal (orthonormal) vectors, but adjacent vertices may not necessarily be mapped into nonorthogonal vectors. If {\bf{u}}_i^{\mathrm{T}} {\bf{u}}_j \neq 0 for all \{i, j\} \in \mathsf{E}({\mathsf{{G}}}) , then such a representation of \mathsf{{G}} is called faithful.
Every graph \mathsf{{G}} on n vertices can be trivially represented by an orthonormal representation in {\mathbb{R}}^n , by assigning each vertex i \in [{n}] to the standard unit-vector {\bf{e}}_i (with a single \tt{1} at the i -th coordinate, and zeros elsewhere). That orthonormal representation is not faithful, unless \mathsf{{G}} is an empty graph. In order to obtain an n -dimensional faithful orthogonal representation, let \mathbf{L} = (L_{i, j}) be the Laplacian matrix of \mathsf{{G}} , which is a positive semidefinite matrix, and let {\bf{u}}_i ( i \in [{n}] ) be the i -th column of the matrix \mathbf{L}^{1/2} . Then, {\bf{u}}_i^{\mathrm{T}} {\bf{u}}_j = L_{i, j} for all i, j \in [{n}] , which implies that \{{\bf{u}}_i\} is a faithful orthogonal representation of \mathsf{{G}} . This idea extends to the signless Laplacian matrix \mathbf{Q} and the normalized Laplacian matrix {\bf{\mathcal{L}}} since these are positive semidefinite matrices by Theorems 2.21–2.23).
Example 2.41 ([29], Example 10.5). In an orthogonal representation of a graph \mathsf{{G}} , every vertex in a clique of \mathsf{{G}} can be represented by an identical vector. Let k \triangleq \chi({\overline{\mathsf{{G}}}}) be the chromatic number of the complement graph \overline{\mathsf{{G}}} . Then, there is a family of k disjoint cliques in \mathsf{{G}} , denoted by \mathcal {B}_1, \ldots, \mathcal {B}_k , covering the vertex set \mathsf{V}({\mathsf{{G}}}) . Mapping all the vertices in the subset \mathcal {B}_i , for i \in [{k}] , into {\bf{e}}_i \in {\mathbb{R}}^k gives an orthonormal representation of \mathsf{{G}} in the k -dimensional Euclidean space. That orthogonal representation is not guaranteed to be faithful. Indeed, unless \mathsf{{G}} is a disjoint union of complete graphs, it is possible for two adjacent vertices in \mathsf{{G}} to belong to different cliques; however, their corresponding vectors are orthogonal.
The construction of low-dimensional orthogonal representations of graphs, particularly those with unique properties, is a significant area of study in graph theory. Detailed discussions on the minimum dimension of orthogonal representations of general graphs, especially those lacking specific subgraphs, can be found in [11,67,68,69] and Chapter 10 of [29]. Some of the bounds on the minimum dimension of such representations involve the Lovász \vartheta -function, which is presented in Section 2.5 (see Item 8 of that section). The minimum dimension of orthonormal representations of a graph \mathsf{{G}} on n vertices is equal to the minimum rank over all positive semidefinite matrices {\bf{M}} = (M_{i, j}) such that M_{i, i} = 1 for all i \in [{n}] , and M_{i, j} = 0 for all \{i, j\} \not\in \mathsf{E}({\mathsf{{G}}}) [69]. Here, {\bf{M}} serves as the Gram matrix of the representing vectors {\bf{u}}_1, \ldots, {\bf{u}}_n , with M_{i, j} \triangleq {\bf{u}}_i^{\mathrm{T}} {\bf{u}}_j for all i, j \in [{n}] . Consequently, the minimum dimension among all orthonormal representations of a graph \mathsf{{G}} is also termed the minimum semidefinite rank of \mathsf{{G}} , and it is denoted by \mathrm{msr}(\mathsf{{G}}) . A notable result by Lovász et al. [67] demonstrates a relationship between graph connectivity and the minimum dimension d required for an orthogonal representation of a graph to ensure that any d of the representing vectors are linearly independent in {\mathbb{R}}^d . Theorem 1 of [67] states that a connected, undirected, and simple graph \mathsf{{G}} on n vertices has such an orthogonal representation in {\mathbb{R}}^d if and only if \mathsf{{G}} is (n-d) -connected. The latter result is also shown in Section 10.3 of [29].
2.4. Vector and strict vector chromatic numbers of graphs
The vector and strict vector colorings of graphs, and their associated chromatic numbers, were defined by Karger et al. [70]. These notions are introduced as follows, and Section 2.5 addresses in part their relations to the Lovász \vartheta -function and its variants, as well as their relations to other graph invariants.
Definition 2.42 (Vector chromatic number). Let \mathsf{{G}} be a nonempty graph on n vertices, and let t \geq 2 be a real number. A vector t -coloring of \mathsf{{G}} in {\mathbb{R}}^d , with d \in {\mathbb{N}} , is an assignment of a unit vector {\bf{u}}_i \in {\mathbb{R}}^d to each vertex i \in \mathsf{V}({\mathsf{{G}}}) such that, for every two adjacent vertices \{i, j\} \in \mathsf{E}({\mathsf{{G}}}) ,
The vector chromatic number of a nonempty graph \mathsf{{G}} , denoted by \chi_{\mathrm{v}}({\mathsf{{G}}}) , is the smallest real number t \geq 2 for which a vector t -coloring of \mathsf{{G}} exists in {\mathbb{R}}^n (namely, the vector t -coloring of \mathsf{{G}} is assumed here to be of dimension n ). The vector chromatic number of an empty graph is defined to be equal to 1.
Let \mathsf{{G}} be a graph on n vertices, and let {\bf{A}} = (A_{i, j}) be its n \times n adjacency matrix. For a real symmetric n \times n matrix {\bf{M}} , the standard notation {\bf{M}} \succeq 0 means that the matrix {\bf{M}} is positive semidefinite. By Definition 2.42, and by setting the n \times n matrix {\bf{M}} = (M_{i, j}) with M_{i, j} \triangleq (t-1) {\bf{u}}_i^{\mathrm{T}} \, {\bf{u}}_j for all i, j \in [{n}] , the vector chromatic number of \mathsf{{G}} can be expressed to be equal to the value of the following semidefinite programming (SDP) problem:
Let {\bf{J}}_n be the all-ones n \times n matrix. The dual of the SDP problem (2.40) is given by
Strong duality holds here since the SDP problems are feasible and bounded, so the solutions of the dual SDP problems in (2.40) and (2.41) coincide. Applying the SDP problem in (2.41) to the complement \overline{\mathsf{{G}}} gives the Schrijver \vartheta -function of the graph \mathsf{{G}} , which is denoted by \vartheta'(\mathsf{{G}}) . In light of (2.41), with \mathsf{{G}} replaced by the complement \overline{\mathsf{{G}}} , the value of \vartheta'(\mathsf{{G}}) is obtained by solving the SDP problem (see Eq (23) in [37]):
The vector chromatic number and Schrijver's \vartheta -function therefore satisfy the equality
for every graph \mathsf{{G}} . By (2.42), it follows that
which holds by selecting a feasible solution in (2.42) as follows. Let \mathcal{I} be a largest independent set in \mathsf{{G}} , and let \mathcal{I} = \{i_1, \ldots, i_\ell\} \subseteq [{n}] with \ell = \alpha({\mathsf{{G}}}) . Define {\bf{B}} to be the n \times n symmetric matrix whose elements are given by B_{i, j} \triangleq \frac{1}{\alpha({\mathsf{{G}}})} whenever i, j \in \mathcal{I} , and B_{i, j} \triangleq 0 otherwise. Then, {\bf{B}} is indeed a positive semidefinite matrix whose trace is equal to 1, and the objective function in (2.42) is then equal to \alpha({\mathsf{{G}}}) . Due to the maximization in (2.42), inequality (2.44) holds.
Schrijver's \vartheta -function of a graph was studied independently by McEliece et al. [36] (with a different notation, where \vartheta'(\mathsf{{G}}) in [37] is replaced by \alpha_{\mathrm{L}}(\mathsf{{G}}) in [36]). In a subsequent study by Szegedy [71], \vartheta'(\mathsf{{G}}) is denoted by \vartheta_{1/2}(\mathsf{{G}}) (an additional variant, denoted by \vartheta_2(\mathsf{{G}}) , was also introduced in [71]). To that end, the SDP problem in (2.42) was modified by replacing the last two lines in (2.42) with the requirement that B_{i, j} \leq 0 for all i, j \in [{n}] such that A_{i, j} = 1 (see Eq (8) in [71]). The Schrijver \vartheta -function of a graph \mathsf{{G}} , \vartheta'(\mathsf{{G}}) , constitutes a variant of the Lovász \vartheta -function \vartheta(\mathsf{{G}}) , which is subsequently introduced in Section 2.5.
Spectral characterizations of the vector chromatic number of a graph, which is equal to the Schrijver \vartheta -function of the graph complement by (2.43), were studied in [72,73], and more recently in [74,75]. We next define the strict vector chromatic number of a graph, which is also shown in Section 2.5 to be related to the Lovász \vartheta -function in a similar way to (2.43) (see (2.50)).
Definition 2.43 (Strict vector chromatic number). Let \mathsf{{G}} be a nonempty graph on n vertices, and let t \geq 2 be a real number. A strict vector t -coloring of \mathsf{{G}} is an assignment of a unit vector {\bf{u}}_i \in {\mathbb{R}}^n to each vertex i \in \mathsf{V}({\mathsf{{G}}}) such that, for every two adjacent vertices \{i, j\} \in \mathsf{E}({\mathsf{{G}}}) , the condition in (2.39) holds with equality. The strict vector chromatic number of a nonempty graph \mathsf{{G}} , denoted by \chi_{\mathrm{sv}}({\mathsf{{G}}}) , is the smallest real number t \geq 2 for which a strict vector t -coloring of \mathsf{{G}} exists. The strict vector chromatic number of an empty graph is defined to be equal to 1.
Clearly, by Definitions 2.42 and 2.43, the inequality
holds for every graph \mathsf{{G}} . By Definition 2.43, the strict vector chromatic number is expressed as a solution of the SDP problem that is almost similar to (2.40); the only difference is that the last inequality constraints in (2.40) turn into equality constraints. Then, similarly to the transition from the SDP problem in (2.40) to the dual SDP problem in (2.41), strong duality gives that the strict vector chromatic number \chi_{\mathrm{sv}}({\mathsf{{G}}}) can be obtained by solving the following SDP problem:
In comparison to (2.41), the condition that all entries of {\bf{B}} are nonnegative is absent in (2.46).
2.5. The Lovász \vartheta -function of graphs
The Lovász \vartheta -function of a graph, as introduced in [11], exhibits intriguing connections to diverse graph parameters such as the independence number, clique number, chromatic number, and Shannon capacity of the graph. Its efficient computability renders it a potent tool in information theory, graph theory, and combinatorial optimization.
Definition 2.44 (Lovász \vartheta -function). Let \mathsf{{G}} be a finite, simple, and undirected graph. Then, the Lovász \vartheta -function of \mathsf{{G}} is defined as
where the minimum is taken over all orthonormal representations \{{\bf{u}}_i: i \in \mathsf{V}({\mathsf{{G}}}) \} of \mathsf{{G}} , and all unit vectors {\bf{c}} . The unit vector \bf{c} is called the handle of the orthonormal representation. The minimization on the right-hand side of (2.47) is implicitly performed over the dimension of the vectors. However, without any loss of generality, it suffices to restrict their dimension to be equal to n = |{ \mathsf{V}({\mathsf{{G}}})}| .
The Lovász \vartheta -function can be expressed as a solution of an SDP problem. To that end, let {\bf{A}} = (A_{i, j}) be the n \times n adjacency matrix of \mathsf{{G}} with n \triangleq |{ \mathsf{V}({\mathsf{{G}}})}| . The Lovász \vartheta -function \vartheta(\mathsf{{G}}) can be expressed by the following convex optimization problem:
The SDP formulation in (2.48) yields the existence of an algorithm that computes \vartheta(\mathsf{{G}}) , for every graph \mathsf{{G}} , with a precision of r decimal digits, and a computational complexity that is polynomial in n and r . A comparison of the optimization problems in (2.41) and (2.48) gives
which holds for every graph \mathsf{{G}} . Indeed, (2.49) follows from the additional constraint in (2.41) that all the entries of the positive semidefinite matrix {\bf{B}} are nonnegative, whereas the latter condition is absent in (2.48). A comparison of the SDP problems in (2.46) and (2.48) also gives (see Theorem 8.2 in [70])
The following properties of the Lovász \vartheta -function and its variant by Schrijver are collected from [3,11,12,22,27,29,34,37,39,68,69,71,76,77,78,79], presented herein for reference and convenience. Some of these properties are employed in the analysis presented in this paper. It is assumed throughout that the graphs are finite, simple, and undirected.
(1) Upper bound on the Shannon capacity of graphs: For every graph \mathsf{{G}}
Although the upper bound in (2.51) is tight in some cases, e.g., for the family of Kneser graphs and the family of self-complementary vertex-transitive graphs [29], it is not a tight bound in general. More explicitly, there exists a sequence of graphs \{\mathsf{{G}}_n\} where \mathsf{{G}}_n is a graph on n vertices such that \Theta(\mathsf{{G}}_n) \leq 3 and \vartheta(\mathsf{{G}}_n) > \sqrt[4]{n} for all n \in {\mathbb{N}} .
(2) Sandwich theorem:
(3) The inequality \vartheta(\mathsf{{G}}) \geq 1 holds in general, with an equality if and only if \mathsf{{G}} is a complete graph.
(4) Computational complexity of graph invariants:
● Computing \alpha({\mathsf{{G}}}) , \alpha_{\mathrm{f}}({\mathsf{{G}}}) , \omega({\mathsf{{G}}}) , \omega_{\mathrm{f}}({\mathsf{{G}}}) , \chi_{\mathrm{f}}({\mathsf{{G}}}) , and \chi({\mathsf{{G}}}) constitutes NP-hard problems.
● Computing bounds on these graph invariants, specifically \vartheta(\mathsf{{G}}) , \vartheta'(\mathsf{{G}}) , \vartheta(\overline{\mathsf{{G}}}) , and \vartheta'(\overline{\mathsf{{G}}}) (by (2.52) and (2.53)), in any desired precision, is feasible. The computational complexity scales polynomially in n , and it is obtained by numerically solving the SDP problems presented in Section 2.4 and (2.48).
(5) For every graph \mathsf{{G}} , combining (2.6) and (2.52) gives
By Item 4, (2.54) gives computable lower bounds on the ratio \frac{ \chi_{\mathrm{f}}({\mathsf{{G}}})}{ \chi({\mathsf{{G}}})} .
(6) In regard to (2.52), the ratios \frac{ \chi({\overline{\mathsf{{G}}}})}{\vartheta(\mathsf{{G}})} and \frac{\vartheta(\mathsf{{G}})}{\alpha({\mathsf{{G}}})} can be made arbitrarily large as follows:
● There exist a constant c > 0 and an infinite sequence of graphs \{\mathsf{{G}}_\ell\} , with increasing orders n_\ell \triangleq |{ \mathsf{V}({\mathsf{{G}}_\ell})}| , for which \alpha({\mathsf{{G}}_\ell}) < 2^{\sqrt{\log n_\ell}} and \vartheta(\mathsf{{G}}_\ell) > n_\ell \, 2^{-c \sqrt{\log n_\ell}} hold for all \ell .
● There exist a constant c > 0 and an infinite sequence of graphs \{\mathsf{{G}}_\ell\} , with increasing orders n_\ell \triangleq |{ \mathsf{V}({\mathsf{{G}}_\ell})}| , for which \vartheta(\mathsf{{G}}_\ell) < 2^{\sqrt{\log n_\ell}} and \chi({\overline{\mathsf{{G}}}_\ell}) > n_\ell \, 2^{-c \sqrt{\log n_\ell}} hold for all \ell .
(7) A counterexample shows that, unlike (2.51), \Theta(\mathsf{{G}}) \not\leq \vartheta'(\mathsf{{G}}) (see Example 5.24 here).
(8) If a graph \mathsf{{G}} has an orthonormal representation in the d -dimensional Euclidean space {\mathbb{R}}^d , then d \geq \vartheta(\mathsf{{G}}) by Theorem 11 of [11], and d \geq \tfrac12 \log_2 \chi({\overline{\mathsf{{G}}}}) by Proposition 10.8 of [11]. Additionally, by Example 2.41, there exists an othornormal representation of \mathsf{{G}} in {\mathbb{R}}^d with d = \chi({\overline{\mathsf{{G}}}}) . The minimum semidefinite rank of \mathsf{{G}} , denoted by \mathrm{msr}(\mathsf{{G}}) , is equal to the minimum dimension d of an orthonormal representation of \mathsf{{G}} in {\mathbb{R}}^d (see Section 2.3), so
This indicates that the minimum dimension of an orthonormal representation of a graph \mathsf{{G}} is somewhat related to the chromatic number of the graph complement \overline{\mathsf{{G}}} .
(9) Factorization under strong products: For all graphs \mathsf{{G}} and \mathsf{{H}} ,
(10) For every graph \mathsf{{G}} on n vertices,
with an equality in (2.57) if the graph \mathsf{{G}} is vertex-transitive or strongly regular.
(11) Let \mathsf{{G}} be a d -regular graph on n vertices. Then,
with an equality in (2.58) if \mathsf{{G}} is an edge-transitive graph.
(12) More generally, if \mathsf{{G}} is a d -regular graph on n vertices, then for every symmetric nonzero n \times n matrix {\mathbf{M}} such that M_{i, j} = 0 for \{i, j\} \in \mathsf{E}({\overline{\mathsf{{G}}}}) and also for i = j , and with {\mathbf{M}} having equal row-sums, the following holds:
If \mathsf{{G}} is a vertex-transitive graph, then there exists such a matrix {\mathbf{M}} attaining equality in (2.59). If \mathsf{{G}} is an edge-transitive graph, then (2.59) holds with equality for {\mathbf{M}} = \mathbf{A}(\mathsf{{G}}) .
(13) Lovász \vartheta -function of subgraphs:
● If \, \mathsf{{H}} is a spanning subgraph of a graph \mathsf{{G}} , then \vartheta(\mathsf{{H}}) \geq \vartheta(\mathsf{{G}}) .
● If \, \mathsf{{H}} is an induced subgraph of a graph \mathsf{{G}} , then \vartheta(\mathsf{{H}}) \leq \vartheta(\mathsf{{G}}) .
(14) For two graphs \mathsf{{G}} and \mathsf{{H}} , let \mathsf{{G}} + \mathsf{{H}} denote their disjoint union (see Definition 2.6). Then,
(15) Let \mathsf{{G}} be a graph on n vertices, and let \alpha({\mathsf{{G}}}) = k . Then,
(16) Let \mathsf{{G}} be a graph on n vertices, and let \vartheta(\overline{\mathsf{{G}}}) = t \geq 2 . Then,
(17) The surplus of a graph \mathsf{{G}} (see Definition 2.2), denoted by \mathrm{sp}(\mathsf{{G}}) , satisfies
The utility of (2.63) in lower bounding the surplus of a graph \mathsf{{G}} follows from the fact that the computational complexity of the max-cut of a graph is NP-complete, whereas the computation of the vector chromatic number in the middle term of (2.63), as well as of the Lovász \vartheta -function in the rightmost term of (2.63), is feasible (see Section 2.4 and Item 4 above).
(18) For every graph \mathsf{{G}} ,
where the supremum is taken over all (simple, finite, and undirected) graphs \mathsf{{H}} .
(19) For every graph \mathsf{{G}} on n vertices, let \tilde{\vartheta}(\mathsf{{G}}) \triangleq \underset{\mathsf{{H}}}{\max} \, \dfrac{|{ \mathsf{V}({\mathsf{{H}}})}|}{\vartheta(\mathsf{{H}})} , where the maximization is taken over all the induced subgraphs \mathsf{{H}} of \mathsf{{G}} (see Eq (10) in [71]). Then, the following holds:
(20) For every graph \mathsf{{G}} on n vertices, the following two equivalent chain of inequalities hold:
(21) Let \mathsf{{G}} be a graph on n vertices, and let \ell(\mathsf{{G}}) be the maximum of \| {\bf{u}}_1 + \ldots + {\bf{u}}_n \| over all orthonormal representations \{{\bf{u}}_i\} of \mathsf{{G}} . Then,
and the upper and lower bounds in (2.67) coincide if \mathsf{{G}} is a vertex-transitive or a strongly regular graph. [By Claim 1.2 in [69], (2.67) holds with equalities if \mathsf{{G}} is vertex-transitive. It also holds with equalities if \mathsf{{G}} is a strongly regular graph, as indicated by the sufficient condition for equality in (2.57) (see Corollary 1 in [34] or Corollary 3.4 here)].
(22) The Lovász \vartheta -function of the complement of the Mycielskian \mathrm{M}(\mathsf{{G}}) of a graph \mathsf{{G}} is uniquely determined by \vartheta(\overline{\mathsf{{G}}}) (see Theorem 2 in [78] for an explicit equation).
(23) For every graph \mathsf{{G}} on n vertices, the following holds:
(a)
where the maximization on the right-hand side of (2.68) is taken over all the unit vectors \mathbf{d} and orthonormal representations \{{\mathbf{v}}_i\}_{i = 1}^n of the complement graph \overline{\mathsf{{G}}} .
(b)
where the minimization on the right-hand side of (2.69) is taken over all n \times n symmetric matrices {\mathbf{U}} = (U_{i, j}) with U_{i, j} = 1 for all i, j \in [{n}] such that \{i, j\} \in \mathsf{E}({\overline{\mathsf{{G}}}}) or i = j .
(c)
where the maximization on the right-hand side of (2.70) is taken over all positive semidefinite n \times n matrices {\mathbf{W}} \succeq 0 with W_{i, j} = 0 for all \{i, j\} \in \mathsf{E}({\mathsf{{G}}}) , and W_{i, i} = 1 for all i \in [{n}] .
(d)
where the maximization on the right-hand side of (2.71) is taken over all symmetric nonzero n \times n matrices {\bf{T}} = (T_{i, j}) with T_{i, j} = 0 for all i, j \in [{n}] such that \{i, j\} \in \mathsf{E}({\mathsf{{G}}}) or i = j .
(e) The SDP problem in (2.48) is given by
where the maximization on the right-hand side of (2.72) is taken over all positive semidefinite n \times n matrices {\bf{B}} \succeq 0 with \mathrm{Tr}({\bf{B}}) = 1 , and B_{i, j} = 0 for all i, j \in [{n}] such that \{i, j\} \in \mathsf{E}({\mathsf{{G}}}) .
(f)
where the minimization on the right-hand side of (2.73) is taken over all positive semidefinite n \times n matrices {\bf{Y}} \succeq 0 with Y_{i, j} = -1 for all i, j \in [{n}] such that \{i, j\} \not\in \mathsf{E}({\mathsf{{G}}}) .
3.
Observations on the Shannon capacity of graphs
Shannon's problem of zero-error communication and the notion of the Shannon capacity of graphs [1] had a major impact on the development of information theory, extremal combinatorics, and graph theory. This section provides new observations on the Shannon capacity of graphs.
3.1. Specialized preliminaries for Section 3
The present section starts with the introduction of specialized preliminaries that are essential for elucidating the subsequent results. These preliminaries encompass bounds and exact findings related to the Lovász \vartheta -function for regular and strongly regular graphs. We also include results pertaining to subclasses of self-complementary regular graphs.
3.1.1. On the Lovász \vartheta -function of regular and strongly regular graphs
Theorem 3.1 (Bounds on the Lovász function of regular graphs, [34]). Let \mathsf{{G}} be a d -regular graph of order n , which is a noncomplete and nonempty graph. Then, the following bounds hold for the Lovász \vartheta -function of \mathsf{{G}} and its complement \overline{\mathsf{{G}}} :
(1)
● Equality holds in the leftmost inequality of (3.1) if \overline{\mathsf{{G}}} is both vertex-transitive and edge-transitive, or if \mathsf{{G}} is a strongly regular graph;
● Equality holds in the rightmost inequality of (3.1) if \mathsf{{G}} is edge-transitive, or if \mathsf{{G}} is a strongly regular graph.
(2)
● Equality holds in the leftmost inequality of (3.2) if \mathsf{{G}} is both vertex-transitive and edge-transitive, or if \mathsf{{G}} is a strongly regular graph;
● Equality holds in the rightmost inequality of (3.2) if \overline{\mathsf{{G}}} is edge-transitive, or if \mathsf{{G}} is a strongly regular graph.
Corollary 3.2. All inequalities in Theorem 3.1 hold with equality if \mathsf{{G}} is a strongly regular graph.
Proof. This follows from the sufficient conditions of the inequalities in Theorem 3.1 to hold with equality. Recall that a graph \mathsf{{G}} is strongly regular if and only if \overline{\mathsf{{G}}} is so. □
Theorem 3.3 (Lovász function of strongly regular graphs, [34]). Let \mathsf{{G}} be a strongly regular graph with parameters \mathsf{srg}({n}, {d}, {\lambda}, {\mu}) . Then,
where
Furthermore, if 2d + (n-1)(\lambda-\mu) \neq 0 , then \vartheta(\mathsf{{G}}), \, \vartheta(\overline{\mathsf{{G}}}) \in {\mathbb{Q}} (i.e., rational numbers).
Corollary 3.4 (An identity for vertex-transitive or strongly regular graphs). The equality
holds for all vertex-transitive graphs and for all strongly regular graphs.
Proof. Equality (3.6) holds for vertex-transitive graphs by Theorem 8 in [11]. For strongly regular graphs, (3.6) follows readily from the expressions for the Lovász \vartheta -functions in (3.3) and (3.4). □
Remark 3.5. By Theorem 5 in [37], equality (3.6) holds more generally for all graphs derived from symmetric association schemes, specifically including the family of strongly regular graphs.
Remark 3.6. (Strongly regular graphs are not necessarily vertex- or edge-transitive graphs). In light of Corollary 3.4, it should be noted that many strongly regular graphs are neither vertex- nor edge-transitive. One such example is Gritsenko's graph [80], which is a conference graph on 65 vertices; it is a strongly regular graph with parameters \mathsf{srg}({65}, {32}, {15}, {16}) that is neither vertex- nor edge-transitive, and it is also not self-complementary. These findings can be verified, for example, by the aid of the SageMath software [51]. The existence of a self-complementary and strongly regular graph that is not vertex-transitive, however, remains an open problem (see Item 6 in Remark 3.12).
3.1.2. The Shannnon capacity of self-complementary vertex-transitive graphs
In some cases, the Shannon capacity of a graph can be calculated exactly, and the Lovász \vartheta -function is a tight bound. This includes the following result.
Theorem 3.7 (Theorem 12 in [11]). Let \mathsf{{G}} be an undirected and simple graph on n vertices.
(1) If \mathsf{{G}} is a vertex-transitive graph on n vertices, then
(2) If \mathsf{{G}} is a self-complementary and vertex-transitive graph on n vertices, then
Remark 3.8. Strengthened and refined versions of Theorem 3.7 are provided in Section 3.2.
3.1.3. On classes of regular and self-complementary graphs
Theorem 3.9 (On symmetry, regularity, and strong regularity). If \mathsf{{G}} is a regular graph, and \mathsf{{G}} and \overline{\mathsf{{G}}} are both edge-transitive, then \mathsf{{G}} is a strongly regular graph.
Theorem 3.10 ([81]). A connected, strongly regular, and edge-transitive graph is vertex-transitive.
Corollary 3.11. If \mathsf{{G}} is a self-complementary, regular, and edge-transitive graph, then \mathsf{{G}} is strongly regular and vertex-transitive.
Proof. Corollary 3.11 follows as a special case of the combination of Theorems 3.9 and 3.10. □
Remark 3.12. This remark refers to subclasses of self-complementary regular graphs.
(1) Self-complementary vertex-transitive graphs and self-complementary strongly regular graphs are nonequivalent classes. These two subclasses of self-complementary regular graphs have gained interest in the literature, as evidenced by their exploration in various works, including [34,82,83,84,85,86,87,88,89,90,91].
(2) Self-complementary regular graphs that are edge-transitive are also strongly regular (Lemma 4.3 in [87]) and vertex-transitive (Theorem 4.12 in [83], and Corollary 3.11 here).
(3) The converse of the statement in Item 2 is false. Even if a graph is self-complementary, strongly regular, and vertex-transitive, it is not necessarily edge-transitive. This can be confirmed using the SageMath software, by showing that there are pseudo Latin square graphs, which are squared skew-Hadamard matrix graphs, possessing the mentioned properties but lacking edge-transitivity.
(4) Self-complementary vertex-transitive graphs are not necessarily strongly regular, as evidenced by a specific construction. This construction involves a self-complementary and vertex-transitive circulant graph on 13 vertices, which is not strongly regular (see Theorems 4.1 and 4.5 in [87,89]).
(5) A conference graph is a strongly regular graph of the form \, \mathsf{srg}({4k+1}, {2k}, {k-1}, {k}) with k \in {\mathbb{N}} . A self-complementary and strongly regular graph is a conference graph, as it can be verified by Item 1 of Theorem 2.36.
(6) It is an open problem to determine if there exists a self-complementary and strongly regular graph that is not vertex-transitive (see page 88 in [82]).
The following results hold for two subclasses of self-complementary regular graphs.
Theorem 3.13 (Theorem 2 in [84]). There exists a self-complementary strongly regular graph on n vertices only if n \equiv 1 \bmod 4 is expressible as a sum of two squares of integers.
Notably, Theorem 3.13 omits the 'if' part, which posits the presence of such graphs for all cases meeting the specified congruence and sum of squares criteria. This aspect remains an unresolved issue.
Theorem 3.14 (Muzychuk [85], Rao [87]). There exists a self-complementary vertex-transitive graph on n vertices if and only if n \equiv 1 \bmod 4 is expressible as a sum of two squares of integers.
● The 'if' part of Theorem 3.14 is due to Theorem 4.6 in [87].
● The 'only if' part of Theorem 3.14 is due to [85].
In light of Theorems 3.13 and 3.14, the following result is presented, which is a well-established finding in number theory (see, e.g., Chapter 4 in [92]).
Theorem 3.15 (Sum of two squares of integers). A natural number n \in {\mathbb{N}} can be represented as a sum of two squares of integers if and only if every prime factor of the form p = 4m+3 appears with an even exponent in the prime decomposition of n .
3.1.4. Latin square graphs
The class of Latin square graphs consists of two types: Strongly regular graphs and complete graphs. To facilitate their presentation, two key notions are briefly introduced.
Definition 3.16 (Transversal 2-designs). Let m \geq 2 and n \geq 1 be integers. A transversal 2-design of order n and block size m is a triple (\mathcal {X}, \mathscr{G}, \mathscr{B}) , satisfying the following conditions:
(1) \mathcal {X} is a set of mn points.
(2) \mathscr{G} = \{ \mathcal {G}_1, \ldots, \mathcal {G}_m\} is a partition of \mathcal {X} into m subsets (called groups), each containing n points.
(3) \mathscr{B} is a class of subsets of \mathcal {X} (called blocks) such that
(a) Every block \mathcal {B} \in \mathscr{B} contains exactly one point from each group \mathcal {G}_j with j \in [{m}] .
(b) Every two points, not contained in the same group, belong together to a single block \mathcal {B} \in \mathscr{B} .
Such a transversal 2-design is denoted by \mathrm{TD}(m, n) .
Theorem 3.17. Let (\mathcal {X}, \mathscr{G}, \mathscr{B}) be a transversal 2-design \mathrm{TD}(m, n) . Then,
(1) Every block \mathcal {B} \in \mathscr{B} contains m points.
(2) Every point x \in \mathcal {X} belongs to n blocks.
(3) Every two distinct blocks \mathcal {B}, \mathcal {B}' \in \mathscr{B} intersect in one element or in no element.
(4) |{\mathscr{B}}| = n^2 .
Definition 3.18 (Latin squares). A Latin square of order n is an n \times n array filled with n different symbols, each occurring exactly once in each row and in each column.
In the continuation, a Latin square of order n is filled with the elements of the set [{n}] \triangleq \{1, \ldots, n\} .
Theorem 3.19. The number of Latin squares of order n , denoted by L(n) , satisfies
and, consequently, the following exact asymptotic result holds:
Proof. See, e.g., Chapter 37 (pages 266–267) of [92]. □
Definition 3.20 (Orthogonal Latin squares). Two Latin squares \mathbf{A} = (a_{i, j}) and \mathbf{B} = (b_{i, j}) of order n are said to be orthogonal Latin squares if for all x, y \in [{n}] , there exists a unique position (i, j) \in [{n}] \times [{n}] such that a_{i, j} = x and b_{i, j} = y . A set of Latin squares of the same order are said to be mutually orthogonal if every pair of squares within the set are orthogonal.
Theorem 3.21 (On mutually orthogonal Latin squares). Let n \in {\mathbb{N}} , and denote by N(n) the largest number of mutually orthogonal Latin squares of order n .
(1) If n is a prime power, then N(n) = n-1 . In general, N(n) \leq n-1 .
(2) The existence of m-2 mutually orthogonal Latin squares of order n is equivalent to the existence of a transversal 2-design of order n and block size m , namely \mathrm{TD}(m, n) .
Definition 3.22 (Latin square graphs). Let (\mathcal {X}, \mathscr{G}, \mathscr{B}) be a \mathrm{TD}(m, n) transversal 2-design with integers m \geq 2 and n \geq 1 . The associated Latin square graph \mathsf{{G}} = (\mathsf{V}, \mathsf{E}) has the vertex set \mathsf{V} = \mathscr{B} , and each two distinct vertices \mathcal {B}, \mathcal {B}' \in \mathscr{B} are adjacent if |{ \mathcal {B} \cap \mathcal {B}'}| = 1 . This graph is said to be an \mathrm{L}_{{m}}({n}) -graph.
The following result characterizes Latin square graphs as either strongly regular or complete graphs.
Theorem 3.23. Let \mathsf{{G}} be an \mathrm{L}_{{m}}({n}) -graph with integers m and n such that 2 \leq m \leq n+1 .
(1) If 2 \leq m \leq n , then \mathsf{{G}} is strongly regular \mathsf{srg}({n^2}, {\, m(n-1)}, {\, m^2-3m+n}, {\, m(m-1)}) .
(2) If m = n+1 , then \mathsf{{G}} is isomorphic to the complete graph \mathsf{K}_{{n^2}} .
Example 3.24 (Lattice graphs). For n \geq 2 , the lattice graph on n^2 vertices is a Latin square graph \mathrm{L}_{{2}}({n}) with vertex set [{n}] \times [{n}] , where distinct vertices (a, b) and (c, d) are adjacent if a = c or b = d . Two vertices in \mathrm{L}_{{2}}({n}) are adjacent if they lie in the same row or column in the Latin square of order n . By Theorem 3.23 with m = 2 , it is a strongly regular graph with parameters \mathsf{srg}({n^2}, {2(n-1)}, {n-2}, {2}) .
Example 3.25 (Latin square graphs with block size 3). The Latin square graph \mathrm{L}_{{3}}({n}) , with n \geq 2 , is constructed as follows. The vertices in the graph represent the n^2 cells of the Latin square of order n , and two vertices are adjacent if they lie in the same row or column, or if the cells of these vertices hold the same element in [{n}] . It is a specialization of the family of Latin square graphs \mathrm{L}_{{m}}({n}) with m = 3 , referring to the row, column and symbol in the cell as the conditions for adjacency of any two vertices. By Theorem 3.23 with m = 3 , it is a strongly regular graph with parameters \mathsf{srg}({n^2}, {3(n-1)}, {n}, {6}) .
3.1.5. Symplectic polar graphs
The symplectic polar graphs are a parametric family of strongly regular graphs with parameters \mathsf{srg}({v}, {k}, {\lambda}, {\mu}) given by
for all n \in {\mathbb{N}} and q \geq 2 that is a prime power, so \lambda = \mu-2 and \mu = \frac{k}{q} . That symplectic polar graph is denoted by \mathsf{Sp}(2n, q) (see Section 2.5 in [52]). The clique number of \mathsf{Sp}(2n, q) is equal to \frac{q^n-1}{q-1} . By Theorem 2.37 and the parameters of the strongly regular graph in (3.11)–(3.14), the eigenvalues of the symplectic polar graph \mathsf{Sp}(2n, q) (with respect to its adjacency matrix) are given by
● \lambda_1 = k = \dfrac{q(q^{2n-2}-1)}{q-1} (the largest eigenvalue) with multiplicity 1;
● \lambda_2 = r (the second-largest eigenvalue) with multiplicity f ;
● \lambda_{\min} = s (the smallest eigenvalue) with multiplicity g ,
where
3.2. New results on the Shannon capacity of graphs
In this subsection, some new results are presented in regard to the Shannon capacity of graphs. The next theorem strengthens and extends Theorem 3.7 (see Theorem 12 in [11]).
Theorem 3.26 (On the Shannon capacity of graphs). Let \mathsf{{G}} be an undirected and simple graph on n vertices.
(1) If \mathsf{{G}} is a vertex-transitive or strongly regular graph, then
(2) If \mathsf{{G}} is a conference graph, then \, \vartheta(\mathsf{{G}}) = \sqrt{n} .
(3) If \mathsf{{G}} is a self-complementary graph with \alpha({\mathsf{{G}}}) = k , then
(4) If \mathsf{{G}} is a self-complementary graph that is vertex-transitive or strongly regular, then
Hence, the minimum Shannon capacity among all self-complementary graphs of a fixed order n is achieved by those that are vertex-transitive or strongly regular, and this minimum is equal to \sqrt{n} .
Proof. See Section 3.3.1. □
Remark 3.27 (Discussion on Theorem 3.26). The following are comments in regard to Theorem 3.26.
(1) Item 1 of Theorem 3.26 extends Theorem 3.7 (i.e., Theorem 12 in [11]) since it holds for all strongly regular graphs, in addition to vertex-transitive graphs. In general, strongly regular graphs are not necessarily vertex-transitive (see Remark 3.6).
(2) In regard to Item 1 of Theorem 3.26, it should be noted that the complement of a vertex-transitive graph is vertex-transitive, and the complement of a strongly regular graph is strongly regular. The strong product of vertex-transitive graphs is vertex-transitive, whereas the strong product of strongly regular graphs is not necessarily strongly regular, but only regular; more explicitly, the strong product of d_1 -regular and d_2 -regular graphs is d -regular with d = (1+d_1)(1+d_2)-1 . If \mathsf{{G}} is a strongly regular graph that is not vertex-transitive, then the regular graph \mathsf{{G}} \boxtimes \overline{\mathsf{{G}}} may not be vertex-transitive nor strongly regular. As a concrete example, let \mathsf{{G}} be the Gritsenko graph [80]. The graph \mathsf{{G}} , a conference graph on 65 vertices, is not vertex- or edge-transitive. Utilizing the SageMath software, it can be verified that the strong product \mathsf{{G}} \boxtimes \overline{\mathsf{{G}}} is not a strongly regular graph, nor is it vertex- or edge-transitive.
(3) Item 2 of Theorem 3.26 states that the Lovász \vartheta -function of a conference graph on n vertices is equal to \sqrt{n} . For a conference graph \mathsf{{G}} on n vertices, d = \tfrac12(n-1) and \lambda_{\min}(\mathsf{{G}}) = -\tfrac12 (1+\sqrt{n}) , so, by Theorem 9 in [11] (see (2.58)), \vartheta(\mathsf{{G}}) \leq \sqrt{n} with an equality if the regular graph \mathsf{{G}} is edge-transitive. Item 2 of Theorem 3.26 shows that the rightmost equality in (3.19) holds for all conference graphs, regardless of the edge-transitivity property of the graph. There are many conference graphs that are not vertex-transitive, nor edge-transitive (for a concrete example, see Remark 3.6).
(4) In regard to Item 4 of Theorem 3.26, recall that self-complementary vertex-transitive graphs and self-complementary strongly regular graphs are not equivalent classes (see Remark 3.12).
The next two theorems provide the Shannon capacity of two infinite subclasses of strongly regular graphs (see Sections 3.1.4 and 3.1.5 for the presentation of these families of graphs).
Theorem 3.28 (The Shannon capacity of complements of Latin square graphs). Let \mathsf{{G}} = \mathrm{L}_{{m}}({n}) be a Latin square graph with m, n \in {\mathbb{N}} and 2 \leq m < n . Then,
Proof. See Section 3.3.2. □
Theorem 3.29 (Graph invariants of symplectic polar graphs and their complements). Let \mathsf{{G}} be the symplectic polar graph \mathsf{Sp}(2n, q) , where n \in {\mathbb{N}} and q \geq 2 is a power of a prime. Then, the following holds:
(1) The independence number, Shannon capacity, and Lovász \vartheta -function of the complement graph \overline{\mathsf{{G}}} coincide, and they are given by
(2) The Lovász \vartheta -function of \mathsf{{G}} , the chromatic number of \overline{\mathsf{{G}}} , and the fractional chromatic number of \overline{\mathsf{{G}}} coincide, and they are given by
Proof. See Section 3.3.3. □
Remark 3.30 (The independence number of symplectic polar graphs). By Proposition 2.5.4 in [52], the independence number of the symplectic polar graph \mathsf{{G}} = \mathsf{Sp}(2n, q) (with n \in {\mathbb{N}} and q \geq 2 that is a prime power) satisfies
● \alpha({\mathsf{{G}}}) = q+1 if n = 1 (an edgeless graph on q+1 vertices);
● \alpha({\mathsf{{G}}}) = 2n+1 if q = 2 and n \in {\mathbb{N}} ;
● \alpha({\mathsf{{G}}}) = 7 if q = 3 and n = 2 ;
● \alpha({\mathsf{{G}}}) \leq 15 \cdot 2^{n-3} - 2 if q = 3 and n \geq 3 ;
● If q \geq 4 is a prime power and n \geq 3 , then
Hence, unless n = 1 (resulting in an edgeless graph on q+1 vertices), in general \alpha({\mathsf{{G}}}) < q^n+1 = \vartheta(\mathsf{{G}}) (the last equality holds by (3.23)).
A new result on the Shannon capacity of two types of joins of graphs is later provided in Section 4.2. The presentation of the Shannon capacity of these types of graphs is deferred to the next section since additional preliminary material is needed for that purpose.
In the following, Section 3.3 provides proofs for the results in this section, and Section 3.4 concludes with numerical experiments illustrating these results.
3.3. Proofs
This section proves the results in Section 3.2.
3.3.1. Proof of Theorem 3.26
Items 1–4 of Theorem 3.26 are proved as follows.
(1) For every undirected and simple graph \mathsf{{G}} on n vertices,
which holds since \{(1, 1), \ldots (n, n)\} is an independent set in the strong product graph \mathsf{{G}} \boxtimes \overline{\mathsf{{G}}} . Indeed, if i, j \in [{n}] , i \neq j , and \{i, j\} \in \mathsf{E}({\mathsf{{G}}}) , then \{i, j\} \not\in \mathsf{E}({\overline{\mathsf{{G}}}}) , which implies that \{(i, i), (j, j)\} \not\in \mathsf{E}({\mathsf{{G}} \boxtimes \overline{\mathsf{{G}}}}) . If \mathsf{{G}} is vertex-transitive or strongly regular, then by (2.56), (3.6), and (3.25),
(2) Let \mathsf{{G}} be a conference graph on n vertices. Then, \mathsf{{G}} and \overline{\mathsf{{G}}} are strongly regular graphs with the same set of parameters \mathsf{srg}(n, \frac{n-1}{2}, \frac{n-1}{5}, \frac{n-1}{4}) . By Theorem 3.3, the Lovász \vartheta -function of a strongly regular graph is determined by its four parameters, so it follows that \vartheta(\mathsf{{G}}) = \vartheta(\overline{\mathsf{{G}}}) . By (3.6) and the rightmost equality in (3.31), it follows that \vartheta(\mathsf{{G}}) = \sqrt{n} .
(3) If \mathsf{{G}} is a self-complementary graph on n vertices, then
where inequality (3.32) holds by (2.36); equality (3.33) holds by the assumption that \mathsf{{G}} is self-complementary, so \mathsf{{G}} \boxtimes \mathsf{{G}} \cong \mathsf{{G}} \boxtimes \overline{\mathsf{{G}}} ; finally, (3.34) holds by (3.25). This proves the leftmost inequality in (3.18). The rightmost inequality in (3.18) holds by combining (2.51) and (2.61) (it should be noted that inequality (2.61) holds by Theorem 11.18 in [29], irrespectively of the self-complementary property of the graph \mathsf{{G}} ).
(4) If a self-complementary graph \mathsf{{G}} on n vertices is vertex-transitive or strongly regular, then by (3.30)
which gives \vartheta(\mathsf{{G}}) = \sqrt{n} . Combined with Item 3 of this proof, it gives
so
Finally, combining (3.31) and (3.37) gives
3.3.2. Proof of Theorem 3.28
The Latin square graph \mathrm{L}_{{m}}({n}) , with m, n \in {\mathbb{N}} and 2 \leq m < n , has the property that each of its edges is contained in a clique of size n , so
By Theorem 3.23, the graph \mathsf{{G}} = \mathrm{L}_{{m}}({n}) is strongly regular with the parameters
By Theorem 3.3, the Lovász \vartheta -function of \mathsf{{G}} is then equal to
with
where equality (3.42) holds by (3.5), equality (3.43) is derived from (3.40), and equality (3.44) is obtained by straightforward algebra (specifically through the cancellation of m ). It therefore follows from (3.40)–(3.44) that
Since \mathsf{{G}} is a strongly regular graph on n^2 vertices, by Corollary 3.4,
Finally, since the Shannon capacity of a graph is bounded between its independence number and its Lovász \vartheta -function, (3.21) follows from (3.39) and (3.48); hence, (3.39) holds with equality. Since the Lovász \vartheta -function of strongly regular graphs only depends on their four parameters ( n, d, \lambda, \mu ), it is identical for all (nonisomorphic) strongly regular graphs with the same set of four parameters. Hence, \vartheta(\mathsf{{G}}) = n holds for all the pseudo Latin square graphs \mathrm{PL}_{{m}}({n}) , which form the class of all the strongly regular graphs with four parameters that are identical to those of the Latin square graph \mathrm{L}_{{m}}({n}) .
3.3.3. Proof of Theorem 3.29
Let \mathsf{{G}} be the symplectic polar graph \mathsf{Sp}(2n, q) , with n \in {\mathbb{N}} and q \geq 2 that is a prime power. By Section 2.5.4 in [52],
The complement graph of a strongly regular graph, \mathsf{srg}(\nu, k, \lambda, \mu) , is a strongly regular graph with parameters \mathsf{srg}(v, v-k-1, v-2k+\mu-2, v-2k+\lambda) (see Item 1 of Theorem 2.36). Substituting v, k, \lambda, \mu in (3.11)–(3.14) gives that \overline{\mathsf{{G}}} is a strongly regular graph on v vertices with the parameters
The complement graph \overline{\mathsf{{G}}} has the 3 distinct eigenvalues q^{2n-1}, \, -1-s = q^{n-1} , and -1-r = -q^{n-1} with multiplicities 1, g , and f , respectively (see (3.15) and (3.16)). Substituting the four parameters of the strongly regular graph \mathsf{{G}} = \mathsf{srg}(v, k, \lambda, \mu) , as given in (3.11)–(3.14), into (3.5) gives
where equality (3.52) holds, by (3.13) and (3.14), since \lambda = \mu-2 ; equality (3.53) further holds by (3.12). Consequently, the Lovász \vartheta -function of the complement graph \overline{\mathsf{{G}}} is equal to
where (3.55) holds by (3.4), and (3.56) follows from the combination of (3.11)–(3.14) and (3.54). Since, by (3.49) and (3.57), \alpha({\overline{\mathsf{{G}}}}) = \vartheta(\overline{\mathsf{{G}}}) = \frac{q^n-1}{q-1} , the Shannon capacity of the complement graph \overline{\mathsf{{G}}} is also equal to that common value, i.e., \Theta(\overline{\mathsf{{G}}}) = \frac{q^n-1}{q-1} . This proves (3.22).
By Theorem 2.4 in [93], the chromatic number of the complement graph \overline{\mathsf{{G}}} is given by
and since \mathsf{{G}} and \overline{\mathsf{{G}}} are strongly regular graphs on v vertices, the combination of equalities (3.6), (3.11), and (3.57) give
Consequently, from (3.58) and (3.59),
This finally proves (3.23) by combining (2.52), which gives \vartheta(\mathsf{{G}}) \leq \chi_{\mathrm{f}}({\overline{\mathsf{{G}}}}) \leq \chi({\overline{\mathsf{{G}}}}) , and (3.60).
3.4. Examples for the results in Section 3.2
Example 3.31 (Paley graphs). Let q be a prime power such that q \equiv 1 \bmod 4 . That is, q is either an arbitrary power of a prime congruent to 1 modulo 4 or it is an even power of a prime congruent to 3 modulo 4. The vertex set of a Paley graph of order q is \{0, 1, \ldots, q-1\} , and any two such distinct vertices are adjacent if their difference is a quadratic residue modulo q . Paley graphs are known to be a class of self-complementary, vertex-transitive, and strongly regular graphs with parameters \mathsf{srg}({q}, {\tfrac12 (q-1)}, {\tfrac14 (q-5)}, {\tfrac14 (q-1)}) (a Paley graph is therefore a conference graph). By Item 4 of Theorem 3.26, the Shannon capacity of a Paley graph \mathsf{{G}}_q of order q is given by \Theta(\mathsf{{G}}_q) = \sqrt{q} , and
If q is an even power of a prime, then \alpha({\mathsf{{G}}_q}) = \sqrt{q} (see [94,95]), so \alpha({\mathsf{{G}}_q \boxtimes \mathsf{{G}}_q}) = q = \alpha({\mathsf{{G}}_q})^2 . If q is equal to a prime number, then the determination of the independence number of such a Paley graph is an unsolved number-theoretic problem, and it is conjectured that \alpha({\mathsf{{G}}_q}) = O\bigl((\log q)^2\bigr) (see Example 11.14 in [29], which refers to the case where q \equiv 1 \bmod 4 is a prime).
Example 3.32 (Shannon capacity of the complements of Latin square graphs with block size 3). By Example 3.25, for any integer n \geq 3 , a Latin square graph with block size m = 3 is a strongly regular graph whose parameters are given by \mathsf{srg}({n^2}, {3(n-1)}, {n}, {6}) . By Item 1 of Theorem 2.36 (see equalities (2.27)–(2.30)), the complement of this graph is a strongly regular graph whose parameters are given by \mathsf{srg}({n^2}, {(n-2)(n-1)}, {(n-3)^2+1}, {(n-3)(n-2)}) . In light of Theorem 3.28, the Shannon capacity of these graphs are given in Table 1 for all 3 \leq n \leq 16 .
Example 3.33 (Shannon capacity of the complements of the symplectic polar graphs). The symplectic polar graphs form an infinite subfamily of the strongly regular graphs; they are briefly addressed in Section 3.1.5 (see also Section 2.5 in [52] for more details). In light of Theorem 3.29, the independence number, Shannon capacity, and the Lovász \vartheta -function of the complements of symplectic polar graphs coincide, and their common value is given by (3.22). Table 2 provides the Shannon capacity of the complements of the symplectic polar graphs \mathsf{{H}} = \overline{ \mathsf{Sp}(2n, q)} where q \geq 2 is a power of a prime and n \in {\mathbb{N}} . The set of parameters of these strongly regular graphs is given in (3.50).
4.
On cospectral and nonisomorphic graphs, and on joins of graphs
The construction of cospectral and nonisomorphic graphs is a nontrivial problem in spectral graph theory, which has gained interest in the literature (see [31,32,33,96,97,98,99,100,101,102,103,104] and references therein).
The present section employs the Lovász \vartheta -function of graphs to unveil novel insights into regular and irregular, cospectral and nonisomorphic graphs. Additionally, it explores new properties of two types of joins of graphs, recently introduced in [32,33], within the context of irregular, cospectral and nonisomorphic graphs.
To facilitate comprehension, we introduce specific preliminaries essential for the present section in Section 4.1. Following this, the new results are presented in Section 4.2. Subsequently, we delve into the proofs of these results in Section 4.3. Finally, in Section 4.4, we engage in discussions, offer illustrative examples, and conduct numerical experimentation to provide further insights into the new results.
4.1. Specialized preliminaries for Section 4
The preliminary material in this subsection forms a continuation to Section 2.1.3.
Definition 4.1 (Cospectral graphs). Let \mathsf{{G}} and \mathsf{{H}} be graphs. Then,
● \mathsf{{G}} and \mathsf{{H}} are said to be X -cospectral, with X \in \{A, L, Q, \mathcal{L}\} , if these graphs have an identical X -spectrum.
● \mathsf{{G}} and \mathsf{{H}} are said to be X -NICS if these graphs are nonisomorphic and X -cospectral.
● Let \mathcal {S} \subseteq \{A, L, Q, \mathcal{L}\} . The graphs \mathsf{{G}} and \mathsf{{H}} are said to be \mathcal {S} -NICS if they are X -NICS for every X \in \mathcal {S} .
Remark 4.2 (Relations between spectra of regular graphs). If \mathsf{{G}} is a d -regular graph on n vertices, then by (2.11)–(2.14) and (2.18)–(2.21), for all i \in [{n}]
If \mathsf{{G}} and \mathsf{{H}} are regular graphs that are X -cospectral for some X \in \{A, L, Q, \mathcal{L}\} , then it follows from the equalities in (4.1) that \mathsf{{G}} and \mathsf{{H}} are X -cospectral for every X \in \{A, L, Q, \mathcal{L}\} . Therefore, for regular graphs, the property of being cospectral remains unchanged regardless of the matrix chosen among \mathbf{A}, \mathbf{L}, \mathbf{Q} , and {\bf{\mathcal{L}}} .
Definition 4.3 (Seidel switching). Let \mathsf{{G}} be a graph with the vertex set \mathsf{V}({\mathsf{{G}}}) , and let \mathcal {X} \subseteq \mathsf{V}({\mathsf{{G}}}) . Constructing a new graph \hat{\mathsf{{G}}} by preserving all the edges in \mathsf{{G}} between vertices in \mathcal {X} and all the edges in \mathsf{{G}} between vertices in \mathsf{V}({\mathsf{{G}}}) \setminus \mathcal {X} , while modifying adjacency and nonadjacency between vertices in \mathcal {X} and \mathsf{V}({\mathsf{{G}}}) \setminus \mathcal {X} , is referred to as Seidel switching.
The next result shows the importance of Seidel switching for the construction of regular, connected, and cospectral graphs.
Theorem 4.4 (Seidel switching and cospectraility). Let \mathsf{{G}} be a connected and d -regular graph, and let \hat{\mathsf{{G}}} be obtained from \mathsf{{G}} by Seidel switching. If \hat{\mathsf{{G}}} remains connected and d -regular, then \mathsf{{G}} and \hat{\mathsf{{G}}} are cospectral graphs.
Definition 4.5 (Determination of a graph by its spectrum). A graph G is determined by its X -spectrum if every graph \mathsf{{H}} that is X -cospectral with \mathsf{{G}} is also isomorphic to \mathsf{{G}} .
Theorem 4.6 ([31]). If \mathsf{{G}} is a regular graph, then the following statements are equivalent:
● \mathsf{{G}} is determined by its adjacency spectrum ( A -spectrum);
● \mathsf{{G}} is determined by its Laplacian spectrum ( L -spectrum);
● \mathsf{{G}} is determined by its signless Laplacian spectrum ( Q -spectrum);
● \mathsf{{G}} is determined by its normalized Laplacian spectrum ( \mathcal{L} -spectrum).
Theorem 4.7 ([31]). All regular graphs on less than 10 vertices are determined by their spectrum. Additionally, there are four pairs of nonisomorphic and cospectral regular graphs on 10 vertices.
The reader is referred to [31,33,99,105,106,107,108,109,110] for analyses on graphs determined by their spectra with respect to their adjacency, Laplacian, signless Laplacian, or normalized Laplacian matrices.
Example 4.8 (Irregular NICS graphs). Figure 1 displays four pairs of irregular, nonisomorphic, and cospectral (NICS) graphs with respect to a single matrix among the matrices \mathbf{A}, \mathbf{L}, \mathbf{Q} , and \mathcal{L} . Notably, each of these pairs of graphs are no longer cospectral with respect to the other three matrices [98]. It can be verified (e.g., by the Sage Math software [51]) that the common characteristic polynomials of the pairs of A -NICS, L -NICS, Q -NICS, and \mathcal{L} -NICS graphs in Figure 1 are, respectively, given by
By Theorem 4.7, there is no pair of cospectral and nonisomorphic regular graphs on less than 10 vertices. The next example shows a pair of regular NICS graphs on 10 vertices.
Example 4.9 (Regular NICS graphs [31]). Let \mathsf{{G}} and \mathsf{{H}} be the regular graphs depicted on the left and right-hand sides of Figure 2, respectively. These are 4-regular graphs on 10 vertices, and they are cospectral while being nonisomorphic [31]. Indeed, the identical A -characteristic polynomials of \mathsf{{G}} and \mathsf{{H}} are given by
so these regular graphs are cospectral. Alternatively, the cospectrality of the regular graphs \mathsf{{G}} and \mathsf{{H}} can be inferred from Theorem 4.4, without needing to compute their characteristic polynomials or eigenvalues. This inference is made by verifying the isomorphism of \mathsf{{H}} and the Seidel switching of \mathsf{{G}} with respect to its four corners, while also ensuring that the latter graph and \mathsf{{G}} are both connected and 4-regular. However, the cospectral graphs \mathsf{{G}} and \mathsf{{H}} are nonisomorphic because each of the two blue edges in \mathsf{{G}} belongs to three triangles, whereas no such edge exists in \mathsf{{H}} (see Figure 2).
It is of interest to explore constructions of irregular \{A, L, Q, \mathcal{L}\} -NICS graphs, as they exhibit cospectrality concerning four matrices that include the adjacency, Laplacian, signless Laplacian, and normalized Laplacian matrices. However, despite this cospectrality, the graphs are nonisomorphic. To delve deeper into this topic, we refer to the recent study by Berman and Hamud [32,33], which begins with essential definitions.
Definition 4.10 (Join of graphs). Let \mathsf{{G}} and \mathsf{{H}} be two graphs with disjoint vertex sets. The join of \mathsf{{G}} and \mathsf{{H}} is defined to be their disjoint union, together with all the edges that connect the vertices in \mathsf{{G}} with the vertices in \mathsf{{H}} . It is denoted by \mathsf{{G}} \vee \mathsf{{H}} .
Remark 4.11 (Join and disjoint union of graphs). Since the edge set of the disjoint union of graphs \mathsf{{G}} and \mathsf{{H}} , denoted by \mathsf{{G}} + \mathsf{{H}} , does not include any edge that connects a vertex in \mathsf{{G}} with a vertex in \mathsf{{H}} (see Definition 2.6), the following equality holds:
Definition 4.12 (Neighbors splitting join of graphs [104]). Let \mathsf{{G}} and \mathsf{{H}} be graphs with disjoint vertex sets, and let \mathsf{V}({\mathsf{{G}}}) = \{v_1, \ldots, v_n\} . The neighbors splitting (NS) join of \mathsf{{G}} and \mathsf{{H}} is obtained by adding vertices v'_1, \ldots, v'_n to the vertex set of \mathsf{{G}} \vee \mathsf{{H}} and connecting v'_i to v_j if and only if \{v_i, v_j\} \in \mathsf{E}({\mathsf{{G}}}) . The NS join of \mathsf{{G}} and \mathsf{{H}} is denoted by \mathsf{{G}} \, \underline{\vee} \, \mathsf{{H}} .
Definition 4.13 (Nonneighbors splitting join of graphs [32,33]). Let \mathsf{{G}} and \mathsf{{H}} be graphs with disjoint vertex sets, and let \mathsf{V}({\mathsf{{G}}}) = \{v_1, \ldots, v_n\} . The nonneighbors splitting (NNS) join of \mathsf{{G}} and \mathsf{{H}} is obtained by adding vertices v'_1, \ldots, v'_n to the vertex set of \mathsf{{G}} \vee \mathsf{{H}} and connecting v'_i to v_j , with i \neq j , if and only if \{v_i, v_j\} \not\in \mathsf{E}({\mathsf{{G}}}) . The NNS join of \mathsf{{G}} and \mathsf{{H}} is denoted by \mathsf{{G}} \, \underline{\underline \vee } \, \mathsf{{H}} .
Remark 4.14. In general, \mathsf{{G}} \, \underline{\vee} \, \mathsf{{H}} \not\cong \mathsf{{H}} \, \underline{\vee} \, \mathsf{{G}} and \mathsf{{G}} \, \underline{\underline \vee } \, \mathsf{{H}} \not\cong \mathsf{{H}} \, \underline{\underline \vee } \, \mathsf{{G}} (unless \mathsf{{G}} \cong \mathsf{{H}} ).
Example 4.15 (NS and NNS join of graphs [32]). Figure 3 shows the NS and NNS joins of the path graphs \mathsf{P}_{{4}} and \mathsf{P}_{{2}} , denoted by \mathsf{P}_{{4}} \, \underline{\vee} \, \mathsf{P}_{{2}} and \mathsf{P}_{{4}} \, \underline{\underline \vee } \, \mathsf{P}_{{2}} , respectively.
Proposition 4.16 (Adjacency matrices of the NS and NNS joins of graphs [32,33,104]). Let \mathsf{{G}}_1 and \mathsf{{G}}_2 be, respectively, finite and simple graphs on n_1 and n_2 vertices. Then, the adjacency matrices of the NS and NNS joins of graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 are, respectively, given by
where {\mathbf{J}}_{n \times m} and {\mathbf{0}}_{n \times m} denote, respectively, the n \times m all-ones and all-zeros matrices. Denoting (for simplicity) \mathbf{J}_{{n}} and {\mathbf{0}}_n to be, respectively, the n \times n all-ones and all-zeros matrices, the equality
relates the adjacency matrices of a graph \mathsf{{G}} and its complement \overline{\mathsf{{G}}} .
Proof. Equality (4.10) holds by Definition 2.4 of a graph complement. The adjacency matrices in (4.8) and (4.9) hold by Definitions 4.12 and 4.13, respectively. In these matrices:
(a) The first n_1 rows and columns correspond to the vertices v_1, \ldots, v_{n_1} in \mathsf{{G}}_1 .
(b) The next n_1 rows and columns refer to the copied vertices v'_1, \ldots, v'_{n_1} that are added to the vertex set of \mathsf{{G}}_1 \vee \mathsf{{G}}_2 to form both vertex sets of the graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 .
(c) The last n_2 rows and columns refer to the vertices in \mathsf{{G}}_2 . □
Consider the NS and NNS joins of two graphs with disjoint vertex sets. The next result gives sufficient conditions for these joins of graphs to be nonisomorphic and cospectral with respect to their adjacency, Laplacian, signless Laplacian, and normalized Laplacian matrices. A partial result was first published in Theorem 5.1 of [104], followed by the next result presented in [32,33].
Theorem 4.17. (Irregular \{A, L, Q, \mathcal{L}\} -NICS graphs). Let \mathsf{{G}}_1 and \mathsf{{H}}_1 be regular and cospectral graphs, and let \mathsf{{G}}_2 and \mathsf{{H}}_2 be regular, nonisomorphic, and cospectral (NICS) graphs. Then, the following statements hold:
(1) \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{H}}_1 \, \underline{\vee} \, \mathsf{{H}}_2 are irregular \{A, L, Q, \mathcal{L}\} -NICS graphs.
(2) \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 and \mathsf{{H}}_1 \, \underline{\underline \vee } \, \mathsf{{H}}_2 are irregular \{A, L, Q, \mathcal{L}\} -NICS graphs.
4.2. New results on cospectral and nonisomorphic graphs, and on joins of graphs
In light of Theorems 2.18–2.25, it is established that every pair of \{A, L, Q, \mathcal{L}\} -NICS graphs share identical structural properties, encompassing identical counts of vertices, edges, triangles, components, bipartite components, spanning trees, and walks (or closed walks) of specific lengths. Moreover, these graphs exhibit either regularity or irregularity, with matching girth, indicating shared characteristics despite being cospectral and nonisomorphic. By Theorem 2.27, the line graphs of these graphs are also A -cospectral, thereby sharing identical counts of vertices, edges, triangles, and walks (or closed walks) of specified lengths. In view of these findings, we introduce two questions as follows.
(1) Is the Lovász \vartheta -function identical for any pair of \{A, L, Q, \mathcal{L}\} -NICS graphs?
(2) If not, are there subfamilies of graphs for which the Lovász \vartheta -function is unique for any pair of \{A, L, Q, \mathcal{L}\} -NICS graphs within that particular subfamily?
These questions are addressed here with the following conclusions:
● By Theorem 4.7, regular graphs with fewer than 10 vertices can be uniquely determined by their spectrum. Therefore, the response to the first question is affirmative for these small regular graphs.
● In general, the response to the first query is negative, as demonstrated by Example 4.18, followed by Theorems 4.19 and 4.20.
● Some subfamilies of regular graphs exhibit a positive response to the second query, as shown in Corollary 4.23, Theorem 4.24, and Corollary 4.25.
Our analysis relies in part on [31,32,33,34], with the background provided in Section 4.1.
Example 4.18 (Regular NICS graphs). The present example continues Example 4.9. Let \mathsf{{G}} and \mathsf{{H}} be the graphs on the left and right plots of Figure 2, respectively. The Lovász \vartheta -functions of these graphs are computed numerically by solving the SDP problem in (2.48) for both \mathsf{{G}} and \mathsf{{H}} . The resulting values are given with a precision of 5 decimal points as follows:
The complements \overline{\mathsf{{G}}} and \overline{\mathsf{{H}}} are 5-regular NICS graphs, whose Lovász \vartheta -functions are equal to
This results in two pairs of regular NICS graphs on 10 vertices, denoted by \{\mathsf{{G}}, \mathsf{{H}}\} and \{\overline{\mathsf{{G}}}, \overline{\mathsf{{H}}}\} . Each pair exhibits distinct values of the Lovász \vartheta -functions, as demonstrated by Eqs (4.11) and (4.12). It is noteworthy that the four graphs \mathsf{{G}} , \overline{\mathsf{{G}}} , \mathsf{{H}} , and \overline{\mathsf{{H}}} share identical independence numbers (3), clique numbers (3), and chromatic numbers (4).
Following Example 4.18, the next result demonstrates the existence of pairs of irregular \{A, L, Q, \mathcal{L}\} -NICS graphs on an arbitrarily large order, such that these cospectral and nonisomorphic graphs have identical pairs of independence numbers, clique numbers, and chromatic numbers, while exhibiting distinct values of their Lovász \vartheta -functions.
Theorem 4.19 (On irregular NICS graphs). For every even integer n \geq 14 , there exist two connected, irregular \{A, L, Q, \mathcal{L}\} -NICS graphs on n vertices with identical independence, clique, and chromatic numbers, yet their Lovász \vartheta -functions are distinct.
Proof. See Section 4.3.1. □
Theorem 4.20 (Graph invariants of NS/NNS joins of graphs). For every finite, undirected, and simple graphs \mathsf{{G}}_1 and \mathsf{{G}}_2 , the following holds:
Moreover, the following sufficient conditions for equalities hold:
● Inequality (4.19) holds with equality if there exists a permutation \pi of the vertex set \mathsf{V}({\mathsf{{G}}_1}) such that \{v_i, v_{\pi(i)}\} \in \mathsf{E}({\mathsf{{G}}_1}) for all i \in \{1, \ldots, |{ \mathsf{V}({\mathsf{{G}}_1})}|\} .
● Inequality (4.20) holds with equality if there exists a permutation \pi of the vertex set \mathsf{V}({\mathsf{{G}}_1}) such that \pi(i) \neq i and \{v_i, v_{\pi(i)}\} \not\in \mathsf{E}({\mathsf{{G}}_1}) for all i \in \{1, \ldots, |{ \mathsf{V}({\mathsf{{G}}_1})}|\} .
● Inequality (4.13) holds with equality if the sufficient condition for equality in (4.19) is satisfied and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) .
● Inequality (4.14) holds with equality if the sufficient condition for equality in (4.20) is satisfied and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) .
Proof. See Section 4.3.2. □
Remark 4.21 (Perfect matchings in graphs). An equivalent formulation of the sufficient conditions in Theorem 4.20, ensuring (4.19) and (4.20) to hold with equalities relies on perfect matchings in graphs. Let \mathsf{{G}} be a graph on n vertices, whose adjacency matrix is \mathbf{A} \triangleq \mathbf{A}(\mathsf{{G}}) . Associate with the graph \mathsf{{G}} the bipartite graph \mathrm{B}(\mathsf{{G}}) = (\mathcal {U} \cup \mathcal {V}, \, \mathcal {E}) on 2n vertices. The vertex set \mathcal {U} \cup \mathcal {V} consists of two disjoint sets \mathcal {U} = {u_1, \ldots, u_n} and \mathcal {V} = {v_1, \ldots, v_n} , and an edge \{u_i, v_j\} \in \mathcal {E} if and only if A_{i, j} = 1 with i, j \in [{n}] .
An equivalent formulation of the sufficient condition for (4.19) to hold with equality is the existence of a perfect matching in the bipartite graph \mathrm{B}(\mathsf{{G}}_1) . Indeed, the number of different perfect matchings in \mathrm{B}(\mathsf{{G}}_1) is equal to the permanent of the adjacency matrix \mathbf{A}(\mathsf{{G}}_1) (see, e.g., Chapter 37 in [92]), so that sufficient condition is given by \mathrm{per}(\mathbf{A}(\mathsf{{G}}_1)) > 0 . Similarly, an equivalent formulation of the sufficient condition for (4.20) to hold with equality is that the bipartite graph \mathrm{B}(\overline{\mathsf{{G}}}_1) has a perfect matching, which can be also represented by the condition \mathrm{per}(\mathbf{A}(\overline{\mathsf{{G}}}_1)) > 0 .
A well-established result is next presented, which hinges on the widely recognized van der Waerden conjecture. Initially posed as a question, this conjecture has been elegantly proven and elucidated in Chapter 24 of [92], [111], and Chapters 11–12 of [112].
Lemma 4.22 (Permanent of the adjacency matrix of a regular graph). Let \mathsf{{G}} be a d -regular graph on n vertices, and let \mathbf{A} be its adjacency matrix. Then,
By Theorem 4.20 and Remark 4.21, the positivity of the permanent of the adjacency matrix of the graph \mathsf{{G}}_1 suffices for (4.19) to hold with equality. Likewise, the positivity of the permanent of the adjacency matrix of the complement graph \overline{\mathsf{{G}}}_1 suffices for (4.20) to hold with equality. Furthermore, by Theorem 4.20, the satisfiability of the supplementary condition \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) implies that (4.13) and (4.14) hold with equalities, respectively, in addition to the equalities in (4.19) and (4.20). If \mathsf{{G}}_1 is a noncomplete and nonempty regular graph, then Lemma 4.22 yields the positivity of the permanent of each of the adjacency matrices \mathbf{A}(\mathsf{{G}}_1) and \mathbf{A}(\overline{\mathsf{{G}}}_1) (since if \mathsf{{G}}_1 is a d -regular graph, then its complement \overline{\mathsf{{G}}}_1 is an (n-d-1) -regular graph). The next result follows.
Corollary 4.23. Let \mathsf{{G}}_1 and \mathsf{{G}}_2 be finite, noncomplete, nonempty, undirected, and simple graphs.
● If \mathsf{{G}}_1 is a regular graph, then (4.19) and (4.20) hold with equalities.
● If \mathsf{{G}}_1 is a regular graph and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) , then (4.13) and (4.14) hold with equalities.
In light of Theorem 4.20, Remark 4.21, and Corollary 4.23, the next result follows.
Theorem 4.24 (The independence number, Shannon capacity, and Lovász \vartheta -function of NS and NNS joins of graphs). Let \mathsf{{G}}_1 and \mathsf{{G}}_2 be finite, undirected, and simple graphs.
(1) If \mathrm{per}(\mathbf{A}(\mathsf{{G}}_1)) > 0 and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) , then
The equalities in (4.22) hold, in particular, if \mathsf{{G}}_1 is a nonempty regular graph and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) .
(2) If \mathrm{per}(\mathbf{A}(\overline{\mathsf{{G}}}_1)) > 0 and the equality \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) holds, then
Equalities in (4.23) hold, in particular, if \mathsf{{G}}_1 is a noncomplete regular graph and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) .
(3) If \, \mathrm{per}(\mathbf{A}(\mathsf{{G}}_1)) > 0 , \, \mathrm{per}(\mathbf{A}(\overline{\mathsf{{G}}}_1)) > 0 , and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) , then the graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 share identical independence numbers, clique numbers, chromatic numbers, Shannon capacities, and Lovász \vartheta -functions. This particulary holds if \mathsf{{G}}_1 is a nonempty and noncomplete regular graph and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) .
Proof. See Section 4.3.3. □
Discussions on the sufficient conditions in Theorem 4.20 are further given in Remarks 4.26 and 4.27 (see Section 4.4). By the above results, a pair of regular or irregular \{A, L, Q, \mathcal{L}\} -NICS graphs may have distinct Lovász \vartheta -functions. A restatement of Theorem 3.1 shows that, within some structured infinite subfamilies of regular graphs, the Lovász \vartheta -functions of NICS graphs are identical.
Corollary 4.25 (On NICS regular graphs). Let \mathsf{{G}} and \mathsf{{H}} be noncomplete, d -regular NICS graphs, and let \{\lambda_i\}_{i = 1}^n be their common A -spectrum in nonincreasing order.
(1) If each of these graphs is either strongly regular or edge-transitive, then
(2) If each of these graphs is either strongly regular or its complement is vertex-transitive and edge-transitive, then
and, for the (n-d-1) -regular cospectral graphs \overline{\mathsf{{G}}} and \overline{\mathsf{{H}}} ,
Proof. See Section 4.3.4. □
4.3. Proofs
This section proves all the new results that are presented in Section 4.2.
4.3.1. Proof of Theorem 4.19
In light of Theorem 4.17, for every k \in {\mathbb{N}} , this proof suggests a construction of two connected, irregular \{A, L, Q, \mathcal{L}\} -NICS graphs on n_k \triangleq 2k + 12 vertices. To that end, let
and let \mathsf{{G}}_2 and \mathsf{{H}}_2 be the 4-regular NICS graphs on 10 vertices, respectively depicted on the left and right-hand sides of Figure 2. By Item 1 of Theorem 4.17, for all k \in {\mathbb{N}} , the graphs \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{H}}_1^{(k)} \, \underline{\vee} \, \mathsf{{H}}_2 are irregular \{A, L, Q, \mathcal{L}\} -NICS graphs. The orders of \mathsf{{G}}_1^{(k)} , \mathsf{{G}}_2 , \mathsf{{H}}_1^{(k)} , and \mathsf{{H}}_2 are given by
By Definition 4.12 and (4.28), it follows that
and similarly, by Definition 4.13 and (4.28),
The graphs \mathsf{{G}}_2 and \mathsf{{H}}_2 can be verified to have identical independence numbers, clique numbers, and chromatic numbers, which are equal to
A largest independent set in the graph \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 is obtained by combining a largest independent set in \mathsf{{G}}_2 along with the vertices v'_1, \ldots, v'_{k+1} that are added to the vertex set of \mathsf{{G}}_1^{(k)} \vee \mathsf{{G}}_2 to form both vertex sets of \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1^{(k)} \, \underline{\underline \vee } \, \mathsf{{G}}_2 . Indeed, this can be deduced as follows:
● The vertices v'_1, \ldots, v'_{k+1} are nonadjacent to each other, and they are also nonadjacent to vertices in \mathsf{{G}}_2 (by Definition 4.12), so the disjoint union of a largest independent set in \mathsf{{G}}_2 and \{v'_1, \ldots, v'_{k+1}\} forms an independent set in \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 whose size is equal to |{ \mathsf{V}({\mathsf{{G}}_1})}| + \alpha({\mathsf{{G}}_2}) = (k+1) + 3 = k+4 .
● Each of the vertices v_1, \ldots, v_{k+1} in \mathsf{{G}}_1^{(k)} is adjacent to all the vertices in \mathsf{{G}}_2 , so none of them can be added to get a larger independent set in \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 .
● When forming an independent set in \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 , by taking a disjoint union of a nonempty subset of vertices in \mathsf{{G}}_1^{(k)} with a subset of the vertices \{v'_1, \ldots, v'_{k+1}\} , it is important to note that no vertex from \mathsf{{G}}_2 can be included in that independent set (since all vertices in \mathsf{{G}}_2 are adjacent to each vertex in \mathsf{{G}}_1^{(k)} ), and also the total cardinality of the two former subsets of vertices cannot exceed |{ \mathsf{V}({\mathsf{{G}}_1^{(k)}})}| = k+1 (by Definition 4.12 and the definition of the graph \mathsf{{G}}_1^{(k)} in (4.27)). This therefore imposes a constraint on the size of that independent set, which is strictly less than k+4 .
The same reasoning holds for the independence number of the NS join of graphs \mathsf{{H}}_1^{(k)} \, \underline{\vee} \, \mathsf{{H}}_2 , so
A largest clique in \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 is obtained by taking the disjoint union of largest cliques in \mathsf{{G}}_1^{(k)} and \mathsf{{G}}_2 . Indeed, this holds since each vertex in \mathsf{{G}}_1^{(k)} is adjacent to each vertex in \mathsf{{G}}_2 , and the vertices v'_1, \ldots, v'_{k+1} (as defined above) are nonadjacent to each other. Likewise, the same reasoning also holds for the clique number of \mathsf{{H}}_1^{(k)} \, \underline{\vee} \, \mathsf{{H}}_2 . By (4.34) where \omega({\mathsf{{G}}_2}) = 3 = \omega({\mathsf{{H}}_2}) , and since \omega({\mathsf{{G}}_1^{(k)}}) = 2 = \omega({\mathsf{{H}}_1^{(k)}}) , it follows that
The chromatic number of the NS join of graphs \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 is next considered. By (4.34), \chi({\mathsf{{G}}_2}) = 4 colors are at least needed for properly coloring the vertices in \mathsf{{G}}_2 so that no two adjacent vertices in \mathsf{{G}}_2 are assigned an identical color. All of the vertices in the set \mathsf{V}({\mathsf{{G}}_1^{(k)}}) = \{v_1, \ldots, v_k\} are adjacent to each vertex in \mathsf{{G}}_2 , so \chi({\mathsf{{G}}_1^{(k)}}) new colors are used for the vertices in \mathsf{{G}}_1^{(k)} . The chromatic number of \mathsf{{G}}_1^{(k)} = \mathsf{C}_{{k+1}} is equal to 2 or 3 if k \geq 2 is odd or even, respectively, and the chromatic number of \mathsf{{G}}_1^{(1)} = \mathsf{K}_{{2}} is equal to 2. Consequently, by (4.27), for all k \in {\mathbb{N}}
Finally, since vertices in \{v'_1, \ldots, v'_{k+1}\} are nonadjacent to one another and also they are nonadjacent to any vertex in \mathsf{{G}}_2 , one of the colors assigned to the vertices in \mathsf{{G}}_2 can be also used for all the vertices v'_1, \ldots, v'_{k+1} . Likewise, the same argument holds for \mathsf{{H}}_1^{(k)} \, \underline{\vee} \, \mathsf{{H}}_2 , so it follows from (4.34) and (4.37) that
Next, we demonstrate that the Lovász \vartheta -functions of the graphs \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{H}}_1^{(k)} \, \underline{\vee} \, \mathsf{{H}}_2 are distinct. We compute the Lovász \vartheta -functions of \mathsf{{G}}_2 and \mathsf{{H}}_2 by solving the SDP problem in (2.48), which yields
Consider a disjoint union of k+1 isolated vertices (i.e., the (k+1) -partite graph \mathrm{K}_{1, 1, \ldots, 1} ) with either \mathsf{{G}}_2 or \mathsf{{H}}_2 , and denote these disjoint unions by the graphs \mathsf{{U}}^{(k)} and \mathsf{{W}}^{(k)} , respectively. In general, the Lovász \vartheta -function of a disjoint union of graphs is equal to the sum of the Lovász \vartheta -functions of the component graphs (see (2.60) with a proof in Section 18 of [12]), so by (4.28)
The graphs \mathsf{{U}}^{(k)} and \mathsf{{W}}^{(k)} are, respectively, induced subgraphs of \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{H}}_1^{(k)} \, \underline{\vee} \, \mathsf{{H}}_2 . Indeed, \mathsf{{U}}^{(k)} and \mathsf{{W}}^{(k)} are obtained by deleting the vertices in \mathsf{{G}}_1^{(k)} and \mathsf{{H}}_1^{(k)} from the graphs \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{H}}_1^{(k)} \, \underline{\vee} \, \mathsf{{H}}_2 , respectively (recall that \mathsf{{G}}_1^{(k)} = \mathsf{{H}}_1^{(k)} by (4.27)). The Lovász \vartheta -function of an induced subgraph is less than or equal to the Lovász \vartheta -function of the original graph (see Item 13 in Section 2.5), so it follows from (4.43) and (4.44) that
We finally show that the leftmost inequalities in (4.45) and (4.46) hold with equality. This is shown by Definition 2.44 of the Lovász \vartheta -function of a graph. For k \in {\mathbb{N}} , let {\bf{u}}^{(k)} be an orthonormal representation of the graph \mathsf{{U}}^{(k)} , \{{\bf{u}}_i^{(k)}: i \in \mathsf{V}({\mathsf{{U}}^{(k)}}) \} , and let the unit vector {\bf{c}}^{(k)} be an optimal handle of that orthonormal representation in the sense of attaining the minimum on the right-hand side of the equality for the Lovász \vartheta -function of the graph \mathsf{{U}}^{(k)} (see (2.47)), i.e.,
Let v'_1, \ldots, v'_{k+1} denote the vertices that are added to the vertex set of the join of graphs \mathsf{{G}}_1^{(k)} \vee \mathsf{{G}}_2 in order to form the vertex set of the NS join of graphs \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 . These added vertices are associated with k+1 vectors, all of which are orthogonal. This orthogonality arises because they correspond to vertices that are nonadjacent in the graph \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 . Furthermore, these vectors are also orthogonal to all the vectors assigned to the vertices in \mathsf{{G}}_2 , as none of the vertices v'_1, \ldots, v'_{k+1} are adjacent to any vertex in \mathsf{{G}}_2 . By (4.27), the vertices v_i and v_{i+1} are adjacent in \mathsf{{G}}_1^{(k)} for all i \in [{k}] , and vertex v_{k+1} is adjacent to v_1 in \mathsf{{G}}_1^{(k)} . The k+1 orthonormal vectors that are assigned to the vertices v'_1, \ldots, v'_{k+1} can be also used to represent the k+1 vertices v_1, \ldots, v_{k+1} of \mathsf{{G}}_1^{(k)} in an orthonormal representation of the graph \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 . Indeed, that can be done by letting, for i \in [{k}] , the vector assigned to v'_i be equal to the vector assigned to the vertex v_{i+1} , and the vector assigned to the vertex v'_{k+1} be equal to the vector assigned to vertex v_1 . This implies that any two unit vectors that are assigned to nonadjacent vertices from \{v'_1, \ldots, v'_{k+1}\} \cup \{v_1, \ldots, v_{k+1}\} in the graph \mathsf{{G}}_1^{(k)} \, \underline{\vee} \, \mathsf{{G}}_2 are orthonormal. Hence, by (2.47) and (4.47),
and the combination of (4.45) and (4.48) gives
Similarly, \vartheta(\mathsf{{H}}_1^{(k)} \, \underline{\vee} \, \mathsf{{H}}_2) = \vartheta(\mathsf{{W}}^{(k)}) , so (4.45) and (4.46) hold with equality, and by (4.41)–(4.44)
This demonstrates that every pair of the constructed irregular \{A, L, Q, \mathcal{L}\} -NICS graphs exhibit identical independence numbers, clique numbers, and chromatic numbers, while also possessing distinct Lovász \vartheta -functions.
4.3.2. Proof of Theorem 4.20
For any finite, undirected, and simple graphs \mathsf{{G}}_1 and \mathsf{{G}}_2 , the arguments presented in the proof of Theorem 4.19 apply directly to the clique numbers \omega({\mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2}) and \omega({\mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2}) , and the chromatic numbers \chi({\mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2}) and \chi({\mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2}) . These considerations therefore validate equalities (4.15)–(4.18).
The remainder of the proof of Theorem 4.19 does not extend, however, to equalities in (4.13), (4.14), (4.19), and (4.20), regarding the independence numbers and Lovász \vartheta -functions of the graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 . Subsequently, we establish inequalities (4.13), (4.14), (4.19), and (4.20), and provide sufficient conditions to assert their validity with equality. [Remarks 4.26 and 4.27 consider some cases where (4.13) and (4.19) hold with strict inequalities].
Let n_1 \triangleq |{ \mathsf{V}({\mathsf{{G}}_1})}| , and let v'_1, \ldots, v'_{n_1} be the vertices added to the vertex set of \mathsf{{G}}_1 \vee \mathsf{{G}}_2 to form both vertex sets of the graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 . According to Definitions 4.12 and 4.13, combining an independent set in \mathsf{{G}}_2 with the vertices v'_1, \ldots, v'_{n_1} yields an independent set in both \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 . By selecting a largest independent set in \mathsf{{G}}_2 , the resulting independent set in both \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 has a cardinality equal to |{ \mathsf{V}({\mathsf{{G}}_1})}| + \alpha({\mathsf{{G}}_2}) . This justifies inequalities (4.13) and (4.14).
Inequalities (4.19) and (4.20) are next proved. Consider the graph \mathsf{{U}} , defined as the disjoint union of an empty graph on n_1 vertices, denoted by \mathsf{E}_{{n_1}} , and the graph \mathsf{{G}}_2 . By (2.60), it follows that
The graph \mathsf{{U}} is an induced subgraph of both graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 since the former graph can be obtained from each of the latter two graphs by removing the vertices in \mathsf{{G}}_1 along with their incident edges. By Item 13 of Section 2.5, it follows that
and then the combination of (4.52)–(4.56) results in (4.19) and (4.20).
Sufficient conditions for inequalities (4.19) and (4.20) to hold as equalities are subsequently proved. Let \{{\bf{u}}_i: i \in \mathsf{V}({\mathsf{{U}}}) \} and {\bf{c}} be, respectively, an orthonormal representation of \mathsf{{U}} and a unit vector such that
The vertex set of the graph \mathsf{{U}} consists of n_1 isolated vertices, denoted by v'_1, \ldots, v'_{n_1} , and the vertex set of \mathsf{{G}}_2 . The vertex set of each of the graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 can be regarded as the disjoint union of the vertex sets of \mathsf{{U}} and \mathsf{{G}}_1 , where \mathsf{V}({\mathsf{{U}}}) = \{v'_1, \ldots, v'_{n_1} \} \cup \mathsf{V}({\mathsf{{G}}_2}) and \mathsf{V}({\mathsf{{G}}_1}) = \{v_1, \ldots, v_{n_1}\} . We next consider separately the Lovász \vartheta -functions of the two graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 .
(1) Consider the graph \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 , where n_1 \triangleq |{ \mathsf{V}({\mathsf{{G}}_1})}| . Also consider an orthonormal representation of the graph \mathsf{{U}} , along with a unit vector \bf{c} , attaining the maximum on the right-hand side of (4.57). Suppose that there exists a permutation \pi \colon [{n_1}] \to [{n_1}] such that \{v_i, v_{\pi(i)}\} \in \mathsf{E}({\mathsf{{G}}_1}) for all i \in [{n_1}] . Select the unit vector representing the vertex v_{\pi(i)} \in \mathsf{V}({\mathsf{{G}}_1}) to be equal to the vector representing the vertex v'_i \in \mathsf{V}({\mathsf{{U}}}) . This facilitates an orthonormal representation of \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 using the same set of vectors as in the orthonormal representation of the induced subgraph \mathsf{{U}} . Indeed, the vertices v'_1, \ldots, v'_{n_1} are nonadjacent to each other in \mathsf{{U}} or also in \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 . Consequently, due to the orthonormality of the set of vectors representing the n_1 vertices v'_1, \ldots, v'_{n_1} , the vector representing any vertex v'_i (with i \in [{n_1}] ) is orthogonal to all vectors representing vertices in \mathsf{{G}}_1 , except for the vertex v_{\pi(i)} . This exception exists because, by construction, the unit vectors that represent v'_i and v_{\pi(i)} are identical. Specifically, for all i \in [{n_1}] , this setup ensures the required orthogonality between the representing vector of v'_i and the representing vectors of all vertices in \mathsf{{G}}_1 that are not adjacent to v'_i .
It is worth noting that the considered orthonormal representation of \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 has two additional features:
● Given that each vertex in \mathsf{{G}}_1 is adjacent to every vertex in \mathsf{{G}}_2 , it is unnecessary to check the orthogonality of pairs of vectors representing any vertex from \mathsf{{G}}_1 and any vertex from \mathsf{{G}}_2 . Despite this, these vector pairs are indeed orthogonal. This orthogonality results from the specific construction of the graph \mathsf{{U}} and its orthonormal representation, ensuring that the vectors representing vertices v'_1, \ldots, v'_{n_1} are orthogonal to those representing the vertices in \mathsf{{G}}_2 . Moreover, there exists an injective mapping (by assumption) between the vectors representing the vertices in \mathsf{{G}}_1 and those representing the vertices v'_1, \ldots, v'_{n_1} , from which the orthogonality between the representing vectors of any vertex pair from \mathsf{{G}}_1 and \mathsf{{G}}_2 follows.
● By assumption, there is an injective mapping from the orthonormal vectors representing the vertices v'_1, \ldots, v'_{n_1} to the vectors representing the vertices in \mathsf{{G}}_1 . Consequently, the vectors representing the vertices in \mathsf{{G}}_1 are also orthonormal. Therefore, any two of these unit vectors that represent nonadjacent and distinct vertices in \mathsf{{G}}_1 are, in particular, orthogonal.
Consequently, under the assumption on the existence of a permutation \pi of [{n_1}] as described, consider \{{\bf{u}}_i: i \in \mathsf{V}({\mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2}) \} as the proposed orthonormal representation of the graph \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 . It then follows that
where inequality (4.58) arises from applying (2.47) to the graph \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 , based on the constructed orthonormal representation of that graph and considering that \mathbf{c} is a unit vector. Equality (4.59) holds because the considered orthonormal representation of \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 utilizes the same set of unit vectors as the orthonormal representation of the induced subgraph \mathsf{{U}} , also incorporating the same unit vector \mathbf{c} . Furthermore, equality (4.60) is due to (4.57). Combining (4.55) with (4.58)–(4.60), under the aforementioned assumption, it follows that
Combining (4.52)–(4.54) and (4.61) gives that inequality (4.19) holds as an equality.
(2) Consider the graph \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 , where n_1 \triangleq |{ \mathsf{V}({\mathsf{{G}}_1})}| . Suppose that there exists a permutation \pi of [{n_1}] such that, for all i \in [{n_1}] , the conditions i \neq \pi(i) and \{v_i, v_{\pi(i)}\} \notin \mathsf{E}({\mathsf{{G}}_1}) hold. The proof that these conditions are sufficient for equality in inequality (4.20) is analogous to the proof for Item 1 regarding the satisfiability of inequality (4.19) with equality. The primary distinction involves a minor modification in the new proof, reflecting differences between the definitions of the NS and NNS joins of graphs, as delineated in Definitions 4.12 and 4.13. This adjustment accounts for the altered assumption compared to that used in Item 1.
The sufficient conditions for the equalities in inequalities (4.13) and (4.14) are finally demonstrated. Assume the above sufficient condition for equality in (4.19) is met and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) . Then,
where (4.62) is justified by the sufficient condition for equality in (4.19); (4.63) holds by assumption; (4.64) holds by (4.13), and (4.65) holds by (2.52) (the Lovász \vartheta -function of a graph is an upper bound on its independence number). Hence, the two inequalities in (4.64) and (4.65) hold with equalities, so (4.13) holds with equality. Similarly, if the above sufficient condition for equality in (4.20) is met and \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) , then also (4.14) holds with equality. This completes the proof of Theorem 4.20.
4.3.3. Proof of Theorem 4.24
Let \mathsf{{G}}_1 and \mathsf{{G}}_2 be finite, undirected, and simple graphs. Consider the NS join of graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 . In light of Remark 4.21, the assumptions in Item 1 of Theorem 4.24 are equivalent to the satisfiability of the sufficient condition for inequality (4.13) to hold with equality. By Theorem 4.20, the satisfiability of the latter condition also suffices for inequality (4.19) to hold with equality. Consequently, by the assumptions in Item 1 of Theorem 4.24,
Since the inequalities \alpha({\mathsf{{G}}}) \leq \Theta(\mathsf{{G}}) \leq \vartheta(\mathsf{{G}}) hold for every graph \mathsf{{G}} , it also follows from (4.66) that
Combining (4.66) and (4.67) gives (4.22), which validates Item 1 of Theorem 4.24.
Consider the NNS join of graphs \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 . Item 2 of Theorem 4.24 is justified likewise by the replacement of the condition \mathrm{per}(\mathbf{A}(\mathsf{{G}}_1)) > 0 with the modified condition \mathrm{per}(\mathbf{A}(\overline{\mathsf{{G}}}_1)) > 0 , while maintaining the condition \alpha({\mathsf{{G}}_2}) = \vartheta(\mathsf{{G}}_2) . Under these assumptions, Item 2 of Theorem 4.24 is justified by combining Theorem 4.20 and Remark 4.21.
Item 3 of Theorem 4.24 finally follows by combining Items 1 and 2 of that theorem.
4.3.4. Proof of Corollary 4.25
By the assumptions outlined in Items 1 and 2 of Corollary 4.25, equalities (4.24)–(4.26) hold in light of the satisfiability of the sufficient conditions for the leftmost and rightmost inequalities in (3.1) and (3.2) to hold as equalities. Additionally, if \mathsf{{G}} and \mathsf{{H}} are cospectral d -regular graphs on n vertices, then their complements \overline{\mathsf{{G}}} and \overline{\mathsf{{H}}} are cospectral (n-d-1) -regular graphs. This assertion is valid since both complement graphs share the largest eigenvalue of their adjacency matrices, which is n-d-1 , and all other eigenvalues, accounting for multiplicities, are uniformly shared and arranged in nonincreasing order as -1 - \lambda_{n+1-i} for each i from 1 to n-1 .
4.4. Discussions and examples for the results in Section 4.2
Remark 4.26 (The independence numbers of NS/NNS joins of graphs). In the construction used in the proof of Theorem 4.19, we encounter a situation where (4.13) holds with equality. Inequalities (4.13) and (4.14) in Theorem 4.20 may hold, however, with strict inequalities. We next show two possible selections of \mathsf{{G}}_1 in the NS join of graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 , for which the difference between the left and right sides of (4.13) can be made arbitrarily large.
● Let \mathsf{{G}}_1 be a graph whose vertex set includes a subset of k_1 isolated vertices, and let \mathsf{{G}}_2 be an arbitrary finite, undirected, and simple graph. Consider the NS join of graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 . In this construction, the k_1 isolated vertices in \mathsf{{G}}_1 , combined with the |{ \mathsf{V}({\mathsf{{G}}_1})}| vertices added to the vertex set of \mathsf{{G}}_1 \vee \mathsf{{G}}_2 to form the complete vertex set of \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 , collectively form an independent set in \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 . Consequently, \alpha({\mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2}) \geq |{ \mathsf{V}({\mathsf{{G}}_1})}| + k_1 , so
The right-hand side of (4.68) can be made arbitrarily large as we let k_1 tend to infinity.
● Let \mathsf{{G}}_1 be a star graph with k_1 leaves (i.e., vertices of degree 1). Let its vertex set be given by \mathsf{V}({\mathsf{{G}}_1}) = \{v_1, \ldots, v_{k_1+1}\} , where v_1 is the central vertex adjacent to all the leaves v_2, \ldots, v_{k_1+1} in \mathsf{{G}}_1 . Consider the NS join of graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 , with an arbitrary finite, undirected, and simple graph \mathsf{{G}}_2 . Denote by v'_1, \ldots, v'_{k_1+1} the k_1+1 vertices that are added to the join of graphs \mathsf{{G}}_1 \vee \mathsf{{G}}_2 to form the vertex set of the NS join of graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 . In that graph, the vertex v'_1 is adjacent to the k_1 vertices v_2, \ldots, v_{k_1+1} in \mathsf{{G}}_1 , and each of the vertices v'_2, \ldots, v'_{k_1+1} is adjacent only to v_1 . Hence, the disjoint union \mathcal {I} \triangleq \{v'_2, \ldots, v'_{k_1+1}\} \cup \{v_2, \ldots, v_{k_1+1}\} is an independent set in the graph \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 , so
Once again, the right-hand side of (4.70) can be made arbitrarily large by letting k_1 tend to infinity.
Remark 4.27 (The Lovász \vartheta -function of NS/NNS joins of graphs). Let \mathsf{{G}}_1 = \mathsf{K}_{{1}, {9}} be the star graph on 10 vertices (with 9 leaves), and let \mathsf{{G}}_2 be the graph on the left side of Figure 2. The star graph \mathsf{{G}}_1 clearly does not satisfy the sufficient condition in Theorem 4.20 for equality in (4.19), but it satisfies the sufficient condition in Theorem 4.20 for equality in (4.20). The Lovász \vartheta -functions of the NS and NNS joints of graphs \mathsf{{G}}_1 \, \underline{\vee} \, \mathsf{{G}}_2 and \mathsf{{G}}_1 \, \underline{\underline \vee } \, \mathsf{{G}}_2 , respectively, are computed by solving the SDP problem presented in (2.48), using the adjacency matrices specified in (4.8) and (4.9). This gives
whereas,
and the equalities (4.73) and (4.75) are justified by (4.41) and since |{ \mathsf{V}({\mathsf{{G}}_1})}| = 10 . This shows that if the sufficient condition in Theorem 4.20 for equality in (4.19) is violated, then (4.19) may hold with strict inequality (see (4.72)). Conversely, (4.20) holds here with equality (see (4.74) and (4.75)), as it is expected in light of the explanation provided above.
Example 4.28 (NS and NNS joins of Kneser graphs). Let \mathsf{{G}}_1 = \mathsf{K}({n_1}, {r_1}) and \mathsf{{G}}_2 = \mathsf{K}({n_2}, {r_2}) be Kneser graphs with n_1 \geq 2r_1 and n_2 \geq 2r_2 (so, these are nonempty graphs). Then, for i \in \{1, 2\} , \mathsf{{G}}_i is a d_i -regular graph with d_i = \binom{n_i-r_i}{r_i} , and
where (4.76), (4.77), and the first equality in (4.78) are justified, e.g., in Chapter 43 of [92]; the second and third equalities in (4.78) are due to Theorem 13 in [11]. In light of Theorems 4.20 and 4.24, it follows from (4.76)–(4.78) that
Specifically, let \mathsf{{G}}_1 = \mathsf{{G}}_2 = \mathsf{{P}} , where \mathsf{{P}} denotes the Petersen graph; \mathsf{{P}} is a graph on 10 vertices, and \mathsf{{P}} \cong \mathsf{K}({5}, {2}) , so (4.79) and (4.80) with n_1 = n_2 = 5 and r_1 = r_2 = 2 give
Equality (4.83) was verified numerically using a combination of the CVX and SageMath software tools [51,113]. This was done by first constructing the NS and NNS join of graphs \mathsf{{P}} \, \underline{\vee} \, \mathsf{{P}} and \mathsf{{P}} \, \underline{\underline \vee } \, \mathsf{{P}} , respectively, based on their adjacency matrices in (4.8) and (4.9). Subsequently, the SDP problem presented in (2.48) was solved for computing the Lovász \vartheta -functions of the two constructed graphs.
Example 4.29 (NS/NNS joins of a regular graph and the Tietze graph). Let \mathsf{{G}}_1 be a nonempty and noncomplete regular graph, and let \mathsf{{G}}_2 be the Tietze graph (see Figure 4). The graph \mathsf{{G}}_2 is a 3-regular graph on 12 vertices, not strongly regular, nor vertex- or edge-transitive (these properties can be verified by the SageMath software [51]).
It is next shown that
Indeed, a maximum independent set in \mathsf{{G}}_2 is given by \{0, 3, 5, 7, 11\} , so \alpha({\mathsf{{G}}_2}) = 5 . Additionally, the equality \vartheta(\mathsf{{G}}_2) = 5 is verified by solving the SDP problem in (2.48):
The maximizing matrix \bf{B} in (4.85), obtained numerically by the CVX software [113], is given by
which gives
For comparison with (4.86), since the graph \mathsf{{G}}_2 is a 3-regular graph on 12 vertices, inequality (2.58) (Theorem 9 in [11]) with d = 3 and \lambda_{\min}(\mathsf{{G}}_2) = -2.30278 \ldots gives
so the upper bound (4.87) is not tight. It should be noted that \mathsf{{G}}_2 is neither edge-transitive nor strongly regular. If it were, then Theorem 3.1 would have transformed inequality (4.87) into an equality. This transformation would have occurred provided the sufficient conditions for equality, specified in regard to the rightmost inequality of (3.1), were met.
By (4.84), it follows that the Shannon capacity of the Tietze graph is equal to 5
The vertices in \mathsf{{G}}_2 can be partitioned into at least three independent sets, e.g., \{0, 2, 5, 11\} , \{1, 4, 7, 10\} , and \{3, 6, 8, 9\} (see Figure 4), so the chromatic number of \mathsf{{G}}_2 is equal to 3
The maximum clique in \mathsf{{G}}_2 (see Figure 4) is the triangle \{9, 10, 11\} , so
In light of Theorem 4.20 and Corollary 4.23, it follows from (4.84), (4.89), and (4.90) that
Example 4.30 (Chang graphs). Chang graphs are three cospectral and strongly regular graphs with the identical parameters \mathsf{srg}({28}, {12}, {6}, {4}) . The line graph of the complete graph \mathsf{K}_{{8}} is also a strongly regular graph with the same set of parameters. By Theorem 2.37, these graphs have an identical spectrum with \lambda_1 = 12 , \lambda_2 = \ldots = \lambda_8 = 4 (multiplicity 7), and \lambda_9 = \ldots = \lambda_{28} = -2 (multiplicity 20). It can be verified, using the SageMath software [51], that all pairs among these cospectral graphs are nonisomorphic and that the three Chang graphs and their complements are neither vertex-transitive nor edge-transitive. In light of Corollary 4.25, those four strongly regular graphs have an identical Lovász \vartheta -function valued at 4, as demonstrated by either (4.24) or (4.25). Furthermore, the graph complements, which are strongly regular, cospectral, and nonisomorphic, share a common value of 7 for their Lovász \vartheta -functions, as demonstrated by (4.26).
5.
Bounds on graph invariants via the Lovász \vartheta -function
Building on preliminaries in Section 2 and introducing additional background in Section 5.1, this section utilizes the Lovász \vartheta -function and its unique properties to derive bounds on various graph invariants. These bounds are presented in Section 5.2, and their proofs are provided in Section 5.3. The tightness of these bounds is examined in Section 5.4, including comparisons with established bounds in the literature.
5.1. Specialized preliminaries for Section 5
5.1.1. Perfect graphs
For all graphs, the chromatic number is greater than or equal to the clique number, but they can be far apart. It is specifically possible to construct finite, connected, and simple graphs whose clique numbers are equal to 2, while having an arbitrarily large chromatic number (see, e.g., page 314 in [92]). Perfect graphs are characterized by the property that not only their chromatic and clique numbers coincide, but also the same coincidence applies to every induced subgraph. These graphs received a lot of attention (see, e.g., the books [114,115,116]), dating back to the paper by Claude Shannon in 1956 [1] and the work by Claude Berge in the early sixties [117]. Perfect graphs include many important families of graphs such as bipartite graphs, line graphs of bipartite graphs, chordal graphs, comparability graphs, and the complements of all these graphs [118]. Unlike general graphs, many graph invariants of all perfect graphs are computationally feasible [28,118].
Definition 5.1 (Perfect graph). A graph \mathsf{{G}} is perfect if \chi({\mathsf{{H}}}) = \omega({\mathsf{{H}}}) for every induced subgraph \mathsf{{H}} of \mathsf{{G}} .
Theorem 5.2 (Weak perfect graph theorem [119]). The complement of a perfect graph retains this perfection. Equivalently, a graph is perfect if and only if its complement is perfect.
A cycle graph of length 2k+1 , with k \geq 2 , satisfies 3 = \chi({ \mathsf{C}_{{2k+1}}}) > \omega({ \mathsf{C}_{{2k+1}}}) = 2 , and its complement satisfies k+1 = \chi({\overline{\mathsf{{ \mathsf{C}_{{2k+1}}}}}}) > \omega({\overline{\mathsf{{ \mathsf{C}_{{2k+1}}}}}}) = k . This shows that cycle graphs of odd length greater than 3, as well as their complements, are imperfect. By definition, the family of perfect graphs is closed under the operation of taking induced subgraphs. Therefore, these graphs can be characterized by the exclusion of a specific family of induced subgraphs, denoted \mathscr{G} . The strong perfect graph theorem, presented as follows, states that these two examples are the only elements within \mathscr{G} .
Theorem 5.3 (Strong perfect graph theorem [120]). A graph is perfect if and only if neither the graph nor its complement contains an induced cycle of odd length greater than 3.
The reader is referred to [121] as a survey paper on perfect graphs, which is mostly focused on the strong perfect graph theorem. This theorem was conjectured by Berge [117], and it was proved four decades later (in 2002) by Chudnovsky, Robertson, Seymour, and Thomas [120].
5.1.2. Triangle-free graphs
A triangle-free graph is a graph that does not contain any triangles, which are cycles of length three, as subgraphs. Triangle-free graphs have garnered attention, as evidenced by their coverage in theoretical graph theory, game theory, and advanced coding techniques for data storage [35,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136]. This interest underscores the importance of investigating graph invariants of triangle-free graphs.
Lower bounds on the independence number of triangle-free graphs were derived in [134,135], as presented in the next result.
Theorem 5.4 (Lower bound on the independence number of triangle-free graphs [135]). Let \mathsf{{G}} be a triangle-free graph on n vertices with a degree sequence \{d_1, \ldots, d_n\} . Let f \colon \{0, 1, 2, \ldots\} \to {\mathbb{R}} be defined by the recursion
with f(0) = 1 . Then,
Corollary 5.5 (Upper bound on the fractional chromatic number). Let \mathsf{{G}} be a triangle-free and vertex-transitive graph on n vertices with degree d . Then,
Proof. The triangle-free graph \mathsf{{G}} is d -regular, which implies by (5.2) that \alpha({\mathsf{{G}}}) \geq n \, f(d) . Also, since \mathsf{{G}} is vertex-transitive on n vertices, \chi_{\mathrm{f}}({\mathsf{{G}}}) = \dfrac{n}{\alpha({\mathsf{{G}}})} \leq \dfrac{n}{\lceil n f(d) \rceil} \leq \dfrac{1}{f(d)} . □
A recent work [127] provides upper bounds on the fractional chromatic number of a triangle-free graph, expressed as a function of the maximal degree of its vertices.
Theorem 5.6 (Upper bound on the fractional chromatic number of a triangle-free graph [127]). For every triangle-free graph \mathsf{{G}} of maximum degree \Delta = \Delta(\mathsf{{G}}) ,
The following result gives an upper bound on the fractional chromatic number of graphs with a large girth (so they are, in particular, triangle-free graphs).
Theorem 5.7 (Upper bound on the chromatic number of graphs with a large girth, [127]). If \mathsf{{G}} is a graph of girth of at least 7, then
Numerical results that rely on Theorem 5.7 are presented in Table 1.4 of [127].
5.1.3. Lower bounds on the fractional chromatic number of a graph
The fractional chromatic number of a graph \mathsf{{G}} is lower-bounded by the Lovász \vartheta -function of the complement \overline{\mathsf{{G}}}
(see Exercise 11.20 in [29], and (2.52) here). For a self-contained presentation in the continuation of this section, we next provide a proof of (5.6).
Proof. By the formulation of the fractional chromatic number of a graph as an LP problem (see (2.5)), let \chi_{\mathrm{f}}({\overline{\mathsf{{G}}}}) \triangleq t be the smallest value for which there exists a family \{ \mathcal {B}_j\}_{j = 1}^p of cliques in \mathsf{{G}} , along with nonnegative weights \{\tau_j\}_{j = 1}^p such that
For every v \in \mathsf{V}({\mathsf{{G}}}) , let the vertex v be assigned the vector
where, for j \in [{p}] , {\bf{e}}_j is the p -dimensional unit column vector characterized by having \tt{1} in its j -th component and zeros in all other components, and
This mapping gives an orthonormal representation of \mathsf{{G}} since these are unit vectors in {\mathbb{R}}^p , and if \{v_1, v_2\} \notin \mathsf{E}({\mathsf{{G}}}) , then there exists no j \in [{p}] such that v_1, v_2 \in \mathcal {B}_j (since the set \mathcal {B}_j forms a clique in \mathsf{{G}} ), so {\bf{u}}(v_1)^{\mathrm{T}} \, {\bf{u}}(v_2) = 0 . Let the p -dimensional handle {\bf{c}} of that orthonormal representation be given by
so it follows from (5.7) that \|{\bf{c}}\| = 1 . For all v \in \mathsf{V}({\mathsf{{G}}}) ,
where equality (5.12) holds by (5.9) and (5.11); (5.13) holds by (5.10), and inequality (5.14) holds by (5.8). Consequently, it follows from (2.47) and (5.14) that
□
Two additional spectral lower bounds on the fractional chromatic number of a graph are presented as follows. These are compared with the lower bound on the right-hand side of Eq (5.6).
(1) For a graph \mathsf{{G}} on n vertices, let \lambda_1(\mathsf{{G}}) and \lambda_n(\mathsf{{G}}) be, respectively, the largest and least eigenvalues of the adjacency matrix of \mathsf{{G}} (see (2.18)). Then, independently by [72,73],
Combining (2.49), (5.6), and (5.16) gives
This demonstrates that the bound expressed on the right-hand side of (5.16) gives a looser lower bound on the fractional chromatic number in comparison to the bound on the right-hand side of (5.6). Alternatively, this conclusion can also be reached by applying (2.71) to the complement graph \overline{\mathsf{{G}}} , which gives
where {\bf{T}} = (T_{i, j}) ranges over all the symmetric nonzero n \times n matrices with T_{i, j} = 0 for all \{i, j\} \not\in \mathsf{E}({\mathsf{{G}}}) , and also for i = j . Selecting a potentially suboptimal choice for {\bf{T}} on the right-hand side of (5.18), namely, the adjacency matrix of \mathsf{{G}} , yields
(2) A recent lower bound by Guo and Sapiro (Theorem 1.1 in [137]) states that
where, on the right-hand side of (5.20), s^{+}(\mathsf{{G}}) and s^{-}(\mathsf{{G}}) respectively denote the sum of squares of the positive and negative eigenvalues of the adjacency matrix \mathbf{A} of \mathsf{{G}} ; these sums are referred to as the positive and negative square energies of the graph \mathsf{{G}} . The interested reader is directed to recent studies in [138,139], which explore the symmetry or asymmetry between the positive and negative square energies of structured and random graphs. These studies also discuss open questions related to this topic.
The lower bound on the fractional chromatic number presented on the right-hand side of (5.20) strengthens Theorem 2.3 from [140], which provides an identical lower bound on the chromatic number of the graph \mathsf{{G}} . It is worth noting that inequality (5.20) was first conjectured in [141] with a proof of a loosened lower bound that was smaller by 1 than the right-hand side of (5.20). In continuation to that line of research, Coutino and Spier [142] recently proved that the right-hand side of (5.20) is even a lower bound on the vector chromatic number of the graph \mathsf{{G}} , i.e.,
The chain of inequalities in (5.21) show that the right-hand side of (5.20) is a looser lower bound on the fractional chromatic number in comparison to the right-hand side of (5.6).
The spectral lower bounds on the fractional chromatic number of a graph \mathsf{{G}} , as presented on the right-hand sides of (5.16) and (5.20), are looser than the bound on the right-hand side of (5.6). The latter is equal to the Lovász \vartheta -function of the graph complement \overline{\mathsf{{G}}} .
We next refer to the so called inertial lower bounds on the chromatic and fractional chromatic numbers of a graph. Let \mathsf{{G}} be a graph on n vertices, and let \mathbf{A} be its adjacency matrix. The inertia of \mathbf{A} is defined as the ordered triple (n^+, n^0, n^-) where n^+ , n^0 , and n^- , respectively, denote the numbers (counting multiplicities) of the positive, zero, and negative eigenvalues of \mathbf{A} (so, n = n^+ + n^0 + n^- ). Note that \mathrm{rank}(\mathbf{A}) = n^{+} + n^{-} and \mathrm{nullity}(\mathbf{A}) = n^0 . Theorem 1 of [143] states that
A graph \mathsf{{G}} is called nonsingular if its adjacency matrix \mathbf{A} is nonsingular, which holds if and only if n^0 = 0 . It is further proved in Section 3 of [143] that if \mathsf{{G}} is a nonsingular graph, then the right-hand side of (5.22) is even a lower bound on its fractional chromatic number, i.e.,
Additionally, (5.23) holds with equality for all Kneser graphs \mathsf{K}({r}, {k}) with r \geq 2k (i.e., for all nonempty Kneser graphs) and for all cycle graphs.
In light of Theorem 2.37, the lower bound in (5.23) holds in particular for all strongly regular graphs (since their adjacency matrices have no zero eigenvalues). Then, for strongly regular graphs, (5.23) gets the form
where m_1 and m_2 on the right-hand side of (5.24), respectively, denote the multiplicities of the second-largest and least eigenvalues of the adjacency matrix of a strongly regular graph \mathsf{{G}} . The expressions for m_{1, 2} are given in (2.33). It is further commented in [143] that the lower bound (5.23) on the fractional chromatic number of a nonsingular graph \mathsf{{G}} cannot serve as a lower bound on the vector chromatic number of \mathsf{{G}} .
5.1.4. Lower bounds on the independence and clique numbers of a graph
Lower bounds on the independence and clique numbers of a graph were established using the vertex degrees by Wei [144]. Let \mathsf{{G}} be a graph on n vertices, and let \{d_i\}_{i = 1}^n represent the degree sequence of its vertices. Then, the following (nonspectral) bounds on the independence and clique numbers of \mathsf{{G}} , respectively, hold:
The equivalent bounds (5.25) and (5.26) are proved by using a probabilistic approach (see, e.g., page 287 in [92]). The reader is referred to [136] for a refinement of Wei's bounds in (5.25) and (5.26) for connected triangle-free graphs.
Spectral lower bounds on the independence and clique numbers of a graph, originally conjectured in [145] and proved in [146], are given by
where m \triangleq |{ \mathsf{E}({\mathsf{{G}}})}| denotes the size of the graph. The equivalent spectral bounds in (5.27) and (5.28) were derived in [146] through a combination of the Motzkin-Straus result (Theorem 1 in [147]), an equality for the largest eigenvalue of the adjacency matrix of the graph \mathsf{{G}} , and the Cauchy-Schwarz inequality. The Motzkin-Starus result states that if \mathsf{{G}} is a graph on n vertices, then
where every edge \{i, j\} and \{j, i\} is counted only once on the left-hand side of (5.29), the maximization is attained by selecting a maximum clique \mathcal {C} in \mathsf{{G}} , and setting x_i \triangleq \frac1{ \omega({\mathsf{{G}}})} for all i \in [{n}] such that v_i \in \mathcal {C} , and x_i \triangleq 0 otherwise. It is noteworthy that [148] appears to be the first paper to identify a relationship between the Motzkin-Straus result and spectral bounds for graphs.
Bounds (5.25)–(5.26) and (5.27)–(5.28), respectively, coincide if \mathsf{{G}} is a regular graph. Indeed, if \mathsf{{G}} is a d -regular graph on n vertices, then m = \tfrac12 \, nd , \lambda_1(\mathsf{{G}}) = d , and \lambda_1(\overline{\mathsf{{G}}}) = n-d-1 , so the right-hand sides of (5.25) and (5.27) are equal to \frac{n}{1+d} , and the right-hand sides of (5.26) and (5.28) are equal to \frac{n}{n-d} . In light of (2.1) and the Brooks' theorem, which provides an upper bound on the chromatic number of a connected graph (see, e.g., Theorem 6.14.2 in [45]), a lower bound on the independence number of a connected d -regular graph on n vertices can be improved to \frac{n}{d} , unless \mathsf{{G}} forms a complete graph or an odd-cycle graph. Further lower bounds on the clique and independence numbers of a general simple graph \mathsf{{G}} , expressed in terms of the average degree of the vertices in \mathsf{{G}} and the smallest eigenvalue of the adjacency matrix of \mathsf{{G}} or its complement \overline{\mathsf{{G}}} , were derived in [149]. The interested reader is also referred to Section 2 in [150] for the derivation of lower bounds on the independence and clique numbers of a graph, based on the spectrum of its Laplacian matrix.
5.2. New bounds and exact results on graph invariants via the Lovász \vartheta -function
The present subsection provides new bounds and exact results on various graph invariants, derived from the properties of the Lovász \vartheta -function. This subsection is organized into four parts:
● Section 5.2.1 discusses strongly regular graphs, offering explicit bounds on several invariants of these graphs;
● Section 5.2.2 derives spectral upper and lower bounds on the vector and strict vector chromatic numbers of regular graphs, including sufficient conditions that facilitate achieving these bounds.
● Section 5.2.3 uses the Lovász \vartheta -function of a graph's complement to establish lower bounds on the fractional chromatic number of a graph, with a focus on perfect and triangle-free graphs.
● Section 5.2.4 provides lower bounds on the independence and clique numbers of a graph, based on the Lovász \vartheta -function of the graph or its complement.
5.2.1. Bounds on graph invariants based on the sandwich theorem for the Lovász \vartheta -function
The sandwich theorem for the Lovász \vartheta -function (see (2.52) and (2.53)) enables the calculation of feasible bounds on the fractional and integral independence, clique, and chromatic numbers of graphs. Although the exact calculation of these graph invariants is NP-hard, determining their bounds, based on the numerical solution of the SDP problem outlined in (2.48), is feasible with a polynomial complexity in the number of vertices (see Theorem 11.11 in [29]).
The following result illustrates the approach by deriving bounds on the considered graph invariants of strongly regular graphs. The upper bounds on the independence and clique numbers are equivalent to those derived in Theorem 2.1.5 of [151]. However, the derivation method here is different, relying on the Lovász \vartheta -function of strongly regular graphs. Through this alternative approach, new lower bounds on the fractional graph invariants are also derived.
Corollary 5.8. Let \mathsf{{G}} be a strongly regular graph with parameters \mathsf{srg}(n, d, \lambda, \mu) . Then,
with
Proof. Inequalities (5.30)–(5.33) follow from (2.52), (2.53), and Theorem 3.3. □
Numerical examinations of the tightness of bounds on graph invariants, as given in Corollary 5.8, are provided in Example 5.21 for several strongly regular graphs. The upper bound on the independence number, presented in (5.30), is a formulation of the Delsarte and Hoffman bound, which was originally developed for regular graphs (see Section 3.3 in [152] and the survey in [153]). This formulation has been specialized in (5.30) to apply to strongly regular graphs. It is noteworthy that this bound, also known as Hoffman's ratio bound, was generalized to simple graphs that are not necessarily regular (Theorem 2.1.3 of [151]), and to graphs that may have self-loops (Corollaries 3.4 and 3.6 of [154]). Additionally, other upper bounds on the independence number of a connected simple graph \mathsf{{G}} are provided in [155], expressed in terms of the largest and smallest eigenvalues of the adjacency matrix of \mathsf{{G}} , along with its maximum and minimum degrees.
5.2.2. Exact results and bounds for the vector and strict vector chromatic numbers of graphs
Upper and lower bounds on the vector and strict vector chromatic numbers are next derived for regular graphs, along with sufficient conditions for the attainability of each of these bounds. For strongly regular graphs or for graphs that are both vertex- and edge-transitive, it leads to exact closed-form expressions of their vector and strict vector chromatic numbers. These results demonstrate that these two types of chromatic numbers coincide for such regular graphs. The subsequent theorem forms a strengthening of Theorem 3.1 (see Remark 5.10).
Theorem 5.9. Let \mathsf{{G}} be a graph on n vertices.
(1) The following inequality holds:
with equality if \mathsf{{G}} is a vertex-transitive or a strongly regular graph.
(2) If \mathsf{{G}} is a d -regular graph, then
Furthermore,
● Equality holds in the leftmost inequality of (5.36) if \mathsf{{G}} is both vertex-transitive and edge-transitive, or if \mathsf{{G}} is a strongly regular graph;
● Equality holds in the rightmost inequality of (5.36) if \overline{\mathsf{{G}}} is edge-transitive, or if \mathsf{{G}} is a strongly regular graph;
● Equality holds in the leftmost inequality of (5.37) if \overline{\mathsf{{G}}} is both vertex-transitive and edge-transitive, or if \mathsf{{G}} is a strongly regular graph;
● Equality holds in the rightmost inequality of (5.37) if \mathsf{{G}} is edge-transitive, or if \mathsf{{G}} is a strongly regular graph.
Proof. See Section 5.3.1. □
Remark 5.10 (Comparison of Item 2 in Theorem 5.9 with Theorem 3.1). By equality (2.50), where \chi_{\mathrm{sv}}({\mathsf{{G}}}) = \vartheta(\overline{\mathsf{{G}}}) holds for every graph \mathsf{{G}} , the rightmost inequalities in (5.36) and (5.37) are, respectively, equivalent to those in (3.2) and (3.1). Furthermore, in light of inequality (2.49), which states that \chi_{\mathrm{v}}({\mathsf{{G}}}) \leq \vartheta(\overline{\mathsf{{G}}}) for all \mathsf{{G}} , the leftmost inequalities in (5.36) and (5.37) are, respectively, stronger than those in (3.2) and (3.1) of Theorem 3.1. These observations affirm that Item 2 in Theorem 5.9 not only corroborates, but also strengthens the assertions made in Theorem 3.1.
Remark 5.11 (Relation to spectral lower bounds in [75]). The spectral lower bound on the vector chromatic number of a regular graph \mathsf{{G}} , as presented in the leftmost term of (5.36), is due to Galtman [73]; it is also referred to as Hoffman's bound for the vector chromatic number [72,75]. Spectral lower bounds on the vector chromatic number of any connected graph \mathsf{{G}} are introduced in Theorems 1 and 6 of [75]. The lower bound in Theorem 1 of [75] is given by
where m \triangleq |{ \mathsf{E}({\mathsf{{G}}})}| is the number of edges in \mathsf{{G}} , and \nu_n(\mathsf{{G}}) denotes the least eigenvalue of the signless Laplacian matrix {\bf{Q}} of the graph \mathsf{{G}} (see (2.20)). Additionally, the lower bound in Theorem 6 of [75] is given by
where \lambda_1(\mathsf{{G}}) , \mu_n(\mathsf{{G}}) , and \nu_1(\mathsf{{G}}) denote, respectively, the largest eigenvalues of the adjacency matrix \mathbf{A} , the Laplacian matrix {\bf{L}} , and the signless Laplacian matrix {\bf{Q}} of the graph \mathsf{{G}} (see (2.18)–(2.20)). For regular graphs, it is mentioned in Section 6 of [75] that these lower bounds coincide. Indeed, this can be verified as follows: For a d -regular graph \mathsf{{G}} on n vertices, the equalities
hold, so the equalities in (5.40) confirm that the lower bounds on the left-hand sides of (5.38) and (5.39) coincide. Furthermore, these lower bounds are identical to the lower bound on \chi_{\mathrm{v}}({\mathsf{{G}}}) as presented in the leftmost term of (5.36).
Based on Theorem 5.9, exact closed-form expressions for the vector and strict vector chromatic numbers are next provided for two important subclasses of regular graphs.
Theorem 5.12 (Vector and strict vector chromatic numbers of strongly regular graphs). Let \mathsf{{G}} be a strongly regular graph with parameters \mathsf{srg}(n, d, \lambda, \mu) . Then, the vector and strict vector chromatic numbers of \mathsf{{G}} and its complement \overline{\mathsf{{G}}} satisfy
where t is given in (5.34). The vector and strict vector chromatic numbers of strongly regular graphs are therefore identical. Additionally, the product of the vector (or strict vector) chromatic numbers of a strongly regular graph and its complement equals the order of the graph, i.e.,
Proof. See Section 5.3.2. □
Corollary 5.13 (Vector and strict vector chromatic numbers of conference graphs). If \mathsf{{G}} is a conference graph on n vertices, then
Proof. The equalities in (5.45) stem from applying Theorem 5.12 with the parameters of a conference graph. Specifically, a conference graph, when considered as a strongly regular graph, is characterized by the parameters d = \frac{1}{2}(n-1) , \lambda = \frac{1}{4}(n-5) , and \mu = \frac{1}{4}(n-1) (see Definition 2.38). The extreme equalities in (5.45) also hold since \mathsf{{G}} and \overline{\mathsf{{G}}} are both conference graphs on n vertices. □
Theorem 5.14 (Vector/ strict vector chromatic numbers of vertex- and edge-transitive graphs). Let \mathsf{{G}} be a graph that is both vertex-transitive and edge-transitive. Then, its vector and strict vector chromatic numbers coincide, and
Proof. See Section 5.3.3. □
Remark 5.15 (On the subclasses of regular graphs in Theorems 5.12 and 5.14). Theorems 5.12 and 5.14 consider, respectively, the class of strongly regular graphs and the class of graphs that are vertex-transitive and edge-transitive. These are nonequivalent subclasses of the regular graphs, where also none of them is contained in the other. Specifically, the complement of the Cameron graph (see Section 10.54 in [52]) is a strongly regular graph, \mathsf{srg}(231,200,172,180) , which is vertex-transitive but not edge-transitive. On the other hand, the Foster graph is 3-regular on 90 vertices (see page 305 of [52]), which is vertex-transitive and edge-transitive, but it is not strongly regular. Another such example is Holt's graph that is 4-regular on 27 vertices, vertex- and edge-transitive, but not strongly regular [156]. The family of Kneser graphs \mathsf{K}({n}, {k}) , where n \geq 2k , forms a family of vertex- and edge-transitive graphs that are not necessarily strongly regular graphs; if, k = 2 and n \geq 4 , then it is a strongly regular graph with parameters \mathsf{srg}({a_n}, {b_n}, {c_n}, {d_n}) with a_n = \binom{n}{2} , b_n = \binom{n-2}{2} , c_n = \binom{n-4}{2} , and d_n = \binom{n-3}{2} . It shows that none of these two subclasses of regular graphs in Theorems 5.12 and 5.14 contains the other. To clarify why a graph that is both vertex- and edge-transitive is not necessarily strongly regular, suppose that \mathsf{{G}} is a vertex- and edge-transitive graph. Then,
● ( \mathsf{{G}} is vertex-transitive) \Rightarrow \mathsf{{G}} is regular;
● ( \mathsf{{G}} is edge-transitive) \Rightarrow (every edge in \mathsf{{G}} is contained in the same number of triangles) \Leftrightarrow (every pair of adjacent vertices in \mathsf{{G}} has the same number of common neighbors).
Hence, the condition that every pair of nonadjacent vertices has the same number of common neighbors, which is a requirement for strongly regular graphs, is not necessarily fulfilled here. To that end, suppose that also \overline{\mathsf{{G}}} is edge-transitive. Then,
● ( \overline{\mathsf{{G}}} is edge transitive) \Rightarrow (for every edge \{u, v\} \in \mathsf{E}({\overline{\mathsf{{G}}}}) , the same number of vertices are not adjacent in \overline{\mathsf{{G}}} to either u or v ) \Leftrightarrow (every pair of nonadjacent vertices in \mathsf{{G}} has the same number of common neighbors).
It is important to note that while the closeness property holds for vertex-transitive graphs under the operation of graph complementation, this property does not extend to edge-transitive graphs.
Remark 5.16 (The vector and strict vector chromatic numbers of vertex-transitive graphs may be distinct). As opposed to graphs that are both vertex- and edge-transitive, whose vector and strict vector chromatic numbers coincide (by Theorem 5.14), the strict vector chromatic number of a graph that is only vertex-transitive (but not edge-transitive) may be strictly greater than its vector chromatic number (see Example 5.23).
5.2.3. Lower bounds on the fractional chromatic number of a graph
The fractional chromatic number of a graph \mathsf{{G}} is lower-bounded by the Lovász \vartheta -function of its complement \overline{\mathsf{{G}}} , as demonstrated by inequality (5.6). Following the derivation of a closed-form lower bound on the fractional chromatic number of any strongly regular graph (see (5.32)), two additional classes of graphs are considered, while linking these results with relevant literature.
On perfect graphs: The strong perfect graph theorem provides an exact characterization of perfect graphs (see Theorem 5.3). This characterization, alongside the sandwich theorem for the Lovász \vartheta -function (see (2.52) and (2.53)) and the weak perfect graph theorem (see Theorem 5.2), establishes that for perfect graphs, the computations of both integral and fractional independence numbers, clique numbers, and chromatic numbers, as well as the Shannon capacity, vector chromatic number, and strict vector chromatic number coincide with the Lovász \vartheta -function of either the graph itself or its complement. Remarkably, the computational complexity of these graph invariants, typically NP-hard for general graphs, can be efficiently computed in polynomial time for perfect graphs by solving the SDP problem outlined in (2.48) [28].
Theorem 5.17 (Graph invariants of perfect graphs). If \mathsf{{G}} is a perfect graph, then
Proof. If \mathsf{{G}} is a perfect graph, so is its complement \overline{\mathsf{{G}}} . Hence, \omega({\mathsf{{G}}}) = \chi({\mathsf{{G}}}) and \alpha({\mathsf{{G}}}) = \chi({\overline{\mathsf{{G}}}}) . The other equalities in (5.47) and (5.48) hold by the sandwich theorem in (2.52) and (2.53). □
If \mathsf{{G}} is a perfect graph, then so is every induced subgraph of \mathsf{{G}} or \overline{\mathsf{{G}}} . It therefore follows that, if \mathsf{{G}} is a perfect graph, then the chains of equalities in (5.47) and (5.48) hold for every induced subgraph of \mathsf{{G}} or \overline{\mathsf{{G}}} .
Theorem 5.17 is illustrated in Examples 5.25 and 5.26, with respect to three-tower Hanoi graphs and windmill graphs (these are all perfect graphs), and with comparisons to lower bounds on the fractional chromatic number. By Theorem 5.17, the lower bound on the right-hand side of (5.6) is tight for perfect graphs, whereas the other lower bounds in (5.16) and (5.20) are not necessarily tight for these graphs.
On triangle-free graphs: The next result gives a lower bound on the fractional chromatic number of triangle-free graphs (i.e., graphs that have no cliques of three vertices).
Theorem 5.18. Let \mathsf{{G}} be a nonempty triangle-free graph on n vertices. Then,
Proof. See Section 5.3.4. □
Remark 5.19 (Relation to [35]). In Theorem 2.1 of [35], Alon proved that for every integer represented as n = 8^k , where k \in {\mathbb{N}} is not divisible by 3, there exists a triangle-free and d_n -regular graph \mathsf{{G}}_n on n vertices, with d_n = 2^{k-1} (2^{k-1}-1) , and
as o(1) \underset{n \to \infty}{\longrightarrow} 0 . The result in Theorem 5.18 shows that, up to a constant factor, \vartheta(\mathsf{{G}}_n) in (5.50) has the smallest scaling in n . A result of a similar focus, examining the minimum chromatic number of a triangle-free graph as a function of its number of vertices or edges, is analyzed in [157].
5.2.4. Lower bounds on the independence and clique numbers of a graph
Section 5.1.4 introduces known lower bounds on the independence and clique numbers of a graph. The following bounds are expressed in terms of the Lovász \vartheta -function of the graph or its complement.
Theorem 5.20 (Lower bounds on the independence and clique numbers of a graph). Let \mathsf{{G}} be a graph on n vertices, excluding the complete graph or its complement. Then,
Proof. See Section 5.3.5. □
5.3. Proofs
This section offers proofs of results outlined in Section 5.2.
5.3.1. Proof of Theorem 5.9
Let \mathsf{{G}} be a graph on n vertices. Inequality (5.35) is derived by combining (2.50) (Theorem 8.2 in [70]) and (2.57) (Corollary 2 in [11]). Additionally, if \mathsf{{G}} is a strongly regular or vertex-transitive graph, then (5.35) is assured to hold with equality by combining (2.50) and Corollary 3.4. This completes the proof of Item 1 in Theorem 5.9.
We now turn to prove Item 2 in Theorem 5.9. Let \mathsf{{G}} be a d -regular graph on n vertices. Referring to Remark 5.10 and (2.49), it suffices to prove the leftmost inequalities in (5.36) and (5.37). This is sufficient because the middle inequalities in (5.36) and (5.37) are (2.45), and the rightmost inequalities in (5.36) and (5.37) are, respectively, equivalent to those in (3.2) and (3.1) (due to equality (2.50)). By Galtman's result [73],
which is the leftmost inequality in (5.36) with \lambda_1(\mathsf{{G}}) = d . The leftmost inequality in (5.37) is obtained as follows:
where (5.54) holds by replacing \mathsf{{G}} with \overline{\mathsf{{G}}} on both sides of (5.53); (5.55) is obtained from (4.10), where the latter reveals the following relation for a d -regular graph \mathsf{{G}} on n vertices (see Section 1.3.2 in [41]):
Specifically, by setting \ell = n in (5.58),
The leftmost inequalities in (5.36) and (5.37) hold by (5.53)–(5.56). Subsequently, by (2.50), the sufficient conditions for equality in the rightmost inequalities of (3.2) and (3.1), respectively, coincide with those required for equality in the rightmost inequalities of (5.36) and (5.37). Furthermore, by (2.50) alongside the leftmost and middle inequalities in (5.36) and (5.37), the sufficient conditions for equality in the leftmost inequalities of (3.2) and (3.1), respectively, also ensure equality in the leftmost inequalities of (5.36) and (5.37).
5.3.2. Proof of Theorem 5.12
Let \mathsf{{G}} be a strongly regular graph with parameters \mathsf{srg}({n}, {d}, {\lambda}, {\mu}) . Then, by the satisfiability of the sufficient conditions in Theorem 5.9 for equality in the leftmost and rightmost inequalities of (5.36) and (5.37), it follows that
We proceed to prove that equality is also attained in the middle inequalities of (5.60) and (5.61). By Theorem 2.37 and the parameter t as defined in (3.5),
which implies that the leftmost and rightmost terms in (5.60) coincide, and
Likewise, by taking reciprocals in (5.63) and (5.64), and multiplying by n , the leftmost and rightmost terms in (5.61) also coincide, and
In light of (5.63)–(5.66), the middle inequalities in (5.36) and (5.37) hold with equalities, establishing all the equalities in (5.41)–(5.44).
5.3.3. Proof of Theorem 5.14
Let \mathsf{{G}} be a graph on n vertices that is both vertex-transitive and edge-transitive. Due to its vertex-transitivity, \mathsf{{G}} is regular, with d denoting the degree of its vertices. By Item 2 in Theorem 5.9, equality holds in the leftmost inequality of (5.36) and the rightmost inequality of (5.37), which gives
By Item 1 of Theorem 5.9, the vertex-transitivity of \mathsf{{G}} yields equality in (5.35), so
Combining (5.67), (5.69), and the equality \lambda_{{1}}({\mathsf{{G}}}) = d (for a d -regular graph \mathsf{{G}} ) gives (5.46).
5.3.4. Proof of Theorem 5.18
Let \mathsf{{G}} be a nonempty triangle-free graph on n vertices, which implies that \alpha({\overline{\mathsf{{G}}}}) = \omega({\mathsf{{G}}}) = 2 . By (2.61) (Theorem 11.18 in [29]), with \mathsf{{G}} replaced by \overline{\mathsf{{G}}} and setting k = 2 , it follows that
Since \vartheta(\mathsf{{G}}) \, \vartheta(\overline{\mathsf{{G}}}) \geq n holds for every graph \mathsf{{G}} on n vertices (see (2.57)), it follows from (5.70) that
The result in (5.49) is deduced by combining (5.71) with the inequality \chi_{\mathrm{f}}({\overline{\mathsf{{G}}}}) \geq \vartheta(\mathsf{{G}}) (see (2.52)).
5.3.5. Proof of Theorem 5.20
Inequalities (5.51) and (5.52) are equivalent since \alpha({\mathsf{{G}}}) = \omega({\overline{\mathsf{{G}}}}) , so the right-hand side of (5.52) is obtained from the right-hand side of (5.51) by replacing \mathsf{{G}} with \overline{\mathsf{{G}}} . For a graph \mathsf{{G}} on n vertices, inequality (5.51) is composed of two lower bounds on its independence number. The first term on the right-hand side of (5.51) is the lower bound on the right-hand of (2.62) with t \triangleq \vartheta(\overline{\mathsf{{G}}}) (by assumption, since neither \mathsf{{G}} nor its complement \overline{\mathsf{{G}}} are complete graphs, it follows that \vartheta(\mathsf{{G}}) \geq \alpha({\mathsf{{G}}}) \geq 2 and \vartheta(\overline{\mathsf{{G}}}) \geq \omega({\mathsf{{G}}}) \geq 2 ). The second term on the right-hand side of (5.51) is an equivalent form of inequality (2.61), where the independence number \alpha({\mathsf{{G}}}) is lower-bounded by a function of \vartheta(\mathsf{{G}}) .
5.4. Examples for the results in Section 5.2
The present subsection provides the utility of the results in Section 5.2, and it also obtains new results by examples and counterexamples.
Example 5.21 (Bounds on graph invariants for strongly regular graphs). The present example aims to illustrate the tightness of the bounds in Corollary 5.8 for four selected strongly regular graphs:
● Petersen graph that is a strongly regular graph with parameters \mathsf{srg}({10}, {3}, {0}, {1}) ;
● Schläfli graph that is a strongly regular graph with parameters \mathsf{srg}({27}, {16}, {10}, {8}) ;
● Shrikhande graph that is a strongly regular graph with parameters \mathsf{srg}({16}, {6}, {2}, {2}) ;
● Hall-Janko graph that is a strongly regular graph with parameters \mathsf{srg}({100}, {36}, {14}, {12}) .
(1) Let \mathsf{{G}}_1 be the Petersen graph. Then, \vartheta(\mathsf{{G}}_1) = 4 , and \vartheta(\overline{\mathsf{{G}}}_1) = \tfrac{5}{2} . The bounds on the independence, clique, and chromatic numbers are tight:
(2) Let \mathsf{{G}}_2, \mathsf{{G}}_3, \mathsf{{G}}_4 be the Schläfli, Shrikhande, and Hall-Janko graphs, respectively. Then,
(3) The lower bounds on the chromatic and fractional chromatic numbers of these graphs are tight:
(4) The upper bounds on their independence numbers are also tight:
(5) The upper bounds on their clique numbers are, however, not tight since
(6) For comparison, the inertial lower bound (5.24) gives
With the exception of the Petersen graph ( \mathsf{{G}}_1 ), it is observed that the lower bounds in (5.88) are not tight. In contrast, the bound provided in Corollary 5.8 proves to be tight for the fractional chromatic numbers of all four graphs.
Example 5.22 (Identical vector and strict vector chromatic numbers in Theorems 5.12 and 5.14). By Theorems 5.12 and 5.14, the vector and strict vector chromatic numbers coincide for every graph that is either strongly regular or both vertex- and edge-transitive. Theorems 5.12 and 5.14 are confirmed numerically by solving the SDP problems in (2.41) and (2.46) for such regular graphs, while getting a match with (5.41), (5.42), and (5.46) (see Table 3). Numerical results in Table 3 also exemplify that the vector and strict vector chromatic numbers may coincide for graphs that do not exhibit either strong regularity or both vertex- and edge-transitivity. That happens to be the case, e.g., for the Frucht graph, whose vector and strict vector chromatic numbers are identical and equal to 3. The Frucht graph is a 3-regular graph on 12 vertices that is neither vertex- nor edge-transitive, and is also not a strongly regular graph.
Example 5.23 (The vector and strict vector chromatic numbers of vertex-transitive graphs may be distinct). In [37] (see page 429), there is an example of a regular graph whose strict vector chromatic number is strictly greater than its vector chromatic number. Since only final results are given in [37], we first elaborate on that example from [37], and we then generalize it to examine the vector and strict vector chromatic numbers of these generalized graphs.
Let \mathsf{{G}} be a graph on 64 vertices, and label its vertices by the 6-length binary strings \{0, 1\}^6 . Let any two vertices be adjacent if and only if their corresponding strings are of Hamming distance that is at most 3. Let \mathsf{{H}} \triangleq \overline{\mathsf{{G}}} denote the complement graph, so any two of its vertices are adjacent if their corresponding strings are of Hamming distance of at least 4. Replacing the binary strings with \pm 1 vectors in the standard way ( 0 \mapsto +1 and 1 \mapsto -1 ) and then normalizing these vectors to be unit vectors in the Euclidean space, the adjacency of vertices in \mathsf{{H}} corresponds to two vectors having an inner product that is less than or equal to -\tfrac13 . By Definition 2.42, it follows that \chi_{\mathrm{v}}({\mathsf{{H}}}) \leq 4 . It can be verified that there exists a clique in \mathsf{{H}} of 4 vertices, so \omega({\mathsf{{H}}}) \geq 4 ; indeed, the vertices that refer to the vectors (+1, +1, +1, +1, +1, +1) , (-1, -1, -1, -1, +1, +1) , (-1, -1, +1, +1, -1, -1) , and (+1, +1, -1, -1, -1, -1) form a clique in \mathsf{{H}} since any pair of vectors differ in four coordinates. Hence, \omega({\mathsf{{H}}}) = 4 = \chi_{\mathrm{v}}({\mathsf{{H}}}) . Numerical calculation of the strict vector chromatic number of the graph \mathsf{{H}} as a solution of the SDP problem in (2.46), which relies on first constructing the adjacency matrix of the graph \mathsf{{H}} by its above definition, gives that \chi_{\mathrm{sv}}({\mathsf{{H}}}) = 5 \tfrac{1}{3} ; it is consistent with Schrijver's paper [37] where it was claimed that \vartheta(\mathsf{{G}}) = 5 \tfrac{1}{3} (by definition, \mathsf{{H}} = \overline{\mathsf{{G}}} , so \chi_{\mathrm{sv}}({\mathsf{{H}}}) = \vartheta(\mathsf{{G}}) ). To conclude, it is obtained that
The regular graph \mathsf{{H}} exhibits vertex-transitivity due to a property in which adding a constant vector to all vertices, using arithmetic over \mathrm{GF}(2) , maintains the Hamming distance between any pair of vertices. This implies that the adjacency relations among the vertices in \mathsf{{H}} remain consistent under such transformations. Consequently, any vector u \in \{0, 1\}^6 can be mapped to any other vector v \in \{0, 1\}^6 by adding the fixed vector v - u \in \{0, 1\}^6 to all vertices in the graph. However, \mathsf{{H}} does not possess edge-transitivity. If it did, according to Theorem 5.14, the vector and strict vector chromatic numbers of \mathsf{{H}} would be identical. The SageMath software tool [51] has confirmed that \mathsf{{H}} is not an edge-transitive graph.
As an extension of the above construction of \mathsf{{H}} , let \ell, d_{\mathrm{L}}, d_{\mathrm{H}} be integers such that 1 \leq d_{\mathrm{L}} \leq d_{\mathrm{H}} \leq \ell . Let \mathsf{{H}} be a graph on n = 2^\ell vertices whose vertices are labeled by all the \ell -length binary strings \{0, 1\}^\ell , and let any pair of vertices in \mathsf{{H}} be adjacent if and only if their corresponding strings are of Hamming distance d that satisfies d_{\mathrm{L}} \leq d \leq d_{\mathrm{H}} . As it is explained above, the regular graph \mathsf{{H}} is vertex-transitive. The above graph \mathsf{{H}} from [37] corresponds to the special case where d_{\mathrm{L}} = 4, d_{\mathrm{H}} = 6 , and \ell = 6 . We next compare the vector and strict vector chromatic numbers of the graph \mathsf{{H}} \triangleq \mathsf{{H}}_{\ell, d_{\mathrm{L}}, d_{\mathrm{H}}} by numerically solving the SDP problems in (2.40) and (2.46) for different selections of the parameters (\ell, d_{\mathrm{L}}, d_{\mathrm{H}}) , showing the existence of other possible combinations of these graph parameters, for which the strict vector chromatic number of the vertex-transitive graph \mathsf{{H}} is strictly greater than its vector chromatic number. The numerical results of the vector and strict vector chromatic numbers of the graph \mathsf{{H}} \triangleq \mathsf{{H}}_{\ell, d_{\mathrm{L}}, d_{\mathrm{H}}} are presented in Table 4 for different values of parameters (\ell, d_{\mathrm{L}}, d_{\mathrm{H}}) . It is shown that, for such vertex-transitive graphs, these two types of chromatic numbers may be distinct, in contrast to graphs that are both vertex- and edge-transitive whose vector and strict vector chromatic numbers coincide by Theorem 5.14.
Example 5.24 (The variant of the \vartheta -function by Schrijver is not an upper bound on the Shannon capacity). By the sandwich theorem in (2.52), the inequality \alpha({\mathsf{{G}}}) \leq \vartheta'(\mathsf{{G}}) \leq \vartheta(\mathsf{{G}}) holds for every finite, undirected, and simple graph \mathsf{{G}} . It is next shown by a counterexample that, unlike the Lovász \vartheta -function of a graph \mathsf{{G}} , which forms an upper bound on the Shannon capacity of \mathsf{{G}} (see (2.51)), the variant of the \vartheta -function by Schrijver does not possess that property, i.e., \Theta(\mathsf{{G}}) \not\leq \vartheta'(\mathsf{{G}}) . It settles a query since the introduction of the latter \vartheta -function in the late seventies [36,37], which was also posed as an open question in the last paragraph of [16].
As a counterexample, let \mathsf{{G}} = \overline{\mathsf{{H}}} with the graph \mathsf{{H}} \triangleq \mathsf{{H}}_{5, 3, 5} that is defined in Example 5.23. In other words, \mathsf{{G}} is a regular graph on 32 vertices that are labeled by the 5-length binary vectors \{0, 1\}^5 , and any two vertices in \mathsf{{G}} are adjacent if and only if the Hamming distance between their corresponding vectors is either equal to 1 or 2. The degree of each vertex in \mathsf{{G}} is therefore equal to \binom{5}{1}+\binom{5}{2} = 15 . By equalities (2.43), (2.50), and Table 4, it follows that
In regard to the different values of \vartheta'(\mathsf{{G}}) and \vartheta(\mathsf{{G}}) in (5.90), it should be noted that the regular graph \mathsf{{G}} is vertex-transitive, and the complement graph \mathsf{{H}} = \overline{\mathsf{{G}}} is not edge-transitive. Indeed, it is proved in Example 5.23 that all graphs \mathsf{{H}}_{\ell, d_{\mathrm{L}}, d_{\mathrm{H}}} , with 1 \leq d_{\mathrm{L}} \leq d_{\mathrm{H}} \leq \ell and \ell \in {\mathbb{N}} , are vertex-transitive; their complements are therefore vertex-transitive as well. On the other hand, the graph \mathsf{{H}} cannot be edge-transitive. Otherwise, due to its vertex-transitivity, the strict inequality in (5.90) could not hold by Theorem 5.14 and equalities (2.43) and (2.50). As a side note, the graph \mathsf{{G}} is edge-transitive, unlike its complement \mathsf{{H}} ; those properties can be verified by the SageMath software tool [51].
The independence number of \mathsf{{G}} satisfies \alpha({\mathsf{{G}}}) = 4 , so inequality (2.44) holds with equality for the considered graph \mathsf{{G}} . This gives an example where the Schrijver \vartheta -function of a graph provides a tight upper bound on its independence number, in contrast to the Lovász \vartheta -function of that graph. The computation of the Shannon capacity of the graph \mathsf{{G}} presents a challenge in this context. However, obtaining a lower bound on \Theta(\mathsf{{G}}) would suffice to demonstrate the claim that \Theta(\mathsf{{G}}) \not\leq \vartheta'(\mathsf{{G}}) . To that end, programming with the SageMath software tool gives
where the leftmost inequality in (5.92) holds by (2.36), and the rest of (5.92) holds by (5.90) and (5.91). It should be noted that the computation of the independence number of the strong product graph \mathsf{{G}} \boxtimes \mathsf{{G}} appears to be significantly more efficient by computing instead the clique number of the complement graph \overline{\mathsf{{\mathsf{{G}} \boxtimes \mathsf{{G}}}}} with the algorithm \mathtt{ Cliquer}; this has been done with the SageMath software, which wraps a set of C routines named \mathtt{ Cliquer} [158]. An example of such a maximum independent set in the graph \mathsf{{G}} \boxtimes \mathsf{{G}} , which is a maximum clique of size 20 in its complement graph, is given by
It appears that there are 368,640 such maximal independent sets of size 20 in the strong product graph \mathsf{{G}} \boxtimes \mathsf{{G}} . The interested reader is referred to the comprehensive review paper [159] on algorithms and applications of the maximum clique problem.
Example 5.25 (Three-tower Hanoi graphs). Three-tower Hanoi graphs, denoted \mathsf{{H}}_3^n for n \in {\mathbb{N}} , form a family of graphs that can be constructed recursively as follows (see Figure 5).
● For n = 1 , the graph is the complete graph \mathsf{K}_{{3}} (a triangle).
● For n > 1 , the graph \mathsf{{H}}_3^n is constructed by converting each vertex at each corner of a triangle in the graph \mathsf{{H}}_3^{n-1} into a new triangle.
By construction,
(1) The graph \mathsf{{H}}_3^n comprises 3^n vertices. It exhibits irregularity as each vertex, except for the three at the corners of the outer triangle, has a degree of 3, while those corner vertices have a degree of 2 (see Figure 5). These graphs are neither edge-transitive nor vertex-transitive.
(2) A three-tower graph is composed of triangles, and it satisfies \chi({\mathsf{{H}}_3^n}) = \omega({\mathsf{{H}}_3^n}) = 3 for all n \in {\mathbb{N}} .
(3) By the sandwich theorem (2.53), it follows that \chi_{\mathrm{f}}({\mathsf{{H}}_3^n}) = \vartheta(\overline{\mathsf{{\mathsf{{H}}_3^n}}}) = 3 for all n \in {\mathbb{N}} .
(4) Table 5 compares lower bounds on the fractional chromatic numbers of these graphs. The lower bound on the right-hand side of (5.6), which is the Lovász \vartheta -function of the graph complement, is tight for the three-tower Hanoi graphs. This is in contrast to the other lower bounds on the right-hand sides of (5.16) and (5.20) that are not tight for the examined graphs.
Example 5.26 (Windmill graphs). Let k \geq 2 and n \geq 2 be integers. The windmill graph \mathsf{{W}}_{k, n} is an undirected, connected, and simple graph, constructed by joining n copies of the complete graph \mathsf{K}_{{k}} at a shared universal vertex (see Figure 6). Specifically, if k = 2 , then \mathsf{{W}}_{2, n} is a star graph with n leaves (see the leftmost graph in Figure 6). The windmill graphs are known to be perfect graphs [116]. The chromatic and fractional chromatic numbers of the graph \mathsf{{G}} = \mathsf{{W}}_{k, n} coincide, being equal to k .
Table 6 compares the fractional chromatic numbers of the windmill graphs \mathsf{{W}}_{k, n} , for several values of k, n \geq 2 , with their corresponding lower bounds on the right-hand sides of (5.6), (5.16), and (5.20). That comparison supports the fact that, by Theorem 5.17, the lower bound on the right-hand side of (5.6) is tight for perfect graphs, in contrast to the other two lower bounds on the right-hand sides of (5.16) and (5.20) that are not necessarily tight for the examined windmill graphs.
Example 5.27 (Independence, capacity and clique numbers of random graphs). The standard model of a random graph is the binomial model \mathsf{{G}}(n, p) , pioneered by Erdös and Rényi. We let 0 < p = p(n) < 1 be a number that may depend on the number of vertices n . Then, the random graph \mathsf{{G}}(n, p) is obtained by independently including each of the \binom{n}{2} possible edges with probability p . The random graph \mathsf{{G}}(n, p) is said to have a certain property with high probability, if the probability that such a random graph has that property tends to 1 as we let n tend to infinity. If n \to \infty and p \in (0, 1) is kept fixed, then with high probability (see Theorem 2 in [160] and Example 11.17 in [29])
and, by replacing the probability p with 1-p for the complement graph, with high probability
The analysis in [160] is extended in [161] to the case where \frac{1}{n} \, (\ln n)^{\tfrac16} \leq p \leq 1-\frac{1}{n} \, (\ln n)^{\tfrac16} , with some concentration inequalities for the Lovász \vartheta -function of random graphs \mathsf{{G}}(n, p) . High-probability lower bounds on the independence number and clique number of a random graph \mathsf{{G}}(n, p) can be obtained by combining the bounds in (5.51), (5.52), (5.94), and (5.95). These high-probability lower bounds consequently hold also for the Shannon capacity of random graphs.
Using (5.94) and (5.95), the inequalities \alpha({\mathsf{{G}}}) \leq \vartheta(\mathsf{{G}}) and \omega({\mathsf{{G}}}) \leq \vartheta(\overline{\mathsf{{G}}}) yield high-probability upper bounds on the independence and clique numbers of random graphs. Since \Theta(\mathsf{{G}}) \leq \vartheta(\mathsf{{G}}) , a high-probability upper bound on their Shannon capacity is also given by the rightmost term in (5.94).
The interested reader is referred to Section 6.1 in [161] in regard to an algorithmic approach and its probabilistic analysis for the approximation of the independence numbers of random graphs. It employs a certain greedy algorithm that, for an input graph \mathsf{{G}} = \mathsf{{G}}(n, p) , the algorithm most probably finds an independent set of cardinality of at least \dfrac{\ln(np)}{2p} , thus providing a lower bound on \alpha({\mathsf{{G}}}) . It then suggests an algorithm that involves the calculation of the Lovász \vartheta -function \vartheta(\mathsf{{G}}) as an upper bound on \alpha({\mathsf{{G}}}) . The expected running time of the latter algorithm is polynomial in n with high probability, and it provides an upper bound that scales like \sqrt{n/p} .
6.
Summary and outlook
The paper primarily focuses on deriving results that hinge on the Lovász \vartheta -function of a graph. These results cover various aspects, including insights into the Shannon capacity of graphs, exploration of cospectral and nonisomorphic graphs, and derivation of bounds on graph invariants. Throughout the paper, numerical results are provided to illustrate the usefulness of the derived findings. This research paper also serves as a tutorial on the subject of the Lovász \vartheta -function, its variants, and its significant roles in algebraic graph theory and zero-error information theory.
This section concludes by posing open questions that are directly relevant to the discussed work.
(1) By Theorem 3.2 of [3], there exists a sequence of graphs \{\mathsf{{H}}_n\} such that \mathsf{{H}}_n is a graph on n vertices whose Shannon capacity is at most 3 and its Lovász \vartheta -function is at least (1+o(1)) \, n^{1/4} . This shows, in particular, that the Lovász \vartheta -function of a graph cannot be upper-bounded by any function of the independence number. In light of that result, it is left for further research to study if Schrijver's variant of the \vartheta -function of a graph can be upper-bounded by any function of the independence number. In other words, by (2.43), it is an open question whether the vector chromatic number of a graph can be upper-bounded by a function of the clique number of the graph. These equivalent questions are akin to an open question posed in Section 6 of [3], which asks whether the Shannon capacity of a graph \Theta(\mathsf{{G}}) can be upper-bounded by any function of the independence number \alpha({\mathsf{{G}}}) . In particular, it is unknown whether there exists a sequence of graphs whose independence numbers are equal to 2, while their Shannon capacity is unbounded.
(2) The self-complementary vertex-transitive graphs and self-complementary strongly regular graphs are two distinct subclasses of self-complementary regular graphs. These subclasses have been studied in various works, including [34,82,83,84,85,86,87,88,89,91]. Notably, self-complementary vertex-transitive graphs do not necessarily fall under the realm of strongly regular graphs, as exemplified in [89]. It remains an open question whether there exists a self-complementary strongly regular graph that is not vertex-transitive, as indicated on page 88 of [82]. This inquiry is relevant to Item 4 of Theorem 3.26. Furthermore, according to that item, the minimum Shannon capacity among all self-complementary graphs of a fixed order n is achieved by those that are vertex-transitive or strongly regular, and this minimum is equal to \sqrt{n} . Another unresolved issue is determining the maximum Shannon capacity among all self-complementary graphs of a fixed order n , and identifying which graphs achieve this maximum.
(3) By Theorems 5.12 and 5.14, vector and strict vector chromatic numbers coincide for every graph that is either strongly regular or both vertex- and edge-transitive. Additionally, Example 5.22 illustrates that these numbers may also coincide for regular graphs that lack strong regularity or both vertex- and edge-transitivity. Consequently, it is of interest to establish further sufficient conditions for the coincidence of the vector and strict vector chromatic numbers of graphs.
Use of AI tools declaration
The author declares that no Artificial Intelligence (AI) tools were utilized in creating this article.
Acknowledgments
The author gratefully acknowledges the timely and constructive reports of the anonymous referees. Special thanks are extended to Clive Elphick for sharing the slides of his recent seminar talk and for pointing out some relevant references, and to Emre Telatar for valuable advice on Latex issues.
Conflict of interest
The author declares no conflicts of interest.









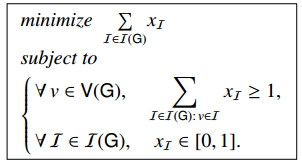
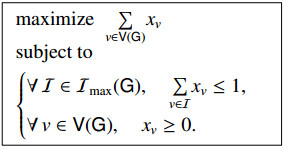
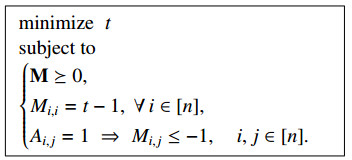




 DownLoad:
DownLoad: