This paper introduces a novel numerical scheme, the conformable finite difference method (CFDM), for solving time-fractional gas dynamics equations. The method was developed by integrating the finite difference method with conformable derivatives, offering a unique approach to tackle the challenges posed by time-fractional gas dynamics models. The study explores the significance of such equations in capturing physical phenomena like explosions, detonation, condensation in a moving flow, and combustion. The numerical stability of the proposed scheme is rigorously investigated, revealing its conditional stability under certain constraints. A comparative analysis is conducted by benchmarking the CFDM against existing methodologies, including the quadratic B-spline Galerkin and the trigonometric B-spline functions methods. The comparisons are performed using L2 and L∞ norms to assess the accuracy and efficiency of the proposed method. To demonstrate the effectiveness of the CFDM, several illustrative examples are solved, and the results are presented graphically. Through these examples, the paper showcases the capability of the proposed methodology to accurately capture the behavior of time-fractional gas dynamics equations. The findings underscore the versatility and computational efficiency of the CFDM in addressing complex phenomena. In conclusion, the study affirms that the conformable finite difference method is well-suited for solving differential equations with time-fractional derivatives arising in the physical model.
Citation: Majeed A. Yousif, Juan L. G. Guirao, Pshtiwan Othman Mohammed, Nejmeddine Chorfi, Dumitru Baleanu. A computational study of time-fractional gas dynamics models by means of conformable finite difference method[J]. AIMS Mathematics, 2024, 9(7): 19843-19858. doi: 10.3934/math.2024969
| [1] | Rabia Noureen, Muhammad Nawaz Naeem, Dumitru Baleanu, Pshtiwan Othman Mohammed, Musawa Yahya Almusawa . Application of trigonometric B-spline functions for solving Caputo time fractional gas dynamics equation. AIMS Mathematics, 2023, 8(11): 25343-25370. doi: 10.3934/math.20231293 |
| [2] | Aisha F. Fareed, Emad A. Mohamed, Mokhtar Aly, Mourad S. Semary . A novel numerical method for stochastic conformable fractional differential systems. AIMS Mathematics, 2025, 10(3): 7509-7525. doi: 10.3934/math.2025345 |
| [3] | Chaeyoung Lee, Yunjae Nam, Minjoon Bang, Seokjun Ham, Junseok Kim . Numerical investigation of the dynamics for a normalized time-fractional diffusion equation. AIMS Mathematics, 2024, 9(10): 26671-26687. doi: 10.3934/math.20241297 |
| [4] | Lakhlifa Sadek, Tania A Lazǎr, Ishak Hashim . Conformable finite element method for conformable fractional partial differential equations. AIMS Mathematics, 2023, 8(12): 28858-28877. doi: 10.3934/math.20231479 |
| [5] | Mahmoud Soliman, Hamdy M. Ahmed, Niveen Badra, Taher A. Nofal, Islam Samir . Highly dispersive gap solitons for conformable fractional model in optical fibers with dispersive reflectivity solutions using the modified extended direct algebraic method. AIMS Mathematics, 2024, 9(9): 25205-25222. doi: 10.3934/math.20241229 |
| [6] | Muhammad Asim Khan, Majid Khan Majahar Ali, and Saratha Sathasivam . High-order finite difference method for the two-dimensional variable-order fractional cable equation in complex systems and neuronal dynamics. AIMS Mathematics, 2025, 10(4): 8647-8672. doi: 10.3934/math.2025396 |
| [7] | Fidel Meléndez-Vázquez, Guillermo Fernández-Anaya, Aldo Jonathan Muñóz-Vázquez, Eduardo Gamaliel Hernández-Martínez . Generalized conformable operators: Application to the design of nonlinear observers. AIMS Mathematics, 2021, 6(11): 12952-12975. doi: 10.3934/math.2021749 |
| [8] | Ahmed A. El-Deeb, Dumitru Baleanu, Nehad Ali Shah, Ahmed Abdeldaim . On some dynamic inequalities of Hilbert's-type on time scales. AIMS Mathematics, 2023, 8(2): 3378-3402. doi: 10.3934/math.2023174 |
| [9] | Tingting Guan, Guotao Wang, Haiyong Xu . Initial boundary value problems for space-time fractional conformable differential equation. AIMS Mathematics, 2021, 6(5): 5275-5291. doi: 10.3934/math.2021312 |
| [10] | Tiecheng Zhang, Liyan Wang, Yuan Zhang, Jiangtao Deng . Finite-time stability for fractional-order fuzzy neural network with mixed delays and inertial terms. AIMS Mathematics, 2024, 9(7): 19176-19194. doi: 10.3934/math.2024935 |
This paper introduces a novel numerical scheme, the conformable finite difference method (CFDM), for solving time-fractional gas dynamics equations. The method was developed by integrating the finite difference method with conformable derivatives, offering a unique approach to tackle the challenges posed by time-fractional gas dynamics models. The study explores the significance of such equations in capturing physical phenomena like explosions, detonation, condensation in a moving flow, and combustion. The numerical stability of the proposed scheme is rigorously investigated, revealing its conditional stability under certain constraints. A comparative analysis is conducted by benchmarking the CFDM against existing methodologies, including the quadratic B-spline Galerkin and the trigonometric B-spline functions methods. The comparisons are performed using L2 and L∞ norms to assess the accuracy and efficiency of the proposed method. To demonstrate the effectiveness of the CFDM, several illustrative examples are solved, and the results are presented graphically. Through these examples, the paper showcases the capability of the proposed methodology to accurately capture the behavior of time-fractional gas dynamics equations. The findings underscore the versatility and computational efficiency of the CFDM in addressing complex phenomena. In conclusion, the study affirms that the conformable finite difference method is well-suited for solving differential equations with time-fractional derivatives arising in the physical model.
Nonlinear differential equations with time-fractional derivatives have emerged as a fundamental tool for modeling complex dynamical systems exhibiting anomalous temporal behaviors. Unlike classical integer-order differential equations, which assume that time evolves linearly and continuously, time-fractional calculus allows for the consideration of non-integer orders of differentiation, enabling the description of processes with memory, hereditary properties, and long-range dependencies. Including nonlinearity further enriches these equations, capturing intricate dynamics that arise in various fields such as physics, biology, finance, and engineering [1,2,3,4,5,6]. Recent studies have explored numerical techniques for investigating nonlinear time-fractional differential equations, encompassing various methodologies. The power series method [7,8,9], Adomian decomposition and variational iteration methods [10], kernel Hilbert space method [11], Taylor wavelet method [12], differential transformation method [13], finite difference method [14], Mohand variational iteration transform [15], and finite element method [16] represent some of the approaches applied in these investigations. Each method offers unique advantages in accuracy, efficiency, and applicability, contributing to the advancement of numerical solutions for time-fractional differential equations.
Gas dynamics is essential for designing equipment, engines, and gas-powered vehicles. Understanding forces in gas interactions, including pressure, temperature, friction, and heat movement, is aided by this. Combustion, detonation, blast waves, and gas propulsion are all included in gas dynamics. Its laws are essential for studying explosions, developing machinery like compressors, turbines, and rocket motors, and studying exterior and interior ballistics. Accurately estimating these phenomena involves mathematical modeling. Finding solutions of nonlinear time-fractional gas dynamics equations presents a formidable challenge due to their inherent complexity, often defying traditional solution techniques. However, various numerical methods have been developed to approximate these solutions effectively. One approach involves combining the Laplace transformation with the power series method, as proposed by [17]. Alternatively, the differential transform method offers another avenue for approximation [18]. Other methods include the quadratic b-spline Galerkin and the cubic b-spline collection methods [19,20]. Trigonometric B-spline functions have also been suggested as a useful tool [21]. Additionally, [22] introduced the integral projected differential transform method, while [23] proposed the homotopy analysis transform method. [24] introduced the optimal q-homotopy analysis method, and [25] suggested employing Elzaki homotopy perturbation and variational iteration methods. In recent years, the utilization of the conformable fractional derivative, as defined by Khalil [26], has garnered attention in fractional differential equations. This derivative has been integrated into various numerical methodologies and modeling techniques, showcasing its versatility and applicability. Afterward, [27] introduced some fundamental properties and definitions of the conformable derivative. For instance, a conformable non-polynomial spline method has also been introduced, further expanding the repertoire of techniques leveraging conformable fractional derivatives [28]. Additionally, a study on the fractional regularized long Wave equation with conformable fractional derivatives highlights the potential of conformable derivatives in modeling physical phenomena [29]. Moreover, exploration of the conformable time Korteweg-de Vries equation using the finite element method provides insights into the effectiveness of conformable fractional derivatives in numerical simulations [30]. These advancements underscore the growing significance of conformable fractional derivatives in enhancing the accuracy and efficiency of numerical solutions for fractional differential equations, paving the way for further developments in this field. The motivation behind this research lies in the inherent complexity of time-fractional gas dynamics equations, which often defy traditional solution techniques. These equations are crucial in understanding various physical phenomena such as explosions, combustion, detonation, and condensation in moving flows. The conformable fractional derivative is a more recent definition that preserves several properties of integer-order differentiation, allowing for a simpler formulation and interpretation, while the Caputo derivative, a well-established concept in fractional calculus, is particularly useful in initial value problems due to its compatibility with classical initial conditions. By introducing the CFDM, we aim to address the challenges posed by these equations and provide a reliable numerical framework for accurately analyzing and predicting the behavior of gas dynamics systems. The development of the CFDM is motivated by the pressing need for efficient and accurate numerical methods to facilitate advancements in gas dynamics research and engineering applications.
This study aims to develop and validate the conformable finite difference method (CFDM) as a robust numerical scheme for accurately solving time-fractional gas dynamics equations. Additionally, we aim to demonstrate the applicability of the CFDM in solving a broader range of time-fractional differential equations encountered in various scientific and engineering fields, thereby showcasing its versatility as a general-purpose numerical scheme. The advantage of the conformable fractional derivative lies in its simpler formulation and preservation of several properties of integer-order differentiation, making it easier to interpret and apply in numerical methods and modeling while maintaining accuracy in describing processes with memory and hereditary properties.
The novelty lies in introducing the CFDM to solve time-fractional gas dynamics equations. This method integrates finite difference techniques with conformable derivatives, offering a unique approach to address the complexities of these equations. It not only accurately analyzes gas dynamics systems, but also showcases versatility for solving various time-fractional differential equations in different fields. This study contributes to advancing numerical methods for fractional differential equations, facilitating computational studies of dynamic systems. The study highlights the versatility and computational efficiency of the CFDM by demonstrating its ability to accurately solve a range of time-fractional gas dynamics equations, capturing complex phenomena such as explosions, combustion, and detonation. Through rigorous stability analysis and comparative assessments using L2 and L∞ norms against existing methods like trigonometric B-spline functions and the quadratic B-spline Galerkin method, the study showcases the CFDM's superior accuracy and efficiency. Additionally, the successful application of the CFDM to various illustrative examples underscores its robustness and adaptability to different problems in time-fractional differential equations.
The rest of the paper is organized as follows. Section 2 presents a detailed description of the conformable finite difference method (CFDM), elucidating its fundamental principles and implementation procedures. Section 3 is dedicated to the stability analysis of the investigated numerical scheme, where we rigorously examine the stability properties under various conditions. In Section 4, we present the numerical results obtained using the CFDM and comprehensively discuss the findings. Through comparative analysis and interpretation of the results, we aim to provide insights into the performance and accuracy of the proposed method. Finally, in the last section, we draw conclusions based on our study, highlighting the contributions, implications, and potential future research directions.
Consider the conformable time-fractional gas dynamics equations
| TξτR(φ,τ)−μR(φ,τ)(1−R(φ,τ))+εR(φ,τ)∂R(φ,τ)∂φ=Ψ(φ,τ),0<ξ≤1,a≤φ≤b,τ≥0, | (1) |
| R(φ,0)=I(φ),φ∈[a,b], | (2) |
| R(a,τ)=B1(τ),R(b,τ)=B2(τ),τ∈[0,T], | (3) |
where μ and ε are reaction and convection parameters, respectively, R(φ,τ) represents the evolution of the state across both space and time, Ψ(φ,τ) is an appropriate predetermined function, and the fractional derivative TξτR(φ,τ) is expressed in the conformable derivative.
This section introduces the combined use of conformable derivatives and the finite difference method, enhancing numerical analysis capabilities. The conformable derivative accommodates functions in diverse domains, while the finite difference method excels in discretization and derivative approximation, which is particularly useful for non-analytic functions or discrete datasets.
Definition 2.1: The conformable time-fractional derivative TξφR(φ,τ) for R:[0,∞]→R, defined by [26], is given as follows:
| TξτR(τ)=limρ→∞R(τ+ρτ1−ξ)−R(τ)ρ,0<ξ≤1. | (4) |
Lemma 2.1: [26,27] Let ξ∈(0,1] and R,H be ξ− differentiable at α point τ>0. Then:
(ⅰ). Tξτ(αR+βH)=αTξτR+βTξτH for α,β∈R,
(ⅱ). Tξτ(τα)=aτα−ξ for all α∈R,
(ⅲ). Tξτc=0 if c is constant function.
(ⅳ) Tξτ(RH)=R(TξτH)+H(TξτR),
(ⅴ) Tξτ(RH)=H(TξτR)−R(TξτH)H2,
(ⅵ). TξτR(τ)=τ1−ξ∂R(τ)∂τ, if R(τ) is differentiable.
Corollary 2.1: Let φ=jh,j=1,2,⋯,L, and τn=nk,n=1,2,⋯,N, with uniform spatial step size h=b−aL and temporal step size k=TN. In the context of the finite difference scheme, we have
| ∂R∂τ≅Rn+1j−Rnjk,whereR(φ,τ)=Rnj, | (5) |
and, according to Lemma 1 (vi) and Eq (5), we have
| TξφR(φ,τ)≅τ1−ξ∂R∂τ=ωRn+1j−Rnjk, | (6) |
where ω=τ1−ξ. Using the Crank-Nicolson finite difference formula, we have
| R(φ,τ)(1−R(φ,τ))≅Rn+1j−Rnj2(1−Rnj), | (7) |
and
| R(φ,τ)∂R(φ,τ)∂φ≅Rnj2(Rn+1j+1−Rn+1j−12h+Rnj+1−Rnj−12h). | (8) |
Therefore, substituting Eqs (6)–(8) into Eq (1), we obtain
| ωRn+1j−Rnjk−μRn+1j−Rnj2(1−Rnj)+εRnj2(Rn+1j+1−Rn+1j−12h+Rnj+1−Rnj−12h)=Ψnj, | (9) |
which implies that
| ωkRn+1j−ωkRnj−μ2Rn+1j−μ2Rnj+μ2RnjRn+1j−μ2(Rnj)2+ε4hRnjRn+1j+1−ε4hRnjRn+1j−1+ε4hRnjRnj+1−ε4hRnjRnj−1=Ψnj. | (10) |
Then, after some simplification, we have
| −ε4hRnjRn+1j−1+(ωk−μ2+μ2Rnj)Rn+1j+ε4hRnjRn+1j+1=ε4hRnjRnj−1+(ωk−μ2+μ2Rnj)Rnj−ε4hRnjRnj+1+Ψnj. | (11) |
System (11) has less than or not enough equations (N–1) compared to its number of unknowns (N+1), necessitating two additional equations to achieve a solution. These additional equations are derived from the initial and boundary conditions, which are as follows:
| MnjRn+1j−1+InjRn+1j−MnjRn+1j+1=−MnjRnj−1+InjRnj+MnjRnj+1+Ψnj, | (12) |
where,
| Mnj=−ε4h|gnj|2,Inj=ωk−μ2+μ2|gnj|2,and|gnj|2=Rnj. |
Rewriting Eq (12) in matrix form:
| ARn+1=BRn+Ψn. | (13) |
Here,
| A=[I1−M10M2I2−M20M3I3000000−M300⋯⋯⋯000⋱000⋱⋯⋯⋯⋱000⋱000⋱000⋱0ML−10⋱0IL−1ML⋱0−ML−1IL], |
| B=[I1M10−M2I2M20−M3I3000000M300⋯⋯⋯000⋱000⋱⋯⋯⋯⋱000⋱000⋱000⋱0−ML−10⋱0IL−1−ML⋱0ML−1IL]. |
| Rn=[Rn1Rn2⋯RnjRnj+1]T, |
| Rn−1=[Rn−11Rn−12⋯Rn−1jRn−1j+1]T. |
In this section, the stability of the numerical scheme is under scrutiny, assuming, according to the Fourier stability principle, that the solution to Eq (12) adheres to a specific structure. This approach leverages the principles of Fourier stability to assess the reliability and performance of the numerical method in question, offering valuable insights into its stability and accuracy.
| Rnj=Ωneiυhj. | (14) |
In this context, υ represents the actual spatial wave number, and i is the imaginary unit i=√−1. By transforming the nonlinear term into a linear form and substituting the expression from Eq (14) into Eq (12), we obtain
| MnjΩn+1eiυh(j−1)+InjΩn+1eiυhj−MnjΩn+1eiυh(j+1)=−MnjΩneiυh(j−1)+InjΩneiυhj+MnjΩneiυh(j+1), | (15) |
After dividing both sides by eiυhj, the resultant expression is
| MnjΩn+1e−iυh+InjΩn+1−MnjΩn+1eiυh=−MnjΩne−iυh+InjΩn+MnjΩneiυh, | (16) |
Then, implementing specific simplifications and grouping pertinent terms, we have
| Ω=−Mnje−iυh+Inj+MnjeiυhMnje−iυh+Inj−Mnjeiυh, | (17) |
Using the Euler formula in complex analysis, we obtain the following:
| Ω=(−Mnjcos(υh)+iMnjsin(υh))+Inj+(Mnjcos(υh)−iMnjsin(υh))(Mnjcos(υh)−iMnjsin(υh))+Inj−(Mnjcos(υh)−iMnjsin(υh)), | (18) |
After some simplification, Eq (17) yields
| |Ω|=|1|. | (19) |
In that case, the numerical scheme (12) is unconditionally stable.
In this section, the accuracy and effectiveness of the developed numerical scheme are thoroughly examined through the investigation of three examples. The obtained numerical results are meticulously compared with existing works, and the outcomes are visually presented through 2D and 3D graphs. The numerical simulations are conducted utilizing MATLAB R2017b, showcasing the robustness and reliability of the implemented scheme. To quantify the accuracy of the proposed scheme, maximum and least square error norms are computed using well-defined formulas:
| L∞=max1≤j≤L|Rjexact−Rjapproximation|, | (20) |
| L2=√hL∑i=1|Rjexact−Rjapproximation|2. | (21) |
Example 4.1. Consider the gas dynamics equation with time-fractional derivative in the following form:
| TξτR(φ,τ)−R(φ,τ)(1−R(φ,τ))+R(φ,τ)∂R(φ,τ)∂φ=0,0<ξ≤1,a≤φ≤b,τ≥0, | (22) |
| R(φ,0)=e−φ,φ∈[0,1], | (23) |
| R(0,τ)=Eξ(τξ),R(1,τ)=e−1Eξ(τξ),τ∈[0,T], | (24) |
where the Mittag-Leffler function Eξ(φ) is defined as
| Eξ(φ)=∞∑m=0φmΓ(ξm+1), | (25) |
and the exact solution of the problem is R(φ,τ)=e−φEξ(τξ).
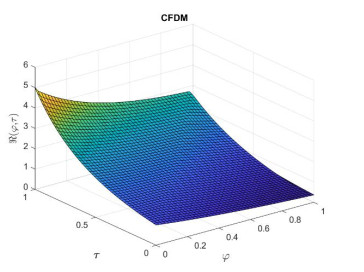
The presented figures collectively offer valuable insights into the behavior and performance of the conformable finite difference method (CFDM) in solving time fractional gas dynamic equations in Example 1. Figure 1 provides a visual representation of CFDM in a 3D plot, illustrating how variations in parameters such as φ and τ within the specified range impact the output. In Figure 2, the comparison between the exact and CFDM methods, with both ξ and τ set to 0.5, demonstrates excellent agreement, confirming the accuracy and efficiency of the numerical scheme employed for time fractional gas dynamic equations. Figure 3 reveals a direct relationship between time τ and the magnitude of the solution R(φ,τ), indicating the temporal influence on system behavior. Finally, Figure 4 highlights the converse effect of the fractional order ξ on R(φ,τ), showcasing how increasing ξ leads to a decrease in the solution magnitude. Figure 5 shows the comparison between the exact and CFDM methods using an absolute error plot. In addition to the graphical representations provided in the figures, Table 1 offers a comparison of the error norms of the presented numerical scheme with that of previous approaches utilizing the trigonometric b-spline method [21] and the quadratic b-spline Galerkin method [20]. The table presents the error norm values, allowing for a direct assessment of the accuracy and performance of each of the methods. The data demonstrate that the solutions obtained using the CFDM outperform those achieved through the trigonometric b-spline and quadratic b-spline Galerkin methods. This superiority in accuracy further underscores the effectiveness and reliability of CFDM in solving time fractional gas dynamic equations. The comparison provided in Table 1 reinforces the conclusions drawn from the graphical analyses, strengthening the argument for the adoption of CFDM as a preferred numerical scheme for such complex fluid dynamic systems.
| τ | CFDM | [21] | [20] | |||||
| L∞ | L2 | L∞ | L2 | L∞ | L2 | |||
| 0.2 | 1.9432×10−5 | 0.5321×10−5 | 3.8746×10−4 | 2.3225×10−4 | 0.4616×10−3 | 0.2339×10−3 | ||
| 0.4 | 1.6476×10−5 | 0.4872×10−5 | 2.0719×10−4 | 1.3005×10−4 | 0.2909×10−3 | 0.1329×10−3 | ||
| 0.6 | 1.3764×10−5 | 0.4187×10−5 | 1.2682×10−4 | 8.5960×10−4 | 0.2239×10−3 | 0.1044×10−3 | ||
| 0.8 | 1.2543×10−5 | 0.3923×10−5 | 7.7522×10−4 | 5.2942×10−4 | 0.1968×10−3 | 0.0940×10−3 | ||
Example 4.2. Consider the gas dynamics equation with time-fractional derivative in the following form:
| TξτR(φ,τ)−R(φ,τ)(1−R(φ,τ))+R(φ,τ)∂R(φ,τ)∂φ=Ψ(φ,τ),0<ξ≤1,a≤φ≤b,τ≥0, | (26) |
| R(φ,0)=0,φ∈[0,1], | (27) |
| R(0,τ)=0,R(1,τ)=τξtan(1),τ∈[0,T], | (28) |
where
| Ψ(φ,τ)=τ2ξtan2φ−τξtanφ+τ2ξtanφsec2φ−πcscπξΓ(−ξ)tanφ, |
and the exact solution of the problem is R(φ,τ)=τξtanφ.
Table 2 provides an error norm comparison between the presented numerical scheme and that of a previous approach utilizing the trigonometric b-spline method [21]. Through direct assessment of the error norm values, the table reveals that the solutions obtained using the CFDM outperform those achieved through the trigonometric b-spline method. This superiority is further evidenced by Figure 6, which presents a 3D plot of the CFDM for Example 2, showcasing its behavior when parameters φ and τ vary within the range [0,1], with ξ=0.5. Figure 7 reinforces the efficacy of the CFDM by illustrating a comparison between exact solutions and CFDM results for Example 2, where ξ=τ=0.5, demonstrating excellent accordance between the two sets of results and confirming the suitability and efficiency of the numerical scheme. Additionally, Figure 8 depicts the effect of time (τ) on the solution R(φ,τ) for Example 2, indicating a direct correlation between R(φ,τ) and increasing τ. Moreover, Figure 9 explores the impact of the fractional order (ξ) on the solution R(φ,τ) for Example 2, concluding that increasing the fractional order leads to a decrease in the solution magnitude, highlighting the sensitivity of the solution to variations in the fractional order parameter within the CFDM framework. Figure 10 shows the comparison between exact and CFDM using an absolute error plot. Collectively, these findings underscore the robustness, accuracy, and superiority of the CFDM approach in accurately modeling and solving Example 2 over alternative numerical methods, providing valuable insights into the behavior of the system under consideration.
| τ | [21] | CFDM | |||
| L∞ | L2 | L∞ | L2 | ||
| 0.05 | 8.3597×10−4 | 9.9531×10−5 | 2.4132×10−5 | 3.2238×10−6 | |
| 0.1 | 8.4173×10−4 | 1.0151×10−4 | 2.3217×10−5 | 3.2431×10−6 | |
| 0.5 | 8.6095×10−4 | 1.2203×10−4 | 2.2619×10−5 | 3.3752×10−6 | |
| 1.0 | 8.5040×10−4 | 1.4138×10−4 | 2.1843×10−5 | 3.4212×10−6 | |
Example 4.3. Consider the gas dynamics equation with time-fractional derivative in the following form:
| TξτR(φ,τ)−R(φ,τ)(1−R(φ,τ))+R(φ,τ)∂R(φ,τ)∂φ=Ψ(φ,τ),0<ξ≤1,a≤φ≤b,τ≥0, | (29) |
| R(φ,0)=0,φ∈[0,1], | (30) |
| R(0,τ)=0,R(1,τ)=τ2+ξsinπ,τ∈[0,T], | (31) |
where
| Ψ(φ,τ)=π2τ4+2ξsin2πφ−τ2+ξsinπφ+τ4+2ξsin2πφ−πτ2cscπξ2Γ(−2−ξ)sinπφ, |
and the exact solution of the problem is R(φ,τ)=τ2+ξsinπφ.
In Figure 11, a 3D plot showcases the application of the CFDM to Example 3, where the parameters τ and φ range from 0 to 1, while ξ remains constant at 0.5. This visualization offers a comprehensive view of the CFDM's behavior within the specified parameter space, shedding light on the dynamics of the solution. Figure 12 compares exact solutions and CFDM results for Example 3, with both ξ and τ set to 0.5. The close agreement between the two sets of results indicates the suitability and efficiency of the CFDM, confirming its reliability in accurately solving Example 3. In Figure 13, the plot illustrates the impact of time (τ) on the solution R(φ,τ) for Example 3, revealing a direct correlation between R(φ,τ) R and increasing τ. This observation offers valuable insights into the temporal behavior of the system under consideration. Furthermore, Figure 14 investigates the effect of the fractional order (ξ) on the solution R(φ,τ) for Example 3, concluding that an increase in the fractional order leads to a decrease in the solution magnitude. Figure 15 shows the comparison between exact and CFDM using an absolute error plot. This finding underscores the sensitivity of the solution to variations in the fractional order parameter within the CFDM framework. Collectively, these results highlight the robustness and accuracy of the CFDM approach in modeling and solving Example 3, providing valuable insights into the behavior of the system.
In conclusion, this study has introduced and validated the conformable finite difference method (CFDM) as a robust numerical scheme for accurately solving time-fractional gas dynamics equations. By integrating the finite difference method with conformable derivatives, the CFDM offers a unique approach to tackle the challenges posed by these equations, which are crucial in capturing various physical phenomena, such as explosions, combustion, detonation, and condensation in a moving flow. Through rigorous stability analysis, we have demonstrated the conditional stability of the proposed scheme under certain constraints, validating its reliability in practical applications. Comparative analysis against existing methodologies, including trigonometric B-spline functions and the quadratic B-spline Galerkin method, using L2 and L∞ norms, highlighted the accuracy and efficiency of the CFDM. Numerical results obtained using the CFDM were presented and discussed in detail, showcasing its capability to accurately capture the behavior of time-fractional gas dynamics equations. Furthermore, several illustrative examples were solved, providing concrete evidence of the effectiveness of the proposed methodology. Overall, this study underscores the versatility and computational efficiency of the CFDM in addressing complex phenomena encountered in time-fractional differential equations arising in various scientific and engineering fields. In conclusion, the CFDM emerges as a promising numerical technique, offering significant potential for advancing research in physical modeling and numerical simulations. Future directions may involve further refinement of the method and its application to a broader range of problems in different disciplines.
Majeed A. Yousif: Conceptualization; Methodology; Software; Formal analysis; Formal analysis; Investigation; Data curation; Writing-original draft preparation; Juan L. G. Guirao: Methodology; Validation; Investigation; Writing-original draft preparation; Project administration; Pshtiwan Othman Mohammed: Conceptualization; Methodology; Validation; Investigation; Resources; Data curation; Supervision; Funding acquisition; Nejmeddine Chorfi: Conceptualization; Software; Investigation; Writing-original draft preparation; Writing-review and editing; Project administration; Funding acquisition; Dumitru Baleanu: Investigation; Project administration; Funding acquisition; Writing-review and editing; Supervision. All authors have read and agreed to the published version of the manuscript.
The authors declare they have not used Artificial Intelligence tools in the creation of this article.
Researchers Supporting Project number (RSP2024R153), King Saud University, Riyadh, Saudi Arabia.
The authors declare that they have no conflicts interests.
| [1] | L. Glass, J. D. Murray, Interdisciplinary Applied Mathematics: Mathematical Biology I, New York: Springer, 2001. |
| [2] | M. Constantin, D. Gheorghe, J. Tenreiro, Introduction to Fractional Differential Equations, New York: Springer, 2019. |
| [3] | P. O. Mohammed, R. P. Agarwal, I. Brevik, M. Abdelwahed, A. Kashuri, M. A. Yousif, On Multiple-Type Wave Solutions for the Nonlinear Coupled Time-Fractional Schrödinger Model, Symmetry, 16 (2024), 553. |
| [4] | L. Sadek, A Cotangent Fractional Derivative with the Application, Fractal Fractional, 7 (2023), 444. |
| [5] | L. Sadek, B. Abouzaid, E. M. Sadek, H. T. Alaoui, Controllability, observability and fractional linear-quadratic problem for fractional linear systems with conformable fractional derivatives and some applications, Int. J. Dyn. Control, 11 (2023), 214–228. |
| [6] |
L. Sadek, T. A. Lazǎr, On Hilfer cotangent fractional derivative and a particular class of fractional problems, AIMS Mathematics, 8 (2023), 28334–28352. https://doi.org/10.3934/math.20231450 doi: 10.3934/math.20231450

|
| [7] | A. M. S. Mahdy, Numerical solutions for solving model time-fractional Fokker–Planck equation, Numer. Methods Partial Differ. Eq., 37 (2021), 1120–1135. |
| [8] | S. Noor, B. M. Alotaibi, R. Shah, S. M. Ismaeel, On the Solitary Waves and Nonlinear Oscillations to the Fractional Schrödinger–KdV Equation in the Framework of the Caputo Operator, Symmetry, 15 (2023), 1616. |
| [9] |
S. Noor, A. S. Alshehry, N. H. Aljahdaly, H. M. Dutt, I. Khan, R. Shah, Investigating the Impact of Fractional Non-Linearity in the Klein–Fock–Gordon Equation on Quantum Dynamics, Symmetry, 15 (2023), 881. https://doi.org/10.3390/sym15040881 doi: 10.3390/sym15040881

|
| [10] | S. Noor, M. A. Hammad, R. Shah, A. W. Alrowaily, S. A. El-Tantawy, Numerical Investigation of Fractional-Order Fornberg–Whitham Equations in the Framework of Aboodh Transformation, Symmetry, 15 (2023), 1353. |
| [11] | N. Attia, A. Akgül, D. Seba, A. Nour, On solutions of time-fractional advection–diffusion equation, Numer. Methods Partial Differ. Eq., 39 (2023), 4489–4516. |
| [12] |
M. Mulimani, S. Kumbinarasaiah, Numerical solution of time-fractional telegraph equations using wavelet transform, Int. J. Dynam. Control, 2023. https://doi.org/10.1007/s40435-023-01318-y doi: 10.1007/s40435-023-01318-y

|
| [13] | S. O. Edeki, G. O. Akinlabi, S. A. Adeosun, Analytic and Numerical Solutions of Time-Fractional Linear Schrödinger Equation, Commun. Math. Appl., 7 (2016), 1–10. |
| [14] | D. Li, W. Sun, C. Wu, A novel numerical approach to time-fractional parabolic equations with nonsmooth solutions, Numer. Math., 14 (2021), 355–376. |
| [15] | A. A. Alderremy, R. Shah, N. A. Shah, S. Aly, K. Nonlaopon, Comparison of two modified analytical approaches for the systems of time fractional partial differential equations, AIMS Mathematics, 8 (2023), 7142–7162. http://doi.org/%2010.3934/math.2023360 |
| [16] | Z. Guang-an, Numerical solutions to time-fractional stochastic partial differential equations, Nume. Algorithms, 82 (2019), 553–571. |
| [17] |
M. Alaroud, O. Ababneh, N. Tahat, S. Al-Omari, Analytic technique for solving temporal time-fractional gas dynamics equations with Caputo fractional derivative, AIMS Mathematics, 7 (2022), 17647–17669. http://doi.org/10.3934/math.2022972 doi: 10.3934/math.2022972

|
| [18] | S. Das, R. Kumar, Approximate analytical solutions of fractional gas dynamic equations, Appl. Math. Comput., 217 (2011), 9905–9915. |
| [19] | A. Esen, O. Tasbozan, Cubic B-spline collocation method for solving time fractional gas dynamics equation, Tbilisi Math. J., 8 (2015), 221–231. |
| [20] | A. Esen, O. Tasbozan, An approach to time fractional gas dynamics equation: Quadratic B-spline Galerkin method, Appl. Math. Comput., 261 (2015), 330–336. |
| [21] | R. Noureen, M. N. Naeem, D. Baleanu, P. O. Mohammed, M. Y. Almusawa, Application of trigonometric B-spline functions for solving Caputo time fractional gas dynamics equation, AIMS Mathematics, 8 (2023), 25343–25370. http://dx.doi.org/%2010.3934/math.20231293 |
| [22] | K. Shah, T. Singh, A. Kılıçman, Combination of integral and projected differential transform methods for time-fractional gas dynamics equations, Ain Shams Eng. J., 9 (2018), 1683–1688. |
| [23] | A. Prakash, M. Kumar, Numerical Method for Time-Fractional Gas Dynamic Equations, Proc. Nat. Acad. Sci. Ind. Sec. A – Phys. Sci., 89 (2019), 559–570. |
| [24] | K. M. Saad, E. H. AL-Shareef, M. S. Mohamed, X. Yang, Optimal q-homotopy analysis method for time-space fractional gas dynamics equation, Eur. Phys. J. Plus, 132 (2017), 23. |
| [25] |
S. S. Zhou, N. A. Shah, I. Dassios, S. Saleem, K. Nonlaopon, A comparative analysis of fractional-order gas dynamics equations via analytical techniques, Mathematics, 9 (2021), 1735. https://doi.org/10.3390/math9151735 doi: 10.3390/math9151735

|
| [26] | R. Khalil, M. Al Horani, A. Yousef, M. Sababheh, A new definition of fractional derivative, J. Comput. Appl. Math., 264 (2014), 65–70. |
| [27] | T. Abdeljawad, On conformable fractional calculus, J. Comput. Appl. Math., 279 (2015), 57–66. |
| [28] | M. A. Yousif, F. K. Hamasalh, Conformable non-polynomial spline method: A robust and accurate numerical technique, Ain Shams Eng. J., 15 (2024), 102415. |
| [29] | A. Jhangeer, M. Muddassar, M. Kousar, B. Infal, Multistability and Dynamics of Fractional Regularized Long Wave equation with Conformable Fractional Derivatives, Ain Shams Eng. J., 12 (2021), 2153–2169. |
| [30] | L. Pedram, D. Rostamy, Numerical solutions of the initial boundary value problem for the perturbed conformable time Korteweg-de Vries equation by using the finite element method, Numer. Methods Partial Differ. Eq., 37 (2021), 1449–1463. |
| 1. | Israr Ahmad, Khursheed Jamal Ansari, Hussam Alrabaiah, Dania Santina, Nabil Mlaiki, Study of 1+1 dimensional fractional order non-linear Benney equation using an analytical technique, 2024, 11, 26668181, 100823, 10.1016/j.padiff.2024.100823 | |
| 2. | Majeed A. Yousif, Ravi P. Agarwal, Pshtiwan Othman Mohammed, Alina Alb Lupas, Rashid Jan, Nejmeddine Chorfi, Advanced Methods for Conformable Time-Fractional Differential Equations: Logarithmic Non-Polynomial Splines, 2024, 13, 2075-1680, 551, 10.3390/axioms13080551 | |
| 3. | Zharasbek Baishemirov, Abdumauvlen Berdyshev, Dossan Baigereyev, Kulzhamila Boranbek, Efficient Numerical Implementation of the Time-Fractional Stochastic Stokes–Darcy Model, 2024, 8, 2504-3110, 476, 10.3390/fractalfract8080476 | |
| 4. | Abdelmjid Benmerrous, Lalla saadia Chadli, Abdelaziz Moujahid, M’hamed Elomari, Said Melliani, On a fractional Cauchy problem with singular initial data, 2024, 11, 2353-0626, 10.1515/msds-2024-0004 | |
| 5. | Rabia Noureen, Muhammad Kashif Iqbal, Maryam Asgir, Bandar Almohsen, Muhammad Azeem, A novel approach to approximate solution of time fractional gas dynamics equation with Atangana–Baleanu derivative, 2025, 116, 11100168, 451, 10.1016/j.aej.2024.11.075 | |
| 6. | Jagjeet Jakhar, Shalu Sharma, Jyotsana Jakhar, Majeed Ahmad Yousif, Pshtiwan Othman Mohammed, Nejmeddine Chorfi, Miguel Vivas-Cortez, Hyers–Ulam–Rassias Stability of Functional Equations with Integrals in B-Metric Frameworks, 2025, 17, 2073-8994, 168, 10.3390/sym17020168 | |
| 7. | Rabia Noureen, Maryam Asgir, Muhammad Kashif Iqbal, Muhammad Azeem, Approximate solution of time-fractional gas dynamics equation using exponential B-spline functions, 2025, 57, 1572-817X, 10.1007/s11082-025-08051-0 |
| τ | CFDM | [21] | [20] | |||||
| L∞ | L2 | L∞ | L2 | L∞ | L2 | |||
| 0.2 | 1.9432×10−5 | 0.5321×10−5 | 3.8746×10−4 | 2.3225×10−4 | 0.4616×10−3 | 0.2339×10−3 | ||
| 0.4 | 1.6476×10−5 | 0.4872×10−5 | 2.0719×10−4 | 1.3005×10−4 | 0.2909×10−3 | 0.1329×10−3 | ||
| 0.6 | 1.3764×10−5 | 0.4187×10−5 | 1.2682×10−4 | 8.5960×10−4 | 0.2239×10−3 | 0.1044×10−3 | ||
| 0.8 | 1.2543×10−5 | 0.3923×10−5 | 7.7522×10−4 | 5.2942×10−4 | 0.1968×10−3 | 0.0940×10−3 | ||
| τ | [21] | CFDM | |||
| L∞ | L2 | L∞ | L2 | ||
| 0.05 | 8.3597×10−4 | 9.9531×10−5 | 2.4132×10−5 | 3.2238×10−6 | |
| 0.1 | 8.4173×10−4 | 1.0151×10−4 | 2.3217×10−5 | 3.2431×10−6 | |
| 0.5 | 8.6095×10−4 | 1.2203×10−4 | 2.2619×10−5 | 3.3752×10−6 | |
| 1.0 | 8.5040×10−4 | 1.4138×10−4 | 2.1843×10−5 | 3.4212×10−6 | |
| τ | CFDM | [21] | [20] | |||||
| L∞ | L2 | L∞ | L2 | L∞ | L2 | |||
| 0.2 | 1.9432×10−5 | 0.5321×10−5 | 3.8746×10−4 | 2.3225×10−4 | 0.4616×10−3 | 0.2339×10−3 | ||
| 0.4 | 1.6476×10−5 | 0.4872×10−5 | 2.0719×10−4 | 1.3005×10−4 | 0.2909×10−3 | 0.1329×10−3 | ||
| 0.6 | 1.3764×10−5 | 0.4187×10−5 | 1.2682×10−4 | 8.5960×10−4 | 0.2239×10−3 | 0.1044×10−3 | ||
| 0.8 | 1.2543×10−5 | 0.3923×10−5 | 7.7522×10−4 | 5.2942×10−4 | 0.1968×10−3 | 0.0940×10−3 | ||
| τ | [21] | CFDM | |||
| L∞ | L2 | L∞ | L2 | ||
| 0.05 | 8.3597×10−4 | 9.9531×10−5 | 2.4132×10−5 | 3.2238×10−6 | |
| 0.1 | 8.4173×10−4 | 1.0151×10−4 | 2.3217×10−5 | 3.2431×10−6 | |
| 0.5 | 8.6095×10−4 | 1.2203×10−4 | 2.2619×10−5 | 3.3752×10−6 | |
| 1.0 | 8.5040×10−4 | 1.4138×10−4 | 2.1843×10−5 | 3.4212×10−6 | |