This paper explored the finite-time stability (FTS) of fractional-order fuzzy inertial neural network with mixed delays. First, the dimension of the model was reduced by the order reduction method. Second, by leveraging the fractional-order finite-time stability theorem, fractional calculus and inequality methods, we established some sufficient conditions to guarantee the FTS of the model under feasible delay-dependent feedback controller and delay-dependent adaptive controller, respectively. Additionally, we derived the settling times (STs) for each control strategy. Finally, we provided two examples to substantiate our findings.
Citation: Tiecheng Zhang, Liyan Wang, Yuan Zhang, Jiangtao Deng. Finite-time stability for fractional-order fuzzy neural network with mixed delays and inertial terms[J]. AIMS Mathematics, 2024, 9(7): 19176-19194. doi: 10.3934/math.2024935
| [1] | Ruoyu Wei, Jinde Cao, Wenhua Qian, Changfeng Xue, Xiaoshuai Ding . Finite-time and fixed-time stabilization of inertial memristive Cohen-Grossberg neural networks via non-reduced order method. AIMS Mathematics, 2021, 6(7): 6915-6932. doi: 10.3934/math.2021405 |
| [2] | Ailing Li, Xinlu Ye . Finite-time anti-synchronization for delayed inertial neural networks via the fractional and polynomial controllers of time variable. AIMS Mathematics, 2021, 6(8): 8173-8190. doi: 10.3934/math.2021473 |
| [3] | Jingfeng Wang, Chuanzhi Bai . Global Mittag-Leffler stability of Caputo fractional-order fuzzy inertial neural networks with delay. AIMS Mathematics, 2023, 8(10): 22538-22552. doi: 10.3934/math.20231148 |
| [4] | Yuehong Zhang, Zhiying Li, Wangdong Jiang, Wei Liu . The stability of anti-periodic solutions for fractional-order inertial BAM neural networks with time-delays. AIMS Mathematics, 2023, 8(3): 6176-6190. doi: 10.3934/math.2023312 |
| [5] | Huizhen Qu, Jianwen Zhou . $ S $-asymptotically $ \omega $-periodic dynamics in a fractional-order dual inertial neural networks with time-varying lags. AIMS Mathematics, 2022, 7(2): 2782-2809. doi: 10.3934/math.2022154 |
| [6] | Jingyang Ran, Tiecheng Zhang . Fixed-time synchronization control of fuzzy inertial neural networks with mismatched parameters and structures. AIMS Mathematics, 2024, 9(11): 31721-31739. doi: 10.3934/math.20241525 |
| [7] | Ivanka Stamova, Gani Stamov . Impulsive control strategy for the Mittag-Leffler synchronization of fractional-order neural networks with mixed bounded and unbounded delays. AIMS Mathematics, 2021, 6(3): 2287-2303. doi: 10.3934/math.2021138 |
| [8] | Ankit Kumar, Subir Das, Vijay K. Yadav, Rajeev, Jinde Cao, Chuangxia Huang . Synchronizations of fuzzy cellular neural networks with proportional time-delay. AIMS Mathematics, 2021, 6(10): 10620-10641. doi: 10.3934/math.2021617 |
| [9] | Wei Liu, Qinghua Zuo, Chen Xu . Finite-time and global Mittag-Leffler stability of fractional-order neural networks with S-type distributed delays. AIMS Mathematics, 2024, 9(4): 8339-8352. doi: 10.3934/math.2024405 |
| [10] | Patarawadee Prasertsang, Thongchai Botmart . Improvement of finite-time stability for delayed neural networks via a new Lyapunov-Krasovskii functional. AIMS Mathematics, 2021, 6(1): 998-1023. doi: 10.3934/math.2021060 |
This paper explored the finite-time stability (FTS) of fractional-order fuzzy inertial neural network with mixed delays. First, the dimension of the model was reduced by the order reduction method. Second, by leveraging the fractional-order finite-time stability theorem, fractional calculus and inequality methods, we established some sufficient conditions to guarantee the FTS of the model under feasible delay-dependent feedback controller and delay-dependent adaptive controller, respectively. Additionally, we derived the settling times (STs) for each control strategy. Finally, we provided two examples to substantiate our findings.
Neural networks (NNs) are computational models inspired by the neuronal structure of the human brain, which consists of numerous artificial neurons (also called nodes or units) that are connected to each other by connection weights. In recent years, various properties of NNs have been widely studied, such as stability [1,2,3] and synchronization [4,5]. It is usually described by a first-order differential equation, and it has been widely used in optimization, classification and solving nonlinear algebraic equations [6,7,8,9].
Furthermore, when modeling the link between flux and current, integer order NNs containing inertial terms, also known as inertial neural networks (INNs), are commonly utilized. In [10,11], Babcock and Westervelt initially presented INN, a second-order differential equation. The inertial term is a key element in causing chaos. INN has received a lot of attention since its introduction and has produced some significant outcomes. Cui et al. investigated the stability of delayed INN with stochastic impulses via using the matrix measure method in [12]. Criteria to ensure exponential stability of INN with proportional delays was given in [13] through applying the non-reduced order method. Dong et al. [14] studied the synchronization between memristive INNs by designing a suitable controller. Mittag-Leffler stability of fractional delayed INN was explored in [15] by utilizing the properties of the Riemann-Liouville integral. Wei et al. analyzed the synchronization between memristive INNs via the interval matrix method in [16] and applied the theoretical results to the field of secret communication.
Fractional-order inertia neural network (FOINN) is a new kind of NN model, that introduces the concept of fractional-order calculus and is better able to describe the dynamic characteristics of the nonlinear system [17,18]. Compared with traditional integer order NNs, FOINNs have better performance and applicability when dealing with nonlinear and complex systems. In practical applications, FOINN has a wide range of application prospects, such as a control system, signal processing and pattern recognition. In recent years, some important progress has been made on the stability and synchronization of FOINNs. In [19], the stability of FOINN with delay-dependent impulses were investigated by constructing Lyapunov-Krasovskii functions (LKFs). Peng and Jian analyzed the Mittag-Leffler synchronization of delayed FOINN under two different control strategies in [20], and obtained sufficient criteria for Mittag-Leffler synchronization between delayed FOINNs through the Lyapunov stability theory and fractional-order differential inequalities. Liu et al. established a class of synchronous control strategies based on the properties of FOINNs, and several conditions to achieve synchronization are given in [21].
Finite-time stability (FTS) is the property that the system can reach a stable state and remain in that state for a finite period of time. For FOINNs, FTS is an important property, which determines whether the system can converge to a stable state in a finite time, and is of great significance for practical applications. When studying the FTS of FOINNs, it is necessary to consider the dynamic characteristics of the system, the topology of the network and the characteristics of fractional-order calculus. In addition, the time delays factors in the modeling process are also factors that affect the FTS of the system [22,23,24,25,26]. Time delays are usually expressed as certain terms in the differential equation that depend on the state of the system at a previous point in time. Time delays can make the dynamic behavior of the system complicated, even oscillating, unstable, or chaotic [27]. In the fields of control systems, biological systems, chemical reaction dynamics, etc., time delays often make stability analysis and control design of systems more difficult. The appearance of time delays may also cause the solution of differential equations to be no longer smooth, but to have a certain piecewise property, which brings challenges to both numerical solution and analysis.
The vagueness can cause the solution of differential equation to become fuzzy or uncertain, which makes the analysis and prediction of the system behavior more difficult. In control systems, artificial intelligence, fuzzy control, and other fields, the existence of vagueness needs to be dealt with by special mathematical tools and methods in [28]. In order to better handle the fuzziness during operation, Yang et al. introduced fuzzy logic into NN models in [29]. Fuzzy logic not only maintains the connectivity between NN nodes, but also integrates the ability of low-level and high-level information processing of NN models. At present, many scholars have designed appropriate feedback control methods to realize the stability and synchronization of FOINNs. In [30], Aouiti et al. studied the stabilization of the fractional-order fuzzy inertial neural network (FOFINN) in finite time by designing nonlinear feedback controllers. Hu et al. explored the stability of complex-valued fractional-order NNs (FONNs) in finite time by designing nonlinear feedback controllers in [31]. By designing a segmented feedback control strategy, synchronization in finite time between fuzzy FONNs was investigated in [32]. In [30,31,32], the feedback control strategy based on system state is the most common and effective control method. However, for many real-world systems, traditional fixed parameter controllers may not effectively deal with the complexity, including nonlinearity, time-variability and uncertainty. Meanwhile, adaptive control technology can adapt to the changes of the system and improve the robustness and performance of the system. Moreover, in fuzzy systems, the dynamic characteristics of the system might not be accurately modeled or measured, which make it difficult to apply traditional control methods. Therefore, it is necessary to consider adaptive controllers in the controller design process of fuzzy NNs.
Based on the above analysis, the main works and contributions of this paper are as follows:
1) Based on FONNs, distributed delay and fuzzy factors are further considered in this paper, which is different from [30,33]. Additionally, the unbounded activation functions are considered in the model.
2) Appropriate order reduction techniques are then employed to convert the model into a first-dimensional FONN model. In contrast to the strategy utilized in [34] to minimize the order of INN, our approach involves two positive parameters ϱi and ξi, which make the model more general.
3) In order to achieve FTS of FOFINN, we design two different controllers, namely state feedback controller and adaptive controller, respectively. By selecting appropriate Lyapunov functions and combining inequality techniques with the FTS theorem, sufficient conditions for FTS of FOFINN models with mixed delays under two control strategies were obtained, and the settling time (ST) is calculated accordingly. Compared with feedback controllers designed in existing works [35,36], the coefficients in the controllers designed in this paper not only depend on constants, but also include functions which change with time.
Finally, we provide the organizational structure of this article. In Section 2, we mainly introduce relevant definitions, assumptions, lemmas, and the NN models. In Section 3, we investigate the problem of FTS of FOFINN with mixed delays by designing delay dependent feedback controller and delay dependent adaptive controller. By using the fractional-order FST theorem, the ST to reach stable state that is independent of the initial value is obtained. Examples are given in Section 4 to verify the results in Theorems 3.1 and 3.2.
Notations: R=(−∞,+∞), R+=(0,+∞). Rn and Rn×m represent the space which combined by real valued n-dimensional vector and real valued n×m-dimensional matrices, respectively. Z+ is the set which contains all positive integers. ⋀ and ⋁ are fuzzy AND and fuzzy OR operations, respectively. |⋅| represents the Euclidean norm. In addition, for simplicity, we denote ∑i=∑ni=1, ⋀i=⋀ni=1, and ⋁i=⋁ni=1.
We review the relevant definitions and properties of fractional order calculus first.
Definition 2.1. [34] The following is the definition of the Caputo fractional-order derivative with non-integer order μ of function y(t):
| Ct0Dμy(t)=1Γ(1−μ)∫tt0y′(t)(t−ζ)μdζ, | (2.1) |
where μ∈(0,1), and
| Γ(t)=∫∞t0e−ζζt−1dζ. | (2.2) |
Definition 2.2. [31] The fractional-order integral of order μ∈(0,1) is defined as follows:
| tIμt0y(t)=1Γ(μ)∫tt0y(ζ)(t−ζ)1−μdζ. | (2.3) |
Remark 2.1. Due to the fact that the fractional derivative depends on the lower bound of the integral, compared to the integer derivative operator, the fractional derivative operator is a nonlocal operator.
Definition 2.3. [37] System (2.8) is finite time stable if it is asymptotically stable in finite time, i.e., y(t)=0,∀t>T(y0), where T(y0) is called the settling time function (STF).
Lemma 2.1. [33] If p∈(0,1) and κj∈R, then
| (n∑j=1|κj|)p≥np−1n∑j=1|κj|p. | (2.4) |
Lemma 2.2. [33] For any 0<μ<1, α,β>0 such that
| C0DμV(t)≤−αV−ν(t)−βV−ε(t) | (2.5) |
holds, where 0≤ν, ν<ε<1+2ν, then, system (2.8) will achieve FTS with following settling time
| T∗=[Γ(1+μ)β2ε−2ν−11+ν(1+ε)((V1+ν(t0)+(βα)1+νε−ν)1+ε1+ν−(βα)1+εε−ν)]1μ. | (2.6) |
Consider the FOFINN shown below.
| C0D2μςi(t)=−aiC0Dμςi(t)−biςi(t)+∑jcijζj(ςj(t))+∑jzijζj(ςj(t−φj(t)))+∑jmij∫t−∞Hj(t−ϵ)ζj(ςj(ϵ))dϵ+⋀jeijζj(ςj(t−φj(t)))+⋁jkijζj(ςj(t−φj(t))), | (2.7) |
where i,j∈Z+ and the term C0Dμ is called the inertial term; ai,bi>0, φj(t)>0 represents the delay function in the jth neuron, and φj(t) is bouned by P; cij,zij,mij,λij represent connection weights between the ith and jth neuron; eij and kij stand for the elements of the fuzzy feedback MIN template, and the fuzzy feedback MAX template, respectively; ζi(⋅) is the activation function; Hj(⋅) is the delay kernel.
Take ˉςi(t)=ϱiC0Dμςi(t)+ξiςi(t), ϱi,ξi∈R+, then
| {C0Dμςi(t)=1ϱiˉςi(t)−ξiϱiςi(t),C0Dμˉςi(t)=(ξiϱi−ai)ˉςi(t)+(aiξi−biϱi−ξ2iϱi)ςi(t)+ϱi[∑jcijζj(ςj(t))+∑jzijζj(ςj(t−φj(t)))+∑jmij∫t−∞Hj(t−ϵ)ζj(ςj(ϵ))dϵ+⋀jeijζj(ςj(t−φj(t)))+⋁jkijζj(ςj(t−φj(t)))], | (2.8) |
where the initial values are given by ςi(s)=ˆϕ(s) and ˉςi(s)=ˆψ(s), s∈(−∞,t0].
Remark 2.2. The addition of fractional calculus greatly enhances the memory and genetic abilities of INN models. Compared with integer order INNs, FOINN has more significance to explore.
Remark 2.3. Different with [34], parameters ϱi in the reduce order method can not only be taken as 1, but also other positive numbers. This makes the model more general.
Remark 2.4. In existing literatures [34,35,38,39,40], models consider only included bounded time delays. However, when they come to unbounded time delays, the controllers designed in [34,35,38,39,40] exhibit some limitations. In addition, there is a lack of fuzzy logic in the current literature [37,41], so the controller designed for the addition of fuzzy logic cannot effectively handle the fuzziness present in the system.
Remark 2.5. This paper relies on the reduced order technique during the analytical phase. Currently, two approaches are offered for analyzing the dynamic characteristics of INN models: The reduced order method and the non-reduced order method. The main advantage of the reduced order method over the non-reduced order method is that it converts the higher order differential equation into the lower order differential equation, which simplifies system analysis; however, the system's stability conditions require additional parameters to verify. For the non-reduced order method, there have been many pioneering results, such as [42,43,44,45]. The advantage of the non-reduced order method is that it directly analyzes the properties of INN by constructing Lyapunov functionals. The structure of the constructor is clear, but the derivation process is relatively complicated.
We assume functions ζi(⋅) and Hi(⋅) meet the following assumptions.
Assumption 2.1. For ζj(⋅),j∈{1,2,…,n}, ∃Lj>0 such that
| |ζj(u)−ζj(v)|≤Lj|u−v|andζj(0)=0, |
where u,v∈R.
Assumption 2.2. Bump functions Hj(⋅)>0, j=1,…,n, and we have
| ∫+∞0Hj(s)ds=1. |
Lemma 2.3. [23] Assume that u and v are two states of FOFINN (2.8), then,
| |⋀jeijζj(u)−⋀jeijζj(v)|≤∑j|eij||ζj(u)−ζj(v)|,|⋁jkijζj(u)−⋁jkijζj(v)|≤∑j|kij||ζj(u)−ζj(v)|. |
In this part, we will analyze the FTS of FOFINN by designing two new control strategies. The controlled system is as follows:
| {C0Dμςi(t)=1ϱiˉςi(t)−ξiϱiςi(t)+ui,C0Dμˉςi(t)=(ξiϱi−ai)ˉςi(t)+(aiξi−biϱi−ξ2iϱi)ςi(t)+ϱi[∑jcijζj(ςj(t))+∑jzijζj(ςj(t−φj(t)))+∑jmij∫t−∞Hj(t−ϵ)ζj(ςj(ϵ))dϵ+⋀jeijζj(ςj(t−φj(t)))+⋁jkijζj(ςj(t−φj(t)))]+vi. | (3.1) |
For simplicity, we introduce the following convenient notations, ςi(t)=ςi, ˉςi(t)=ˉςi, and ςi(t−φi(t))=ςφi, ˉςi(t−φi(t))=ˉςφi, ui=ui(t), vi=vi(t).
To achieve the FTS of FOFINN (2.8), we design a feedback controller and have the following theorem.
Theorem 3.1. Based on the Assumptions 2.1–2.2, the FOFINN (2.8) is said to achieve FTS under the following controller:
| {ui=−ρi1ςi−ρi2sign(ςi)|ˉςφi|−ρi3sign(ςi)|ςi|−ℓ−ρi4sign(ςi)|ςi|−ϖ,vi=−ℵi1ˉςi−sign(ˉςi)∑jˉμij|ςφj|−ϱi∑jmij∫t−∞Hj(t−ϵ)ζj(ςj)dϵ−ℵi3sign(ˉςi)|ˉςi|−ℓ−ℵi4sign(ˉςi)|ˉςi|−ϖ, | (3.2) |
where i,j∈{1,…,n},0≤ℓ, ℓ<ϖ<1+2ℓ, ρi3,ρi4,ℵi3,ℵi4 are positive constants, if the following conditions hold
| ρi1≥−ξiϱi+|aiξi−biϱi−ξ2iϱi|+∑jϱj|cji|Lj, | (3.3) |
| ℵi1≥1ϱi+ξiϱi−ai, | (3.4) |
| ˉμij≥ϱi(|zij|+|eij|+|kij|)Lj, | (3.5) |
| ρi2≥0. | (3.6) |
In addition, the settling time is estimated by
| T∗=[Γ(1+μ)B2ϖ−2ℓ−11+ℓ(1+ϖ)((V1+ℓ(t0)+(BA)1+ℓϖ−ℓ)1+ϖ1+ℓ−(BA)1+ϖϖ−ℓ)]1μ, | (3.7) |
where A=nmini{ρi3,ℵi3}, B=nmini{ρi4,ℵi4}.
Proof. Take V=V(t)=∑i|ςi|+∑i|ˉςi|. Then, we have
| C0DμV≤∑isign(ςi)C0Dμςi+∑isign(ˉςi)C0Dμˉςi≤∑isign(ςi){1ϱiˉςi−ξiϱiςi−ρi1ςi−ρi2sign(ςi)|ˉςφi|−ρi3sign(ςi)|ςi|−ℓ−ρi4sign(ςi)|ςi|−ϖ}+∑isign(ˉςi){(ξiϱi−ai)ˉςi+(aiξi−biϱi−ξ2iϱi)ςi+ϱi[∑jcijζj(ςj)+∑jzijζj(ςφj)+⋀jeijζj(ςφj)+⋁jkijζj(ςφj)]−ℵi1ˉςi−sign(ˉςi)∑jˉμij|ςφj|−ℵi3sign(ˉςi)|ˉςi|−ℓ−ℵi4sign(ˉςi)|ˉςi|−ϖ}. | (3.8) |
Combined with Lemma 2.3 and Assumptions 2.1–2.2, we can obtain
| C0DμV≤∑i{1ϱi|ˉςi|−ξiϱi|ςi|−ρi1|ςi|−ρi2|ˉςφi|−ρi3|ςi|−ℓ−ρi4|ςi|−ϖ}+∑i{(ξiϱi−ai)|ˉςi|+|aiξi−biϱi−ξ2iϱi||ςi|+ϱi[∑j|cij|Lj|ςj|+∑j|zij|Lj|ςφj|+∑j|eij|Lj|ςφj|+∑j|kij|Lj|ςφj|]−ℵi1|ˉςi|−∑jˉμij|ςφj|−ℵi3(t)|ˉςi|−ℓ−ℵi4(t)|ˉςi|−ϖ}. | (3.9) |
From Lemma 2.1, we can get
| C0DμV≤∑i{1ϱi+ξiϱi−ai−ℵi1}|ˉςi|−∑iρi2|ˉςφi|+∑i{−ξiϱi−ρi1+aiξi−biϱi−ξiϱi+∑jϱj|cji|Li}|ςi|+∑i{∑j[ϱi(|zij|+|eij|+|kij|)Lj−ˉμij]}|ςφj|−∑iρi3(t)|ςi|−ℓ−∑iρi4(t)|ςi|−ϖ−∑iℵi3(t)|ˉςi|−ℓ−∑iℵi4(t)|ˉςi|−ϖ≤−∑iρi3|ςi|−ℓ−∑iρi4|ςi|−ϖ−∑iℵi3|ˉςi|−ℓ−∑iℵi4|ˉςi|−ϖ≤−nmini∈R+{ρi3,ℵi3}[∑i(|ςi|+|ˉςi|)]−ℓ−nmini∈R+{ρi4,μi4}[∑i(|ςi|+|ˉςi|)]−ϖ≤−AV(t)−ℓ−BV(t)−ϖ. | (3.10) |
From Lemma 2.2, we can obtain that FOFINN 3.1 could achieve FTS within the ST (3.7).
Adaptive control provides techniques that adjust a controller for a system with parametric uncertainty, structural uncertainty, and environmental uncertainty, where fuzzy logic is the typical structural uncertainty. The adaptive controller can adaptively adjust the output values based on the current state of the system, which to some extent reduces the loss of control input. Thus, we design a type of adaptive controller to achieve the predetermined performance of FOFINN. On the basis of controller (3.2), we replace the control parameters ρi1 and ℵi1 with variable parameters which related to the system states, then the controller becomes an adaptive controller. Hence, we have the following theorem.
Theorem 3.2. Assume the Assumptions 2.1–2.2 and conditions (3.4)–(3.6), FOFINN (2.8) is said to be FTS under the following adaptive controllers
| {ui=−|ρi1(t)|ςi−ρi2sign(ςi)|ˉςφi|−ρi3sign(ςi)|ςi|−ℓ−ρi4sign(ςi)|ςi|−ϖ,vi=−|ℵi1(t)|ˉςi−sign(ˉςi)∑jˉμij|ςφj|−ϱi∑jmij∫t−∞Hj(t−ϵ)ζj(ςj)dϵ−ℵi3sign(ˉςi)|ˉςi|−ℓ−ℵi4sign(ˉςi)|ˉςi|−ϖ. | (3.11) |
Additionally, the settling time is estimated by
| T∗=[Γ(1+μ)Υ22ϖ−2ℓ−11+ℓ(1+ϖ)((V1+ℓ(t0)+1)1+ϖ1+ℓ−1)]1μ, | (3.12) |
where
| C0Dμρi1(t)=(ρi1(t)−δsign(ρi1(t)))|ςi|−ρi4sign(ρi1(t))|ρi1(t)|−ℓ−ρi3sign(ρi1(t))|ρi1(t)|−ϖ, | (3.13) |
| C0Dμℵi1(t)=(ℵi1(t)−δsign(ℵi1(t)))|ˉςi|−ℵi4sign(ℵi1(t))|ℵi1(t)|−ℓ−ℵi3sign(ℵi1(t))|ℵi1(t)|−ϖ, | (3.14) |
and Υ1=nmini∈Z+{mini∈Z+{ρi3,ℵi3},mini∈Z+{ρi4,ℵi4}}, Υ2=Υ1, δ≥maxi∈Z+{1ϱi+ξiϱi−ai,−ξiϱi+|aiξi−biϱi−ξ2iϱi|+∑jϱj|cji|Li|}.
Proof. In order to keep it simple, we denote ρi1=ρi1(t) and ℵi1=ℵi1(t), respectively. Take the following Lyapunov functional:
| V=V(ςi,ˉςi,ρi1,ℵi1)=∑i(|ςi|+|ˉςi|+|ρi1|+|ℵi1|). | (3.15) |
Then, similarly to (3.8), we obtain
| C0DμV≤∑isign(ςi)C0Dμςi+∑isign(ˉςi)C0Dμˉςi+∑isign(ρi1)C0Dμρi1+∑isign(ℵi1)C0Dμℵi1. | (3.16) |
From the model (2.8), Lemma 2.1, Lemma 2.3, as well as (3.11), we have
| C0DμV≤∑isign(ςi){1ϱiˉςi−ξiϱiςi−|ρi1(t)|ςi−ρi2sign(ςi)|ˉςφi|−ρi3sign(ςi)|ςi|−ℓ−ρi4sign(ςi)|ςi|−ϖ}+∑isign(ˉςi){(ξiϱi−ai)ˉςi+(aiξi−biϱi−ξ2iϱi)ςi+ϱi[∑jcijζj(ςj)+∑juijζj(ςφj)+⋀jeijζj(ςφj)+⋁jkijζj(ςφj)]−|ℵi1(t)|ˉςi−sign(ˉςi)∑jˉμij|ςφj|−ℵi3sign(ˉςi)|ˉςi|−ℓ−ℵi4sign(ˉςi)|ˉςi|−ϖ}+∑isign(ρi1(t))((ρi1(t)−δsign(ρi1(t)))|ςi|−sign(ρi1(t))ρi4|ρi1(t)|−ℓ−sign(ρi1(t))ρi3|ρi1(t)|−ϖ)+∑isign(ℵi1(t))((ℵi1(t)−δsign(ℵi1(t)))|ˉςi|−sign(ℵi1(t))ℵi4|ℵi1(t)|−ℓ−sign(ℵi1(t))ℵi3|ℵi1(t)|−ϖ)≤∑i{1ϱi|ˉςi|−ξiϱi|ςi|−|ρi1(t)||ςi|−ρi2|ˉς−φi|−ρi3|ςi|−ℓ−ρi4|ςi|−ϖ}+∑i{(ξiϱi−ai)|ˉςi|+|aiξi−biϱi−ξ2iϱi||ςi|+ϱi∑j[|cij|Lj|ςj|+|uij|Lj|ςφj|+|eij|Lj|ςφj|+|kij|Lj|ςφj|]−|ℵi1||ˉςi|−∑jˉμij|ςφj|−ℵi3|ˉςi|−ℓ−ℵi4|ˉςi|−ϖ}+∑i((|ρi1(t)|−δ)|ςi|−ρi4|ρi1(t)|−ℓ−ρi3|ρi1(t)|−ϖ)+∑i((|ℵi1(t)|−δ)|ˉςi|−ℵi4|ℵi1(t)|−ℓ−ℵi3|ℵi1(t)|−ϖ). | (3.17) |
Combine with conditions (3.3)–(3.6), we have
| C0DμV≤∑i{1ϱi+ξiϱi−ai−δ}|ˉςi|−∑iρi2|ˉςφi|+∑i{−ξiϱi+|aiξi−biϱi−ξ2iϱi|+∑jϱj|cji|Li|−δ}|ςi|+∑i{∑j[ϱi(|zij|+|eij|+|kij|)Lj−ˉμij]}|ςφj|−∑iρi3|ςi|−ℓ−∑iℵi3|ˉςi|−ℓ−∑iρi4|ρi1(t)|−ℓ−∑iℵi4|ℵi1(t)|−ℓ−∑iρi4|ςi|−ϖ−∑iℵi4|ˉςi|−ϖ−∑iρi3|ρi1(t)|−ϖ−∑iℵi3|ℵi1(t)|−ϖ≤−Υ1V−ℓ−Υ2(t)V−ϖ. | (3.18) |
Hence, from Lemma 2.2, we can see that FOFINN (2.8) could achieve FTS within the settling time (3.12).
Remark 3.1. Due to the inclusion of a time driven variable coefficients in the adaptive controller (3.11) that we designed, it is more flexible than the feedback controllers in [35,36]. At the same time, from Lemma 2.2, it can be found that the settling time can be estimated by adjusting the size of parameters μ, ℓ, and ϖ.
Several numerical examples are given in this part to validate the results we obtained.
Example 4.1. Take the following controlled FOFINN into consideration.
| {C0Dμz1(t)={1η1ˉz1(t)−ξ1η1z1(t)}+u1,C0Dμz2(t)={1η2ˉz2(t)−ξ2η2z2(t)}+u2,C0Dμˉz1(t)={(ξ1η1−a1)ˉz1(t)+(a1ξ1−b1η1−ξ21η1)z1(t)+η1[∑jc1jζj(ςj(t))+∑jh1jζj(ςj(t−φj(t)))+∑jm1j∫t−∞Hj(t−ϵ)ζj(ςj(ϵ))dϵ+⋀je1jζj(ςj(t−φj(t)))+⋁jk1jζj(ςj(t−φj(t)))]}+v1,C0Dμˉz2(t)={(ξ2η2−a2)ˉz2(t)+(a2ξ2−b2η2−ξ22η2)z2(t)+η2[∑jc2jζj(ςj(t))+∑jh2jζj(ςj(t−φj(t)))+∑jm2j∫t−∞Hj(t−ϵ)ζj(ςj(ϵ))dϵ+⋀je2jζj(ςj(t−φj(t)))+⋁jk2jζj(ςj(t−φj(t)))]}+v2, | (4.1) |
where ϱi=[1,1], ξi=[1,1], ai=[2,2], bi=[3,3], cij=[3,2;−5,1], zij=[−0.7,−0.5;−0.3,0.9], mij=[−0.6,0.3;0.5,0.6], eij=[−0.3,0.4;−0.5,0.6], kij=[0.7,−0.9;−0.8,0.5] and φi(t)=0.6exp(sin(t))+0.6exp(sin(t)), Hj(t)=exp(−t).
From Theorem 3.1, we can obtain that ˉμ11≥1.7, ˉμ12≥1.8, ˉμ21≥1.6, ˉμ22≥2, ρ11≥7, ρ21≥4, ℵi1≥0.
Take ρ11=14, ρ21=9, ρ12=1.086, ρ22=2.5, ℵ11=ℵ21=2, ˉμij=[3.7,3.8;3.6,4], ρ13=0.055, ρ23=0.135, ρ14(t)=0.09, ρ24(t)=0.026, ℵ13=ℵ23=0.015, ℵ14=0.016, ℵ24=0.014, ℓ=0.7, ϖ=0.01, then, we can find that conditions (3.3)–(3.6) are all met. Therefore, the ST of controlled FOFINN (3.1) is
| T∗=[Γ(1+μ)B2ϖ−2ℓ−11+ℓ(1+ϖ)((V1+ℓ(t0)+(BA)1+ℓϖ−ℓ)1+ϖ1+ℓ−(BA)1+ϖϖ−ℓ)]1μ=45.1461. | (4.2) |
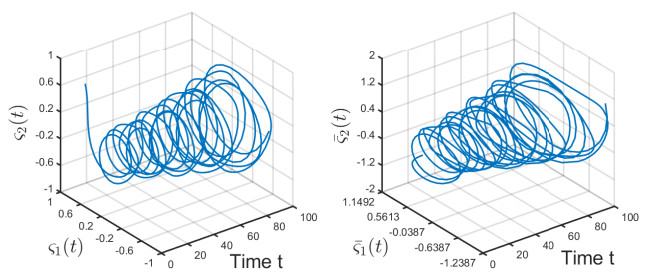
Figures 1 and 2 show the state trajectory of FOINN (4.1) without controller and the values of delay function φj(t), respectively. We can find that FOFINN can converge to a stable state before 1.2. This further demonstrates the effectiveness of our designing controller.
Figures 3 and 4 show the state of FOFINN (4.1) under feedback controller (3.2) and the values of controller (3.2). It can be observed that under controller (3.11), the state of FOFINN converges to a stable state before reaching the ST, i.e., FOFINN could achieve FTS. This also proves that the feedback controller (3.2) we designed is effective.
Example 4.2. We consider the same system as in Example 4.1 and consider the following adaptive controller:
| {ui=−|ρi1(t)|ςi−ρi2sign(ςi)|ˉςφi|−ρi3sign(ςi)|ςi|−ℓ−ρi4sign(ςi)|ςi|−ϖ,vi=−|ℵi1(t)|ˉςi−sign(ˉςi)∑jˉμij|ςφj|−ϱi∑jmij∫t−∞Hj(t−ϵ)ζj(ςj)dϵ−ℵi3sign(ˉςi)|ˉςi|−ℓ−ℵi4sign(ˉςi)|ˉςi|−ϖ, | (4.3) |
where parameters ρi2, ρi3, ρi4, ˉμij, mij, ϱi, ℵi3, ℵi4 are the same as we take in Example 4.1, and
| C0Dμρi1(t)=(ρi1(t)−δsign(ρi1(t)))|ςi|−ρi4sign(ρi1(t))|ρi1(t)|−ℓ−ρi3sign(ρi1(t))|ρi1(t)|−ϖ, | (4.4) |
| C0Dμℵi1(t)=(ℵi1(t)−δsign(ℵi1(t)))|ˉςi|−ℵi4sign(ℵi1(t))|ℵi1(t)|−ℓ−ℵi3sign(ℵi1(t))|ℵi1(t)|−ϖ. | (4.5) |
Take δ=10 and after verification, the conditions (3.3) and (3.6) are still met, so, from Lemma 2.2, the system can achieve FTS with the following ST:
| T∗=[Γ(1+μ)Υ22ϖ−2ℓ−11+ℓ(1+ϖ)((V1+ℓ(t0)+1)1+ϖ1+ℓ−1)]1μ=46.1001. | (4.6) |
The state of FOFINN (4.1) under controller (3.11) is shown in Figure 5. We can find that FOFINN converges to a stable state before reaching ST. Due to the fact that the control parameters change with the state of FOFINN, the convergence speed to stable state is slower and the ST under adaptive controller (3.11) is larger than under feedback controller (3.2).
Figure 6 is the values of adaptive parameters ρ11(t), ℵ11(t), ρ21(t), ℵ21(t) in controller (3.11).
Remark 4.1. The symbol function in the controller will generate chattering effects in the control process, increasing the control cost. To avoid the buffeting effect, sign function can be replaced by function tanh(⋅).
Remark 4.2. To the best of our knowledge, the stability of FOFINNs has scarcely been explored, particularly the fixed-time synchronization of such networks with mixed delay and neutral terms. Therefore, the findings presented in this paper are groundbreaking.
Remark 4.3. In [30,46], authors previously required that activation functions be bounded. However, this paper removes the boundedness assumption, making our results more general and lessening the conservativeness of the derived stibility criteria to some extent. The results in this paper can be generalized to those in [30,46], but the opposite is not true.
Remark 4.4. In [39,40,41], the criteria of FTS for integer order NNs have been obtained. We know that non-integer derivatives are more widely used than integer derivatives, so fractional derivatives are one of the factors that must be considered in modeling. In [47], the FTS criteria of memristor-based FONN are given based on the linear controller, but the calculation expression of the settling time is not given in detail. Compared to the results presented in [39,40,41,47], our results significantly enhance and broaden their theoretical outcomes to a certain extent.
Remark 4.5. In the design of control systems and mechanical systems, the inertia term is an important part, which affects the dynamic response and stability of the system. In the recent results [26,27,31,32], the FTS of NN models with inertial terms is not analyzed. Compared to their results, our results are more general.
Remark 4.6. Since the settling time of the system is derived according to the inequality techniques, there may be some errors in the estimation of the system settling time. In order to solve this problem, we can consider applying the less conservative inequality techniques.
This paper delves into the FTS of FOFINNs with mixed delays. Leveraging the fractional-order FTS theorem, properties of fractional calculus, and inequality approaches, we derive some novel sufficient conditions to ensure the globally FTS of FOFINN. Additionally, we design two types of controllers, namely the feedback controller and adaptive controller, and compute the settling times for each controller. Finally, we provide two examples to validate our results. Future research will focus on designing more concise and easy to implement controllers to achieve FTS of FONNs.
Tiecheng Zhang: Conceptualisation, writing - original draft, formal analysis, writing - review & editing; Liyan Wang: Methodology, software; Yuan Zhang: Supervision, validation; Jiangtao Deng: Writing - review & editing. All authors have read and approved the final version of the manuscript for publication.
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
This research is supported by the Guiding Project for 2023 of Scientific Research Plan of Hubei Provincial Department of Education, the Open Subject for Teacher Education Research of Hubei Normal University (Grant No. 2022TEZ06), the Philosophy and Social Science Research Project of Hubei Provincial Department of Education (Grant No. 23Y122), Science Research Project of Hubei Normal University (Grant No. 2023046, 2023049), and Guiding Project of Hubei Provincial Department of Education's Scientific Research Program (Grant No. B2022187).
The authors declare that there are no conflicts of interest regarding the publication of this paper.
| [1] |
Y. Ni, Z. Wang, X. Huang, Q. Ma, H. Shen, Intermittent sampled-data control for local stabilization of neural networks subject to actuator saturation: A work-interval-dependent functional approach, IEEE Trans. Neural Netw. Learn. Syst., 35 (2024), 1087–1097. https://doi.org/10.1109/TNNLS.2022.3180076 doi: 10.1109/TNNLS.2022.3180076

|
| [2] |
H. B. Zeng, Y. He, K. L. Teo, Monotone-delay-interval-based Lyapunov functionals for stability analysis of systems with a periodically varying delay, Automatica, 138 (2022), 110030, 2022. https://doi.org/10.1016/j.automatica.2021.110030 doi: 10.1016/j.automatica.2021.110030

|
| [3] |
Y. Sheng, F. L. Lewis, Z. Zeng, T. Huang, Lagrange stability and finite-time stabilization of fuzzy memristive neural networks with hybrid time-varying delays, IEEE Trans. Cybernet., 50 (2020), 2959–2970. https://doi.org/10.1109/TCYB.2019.2912890 doi: 10.1109/TCYB.2019.2912890

|
| [4] |
S. Ding, Z. Wang, Synchronization of coupled neural networks via an event-dependent intermittent pinning control, IEEE Trans. Syst. Man Cybernet., 52 (2022) 1928–1934. https://doi.org/10.1109/TSMC.2020.3035173 doi: 10.1109/TSMC.2020.3035173

|
| [5] |
Y. Wu, Y. Gao, W. Li, Finite-time synchronization of switched neural networks with state-dependent switching via intermittent control, Neurocomputing, 384 (2020), 325–334. https://doi.org/10.1016/j.neucom.2019.12.031 doi: 10.1016/j.neucom.2019.12.031

|
| [6] |
M. J. A. Schuetz, J. K. Brubaker, H. G. Katzgraber, Combinatorial optimization with physics-inspired graph neural networks, Nat. Mach. Intell., 4 (2022), 367–377. https://doi.org/10.1038/s42256-022-00468-6 doi: 10.1038/s42256-022-00468-6

|
| [7] |
A. Sellami, S. Tabbone, Deep neural networks-based relevant latent representation learning for hyperspectral image classification, Pattern Recogn., 121 (2022), 108224. https://doi.org/10.1016/j.patcog.2021.108224 doi: 10.1016/j.patcog.2021.108224

|
| [8] |
S. Panghal, M. Kumar, Optimization free neural network approach for solving ordinary and partial differential equations, Eng. Comput., 37 (2021), 2989–3002. https://doi.org/10.1007/s00366-020-00985-1 doi: 10.1007/s00366-020-00985-1

|
| [9] |
S. Wen, Z. Zeng, T. Huang, Q. Meng, W. Yao, Lag synchronization of switched neural networks via neural activation function and applications in image encryption, IEEE Trans. Neural Netw. Learn. Syst., 26 (2015), 1493–1502. https://doi.org/10.1109/TNNLS.2014.2387355 doi: 10.1109/TNNLS.2014.2387355

|
| [10] |
K. L. Babcock, R. M. Westervelt, Stability and dynamics of simple electronic neural networks with added inertia, Phys. D, 23 (1986), 464–469. https://doi.org/10.1016/0167-2789(86)90152-1 doi: 10.1016/0167-2789(86)90152-1

|
| [11] |
K. L. Babcock, R. M. Westervelt, Dynamics of simple electronic neural networks, Phys. D, 28 (1987), 305–316. https://doi.org/10.1016/0167-2789(87)90021-2 doi: 10.1016/0167-2789(87)90021-2

|
| [12] |
Q. Cui, L. Li, J. Cao, Stability of inertial delayed neural networks with stochastic delayed impulses via matrix measure method, Neurocomputing, 471 (2022), 70–78. https://doi.org/10.1016/j.neucom.2021.10.113 doi: 10.1016/j.neucom.2021.10.113

|
| [13] |
C. Huang, Exponential stability of inertial neural networks involving proportional delays and non-reduced order method, J. Exp. Theor. Artif. In., 32 (2020), 133–146. https://doi.org/10.1080/0952813X.2019.1635654 doi: 10.1080/0952813X.2019.1635654

|
| [14] |
S. Dong, H. Zhu, S. Zhong, K. Shi, Y. Liu, New study on fixed-time synchronization control of delayed inertial memristive neural networks, Appl. Math. Comput., 399 (2021), 126035. https://doi.org/10.1016/j.amc.2021.126035 doi: 10.1016/j.amc.2021.126035

|
| [15] |
L. Ke, Mittag-Leffler stability and asymptotic ω-periodicity of fractional-order inertial neural networks with time-delays, Neurocomputing, 465 (2021), 53–62. https://doi.org/10.1016/j.neucom.2021.08.121 doi: 10.1016/j.neucom.2021.08.121

|
| [16] |
F. Wei, G. Chen, Z. Zeng, N. Gunasekaran, Finite/fixed-time synchronization of inertial memristive neural networks by interval matrix method for secure communication, Neural Netw., 167 (2023), 168–182. https://doi.org/10.1016/j.neunet.2023.08.015 doi: 10.1016/j.neunet.2023.08.015

|
| [17] |
C. Li, W. Deng, Remarks on fractional derivatives, Appl. Math. Comput., 187 (2007), 777–784. https://doi.org/10.1016/j.amc.2006.08.163 doi: 10.1016/j.amc.2006.08.163

|
| [18] |
Y. Gu, H. Wang, Y. Yu, Stability and synchronization for Riemann-Liouville fractional-order time-delayed inertial neural networks, Neurocomputing, 340 (2019), 270–280. https://doi.org/10.1016/j.neucom.2019.03.005 doi: 10.1016/j.neucom.2019.03.005

|
| [19] |
L. Luo, L. Li, W. Huang, Q. Cui, Stability of the Caputo fractional-order inertial neural network with delay-dependent impulses, Neurocomputing, 520 (2023), 25–32. https://doi.org/10.1016/j.neucom.2022.11.060 doi: 10.1016/j.neucom.2022.11.060

|
| [20] |
Q. Peng, J. Jian, Synchronization analysis of fractional-order inertial-type neural networks with time delays, Math. Comput. Simul., 205 (2023), 62–77. https://doi.org/10.1016/j.matcom.2022.09.023 doi: 10.1016/j.matcom.2022.09.023

|
| [21] |
Y. Liu, Y. Sun, L. Liu, Stability analysis and synchronization control of fractional-order inertial neural networks with time-varying delay, IEEE Access, 10 (2022), 56081–56093. https://doi.org/10.1109/ACCESS.2022.3178123 doi: 10.1109/ACCESS.2022.3178123

|
| [22] |
G. Rajchakit, R. Sriraman, Robust passivity and stability analysis of uncertain complex-valued impulsive neural networks with time-varying delays, Neural Process Lett., 53 (2021), 581–606. https://doi.org/10.1007/s11063-020-10401-w doi: 10.1007/s11063-020-10401-w

|
| [23] |
F. Kong, Q. Zhu, R. Sakthivel, A. Mohammadzadeh, Fixed-time synchronization analysis for discontinuous fuzzy inertial neural networks with parameter uncertainties, Neurocomputing, 422 (2021), 295–313. https://doi.org/10.1016/j.neucom.2020.09.014 doi: 10.1016/j.neucom.2020.09.014

|
| [24] |
S. Wen, G. Bao, Z. Zeng, Y. Chen, T. Huang, Global exponential synchronization of memristor-based recurrent neural networks with time-varying delays, Neural Netw., 48 (2013), 195–203. https://doi.org/10.1016/j.neunet.2013.10.001 doi: 10.1016/j.neunet.2013.10.001

|
| [25] |
F. Du, J. G. Lu, Finite-time stability of fractional-order fuzzy cellular neural networks with time delays, Fuzzy Sets Syst., 438 (2022), 107–120. https://doi.org/10.1016/j.fss.2021.08.011 doi: 10.1016/j.fss.2021.08.011

|
| [26] |
F. Yan, D. Luo, Finite-time stability of Caputo fractional fuzzy differential equations with delay in granular sense, Commun. Nonlinear Sci. Numer. Simul., 134 (2024), 108022. https://doi.org/10.1016/j.cnsns.2024.108022 doi: 10.1016/j.cnsns.2024.108022

|
| [27] |
B. Zheng, Z. Wang, Mittag-Leffler synchronization of fractional-order coupled neural networks with mixed delays, Appl. Math. Comput., 430 (2022), 127303. https://doi.org/10.1016/j.amc.2022.127303 doi: 10.1016/j.amc.2022.127303

|
| [28] |
S. Wen, M. Z. Q. Chen, Z. Zeng, T. Huang, C. Li, Adaptive neural-fuzzy sliding-mode fault-tolerant control for uncertain nonlinear systems, IEEE Trans. Syst. Man Cybernet., 47 (2017), 2268–2278. https://doi.org/10.1109/TSMC.2017.2648826 doi: 10.1109/TSMC.2017.2648826

|
| [29] | T. Yang, L. Yang, C. W. Wu, L. O. Chua, Fuzzy cellular neural networks: theory, In: 1996 Fourth IEEE international workshop on cellular neural networks and their applications proceedings (CNNA-96), IEEE, 1996,181–186. https://doi.org/10.1109/CNNA.1996.566545 |
| [30] |
C. Aouiti, J. Cao, H. Jallouli, C. Huang, Finite-time stabilization for fractional-order inertial neural networks with time varying delays, Nonlinear Anal. Model. Control, 27 (2022), 1–18. https://doi.org/10.15388/namc.2022.27.25184 doi: 10.15388/namc.2022.27.25184

|
| [31] |
T. Hu, Z. He, X. Zhang, S. Zhong, Finite-time stability for fractional-order complex-valued neural networks with time delay, Appl. Math. Comput., 365 (2020), 124715. https://doi.org/10.1016/j.amc.2019.124715 doi: 10.1016/j.amc.2019.124715

|
| [32] |
H. L. Li, C. Hu, L. Zhang, H. Jiang, J. Cao, Complete and finite-time synchronization of fractional-order fuzzy neural networks via nonlinear feedback control, Fuzzy Sets Syst., 443 (2022), 50–69. https://doi.org/10.1016/j.fss.2021.11.004 doi: 10.1016/j.fss.2021.11.004

|
| [33] |
F. Du, J. Lu, Finite-time synchronization of fractional-order delayed fuzzy cellular neural networks with parameter uncertainties, IEEE Trans. Fuzzy Syst., 31 (2023), 1769–1779. https://doi.org/10.1109/TFUZZ.2022.3214070 doi: 10.1109/TFUZZ.2022.3214070

|
| [34] |
L. Ke, Mittag-Leffler stability and asymptotic ω-periodicity of fractional-order inertial neural networks with time-delays, Neurocomputing, 465 (2021), 53–62. https://doi.org/10.1016/j.neucom.2021.08.121 doi: 10.1016/j.neucom.2021.08.121

|
| [35] |
E. Arslan, G. Narayanan, M. S. Ali, S. Arik, S. Saroha, Controller design for finite-time and fixed-time stabilization of fractional-order memristive complex-valued BAM neural networks with uncertain parameters and time-varying delays, Neural Netw., 130 (2020), 60–74. https://doi.org/10.1016/j.neunet.2020.06.021 doi: 10.1016/j.neunet.2020.06.021

|
| [36] |
M. Zheng, L. Li, H. Peng, J. Xiao, Y. Yang, Y. Zhang, et al., Finite-time stability and synchronization of memristor-based fractional-order fuzzy cellular neural networks, Commun. Nonlinear Sci. Numer. Simul., 59 (2018), 272–291. https://doi.org/10.1016/j.cnsns.2017.11.025 doi: 10.1016/j.cnsns.2017.11.025

|
| [37] |
A. Polyakov, Nonlinear feedback design for fixed-time stabilization of linear control systems, IEEE Trans. Automat. Control, 57 (2012), 2106–2110. https://doi.org/10.1109/TAC.2011.2179869 doi: 10.1109/TAC.2011.2179869

|
| [38] |
Y. Li, Y. Kao, C. Wang, H. Xia, Finite-time synchronization of delayed fractional-order heterogeneous complex networks, Neurocomputing, 384 (2020), 368–375. https://doi.org/10.1016/j.neucom.2019.11.043 doi: 10.1016/j.neucom.2019.11.043

|
| [39] |
C. Aouiti, Q. Hui, H. Jallouli, E. Moulay, Fixed-time stabilization of fuzzy neutral-type inertial neural networks with time-varying delay, Fuzzy Sets Syst., 411 (2021), 48–67. https://doi.org/10.1016/j.fss.2020.10.018 doi: 10.1016/j.fss.2020.10.018

|
| [40] |
Y. Liu, G. Zhang, J. Hu, Fixed-time stabilization and synchronization for fuzzy inertial neural networks with bounded distributed delays and discontinuous activation functions, Neurocomputing, 495 (2022), 86–96. https://doi.org/10.1016/j.neucom.2022.04.101 doi: 10.1016/j.neucom.2022.04.101

|
| [41] |
C. Aouiti, H. Jallouli, State feedback controllers based finite-time and fixed-time stabilisation of high order BAM with reaction-diffusion term, Int. J. Syst. Sci., 52 (2021), 905–927. https://doi.org/10.1080/00207721.2020.1849861 doi: 10.1080/00207721.2020.1849861

|
| [42] |
G. Zhang, Z. Zeng, Stabilization of second-order memristive neural networks with mixed time delays via nonreduced order, IEEE Trans. Neural Netw. Learn. Syst., 31 (2020), 700–706. https://doi.org/10.1109/TNNLS.2019.2910125 doi: 10.1109/TNNLS.2019.2910125

|
| [43] |
G. Zhang, J. Cao, New results on fixed/predefined-time synchronization of delayed fuzzy inertial discontinuous neural networks: Non-reduced order approach, Appl. Math. Comput., 440 (2023), 127671. https://doi.org/10.1016/j.amc.2022.127671 doi: 10.1016/j.amc.2022.127671

|
| [44] |
J. Yu, C. Hu, H. Jiang, L. Wang, Exponential and adaptive synchronization of inertial complex-valued neural networks: A non-reduced order and non-separation approach, Neural Netw., 124 (2020), 50–59. https://doi.org/10.1016/j.neunet.2020.01.002 doi: 10.1016/j.neunet.2020.01.002

|
| [45] |
J. Wang, X. Wang, Y. Wang, X. Zhang, Non-reduced order method to global h-stability criteria for proportional delay high-order inertial neural networks, Appl. Math. Comput., 407 (2021), 126308. https://doi.org/10.1016/j.amc.2021.126308 doi: 10.1016/j.amc.2021.126308

|
| [46] |
J. Jian, L. Duan, Finite-time synchronization for fuzzy neutral-type inertial neural networks with time-varying coefficients and proportional delays, Fuzzy Sets Syst., 381 (2020), 51–67. https://doi.org/10.1016/j.fss.2019.04.004 doi: 10.1016/j.fss.2019.04.004

|
| [47] |
M. Zheng, L. Li, H. Peng, J. Xiao, Y. Yang, Y. Zhang, et al., Finite-time stability and synchronization of memristor-based fractional-order fuzzy cellular neural networks, Commun. Nonlinear Sci. Numer. Simul., 59 (2018), 272–291. https://doi.org/10.1016/j.cnsns.2017.11.025 doi: 10.1016/j.cnsns.2017.11.025

|