Global Mittag-Leffler stability of Caputo fractional-order fuzzy inertial neural networks with delay

1.   Introduction

In 1986, Babcock and Westervelt ^[1] first introduced an inertial term into neural networks. Second-order inertial neural networks are an extension of traditional neural networks that include a second-order term in their update formula. In the practical application of neural networks, such addition of inertial terms can lead to more complicated dynamical behaviors, such as bifurcation and chaos ^[2]. In the past decade, researchers have applied second-order inertial neural networks to various tasks, including recommendation systems, image recognition, and natural language processing. They have shown that these networks can achieve faster convergence and better generalization compared to traditional neural networks. Many efforts have been devoted for stability analysis of the inertial neural networks, and many interesting results have been established, such as ^[3,4,5].

Fuzzy cellular neural networks are combined with fuzzy logic and neural networks, which were initially introduced by Yang and Yang ^[6] in 1996. For neural networks, fuzzy logic can be used to handle uncertain inputs or outputs by defining fuzzy membership functions, which enables the network to make decisions based on partial or ambiguous information. Since fuzzy neural networks are more suitable and potential to tackle practical general problems, during the past few decades, a lot of results on the stability behaviors for fuzzy neural networks with delay have been obtained, see ^{[7,8,9,10,11,12,13,14]} and the references therein.

As we all know, compared with integer-order derivative, fractional-order derivatives provide a magnificent approach to describe memory and hereditary properties of various processes. Thus, it becomes more convenient and accurate to neural networks using fractional-order derivatives than integer-order ones. Dynamical behavior analysis, as well as existence, uniqueness, and stability of the equilibrium point of fractional order neural networks, has concerned growing interest in the past decades. Recently, the various kinds of stability problems for fractional-order neural networks, including Mittag-Leffler stability, asymptotic stability and uniform stability have been widely discussed, and some excellent results were obtained in both theory and applications. See, for example, previous works ^{[15,16,17,18,19,20,21,22,23]}, and the references therein.

Fractional-order fuzzy cellular neural networks (FOFCNNs) are a type of neural network that combines the concepts of fuzzy logic and fractional calculus. They have been applied in various fields, including image processing, control systems, and pattern recognition. The analysis of stability for fractional-order fuzzy cellular neural networks requires the use of specialized methods, such as the fractional Lyapunov method and the Lyapunov function based on fuzzy sets to verify global, asymptotic and finite-time stability. For example, by using the fractional Barbalats lemma, Riemann-Liouville operator and Lyapunov stability theorem, Chen et.al. in ^[24] studied the asymptotic stability of delayed fractional-order fuzzy neural networks with fixed-time impulse. Zhao et.al. ^[25] investigated the finite-time synchronization for a class of fractional-order memristive fuzzy neural networks with leakage and transmission delays. In ^[26], Yang et.al. studied the finite-time stability for fractional-order fuzzy cellular neural networks involving leakage and discrete delays. By applying Lyapunov stability theorem and inequality scaling skills, Syed Ali et.al. ^[27] considered the impulsive effects on the stability equilibrium solution for Riemann-Liouville fractional-order fuzzy BAM neural networks with time delay. Recently, Hu et.al. ^[28] studied the finite-time stabilization of fractional-order quaternion-valued fuzzy NNs.

To the best of our knowledge, there is no paper on the global Mittag-Leffler stability of the fractional order fuzzy inertial neural networks with delays in the literature. There are several difficulties in handling fractional-order fuzzy inertial neural networks (FOFINNs). First, designing the structure and parameters of FOFINNs is challenging because of the high dimensionality of the network. Second, training FOFINNs is computationally intensive and requires specialized optimization algorithms. Finally, the interpretability and explainability of FOFINNs can be difficult, as the fuzzy logic, fractional calculus components and inertial terms can make it difficult to understand the underlying mechanisms of the model.

Motivated by the previous works mentioned above, we first propose a class of new Capoto fractional-order fuzzy inertial neural networks (CFOFNINND) with delays. The primary contributions of this paper can be summarized as follows:

(1) The global fractional Halanay inequalities and Lyapunov functional approach for studying the global Mittag-Leffler stability (MLS) of Caputo fractional-order fuzzy neural-type inertial neural networks with delay (CFOFNINND) are introduced;

(2) A new sufficient condition of the existence and uniqueness of the equilibrium solution for an CFOFNINND is established by means of Banach contraction mapping principle;

(3) The GMLS conditions are established, which are concise and easy to verify.

The remaining of this paper is structured as follows. In section 2, we will provide some lemmas that will help us to prove our main results. In section 3, the existence and uniqueness of equilibrium point of CFOFNINND are proved by using contraction mapping principle. Moreover, by constructing suitable Lyapunov functional, using the global fractional Halanay inequalities, the global Mittag-Leffler stability of CFOFNINND is derived. Additionally, a numerical example is provided to show the feasibility of the approaches in section 4. Finally, this article is concluded in Section 5.

2.   Preliminaries

In this paper, we consider the following fractional-order fuzzy neural-type inertial neural networks with delay (FOFNINND):

where $^C D^{\beta} x_i(t) = \frac{1}{\Gamma(1-\beta)}\int_0^t (t-\tau)^{-\beta} x_i^{\prime}(\tau) d \tau$ denotes the Caputo fractional derivative of order $\beta$ ($0 < \beta \le 1)$, $n$ is the amount of units in the neural networks, $x_i(t)$ represents the state of $i$th neuron, $a_i > 0$, $c_i > 0$ are constants, $\tau > 0$ is the time delay, $f_j(x_j(t))$ represents the output of neurons at time $t$, $g_j(x_j(t-\tau))$ represents the output of neurons at time $t-\tau$, $a_{ij}$ responds to the synaptic connection weight of the unit $j$ to the unit $i$ at time $t$, $c_{ij}$ responds to the synaptic connection weight of the unit $j$ to the unit $i$ at time $t-\tau_j$, and represent the fuzzy OR and fuzzy AND mapping, respectively; $\alpha_{ij}$, $\beta_{ij}$, $T_{ij}$ and $H_{ij}$ denote the elements of fuzzy feedback MIN template, fuzzy feedback MAX template, fuzzy feed-forward MIN template and fuzzy feed-forward MAX template, respectively; $\mu_{ij}$ denotes the external input; $I_i$ represents the external bias of $i$th neuron.

The initial conditions for system (2.1) is

Remark 2.1. If $\beta = 1$, then system (2.1) is reduce to the following delayed fuzzy inertial neural networks :

In this section, we present some definitions and lemmas about Caputo fractional calculus, which will be used in the subsequent theoretical analysis.

Definition 2.1 ^[29]. The fractional integral of order $\alpha > 0$ for a function $x(t)$ is defined as

Definition 2.2 ^[30]. The Caputo derivative with fractional order $\alpha$ for a continuous function $x(t)$ is denotes as

in which $m-1 < \alpha < m$, $m \in Z^+$. Particularly, when $0 < \alpha < 1$

According to Definition 2.2, we have

Definition 2.3 ^[31]. The equilibrium point $x^* = (x_1^*, x_2^*, \cdots, x_n^*)^T$ of CFOFNINND (2.1) is said to be globally Mittag-Leffler stable, if there exists positive constant $\gamma$, such that for any solution $x(t) = (x_1(t), x_2(t), \cdots, x_n(t))$ of (2.1) with initial value (2.2), we have

where

$M(\|\phi\|, \|\psi\|) \ge 0$ and $E_{\alpha}(\cdot)$ is a Mittag-Leffler function.

Remark 2.2. The global Mittag-Leffler stability implies global asymptotic stability.

Lemma 2.1 ^[31]. Let $0 < \alpha < 1$. If $G(t) \in C^1[t_0, +\infty)$, then

Lemma 2.2 ^[32]. Assume $x(t)$ and $y(t)$ be two states of system (2.1), then we have

Lemma 2.3 ^[33]. Let $a, b, c, \rho : [0, \infty) \to \mathbb{R}$ be continuous functions and $b, c, \rho$ be nonnegative. Assume that

If a nonnegative continuous function $u: [-h, T] \to \mathbb{R}$ satisfies the following fractional inequality

then

where $\lambda^* = \inf \limits_{\lambda} \left\{\lambda - a(t) - \frac{b(t)}{E_{\alpha}(\lambda h^{\alpha})} \ge 0, \ \forall t \ge 0\right\}$.

In particular, if $b(t)$ and $c(t)$ are bounded functions, namely $0 \le b(t) \le \bar{b}$ and $0 \le c(t) \le \bar{c}$ for all $t > 0$, then

where $\bar{\lambda} = (1+ \Gamma(1-\alpha) \bar{b} h^{\alpha})^{-1} \Lambda$.

From Lemma 2.3, we obtain

Corollary 2.4. If a nonnegative continuous function $u: [-h, T] \to \mathbb{R}$ satisfies the following fractional inequality

where $\mu > \gamma > 0$ and $\rho(t) \le h$, then

where $\bar{\lambda} = - (1+ \Gamma(1-\alpha) \gamma h^{\alpha})^{-1} (\mu - \gamma) < 0$.

3.   Main results

In this section, we will study the existence, uniqueness and globally Mittag-Leffler stability of the equilibrium point for delayed Caputo fractional-order fuzzy inertial neural networks (2.1).

For $\beta > 0$, we know that $\mbox{}^C D^{\beta} a = 0$ for a constant $a$. Thus, we have the following definition.

Definition 3.1. A constant vector $x^* = (x_1^*, x_2^*, ..., x_n^*)^T$ is an equilibrium point of system (2.1) if and only if $x^*$ is a solution of the following equations:

Theorem 3.1. Assume that

($H_1$) The functions $f_j, g_j$ ($j = 1, 2, ..., n$) are Lipschitz continuous. That is, there exist positive constants $F_j, G_j$ such that

hold. If there exist constants $m_i$ ($i = 1, 2, ..., n$) such that the following inequality holds

then CFOFNINND (2.1) has a unique equilibrium point.

Proof. $\forall u = (u_1, u_2, ..., u_n)^T$, we constructing a mapping $P(u) = (P_1(u), P_2(u), ..., P_n(u))^T$ as follows

Let $u = (u_1, u_2, ..., u_n)^T$ and $v = (v_1, v_2, ..., v_n)^T$. From $(H_1)$ and Lemma 2.2, we obtain that

Moreover, we obtain by (3.2) that

which implies that $\|P(u) - P(v)\| < \|u - v\|$. That is, $P$ is a contraction mapping on $R^n$. So, we can conclude that there exists a unique fixed pint $u^*$ such that $P(u^*) = u^*$, i.e.,

Assume $x_i^* = \frac{u_i^*}{c_i m_i}$, we can get

which indicates that $x_i^*$ is a unique solution of (3.1). So, $x^*$ is the unique equilibrium point of system (2.1). This proof is completed. □

By using the transformation $x_i(t) = y_i(t) + x_i^*$, the equilibrium point of (2.1) can be shifted to the origin, that is, system (2.1) can be transformed into

In (3.4), we adopt a variable transformation : $z_i(t) = D^{\beta} y_i(t) + k_i y_i(t)$. Then system (3.4) can be rewritten as follows:

The initial conditions for system (3.5) is

Theorem 3.2. Let $0 < \beta \le 1$. Assume that $(H_1)$ holds. If there exist proper positive parameters $m_i$ and $p_i$, satisfying (3.2) and the following inequality :

then CFOFNINND (2.1) has a unique equilibrium point which is globally Mittag-Leffler stable.

Proof. By Theorem 3.1 we know that (2.1) has a unique equilibrium point $(x_1^*, x_2^*, ..., x_n^*)$. Construct the Lyapunov function candidate defined by

where $m_i$, $p_i$ are unknown positive constants, which need to be determined. Based on Lemma 2.1 and (3.5), calculating the fractional-order derivative of $V(t)$ :

where

and

Based on Corollary 2.4, one can infer that

where $\bar{\lambda} = - (1+\Gamma(1-\alpha) \gamma \tau^{\alpha})^{-1} (\mu - \gamma)$, and

Obviously, we have

where $L_1 = \max \limits_{1 \le i \le n} \left\{m_i + k_i p_i, \ p_i\right\} > 0$ and $L_2 = \max \limits_{1 \le i \le n} (m_i + k_i p_i) \|x^*\| > 0$. Thus, one obtain

where $\Omega = \frac{1}{\min_{1 \le i \le n}\{m_i, p_i\}} > 0$, which implies that the unique equilibrium point $(x_1^*, x_2^*, ..., x_n^*)$ of CFOFNINND (2.1) is globally Mittag-Leffler stable. The theorem 3.2 is proved. □

4.   An example

Example 4.1. Consider a two-dimensional Caputo fractional fuzzy inertial neural network with delay:

Two initial values of system (4.1) are given by

and

The parameters of system (4.1) are set as $\beta = 0.85$, $\tau_1 = \tau_2 = 1$, $a_1 = 7$, $a_2 = 6$, $c_1 = 11.3$, $c_2 = 8.7$, $a_{11} = 0.3$, $a_{12} = -0.2$, $c_{11} = -0.4$, $c_{12} = 0.1$, $\alpha_{11} = 0.2$, $\alpha_{12} = -0.6$, $\beta_{11} = 0.1$, $\beta_{12} = 0.3$, $a_{21} = - 0.2$, $a_{22} = 0.3$, $c_{21} = 0.1$, $c_{22} = -0.2$, $\alpha_{21} = -0.35$, $\alpha_{22} = 0.2$, $\beta_{21} = -0.2$, $\beta_{22} = 0.3$, $I_1 = 3.4490$, $I_2 = 3.3377$, $\mu_i = 0.3$ ($i = 1, 2$), and

The Lipchitz constants $F_j = 1$ for $f_j(\cdot) = \tanh(\cdot)$ and $G_j = 1$ for $g_j(\cdot) = \sin(\cdot)$ ($j = 1, 2$). Let parameters $m_i = p_i = 1$ ($i = 1, 2$). Then,

and

which implies that (3.2) holds. Thus, by Theorem 3.1, the equilibrium point $(x_1^*, x_2^*)$ of system (4.1) is the unique solution of the following system:

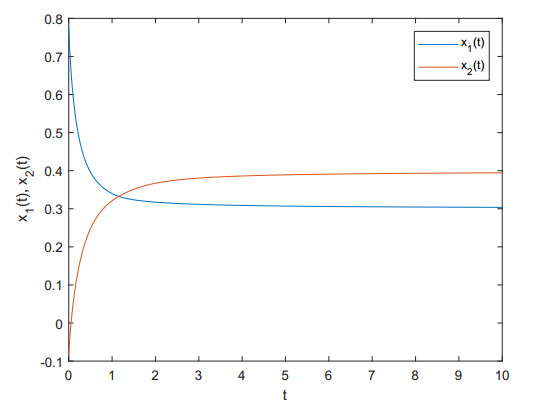
By matlab, we easy to get that $x_1^* = 0.3$ and $x_2^* = 0.4$. Obviously, the conditions $(H_1)$ hold. Moreover, letting parameters $k_1 = 4$ and $k_2 = 3$, one has

and

Thus $\mu = 2 > \gamma = 1.7$, that is the inequality (3.7) holds. Thus, by Theorem 3.2, the unique equilibrium point $(0.3, 0.4)$ of the system (4.1) is globally Mittag-Leffler stable (see Figures 1 and 2).

5.   Conclusions

The theoretical research on the fractional-order neural-type inertial neural networks is still relatively few. In this paper, we first propose and investigate a class of delayed fractional-order fuzzy inertial neural networks. With the help of contraction mapping principle, the sufficient condition is obtained to ensure the existence and uniqueness of equilibrium point of system (2.1). Based on the global fractional Halanay inequalities, and by constructing suitable Lyapunov functional, some sufficient conditions are obtained to ensure the global Mittag-Leffler stability of system (2.1). These conditions are relatively easy to verify. Finally, a numerical example is presented to show the effectiveness of our theoretical results.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We are really thankful to the reviewers for their careful reading of our manuscript and their many insightful comments and suggestions that have improved the quality of our manuscript. This work is supported by Natural Science Foundation of China (11571136).

Conflict of interest

The authors declare that there are no conflicts of interest.