New criteria on global Mittag-Leffler synchronization for Caputo-type delayed Cohen-Grossberg Inertial Neural Networks

1.   Introduction

Fractional calculus, as a prominent branch of mathematics, traces back to the 17th century ^[1]. It has been extensively used in environmental mechanics, engineering applications, automatic control and signal processing ^[2,3,4,5]. In contrast to integer order integrals, fractional order integrals can additionally describe procedures of all kinds with memory and hereditary properties. It was first developed in the 1940s to model neural computation, which is the foundation of Neural Networks (NNs) models. In the last few years, NNs have received significant attention from several scholars, and rich results are available in the reports ^[6,7,8,9,10].

In 1986, as can be noticed, Babcock and Westervelt brought inductance into a class of circuit models, resulting in inertial NNs (INNs). As a particular class of NNs, INNs take the form of second-order differential systems. The inclusion of the inertial term gives rise to some complicated behavior, such as instabilities and chaos. Therefore, INNs have caught sufficient attention of numerous researchers to yield some fascinating results. It is not difficult to see from these studies that the treatment of the inertial term is in general a method of order reduction or direct analysis. ^[8] discussed the problem of stabilization of INNs, which used analysis approach. ^[9] considered the inertial system by the method of non-separation. Based on integer order INNs, various synchronization and stability problems were widely discussed ^{[9,10,11,12,13,14]}. Compared to integer-order NNs, fractional-order NNs (FONNs) have the property of infinite storage and have the superior ability to describe dynamic behavior. As a result, a growing number of scholars have introduced inertial terms into fractional systems to form FOINNs, with a plethora of intriguing results ^{[15,16,17,18]}. In actual applications, INNs are widely used in engineering, such as secure communication ^[19], image encryption ^[20], etc.

It may be noted that the CGNNs were raised by Cohen and Grossberg as a generalization of the network models. This class of exceptional NNs model has attracted considerable attention in the areas of associative memory, classification, solving optimization problems and pattern recognition ^{[21,22,23,24]}. Recently, a large amount of results for CGNNs have been reported. In ^[25], the problem of synchronization of complex-valued CGNNs is addressed by constructing appropriate controllers. In ^[26], proposed the model of delayed fuzzy CGNNs with discontinuous activations and uncertain term. Due to the particularity of INNs and CGNNs, some scholars add inertial term to CGNNs to form a kind of inertial CGNNs (ICGNNs) and the dynamic behavior analysis of this class of NNs has received wide attention ^[8,27,28,29]. For example, ^[8] proposed the condition of judging the stability by the direct approach of ICGNNs with generalized delays. ^[27] gained several new criteria to verify the ICGNNs with proportional delays. ^[28] established the criterion of fixed-time synchronization for ICGNNs by constructing a controller with two exponential terms. To better describe the dynamic behavior of some neurons, ^[30] proposed the delayed of FOICGNNs. As a matter of fact, some results of FOCGNNs have been reported ^{[31,32,33,34]}, where the models do not take into account the inertia term. Furthermore, there are some systems of FOINNs that are not combined with CGNNs ^{[15,16,17,18]}. It should be pointed out that model is based on the Riemann-Liouville type FOICGNNs in ^[30]. Thus, we found that there is relatively little research on FOICGNNs in the Caputo sense. It is noteworthy that various types of synchronization have been extensively discussed, including but not limited to anti-synchronization ^[12], fixed-time synchronization ^{[7,11,19,26,28]}, finite time synchronization ^[25,35,36], quasi projective synchronization ^[25], global asymptotic synchronization (GAS) ^[16,27] and GMLS ^[17,18]. Currently, various effective control strategies have been applied to solve the synchronization problem, such as impulsive control ^[37], predefined-time control ^[12], linear control ^[25,29], pinning control ^[13,38] and sliding mode control ^[14]. Therefore, the problem of GMLS for Caputo-type FOICGNNs with discrete and distributed delays is not yet considered.

Motivated by the front statement, our main goal of this paper is to study the GMLS of Caputo-type delayed ICGNNs. The following innovations are listed:

(1) The model being considered is constructed on the basis of Caputo-type ICGNNs that have both discrete and distributed delays. The model takes into account two distinct time delays, thus making it more comprehensive and more practical than the models of ICGNNs ^[28,29].

(2) The inertial system is converted into two ordinary fractional systems by variable substitution. The difficulties caused by delays are overcome using two novel control strategies. Different from ^[30], the novel controllers are designed to achieve the GMLS of Caputo-type ICGNNs, which reduces the control cost and improves the control precision to a certain extent.

(3) Compared with the matrix inequalities approach ^[32], the novel conditions of GMLS are derived by the algebraic inequality technique, which can avoid the complex calculation and facilitate the verification.

(4) The derived conditions are characterized by the form of algebraic inequalities, which are easy to put into effect in reality. The validity of theoretical results is confirmed via simulation results.

2.   Preliminaries

Subsequently, the basic concepts, lemmas and the Caputo-type delayed ICGNNs model are described.

Definition 1. ^[1] For a function $u(\cdot)$, its fractional integral with order $\beta$ is

Definition 2. ^[39] For $u(\cdot)\in \mathbb{C}^n([0, +\infty], R)$, its Caputo derivative of the $\beta$-order is

Lemma 1. ^[40] If $\phi(t)$ is differentiable and $\phi(t)\in \mathbb{C} [t_0, +\infty)$, then

Lemma 2. ^[41] If $\varepsilon > 0$, $\sigma_1, \sigma_2 \in R$, then

Lemma 3. ^[42] For $V(t)\in \mathbb{C} [0, +\infty)$, if satisfies $_0^cD_t^\beta V(t)\leqslant-\Lambda V(t)$, then

where $\beta \in (0, 1)$ and $\Lambda \in \mathbb{R}$.

The Caputo-type delayed FOICGNNs is investigated as follows:

where $\alpha_\kappa(r_\kappa(t))$ is the amplification function; $h_\kappa(r_\kappa(t))$ means well behaved function; $r_\kappa(t)$ stands for the state of the $k$ th neuron, $\psi_\hbar(r_\hbar(t))$ refers to the activation function, $\tau_1$ denotes the constant time delay, $\tau_2$ is the distributed delay; $d_{\kappa \hbar}, b_{\kappa \hbar}$ and $c_{\kappa \hbar}$ are connection weights, $I_\kappa(t)$ represents the external input and $0 < |I_\kappa(t)|\leqslant I_\kappa.$

Considering the following variable transform:

then, the system (2.1) is expressed as:

Analogously, the response system of the system (2.3) can be depicted as:

We set the initial-value of systems (2.3) and (2.4) as:

Let ${\widetilde{e}_\kappa}(t) = {y_\kappa}(t) - {r_\kappa}(t)$, ${\widetilde{z}_\kappa}(t) = {v_\kappa}(t) - {w_\kappa}(t)$, the above error systems are given by:

Assumption 1. The function of $\alpha(\cdot)$ satisfies:

where $y, r\in R$ and $\alpha_\kappa > 0$.

Assumption 2. If exists $\varpi_\kappa > 0$, the functions $\alpha(\cdot)$ and $h(\cdot)$ satisfy:

where $r\neq y, r, y\in \mathbb{R}.$

Assumption 3. $\forall y, r \in \mathbb{R}$, if the activation function $\psi_\hbar(\cdot)$ satisfies:

where $\Psi_\hbar > 0.$

Assumption 4. For $\psi_\hbar(\cdot)$, the constant $M_\hbar > 0$ exist such that

Definition 3. The systems (2.3) and (2.4) can reach GMLS under the controllers $P_\kappa(t)$ and $Q_\kappa(t)$, if there exists one constant $\ell > 0$, such that

3.   Main results

The controllers of system (2.5) are designed:

where $\widetilde{e}_\kappa(t)\neq0.$

Theorem 1. The systems (2.3) and (2.4) can realize GMLS, when $\Lambda > 0, \Lambda = \min\{\Lambda_1, \Lambda_2\}$

Proof. Constructing $V(\cdot)$ as:

Based on Lemma 1, one has:

Substituting (2.5) into (3.3), we have

From Assumptions 1 and 2, it gives

By Assumptions 3 and 4, one obtains

From Lemma 2, one has

Substituting (3.7)–(3.10) into (3.6), then

Because of the condition $\Lambda = \min\{\Lambda_1, \Lambda_2\} > 0$, where,

From Lemma 3, one can get

Therefore,

By Definition 3, the systems (2.3) and (2.4) can realize the GMLS. □

In order to realize the automatic adjustment of control gains, the controller of system (2.5) are designed as follows:

where $\widetilde{e}_\kappa(t)\neq0.$

Theorem 2. If $\vartheta_\kappa^\ast$ satisfies $\Lambda > 0$, when $\Lambda = \min\{\Lambda_1, \Lambda_2\}$,

the systems (2.3) and (2.4) can realize GMLS.

Proof. Designing $V(\cdot)$ is

By utilizing Lemma 1, the Caputo type derivative of (3.13) can be obtained,

Substituting (2.5) into (3.16) yields

From Assumptions 1 and 2, one has

According to Assumptions 3 and 4, we get

From (3.7)–(3.10), then we get

Based on the condition $\Lambda = \min\{\Lambda_1, \Lambda_2\} > 0$, there,

From Lemma 3, then

Therefore,

Note that,

where $H$ is a positive constant.

Thus,

From Definition 3, the systems (2.3) and (2.4) can realize GMLS. □

Remark 1. Different with the GAS ^[37], quasi projective synchronization ^[25], finite-time synchronization ^[26,35,36], Mean-square synchronization ^[38], fixed-time synchronization ^[7,26,28], exponential synchronization ^[29], pinning synchronization ^[43] and adaptive quantitative exponential synchronization ^[44]. The GMLS of ICGNNs is discussed in the article.

Remark 2. Note that the attack resistant control ^[44], sliding mode control ^[14,45], pinning control ^[13,38] and intermittent control ^[46] are inconvenient and undesirable in practical applications. Two novel feedback controllers are designed to achieve GMLS in this article, which is more convenient. Different with the linear control and adaptive control, in this paper, two control inputs $P_\kappa(t)$ and $Q_\kappa(t)$ are incorporated into the the model of response systems. It can be seen that the selection of the novel feedback controller with time delays is more efficient and extensive.

Remark 3. Compared with the models of integer order ICGNNs considered in some literature ^{[8,24,27,28,29]}, we study the FOICGNNs. Different with the dynamic properties exhibited by integer-order ICGNNs, FOICGNNs possess infinite memory characteristics and offer a more accurate depiction of neuronal dynamics. Consequently, they are particularly well-suited for application in realistic domains. Different from the model ^[30], the model of this article is based on the derivative of Caputo' sense. In other researches, various types of time delays have been considered such as proportional delay ^[27,31], discrete delay ^[30,47], time-varying delay ^[13,33] and leakage delay ^[47]. However, the system of this article are considered both discrete and distributed delays. For these reasons, the proposed model of the nervous system is less conservative.

Remark 4. Different from some approaches such as event-triggered approach ^[28], matrix inequalities approach ^[33] and contraction mapping principle ^[32], several efficient guidelines are derived to implement the GMLS of Caputo FOICGNNs through the method of variable substitution and inequality technique. The resulting criterion is formulated in the form of an algebraic inequality, which greatly reduces the computational complexity and is easier to prove and implement in practical applications.

Remark 5. In ^[37], the GAS of fractional-order dynamic systems was realized within the framework of event-based delayed impulsive control. However, in this paper, the GMLS of Caputo-type delayed ICGNNs is considered. As a matter of fact, the GMLS is simplified to the GAS. Thus, the GMLS of this paper can apply to the GAS. In ^[43], pinning synchronization of integer-order NNs was achieved. Instead, the model of fractional-order is discussed in this paper, which can overcome the disadvantage that the integer order model does not agree well with the experimental results. In addition, the fractional-order model is more clear and concise in describing complex physical and mechanical problems.

4.   Illustrative examples

Some simulations are provided to check the availability of the results in this part.

Example 1. Considering two-dimensional FOICGNNs with discrete and distributed delays:

where $\kappa = 1, 2,$ and $0 < \beta < 1,$ let: $\beta = 0.95$, $\alpha_1(r_1) = 0.9+{\frac{0.2}{1+{r_1}^2}}$, $\alpha_2(r_2) = 0.9+\frac{0.2}{1+{r_2}^2}$, $I_\kappa(t) = sint$, $\psi_\hbar(\cdot) = cos(\cdot)$, $h_1(r_1) = 0.2{r_1}-\frac{0.2}{1+{r_1}^2}$, $h_2(r_2) = 0.2{r_2}-\frac{0.2}{1+{r_2}^2}$. By calculating $\underline{\alpha} = 0.9$, $\overline{\alpha} = 1.1$, $\alpha_1 = \alpha_2 = 0.2$, $\varpi_1 = \varpi_2 = 0.18$.

Then, choose $\pi_1 = 2.9$, $\pi_2 = 2.9$, $\hat{\delta}_1 = 4.6$, $\hat{\delta}_2 = 4.6$ $\ d_{11} = 0.23$, $\ d_{12} = -1.5$, $\ d_{21} = -0.64$, $\ d_{22} = 0.3$, $\ b_{11} = 0.12$, $\ b_{12} = -0.1$, $\ b_{21} = -0.2$, $\ b_{22} = 0.16$, $\ c_{11} = 0.15$, $\ c_{12} = -0.3$, $\ c_{21} = 0.2$, $\ c_{22} = -0.15$, $\tau_1 = \tau_2 = 1$. $\epsilon_1 = 1.$ The Lipchitz constants $\Psi_1 = \Psi_2 = 0.5$, $\ \psi_\hbar(\cdot) = cos(\cdot)$. $\ I_1 = I_2 = 1.$

The parameters of the controllers, we choose: $\ {\breve{\eta}_1} = 8.6$, $\ {\breve{\eta}_2} = 9.1$, $\ {\breve{\varrho}_1} = 9.0$, $\ {\breve{\varrho}_2} = 8.7$, $\ \mu_1 = 0.088$, $\ \mu_2 = 0.0715$, $\ 2\bar{\alpha}(c_{11}+c_{12}) = 0.99$, $2\bar{\alpha}(c_{21}+c_{22}) = 0.77.$ The initial values are given as $r_1(0) = 2.9$, $r_2(0) = -1.5$, $w_1(0) = 5.7$, $w_2(0) = 1.5$, $y_1(0) = 0.4$, $y_2(0) = 2.3$, $v_1(0) = -1.9$, $v_2(0) = -0.1$. Therefore,

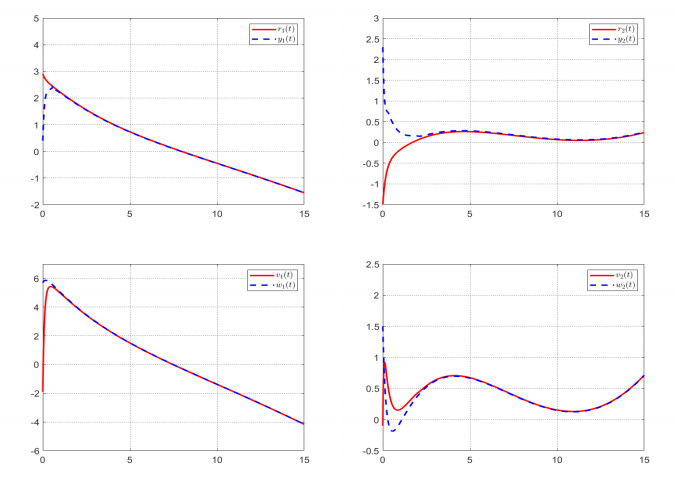
when $\kappa = 1$, $\Lambda_1 = 7.86575,$ $\Lambda_2 = 6.76875;$ $\kappa = 2$, $\Lambda_1 = 8.185,$ $\Lambda_2 = 6.7225;$ then $\Lambda = \min\{\Lambda_1, \Lambda_2\} = 6.7225 > 0$. Thus, the systems (2.3) and (2.4) can realize the GMLS. The figures of each state variable of the systems (2.3) and (2.4) are given in Figure 1. As is shown in the picture, the curves for the state of the system are eventually coeval. The error curves of systems (2.3) and (2.4) are portrayed in Figure 2.

Example 2. Considering two-dimensional models (2.3) and (2.4): Where $\kappa = 1, 2,$ and $0 < \beta < 1,$ let: $\beta = 0.9$, $\alpha_1(r_1) = 0.3+\frac{0.6}{1+{r_1}^2}$, $\alpha_2(r_2) = 0.3+\frac{0.6}{1+{r_2}^2}$, $I_\kappa(t) = sint$, $\psi_\hbar(\cdot) = cos(\cdot)$, $I_1 = I_2 = 1,$ $h_1(r_1) = \cos({r_1})-\frac{0.4}{1+{r_1}^2}$, $h_2(r_2) = \cos({r_2})-\frac{0.4}{1+{r_2}^2}.$ By calculating $\underline{\alpha} = 0.3$, $\overline{\alpha} = 0.9$, $\alpha_1 = \alpha_2 = 0.6$, $\varpi_1 = \varpi_2 = 0.3$.

The relevant parameters are selected as $\pi_1 = 3.4$, $\pi_2 = 3.4$, $\hat{\delta}_1 = 3.9$, $\hat{\delta}_2 = 3.9$ $\ d_{11} = 0.3$, $\ d_{12} = -1.4$, $\ d_{21} = 0.03$, $\ d_{22} = 1.0$, $\ b_{11} = 0.12$, $\ b_{12} = -0.1$, $\ b_{21} = -0.18$, $\ b_{22} = 0.13$, $\ c_{11} = -0.45$, $\ c_{12} = -0.14$, $\ c_{21} = 0.2$, $\ c_{22} = 0.4$, $\tau_1 = 1$, $\tau_2 = 1$. The Lipchitz constants $\Psi_1 = \Psi_2 = 0.5$. Taking the initial values as: $r_1(0) = 2.9$, $r_2(0) = -3.5$, $w_1(0) = 2.5$, $w_2(0) = -1.9$, $y_1(0) = -0.8$, $y_2(0) = 2.4$, $v_1(0) = -1.9$, $v_2(0) = 1.5$.

Under the controller (3.14), select $\rho_1 = 1$, $\rho_2 = 1.5$, $\vartheta_1(0) = 1.2$, $\vartheta_2(0) = 1.8$, $\vartheta_1^\ast = 7$, $\vartheta_2^\ast = 5$, $\ {\breve{\eta}_1} = 7.0$, $\ {\breve{\eta}_2} = 7.4$, $\ \mu_1 = 0.0675$, $\ \mu_2 = 0.05175$, $2\bar{\alpha}(c_{11}+c_{12}) = 1.062$, $2\bar{\alpha}(c_{21}+c_{22}) = 1.08,$ Therefore,

when $\kappa = 1$, $\Lambda_1 = 7.76375,$ $\Lambda_2 = 4.515;$ $\kappa = 2$, $\Lambda_1 = 7.878,$ $\Lambda_2 = 2.8165;$ then $\Lambda = \min\{\Lambda_1, \Lambda_2\} = 6.7225 > 0$.

Therefore, the simulations confirm the validity of proposed Theorem 2, the systems (2.3) and (2.4) can reach GMLS. The curves of control gains are provided in Figure 5. In Figure 3 represents the state trajectories of the systems (2.3) and (2.4). The synchronization error of systems (2.3) and (2.4) are exhibited in Figure 4.

5.   Conclusions

The GMLS analysis of delayed FOICGNNs is presented in this article. By means of variable substitution and Caputo-type derivative property, the $2\beta$ order inertial system is converted into two general systems with $\beta$ order. Some criteria are formulated by the use of the differential mean-value theorem and fractional differential inequality techniques, the GMLS of FOICGNNs is implemented by designing the novel controllers. Ultimately, two numerical simulations are furnished to demonstrate the feasibility of the results. In our future works, we will further investigate event-triggered control on finite-time Mittag-Leffler synchronization of FOICGNNs with time-varying delays.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Natural Science Foundation of Anhui Province of China (No.1908085MA01), the Top Young Talents Program of Higher Learning Institutions of Anhui Province of China (No.gxyq2019048) and the Natural Science Foundation of the Higher Education Institutions of Anhui Province of China (No.2023AH050478).

Conflict of interest

The authors declare that they have no competing interests.