Finite-time and global Mittag-Leffler stability of fractional-order neural networks with S-type distributed delays

1.   Introduction

The study of neural networks (NNs) with time delays is crucial for addressing practical problems. Time delays can be generally categorized as discrete delays, leakage delays, and distributed delays. Fractional-order calculus extends the order of nonlinear system models from integer-order to fractional-order. The control problem of fractional-order nonlinear systems has been a prominent and challenging research area in control theory and numerous research results have been obtained in this field. In ^[1], a novel decentralized non-integer order controller applied on the nonlinear fractional-order composite system was proposed, and some novel results for the asymptotic stabilization were obtained. In ^[2], a variable structure adaptive fuzzy control scheme was designed to solve the unknown dead-zone input nonlinearities which are considered in the Riemann-Liouville and Caputo fractional-order nonlinear systems. The authors in ^[3] proposed some novel stabilization methods and investigated the gradient control of a nonlinear fractional-order system. An adaptive composite dynamic surface control scheme was first proposed for nonlinear fractional-order systems subject to delayed input in ^[4]. In ^[5], the authors introduced a composite learning adaptive backstepping fuzzy control method for functional uncertainties of fractional-order nonlinear systems. In ^[6], the event-triggered predefined-time output feedback control problem was investigated for fractional-order nonlinear systems with input saturation. In the past decade, fractional-order neural networks (FNNs) with time delays have attracted wide and considerable attention because incorporating fractional-order derivatives into NNs can well describe the dynamical behavior of neurons, holding significant relevance across a broad spectrum of applications. Therefore, the study of the dynamical properties of FNNs with time delays has received considerable attention among many scholars and there have been numerous results, such as bifurcation properties ^[7,8], Mittag-Leffler synchronization ^[9,10], finite-time stability and synchronization^{[11,12,13,14,15]}, asymptotical stability ^{[16,17,18,19,20,21]}, multistability ^[22], quasi-uniform stability ^[23], and synchronization control ^[24,25].

In 2002, Wang and Xu firstly introduced S-type distributed delays into bidirectional associative memory (BAM) NNs ^[26], which comprises discrete delays and continuously distributed delays in terms of Lebesgue-Stieltjes integral. The emergence of S-type distributed delays has aroused the interest of numerous scholars, leading investigations into the stability problems of NNs with S-type distributed delays (SDNNs), including global asymptotic stability ^[26], robust stability ^[27], global exponential robust stability ^[28,29], global exponential stability ^[30,31], and some solution problems of SDNNs, such as mild solution ^[32] and periodic solution ^[33].

However, to the best of our knowledge, research on the dynamical properties of fractional-order neural networks with S-type distributed delays (FSDNNs) has not been found. Therefore, the investigation of finite-time stability (FTS) and global Mittag-Leffler stability (GMLS) of FSDNNs in this paper is more interesting and meaningful in both theoretical development and practical application. The main contributions of this paper are summarized as follows.

● FSDNNs incorporating discrete delays and continuously distributed delays as S-type distributed delays in the sense of Lebesgue-Stieltjes integral are established.

● Fractional-order integrals of the state function with S-type distributed delays are transformed into fractional-order integrals of the state function without S-type distributed delays.

● Sufficient conditions for FTS and GMLS of FSDNNs are obtained when certain conditions are satisfied. This provides a new basis for further expanding NNs research and practical applications.

The paper is structured as follows: In Section 2, the FSDNNs formulation and some preliminaries contents are presented. In Section 3, some criteria for FTS and GMLS of FSDNNs are derived. In Section 4, two numerical simulations examples are presented to illustrate the correctness and realizability of our conclusion. In the end, a conclusion is drawn in Section 5.

2.   Preliminaries

We consider a class of FSDNNs described by

with initial condition

In system (2.1), $\mathcal{D}_t^{\alpha}$ is an $\alpha$-order $(0 < \alpha < 1)$ Riemann-Liouville derivative, $f_j(x_j(t))$ denotes activation function, $a_{ij}$ and $b_{ij}$ represent the weight between the $j$th neuron and the $i$th neuron, $I_i$ is an input signal introduced from outside to the $i$th neuron, $d_i > 0$ denotes the rate of the $i$th neuron returning to resting state without any connection, and the past effect of the $j$th neuron on the $i$th neuron is given by the Lebesgue-Stieltjes integral $\int_{-\infty}^0 x_j(t+\theta)dw_j(\theta)$ with nondecreasing bounded variation function $w_j(\theta)$ and satisfies $\int_{-\infty}^0 dw_j(\theta) = k_j > 0, j = 1, \cdots, n$.

The assumption that accompanies system (2.1) is given as follows:

Assumption $\boldsymbol{A}_{\bf{1}}$: The output functions $f_i(\cdot)$ satisfying Lipschitz condition, i.e., exists $F_i > 0$, which satisfies

Definition 2.1. ^[34] The Riemann-Liouville fractional integral with order $q$ of function $f(t)$ is defined as

for all $t\geq t_0$, $q > 0 \in \mathbb{R}$, where $\Gamma(\tau) = \int_{0}^{+\infty}t^{\tau-1}e^{-t}dt$.

Definition 2.2. ^[34] The Riemann-Liouville fractional derivative with order $q$ is defined as

where $n-1\leq q < n$, $n\in \mathbb{Z}^+$, $q \in \mathbb{R}$.

Definition 2.3. ^[34] The Mittag-Leffler function with one parameter is defined as

where $\alpha > 0$ and $z\in \mathbb{C}$.

Lemma 2.4. ^[35] If $u(t)\in \mathbb{C}[0, +\infty]$, and there exist $c_1 > 0, c_2 > 0$, which satisfy $u(t) \leq -c_1\mathcal{I}_{t}^{q} u(t) + c_2$, then

where $0 < q < 1$ and $E_q(\cdot)$ denotes the one-parameter Mittag-Leffler function.

Lemma 2.5. (Bellman-Gronwall inequality ^[36]) Assume that function $y(t)$ satisfies

with $\alpha(t)$ and $\beta(t)$ being known real-valued positive functions. If $\alpha(t)$ is differentiable, then

Definition 2.6. ^[37] The equilibrium point $u^* = (u^*_1, \cdots, u^*_n)^T$ of system (2.1) is FTS with respect to $\{\delta, \varepsilon, t_0, J\}, J = [t_0, t_0+H], 0 < H < +\infty, t_0$ denoting the initial time observation of the system, $0 < \delta < \varepsilon, \delta, \varepsilon \in\mathbb{R}$, and any solution $u(t, t_0, \varphi)$ with initial condition $u_i(s) = \varphi_i (s), s\in(-\infty, 0], i = 1, \cdots, n,$ if and only if $\|\varphi-u^*\| < \delta,$ implies

where $\|\varphi-u^*\| = \sup\limits_{-\infty\leq s \leq 0} \sum \limits_{i = 1}^{n}|\varphi_i(s)-u^*_i|, \ \|u(t)-u^*\| = \sum\limits_{i = 1}^{n}|u_i(t)-u^*_i|.$

Definition 2.7. ^[35] If there exist constants $\rho_1\geq0$ and $\rho_2\geq 0$, let $x(t)$ and $y(t)$ be two different solutions of system (2.1) with different initial values $x_i(s) = \varphi_i(s)$ and $y_i(s) = \psi_i(s)$, $s\in (-\infty, 0]$. The solution of system (2.1) is said to be GMLS if $x(t)$ and $y(t)$ satisfy

where $x(t) = (x_1(t), \cdots, x_n(t))^T$, $y(t) = (y_1(t), \cdots, y_n(t))^T$, $\varphi(t) = (\varphi_1(t), \cdots, \varphi_n(t))^T$, $\psi(t) = (\psi_1(t), \cdots, \psi_n(t))^T$, $M(\varphi-\psi)\geq 0$, $M(0) = 0$, $E_q$ is the Mittag-Leffler function with one parameter.

3.   Main results

Theorem 3.1. For $\delta, \varepsilon, J$ is defined in Definition 2.6 and $0 < \delta < \varepsilon$. If Assumption $A_1$ and

hold, then there exists a unique equilibrium point in FSDNNs (2.1), which is FTS.

Proof. Let $x(t) = (x_1(t), \cdots, x_n(t))^T \in \mathbb{R}^n$ and define a mapping $P: \mathbb{R}^n\rightarrow \mathbb{R}^n$ by $P(x) = (P_{x_1}, \cdots, P_{x_n})^T$, where

We prove that the mapping $P$ is contractive:

$y(t) = (y_1(t), \cdots, y_n(t))^T \in \mathbb{R}^n$, which yields

Thus, $P$ is the contractive mapping. In light of contractive mapping theory, there exists the unique point $u^{\ast} = (u_1^{\ast}, \cdots, u_n^{\ast})^T$ satisfying $P(u^{\ast}) = u^{\ast}$, $P_{u_i^{\ast}} = u_i^{\ast}$, $i = 1, \cdots, n$. Thus

and we have

then $u^{\ast}$ is the unique equilibrium point in FSDNNs (2.1).

We prove the unique equilibrium point $u^{\ast}$ is finite-time stable as follows.

Let $y_i(t) = x_i(t) - u_i^{\ast}$, for $0 < \delta < \varepsilon$, and solution $x(t, t_0, \varphi)$ satisfies initial condition $x_i(s) = \varphi_i (s), s\in (-\infty, 0], \ i = 1, \cdots, n,$ such that $\|\varphi-u^*\| < \delta.$ From FSDNNs (2.1), we have

Case $(a)$. When $-\infty < \theta \leq 0$, $t > 0$, $t+\theta \leq 0$,

Case $(b)$. When $-\infty < \theta \leq 0$, $t > 0$, $t+\theta\geq 0$,

When $-\infty < \theta \leq 0$, $t > 0$, it follows from (3.4) and (3.5) that

Substituting (3.6) into (3.3), we have

where

By Lemma 2.5 and from (3), we obtain

By Definition 2.6, the equilibrium point of FSDNNs (2.1) is FTS. This proves the theorem. □

Theorem 3.2. Under the Assumption $A_1$, for $t\in[0, T]$, $(0 < T < +\infty)$, if

the solution of FSDNNs (2.1) is GMLS.

Proof. Let $x(t) = (x_1(t), \cdots, x_n(t))^T$ and $y(t) = (y_1(t), \cdots, y_n(t))^T$ be two solutions of FSDNNs (2.1), satisfying initial conditions $x_i(s) = \varphi_i(s)$ and $y_i(s) = \psi_i(s)$, $s \in (-\infty, 0]$.

Let $z_i(t) = x_i(t) - y_i(t)$, $i = 1, \cdots, n$. From FSDNNs (2.1), we obtain

Similar to the derivation of (3.6), we can have

Substituting (3.11) into (3.10), we obtain

where

By Lemma 2.4, it follows from (3.12) that $\sum\limits_{i = 1}^n |z_i(t)| \leq M(\varphi - \psi)E_\alpha(-\underline{\eta} t^\alpha)$, or $\|x-y\|\leq M(\varphi - \psi)E_\alpha(-\underline{\eta} t^\alpha).$ Moreover, $M(\varphi - \psi) \geq 0$, $M(0) = 0$, where $E_\alpha(\cdot)$ denotes the one-parameter Mittag-Leffler function. Thus, by Definition 2.7, the solution of FSDNNs (2.1) is GMLS. □

Remark. Theorem 3.1 presents sufficient condition for FTS of FSDNNs when

and Theorem 3.2 presents sufficient condition for GMLS of FSDNNs when

Thus, the parameter

is the dividing quantity of two kinds of stability of FSDNNs, and we can choose the appropriate parameter and theorem to determine the stability of FSDNNs according to the requirements of practical applications and problems.

4.   Numerical example

In this section, two numerical examples are presented to illustrate our theorems.

We consider a class of FSDNNs as follows:

where $w_j(\theta)$ is a nondecreasing bounded variation function on the interval of $(-\infty, 0]$, and we set

Thus, we see that

Example 4.1. Let the parameters and the functions in FSDNNs (4.1) be: $\alpha = 0.8, \ d_{1} = 0.1, \ d_{2} = 0.11, \ a_{11} = 0.01,$ $a_{12} = 0.015, \ a_{21} = -0.01,$ $a_{22} = 0.015, \ b_{11} = 0.012, \ b_{12} = 0.02, \ b_{21} = -0.0125,$ $b_{22} = 0.015.\ I_{1} = 0.6, \ I_{2} = 0.4, \ f_{j}(x_{j}(t)) = 2.5\sin(x_{j}(t)), \ j = 1, 2.$

Let $F_j = 2.5, k_j = 1, j = 1, 2,$ $\varepsilon = 0.02, \delta = 0.015,$ $t_0 = 2.5, H = 1.5, t\in J = [t_0, t_0+H] = [2.5, 4].$ We can see Assumptions $A_{1}$ are satisfied. It can be obtained by calculation:

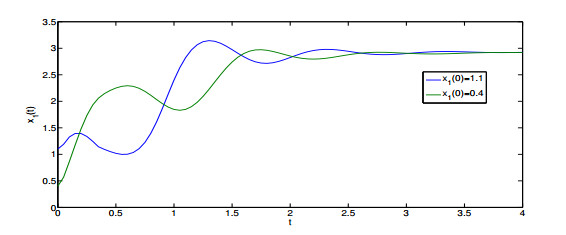
which satisfies the conditions in Theorem 3.1. According to Theorem 3.1, there exists a unique equilibrium point in FSDNNs (4.1), which is FTS. According to simulation, we can see the trajectories of state variables in Example 4.1 (Figures 1 and 2).

Example 4.2. Let the parameters and the functions in FSDNNs (4.1) be: $\alpha = 0.8, \ d_{1} = 2.5, \ d_{2} = 3, \ a_{11} = 0.3, \ a_{12} = 0.5,$ $a_{21} = -0.4,$ $a_{22} = 0.15, \ b_{11} = 0.2, \ b_{12} = 0.2, \ b_{21} = -0.25,$ $b_{22} = 0.35.\ I_{1} = 0, 3,$ $I_{2} = 0, 2, \ f_{j}(x_{j}(t)) = \frac{1}{10}\sin(x_{j}(t)),$ $j = 1, 2.$

Let $F_j = \dfrac{1}{10}, \ k_j = 1, \ j = 1, 2$.

We can see Assumptions $A_{1}$ are satisfied and the parameters are

which satisfy the conditions in Theorem 3.2. According to Theorem 3.2, FSDNNs (4.1) are GMLS. According to simulation, we can see the trajectories of state variables in Example 4.2 (Figures 3 and 4). Obviously, the simulation and Theorem 3.2 are consistent.

5.   Conclusions

In this paper, we mainly investigate the stability of a class of FSDNNs and obtain the sufficient conditions for FTS and GMLS of FSDNNs, i.e., Theorems 3.1 and 3.2, which comprise discrete and continously distributed delays. Specially, when the parameter satisfies $\sum \limits_{j = 1}^{n}(|a_{ji}| + |b_{ji}|k_i)F_i - d_i > 0, i = 1, \cdots, n,$ the solution of FSDNNs is FTS, and when the parameter satisfies $\sum \limits_{j = 1}^{n}(|a_{ji}| + |b_{ji}|k_i)F_i - d_i < 0, i = 1, \cdots, n,$ the solution of FSDNNs is GMLS. The results are complementary, which provides a new basis for further expanding NNs research and practical applications.

The conclusion is obtained by using Riemann-Liouville fractional-order derivatives in this paper. However, our next research endeavor will involve investigating FTS and GMLS with Caputo fraction-order derivatives. Moreover, this paper provides new useful tools and methods to investigate the stability problem of other types of NNs with S-type distributed delays, such as the stability of fractional-order Cohen-Grossberg NNs with S-type distributed delays and fractional-order BAM NNs with S-type distributed delays.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors acknowledge The Ministry of Education's Cooperative Education Program for Industry-University Cooperation (220505876312732), The Science Research Key Project of Shaoxing University (2023LG017), The Science Research Project of Shaoxing University Yuanpei College (KY2022C03), and The Science Project of Zhejiang Educational Department (Y202145903).

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.