Global co-dynamics of viral infections with saturated incidence

1.   Introduction

Human viral infections such as human immunodeficiency virus (HIV), hepatitis B virus (HBV), hepatitis C virus (HCV), ebola virus, influenza A virus (IAV), influenza B virus (IBV), chikungunya virus (CHIKV), middle east respiratory syndrome coronavirus (MERS-CoV), human T-cell lymphotropic virus (HTLV), zika virus (ZIKV), dengue virus (DENV), and severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) are a global health concern. It is possible for a person to be infected with two or more types of viruses (or different viral strains) simultaneously or successively. This situation is defined as viral coinfection ^[1]. Examples of viral coinfections include: HIV and viral hepatitis ^[2]; HBV and HCV ^[3]; different strains of SARS-CoV-2 ^[4]; and SARS-CoV-2 and HBV ^[5].

Many researchers are interested in mathematical modeling of viral infections within the host. The development of antiviral drug therapies and vaccines, the understanding of the dynamics of viral infection and the immune system's response to viruses, and the identification of the minimum number of variables needed to analyze experimental data and explain biological phenomena are all made possible by mathematical models. In ^[6], a basic model for viral single-infection within a host has been formulated. A mathematical model that describes competition of two virus types (or virus variants) for uninfected cells can be given as ^[7]:

where $H(t)$, $Y(t)$, $Z(t)$, $C(t)$, and $B(t)$ are the concentrations of the uninfected cells, infected cells by virus type $C$, infected cells by virus type $B$, free virus type $C$ particles, and free virus type $B$ particles at time $t$, respectively.

Examples of viruses (or virus strains) which compete for the same target cells including:

● Respiratory viruses: Such SARS-CoV-2 and IAV which compete for the epithelial cells in the respiratory tract ^[1,8]. Human rhinovirus, respiratory syncytial virus, human enterovirus, human metapneumovirus, influenza A/B viruses, parainfluenza virus, coronavirus, and human bocavirus and adenovirus are among the respiratory viruses that have been found to be able to participate in simultaneous infections ^[9].

● Chronic viruses: HIV and HTLV infect the CD4$^{+}$ T cells, often known as "helper" T cells which play a central role in immune system ^[10]. HBV and HCV target hepatocytes in the human liver ^[11].

● Victor-born infections: Both DENV and CHIKV infect the monocytes ^[12].

● Virus strains: As new mutants continue to evolve, the genotypes of the same virus in infected hosts that are wild-type and mutant overlap ^[13]. A number of recombinant viral strains of worldwide epidemiologic significance have been observed as a result of co-occurring HIV infections, which has significant implications for our knowledge of HIV transmission and the development of the AIDS vaccine ^[14]. Recent research has shown that coinfection can act as a catalyst for the recombination of distinct SARS-CoV-2 subtypes ^[15].

Several mathematical models have been developed for viral coinfections including: HIV-1/HTLV-I ^[16], SARS-CoV-2/IAV ^[8,17], SARS-CoV-2/HTLV-I^[18], SARS-CoV-2/HIV-1 ^[19], HIV-1/HBV ^[20] and HIV-1/HCV ^[21]. Moreover, coinfection with two viral strains have been modeled in several works (see e.g., ^[13,22,23]).

In the case of HIV infection, there is no medicine to cure acquired immune deficiency syndrome (AIDS) completely to date, but highly active antiretroviral therapy (HAART) has been used for the last two decades to treat HIV patients, and it has been found successful in suppressing HIV replication and reconstituting the immune system in the human body. However, using HAART cannot eradicate the virus completely ^[24]. An important reason is that HIV provirus can reside in latently infected cells, which live long, but can be activated to produce virus by relevant antigens, ^[25]. It has been reported in ^[26] that a coexistence of two HIV strains in the latent reservoirs is possible.

Models (1.1)–(1.5) operate under the premise that, upon entry of the virus into an uninfected cell, the cell becomes infected and produces new mature viruses. It is commonly recognized that the infection of free viruses into uninfected cells and the generation of new mature viruses often do not occur instantly but develop over a period of time ^[27]. Regarding HIV infection, it is believed that the duration between HIV entry into an uninfected cell and the production of new mature HIV particles is around 0.9 days ^[28]. Consequently, the delay finds extensive application in several models of viral infection, which are essential for studying biological processes that are more like reality (see e.g., ^[29,30,31]).

The infection rate is one important factor influencing the propagation of viruses ^[32]. A number of mathematical models of two competing viruses (or strains of viruses) that have appeared in the literature (see, e.g., ^[7,23]) include the assumption that bilinear incidence determines the infection rate. In this case, the infection rate per target cell and per virus is a constant. This situation implies that the rate of infection is precisely proportional to the product of the concentrations of the viruses $B$ (or $C$) interacting with uninfected cells ($H$), a phenomenon known as the mass-action principle. The incidence rate is linear in each variable over the entire range of $B$ (or $C$) and $H$. However, as reported in ^[33], experiments have demonstrated that the infection rate of microparasitic infections generally increases with the parasite dose and typically exhibits a sigmoidal shape. The law of mass action, for instance, will not apply if the concentration of viruses is higher than the concentration of uninfected cells. In such a scenario, an increase in virus concentration will not result in a rise in infection. A sublinear response in virus concentration might arise from saturation at high virus concentrations, where the infectious fraction is high, leading to a high likelihood of exposure ^[34]. The goal of the saturation incidence function in epidemiology is to characterize the variance in infection force brought on by the crowding impact of infectious ^[35]. It is important to note that the models of two competing viruses with bilinear incidences shown in ^[7,23] do not exhibit the co-existence equilibrium. As a result, these models might not be able to explain situations in which two chronic viruses co-exist, such as HIV, HTLV, HBV, and HCV.

Papers ^[27,36,37] studied two strain viral dynamics models with saturated incidence. Nevertheless, these models do not incorporate latently infected cells. Further, the maturation delay of newly released virions was not included in the model given in ^[27]. Furthermore, it has not been addressed how saturation affects the conditions in which the two strains coexist. Thus, the aim of this study is to construct and analyze mathematical models that characterize the co-dynamics of two competing viruses (or virus variants) with saturated incidence and latently infected cells. The paper's novelty resides in the following aspects:

A1: Two models (one with discrete delay and the other with distributed delay) have been developed to describe the co-dynamics of two competing viruses within a host.

A2: Three kinds of discrete (or distributed) time delays have been incorporated into the model: (ⅰ) The formation delay of latently infected cells; (ⅱ) the activation delay of latently infected cells; and (ⅲ) the maturation delay of newly released virions.

A3: The non-negativity and boundedness of the model's solutions are rigorously analyzed, confirming that the presented models are both mathematically well-posed and biologically plausible.

A4: Global stability analysis has been presented for both models.

A5: Conditions for the co-existence of competing viruses that target the same host cells have been established.

A6: The theoretical findings have been validated through numerical simulations.

Our proposed model could be valuable for modeling the competitive transmission dynamics of different strains of COVID-19, such as Omicron and Delta ^[38,39].

The paper is organized as follows: Sections 2 and 4 focus on formulating the two models, proving the non-negativity and boundedness of the model's solutions, determining the model's equilibria and threshold parameters, and establishing the global stability of the equilibria. Section 3 contains comparison results. Section 5 presents numerical simulations for the model with discrete delays, while Section 6 summarizes our findings and outlines future perspectives.

2.   Model with discrete-time delays

2.1.   Model formulation

In this section, we develop a two-virus co-dynamics model with a saturated incidence rate, latently infection cells, and six discrete-time delays as follows:

where $L$ and $E$ are the concentrations of the latent cells infected by virus types $C$ and $B$, respectively. The activation and death rate constants of compartments ($L$, $E$) are denoted by ($\delta_{L}$, $\delta_{E})$ and ($\eta_{L}$, $\eta_{E}$), respectively. The terms $\frac{\gamma_{HC}HC} {1+\psi_{C}C}$ and $\frac{\gamma_{HB}HB}{1+\psi_{B}B}$ represent saturated incidence for virus types $C$ and $B$, respectively, where $\psi_{C}\geq0$ and $\psi_{B}\geq0$ are saturation parameters. Saturated incidence leads to bilinear incidence when $\psi_{C} = \psi_{B} = 0$. There are three types of time delays:

(ⅰ) $\omega_{1}$ and $\omega_{4}$, the formation times of latent cells infected by viruses type $C$ and $B$, respectively;

(ⅱ) $\omega_{2}$ and $\omega_{5}$, the activation times of latent cells infected by viruses type $C$ and $B$, respectively;

(ⅲ) $\omega_{3}$ and $\omega_{6}$, the maturation times of newly released virions type $C$ and $B$, respectively.

The factor $e^{-\alpha_{i}\omega_{i}}$, $i = 1, 2, \ldots, 6$ represents the probability of survival of a cell or virion throughout the delay time $[t-\omega_{i}, t]$, and $\alpha_{i} > 0$.

The initial conditions for system (2.1)–(2.7) are:

where

and $\mathbb{C}$ is the Banach space of continuous functions mapping the interval $[-\omega^{\ast}, 0]$ into $\mathbb{R} _{\geq0}$ with

for $\ell_{i}\in \mathbb{C}$. System (2.1)–(2.7), with initial conditions (2.8), has a unique solution ^[40,41].

Remark 1. The production rate of uninfected cells has been represented by a variety of functions in virology literature, including: constant, $\phi$, saturated, $\frac{\phi V}{1+\epsilon V}$ ^[42], exponential, $\phi e^{-\epsilon V}$ ^[43], decreasing, $\frac{\phi \epsilon}{\epsilon+V}$ ^[44], and general, $H\Xi(H)$ ^[45], where $\epsilon$ is constant and $\Xi$ is a general function.

2.2.   Preliminaries

Proposition 1. The solutions of system (2.1)–(2.7) with initial (2.8) are nonnegative and ultimately bounded.

Proof. We have that

Hence, $H(t) > 0$ for all $t\geq0$. Moreover, for all $t\in \lbrack0, \omega^{\ast}],$ we have:

Hence, $L(t), Y(t), E(t), Z(t), C(t), B(t)\geq0$ for all $t\in \lbrack0, \omega ^{\ast}].$ Through recursive argumentation, we get $L(t), Y(t), E(t), Z(t), C(t), B(t)$ for all $t\geq0$. Therefore, $H, L, Y, E, Z, C$ and $B$ are nonnegative.

The nonnegativity of the system's solution implies that

Let us define

then

where

It follows that

Let

then,

where

Thus

From Eq (2.3) we get

Equation (2.5) implies that

Similarly from Eqs (2.6) and (2.7) we get

This completes the proof.□

Based on Proposition 1 we can show that

is positively invariant for system (2.1)–(2.7).

2.3.   Equilibria

We calculate the model's equilibria and deduce the conditions of their existence. Any equilibrium point $\Xi = (H, L, Y, E, Z, C, B)$ satisfies

System (2.9) admits four equilibria.

(Ⅰ) Infection-free equilibrium, $\Xi_{0} = (H_{0}, 0, 0, 0, 0, 0, 0)$, where $H_{0} = \phi/\eta_{H}$.

(Ⅱ) Virus type $C$ single-infection equilibrium $\Xi_{1} = (H_{1}, L_{1, } Y_{1}, 0, 0, C_{1}, 0),$ where

and

which represents the basic reproduction number for virus type $C$ single-infection. It follows that, $\Xi_{1}\, \ $exists if $\Re_{1} > 1$.

(Ⅲ) Virus type $B$ single-infection equilibrium $\Xi_{2} = (H_{2}, 0, 0, E_{2, } Z_{2}, 0, B_{2})$, where

and

which represents the basic reproduction number for virus type $B$ single-infection. Therefore, $\Xi_{2}\, \ $exists if $\Re_{2} > 1.$

(Ⅳ) Coexistence equilibrium $\Xi_{3} = (H_{3}, L_{3, }Y_{3}, E_{3}, Z_{3}, C_{3}, B_{3})$, where

and

Clearly, $\Xi_{3}$ exists when $\Re_{3} > 1$ and $\Re_{4} > 1$.

Remark 2. We note that we have calculated the basic reproduction numbers $R_{1}$ and $R_{2}$ from the existence's conditions of equilibria $\Xi_{1}$ and $\Xi_{2}$, respectively. It is worth noting that $R_{1}$ and $R_{2}$ can also be calculated using the next-generation matrix method of van den Driessche and Watmough ^[46] or by analyzing the local stability of the infection-free equilibrium.

2.4.   Global stability analysis

In this part, we use the Lyapunov function construction approach described in ^[47] to demonstrate the global asymptotic stability of all equilibria. Let $\Lambda_{j}(H, L, Y, E, Z, C, B)$ be a Lyapunov function candidate and $\tilde{\Omega}_{j}$ be the largest invariant subset of

Define a function

as

We denote

Theorem 1. Consider (2.1)–(2.7) and suppose that $\Re_{1}\leq1$ and $\Re_{2}\leq1$, then $\Xi_{0}$ is globally asymptotically stable (GAS).

Proof. Define

It is seen that, $\Lambda_{0} > 0$ for all $H, L, Y, E, Z, C, B > 0,$ and $\Lambda _{0}(H_{0}, 0, 0, 0, 0, 0, 0) = 0$. We calculate $\frac{d\Lambda_{0}}{dt}$ along the solutions of system (2.1)–(2.7) as:

From Eqs (2.1)–(2.7), we obtain

Then, we collect terms as:

Using the equilibrium condition $\phi = \eta_{H}H_{0}$, we get

Since $\Re_{1}\leq1$ and $\Re_{2}\leq1,$ then $\frac{d\Lambda_{0} }{dt}\leq0$ for all $H, C, B > 0$. In addition $\frac{d\Lambda_{0}}{dt} = 0$ when $H = H_{0}$ and $C = B = 0.$ The solutions of system (2.1)–(2.7) tend to $\tilde{\Omega}_{0}$ ^[40] where $C = B = 0$. Thus, $\dot{C} = \dot{B} = 0$ and from Eqs (2.6) and (2.7) we have

Then from Eqs (2.3) and (2.5) we get

Therefore, $\tilde{\Omega}_{0} = \left \{ \Xi_{0}\right \}$ and applying LaSalle's invariance principle (LIP) ^[48], we obtain that $\Xi_{0}$ is GAS.□

Theorem 2. Consider (2.1)–(2.7) and suppose that $\Re_{1} > 1$ and $\Re_{4}\leq1$, then $\Xi_{1}$ is GAS.

Proof. Define $\Lambda_{1}$ as:

We calculate $\frac{d\Lambda_{1}}{dt}$ as:

So, we get

Simplifying Eq (2.12), and using the equilibrium conditions for $\Xi_{1}$:

we obtain

Using the following equalities:

where $i = 1, 3,$ we get

Since $\Re_{4}\leq1$ then, $\frac{d\Lambda_{1}}{dt}\leq0$ for all $H, L, Y, E, Z, C, B > 0$. Moreover, $\frac{d\Lambda_{1}}{dt} = 0$ when $H = H_{1}$, $L = L_{1}$, $Y = Y_{1}$, $C = C_{1}$, and $B = 0.$ The solutions of system (2.1)–(2.7) tend to $\tilde{\Omega}_{1}$ which includes elements with $B = 0$ which gives $\dot{B} = 0$. From Eq (2.7) we get

Then from Eq (2.5) we have

Hence, $\tilde{\Omega}_{1} = \left \{ \Xi \text{ _{1} }\right \}$ and $\Xi_{1}$ is GAS using LIP.□

Theorem 3. Consider (2.1)–(2.7) and suppose that $\Re_{2} > 1$ and $\Re_{3}\leq1$, then $\Xi_{2}$ is GAS.

Proof. Consider

We calculate $\frac{d\Lambda_{2}}{dt}$ as:

Then simplifying Eq (2.14) and using the equilibrium conditions for $\Xi_{2}$:

and using the following equalities:

where $i = 2, 3,$ we get:

Since $\Re_{3}\leq1$ then, $\frac{d\Lambda_{2}}{dt}\leq0$ for all $H, L, Y, E, Z, C, B > 0$. Further, $\frac{d\Lambda_{2}}{dt} = 0$ when $H = H_{2},$ $E = E_{2, }\ Z = Z_{2},$ $B = B_{2}$ and $C = 0.$ The solutions of system (2.1)–(2.7) tend to $\tilde{\Omega}_{2}$ which contains elements with $C = 0$, which gives $\dot{C} = 0$. Equation (2.6) implies

Then, Eq (2.3) becomes

Therefore, $\tilde{\Omega}_{2} = \left \{ \Xi \text{ _{2} }\right \}$. Applying LIP, we get $\Xi_{2}$ is GAS.□

Theorem 4. Consider (2.1)–(2.7) and suppose that $\Re_{3} > 1$ and $\Re_{4} > 1$, then $\Xi_{3}$ is GAS.

Proof. Define

We calculate $\frac{d\Lambda_{3}}{dt}$ as:

Then collecting terms of Eq (2.16) and using the equilibrium conditions for $\Xi_{3}$:

and equalities (2.13) and (2.15), we get:

So, we get $\frac{d\Lambda_{3}}{dt}\leq0$ for all $H, L, Y, E, Z, C, B > 0$. Further, $\frac{d\Lambda_{3}}{dt} = 0$ when $H = H_{3},$ $L = L_{3}, \ Y = Y_{3},$ $E = E_{3}, \ Z = Z_{3}$, $C = C_{3}$ and $Z = Z_{3}.$ Therefore, $\tilde{\Omega} _{3} = \left \{ \Xi \text{ _{3} }\right \}$. Applying LIP, we find that $\Xi _{3}$ is GAS. □

We have compiled the existence and global stability conditions for each equilibrium point in Table 1 based on the aforementioned results.

3.   Model with distributed-time delays

In the preceding section, we assumed that:

(ⅰ) The formation time of each latently infected cell is fixed;

(ⅱ) The activation time of each latently infected cell is fixed;

(ⅲ) The maturation time of each newly released viron is fixed. It is evident from a mathematical and biological perspective that the distributed delay (where the time delay is taken as a random variable drawn from the probability distribution function) is more appropriate in real-world scenarios than the discrete delay. There have been several studies on virus infection models with distributed-time delays (see ^[27,31]).

3.1.   Model formulation

In this section, we extend the two-virus model presented in the previous section by including six distributed-time delays as:

Here $\omega$ is random taken from probability distributed function $P_{i}(\omega)$ during time interval $[0, \varkappa_{i}],$ where $\varkappa _{i}$ is the limit superior of the delay period, $i = 1, 2, \ldots, 6$. We have the assumptions:

(ⅰ) The probability of uninfected cells touched by viral types $C$ and $B$ at time $t-\omega$ surviving $\omega$ time units and becoming latent infected cells at time $t$ are represented by factors $P_{i}(\omega)e^{-\alpha_{i}\omega}$, where $i = 1$ and $4$, respectively.

(ⅱ) The probability that latent cells infected with viruses type $C$ and $B$ at time $t-\omega$ would survive $\omega$ time units and become active are shown by factors $P_{i}(\omega)e^{-\alpha_{i}\omega}$, where $i = 2$ and $5$, respectively.

(ⅲ) The probability that immature viruses type $C$ and $B$ at time $t-\omega$ survive $\omega$ time units to become mature viruses at time $t$ are shown by factors $P_{i}(\omega)e^{-\alpha_{i}\omega}$, where $i = 3$ and $6$, respectively.

Function $P_{i}(\omega)$, $i = 1, 2, \ldots, 6$ satisfy $P_{i}(\omega) > 0$ and

where $n > 0$. Let us denote that

This implies that $0 < \mathcal{P}_{i}\leq1$. The initial conditions for system (3.1)–(3.7) are the same as given by Eq (2.8), where $\omega^{\ast} = \max \{ \varkappa_{1}, \varkappa_{2}, \ldots, \varkappa_{6}\}$.

3.2.   Preliminaries

Proposition 2. The solutions of system (3.1)–(3.7) with initial (2.8) are nonnegative and ultimately bounded.

Proof. We have that

Hence, $H(t) > 0$ for all $t\geq0$. Moreover, for all $t\in \lbrack0, \omega^{\ast}],$ we have:

Hence, $L(t), Y(t), E(t), Z(t), C(t), B(t)\geq0$ for all $t\in \lbrack0, \omega^{\ast}].$ Through recursive argumentation, we get $L(t), Y(t), E(t), Z(t), C(t), B(t)$ for all $t\geq0$. Therefore, $H, L, Y, E, Z, C$ and $B$ are nonnegative.

The nonnegativity of the system's solution implies that:

Let us define

Then

It follows that

Let

then,

It follows that

From Eq (3.3) we get

Equation (3.5) implies that

Similarly from Eqs (3.6) and (3.7) we get

Based on Proposition 2 we can show that $\Gamma$ is positively invariant for system (3.1)–(3.7).□

3.3.   Equilibria

We calculate the model's equilibria deduce when they exist. Any equilibria point $\Xi = (H, L, Y, E, Z, C, B)$ satisfies:

System (3.8) admits four equilibria.

(Ⅰ) Infection-free equilibrium, $\Xi_{0} = (H_{0}, 0, 0, 0, 0, 0, 0)$, where $H_{0} = \phi/\eta_{H}$.

(Ⅱ) Virus type $C$ single-infection equilibrium $\Xi_{1} = (H_{1}, L_{1, } Y_{1}, 0, 0, C_{1}, 0),$ where

where, $\mathcal{R}_{1}$ is given by

It follows that, $\Xi_{1}\, \ $exists if $\mathcal{R}_{1} > 1$.

(Ⅲ) Virus type $B$ single-infection equilibrium $\Xi_{2} = (H_{2}, 0, 0, E_{2, } Z_{2}, 0, B_{2})$, where

where

Therefore, $\Xi_{2}\, \ $exists if $\mathcal{R}_{2} > 1$.

(Ⅳ) Coexistence equilibrium $\Xi_{3} = (H_{3}, L_{3, }Y_{3}, E_{3}, Z_{3}, C_{3}, B_{3})$, where

where

Clearly, $\Xi_{3}$ exists when $\mathcal{R}_{3} > 1$ and $\mathcal{R}_{4} > 1$.

3.4.   Global stability analysis

Let $\Theta_{j}(H, L, Y, E, Z, C, B)$ be a Lyapunov function candidate and $\tilde{\Upsilon}_{j}$ be the largest invariant subset of

We denote

and

Theorem 5. For system (3.1)–(3.7) suppose that $\mathcal{R}_{1}\leq1$ and $\mathcal{R}_{2}\leq1$, then $\Xi_{0}$ is GAS.

Proof. Define

It is seen that, $\Theta_{0} > 0$ for all $H, L, Y, E, Z, C, B > 0,$ and $\Theta_{0}(H_{0}, 0, 0, 0, 0, 0, 0) = 0$. Calculate $\frac{d\Theta_{0}}{dt}$ as:

Collecting terms and using the equilibrium condition $\phi = \eta _{H}H_{0}$, we get:

Since $\mathcal{R}_{1}\leq1$ and $\mathcal{R}_{2}\leq1,$ then $\frac{d\Theta_{0}}{dt}\leq0$ for all $H, C, B > 0$. In addition $\frac {d\Theta_{0}}{dt} = 0$ when $H = H_{0}$ and $C = B = 0.$ The solutions of system (3.1)–(3.7) tend to $\tilde{\Upsilon}_{0}$ ^[40] which includes elements with $C = B = 0$. Thus, $\dot{C} = \dot{B} = 0$ and from Eqs (3.6) and (3.7) we have:

Then from Eqs (3.3) and (3.5) we get

Therefore, $\tilde{\Upsilon}_{0} = \left \{ \Xi_{0}\right \}$ and applying LIP, we obtain that $\Xi_{0}$ is GAS. □

Theorem 6. For system (3.1)–(3.7) suppose that $\mathcal{R}_{1} > 1$ and $\mathcal{R}_{4}\leq1$, then $\Xi_{1}$ is GAS.

Proof. Let us formulate a Lyapunov function $\Theta_{1}$ as:

We calculate $\frac{d\Theta_{1}}{dt}$ as:

Simplifying Eq (3.9) and using the equilibrium conditions for $\Xi_{1}$:

and the following equalities:

where $i = 1, 3,$ we get:

Since $\mathcal{R}_{4}\leq1$ then, $\frac{d\Theta_{1}}{dt}\leq0$ for all $H, L, Y, E, Z, C, B > 0$. Moreover, $\frac{d\Theta_{1}}{dt} = 0$ when $H = H_{1}$, $L = L_{1}$, $Y = Y_{1}$, $C = C_{1}$, and $B = 0.$ The solutions of system (3.1)–(3.7) tend to $\tilde{\Upsilon}_{1}$ which includes elements with $B = 0$ which gives $\dot{B} = 0$. From Eq (3.7) we get

Then from Eq (3.5) we have

Hence, $\tilde{\Upsilon}_{1} = \left \{ \Xi \text{ _{1} }\right \}$ and $\Xi _{1}$ is GAS using LIP.□

Theorem 7. For system (3.1)–(3.7) suppose that $\mathcal{R}_{2} > 1$ and $\mathcal{R}_{3}\leq1$, then $\Xi_{2}$ is GAS.

Proof. Consider

We calculate $\frac{d\Theta_{2}}{dt}$ as:

Then simplifying Eq (3.11) and using the equilibrium conditions for $\Xi_{2}$:

and the following equalities:

where $i = 2, 3,$ we get:

Since $\mathcal{R}_{3}\leq1$ then, $\frac{d\Theta_{2}}{dt}\leq0$ for all $H, L, Y, E, Z, C, B > 0$. Further, $\frac{d\Theta_{2}}{dt} = 0$ when $H = H_{2},$ $E = E_{2, }\ Z = Z_{2},$ $B = B_{2}$ and $C = 0.$ The solutions of system (3.1)–(3.7) tend to $\tilde{\Upsilon}_{2}$ which contains elements with $C = 0$, which gives $\dot{C} = 0$. Equation (3.6) implies

Then, Eq (3.3) becomes

Therefore, $\tilde{\Upsilon}_{2} = \left \{ \Xi \text{ _{2} }\right \}$. Applying LIP, we get $\Xi_{2}$ is GAS.□

Theorem 8. For system (3.1)–(3.7) assume that $\mathcal{R}_{3} > 1$ and $\mathcal{R}_{4} > 1$, then $\Xi_{3}$ is GAS.

Proof. Define a function $\Theta_{3}$ as:

We calculate $\frac{d\Theta_{3}}{dt}$ as:

Then collecting terms of Eq (3.13) and using the equilibrium conditions for $\Xi_{3}$:

and equalities (3.10) and (3.12), we get:

So, we get $\frac{d\Theta_{3}}{dt}\leq0$ for all $H, L, Y, E, Z, C, B > 0$. Further, $\frac{d\Theta_{3}}{dt} = 0$ when $H = H_{3},$ $L = L_{3}, \ Y = Y_{3},$ $E = E_{3}, \ Z = Z_{3}$, $C = C_{3}$ and $Z = Z_{3}.$ Therefore, $\tilde{\Upsilon} _{3} = \left \{ \Xi \text{ _{3} }\right \}$. Applying LIP, we find that $\Xi _{3}$ is GAS. □

4.   Comparison results

We compare our model (2.1)–(2.7) with the following model, where saturation is ignored:

Model (4.1)–(4.7) has only three equilibria:

(Ⅰ) Infection-free equilibrium, $\tilde{\Xi}_{0} = (\tilde{H}_{0}, 0, 0, 0, 0, 0, 0)$, where $\tilde{H}_{0} = \phi/\eta_{H}$.

(Ⅱ) Virus type $C$ single-infection equilibrium $\tilde{\Xi}_{1} = (\tilde{H}_{1}, \tilde{L}_{1}, \tilde{Y}_{1}, 0, 0, \tilde{C}_{1}, 0),$ where

(Ⅲ) Virus type $B$ single-infection equilibrium $\tilde{\Xi}_{2} = (\tilde {H}_{2}, 0, 0, \tilde{E}_{2}, \tilde{Z}_{2}, 0, \tilde{B}_{2})$, where

We note that the basic reproduction numbers $\Re_{1}$ and $\Re_{2}$ do not depend on the saturation parameters $\psi_{B}$ and $\psi_{C}$. It should be noted that the co-existence equilibrium is absent from this model and a number of other models that have been published in the literature (see, for example, ^[7,23]). Consequently, one of the elements that can lead to the coexistence of the two rival viruses is saturation.

Remark 1. When $\psi_{B} = 0$ and $\psi_{C} = 0$, then $\Re_{3} = \frac {\Re_{1}}{\Re_{2}}$ and $\Re_{4} = \frac{\Re_{2}}{\Re1}.$

Corollary 1. Consider (4.1)–(4.7) then:

(ⅰ) If $\Re_{1}\leq1$ and $\Re_{2}\leq1$, then $\tilde{\Xi}_{0}$ is GAS;

(ⅱ) If $\Re_{1} > 1$ and $\Re_{1}\geq \Re_{2}$, then $\tilde{\Xi}_{1}$ is GAS;

(ⅲ) If $\Re_{2} > 1$ and $\Re_{2}\geq \Re_{1}$, then $\tilde{\Xi}_{2}$ is GAS.

Next we show the range of the saturation parameters $\psi_{B}$ and $\psi_{C}$ that ensure the coexistence equilibrium will appear.

4.1.   Coexistence conditions of the two competing viruses in terms of the saturation parameters $\psi_{B}$ and $\psi_{C}$

We have shown that the coexistence equilibrium $\Xi$$_{3}$appears when $\Re_{3} > 1$ and $\Re_{4} > 1$. When all other parameters are fixed, $\Re_{3}\ $and $\Re_{4}$ are functions of $\psi_{B}$ and $\psi_{C}$, respectively. In addition, we have

Hence, if $\Re_{1} > 1$ and $\Re_{2} > 1$, then $\Re_{3}\ $and $\Re_{4}$ are increasing functions of $\psi_{B}$ and $\psi_{C}$, respectively.

Let us compute $\psi_{B}^{\min}$ and $\psi_{C}^{\min}$ such that

Then the coexistence conditions are

We have two cases:

(ⅰ) If $\Re_{2} > \Re_{1} > 1$, then

(ⅱ) If $\Re_{1} > \Re_{2} > 1$, then

We see that model (4.1)–(4.7) does not include the scenario where two types of viruses coexist. It was noted that several patients in the studies reported in ^[14] had co-infections with two different strains of HIV. As such, ignoring saturation might not provide an adequate description of the coinfection dynamics between the two types of viruses (or strains). This lends credence to the notion of including saturation in the coinfection model of two types of viruses, in which the coexistence of two types of viruses is seen. Chronic viral coinfections can also result from other reasons, including immune response ^[16] and superinfection ^[49].

4.2.   Models under the influence of antiviral treatment

To demonstrate why it is crucial to incorporate latently infected cells and time delays in our proposed model, we examine the model (2.1)–(2.7) in the presence of reverse transcriptase inhibitors (RTIs), a class of medications that may effectively block the free viral infection of target cells. Let $\epsilon_{C}\in \lbrack0, 1]$ and $\epsilon_{B}\in \lbrack0, 1]\ $be the efficacies of RTIs for the viruses types $C$ and $B$, respectively ^[22]. Under the effect of RTIs, model (2.1)–(2.7) becomes:

The basic reproduction numbers of system (4.9)–(4.15) are:

We now compute the drug efficacies $\epsilon_{C}$ and $\epsilon_{B}$, which make $\Re_{1}^{\epsilon_{C}}\leq1$ and $\Re_{1}^{\epsilon_{B}}\leq1$, and then stabilize system (4.9)–(4.15) about the infection-free equilibrium $\Xi _{0}$

If the latently infected cells in model (4.9)–(4.15) are disregarded, we get

and the basic reproduction numbers of model (4.18)–(4.22) are given by

We determine the drug efficacies $\epsilon_{C}$ and $\epsilon_{B}$, which make $\bar{\Re}_{1}^{\epsilon_{C}}\leq1$ and $\bar{\Re}_{1}^{\epsilon_{B}}\leq1$ and stabilizes the infection-free equilibrium of system (4.18)–(4.22) as:

Since $0 < e^{-\alpha_{2}\omega_{2}}\leq1$ and $0 < e^{-\alpha_{5}\omega_{5}} \leq1$, then

Hence, $\Re_{1}^{\epsilon_{C}} < \bar{\Re}_{1}^{\epsilon_{C}}$ and $\Re _{2}^{\epsilon_{B}} < \bar{\Re}_{2}^{\epsilon_{B}}$ and thus eliminating the latently infected cells from the two-virus co-dynamics model would lead to an overestimation of the basic reproduction numbers. By comparing Eqs (4.16), (4.17) and (4.23), (4.24) we get that $\epsilon _{C}^{\min} < \bar{\epsilon}_{C}^{\min}$ and $\epsilon_{B}^{\min} < \bar{\epsilon }_{B}^{\min}$. Thus, in order to keep the system at the infection-free equilibrium and remove the two types of viruses from the body, fewer treatment efficacies will be needed when utilizing a model with latently infected cells.

Similar to the discussion, one can find that the presence of time delays reduces the basic reproduction numbers. Then, when using a model with time delays, fewer treatment efficacies will be needed to keep the system at infection-free equilibrium and remove the two types of viruses from the body.

5.   Numerical simulations

We perform numerical simulation for the model with discrete-time delays (2.1)–(2.7) in this section. We use the values of the parameters given in Table 2. Using MATLAB's dde23 solver, the system of DDEs is numerically solved.

5.1.   Stability of the equilibria

In this subsection, we fix the delay parameters as: $\omega_{1} = 1,$ $\omega_{2} = 0.8,$ $\omega_{3} = 0.6,$ $\omega_{4} = 0.4,$ $\omega_{5} = 0.2,$ and $\omega_{6} = 0.1.$ Moreover, we solve system (2.1)–(2.7) with the following initial conditions:

I-1: $(H(u), L(u), Y(u), E(u), Z(u), C(u), B(u)) = (800, 5, 1.5,100, 1, 1, 0.6)$,

I-2: $(H(u), L(u), Y(u), E(u), Z(u), C(u), B(u)) = (600, 10, 3,150, 2, 1.5, 1),$ I-3: $(H(u), L(u), Y(u), E(u), Z(u), C(u), B(u)) = (300, 15, 4.5,200, 3, 2, 1.4)$,

where $u\in \lbrack-1, 0].$

Selecting the values of $\gamma_{HC}$, $\gamma_{HB}$, $\psi_{C}$ and $\psi_{B}$ leads to the following plans:

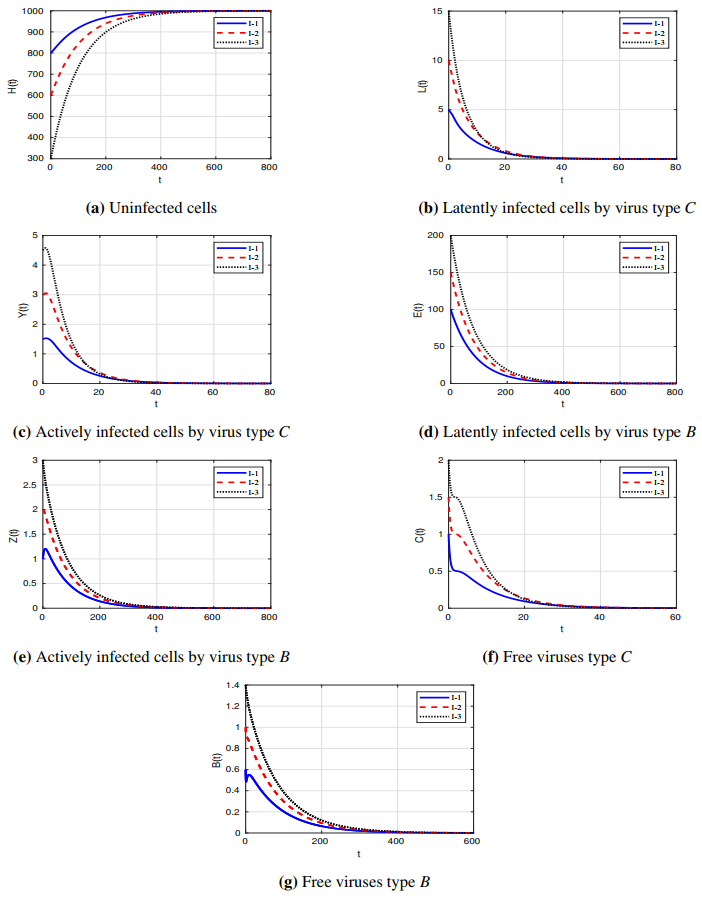
Plan 1. $\gamma_{HC} = 0.001$, $\gamma_{HB} = 0.0003$ and $\psi_{C} = \psi_{B} = 0.01$. These values yield $\Re_{1} = 0.38 < 1$ and $\Re_{2} = 0.11 < 1$. Figure 1 displays that the solutions initiating with I-1, I-2 and I-3 converge the equilibrium $\Xi_{0} = (1000, 0, 0, 0, 0, 0, 0)$. This illustrates the global asymptotic stability of $\Xi_{0}$ proven Theorem 1. Both virus types $C$ and $B$ will finally be eradicated in this case.

Plan 2. $\gamma_{HC} = 0.005$, $\gamma_{HB} = 0.0005$ and $\psi_{C} = \psi_{B} = 0.01$. For such choice, we have $\Re_{1} = 1.92 > 1$ and $\Re_{4} = 0.10 < 1$. It is evident from Figure 2 that for the three selected initial values, the system's solutions converge to the equilibrium $\Xi_{1} = (530.5, 17.47, 5.5, 0, 0, 1.8, 0)$. This shows that $\Xi_{1}$ is GAS, according to Theorem 2. This situation represents the infection of virus type $C$ only.

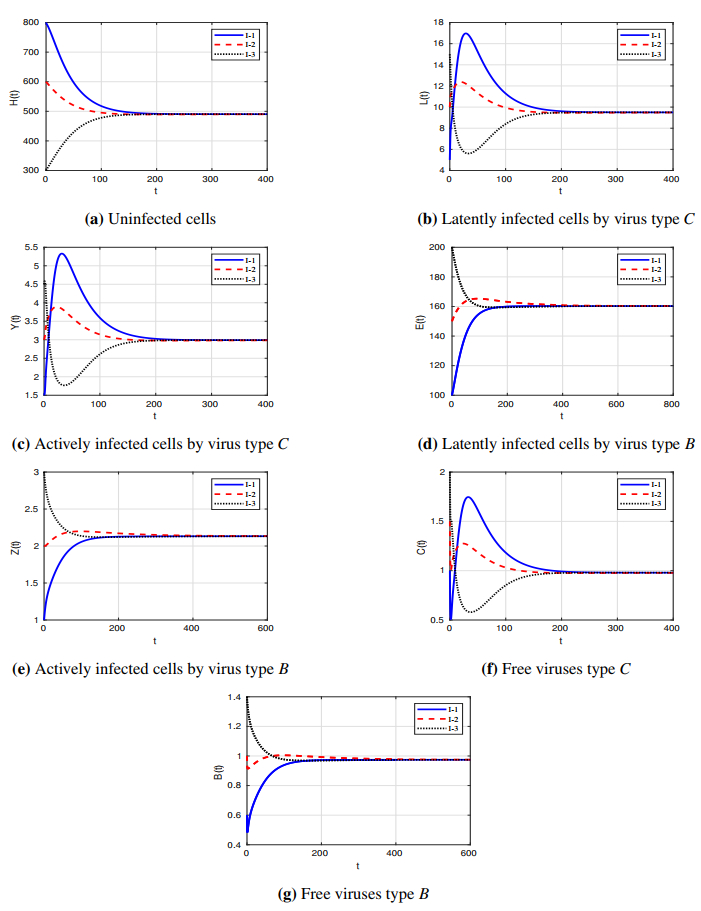
Plan 3. $\gamma_{HC} = 0.001, \gamma_{HB} = 0.005$ and $\psi _{C} = \psi_{B} = 0.01$. These parameters provide that $\Re_{2} = 1.91 > 1$ and $\Re _{3} = 0.20 < 1$. In Figure 3, we display that the equilibrium $\Xi _{2} = (531.73, 0, 0,294.91, 3.92, 0, 1.79)$ is reached for all initials I-1, I-2 and I-3. This shows that $\Xi_{2}$ is GAS, according to Theorem 3. This situation represents the infection of virus type $B$ only.

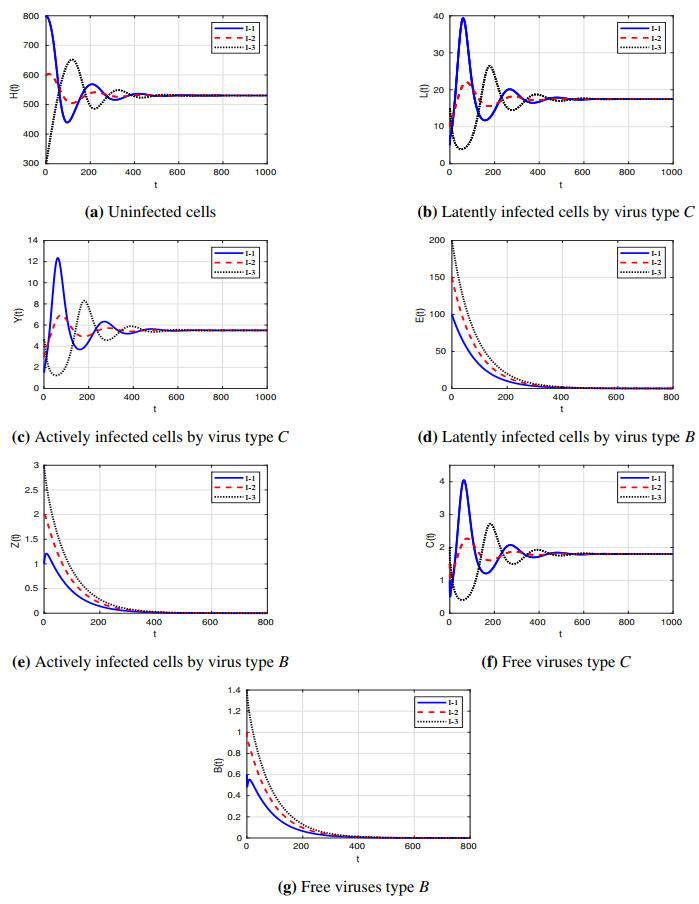
Plan 4. $\gamma_{HC} = \gamma_{HB} = 0.01$ and $\psi_{C} = \psi_{B} = 0.9$. For such values, we get that $\Re_{3} = 2.35 > 1$ and $\Re_{4} = 2.34 > 1$. From Figure 4, we can see that the equilibrium $\Xi_{3} = (490.25, 9.5, 2.99,160.3, 2.12, 0.98, 0.97)$ is reached for the three selected initials. This illustrates the global asymptotic stability of $\Xi_{3}$ proven Theorem 1. This case show the coexistence of the two type of viruses.

5.2.   Impact of saturation on viral co-dynamics

In this part we show the effect of the saturation parameters $\psi_{B}$ and $\psi_{C}$ on viral co-dynamics. Here, we fix the delay parameters as

We have two situations to identify the values of $\psi_{B}$ and $\psi_{C}$ that lead to the coexistence of the two types of viruses:

Situation (Ⅰ). $\Re_{2} > \Re_{1} > 1$. In this case we choose

Then we get

Therefore, $\Xi _{3}$ exists when

Situation (Ⅱ). $\Re_{1} > \Re_{2} > 1$. We take

Then we get

It follows that, $\Xi$$_{3}$exists when

Now we show the effect of the saturation parameters $\psi_{B}$ and $\psi_{C}$ on the solutions of model (2.1)–(2.7) in case of Situation (Ⅱ). We consider the initial condition

I-4: $(H(u), L(u), Y(u), E(u), Z(u), C(u), B(u)) = (600, 10, 3, 80, 1, 1, 0.5), \; \; u\in \lbrack-\omega^{\ast}, 0].$

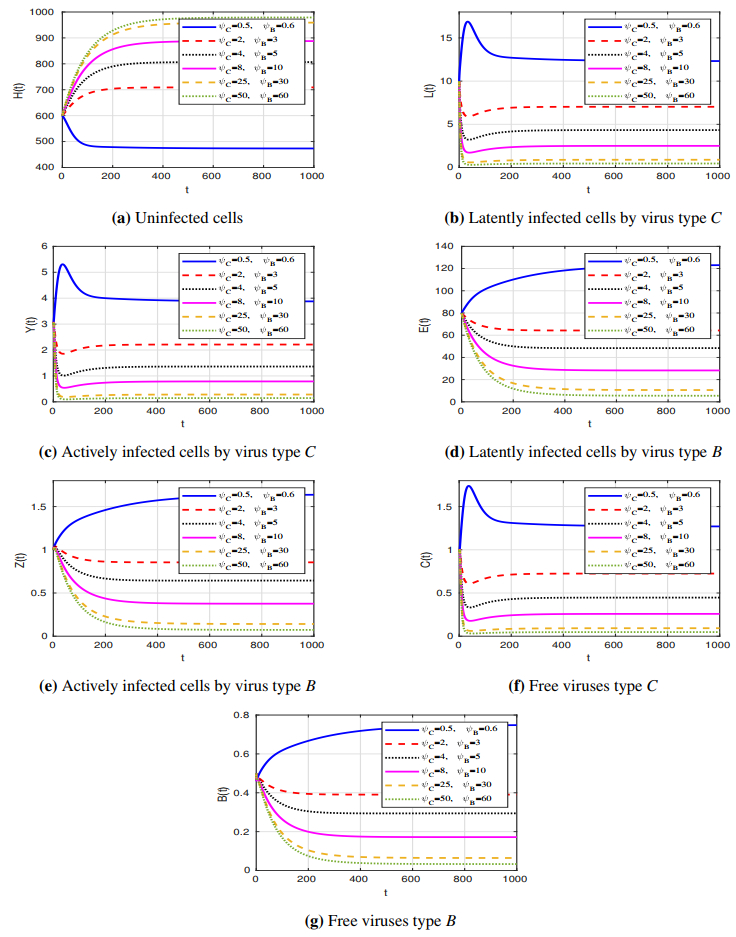
Figure 5 shows the effect of saturation on the viral co-dynamics. We note that a rise in $\psi_{C}$ and $\psi_{B}$ results in a drop in the incidence rate between uninfected cells and the two types of viruses. This decrease is followed by an increase in the concentration of uninfected cells and a decrease in the concentrations of infected cells and free viruses. The infection-free equilibrium $\Xi_{0}$ will not be maintained by raising $\psi_{B}$ and $\psi_{C}$ because the basic reproduction numbers $\Re_{1}$ and $\Re_{2}$ are independent of the saturation parameters.

5.3.   Effect of the delay parameters on viral co-dynamics

In this subsection, we analyze the impact of time delay parameters $\omega _{i},$ $i = 1, 2, \ldots, 6$ on the co-dynamics of the two types of viruses. We fix the parameters that $\gamma_{HC} = 0.009,$ $\gamma_{HB} = 0.08$, and $\psi_{C} = \psi _{B} = 0.9$. We consider the scenarios given in Table 3. We solve the system (2.1)–(2.7) under the following initial condition:

I-5: $(H(u), L(u), Y(u), E(u), Z(u), C(u), B(u)) = (600, 10, 3,150, 2, 1.5, 1), \; \; u\in \lbrack-\omega^{\ast}, 0].$

The numerical results are shown in Figure 6. It is observed that time delays might lead to a notable rise in the quantity of uninfected cells and a decrease in the quantity of remaining compartments. We note that, $\Re_{1}$ and $\Re_{2}$ given by Eqs (2.10) and (2.11) depend on $\omega_{i},$ $i = 1, 2, \ldots, 6$ when all other parameters are fixed. We observe from Table 4 that $\Re_{1}$ and $\Re_{2}$ decrease if $\omega_{i}$ increases; hence, the stability of $\Xi_{0}$ will be changed.

Now, we need to calculate the critical values of the delay parameters $\omega_{i}$, $i = 1, 2, \ldots, 6$ that make the system stable around the equilibrium point $\Xi_{0}$. Let $\omega_{C} = \omega_{1} = \omega_{2} = \omega_{3}$ and $\omega_{B} = \omega_{4} = \omega_{5} = \omega_{6}$, and we write $\Re_{1} (\omega_{C})$ and $\Re_{2}(\omega_{B})$ as:

Clearly, when all other parameters are fixed, $\Re_{1}$ and $\Re_{2}$ are decreasing functions of $\omega_{C}$ and $\omega_{B}$, respectively. Let us calculate $\omega_{C}^{\min}$ and $\omega_{B}^{\min}$ such that $\Re _{1}(\omega_{C}^{\min}) = 1$ and $\Re_{2}(\omega_{B}^{\min}) = 1$ as:

Consequently,

Therefore, $\Xi_{0}$ is GAS when $\omega_{C}\geq \omega_{C}^{\min}$ and $\omega_{B}\geq \omega_{B}^{\min}$. Using the values of the parameters in Table 2, we get $\omega_{C} = 2.1229$ and $\omega_{B} = 1.9160$. It follows that:

(ⅰ) If $\omega_{C}\geq2.1229$ and $\omega_{B}\geq1.9160,$ then $\Re_{1} (\omega_{C})\leq1$ and $\Re_{2}(\omega_{B})\leq1$, and then $\Xi_{0}$ is GAS.

(ⅱ) If $\omega_{C} < 2.1229$ and/or $\omega_{B} < 1.9160,$ then $\Re_{1} (\omega_{C}) > 1$ and/or $\Re_{2}(\omega_{B}) > 1$. In this case, $\Xi_{0}$ will lose its stability. We see that the effects of antiviral medications and time delays can be comparable. This can help scientists develop novel therapies that lengthen time delays in cases of coinfection between the $C$ and $B$ viruses.

6.   Conclusions and future perspectives

In this work, we examined a mathematical model of the population co-dynamics of two types of viruses (or virus variants) infecting the same target cells. The infection rate is given by the saturated incidence. The model included the latently infected cells. Three kinds of discrete (or distributed) time delays were incorporated into the model:

(ⅰ) The formation delay of latently infected cells;

(ⅱ) The activation delay of latently infected cells;

(ⅲ) The maturation delay of newly released virions.

First, we demonstrated nonnegativity and boundedness, which are the key characteristics of the solutions. Second, we proved that the model admits four equilibria. We derived four threshold parameters, which decide whether the model's equilibria exist and are globally asymptotically stable. We demonstrated the global asymptotic stability for every equilibrium point using the Lyapunov approach. We used a numerical method to solve the model, and then we displayed the findings graphically. We found a correlation between the theoretical and numerical results. Our findings are contrasted with models that do not account for saturation incidence, latently infected cells, or time delays. We have the following observations:

● When saturation is not present, only one type of virus with the highest reproduction number can survive in equilibrium. The rivalry between two virus kinds for shared resources leads to the survival of just one viral type with the highest reproduction number. In our proposed model with saturated incidence, two types of viruses can coexist in equilibrium. We can think of this situation as follows: Two viral kinds can coexist because saturation incidence lowers infection rates, which also lessens rivalry between the two virus types. We established conditions under which these types of viruses can coexist. The coexistence conditions are formulated in terms of saturation constants.

● The presence of latently infected cells and/or time delays reduces the basic reproduction numbers. Then, when using a model with latently infected cells and/or time delays, fewer treatment efficacies will be needed to keep the system at infection-free equilibrium and remove the two types of viruses from the body. This may help scientists develop novel therapies that lengthen time delays.

● Our results indicate that saturated, latently infected cells and time delay are essential elements of the two-virus model that cannot be ignored.

Our study's main flaw is that we were unable to use actual data to estimate the model's parameter values. The following are the causes:

(ⅰ) Genuine data on two-virus infections is lacking;

(ⅱ) Comparing our findings to a limited number of genuine studies may not be particularly reliable;

(ⅲ) It can be challenging to collect real data from patients who have two virus infections.

Our proposed model can be extended by considereing different incidene rate forms, such as: Beddington-DeAngelis incidence $\frac{\gamma_{HV} HV}{1+\psi_{V}V+\psi_{H}H}$ ^[56]; Crowley-Martin incidence $\frac{\gamma_{HV}HV}{(1+\psi_{V}V)(1+\psi_{H}H)}$ ^[57]; Hattaf-Yousf incidence $\frac{\gamma_{HV}HV}{\psi_{0} +\psi_{V}V+\psi_{H}H+\psi_{VH}HV}$, ^[58]; general incidence $\xi(H, V)$ ^[59], where $V$ is the concentration of the viruses, $\psi_{0}, \psi_{V}, \psi_{H}, \psi_{VH}\geq 0$ and $\xi$ is a general function. Investigating the memory effect on the dynamics of our model using fractional differential equations (FDEs) sounds like a fascinating direction ^[60]. FDEs can capture non-local and memory-dependent effects, which are often crucial in viological systems ^[61], and epidemical systems ^[62,63]. Additionally, we would like to contrast the results with real data from people who have the infection.

We observe that active-particle methods have recently been used to model epidemics through a detailed description of the immune competition at the cellular scale. Specifically, the competition between the primary virus and variants has been considered, see ^[64,65]. This approach has not yet considered comorbidities. We believe that our approach can contribute to include different types of viruses within the model proposed in ^[64,65].

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflicts of interest.