1.
Introduction
Fractional calculus has been a popular topic among scholars for almost three centuries. It is a branch of mathematical analysis that deviates from classical calculus and extends the concepts of derivatives and integrals to fractional-order. Differential equations under fractional-order are known as fractional differential equations (FDEs), and they are used in various domains of real-world phenomena problems. It can be distinguished based on various criteria, such as the linearity of the equation (linear or nonlinear). Its distinguishing traits, including flexibility, memory, and hereditary properties, make it a powerful tool for modeling, evaluating, and regulating complex systems in many disciplines, including applied science and engineering (see the books of Podlubny [1], Hilfer [2], Kilbas, et al. [3], and Diethelm [4]), and a comprehensive work on boundary value problems with fractional-order [5].
It is well known that fractional derivative operators (FDOs) are often defined in the sense of fractional integral operators (FIOs) under the gamma function. In the field of fractional calculus, various definitions of fractional derivatives have emerged, such as Riemann-Liouville (RL), Caputo, Hadamard, Erdélyi-Kober, Katugampola, Hilfer, proportional, and so on, and each has different uses. The RL-FIOs and RL-FDOs concerning a function ψ are studied as in [3]. These were used to develop the ψ-Hilfer-FDO [6]. One FDO gaining attention is the proportional FDO [7]. This operator has exponential functions in the kernels, which are more advantageous than other fractional operators. For work regarding qualitative theory on proportional FDEs, see [8,9,10,11,12,13,14] and references cited therein. In parallel, the k-gamma function defines and develops fractional calculus concepts, especially the k-RL-FIOs and the k-RL-FDOs [15,16]. After that, in 2018, the (k,ψ)-RL fractional operators were proposed by [17]. Later, in 2021, Kucche and Mali proposed FDO under the (k,ψ)-Hilfer type [18], which attracted many scholars' curiosity. There are some other intriguing pieces, including those of Aljaaidi et al. [19], which proved some properties of the (k,ψ)-proportional fractional operator ((k,ψ)-PFO) and presented a new technique to investigate the k-Pólya-Szegö integral inequalities in 2021. In the same year, Boucenna et al. [20] studied the existence and uniqueness of results and a numerical technique for the Caputo proportional fractional Cauchy-type problem. While a numerical technique based on the decomposition formula was used to solve the fractional Caputo-Katugampola derivative operator [21], the analytical solutions of fractional differential equations are difficult and complex, so numerical techniques are popular for solving these equations [22,23,24]. Sudsutad et al. [25] developed the (k,ψ)-Hilfer-PFO, which cooperates the (k,ψ)-proportional fractional derivative of RL's and Caputo's senses ((k,ψ)-RL-PFDO / (k,ψ)-Caputo-PFDO). They constructed the Laplace transform concerning a function ψ of the proposed operator and applied it to solving the initial value Cauchy-type problems. In the extension, a Cauchy-type problem for FDEs is commonly defined as an initial value problem in which the goal is to find a function corresponding to the equation and the provided beginning conditions. Furthermore, numerous researchers have popularly expressed their robust findings by using a realistic application of fractional calculus in the context of diverse operators for various real-world issues such as medicine, engineering, electrical, science, and finance. For example, in 2019, Qureshi et al. [26] proposed the fractional modeling of the blood ethanal concentration using three fractional operators such as Caputo, Atangana-Baleanu, and Caputo-Fabrizio with the real data. In 2021, Norouzi and N'Guérékata [27] studied FDEs in the sense of ψ-Hilfer-FDO and used the financial crisis as an application. In 2022, Awadalla et al. [28] used a FDE in the sense of ψ-Caputo-FDO to study the model of drug concentration. In 2024, Wanassi and Torres [29] utilized the blood alcohol model as an application of the fractional analysis based on the ψ-Caputo-FDO. We refer the reader for more works in [30,31,32,33,34,35,36]. On the other hand, Ulam stability is a popularly efficient tool for ensuring that the approximate solutions generated by numerical methods remain close to the exact solutions. Numerous researchers have provided this to analyze the mathematical stability of solutions in various fields, including fractional calculus and control theory. It was initially created by Ulam in 1940 [37]. The following year, Hyer designed the Ulam-Hyers stability [38]. Presently, stability in the context of the Ulam's type has developed into various stabilities, such as Ulam-Hyers-Rassias stability [39] and Ulam-Hyer-Mittag-Leffler (UH-ML) stability, which are extensions of Ulam stability that incorporates the Mittag-Leffler function [40], and so on.
Motivated by the works [9,20,25], our major goals are to investigate the qualitative results and numerical approximations for the following Cauchy-type problem under (k,ψ)-Caputo-PFDO
where Ca,kDα,ρ;ψ is the (k,ψ)-Caputo-PFDO of α and f∈C([a,b]×R,R). To the best of our knowledge, this problem has yet to be considered. Specifically, we provide an extended Gronwall inequality under the (k,ψ)-PFOs to establish bounds on solutions, which is crucial in stability analysis. We investigate the existence and uniqueness of results utilizing the standard fixed point theory of Banach's and Leray-Schauder's types. Moreover, various UH–MT stability results are studied utilizing nonlinear functional analysis techniques. In addition, we develop a novel numerical approach based on a decomposition formula for solving the Cauchy-type problems. In the end, a blood alcohol level problem is presented as an application to the proposed system. The following structure governs the remaining sections of this work: In Sect. 2, we introduce the fundamental principles and some properties of the (k,ψ)-PFDO and the (k,ψ)-PFIO. The required lemmas utilized throughout this paper are also presented. In addition, we look at the extended Gronwall inequality under the aforementioned operators. The qualitative results for a Cauchy-type problem are accomplished in the remaining sections. In Section 3, we investigate the existence of the solution using a fixed point theory of Leray-Schauder's type, while the uniqueness of the solution is proved using Banach's contraction mapping principle. Then, a variety of UH-ML stability results are established to ensure the results. In Section 4, we demonstrate the numerical approach based on a decomposition formula for solving the Cauchy-type problems under the (k,ψ)-Caputo-PFDO. Some illustrative examples, particularly the blood alcohol level problem, are provided to help the accuracy of the theoretical results found in Section 5. In the final section, we outline the course of our work.
2.
Preliminaries
Suppose that C([a,b],R) is the Banach space of the continuous function u on [a,b] supplemented with the supremum norm ‖u‖=supτ∈[a,b]{|u(τ)|}. The space of the n-times absolutely continuous function u on [a,b] is defined by ACn([a,b],R)={u:[a,b]→R;u(n−1)∈AC([a,b],R)} and Lp([a,b],R) is the Banach space of all Lebesgue measurable g:[a,b]→R supplemented with ‖g‖Lp<+∞. Assume that ψ:[a,b]→R is a strictly increasing continuous function under ψ′(τ) not equal zero. For ease of calculation through this work, we provide a notation as follows:
Now, we recall some definitions and lemmas of the (k,ψ)-PFDO and the (k,ψ)-PFIO that will be applied in this work.
Definition 2.1. ([25]). Let α, k∈R+, 0<ρ≤1, and f∈L1([a,b],R). Then, the (k,ψ)-RL-PFIO of α of f is defined by
where Γk(z)=∫∞0sz−1e−skkds, z∈C, Re(z)>0 and
Definition 2.2. ([25]). Let α, k∈R+, 0<ρ≤1, f∈C([a,b],R), ψ(τ)∈Cn([a,b],R) with ψ′(τ)≠0, and n=1,2,…, such that n=⌊α/k⌋+1. Then, the (k,ψ)-RL-PFDO for α of f is defined by
where kDn,ρ;ψ=kDρ;ψkDρ;ψ⋯kDρ;ψ⏟ntimes and kD1,ρ;ψf(τ)=kDρ;ψf(τ)=(1−ρ)f(τ)+kρf′(τ)ψ′(τ).
Definition 2.3. ([25]). Let α, k∈R+, 0<ρ≤1, f∈Cn(J,R), ψ(τ)∈Cn([a,b],R) with ψ′(τ)≠0, and n∈1,2,…, such that n=⌊α/k⌋+1. Then, the (k,ψ)-Caputo-PFDO for α of f is defined by
Next, we give some important properties that are applied in this work.
Lemma 2.4. ([25]). Let α, δ∈R+∪{0}, k, η∈R+, 0<ρ≤1, ω∈R, ω/k>−1, and n=⌊ω/k⌋+1. Then,
(i) a,kIα,ρ;ψ[ρkΨωk−1ψ(τ,a)]=Γk(ω)ραkΓk(ω+α)ρkΨω+αk−1ψ(τ,a).
(ii) Ca,kDα,ρ;ψ[ρkΨωk−1ψ(τ,a)]=ραkΓk(ω)Γk(ω−α)ρkΨω−αk−1ψ(τ,a). Particularly, for m=0,1,…,n−1, we obtain Ca,kDα,ρ;ψ[ρkΨmψ(τ,a)]=0.
(iii) a,kIα,ρ;ψ[a,kIδ,ρ;ψf(τ)]=a,kIδ+α,ρ;ψf(τ)=a,kIδ,ρ;ψ[a,kIα,ρ;ψf(τ)].
(iv) Ca,kDω,ρ;ψ(a,kIη,ρ;ψf(τ))=a,kIη−ω,ρ;ψf(τ), where ω∈R+, ω<k, and η>nk.
(v) a,kIα,ρ;ψ(Ca,kDα,ρ;ψf(τ))=f(τ)−n∑i=1ρkΨn−ik−1ψ(τ,a)(ρk)n−i(n−i)!kDn−i,ρ;ψf(a), α∈(n−1,n].
Now, we prove an extended Gronwall inequality under the (k,ψ)-PFOs, and its properties are analyzed in the below Theorem.
Theorem 2.5. (An Extended (k,ψ)-Proportional Fractional Gronwall Inequality). Suppose that α>0, k>0, ρ∈(0,1], and ψ∈C1([a,b],R) is an increasing function so that ψ′(τ) not equal zero for every τ∈[a,b]. Assume that the following hypotheses hold:
(H1) The two non-negative functions u(τ) and v(τ) are locally integrable on [a,b];
(H2) The function w(τ) is a non-decreasing, non-negative, and continuous function defined on [a,b] such that w(τ)≤w∗∈R.
If
then, for any τ∈[a,b], we obtain
Proof. First, we define an operator
From (2.5), we have u(τ)≤v(τ)+Au(τ). By applying the monotonicity of the operator A, we obtain inequalities as follows:
By applying iterative technique, n=1,2,…, which yields that u(τ)≤∑n−1i=0Aiv(τ)+Anu(τ), τ∈[a,b], where A0v(τ)=v(τ). Next, we claim that
and Anu(τ)→0 as n→∞ for any τ∈[a,b]. If n=1, we get that the inequality (2.7) holds. Next, assume that the inequality (2.7) is held under n=m, that is
If n=m+1, using the induction procedure, we have
Since the function w(τ) is a non-decreasing, w(s)≤w(τ), for every s≤τ and taking z=(ψ(s)−ψ(r))/(ψ(τ)−ψ(r)), then
Since w∈C([a,b],R), then there is w∗∈R such that w(τ)≤w∗, for all τ∈[a,b], one has
Since 0≤eρ−1kρ(ψ(τ)−ψ(r))≤1, and u is non-negative and locally integrable on [a,b]. Hence, u is bounded on [a,b], and there is Mu∈R such that |u(τ)|≤Mu. The inequality (2.8) can be obtained
Applying the Stirling's formula, that is n!∼√2πn(n/e)n, into (2.9) with (2.2), we obtain that
where θ, ρ, k, α∈R+. This yields that, if n→∞, we obtain that Anu(τ)→0. Then,
The inequality (2.4) is achieved.
Corollary 2.6. Let α, k∈R+, 0<ρ≤1, and ψ∈C1([a,b],R) be an increasing function such that ψ′(τ)≠0, τ∈[a,b]. Let u(τ) and v(τ) be two non-negative locally integrable functions on [a,b], and w(τ)≡M≥0. If
then,
Corollary 2.7. Assume all conditions in Theorem 2.5 are held, and the function v(τ) is non-decreasing on τ∈[a,b]. Hence, we obtain the following inequality:
where
Proof. From the inequality (2.12) with the help of the non-decreasing property of v(τ), that is v(s)≤v(τ) for any τ∈[a,b], we obtain that
Since 0≤eρ−1kρ(ψ(τ)−ψ(s))≤1, which yields that
Applying Definition 2.7, the inequality (2.13) is obtained.
3.
Existence and stability results
Here, we analyze the qualitative results for the proposed problem, including existence and uniqueness results and various results for Ulam's stability. First, we prove an integral equation is equivalent to the proposed problem (1.1).
Lemma 3.1. Suppose that f∈C([a,b]×R,R), α, ρ∈(0,1] and k∈R+. Then, the proposed problem (1.1) can be stated equivalently as
Proof. Let u be a solution to the problem (1.1). Taking the operator a,kIα,ρ;ψ into the proposed problem (1.1) and applying (v) in Lemma 2.4, which implies that
By using u(a)=ua into (3.2) and inserting the obtained value into itself, we get the achieved (3.1).
On the other hand, by applying (ii) and (iv) in Lemma 2.4 into (3.1), it follows that
The proof is done.
3.1. Existence and uniqueness results
From Lemma 3.1, we provide the operator Q:C([a,b],R)→C([a,b],R) by
The first result is based on the Banach's contraction mapping [41].
Theorem 3.2. Suppose that α, ρ∈(0,1], k∈R+, and f∈C([a,b]×R,R). Suppose that
(A1) There is a positive real constant L such that
Then, the proposed problem (1.1) has a unique solution on [a,b], provided that
Proof. Assume that Br1:={u∈C([a,b],R):‖u‖≤r1} is a closed bounded and convex subset of C([a,b],R), where the radius r1 corresponds to the following condition
We prove that (ⅰ) QBr1 is bounded, i.e. QBr1⊆Br1 and (ⅱ) Q is a contraction.
Step (i). We show that QBr1⊆Br1.
For any u∈Br1 with the property of 0≤eρ−1kρ(ψ(τ)−ψ(a))≤1 and the assumption (A1), we have
This implies that QBr1⊆Br1.
Step (ii). We show that Q is a contraction.
Let u, v∈C([a,b],R). Then, for every τ∈[a,b], we get
Then, ‖Qu−Qv‖≤(ψ(b)−ψ(a))αkραkΓk(α+k)L‖u−v‖. Since the condition (3.4) holds, which implies that Q has a contraction property. Hence, by [41], Q has a unique fixed point. Then, there is a unique solution of the proposed problem (1.1) on [a,b].
Next, the existence result is achieved by utilizing the fixed point theory of Leray-Schauder's [42].
Theorem 3.3. Suppose that
(A2) There are a continuous non-decreasing function h:[a,∞)→(0,∞) and a function ϕ∈C([a,b],R+) such that the following condition:
(A3) There is a number N∈R+ such that the following inequality:
Then the proposed problem (1.1) has at least one solution on J.
Proof. Assume that Q is given by (3.3). The technique is done in three phases.
Step (i). We show that Q maps bounded sets (balls) into bounded sets in C([a,b],R).
Assume that Br2={u∈C([a,b],R):‖u‖≤r2} is a bounded ball in C([a,b],R) and ‖ϕ‖=supτ∈[a,b]|ϕ(τ)|. By applying the fact of 0≤eρ−1kρ(ψ(τ)−ψ(a))≤1 and (A2), for every τ∈[a,b], which yields that
Step (ii). We show that Q maps bounded sets into equicontinuous sets of C([a,b],R).
Assume that τ1, τ2∈[a,b] with τ1<τ2, and u∈Br2. Hence
Clearly, the right-hand side of (3.5) tends to zero independently of u∈Br2 as τ2→τ1. Then, by utilizing the Arzelá-Ascoli theorem, we get that Q:C([a,b],R)→C([a,b],R) is completely continuous.
Step (iii). We show that there exists an open set D⊆C([a,b],R) with u≠λQ(u), 0<λ<1 and u∈∂D.
Assume that u∈C([a,b],R) is the solution of u=λQu, 0<λ<1. For any τ∈[a,b], we obtain that
Then
Consequently,
In view of (A3), there exists N such that ‖u‖≠N. Let us take D={u∈C([a,b],R):‖u‖<N} and U=D∩Br2.
Finally, Q:¯U→C([a,b],R) is continuous and completely continuous. Using the choice of U, there is no 0∈∂U so that u=λ(Qu) for some 0<λ<1. Hence, by [42], we obtain that Q has a fixed point u∈¯U, which is a solution of the problem (1.1).
3.2. Ulam-Mittag-Leffler stability results
Next, we establish various of UH–ML stability results for the proposed problem (1.1).
Definition 3.4. The proposed problem (1.1) is called UH-ML stable, if there is a number Cf∈R+ so that for any ϵ>0 and w∈C([a,b],R+) of
there exists u∈C([a,b],R+) of the proposed problem (1.1) under the assumption
Definition 3.5. The proposed problem (1.1) is called generalized UH-ML stable, if there is a function Gf∈C(R+,R+) via Gf(0)=0, such that for any ϵ>0 and w∈C([a,b],R+) of
there exists u∈C([a,b],R+) of the proposed problem (1.1) under the assumption
Definition 3.6. The proposed problem (1.1) is called Ulam-Hyers-Rassias-Mittag-Leffler (UHR-ML) stable with respect to another function Φ(τ), if there is a number CfΦ∈R+ so that for any ϵ>0 and w∈C([a,b],R+) of
there exists u∈C([a,b],R+) of the proposed problem (1.1) under the assumption
Definition 3.7. The proposed problem (1.1) is called generalized UHR-ML stable concerning function Φ(τ) so that for any ϵ>0 and w∈C([a,b],R+) of
there exists u∈C([a,b],R+) of the proposed problem (1.1) under the assumption
Remark 3.8. Assume that w∈C([a,b],R) is the solution of (3.6) if and only if there is uw∈C([a,b],R), which depends on w, so that (i). |uw(τ)|≤ϵ, τ∈[a,b]; (ii). Ca,kDα,ρ;ψw(τ)=f(τ,w(τ))+uw(τ), τ∈[a,b].
Remark 3.9. Assume that w∈C([a,b],R) is the solution of (3.10) if and only if there is vw∈C([a,b],R), that is depends on w, such that (i). |vw(τ)|≤ϵΦ(τ), τ∈[a,b]; (ii). Ca,kDα,ρ;ψz(τ)=f(τ,w(τ))+vw(τ), τ∈[a,b].
Theorem 3.10. Suppose that f∈C([a,b]×R,R), (A1), and (3.2) hold. Then, the proposed problem (1.1) is UH–ML stable and consequently generalized UH-ML stable on [a,b].
Proof. Let ϵ>0 and w∈C([a,b],R) be a solution of (3.6). From (ii) in Remark 3.8, we have
Applying Lemma 3.1, the solution of the problem (3.14) is
Let u∈C([a,b],R) be a solution of (1.1). Hence,
By applying the property |u−v|≤|u|+|v|, τ∈J with (3.15)-(3.16), one has
By using the property 0≤eρ−1kρ(ψ(τ)−ψ(a))≤1, (H1), and (i) in Remark 3.8, the inequality (3.17) can be written
From Theorem 2.5 and Corollary 2.7, which implies that
By setting a constant Cf:=(ψ(b)−ψ(a))αkραkΓk(α+k) and κf:=Lρ−αk, which yields that
Hence, the proposed problem (1.1) is UH–ML stable. In addition, by setting Gf(ϵ)=Cfϵ under the condition Gf(0)=0, then
Therefore, the solution of the proposed problem (1.1) is generalized UH-ML stable.
Now, we give the required assumption that is used in Theorem 3.11.
(P1) Suppose that Φ∈C([a,b],R) is a non-decreasing function. There exists χΦ>0 so that
Theorem 3.11. Suppose that f∈C([a,b]×R,R), (A1), and (3.2) hold. Then, the proposed problem (1.1) is UHR-ML stable and consequently generalized UHR-ML stable on [a,b].
Proof. Let ϵ>0 and w∈C([a,b],R) be the solution of (3.6). From (ii) in Remark 3.9, it follows form
From Lemma 3.1, the solution of the problem (3.19) is defined by
Let u∈C([a,b],R) be the solution of (1.1). It follows that
By applying the property |u−v|≤|u|+|v|, for τ∈[a,b] with (3.20)-(3.21), which yields that
By using 0≤eρ−1kρ(ψ(τ)−ψ(a))≤1, (A1), (P1), and (i) in Remark 3.9, the inequality (3.22) can be written
Applying Theorem 2.5 and Corollary 2.7, which implies that
By choosing CfΦ:=χΦ and κf:=Lρ−αk, then
Thus, the proposed problem (1.1) is UHR-ML stable. Additionally, by setting ϵ=1, one has
Then, the solution of the proposed problem (1.1) is generalized UHR-ML stable.
4.
Numerical approach
Now, we construct an approximation form for the (k,ψ)-PFDO in Caputo's sense under α∈(0,1] of a function u(τ). We may generate a sequence of N+1 equations with N+1 conditions for a given (k,ψ) proportional fractional Cauchy-type problem under this tool. A sequence (uN) of solutions to such systems eventually leads to the solution of the proposed problem.
Theorem 4.1. Assume that N=1,2,…, and u∈AC2([a,b],R). Let
and let Vi:[a,b]→R be a function, which is given by
Hence,
where kDρ;ψu(τ)=(1−ρ)u(τ)+kρu′(τ)ψ′(τ) and limN→∞Etr(τ)=0, τ∈[a,b].
Proof. By using Definition 2.3 and kDρ;ψu(τ)=(1−ρ)u(τ)+kρu′(τ)ψ′(τ), for any α∈(0,1], we have
Changing new variables
and by helping the integrating by parts technique, the equation (4.5) can be solved as
Applying the Newton's generalized binomial theorem, it follows that
Inserting (4.7) into (4.6), we have
where
Then, we have
By using integrating by parts with changing variable x(s)=(ψ(s)−ψ(a))i and y′(s)=dds(e1−ρkρψ(s)[(1−ρ)u(s)+kρu′(s)ψ′(s)]), which yields that
Next, we study the term Etr(τ), which is the error caused by truncation error. Finally, we show that Etr(τ)→0 as N→∞, τ∈[a,b], and to prove this, we provide an upper bound for the error. Since 0≤ψ(s)−ψ(a)ψ(τ)−ψ(a)≤1 for s, τ∈J, The equation (4.10) can be computed that
which implies that
Taking M(τ)=maxs∈[a,τ]|dds(eρ−1kρ(ψ(τ)−ψ(s))[(1−ρ)u(s)+kρu′(s)ψ′(s)])| and (4.11) into (4.9), we obtain the following upper bound
The right-sided of (4.12) tends to zero as N→∞, τ∈[a,b]. The proof is done.
From the property (iv) in Lemma 2.4, the integral equation (3.1) in Lemma 3.1 can be reformed as
By applying Theorem 4.1, the equation (4.13) can be re-written as
where
In order to obtain the formula of an approximated solution, uN(τ), we truncate the formula up to order N, getting
where
Note that uN(a)=u(a).
Theorem 4.2. Assume that f∈C([a,b]×R,R) which verifies (A1), and assume that u and uN as in (4.14) and (4.15), respectively, for N∈N. Also, suppose that b∈R is a real in the open interval
Then, uN(τ)→u(τ) as N→∞, for all τ∈[a,b].
Proof. From the equations (4.14) and (4.15), for any τ∈[a,b], we have
Now, we define δuN:=maxτ∈[a,b]|uN(τ)−u(τ)|. Then, we have
By using the formula (3) in [43], we have
and using (4.19), it follows that
Substitution (4.18), (4.20), and (4.21) into the inequality (4.17), for any τ∈[a,b], one has
Applying the maximum into the inequality (4.22) over τ∈[a,b], we obtain that
Clearly, limN→∞|E∗tr(τ)|=0. In addition, by applying the Stirling's formula [44], we have
Then, taking N→∞ in (4.23), one has
By the condition (4.16), we get that δuN→0 as N→∞. From (4.23), which implies that
Applying the condition (4.16), we obtain the following result
Then,
For N sufficiently large number, we obtain the property (4.24). Therefore, there exists a function B (depending on α, ρ, k, τ but independent of N), such that
where
Remark 4.3. Under Theorem 4.1 and Theorem 4.2, we have the following results:
(ⅰ) If k=1 and ψ(τ)=τ then, Theorem 4.1 and Theorem 4.2 reduce to the results as in [20].
(ⅱ) If k>1, ρ=1, and ψ(τ)=τμ, where μ>0 then, Theorem 4.1 and Theorem 4.2 reduce to the results as in [21].
(ⅲ) If k>1, ρ=1 and ψ(τ)=τ then, Theorem 4.1 and Theorem 4.2 reduce to the results as in [22,23].
(ⅳ) If k>1, ρ=1, and ψ(τ)=τμ, where μ→0+ then, Theorem 4.1 and Theorem 4.2 reduce to the results as in [24].
5.
Applications
This section provides two different numerical examples of applications to verify the theoretical results of our main results.
5.1. A numerical example
Example 5.1. Consider the following Cauchy-type problem under the (k,ψ)-Caputo-PFDO:
The exact solution of the problem (5.1) is provided by u(τ)=ρkΨωkψ(τ,0), where ω∈R and ω>k.
From the problem (5.1), we get
For every u, v∈R, τ∈[0,1], we get that
It is noticed that the assumption (A1) is held with L=1/8. By setting α=22/25, ρ=1/4, k=5/4, ω=3/2, and ψ(τ)=τ, then (L(ψ(b)−ψ(a))αk)/(ραkΓk(α+k))≈0.311730513<1. Since all assumptions in Theorem 3.2 are satisfied, the proposed problem (5.1) has a unique solution on [0,1]. From Theorem 3.10, we can compute that
Then, the proposed problem (5.1) is UH-ML stable on [0,1]. If we set Gf(ϵ)=Cfϵ under the condition Gf(0)=0, then we obtain the proposed problem (5.1) is generalized UH-ML stable on [0,1]. In addition, by setting a non-decreasing function Φ(τ)=ρkΨ3kψ(τ,a), we have
This yields that CfΦ:=χΦ=(Γk(3))/(ραkΓk(3+α))(ψ(τ)−ψ(a))αk≈1.276974061>0 and κfΦ:=Lρ−αk≈0.331711285≥0. Hence, the proposed problem (5.1) is UHR-ML stable on [0,1]. If we take ϵ=1, then the proposed problem (5.1) is generalized UHR-ML stable on [0,1].
To achieve the numerical approximation of the proposed problem (5.1), we apply (4.4) in Theorem 4.1. Then, the operator C0,kDα,ρ;ψu(τ) can be replaced as follows:
where AN, BN,i, and Vi(τ) are given by (4.1), (4.2), and (4.3), respectively, in Theorem 4.1. Then
By applying (5.3) and (5.4), then
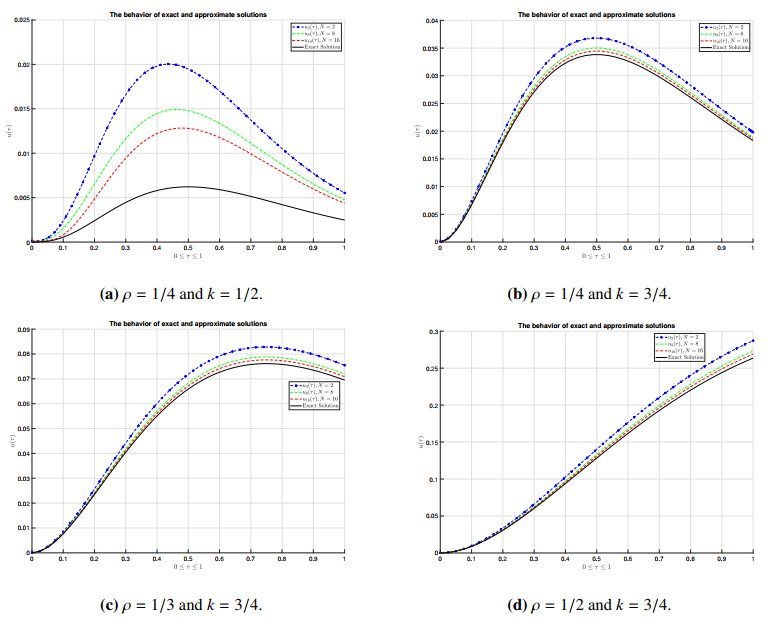
The proposed system (5.5) can solve the numerical solution by applying ode45 in MATLAB software, which applies the explicit Runge-Kutta technique to achieve the approximated solution. The exact solution (continuous line) and numerical approximations (dot lines) of the proposed problem are compared with different parameters ρ=1/4, 1/3, 1/2, and k=1/2, 3/4.
Figure 1 displays the behavior of the exact and approximate solutions under the fixed value α=9/10, and vary values ρ=1/4, 1/3, 1/2, k=1/2, 3/4, N=2,8,16 for the proposed problem (5.1). While Figure 2 displays the behavior of the absolute error between the exact and approximate solutions under the fixed values α=9/10, and vary values ρ=1/4, 1/3, 1/2 , k=1/2, 3/4, N=2,8,16 for the proposed problem (5.1). Figures 1a–1b illustrate that as the value k increases, the approximate solution quickly converges to the exact solution. Moreover, the absolute error values rapidly decrease to zero, as can be seen from Figures 2a–2b. Conversely, Figures 1c–1d indicate that as the value ρ increases, the approximate solution converges to the exact solution more quickly and to greater values. While the absolute error values increase, as can be seen from the Figures 2c–2d.
5.2. An Application to Blood Alcohol Levels (BALs) problem
Now, an application has been developed to support our theoretical results. We study a basic model for determining BALs that is characterized by two differential equations with real-data individuals. The BALs problem is explained by the following Cauchy-type system of the form:
where S(τ) and B(τ) denote the concentrations (mg/L) of alcohol in the stomach and blood of a human body at time τ (min), respectively. The rate law constants i (min−1) are given by ci, i=1,2, and S0, B0 represent the subject's initial alcohol intake in the stomach and blood, respectively. The exact solution for the system (5.6) is fairly simple and may be determined using the Laplace transform approach
Fractional-order models have been recognized as being more useful in estimating experimental data than integer-order models. Another reason is that various parameters can be adjusted accordingly. Then, by taking the (k,ψ)–Caputo–PFDO into the left-sided of the problem (5.6), the problem (5.6) can be rewritten as:
Similarly procedure in Example 5.1, we obtain that
In all graphical simulations, we use the parameters k1=0.12, k2=0.01, and ψ(τ)=τ based on the experimental results for the BALs of a real individual in Table 1. We separated them into three cases, which are shown in Figure 3.
Case (1): We set the initial conditions S0=330, B0=0, ρ=0.988, and k=0.995 with the varied α∈{0.80,0.85,0.90,0.95,1.00}. The graphical simulation of B(τ) with the common parameters is shown as in Figure 3a. Case (2): We set the initial conditions S0=280, B0=0, α=0.95, and k=0.9 with the varied ρ∈{0.992,0.994,0.996,0.998,1.000}. The graphical simulation of B(τ) with the common parameters is shown as in Figure 3b. Case (3): We set the initial conditions S0=255, B0=0, α=0.95, and ρ=0.998 with the varied k∈{0.88,0.90,0.92,0.94,0.96}. The graphical simulation of B(τ) with the common parameters is shown as in Figure 3c. Case (4): We set the initial conditions S0=255, B0=0, α=0.90, ρ=0.25, k=0.5, and N=2,5,20. The graphical simulation of B(τ) with the common parameters is shown as in Figure 4.
We calculate the relative absolute error, EN=|(xe−xa)/xe| between the exact solution x_{e}(\tau) and the approximation solution x_{a}(\tau) for the concentration of alcohol in the blood of a human body at time \tau , B(\tau) , as displayed in Table 2. The presented technique is applicable. Also, the results agree with the exact solutions, and the error decreases as N increases.
6.
Conclusions
In this work, we analyzed an extended Gronwall inequality in the context of the (k, \psi) -PFOs and proved its properties. A Cauchy-type problem under the (k, \psi) -Caputo-PFDO is the highlight of our presentation. First, the existence and uniqueness results of the proposed problem (1.1) were established by applying Banach's contraction mapping principle and Leray-Schauder's nonlinear alternative. Then, UH-ML stability was studied to guarantee the existing results. Moreover, a numerical technique is demonstrated based on a decomposition formula for the (k, \psi) -Caputo-PFDO. Finally, numerical examples are shown to verify the theoretical results. As seen in Example 5.1, we set the specific type of Cauchy problem and showed numeric calculations to confirm the accuracy of Theorem 3.2, which expresses the unique solution. We also showed the calculation satisfied the conditions for various Ulam stability to guarantee the results. For the fixed value of order \alpha and with the different parameters \rho and k , we found the result's behavior through the graphic numerical simulation that the approximate solution of the system converges to the exact solution as \rho and k increased. In contrast, the absolute error values decreased to zero for increasing value k but increased for decreasing value \rho . Furthermore, to strengthen our study in a broader domain, we applied the established numerical technique to the BALs problem as seen in Example 5.2. We expressed a numerical simulation of this problem under different parameters. The graphical results illustrated that various values of \alpha, \rho, and k gave the corresponding behavior of the system in the same trend as the data. Consequently, the fractional-order form may approximate the alcohol concentration in a human's blood under a range of circumstances, as proven with data.
In future works, we can discuss applying (k, \psi) -Caputo-PFDO to real-world problems. This larger paradigm greatly contributes to the development of fractional calculus. It is paving the way for exciting future studies in this dynamic and developing discipline.
Author contributions
Weerawat Sudsutad: Problem statement, conceptualization, methodology, investigation, software, writing the original draft, writing, reviewing, and editing; Jutarat Kongson: Supervision, problem statement, conceptualization, methodology, investigation, writing the original draft, reviewing, and editing; Chatthai Thaiprayoon: Methodology, software, investigation, writing the original draft, reviewing, and editing; Aphirak Aphithana, Weerapan Sae-dan: Investigation, software, writing, reviewing, and editing. All the authors read and approved the final manuscript.
Acknowledgments
W. Sudsutad (weerawat.s@rumail.ru.ac.th), A. Aphithana (aphirak.apt@gmail.com), W. Sae-dan (weerapan.s@rumail.ru.ac.th) would like to thank Ramkhamhaeng University, J. Kongson and C. Thaiprayoon (chatthai@go.buu.ac.th) thank Burapha University for supporting this work.
Conflict of interest
The authors declare no conflicts of interest.









 DownLoad:
DownLoad:






