Practical consensus of time-varying fuzzy positive multi-agent systems

1.   Introduction

Recently, the cooperative control of multi-agent systems (MASs) has been widely studied ^[1,2,3]. In ^[4], distributed consensus was explored for MASs with attacks. An event-triggered protocol was proposed for nonlinear MASs ^[5]. The interactions in MAS are often not linear relationships but full of nonlinear characteristics. In ^[6], the finite-time control of uncertain planar nonlinear systems was studied. The global finite-time stability of planar nonlinear systems was considered in ^[7] with mismatched unknown perturbations. A method for prescriptive-time stabilization of uncertain planar nonlinear systems was reported in ^[8] with output constraints. However, uncertainty and ambiguity exist in the real process, and they induce new challenges when making decisions and actions. By introducing fuzzy logic, Takagi–Sugeno fuzzy multi-agent systems (T-S FMASs) can quantify and process uncertain and fuzzy information. In ^[9], a consensus protocol was designed to reach the time-delay consensus of T-S FMASs. Fixed-time consensus was introduced in ^[10] for MASs. Positive systems are an interesting research topic in the field of control, which are characterized as dynamic systems with non-negative state variables and input variables. Relevant theory and applications of positive systems were explained in ^[11]. In ^[12], linear programming was applied for the routine control of networked positive systems. In ^[13], disturbance observers were developed for positive systems. As the number of application scenarios increases, the performance requirements for MASs are also getting higher and higher. Combining MASs with positive systems, positive multi-agent systems (PMASs) can not only broaden the application scope of agents but also improve their performance when dealing with non-negative constraint problems. The literature ^[14] discussed the leader-following consensus problem of PMASs. A supervisory control scheme was considered in ^[15] to achieve asymptotic stability of PMASs. Regrettably, there are few studies on T-S fuzzy positive multi-agent systems (T-S FPMASs). The main reasons lie in that (i) Positivity and consensus may not be simultaneously guaranteed when combining T-S FPMASs with positive systems, and (ii) a fuzzy control framework has not yet been constructed for T-S FPMASs.

With the increase in system complexity and rapid changes in the external environment, invariant systems are no longer able to meet actual requirements. Time-varying MASs, as a type of dynamic system that can describe changes in parameters or characteristics over time, exhibit strong flexibility and adaptability. In ^[16], the stability of time-varying positive systems was addressed using linear Lyapunov functions. A proportional derivative controller was designed in ^[17] to enable the time-varying system to achieve both positivity and stability. The leader-follower consensus problem was considered in ^[18] of time-varying MASs under switching topology. In ^[19], a mean square consensus controller was designed for time-varying MASs to reflect the instantaneous state consensus behavior. Asymptotic consensus of time-varying MASs was established in ^[20]. More results on time-varying MASs can refer to ^[21,22,23]. However, few results are devoted to time-varying T-S FPMASs. The main difficulties have three aspects. First, the characteristics of time-varying T-S FPMASs change with time, which induces a complicated mathematical model. Second, since parameters change with time, the consensus of T-S FPMASs may also change, which increases the difficulty of analyzing system consensus. Finally, fuzzy systems require the design of fuzzy rules, which means that fuzzy rules and membership functions may change over time. This greatly increases the complexity of system modeling. These lead to the difficulty of achieving the positivity and consensus of the system.

This paper aims to explore the positivity and consensus of time-varying T-S FPMASs. A new consensus framework is constructed. Under this framework, the conditions for positivity and consensus are addressed using time-varying Lyapunov functions and time-varying linear programming, and the corresponding protocol design is proposed based on matrix decomposition. The contributions and innovations of this paper are as follows: (i) A novel error variable is introduced to achieve practical consensus, which effectively improves the accuracy and stability of the system operation; (ii) A novel control framework is established for time-varying T-S fuzzy multi-agent systems, which can ensure the robustness and reliability of the systems under external attacks; and (iii) A simple computation method is presented by combining linear programming with a co-positive Lyapunov function; The structure of the remainder is: Section 2 formulates the problem formulation, Section 3 presents main results, Section 4 gives two examples, and Section 5 summarizes the paper.

2.   Problem formulation

For convenience of development, some notations are listed. Kronecker product is represented by $\bigotimes$. The $N$-dimensional identity matrix is described by $I_{N}$. For a matrix $\mathcal{B} \in \Re^{m \times m}$, $\mathcal{B} \succeq 0$ ($\succ 0$, $\preceq 0$, $\prec 0$) implies that $[\mathcal{B}]_{ij}\geq0$ ($> 0, \leq0, < 0$), $\forall i, j = 1, 2, \cdots, m$, where $[\mathcal{B}]_{ij}$ is the $i$th and $j$th column element. $\mathbb{E} \{\cdot \}$ represents the mathematical expectation. All elements in the $z$-dimension vector $1_{z}$ are 1, and the $s$th element is 1 and other ones are zero in the vector $1_{z}^{(s)}$.

Consider a time-varying system:

where $x(k) \in \Re^{m}$, $y(k) \in \Re^{n}$, and $u(k) \in \Re^{s}$ are state, output, and control input, respectively. The system matrices satisfy $\mathcal{A}(k) \succeq 0$, $\mathcal{B}(k) \succeq 0$, and $\mathcal{C}(k) \succeq 0$. For convenience, denote the time-varying matrices as $\mathcal{A}_k$, $\mathcal{B}_k$, and $\mathcal{C}_k$ in the latter section. A similar use is suitable for time-varying vectors.

Definition 1. ^[11] A system is positive if all states and outputs are nonnegative for any nonnegative initial state and input.

Lemma 1. System (1) is positive if $\mathcal{A}_k \succeq 0$, $\mathcal{B}_k \succeq 0$, and $\mathcal{C}_k \succeq 0$.\\ Lemma 1 is an extension of the positivity definition of time-invariant systems ^[11].

Lemma 2. ^[11] For a matrix $\mathcal{A}$ with $\mathcal{A} \succeq 0$, the condition that $\mathcal{A}$ is a Schur matrix is equivalent to the condition that there exists a vector $\sigma \in \Re^{m}$ with $\sigma \succ 0$ such that $(\mathcal{A} - I_{m})\sigma \prec 0$.

In this paper, we assume that the communication topology of MASs with $N$ agents is represented by a directed graph $\mathcal{G} = \{\mathcal{D}, \mathcal{E}\}$. $\mathcal{E} \subset \mathcal{D} \times \mathcal{D}$ and $\mathcal{D} = \{\upsilon_{1}, \upsilon_{2}, \dots, \upsilon_{N}\}$ denote the set of edges and nodes, respectively. In $\mathcal{G}$, each node is represented by an integer $i$ belonging to the node set $\mathcal{S} = \{1, 2, \ldots, N\}$. If $(\upsilon_{i}, \upsilon_{j}) \in \mathcal{E}$, then $\upsilon_{i}$ is called an adjacent node of $\upsilon_{j}$. If there is a path between any two nodes, the graph $\mathcal{G}$ is a connected graph. The row-stochastic matrix $\mathcal{R} = [\mathcal{R}_{ij}] \in \Re^{N \times N}$ is defined by $\sum_{j = 1}^{N}[\mathcal{R}]_{ij} = 1$, where $[\mathcal{R}]_{ij} > 0$ implies that the information is transferred from agent $j$ to agent $i$, otherwise $[\mathcal{R }]_{ij} = 0$. Throughout this paper, the directed graph is strongly connected. Let $\mathcal{L}_{max} = \max_{i \in N}\{1-\sum_{i = 1}^{N}[\mathcal{R}]_{i1} \}$ and $\mathcal{L}_{min} = \min_{i \in N}\{1-\sum_{i = 1}^{N}[\mathcal{R}]_{i1} \}$.

Lemma 3. ^[24] A simple eigenvalue of $I_{N} - \mathcal{R}$ is zero if and only if the directed graph $\mathcal{G}$ is connected. Furthermore, $I_{N}-\mathcal{R}$ has a nonnegative left eigenvector $\psi$ associated with zero eigenvalues that satisfies $\psi^{\top}(I_{N}-\mathcal{R}) = 0$ and $\psi^{\top} {\bf 1} = 1$.

Consider a time-varying T-S FMAS with $N$ agents described by the T-S fuzzy rule: IF $\tau_{1, k}$ is $W_{a1}$, $\tau_{2, k}$ is $W_{a2}$, $\cdots$, and $\tau_{q}(k)$ is $W_{aq}$, THEN

where $i\in \mathcal{S}, x_{i}(k)\in\Re^n$, $y_{i}(k)\in\Re^m$, and $u_{i}(k)\in\Re^p$ are state, output, and control input of agent $i$, respectively, and the system matrices $A_{a, k}$, $B_{a, k}$ and $C_{a, k}$ are nonnegative, $a = 1, 2, \cdots, M$ is the rule number, $\tau_{1, k}, \tau_{2, k}, \cdots, \tau_{q, k}$ are the premise variables, and $W_{ag}$ $(a = 1, 2, \cdots, M$; $g = 1, 2, \cdots, q)$ denotes the fuzzy set. Then,

where $h_{a}(\tau(k)) = \frac{u_{a}(\tau(k))}{\sum_{a = 1}^M u_{a}(\tau(k))}$, $\sum_{a = 1}^M h_{a}(\tau(k)) = 1$, and $u_{a}(\tau(k)) = \prod_{g = 1}^q M_{ag}(\tau_{g, k})$ with $h_{a}(\tau(k)) \geq 0$.

Definition 2. System (2) achieves the practical consensus if $\lim_{k \to \infty} {\left\lVert x_{i}(k) - \mu \right\rVert}_{1} \leq \lambda$ holds $\forall i \in \mathcal{S}$, where $\lambda > 0$ and $\mu \succ 0$.

Remark 1. Definition 2 introduces the practical consensus by replacing the common Euclidean norm by 1-norm. The core of this improvement is to drive the states of MASs to the neighborhood of a specific vector $\mu_i$. One can also unify the target vector $\mu_i$ of each agent into a global target vector $\mu$. It means that $\mu_i = \mu$ for any agent $i\in\mathcal{S}$, where $\mu \succ 0$. In this way, the state adjustment of MASs will point to a common neighborhood. By specifying different target vectors $\mu_i$ for different agents, the solution to the consensus problem is expanded and the design flexibility is enhanced.

3.   Main results

3.1.   Practical consensus

A time-varying control protocol is designed as:

where $\mathcal{K}_{Ps, k} \in \Re^{p \times m}$, $\mathcal{F}_{s} \in \Re^{p \times m}$ and $\mathcal{T}_{s, k} \in \Re^{p \times n}$ are the gain matrix to be determined, and $\Re^{n}$ vector $\beta_0 \succ 0$. A variable $\xi_{i}(k)$ is introduced:

where $\varphi = \{\varphi_{1}, \varphi_{2}, \ldots, \varphi_{N}\}^{\top}$, where $\varphi = \phi \psi$, $\psi$ is the left eigenvector of $I_{N}-\mathcal{R}$, $\phi > \frac{1}{\psi_{\min}}$, and $\psi_{\min}$ is the minimum element of $\psi$.

Theorem 1. If there exist scalars $\alpha > 0$, $0 < \underline{\delta} \leq 1 \leq \overline{\delta}$, $\Re^{n}$ vectors $v_{1, k} \succ 0$, $\zeta_{l, k} \succ 0$, $\zeta_{k} \succ 0$, $\varpi_{k} \succ 0$, and $\Re^{m}$ vectors $\varepsilon_{l, k} \succ 0$, $\varsigma_{l, k} \succ 0$, $\varsigma_{k} \succ 0$ such that

where $l = 1, 2, \cdots, p$, $g = 1, 2, \cdots, M$, $s = 1, 2, \cdots, M$ and $r = 1, 2, \cdots, M$, then the time-varying system (2) achieves the consensus and positivity under the protocol (3) with

Proof. Define $X(k) = (x_{1}^{\top}(k), \ldots, x_{N}^{\top}(k))^{\top}$, $U(k) = (u_{1}^{\top}(k), \ldots, u_{N}^{\top}(k))^{\top}$, and $Y(k) = (y_{1}^{\top}(k), \ldots, y_{N}^{\top}(k))^{\top}$. By (2), we have

Define $\beta = (\underbrace{\beta_{0}^{\top}, \ldots, \beta_{0}^{\top}}_{N})^{\top}$. By (3), it follows that

Substituting (8) into (7) gives

Define $\xi(k) = (\xi_{1}^{\top}(k), \ldots, \xi_{N}^{\top}(k))^{\top}$. Together with (4) gives

By Lemma 3, $1_{N}\varphi^{\top}(I_{N}-\mathcal{R}) = (I_{N}-\mathcal{R})1_{N}\varphi^{\top} = 0$. Then,

where

It follows that $[{\mathcal{A}}_{asg, k}]_{ij} \succeq 0$ and $[{\mathcal{B}}_{asg, k}]_{ij} \succeq 0$. Due to (5a) and (5b), it holds that

Using (6) it follows that $[{\mathcal{A}}_{asg, k}]_{ii} \succeq 0$ and $[{\mathcal{B}}_{asg, k}]_{ii} \succeq 0$. The positivity of the system (11) is obtained.

Next, the time-varying Lyapunov function is constructed as $\mathcal{V}(\xi(k)) = \xi^{\top}(k) v_{k}$, where $v_{k} = (\underbrace{v_{1, k}^{\top}, v_{1, k}^{\top}, \dots, v_{1, k}^{\top}}_{N})^{\top}$. Then,

where

By (5e) and (6), we obtain

By (5c) and (5d), it holds that

Together with (12) yields that $\mathcal{V}(\xi(k)) < (1 - \alpha)^{k}\mathcal{V}(\xi(0)) + \frac{(1 - \alpha)^{k}-1}{(1 - \alpha)-1} \beta^{\top}(1_{N} \bigotimes \varpi_{k})$. Additionally, it is easy to obtain that $\mathcal{V}(\xi(k)) = \xi^{\top}(k) v_{k} \geq \chi \xi^{\top}(k) 1_{Nn} = \chi {\left\lVert \xi(k) \right\rVert}_{1}$, where $\chi$ is the minimum elements of $v_{k}$. Then,

Therefore, $\lim_{k \to \infty} ({\lVert x_{i}(k) - \frac{\beta_{0}}{\sum_{i = 1}^{N}\varphi_{i}-1} \rVert}_{1})$ $\leq$ $\frac{\kappa}{\chi}$, where $\kappa = \frac{1}{\alpha} \beta^{\top}(1_{N} \bigotimes \varpi_{k})$. By Definition 2, the practical consensus is achieved. □

Remark 2. The positivity and stability problems of time-varying systems are discussed in ^[16,17]. In ^{[18,19,20,21,22,23]}, the consensus design was explored for time-varying MASs. However, there are still many open issues of time-varying MASs that have not been adequately addressed. On the one hand, there is no unified framework on positivity and consensus of time-varying T-S FPMASs. On the other hand, the introduction of the time-varying Lyapunov function induces new challenges in achieving the consensus. The time-varying property brings much design and computational burden. More importantly, there is no good method to solve time-varying linear programming. Theorem 1 constructs a novel consensus framework on time-varying T-S FPMASs and solves the mentioned issues.

Remark 3. When dealing with general time-varying systems, linear matrix inequality is used ^{[25,26,27,28]}. Due to the characteristics of positive systems, it is unnecessary to employ a quadratic Lyapunov function, and a co-positive Lyapunov function is more suitable for positive systems. Under the framework of the co-positive Lyapunov function, the corresponding variables are vectors, and they are solveable via linear programming. Moreover, linear programming is powerful in dealing with large-scale systems, which can effectively reduce the computation burden.

To reduce the computational burden of Theorem 1, we further provide the following corollary 1.

Corollary 1. If there exist scalars $\alpha > 0$, $0 < \underline{\delta} \leq 1 \leq \overline{\delta}$, $\Re^{n}$ vectors $v_{1} \succ 0$, $\zeta_{l} \succ 0$, $\zeta \succ 0$, $\varpi \succ 0$, and $\Re^{m}$ vectors $\varepsilon_{l} \succ 0$, $\varepsilon \succ 0$, $\varsigma_{l} \succ 0$, $\varsigma \succ 0$ such that

where $l = 1, 2, \cdots, p$, $g = 1, 2, \cdots, M$, $s = 1, 2, \cdots, M$ and $r = 1, 2, \cdots, M$, then the time-varying system (2) achieves the consensus and positivity under the control protocol (3) with

Corollary 1 is obtained by sampling and scaling the time-varying function in Theorem 1, and the proof is similar to Theorem 1, so it is omitted. Verified by the linear programming toolkit in the MATLAB toolbox, the final result agrees with Theorem 1, realizing the practical consensus.

3.2.   False Data-Injection attacks

Under false Data-Injection attacks, a control protocol is given as:

where $d^{u}_{i}(k)$ is the inject false data, $d^{u}_{i}(k)$ is a random bounded energy signal, $\Lambda^{u}_{i}(k)$ represents the decision variable, and $\Lambda^{u}_{i}(k)$ is a Bernoulli distribution with: $Prob\{\Lambda^{u}_{i}(k) = 1\} = \Lambda_{i}, Prob\{\Lambda^{u}_{i}(k) = 0\} = 1 - \Lambda_{i}.$ Then,

where $\widehat{y}_{i}(k) = {y}_{i}(k) + \Lambda^{y}_{i}(k) d^{y}_{i}(k)$ is the false data injected into the output; $\triangle \widehat{y}_{i}(k) = \widehat{y}_{i}(k) - \widehat{y}_{i}(k - 1)$ and $e_{i}(k) = (1-\beta)e_{i}(k-1) + y_{i}(k-1) + \mathcal{F}_{k} e_{\varphi}$ are derivative and integral parts for agent $i$, $0 < \beta \leq 1$ is a tuning parameter, and $\mathcal{K}_{Ps, k}$, $\mathcal{K}_{Is1, k}$, $\mathcal{K}_{Ds, k}$, $\mathcal{K}_{Is2, k}$, $\mathcal{H}_{s, k}$, $\mathcal{T}_{s, k}$, $\mathcal{Y}_{s, k}$, and $\mathcal{F}_{k}$ are the gain matrices, and $\Re^n$ vector $x_{\delta} \succ 0$ and $\Re^m$ vector $e_{\varphi} \succ 0$ are known. Two variables $\delta_{i}(k)$ and $\varphi_{i}(k)$ are introduced as follows:

where $\psi = (\psi_{1}, \ldots, \psi_{N})^{\top}$, where $\psi = \hbar \rho$, $\rho$ is the left eigenvector of $I_M - \mathcal{R}$, $\hbar > \frac{1}{\rho_{\min}}$, and $\rho_{\min}$ is the minimal element of $\rho$.

Remark 4. The cooperative consensus of MASs requires each agent to share information with its neighbor agents. False data may cause the failure of cooperative behavior because the agents' decision is based on wrong data. Thus, the cooperation efficiency and consensus of MASs are destroyed. The false data used in this paper is injected into the control protocol. These data appear as signals with randomness and bounded energy, and their attack strength is uncertain due to fuzzy rules. In addition, this paper introduces a key decision variable in the controller, which will monitor the variable to determine whether the system is under attacks and take the corresponding strategies to deal with it.

Theorem 2. If there exist scalars $0 < \beta \leq 1$, ${0 < \underline{\ell} \leq 1 \leq \overline{\ell}}$, $\alpha > 0$, $\Re^n$ vectors $v_{1, k} \succ 0$, $v'_{1, k} \succ 0$, $\zeta_{l, k} \succ 0$, $\zeta_{k} \succ 0$, $\gamma_{\delta} \succ 0$, $\Re^m$ vectors $v_{2, k} \succ 0$, $v'_{2, k} \succ 0$, $\xi_{l, k} \succ 0$, $o_{l, k} \succ 0$, $\eta_{l, k} \succ 0$, $\eta_{k} \succ 0$, $\theta_{l, k} \prec 0$, $\overline{\theta}_{k} \prec 0$, $\underline{\theta}_{k} \prec 0$, $\varepsilon_{l, k} \succ 0$, $\varepsilon_{k} \succ 0$, $\vartheta_{l, k} \succ 0$, $\vartheta_{k} \succ 0$, $\varsigma_{l, k} \succ 0$, $\varsigma_{k} \succ 0$, $\gamma_{\varphi} \succ 0$, $\gamma_{y} \succ 0$, $\gamma_{y-1} \succ 0$, and $\Re^p$ vector $\gamma_{u} \succ 0$ such that

where $l = 1, 2, \cdots, p$, $g = 1, 2, \cdots, M$, $s = 1, 2, \cdots, M$ and $r = 1, 2, \cdots, M$, then the time-varying system (2) achieves the consensus and positivity under the protocol (13) with

Proof. Define $X(k) = (x_{1}^{\top}(k), \ldots, x_{N}^{\top}(k))^{\top}$, ${U}(k) = ({u}_{1}^{\top}(k), \ldots, {u}_{N}^{\top}(k))^{\top}$ and $Y(k) = (y_{1}^{\top}(k), \ldots, y_{N}^{\top}(k))^{\top}$. By (2), we have

Define $E(k) = (e_{1}^{\top}(k), \dots, e_{N}^{\top}(k))^{\top}$, $X_{\delta} = (\underbrace{{x_{\delta}}^{\top}, \ldots, {x_{\delta}}^{\top}}_{N})^{\top}$, $E_{\varphi} = (\underbrace{{e_{\varphi}}^{\top}, \ldots, {e_{\varphi}}^{\top}}_{N})^{\top}$, $D_{y}(k) = ({\Lambda^{y}_{1}(k) d^{y}_{1}(k)}^{\top}, \ldots, {\Lambda^{y}_{N}(k) d^{y}_{N}(k)}^{\top})^{\top}$, and $D_{u}(k) = ({\Lambda^{u}_{1}(k) d^{u}_{1}(k)}^{\top}, \ldots, {\Lambda^{u}_{N}(k) d^{u}_{N}(k)}^{\top})^{\top}$. By (13), it follows that

and

Substituting (18) into (17) gives

Define $\widetilde{X}(k) = (X^{\top}(k) \; E^{\top}(k))^{\top}$, $\widetilde{X}_{\delta} = (X_{\delta}^{\top} \; E_{\varphi}^{\top})^{\top}$ and $\Lambda_{D}(k) = (D_{y}^{\top}(k) \; D_{u}^{\top}(k))^{\top}$. Combining (19) and (20) yields that

where

Define $\delta(k) = (\delta_{1}^{\top}(k), \ldots, \delta_{M}^{\top}(k))^{\top}$, $\varphi(k) = (\varphi_{1}^{\top}(k), \ldots, \varphi_{M}^{\top}(k))^{\top}$, and $\widetilde{\delta}(k) = (\delta^{\top}(k) \; \varphi^{\top}(k))^{\top}$. Together with (21) gives

By Lemma 3, $1_{N}\varphi^{\top}(I_{N}-\mathcal{R}) = (I_{N}-\mathcal{R})1_{N}\varphi^{\top} = 0$. Then,

where

It follows that $[{\mathcal{A}}_{asg, k}]_{ij} \succeq 0$, $[{\mathcal{B}}_{as, k}]_{ij} \succeq 0$, ${\mathcal{C}}_{a, k} \succeq 0$, ${\mathcal{D}} \succeq 0$, ${\mathcal{E}}_{asz, k} \succeq 0$, $[{\mathcal{O}}_{asgz, k}]_{ij} \succeq 0$, $[{\mathcal{P}}_{k}]_{ij} \succeq 0$, ${\mathcal{W}}_{a, k} \succeq 0$, and ${\mathcal{Z}}_{as, k} \succeq 0$. Due to (15a)–(15c), it holds that

and

Using (16) it follows that $[{\mathcal{A}}_{asg, k}]_{ii} \succeq 0$, $[{\mathcal{B}}_{asg, k}]_{ii} \succeq 0$, and $[{\mathcal{O}}_{asgz, k}]_{ii} \succeq 0$. Together with (15d)–(15f) gives

and

Using (16) again, it follows that $[{\mathcal{P}}_{k}]_{ii} \succeq 0$ and ${\mathcal{S}}_{asg, k} \succeq 0$. The positivity of the system (23) is obtained.

Next, the time-varying Lyapunov function is constructed as

where $v_{k} = (\varpi_{k}^\top \; \chi_{k}^\top)^\top$, $v'_{k} = ({\varpi'}_{k}^\top \; {\chi'}_{k}^\top)^\top$, $\varpi_{k} = (\underbrace{v_{1, k}^\top \ldots v_{1, k}^\top}_{N})^\top$, $\chi_{k} = (\underbrace{v_{2, k}^\top \ldots v_{2, k}^\top}_{N})^\top$, $\varpi'_{k} = (\underbrace{v_{1, k}'^{\top} \ldots v_{1, k}'^{\top}}_{N})^\top$, $\chi'_{k} = (\underbrace{v_{2, k}'^\top \ldots v_{2, k}'^\top}_{N})^\top$. The difference of $V(\widetilde{X}(k))$ is

Together with (23) follows that

where

By (15o) and (16), we obtain

and

By (15g)–(15j), it holds that

and

Using (15o) and (16) again, it holds that

By (15k) and (15n), it holds that

Together with (25) yields that

Additionally, it is easy to obtain that $\mathcal{V}(\widetilde{\delta}(k)) = \widetilde{\delta}^\top(k)v_{k} + \widetilde{\delta}^\top(k-1)v'_{k} \geq \delta^\top(k)\varpi_{k} + \delta^\top(k-1)\varpi_{k}' \geq \hslash \delta^{\top}(k) 1_{Nn} + \hslash' \delta^{\top}(k-1) 1_{Nn} = \hslash {\left\lVert \delta(k) \right\rVert}_{1} + \hslash' {\left\lVert \delta(k-1) \right\rVert}_{1}$, where $\hslash$ and $\hslash'$ are the minimum elements of $\varpi_{k}$ and $\varpi_{k}'$, respectively. Then,

Therefore, $\lim_{k \to \infty} ({\lVert x_{i}(k) - \frac{x_{\delta}}{\sum_{i = 1}^{N}\varphi_{i}-1} \rVert}_{1})$ $\leq$ $\frac{\kappa}{\underline{\hslash}}$, where $\underline{\hslash} = \min\{\hslash, \hslash'\}$, $\kappa = \frac{1}{\alpha} \big({X_{\delta}^{\top}}(I_{N} \otimes \gamma_{\delta}) + {E_{\varphi}^{\top}}(I_{N} \otimes \gamma_{\varphi}) + {D_{y}^\top(k-1)} (I_{N} \otimes \gamma_{y-1}) + {D_{y}^\top(k)} (I_{N} \otimes \gamma_{y}) + {D_{u}^\top(k)} (I_{N} \otimes \gamma_{u}) \big)$. By Definition 2, the consensus of Theorem 2 is achieved. □

A suggested algorithm is provided for Theorem 2 in Algorithm 1.

Remark 5. Theorem 2 establishes a new framework for ensuring the positivity and consensus of the time-varying fuzzy positive multi-agent system when it suffers from false data injection attacks. In the designed PID control protocol (13), attacks will cause interference to the positivity and consensus of the system, and $\mathcal{Y}_{s, k}\Lambda^{y}_{i}(k) d^{y}_{i}(k)$ is the key to achieving the positivity of the system; otherwise, the positivity and consensus of the system cannot be achieved at the same time. When being attacked, a large amount of false data will be injected into the system, and the gain matrix $\mathcal{Y}_{s, k}$ will correct the system according to the false data to reduce the interference and impact on the system.

4.   Illustrative Example

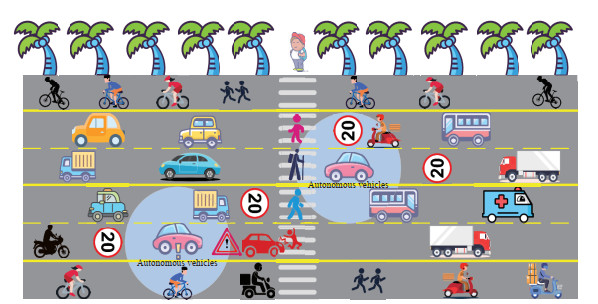
Autonomous vehicles, as a cutting-edge transportation technology, require control algorithms to determine the vehicle's driving route, speed, and other parameters. These algorithms need to make real-time decisions based on the environment and current status of the vehicle and respond accordingly in different traffic scenarios to ensure safe and stable driving of the vehicle. In ^[29], a distributed adaptive cooperative control strategy was proposed to achieve leader synchronization of autonomous vehicles. In ^[30], a formation tracking control method was proposed for multi-agent velocity control autonomous vehicles. In ^[31], the preview control theory was proposed to solve the system disturbance and uncertainty of autonomous vehicles in the path tracking control. The research object of the above literature is autonomous vehicles. Carsim full-vehicle model and general tracking methods are employed. Traditional control strategies often require precise mathematical models, while fuzzy systems reduce the dependence on such models and increase the flexibility of autonomous vehicle systems. By combining with time-varying systems and the proposed fuzzy design, the following simulation example is given. Figure 1 shows the simulated driving environment of autonomous vehicles, where its objects are autonomous vehicles and the circle in the figure is the real-time visual scanning area. In system (2), the time-varying factor reflects the dynamic changes of the external environment, where the expression $\sum_{a = 1}^{M}h_{a}(\tau(k))$ quantifies the uncertainty and complexity of the road conditions. The state of the autonomous vehicle at the $k$th sampling instant is represented by $x_{i}(k)$, while $u_{i}(k)$ represents the control command received by the vehicle at that time. Through two different sets of simulation experiments, the effectiveness and stability of the controller in dealing with various situations are verified.

Example 1. Based on the above analysis, the autonomous vehicle is modeled using system (2) and controller (3), where

The membership functions $h_{1}(\tau(k))$ and $h_{2}(\tau(k))$ are: $h_{1}(\tau(k)) = \frac{1 + \cos^{2}(\sin^{2}(k))}{3}$ and $h_{2}(\tau(k)) = \frac{1 + \sin^{2}(\sin^{2}(k))}{3}$. In this case, the communication topology of the T-SFMAS(2) is described by a directed communication graph $\mathcal{G}$ shown in Figure 2.

By Theorem 1, we have

The initial conditions are given as: $x_{1}(0) = (20.5, 14.3, 9.1)^{\top}$, $x_{2}(0) = (15.4, 23.3, 8.9)^{\top}$, $x_{3}(0) = (10.2, 21.0, 18.8)^{\top}$, $x_{4}(0) = (13.7, 8.6, 22.4)^{\top}$, $x_{5}(0) = (9.8, 25.1, 17.9)^{\top}$. Figures 3–5 are the state simulations of the system (2) under the control protocol (3). By observing the embedding figures in Figures 3–5, it is seen that the consensus error does not converge to zero and the states of the agents do not keep the same values but fluctuate in a range. From Figures 3–5, it can be noticed that the agents achieve practical consensus around $k = 10.$ Figure 6 shows the time-varying function $v_{1, k}$. Based on these simulation results, it can be found that the designed control protocol (3) is effective.

Example 2. Consider the systems (2) under the false data injection attacks with five agents, where

The membership function and row-stochastic matrix of Theorem 2 are the same as those of Theorem 1. By Theorem 2, we can obtain the control gain matrices:

Figures 7–9 are the state simulations of system (2) under control protocol (13). By observing the embedding diagram in Figures 7–9, it is found that the agents achieved practical consensus at k = 10. Figures 10–13 shows the time-varying functions $v_{1, k}$, $v_{1, k}'$, $v_{2, k}$ and $v_{2, k}'$, respectively.

5.   Conclusions

This paper constructs a consensus protocol framework for time-varying T-S FPMASs. A novel fuzzy consensus protocol is proposed to achieve the practical consensus of the systems. Time-varying Lyapunov functions and time-varying linear programming are employed to analyze and design the control protocol. In this paper, the time-varying linear programming conditions are computed using a piecewise strategy. The control framework for false data injection attacks is not limited to the current type of attacks, and its application scope can be extended to other forms of attacks, including denial of service attacks and deception attacks. When dealing with these different types of attacks, the positivity and consensus issues of the systems need to be fully considered. The proposed fuzzy control approach can be further developed for other issues of FPMASs, such as the filter, cooperative observation, etc. Moreover, it is interesting to apply the proposed control framework to other classes of positive systems, such as time-varying positive complex networks, time-varying positive neural networks, etc.

Author contributions

Junfeng Zhang: Supervision, conceptualization, investigation, writing-review and editing; Renjie Fu: formal analysis, writing-original draft, methodology, software, validation; Yuanyuan Wu: validation, writing-review and editing, conceptualization, visualization; Bhatti Uzair Aslam: Investigation, formal analysis, visualization, writing-original draft. All authors have read and agreed to the published version of the manuscript.

Acknowledgment

This work was supported by National Natural Science Foundation of China (62463007 and 62073111), Hainan Provincial Natural Science Foundation of China (622RC618), Science Research Funding of Hainan University (KYQD(ZR)21007 and KYQD(ZR)22180) and Postgraduate Innovative Research Funding of Hainan Province (Qhys2023-279, Qhys2023-278 and Qhys2023-280).

Conflict of interest

The authors declare that they have no conflict of interest.