Existence and uniqueness of nonlinear fractional differential equations with the Caputo and the Atangana-Baleanu derivatives: Maximal, minimal and Chaplygin approaches

Abdon Atangana; Abdon Atangana

doi:10.3934/math.20241282

AIMS Mathematics

2024, Volume 9, Issue 10: 26307-26338. doi: 10.3934/math.20241282

Previous Article Next Article

Research article Special Issues

Existence and uniqueness of nonlinear fractional differential equations with the Caputo and the Atangana-Baleanu derivatives: Maximal, minimal and Chaplygin approaches

Abdon Atangana ^{1,2,3
,
,}

1.
Institute for Groundwater Studies, Faculty of Natural and Agricultural Sciences, University of the Free State, Bloemfontein, 9301, South Africa
2.
Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
3.
IT4Innovations, VSB – Technical University of Ostrava, Czech Republic

Received: 25 June 2024 Revised: 06 August 2024 Accepted: 07 August 2024 Published: 11 September 2024
MSC : 34A08, 34A12

This work provided a detailed theoretical analysis of fractional ordinary differential equations with Caputo and the Atangana-Baleanu fractional derivative. The work started with an extension of Tychonoff's fixed point and the Perron principle to prove the global existence with extra conditions due to the properties of the fractional derivatives used. Then, a detailed analysis of the existence of maximal and minimal solutions was presented for both cases. Then, using Chaplygin's approach with extra conditions, we also established the existence and uniqueness of the solutions of these equations. The Abel and the Bernoulli equations were considered as illustrative examples and were solved using the fractional middle point method.

Keywords:

Citation: Abdon Atangana. Existence and uniqueness of nonlinear fractional differential equations with the Caputo and the Atangana-Baleanu derivatives: Maximal, minimal and Chaplygin approaches[J]. AIMS Mathematics, 2024, 9(10): 26307-26338. doi: 10.3934/math.20241282

Related Papers:

[1]	Mohammed A. Almalahi, Satish K. Panchal, Fahd Jarad, Mohammed S. Abdo, Kamal Shah, Thabet Abdeljawad . Qualitative analysis of a fuzzy Volterra-Fredholm integrodifferential equation with an Atangana-Baleanu fractional derivative. AIMS Mathematics, 2022, 7(9): 15994-16016. doi: 10.3934/math.2022876
[2]	Kishor D. Kucche, Sagar T. Sutar, Kottakkaran Sooppy Nisar . Analysis of nonlinear implicit fractional differential equations with the Atangana-Baleanu derivative via measure of non-compactness. AIMS Mathematics, 2024, 9(10): 27058-27079. doi: 10.3934/math.20241316
[3]	Najat Almutairi, Sayed Saber . Chaos control and numerical solution of time-varying fractional Newton-Leipnik system using fractional Atangana-Baleanu derivatives. AIMS Mathematics, 2023, 8(11): 25863-25887. doi: 10.3934/math.20231319
[4]	Saeed M. Ali, Mohammed S. Abdo, Bhausaheb Sontakke, Kamal Shah, Thabet Abdeljawad . New results on a coupled system for second-order pantograph equations with $ \mathcal{ABC} $ fractional derivatives. AIMS Mathematics, 2022, 7(10): 19520-19538. doi: 10.3934/math.20221071
[5]	Muhammad Altaf Khan, Muhammad Ismail, Saif Ullah, Muhammad Farhan . Fractional order SIR model with generalized incidence rate. AIMS Mathematics, 2020, 5(3): 1856-1880. doi: 10.3934/math.2020124
[6]	Mohamed I. Abbas, Maria Alessandra Ragusa . Nonlinear fractional differential inclusions with non-singular Mittag-Leffler kernel. AIMS Mathematics, 2022, 7(11): 20328-20340. doi: 10.3934/math.20221113
[7]	Hasib Khan, Jehad Alzabut, J.F. Gómez-Aguilar, Praveen Agarwal . Piecewise mABC fractional derivative with an application. AIMS Mathematics, 2023, 8(10): 24345-24366. doi: 10.3934/math.20231241
[8]	Eman A. A. Ziada, Salwa El-Morsy, Osama Moaaz, Sameh S. Askar, Ahmad M. Alshamrani, Monica Botros . Solution of the SIR epidemic model of arbitrary orders containing Caputo-Fabrizio, Atangana-Baleanu and Caputo derivatives. AIMS Mathematics, 2024, 9(7): 18324-18355. doi: 10.3934/math.2024894
[9]	Abdelatif Boutiara, Mohammed M. Matar, Jehad Alzabut, Mohammad Esmael Samei, Hasib Khan . On $ \mathcal{A B C} $ coupled Langevin fractional differential equations constrained by Perov's fixed point in generalized Banach spaces. AIMS Mathematics, 2023, 8(5): 12109-12132. doi: 10.3934/math.2023610
[10]	Rahat Zarin, Abdur Raouf, Amir Khan, Aeshah A. Raezah, Usa Wannasingha Humphries . Computational modeling of financial crime population dynamics under different fractional operators. AIMS Mathematics, 2023, 8(9): 20755-20789. doi: 10.3934/math.20231058

Abstract

1. Introduction

Many real-world problems occurring in various disciplines of study exhibit nonlinear characteristics; see, for example, the identification of nonlinear biological systems ^[1], fresh breath ^[2], and some nonlinear challenges in biology ^[3]. Many researchers from various backgrounds have expressed an interest in modeling these processes. Nonlinear ordinary differential equations, in particular, have been utilized by mathematicians to recreate such tendencies. Indeed, order exists beneath the diversity of life and the complexity of ecology, reflecting the operation of fundamental physical and biological processes. Power laws are emergent quantitative aspects of biodiversity that represent empirical scaling connections; see, for instance, power law and the Pareto distribution ^[4], Fechner's and Steven's law ^[5], and the theory of behavioral power function ^[5]. These characteristics are structural or dynamic patterns that are self-similar or fractal-like over many orders of magnitude. We can list the scaling of tropical cyclone dissipation ^[6]. Extrapolation and prediction over a wide range of scales are possible with power laws. Some appear to be ubiquitous, appearing in almost all taxa of creatures and situations. They provide insights into the underlying mechanisms that powerfully and nonlinearly restrict biodiversity. We outline recent accomplishments and future prospects for understanding the mechanisms that generate these power laws, as well as for explaining species variety and ecosystem complexity in terms of fundamental nonlinear physics and nonlinear biological science principles; see, for instance, the power law of dust devil diameters on earth and mars ^[7], the gene family ^[8], decreasing failure rates ^[9], and polymetric damping materials ^[10]. While many natural processes exhibit nonlinearities approximating power-law-like tendencies ^[11], many also exhibit crossover patterns. The transition from stretched exponential to power law is a good example. This means that after a certain amount of time, the process exhibits behaviors such as stretched exponential, after which power-law behaviors are noticed ^[12,13]. Modeling fractional-order viscoelastic materials is one application of the Mittag-Leffler function ^[13]. Experiments on the time-dependent relaxation behavior of viscoelastic materials reveal a very fast decrease in stress at the start of the relaxation process and an exceedingly sluggish decay for long timeframes. It may even take a long time to obtain a constant asymptotic value. The Caputo and Riemann-Liouville derivatives are differential operators based on the power law in the realm of fractional differentiation, making them good candidates for modeling processes with similar power-law behavior. The Atangana-Baleanu derivative, on the other hand, is based on the generalized Mittag-Leffler kernel, which has the property of crossing from the stretched exponential to the power law ^[12,13]. As a result, it is the best contender for modeling processes that follow these difficulties. While nonlinear ordinary differential equations with the Caputo and Atangana-Baleanu fractional derivatives are essential classes for modeling power law and crossover processes, there are no analytical methods for solving these equations. To solve these equations, researchers primarily employ numerical methods ^[14]. But first, it is a good idea to research the existence and originality of their solutions ^[15,16]. There are numerous methods for investigating the existence and uniqueness of nonlinear classical ordinary differential equations. The maximal-minimal principle and the Chaplygin approach ^[17,18] were two ideas that piqued our interest ^{[15,16,17,18]}, as was the Perron method for global existence and uniqueness ^[19,20]. To highlight the importance of the Mittag-Leffler kernel used to obtain the Atangana-Baleanu fractional derivative, we ask the readers to see the following reference: ^[21] In this work, the authors presented a detailed analysis of the properties of the power law kernel that is used in the Caputo and the Riemann-Liouville fractional derivatives, the Mittag-Leffler kernel that is used in the Atangana-Baleanu fractional derivative, and the exponential decay function used in the Caputo-Fabrizio derivative. They have also highlighted the possible applications of these kernels in modeling complex real-world problems. Beside these outstanding results, different authors have also presented the importance of the Mittag-Leffler used in the Atangana-Baleanu in Caputo sense (ABC) derivative; see, for instance, this paper ^[22]. While these papers have been recognized as outstanding results within the field of fractional calculus, an argument about the initial condition for differential equations with the ABC derivative was raised; however, the following paper ^[23] showed that this argument was not mathematically correct. The fundamental theorem between the differential and integral operators for the ABC case was presented in many papers. These results then show that there is equivalence between fractional ordinary differential equations with the ABC derivative and their component with the AB integral ^[24]. In this paper, these results will not be repeated as they have been well-established and are very well-known. The first strategy requires finding maximal and minimal solutions to the equations, while the second requires constructing rising and decreasing sequences that bound the solution, and these two converge as n approaches infinity. This will be the focus of this project.

2. Global existence and uniqueness via Tychonoff's fixed-point and Perron principle

In this part, we will show how to use Tychonoff's fixed-point and the Perron principle to prove the global existence of a fractional Cauchy problem using the Caputo and Atangana-Baleanu differential operators. Because of the features of fractional differential operators, this will be accomplished with additional conditions.

2.1. Global existence and uniqueness for fractional differential equations with Caputo derivative

In this work, we shall consider the following general Caputo fractional differential equations:

$\begin{align} _{t_{0}}^{C}D_{t}^{\alpha}y(t) & = f\left( t, y(t)\right) , { \ }0 < \alpha < 1\ \ \ \text{if }t > t_{0}, \\ y(t_{0}) & = y_{0} , \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{if } t = t_{0}. \end{align}$

(2.1)

2.1.1. Global existence

We shall make use of the Tychonoff's fixed-point which uses the locally convex linear spaces to demonstrate the global existence of the solution of the fractional differential equations with the Caputo derivative. We shall note that $f\in C\left[I\times R, R\right]$ , where indeed $I = [t_{0}, \infty).$

Theorem 2.1. Let A be a complete locally convex, linear space and $A_{0}$ is a closed convex subset of $A.$ Let $\overline{\Gamma}$ be a mapping continuous and $\overline{\Gamma}\left(A_{0}\right) \subset A_{0}$ . If $\overline{\Gamma}\left(A_{0}\right)$ is compact, then $\overline {\Gamma}$ has a fixed point in $A_{0}$ .

Theorem 2.2. Let $f\in C\left[I\times R, R\right]$ and $\forall\left(t, y\right) \in I\times R,$

$\begin{equation} \left\vert f\left( t, y\right) \right\vert \leq g\left( t, \left\vert y\right\vert \right) . \end{equation}$

(2.2)

Here, if $f\in C\left[I\times R, R\right]$ and the function $g\left(t, y\right)$ is monotonic nondecreasing in $y$ , $\forall t\in I,$ let us assume that $\forall x_{0} > 0$ , the differential equation

$\begin{align} _{t_{0}}^{C}D_{t}^{\alpha}x(t) & = g\left( t, x(t)\right) , 0 < \alpha < 1\ \ \ \;\mathit{\text{if}}\;t\in(t_{0}, \infty), \\ x(t_{0}) & = x_{0} , \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;\mathit{\text{if}}\; t = t_{0}, \end{align}$

(2.3)

has a solution $x(t) = x\left(t, t_{0}, x_{0}\right)$ when $t > t_{0}.$ Then $\forall y_{0}\in R$ , such that $\left\vert y_{0}\right\vert \leq x_{0}$ , and there exists a solution $y(t) = y\left(t, t_{0}, y_{0}\right)$ of the fractional differential equations with Caputo derivative for $t\geq t_{0}$ that satisfies

$\begin{equation} \left\vert y(t)\right\vert \leq\left\vert x(t)\right\vert \mathit{\text{, }}t > t_{0}. \end{equation}$

(2.4)

Proof. We consider $A$ the space of all continuous functions from $[t_{0}, \infty)\rightarrow R$ , with the topology of $A$ equipped with norm

$\begin{equation} \left\Vert y\right\Vert _{\infty} = \underset{t_{0}\leq t < \infty}{\sup }\left\vert y(t)\right\vert . \end{equation}$

(2.5)

A fundamental neighborhood is given by

$\begin{equation} A_{0} = \left\{ y\in A:p\left( y\right) \leq1\right\} . \end{equation}$

(2.6)

Of course, within the defined topology, the set $A$ is a complete, locally convex, linear space and $p$ is a defined norm. Let $A_{0}\subset A$ defined as

$\begin{equation} A_{0} = \left\{ y\in A:\left\vert y(t)\right\vert \leq\left\vert x(t)\right\vert , \;\forall t > t_{0}\right\} , \end{equation}$

(2.7)

where $x(t)$ is the same as defined before. From ^[15], we have that $A_{0}\subset A$ is a closed set, convex, and bounded. We now consider the mapping

$\begin{equation} \overline{\Gamma}y(t) = y_{0}+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau , y(\tau)\right) d\tau, \end{equation}$

(2.8)

$\overline{\Gamma}y(t) = y(t)$ is the solution of the fractional differential equations with the Caputo fractional derivative. It is clear that for any bounded sequence $\left(y_{n}\right) _{n}\in A_{0}$ , the sequence $\left(\overline{\Gamma}y_{n}\right) _{n\in N}$ contains a converging subsequence, therefore $\overline{\Gamma}$ is compact; thus, $\overline{\Gamma}\left(A_{0}\right)$ in the view of the boundness of $A_{0}.$ We shall now show that $\overline{\Gamma}\left(A_{0}\right) \subset A_{0}$ , let $y\in A$ and

$\begin{align} \overline{\Gamma}y(t) & = y_{0}+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau , y(\tau)\right) d\tau, \\ \left\vert \overline{\Gamma}y(t)\right\vert & = \left\vert y_{0}+\frac {1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, y(\tau)\right) d\tau\right\vert \\ & \leq\left\vert y_{0}\right\vert +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert f\left( \tau, y(\tau)\right) \right\vert d\tau\\ & \leq\left\vert y_{0}\right\vert +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}g\left( \tau, \left\vert y(\tau)\right\vert \right) d\tau. \end{align}$

(2.9)

By definition, $g$ is monotone in $y$ , the formula of $A_{0}$ , and the solution $x(t)$ such that $\left\vert y_{0}\right\vert \leq x_{0}$ leads to

$\begin{equation} \left\vert \overline{\Gamma}y(t)\right\vert \leq x_{0}+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha -1}g\left( \tau, x(\tau)\right) d\tau = x(t). \end{equation}$

(2.10)

Therefore,

$\begin{equation} \left\vert \overline{\Gamma}y(t)\right\vert \leq x(t), \end{equation}$

(2.11)

which completes the proof. That is to say,

$\begin{equation} \overline{\Gamma}\left( A_{0}\right) \subset A_{0}. \end{equation}$

(2.12)

□

2.1.2. Uniqueness

We shall borrow the Perron's criteria to show the uniqueness of the equation under investigation ^[19].

Theorem 2.3. Let us assume that the defined function $g\left(t, x\right)$ is continuous for $t_{0}\leq t\leq t_{0}+c$ , $0\leq x\leq2d$ and that for $t_{0}\leq t_{1}\leq t_{0}+c$ , $x(t) = 0$ is the only differentiable function on $t_{0}\leq t\leq t_{1}$ that satisfies

$\begin{equation} _{t_{0}}^{C}D_{t}^{\alpha}x(t) = g\left( t, x(t)\right) , \; 0 < \alpha < 1, \;x(t_{0}) = 0, \;\forall t\in\lbrack t_{0}, t_{1}]. \end{equation}$

(2.13)

Let $f\in C\left[\overline{R}_{0}, R\right]$ where we define

$\begin{equation} \overline{R}_{0} = \left\{ \left( t, y\right) :t_{0}\leq t\leq t_{0}+c, \;\left\vert y-y_{0}\right\vert < 2d\right\}, \end{equation}$

(2.14)

$\forall(t, y_{1})\in\overline{R}_{0}$ and $\forall(t, y_{2})\in\overline{R} _{0}$ ,

$\begin{equation} \left\vert f(t, y_{1})-f(t, y_{2})\right\vert \leq g\left( t, \left\vert y_{1}-y_{2}\right\vert \right). \end{equation}$

(2.15)

Then, $_{t_{0}}^{C}D_{t}^{\alpha}y(t) = f\left(t, y(t)\right)$ has one unique solution in $\left[t_{0}, t_{0}+c\right].$

Proof. Let $y_{1}(t)$ and $y_{2}(t)$ be two different solutions $\forall t\in\left[t_{0}, t_{0}+c\right]$ with

$y_{1}(t_{0}) = y_{2}(t_{0}) = x(t_{0}) = 0.$

We let

$\begin{equation} z(t) = y_{1}(t)-y_{2}(t), \end{equation}$

(2.16)

$\begin{align} z(t) & = \frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left( t-\tau\right) ^{\alpha-1}\left( f\left( \tau, y_{1} (\tau)\right) -f\left( \tau, y_{2}(\tau)\right) \right) d\tau, \\ \left\vert z(t)\right\vert & = \left\vert \frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha -1}\left( f\left( \tau, y_{1}(\tau)\right) -f\left( \tau, y_{2} (\tau)\right) \right) d\tau\right\vert \\ & \leq\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert f\left( \tau, y_{1}(\tau)\right) -f\left( \tau, y_{2}(\tau)\right) \right\vert d\tau. \end{align}$

(2.17)

By hypothesis, we have that

$\begin{equation} \left\vert z(t)\right\vert \leq\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}g\left( t, \left\vert y_{1}-y_{2}\right\vert \right) d\tau, \end{equation}$

(2.18)

but note that

$\begin{equation} z(t_{0}) = y_{1}(t_{0})-y_{2}(t_{0}). \end{equation}$

(2.19)

Since the initial condition is unique, therefore

$\begin{equation} z(t_{0}) = 0. \end{equation}$

(2.20)

For any $t_{1}$ such that $t_{0} < t_{1} < t_{0}+c$ , we have that

$\begin{equation} z(t)\leq\Omega\left( t\right) \text{, }t_{0}\leq t < t_{1}, \end{equation}$

(2.21)

where $\Omega\left(t\right)$ is the maximum solution of Eq (2.13). From the first hypothesis of the theorem, we have that $z(t) = 0$ in $[t_{0}, t_{1}]$ is to say

$\begin{equation} y_{1}(t) = y_{2}(t), \;\forall t\in\lbrack t_{0}, t_{1}], \end{equation}$

(2.22)

which completes the proof. □

2.2. Global existence and uniqueness for fractional differential equations with the Atangana-Baleanu fractional derivative

In this section, using the Tychonoff's fixed-point and the Perron principle with some extra conditions, we shall investigate the existence and the uniqueness of a general Cauchy problem with the Atangana-Baleanu fractional differential operator.

In this section, we shall consider the following fractional differential equations with

$\begin{align} _{t_{0}}^{ABC}D_{t}^{\alpha}y(t) & = f\left( t, y(t)\right) , { \ }0 < \alpha < 1\ \text{if }\;t > t_{0}, \\ y(t_{0}) & = y_{0} , \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{if }t = t_{0} . \end{align}$

(2.23)

2.2.1. Existence

We shall assume that all the conditions prescribed before hold. We also assume that the defined sets $A$ and $A_{0}$ hold here, too. Here, we shall define the following mapping

$\begin{equation} \Lambda y(t) = y(t_{0})+\left( 1-\alpha\right) f\left( t, y(t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, y(\tau)\right) d\tau. \end{equation}$

(2.24)

$\Lambda y(t) = y(t)$ is indeed the solution of the fractional differential equations with the Atangana-Baleanu fractional derivative. Clearly, $\Lambda$ is a linear mapping if $f$ is linear with respect to $y.$ Let $\left(y_{n}\right) _{n\in N}\in A_{0}$ be bounded, and we have that

$\begin{align} \Lambda y_{n}(t) & = y(t_{0})+\left( 1-\alpha\right) f\left( t, y_{n} (t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, y_{n}(\tau)\right) d\tau, \\ \left\vert \Lambda y_{n}(t)\right\vert & = \left\vert y_{0}\right\vert +\left( 1-\alpha\right) \left\vert f\left( t, y_{n}(t)\right) \right\vert +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert f\left( \tau, y_{n}(\tau)\right) \right\vert d\tau \\ & \leq\left\vert y_{0}\right\vert +\left( 1-\alpha\right) g\left( t, \left\vert y_{n}\right\vert \right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha -1}g\left( \tau, \left\vert y_{n}(\tau)\right\vert \right) d\tau. \end{align}$

(2.25)

Since $\left(y_{n}\right) _{n\in N}$ is bounded in $A_{0},$ $\exists N$ such that $\forall n\geq N,$ $\left\vert y_{n}\right\vert < M$ with $M > 0$ , therefore

$\begin{align} \left\vert \Lambda y_{n}(t)\right\vert & \leq\left\vert y_{0}\right\vert +\left( 1-\alpha\right) g\left( t, M\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha -1}g\left( \tau, M\right) d\tau\\ & \leq\left\vert y_{0}\right\vert +\left( 1-\alpha\right) \underset{t\in I}{\sup}\left\vert g\left( t, M\right) \right\vert +\frac{\alpha} {\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\underset{\tau\in I}{\sup}\left\vert g\left( \tau, M\right) \right\vert d\tau\\ & \leq\left\vert y_{0}\right\vert +\left( 1-\alpha\right) M_{g} +\frac{\alpha M_{g}}{\Gamma\left( \alpha+1\right) }\left( t-t_{0}\right) ^{\alpha} < \infty. \end{align}$

(2.26)

Therefore, $\left(\Lambda y_{n}\right) _{n\in N}$ is bounded. Since $\left(\Lambda y_{n}\right) _{n\in N}$ is bounded in real space, we have that there exists a subsequence of $\left(\Lambda y_{nl}\right) _{n\in N}$ of $\left(\Lambda y_{n}\right)$ that converges. Therefore, the mapping is compact in the topology of $A$ and thus $\Lambda\left(A_{0}\right)$ is compact because of the boundness of $A_{0}$ . We shall now show that

$\begin{equation} \Lambda\left( A_{0}\right) \subset A_{0}, \end{equation}$

(2.27)

$\forall y\in A_{0}$ , and we have

$\begin{align} \left\vert \Lambda y(t)\right\vert & = \left\vert y(t_{0})+\left( 1-\alpha\right) f\left( t, y(t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha -1}f\left( \tau, y(\tau)\right) d\tau\right\vert \\ & \leq\left\vert y(t_{0})\right\vert +\left( 1-\alpha\right) \left\vert f\left( t, y(t)\right) \right\vert +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha -1}\left\vert f\left( \tau, y(\tau)\right) \right\vert d\tau\\ & \leq\left\vert y(t_{0})\right\vert +\left( 1-\alpha\right) g\left( t, \left\vert y\right\vert \right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}g\left( \tau, \left\vert y\right\vert \right) d\tau \\ & \leq\left\vert y(t_{0})\right\vert +\left( 1-\alpha\right) g\left( t, x(t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int \limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}g\left( \tau , x(\tau)\right) d\tau \\ & = x(t). \end{align}$

(2.28)

Therefore,

$\begin{equation} \left\vert \Lambda y(t)\right\vert \leq x(t), \end{equation}$

(2.29)

which shows

$\begin{equation} \Lambda\left( A_{0}\right) \subset A_{0}, \end{equation}$

(2.30)

and the proof is completed.

2.2.2. Uniqueness

For the uniqueness, we set all the hypotheses as before, then let $y_{1}(t)$ and $y_{2}(t)$ be different solutions in $R,$ $\forall t\in\left[t_{0}, t_{0}+c\right]$ with

$y_{1}(t_{0}) = y_{2}(t_{0}) = x(t_{0}) = 0.$

We let

$\begin{align} z(t)& = \left\vert y_{1}(t)-y_{2}(t)\right\vert, \end{align}$

(2.31)

$\begin{align} z(t) & \leq\left( 1-\alpha\right) \left\vert f\left( t, y_{1}(t)\right) -f\left( t, y_{2}(t)\right) \right\vert \\ &\quad +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert f\left( \tau, y_{1}(\tau)\right) -f\left( \tau, y_{2}(\tau)\right) \right\vert d\tau \\ & \leq\left( 1-\alpha\right) g\left( t, \left\vert y_{1}-y_{2}\right\vert \right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left( t-\tau\right) ^{\alpha-1}g\left( \tau, \left\vert y_{1} -y_{2}\right\vert \right) d\tau \\ & \leq\left( 1-\alpha\right) g\left( t, z(t)\right) +\frac{\alpha} {\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}g\left( \tau, z(\tau)\right) d\tau.\nonumber \end{align}$

(2.32)

Noting $z(t_{0}) = 0$ by the theorem hypothesis, and $\forall t_{1}$ such that $t_{0} < t_{1} < t_{0}+c$ , we have that

$\begin{equation} z(t)\leq r\left( t\right) , \;t_{0}\leq t < t_{1}. \end{equation}$

(2.33)

Assuming $r\left(t\right)$ is the maximal solution, we shall have

$\begin{equation} z(t) = 0, \;\forall t\in t_{0}\leq t < t_{1}, \end{equation}$

(2.34)

which completes the proof.

3. Existence of maximal and minimal solution

In this section, we shall present the existence of the maximal and minimal solution of the fractional differential equations with the ABC and Caputo fractional derivative ^[15]. We shall start with the Caputo case.

Theorem 3.1. Let $f\in C\left[R_{0}, R\right],$ where $R_{0}$ is defined as

$\begin{equation} R_{0} = \left\{ \left( t, y\right) \left\vert t_{0} < t < t_{0}+a, \;\left\vert y-y_{0}\right\vert \leq b\right. \right\}, \end{equation}$

(3.1)

and we assume that $f\left(t, y(t)\right)$ is bounded for any fixed $t$ and $y$ in $R_{0}.$ Then there exist a maximal and minimal solution of

$\begin{align} _{t_{0}}^{C}D_{t}^{\alpha}y(t) & = f\left( t, y(t)\right) , \;0 < \alpha < 1, \ \;\mathit{\text{if}}\;t > t_{0}, \\ y(t_{0}) & = y_{0} , \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;\mathit{\text{if}}\; t = t_{0}, \end{align}$

(3.2)

on $\left[t_{0}, t_{0}+\beta\right]$ , $\beta = \min\left\{ a, \left(\frac{b\Gamma\left(\alpha+1\right) }{2M+b}\right) ^{\frac{1}{\alpha} }\right\}.$

Proof. We shall prove maximal first since minimal will be deduced similary. Let $0 < \xi\leq\frac{b}{2}.$ Let us consider

$\begin{equation} _{t_{0}}^{C}D_{t}^{\alpha}y(t) = f\left( t, y(t)\right) +\xi\text{, }y_{\xi }\left( t_{0}\right) = y_{0}+\xi. \end{equation}$

(3.3)

We can define

$\begin{equation} f_{\xi}\left( t, y\right) = f\left( t, y\right) +\xi. \end{equation}$

(3.4)

Since $f\in C\left[R_{0}, R\right]$ , clearly $f_{\xi}$ is continous on

$\begin{equation} R_{\xi}:t_{0}\leq t\leq t_{0}+a, \;\left\vert y-y_{\xi}\left( t_{0}\right) \right\vert \leq\frac{b}{2}. \end{equation}$

(3.5)

Then, let $\left(\overline{t}, \overline{y}\right) \in R_{\xi},$ and indeed $\overline{t}\in\left[t_{0}, t_{0}+a\right],$

$\begin{align} \overline{y}& = y_{\xi}\left( t_{0}\right) +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{\overline{t}}\left( \overline{t} -\tau\right) ^{\alpha-1}f_{\xi}\left( \tau, \overline{y}\right) d\tau, \end{align}$

(3.6)

$\begin{align} \left\vert \overline{y}-y_{\xi}\left( t_{0}\right) \right\vert & \leq \frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{\overline{t} }\left( \overline{t}-\tau\right) ^{\alpha-1}\left\vert f_{\xi}\left( \tau, \overline{y}\right) \right\vert d\tau \\ & \leq\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{\overline{t}}\left( \overline{t}-\tau\right) ^{\alpha-1}\left\vert f\left( \tau, \overline{y}\right) +\xi\right\vert d\tau\\ & \leq\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{\overline{t}}\left( \overline{t}-\tau\right) ^{\alpha-1}\left\vert f\left( \tau, \overline{y}\right) \right\vert d\tau+\frac{\left( \overline{t}-t_{0}\right) ^{\alpha}}{\Gamma\left( \alpha+1\right) }\xi\\ & \leq\frac{M\left( \overline{t}-t_{0}\right) ^{\alpha}}{\Gamma\left( \alpha+1\right) }+\frac{\left( \overline{t}-t_{0}\right) ^{\alpha}} {\Gamma\left( \alpha+1\right) }\xi.\nonumber \end{align}$

(3.7)

Since $f(t, y)$ is bounded,

$\begin{align} \left\vert \overline{y}-y_{\xi}\left( t_{0}\right) \right\vert & \leq \frac{\left( \overline{t}-t_{0}\right) ^{\alpha}}{\Gamma\left( \alpha+1\right) }\left\{ M+\xi\right\} \\ & \leq\frac{a^{\alpha}}{\Gamma\left( \alpha+1\right) }\left\{ M+\xi\right\} \leq\frac{a^{\alpha}}{\Gamma\left( \alpha+1\right) }\left\{ 2M+b\right\}. \end{align}$

(3.8)

Therefore,

$\begin{equation} R_{\xi}\subset R_{0}. \end{equation}$

(3.9)

In Peano's existence theorem, there exists a solution to the initial value problem,

$\begin{equation} _{t_{0}}^{C}D_{t}^{\alpha}y(t) = f\left( t, y(t)\right) +\xi, \; \end{equation}$

(3.10)

say $y\left(t, \xi\right)$ on $\left[t_{0}, t_{0}+\beta\right]$ where $\beta = \min\left\{ a, \left(\frac{b\Gamma\left(\alpha+1\right) } {2M+b}\right) ^{\frac{1}{\alpha}}\right\}.$

We proceed with $\xi_{1}$ and $\xi_{2}$ such that $0 < \xi_{2} < \xi_{1}\leq\xi.$ We shall have that

$\begin{equation} y_{\xi_{2}}(t_{0}) < y_{\xi_{1}}(t_{0})\leq y_{\xi}(t_{0}), \end{equation}$

(3.11)

therefore

$\begin{align} y_{\xi_{2}}(t) & = y_{\xi_{2}}\left( t_{0}\right) +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}f_{\xi_{2}}\left( \tau, y\right) \left( t-\tau\right) ^{\alpha-1}d\tau, \\ \left\vert y_{\xi_{2}}(t)\right\vert & \leq\left\vert y_{\xi_{2}}\left( t_{0}\right) \right\vert +\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\left\vert f_{\xi_{2}}\left( \tau, y\right) \right\vert \left( t-\tau\right) ^{\alpha-1}d\tau\\ & \leq\left\vert y_{\xi_{2}}\left( t_{0}\right) \right\vert +\frac {1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left\vert f\left( \tau, y\right) +\xi_{2}\right\vert \left( t-\tau\right) ^{\alpha-1} d\tau\\ & \leq\left\vert y_{\xi_{2}}\left( t_{0}\right) \right\vert +\frac {1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left\vert f\left( \tau, y\right) \right\vert \left( t-\tau\right) ^{\alpha-1}d\tau +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\xi _{2}\left( t-\tau\right) ^{\alpha-1}d\tau\\ & \leq\left\vert y_{\xi_{2}}\left( t_{0}\right) \right\vert +\frac{\left( t-t_{0}\right) ^{\alpha}\xi_{2}}{\Gamma\left( \alpha+1\right) } +\frac{\left( t-t_{0}\right) ^{\alpha}M}{\Gamma\left( \alpha+1\right) }\\ & \leq\left\vert y_{\xi_{2}}\left( t_{0}\right) \right\vert +\frac {a^{\alpha}\xi_{2}}{\Gamma\left( \alpha+1\right) }+\frac{a^{\alpha}M} {\Gamma\left( \alpha+1\right) } < \left\vert y_{\xi_{1}}(t)\right\vert. \end{align}$

(3.12)

This can also be demonstrated by simple evaluating

$\begin{equation} \left\vert y_{\xi_{1}}(t)-y_{\xi_{2}}(t)\right\vert = \left\vert \xi_{1} -\xi_{2}\right\vert +\frac{1}{\Gamma\left( \alpha\right) }\int \limits_{t_{0}}^{t}\left\vert \xi_{1}-\xi_{2}\right\vert \left( t-\tau\right) ^{\alpha-1}d\tau. \end{equation}$

(3.13)

Noting $\exists\overline{\xi} = \xi_{1}-\xi_{2} > 0$ , we have that

$\begin{align} \left\vert y_{\xi_{1}}(t)-y_{\xi_{2}}(t)\right\vert & = \overline{\xi} +\frac{\left( t-t_{0}\right) ^{\alpha}\overline{\xi}}{\Gamma\left( \alpha+1\right) } = \overline{\xi}\left( 1+\frac{a^{\alpha}}{\Gamma\left( \alpha+1\right) }\right)\\ & = \overline{\xi}\left( 1+\frac{a^{\alpha}}{\Gamma\left( \alpha+1\right) }\right) > 0. \end{align}$

(3.14)

Then, again $R_{\xi_{2}} < R_{\xi_{1}}\leq R_{\xi} < R_{0}.$ We can indeed conclude that the functions $y\left(t, \xi\right)$ are equi-continuous and uniformly bounded on $\left[t_{0}, t_{0}+\beta\right].$ Therefore, we can find a decreasing sequence $\left(\xi_{n}\right)$ such that $\xi_{n}\rightarrow0$ and the uniform limit $n\rightarrow \infty$

$\begin{equation} \overline{y}(t) = \underset{n\rightarrow \infty}{\lim}y\left( t, \xi_{n}\right) , \end{equation}$

(3.15)

exists on $\left[t_{0}, t_{0}+\beta\right],$ ; for a start, see $\overline {y}(t_{0}) = y_{0}.$

$\begin{align} y\left( t, \xi_{n}\right) & = y_{0}+\xi_{n}+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}f\left( \tau, y\left( \tau, \xi _{n}\right) \right) \left( t-\tau\right) ^{\alpha-1}d\tau, \end{align}$

(3.16)

$\begin{align} \overline{y}(t) & = \underset{n\rightarrow \infty}{\lim}y\left( t, \xi _{n}\right) = \underset{n\rightarrow \infty}{\lim}\left( y_{0}+\xi_{n} +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}f\left( \tau, y\left( \tau, \xi_{n}\right) \right) \left( t-\tau\right) ^{\alpha -1}d\tau\right) \\ &= y_{0}+\underset{n\rightarrow \infty}{\lim}\xi_{n}+\underset{n\rightarrow \infty}{\lim}\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}f\left( \tau, y\left( \tau, \xi_{n}\right) \right) \left( t-\tau\right) ^{\alpha-1}d\tau.\nonumber \end{align}$

(3.17)

However, we have $f$ being a uniform continuous function on $\left[t_{0}, t_{0}+\beta\right]$ , therefore

$\begin{align} &\underset{n\rightarrow \infty}{\lim}f\left( t, y\left( t, \xi_{n}\right) \right) = f\left( t, \overline{y}(t)\right), \end{align}$

(3.18)

$\begin{align} &\overline{y}(t) = y_{0}+\frac{1}{\Gamma\left( \alpha\right) }\int \limits_{t_{0}}^{t}f\left( \tau, \overline{y}\left( \tau\right) \right) \left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.19)

Therefore, $\overline{y}(t)$ is a solution of

$\begin{equation} y(t) = y_{0}+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}f\left( \tau, y\left( \tau\right) \right) \left( t-\tau\right) ^{\alpha-1}d\tau, \end{equation}$

(3.20)

$\forall y\left(t\right)$ solution of

$\begin{align} _{t_{0}}^{C}D_{t}^{\alpha}y(t) & = f\left( t, y(t)\right) , \ \ \text{if }t > t_{0}, \\ y(t_{0}) & = y_{0}, \ \ \ \ \ \ \ \ \ \ \ \text{if }t = t_{0}, \end{align}$

(3.21)

on $\left[t_{0}, t_{0}+\beta\right]$ , then

$\begin{align} &y(t_{0}) = y_{0} < y_{0}+\xi = y\left( t_{0}, \xi\right) , \\ & _{t_{0}}^{C}D_{t}^{\alpha}y(t) \leq_{t_{0}}^{C}D_{t}^{\alpha} y(t, \xi), \end{align}$

(3.22)

for $t\in\left[t_{0}, t_{0}+\beta\right]$ and $\xi\leq\frac{b}{2}$ , and we surely have that

$\begin{equation} y(t) < y(t, \xi){ \ \ \ \ \ }\forall t\in\left[ t_{0}, t_{0}+\beta\right]. \end{equation}$

(3.23)

The uniqueness of the maximal solution shows that

$\begin{equation} \underset{\xi\rightarrow0}{\lim}y(t, \xi) = \overline{y}(t), \end{equation}$

(3.24)

uniformly. The proof is therefore completed. For minimal, it is only to consider

$\begin{equation} y_{\xi}(t_{0}) = y_{0}-\xi. \end{equation}$

(3.25)

□

We assume that all the conditions of the theorem above holds only with the adjustment that

$\begin{align} &\beta = \min\left\{ a, \left( \frac{b+\left( \alpha-1\right) \left( M+\frac{b}{2}\right) \Gamma\left( \alpha+1\right) }{M+\frac{b}{2}}\right) ^{\frac{1}{\alpha}}\right\}, \end{align}$

(3.26)

$\begin{align} &_{t_{0}}^{ABC}D_{t}^{\alpha}y(t) = f\left( t, y(t)\right) +\xi, \ \ \text{ if }t > t_{0}, \\ &y(t_{0}) = y_{0}+\xi, \ \ \ \text{if }t = t_{0}.\nonumber \end{align}$

(3.27)

We shall put

$\begin{align} y_{\xi}\left( t\right) = y_{\xi}\left( t_{0}\right) +\frac{\alpha }{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}f_{\xi}\left( \tau, y(\tau)\right) \left( t-\tau\right) ^{\alpha-1}d\tau +(1-\alpha)f_{\xi}\left( t, y(t)\right). \end{align}$

(3.28)

We have that $R_{\xi}\subset R_{0}$ since $\forall(t, y)\in R_{\xi}$ , and we have

$\begin{align} \left\vert y\left( t, \xi\right) -y_{\xi}\left( t_{0}\right) \right\vert & \leq(1-\alpha)\left\{ M+\xi\right\} +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left\{ M+\xi\right\} \left( t-\tau\right) ^{\alpha-1}d\tau\\ & \leq(1-\alpha)\left\{ M+\xi\right\} +\frac{\alpha\left( t-t_{0}\right) ^{\alpha}}{\Gamma\left( \alpha+1\right) }\left\{ M+\xi\right\}\\ & < (1-\alpha)\left\{ M+\frac{b}{2}\right\} +\frac{\alpha a^{\alpha}}{\Gamma\left( \alpha+1\right) }\left\{ M+\frac{b}{2}\right\} \\ & < \left( (1-\alpha)+\frac{a^{\alpha}}{\Gamma\left( \alpha\right) }\right) \left\{ M+\frac{b}{2}\right\} . \end{align}$

(3.29)

Therefore, $R_{\xi}\subset R_{0}.$ We can also deduce that from the Peano's existence theorem, the equation

$\begin{align} y(t) = y(t_{0})+\xi+\left( f\left( t, y(t)\right) +\xi\right) (1-\alpha) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( f\left( \tau, y(\tau)\right) +\xi\right) \left( t-\tau\right) ^{\alpha -1}d\tau, \end{align}$

(3.30)

has a solution on $\left[t_{0}, t_{0}+\beta\right]$ , where

$\begin{equation} \beta = \min\left\{ a, \left( \frac{b+\left( \alpha-1\right) \left( M+\frac{b}{2}\right) \Gamma\left( \alpha\right) }{M+\frac{b}{2}}\right) ^{\frac{1}{\alpha}}\right\} . \end{equation}$

(3.31)

Again, we want to construct a decreasing sequence that converges toward zero when $n\rightarrow \infty$ as done before. We proceed with $\xi_{1}$ and $\xi_{2}$ such that $0 < \xi_{2} < \xi_{1}\leq\xi\$ , then we have that

$\begin{align} \left\vert y(t, \xi_{1})-y(t, \xi_{2})\right\vert & = \left\vert \xi_{1} -\xi_{2}\right\vert +(1-\alpha)\left\vert \xi_{1}-\xi_{2}\right\vert +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left\vert \xi_{1}-\xi_{2}\right\vert \left( t-\tau\right) ^{\alpha -1}d\tau\\ & = \overline{\varphi}+(1-\alpha)\overline{\varphi}+\frac{ \overline{\varphi}\left( t-t_{0}\right) ^{\alpha}}{\Gamma\left( \alpha\right) }\\ & = \overline{\varphi}\left( 2-\alpha+\frac{\left( t-t_{0}\right) ^{\alpha}}{\Gamma\left( \alpha\right) }\right) > 0. \end{align}$

Therefore,

$\begin{equation} y(t, \xi_{1}) > y(t, \xi_{2})\text{, }\forall t\in\left[ t_{0}, t_{0} +\beta\right] . \end{equation}$

(3.32)

We can repeat this until we reach

$\begin{equation} y(t, \xi) > y(t, \xi_{1}), \end{equation}$

(3.33)

where

$\begin{align} &\xi_{n} < \xi_{n-1} < ... < \xi, \end{align}$

(3.34)

$\begin{align} &y(t)\leq y(t, \xi_{n}) < y(t, \xi). \end{align}$

(3.35)

Taking

$\begin{equation} \overline{y}(t) = \underset{n\rightarrow \infty}{\lim}y(t, \xi_{n}), \text{ }\overline{y}(t_{0}) = y_{0}, \end{equation}$

(3.36)

with $f$ uniformly continuous, we have that

$\begin{align} y(t, \xi_{n}) = y_{0}+\xi_{n}+(1-\alpha)f\left( t, y\left( t, \xi _{n}\right) \right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}f\left( \tau, y\left( \tau, \xi_{n}\right) \right) \left( t-\tau\right) ^{\alpha-1}d\tau, \end{align}$

(3.37)

$\begin{align} \overline{y}(t) & = \underset{n\rightarrow \infty}{\lim}y\left( t, \xi _{n}\right) = \underset{n\rightarrow \infty}{\lim}\left( \begin{array} [c]{c} y_{0}+\xi_{n}+(1-\alpha)f\left( t, y\left( t, \xi_{n}\right) \right) \\ +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}f\left( \tau, y\left( \tau, \xi_{n}\right) \right) \left( t-\tau\right) ^{\alpha -1}d\tau \end{array} \right) , \\ \overline{y}(t) & = \underset{n\rightarrow \infty}{\lim}y\left( t, \xi _{n}\right) = y_{0}+(1-\alpha)f\left( t, \overline{y}\left( t\right) \right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}f\left( \tau, \overline{y}\left( \tau\right) \right) \left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.38)

Let $y(t)$ be any solution to our equation on $\left[t_{0}, t_{0} +\beta\right]$ , then

$\begin{align} &y(t_{0}) = y_{0} < y_{0}+\xi = y_{\xi}(t_{0}), \end{align}$

(3.39)

$\begin{align} &y(t) < y(t_{0})+\xi+(1-\alpha)f\left( t, y\left( t, \xi\right) \right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}f\left( \tau, y\left( \tau, \xi\right) \right) \left( t-\tau\right) ^{\alpha-1}d\tau, \\ & y\left( t, \xi\right) \leq y\left( \left( t, \xi\right) , \xi\right) , \nonumber \end{align}$

(3.40)

for $t\in\left[t_{0}, t_{0}+\beta\right]$ , $\xi\leq\frac{b}{2}.$

3.1. Extension of the Chaplygin's existence and uniqueness approach to fractional differential equations with singular and nonsingular kernel

In this section, we will apply Chaplygin's strategy, which consists of constructing two convergent sequences, one growing and serving as the solution's low bound and the other decreasing and serving as the solution's upper bound ^[18]. Both sequences converge toward the solution of the nonlinear equations as $n$ approaches infinity. To fit the content of nonlinear fractional differential equations with the Atangana-Baleanu and Caputo derivatives, we shall add more conditions to this technique.

Theorem 3.2. Extension of Chaplygin's method: Let $f\in C\left[R_{0}, R\right],$ where $R_{0}$ is defined as

$\begin{equation} R_{0}:\left\{ \left( t, y\right) \left\vert \left\vert t-t_{0}\right\vert < a, \;\left\vert y-y_{0}\right\vert \leq b\right. \right\} . \end{equation}$

(3.41)

We assume that $f\left(t, y(t)\right)$ is bounded for any fixed $t$ and $y$ in $R_{0}$ and

$\begin{equation} \beta = \min\left\{ a, \left( \frac{b\Gamma\left( \alpha+1\right) } {M}\right) ^{\frac{1}{\alpha}}\right\} , \end{equation}$

(3.42)

in case of Caputo, and in case of the Atangana-Baleanu,

$\beta = \min\left\{ a, \left( \frac{\left( b+\left( \alpha-1\right) M\right) \Gamma\left( \alpha\right) }{M}\right) ^{\frac{1}{\alpha} }\right\} .$

We assume that $f_{x}, f_{xx}$ exist and $f_{xx} > 0$ on $R_{0}.$ Let $u_{0} = u_{0}(t)$ , $v_{0} = v_{0}(t)$ , be differentiable for $t_{0}\leq t\leq t_{0}+\beta$ such that $\left(t, u_{0}(t)\right),$ $\left(t, v_{0} (t)\right) \in R_{0}$ , and

$\begin{equation} \left\{ \begin{array} [c]{c} _{t_{0}}^{F}D_{t}^{\alpha}u_{0}(t) < f\left( t, u_{0}(t)\right) \\ u_{0}(t_{0}) = y_{0} \end{array} \right. , \end{equation}$

(3.43)

$\begin{equation} \left\{ \begin{array} [c]{c} _{t_{0}}^{F}D_{t}^{\alpha}v_{0}(t) > f\left( t, v_{0}(t)\right) \\ v_{0}(t_{0}) = y_{0} \end{array} \right. . \end{equation}$

(3.44)

Then, we can find a fractional Chaplygin sequence $\left(u_{n} (t), v_{n}(t)\right)$ such that

$\begin{align} u_{n}(t) & < u_{n+1}(t) < y\left( t\right) \leq v_{n+1}(t) < v_{n}(t)\;t\in(t_{0}, t_{0}+\beta], \\ u_{n}(t_{0}) & = y_{0} = v_{n}(t_{0}), \end{align}$

(3.45)

where $y\left(t\right)$ is the unique solution of

$\begin{equation} \left\{ \begin{array} [c]{c} _{t_{0}}^{F}D_{t}^{\alpha}y(t) = f\left( t, y(t)\right) , \;t\in (t_{0}, t_{0}+\beta], \\ y(t_{0}) = y_{0}, \;t = t_{0}. \end{array} \right. \end{equation}$

(3.46)

Also, $u_{n}(t)$ and $v_{n}(t)\rightarrow y(t)$ uniformly on $\left[t_{0}, t_{0}+\beta\right]$ as $n\rightarrow \infty.$ If in addition, for an adequate $\lambda$ ,

$\begin{equation} 0\leq v_{0}(t)-u_{0}(t)\leq\lambda. \end{equation}$

(3.47)

Then

$\begin{equation} \left\vert u_{n}(t)-v_{n}(t)\right\vert \leq\frac{2\lambda}{2^{2n}}\;t\in\left[ t_{0}, t_{0}+\beta\right] . \end{equation}$

(3.48)

Case with the Caputo fractional derivative:

Proof.

$\begin{equation} \beta = \min\left\{ a, \left( \frac{b\Gamma\left( \alpha+1\right) } {M}\right) ^{\frac{1}{\alpha}}\right\} , \end{equation}$

(3.49)

since indeed

$\begin{equation} \left\vert y(t)-y_{0}\right\vert \leq b\text{, }\forall t\in\left[ t_{0}, t_{0}+a\right] . \end{equation}$

(3.50)

If indeed $u_{0}(t)$ , $v_{0}(t)$ , and $y(t)$ satisfy the hypothesis of this theorem, then the principle is

$\begin{equation} u_{0}(t) < y(t) < v_{0}(t)\;\forall t\in(t_{0}, t_{0}+\beta]. \end{equation}$

(3.51)

Since

$\begin{align} u_{0}(t) & < u_{0}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau , u_{0}(\tau)\right) d\tau\\ & \leq y(t_{0})+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, y(\tau)\right) d\tau\\ & = y(t). \end{align}$

(3.52)

Similary, we have

$\begin{equation} y(t) < v_{0}(t). \end{equation}$

(3.53)

We define the function

$\begin{align} \overline{f}\left( t, y;u_{0}, v_{0}\right) & = f\left( t, u_{0}(t)\right) +f_{x}\left( t, u_{0}(t)\right) \left( y(t)-u_{0}(t)\right) , \\ \overline{f}_{1}\left( t, y;u_{0}, v_{0}\right) & = f\left( t, u_{0} (t)\right) +\frac{f\left( t, u_{0}(t)\right) -f\left( t, v_{0}(t)\right) }{u_{0}(t)-v_{0}(t)}\left( y(t)-u_{0}(t)\right) . \end{align}$

(3.54)

When $t = t_{0}$ ,

$\begin{equation} \overline{f}_{1}\left( t_{0}, y;u_{0}, v_{0}\right) = \overline{f}\left( t_{0}, y;u_{0}, v_{0}\right) . \end{equation}$

(3.55)

We now have $u_{1}(t)$ and $v_{1}(t)$ as the linear differential fractional equations,

$\begin{align} _{t_{0}}^{C}D_{t}^{\alpha}u_{1}(t) & = \overline{f}\left( t, u_{1} (t);u_{0}, v_{0}\right) , \;u_{1}(t_{0}) = y_{0}, \\ _{t_{0}}^{C}D_{t}^{\alpha}v_{1}(t) & = \overline{f_{1}}\left( t, v_{1} (t);u_{0}, v_{0}\right) , \;v_{1}(t_{0}) = y_{0}, \end{align}$

(3.56)

which exist on $\left[t_{0}, t_{0}+\beta\right]$ since

$\begin{align} \left\vert u_{1}(t)-u_{1}(t_{0})\right\vert & \leq\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha -1}\left\vert \overline{f}\left( \tau, u_{1}(\tau);u_{0}, v_{0}\right) \right\vert d\tau, \\ & \leq\frac{M\left( t-t_{0}\right) ^{\alpha}}{\Gamma\left( \alpha +1\right) }\leq\frac{Ma^{\alpha}}{\Gamma\left( \alpha+1\right) } < b. \end{align}$

(3.57)

We have that

$\begin{align} u_{0}(t) & < y_{0}+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, u_{0}(\tau)\right) d\tau\\ & = y_{0}+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left( t-\tau\right) ^{\alpha-1}\overline{f}\left( \tau, u_{0} (\tau);u_{0}, v_{0}\right) d\tau\\ & = u_{0}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}\overline{f}\left( \tau, u_{0} (\tau);u_{0}, v_{0}\right) d\tau\\ & \leq u_{0}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) }\int \limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\overline{f}\left( \tau, u_{1}(\tau);u_{0}, v_{0}\right) d\tau\\ & = u_{1}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}\overline{f}\left( \tau, u_{1} (\tau);u_{0}, v_{0}\right) d\tau = u_{1}(t). \end{align}$

(3.58)

That is to say,

$\begin{equation} u_{0}(t) < u_{1}(t)\text{, }\forall t\in(t_{0}, t_{0}+\beta], \end{equation}$

(3.59)

$\begin{align} v_{1}(t) & = v_{1}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\overline{f} _{1}\left( \tau, v_{1}(\tau);u_{0}, v_{0}\right) d\tau\\ & = v_{0}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}\overline{f}_{1}\left( \tau, v_{1} (\tau);u_{0}, v_{0}\right) d\tau\\ & < v_{0}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}\overline{f}_{1}\left( \tau, v_{0} (\tau);u_{0}, v_{0}\right) d\tau\\ & = v_{0}(t). \end{align}$

(3.60)

Thus,

$\begin{equation} v_{1}(t) < v_{0}(t)\text{, }\forall t\in(t_{0}, t_{0}+\beta]. \end{equation}$

(3.61)

We note that

$\begin{align} & \overline{f}\left( t, u_{0};u_{0}, v_{0}\right) = f(t, u_{0}(t)), \\ & \overline{f}_{1}(t, u_{0}) = f(t, u_{0}(t)) = \overline{f}\left( t, u_{0} ;u_{0}, v_{0}\right), \\ & \overline{f}\left( t, u_{0};u_{0}, v_{0}\right) = f(t, u_{0}) = \overline {f}_{1}\left( t, u_{0};u_{0}, v_{0}\right). \end{align}$

(3.62)

We shall show that

$\begin{equation} \begin{array} [c]{c} _{t_{0}}^{C}D_{t}^{\alpha}u_{1}(t) < f\left( t, u_{1}(t)\right) , \\ _{t_{0}}^{C}D_{t}^{\alpha}v_{1}(t) > f\left( t, v_{1}(t)\right) . \end{array} \end{equation}$

(3.63)

We have in principle that $f_{y}(t, y)$ increases with respect to $y$ ,

$\begin{align} u_{1}(t) & = u_{1}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{1}\left( \tau, u_{1}(\tau);u_{0}, v_{0}\right) d\tau\\ & = u_{1}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left[ f(\tau, u_{0}(\tau))+f_{y}(\tau, u_{0}(\tau))\left( y-u_{0} (\tau)\right) \right] \left( t-\tau\right) ^{\alpha-1}d\tau\\ & = u_{1}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}f(\tau, u_{0}(\tau))\left( t-\tau\right) ^{\alpha-1}d\tau\\ & \quad +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left[ f_{y}(\tau, u_{0}(\tau))\left( y-u_{0}(\tau)\right) \right] \left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.64)

Using the fact that $f_{y}(t, y)$ increases with respect to $y$ , we have

$\begin{align} u_{1}(t) & < \frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}f(\tau, u_{0}(\tau))\left( t-\tau\right) ^{\alpha-1}d\tau +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left[ f_{y}(\tau, u_{1}(\tau))\left( y-u_{0}(\tau)\right) \right] \left( t-\tau\right) ^{\alpha-1}d\tau\\ & < \frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\overline {f}\left( \tau, u_{1}(\tau);u_{0}, v_{0}\right) \left( t-\tau\right) ^{\alpha-1}d\tau+u_{1}(t_{0}). \end{align}$

(3.65)

Therefore,

$\begin{equation} _{t_{0}}^{C}D_{t}^{\alpha}y(t) < f_{1}\left( t, u_{1}(t);u_{0}, v_{0}\right) . \end{equation}$

(3.66)

On the other hand, we have that

$\begin{align} u_{0}(t) & < u_{0}(t)+\frac{1}{\Gamma\left( \alpha\right) }\int \limits_{t_{0}}^{t}f(\tau, u_{0}(\tau))\left( t-\tau\right) ^{\alpha-1} d\tau\\ & = u_{0}(t)+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\overline{f}_{1}\left( \tau, u_{0}(\tau);u_{0}, v_{0}\right) \left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.67)

Then, we have that

$\begin{equation} u_{0}(t) < v_{1}(t)\text{, }\forall t\in(t_{0}, t_{0}+\beta]. \end{equation}$

(3.68)

Nevertheless,

$\begin{equation} f_{y}(t, u_{0}(t)) < \frac{f\left( t, u_{0}(t)\right) -f\left( t, v_{0} (t)\right) }{u_{0}(t)-v_{0}(t)}. \end{equation}$

(3.69)

$\begin{align} f\left( t, v_{1}(t)\right) & = f\left( t, u_{0}(t)\right) +f_{y} (t, u_{0}(t))\left[ v_{1}(t)-u_{0}(t)\right] +\frac{1}{2}f_{yy}\left( t, \xi\right) \left[ v_{1}(t)-u_{0}(t)\right] ^{2}, \\ u_{0}(t) & < \xi < v_{1}(t). \end{align}$

(3.70)

With the Taylor series expansion, repeating the mean value theorem, and using the fact that $f_{yy}(t, \xi) > 0$ , we get

$\begin{align} v_{1}(t) & = v_{1}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\overline{f}_{1}(\tau, v_{1}(\tau), u_{0}, v_{0})\left( t-\tau\right) ^{\alpha-1}d\tau\\ & > v_{1}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}f(\tau, v_{1}(\tau))\left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.71)

Therefore,

$\begin{equation} _{t_{0}}^{C}D_{t}^{\alpha}v_{1}(t) > f\left( t, v_{1}(t)\right) \text{, }\forall t\in\left[ t_{0}, t_{0}+\beta\right] . \end{equation}$

(3.72)

Note that $v_{1}(t),$ $y(t)$ , and $u_{1}(t)$ verify the under and over function with respect to the initial condition

$\begin{equation} v_{1}(t_{0}) = y\left( t_{0}\right) = u_{1}(t_{0}), \end{equation}$

(3.73)

within $\forall t\in\left[t_{0}, t_{0}+\beta\right].$ Then,

$\begin{equation} u_{1}(t) < y(t) < v_{1}(t)\text{, }\forall t\in(t_{0}, t_{0}+\beta]. \end{equation}$

(3.74)

This is to say,

$\begin{equation} u_{0}(t) < u_{1}(t) < y(t) < v_{1}(t) < v_{0}(t), \;\forall t\in(t_{0} , t_{0}+\beta]. \end{equation}$

(3.75)

We can repeat this process by defining a transformation $\overline{\Lambda}$ such that

$\begin{align} \left( u_{1}, v_{1}\right) & = \overline{\Lambda}\left[ \left( u_{0} , v_{0}\right) \right] , \\ \left( u_{2}, v_{2}\right) & = \overline{\Lambda}\left[ \left( u_{1} , v_{1}\right) \right] , \\ & \vdots\\ \left( u_{n+1}, v_{n+1}\right) & = \overline{\Lambda}\left[ \left( u_{n}, v_{n}\right) \right], \end{align}$

(3.76)

of functions that meet the following conditions,

$\begin{align} u_{n}(t) & < u_{n}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}f(\tau, u_{n}(\tau))\left( t-\tau\right) ^{\alpha -1}d\tau, \\ u_{n}(t_{0}) & = y_{0}, \\ v_{n}(t) & > v_{n}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}f(\tau, v_{n}(\tau))\left( t-\tau\right) ^{\alpha -1}d\tau, \\ v_{n}(t_{0}) & = y_{0}. \end{align}$

(3.77)

$\begin{align} u_{n}(t) & < u_{n+1}(t) < y(t) < v_{n+1}(t) < v_{n}(t)\text{, }\forall t\in (t_{0}, t_{0}+\beta], \\ u_{n+1}(t) & < u_{n+1}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\overline{f}(\tau, u_{n+1}(\tau);u_{n}(\tau), v_{n} (\tau))\left( t-\tau\right) ^{\alpha-1}d\tau, \\ v_{n+1}(t) & < v_{n+1}(t_{0})+\frac{1}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\overline{f_{1}}(\tau, v_{n+1}(\tau);u_{n}(\tau ), v_{n}(\tau))\left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.78)

$\left(u_{n}(t)\right) _{n\in N}$ , $\left(v_{n}(t)\right) _{n\in N}$ are monotonic uniformly bounded on $\left[t_{0}, t_{0}+\beta\right].$ They are also equi-continuous for each fixed $n,$ and $u_{n},$ $v_{n}$ are solutions of linear fractional equations. The uniform convergence leads us to

$\begin{equation} \underset{n\rightarrow \infty}{\lim}u_{n}(t) = \underset{n\rightarrow \infty} {\lim}v_{n}(t) = y(t). \end{equation}$

(3.79)

Let

$\begin{align} \Omega & = \underset{ \begin{array} [c]{l} u_{0}(t)\leq y\leq v_{0}(t)\\ t_{0}\leq t\leq t_{0}+\beta \end{array} }{\sup}\left\vert f_{y}\left( t, y(t)\right) \right\vert , \\ \overline{\Omega} & = \underset{ \begin{array} [c]{l} u_{0}(t)\leq y\leq v_{0}(t)\\ t_{0}\leq t\leq t_{0}+\beta \end{array} }{\sup}\left\vert f_{yy}\left( t, y(t)\right) \right\vert . \end{align}$

(3.80)

Following the discussion presented above, we have that $\forall t\in\left[t_{0}, t_{0}+\beta\right]$ ,

$\begin{align} \left\vert v_{0}(t)-u_{0}(t)\right\vert & \leq\left\vert v_{0} (t)-y(t)\right\vert +\left\vert y(t)-u_{0}(t)\right\vert \\ & \leq\underset{t\in\left[ t_{0}, t_{0}+\beta\right] }{\sup}\left\vert v_{0}(t)-y(t)\right\vert +\left\vert y(t)-u_{0}(t)\right\vert \\ & \leq\Delta+\left\vert y(t)-u_{0}(t)\right\vert \\ & \leq\Delta+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left\vert f(\tau, y(\tau)-f(\tau, u_{0}(\tau))\right\vert -\left( t-\tau\right) ^{\alpha-1}d\tau\\ & \leq\Delta+\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left\vert f_{y}\left( \tau, y(\tau)\right) \right\vert \left\vert y(\tau)-u_{0}(\tau)\right\vert \left( t-\tau\right) ^{\alpha-1} d\tau\\ & \leq\Delta +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\underset{ \begin{array} [c]{l} u_{0}(\tau)\leq y\leq v_{0}(\tau)\\ { \ \ \ \ }t_{0}\leq\tau\leq t \end{array} }{\sup}\left\vert f_{y}\left( \tau, y(\tau)\right) \right\vert \left\vert y(\tau)-u_{0}(\tau)\right\vert \left( t-\tau\right) ^{\alpha-1} d\tau\\ & \leq\Delta+\frac{\Omega}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left\vert y(\tau)-u_{0}(\tau)\right\vert \left( t-\tau\right) ^{\alpha-1}d\tau\\ & \leq\Delta+\frac{\Omega}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left\vert v_{0}(\tau)-u_{0}(\tau)\right\vert \left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.81)

We put

$\begin{equation} z_{0}(t) = v_{0}(t)-u_{0}(t). \end{equation}$

(3.82)

Then, we get

$\begin{equation} z_{0}(t)\leq\Delta+\frac{\Omega}{\Gamma\left( \alpha\right) }\int \limits_{t_{0}}^{t}z_{0}(\tau)\left( t-\tau\right) ^{\alpha-1}d\tau. \end{equation}$

(3.83)

The Gronwall inequality teaches us that

$\begin{equation} z_{0}(t)\leq\Delta\exp\left[ \frac{\Omega\beta^{\alpha}}{\Gamma\left( \alpha+1\right) }\right] . \end{equation}$

(3.84)

Therefore, $\forall t\in\left[t_{0}, t_{0}+\beta\right]$ , we will have

$\begin{equation} 0\leq v_{0}(t)-u_{0}(t)\leq\Delta\exp\left[ \frac{\Omega\beta^{\alpha} }{\Gamma\left( \alpha+1\right) }\right] = \lambda. \end{equation}$

(3.85)

Then,

$v_{0}(t)-u_{0}(t)\leq\lambda.$

We now assume that $\forall n$

$\begin{equation} \left\vert u_{n}(t)-v_{n}(t)\right\vert \leq\frac{2\lambda}{2^{2n}}. \end{equation}$

(3.86)

We want to verify this for $n+1,$

$\begin{align} v_{n+1}(t)-u_{n+1}(t)\ = \frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\left[ \begin{array} [c]{c} \left( v_{n+1}(\tau)-u_{n+1}(\tau)\right) \frac{f\left( \tau, u_{n} (\tau)\right) -f\left( \tau, v_{n}(\tau)\right) }{u_{n}(\tau)-v_{n}(\tau)}\\ -\left[ u_{n+1}(\tau)-u_{n}(\tau)\right] f_{y}\left( \tau, u_{n}\left( \tau\right) \right) \end{array} \right] d\tau. \end{align}$

(3.87)

Applying the mean value theorem, $\exists\xi\in\left[u_{n}(t)-v_{n} (t)\right].$ We shall have

$\begin{align} f_{y}\left( t, \xi\right) -f_{y}\left( t, u_{n}(t)\right) = f_{yy}\left( t, \eta\right) \left( \xi-u_{n}(t)\right), \quad u_{n}(t) < \eta < \xi. \end{align}$

(3.88)

$\begin{align} v_{n+1}(t)-u_{n+1}(t) & = \frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1} \left[ \begin{array} [c]{c} f_{y}\left( \tau, \xi\right) \left( v_{n+1}(\tau)-u_{n+1}(\tau)\right) \\ +\left( u_{n+1}(\tau)-u_{n}(\tau)\right) \left( f_{y}\left( \tau , \xi\right) -f_{y}\left( \tau, u_{n}\left( \tau\right) \right) \right) \end{array} \right] d\tau, \\ \left\vert v_{n+1}(t)-u_{n+1}(t)\right\vert & \leq\frac{\Omega} {\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert v_{n+1}(\tau)-u_{n+1}(\tau)\right\vert d\tau\\ & \quad +\frac{\overline{\Omega}}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( \xi-u_{n}(\tau)\right) \left( t-\tau\right) ^{\alpha -1}\left\vert u_{n+1}(\tau)-u_{n}(\tau)\right\vert d\tau. \end{align}$

(3.89)

Additionally, we have

$\begin{equation} \left\vert \xi-u_{n}(t)\right\vert \leq\left\vert u_{n}(t)-v_{n}(t)\right\vert, \end{equation}$

(3.90)

and

$\begin{align} \left\vert v_{n+1}(t)-u_{n}(t)\right\vert & \leq\left\vert v_{n} (t)-u_{n}(t)\right\vert , \\ \left\vert v_{n+1}(t)-u_{n+1}(t)\right\vert & \leq\frac{\Omega} {\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert v_{n+1}(\tau)-u_{n+1}(\tau)\right\vert d\tau\\ & \quad +\frac{\overline{\Omega}}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert v_{n}(\tau)-u_{n} (\tau)\right\vert d\tau\\ & \leq\frac{\Omega}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert v_{n+1}(\tau)-u_{n+1} (\tau)\right\vert d\tau +\frac{\overline{\Omega}}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( \frac{2\lambda}{2^{2n}}\right) ^{2}\left( t-\tau\right) ^{\alpha-1}d\tau\\ & \leq\frac{\Omega}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert v_{n+1}(\tau)-u_{n+1} (\tau)\right\vert d\tau +\frac{\overline{\Omega}}{\Gamma\left( \alpha+1\right) }\left( \frac{2\lambda}{2^{2n}}\right) ^{2}\beta^{\alpha}\\ & \leq\frac{\Omega}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left( t-\tau\right) ^{\alpha-1}\left\vert v_{n+1}(\tau)-u_{n+1} (\tau)\right\vert d\tau +\frac{\overline{\Omega}}{\Gamma\left( \alpha+1\right) }\frac {2^{2}\lambda^{2}}{2^{2n+1}}\beta^{\alpha}. \end{align}$

(3.91)

Put

$\begin{align} m(t) & = v_{n+1}(t)-u_{n+1}(t), \\ m(t) & \leq\frac{\overline{\Omega}\beta^{\alpha}2^{2}\lambda^{2}} {\Gamma\left( \alpha+1\right) 2^{2n+1}}+\frac{\Omega}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}m(t)\left( t-\tau\right) ^{\alpha -1}d\tau. \end{align}$

(3.92)

The Gronwall inequality helps us to obtain

$\begin{align} m(t) & \leq\frac{\overline{\Omega}\beta^{\alpha}2^{2}\lambda^{2}} {\Gamma\left( \alpha+1\right) 2^{2n+1}}\exp\left( \frac{\Omega\beta ^{\alpha}}{\Gamma\left( \alpha+1\right) }\right) \\ & \leq\frac{2\lambda}{2^{2n+1}}, \\ & \frac{\overline{\Omega}\beta^{\alpha}}{\Gamma\left( \alpha+1\right) } \exp\left( \frac{\Omega\beta^{\alpha}}{\Gamma\left( \alpha+1\right) }\right) \lambda = 1, \end{align}$

(3.93)

which is true for all $n$ consequently,

$\begin{align} \left\vert y(t)-u_{n}(t)\right\vert & \leq\frac{2\lambda}{2^{2n}}, \\ \left\vert y(t)-v_{n}(t)\right\vert & \leq\frac{2\lambda}{2^{2n}}. \end{align}$

(3.94)

□

Case with the Atangana-Baleanu fractional derivative:

Proof. For the case of Atangana-Baleanu as presented before, we shall also have that

$\begin{align} u_{0}(t) & \leq u_{0}(t_{0})+\left( 1-\alpha\right) f\left( t, u_{0}(t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) } \int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau , u_{0}(\tau)\right) d\tau\\ & < y(t_{0})+\left( 1-\alpha\right) f\left( t, y(t)\right) +\frac{\alpha }{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, y(\tau)\right) d\tau\\ & < v_{0}(t_{0})+\left( 1-\alpha\right) f\left( t, v_{0}(t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, v_{0}(\tau)\right) d\tau, \end{align}$

(3.95)

therefore

$\begin{equation} u_{0}(t) < y(t) < v_{0}(t)\text{, }\forall t\in(t_{0}, t_{0}+\beta]. \end{equation}$

(3.96)

The functions $f_{1}(t, y, u_{0}, v_{0})$ and $f_{2}(t, y, u_{0}, v_{0})$ are the same like before. At the initial time, we have that $f_{1}$ and $f_{2}$ coincide. We now consider $u_{1}(t)$ and $v_{1}(t)$ . To be the solutions of the fractional linear differential equation with the Atangana-Baleanu derivative,

$\begin{align} _{t_{0}}^{ABC}D_{t}^{\alpha}u_{1}(t) & = f_{1}\left( t, u_{1}(t);u_{0} , v_{0}\right) , \;u_{1}(t_{0}) = y_{0}, \\ _{t_{0}}^{ABC}D_{t}^{\alpha}v_{1}(t) & = f_{2}\left( t, v_{1}(t);u_{0} , v_{0}\right) , \;v_{1}(t_{0}) = y_{0}. \end{align}$

(3.97)

Indeed,

$\begin{align} u_{1}(t) & = u_{1}(t)+\left( 1-\alpha\right) f_{1}\left( t, u_{1} (t);u_{0}, v_{0}\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{1}\left( \tau, u_{1}(\tau);u_{0}, v_{0}\right) d\tau, \\ v_{1}(t) & = v_{1}(t)+\left( 1-\alpha\right) f_{2}\left( t, v_{1} (t);u_{0}, v_{0}\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{2}\left( \tau, v_{1}(\tau);u_{0}, v_{0}\right) d\tau, \end{align}$

(3.98)

which exist on $\left[t_{0}, t_{0}+\beta\right].$ However, we note that

$\begin{align} u_{0}(t) & < u_{0}(t)+\left( 1-\alpha\right) f\left( t, u_{0}(t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, u_{0}(\tau)\right) d\tau\\ & = u_{0}(t_{0})+\left( 1-\alpha\right) f_{1}\left( t, u_{0}(t);u_{0} , v_{0}\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{1}\left( \tau, u_{0}(\tau);u_{0}, v_{0}\right) d\tau. \end{align}$

(3.99)

We shall then obtain

$\begin{equation} u_{0}(t) < u_{1}(t);\;t\in(t_{0}, t_{0}+\beta]. \end{equation}$

(3.100)

In a similar way, we shall have

$\begin{equation} v_{1}(t) < v_{0}(t);\;t\in(t_{0}, t_{0}+\beta]. \end{equation}$

(3.101)

We will now show that the function $u_{1}(t)$ and $v_{1}(t)$ satisfy the inequalities with the property of $f_{y}$ together with the mean square value, we have

$\begin{align} u_{1}(t) & = u_{1}(t_{0})+\left( 1-\alpha\right) f_{1}\left( t, u_{1}(t);u_{0}, v_{0}\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{1}\left( \tau, u_{1}(\tau);u_{0}, v_{0}\right) d\tau\\ & \leq u_{1}(t_{0})+\left( 1-\alpha\right) f_{1}\left( t, u_{1}(t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{1}\left( \tau, u_{1}(\tau)\right) d\tau , \\ \;\forall t & \in\left[ t_{0}, t_{0}+\beta\right] . \end{align}$

(3.102)

We also have

$\begin{align} u_{0}(t) & < u_{0}(t)+\left( 1-\alpha\right) f\left( t, u_{0}(t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, u_{0}(\tau)\right) d\tau, \\ & = u_{0}(t_{0})+\left( 1-\alpha\right) f_{2}\left( t, u_{0}(t);u_{0} , v_{0}\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{2}\left( \tau, u_{0}(\tau);u_{0}, v_{0}\right) d\tau. \end{align}$

(3.103)

Therefore, we shall have

$\begin{equation} v_{0}(t) < v_{1}(t);\;t\in(t_{0}, t_{0}+\beta]. \end{equation}$

(3.104)

Additionally, we have

$\begin{equation} f_{y}(t, u_{0}(t)) < \frac{f\left( t, u_{0}(t)\right) -f\left( t, v_{0} (t)\right) }{u_{0}(t)-v_{0}(t)}. \end{equation}$

(3.105)

Due to the value of $f\left(t, v_{1}(t)\right)$ , $f_{xx}\left(t, \xi\right) > 0$ , and the mean value theorem, we have

$\begin{align} v_{1}(t) & = v_{1}(t_{0})+\left( 1-\alpha\right) f_{2}\left( t, v_{1}(t);u_{0}, v_{0}\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{2}\left( \tau, v_{1}(\tau);u_{0}, v_{0}\right) d\tau\\ & > v_{1}(t_{0})+\left( 1-\alpha\right) f_{2}\left( t, v_{1}(t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{2}\left( \tau, v_{1}(\tau)\right) d\tau, \\ \;\forall t & \in\left[ t_{0}, t_{0}+\beta\right]. \end{align}$

(3.106)

Therefore, we have

$\begin{equation} u_{0}(t) < u_{1}(t) < y(t) < v_{1}(t) < v_{0}(t)\text{, }\forall t\in(t_{0} , t_{0}+\beta]. \end{equation}$

(3.107)

We shall again consider the mapping

$\begin{equation} \left( u_{n+1}, v_{n+1}\right) = \overline{\Lambda}\left[ \left( u_{n} , v_{n}\right) \right] , \end{equation}$

(3.108)

of functions that hold the following inequalities:

$\begin{align} u_{n}(t) & < u_{n}(t_{0})+\left( 1-\alpha\right) f\left( t, u_{n} (t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, u_{n}(\tau)\right) d\tau, \\ v_{n}(t) & > v_{n}(t_{0})+\left( 1-\alpha\right) f\left( t, v_{n} (t)\right) +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0} }^{t}\left( t-\tau\right) ^{\alpha-1}f\left( \tau, v_{n}(\tau)\right) d\tau, \\ u_{n}(t) & < u_{n+1}(t) < y(t) < v_{n+1}(t) < v_{n}(t)\text{, }\forall t\in\left[ t_{0}, t_{0}+\beta\right] . \end{align}$

(3.109)

$\begin{align} u_{n+1}(t) & = u_{n+1}(t_{0})+\left( 1-\alpha\right) f_{1}\left( t, u_{n+1}(t);u_{n}(t), v_{n}(t)\right) \\ & \quad +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{1}\left( \tau, u_{n+1}(\tau);u_{n}(\tau ), v_{n}(\tau)\right) d\tau, \\ v_{n+1}(t) & = v_{n+1}(t_{0})+\left( 1-\alpha\right) f_{1}\left( t, v_{n+1}(t);u_{n}(t), v_{n}(t)\right) \\ & \quad +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}f_{2}\left( \tau, v_{n+1}(\tau);u_{n}(\tau ), v_{n}(\tau)\right) d\tau. \end{align}$

(3.110)

$\left\{ u_{n}, v_{n}\right\}$ are indeed monotonic and uniformly bounded on $\left[t_{0}, t_{0}+\beta\right].$ Since they are linear, they are equi-continuous, therefore $u_{n}(t)$ and $v_{n}(t)$ converges when $n\rightarrow \infty.$ $\Omega$ and $\overline{\Omega}$ are the same as before. Note that

$\begin{align} 0&\leq v_{0}(t)-y(t) < v_{0}(t)-u_{0}(t), \\ \left\vert v_{0}(t)-u_{0}(t)\right\vert & \leq\left\vert v_{0} (t)-y(t)\right\vert +\left\vert y(t)-u_{0}(t)\right\vert \\ & \leq\underset{t\in\left[ t_{0}, t_{0}+\beta\right] }{\sup}\left\vert v_{0}(t)-y(t)\right\vert +\left\vert y(t)-u_{0}(t)\right\vert \\ & \leq\overline{\Delta}+\left\vert y(t)-u_{0}(t)\right\vert\\ & \leq\overline{\Delta}+\left\vert \begin{array} [c]{c} \left( 1-\alpha\right) \left( f(t, y(t)-f(t, u_{0}(t))\right) \nonumber\\ +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( f(\tau, y(\tau)-f(\tau, u_{0}(\tau))\right) -\left( t-\tau\right) ^{\alpha-1} \end{array} \right\vert d\tau\\ & \leq\overline{\Delta}+ \begin{array} [c]{c} \left( 1-\alpha\right) \left\vert f(t, y(t)-f(t, u_{0}(t))\right\vert \\ +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left\vert f(\tau, y(\tau)-f(\tau, u_{0}(\tau))\right\vert -\left( t-\tau\right) ^{\alpha-1} \end{array} d\tau. \end{align}$

(3.111)

Since $f_{y}\left(t, y(t)\right)$ exists by hypothesis, we can find by the mean of the well-known mean value theorem

$y < \xi < u_{0},$

such that

$\begin{equation} f\left( t, y\right) -f\left( t, u_{0}\right) = f_{y}^{\prime}\left( t, \xi\right) \left( y-u_{0}\right) . \end{equation}$

(3.112)

Therefore,

$\begin{equation} v_{0}(t)-u_{0}(t)\leq\overline{\Delta}+ \begin{array} [c]{c} \left( 1-\alpha\right) \underset{t\in\left[ t_{0}, t_{0}+\beta\right] }{\sup}\left\vert f_{y}^{\prime}\left( t, \xi\right) \right\vert \left( y(t)-u_{0}(t)\right) \\ +\frac{\alpha}{\Gamma\left( \alpha\right) }\underset{t\in\left[ t_{0} , t_{0}+\beta\right] }{\sup}\left\vert f_{y}^{\prime}\left( t, \xi\right) \right\vert \int\limits_{t_{0}}^{t}\left( y(\tau)-u_{0}(\tau)\right) -\left( t-\tau\right) ^{\alpha-1}d\tau, \end{array} \end{equation}$

(3.113)

having that $\forall t\in\left[t_{0}, t_{0}+\beta\right]$

$\begin{equation} u_{0}(t) < y(t) < v_{0}(t). \end{equation}$

(3.114)

We will have

$\begin{align} v_{0}(t)-u_{0}(t) \leq\overline{\Delta}+\left( 1-\alpha\right) \Omega\left\vert v_{0}(t)-u_{0}(t)\right\vert +\frac{\alpha\Omega}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left( t-\tau\right) ^{\alpha-1}\left( v_{0}(\tau)-u_{0}(\tau)\right) d\tau. \end{align}$

(3.115)

We need, in addition,

$\begin{equation} 1+\left( \alpha-1\right) \Omega > 0, \end{equation}$

(3.116)

such that

$\begin{align} v_{0}(t)-u_{0}(t) \leq\frac{\overline{\Delta}}{1+\left( \alpha-1\right) \Omega} +\frac{\alpha\Omega}{\Gamma\left( \alpha\right) \left\{ 1+\left( \alpha-1\right) \Omega\right\} }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\left( v_{0}(\tau)-u_{0}(\tau)\right) d\tau. \end{align}$

(3.117)

We put

$\begin{equation} m(t) = v_{0}(t)-u_{0}(t). \end{equation}$

(3.118)

Thus, by the Gronwall inequality, we have

$\begin{equation} m(t)\leq\frac{\overline{\Delta}}{1+\left( \alpha-1\right) \Omega}\exp\left( \frac{\Omega\beta^{\alpha}}{\Gamma\left( \alpha\right) \left\{ 1+\left( \alpha-1\right) \Omega\right\} }\right) . \end{equation}$

(3.119)

Therefore, we assume that

$\begin{equation} v_{0}(t)-u_{0}(t)\leq\lambda. \end{equation}$

(3.120)

The formula is true when $n = 0$ , and we assume that $\forall n\geq0$

$\begin{equation} \left\vert v_{n}(t)-u_{n}(t)\right\vert \leq\frac{2\lambda}{2^{2n}}. \end{equation}$

(3.121)

We want to verify the above formula when we reach $n+1$ .

$\begin{align} v_{n+1}(t)-u_{n+1}(t) & = \left( 1-\alpha\right) \left[ \begin{array} [c]{c} \overline{f}_{1}(t, v_{n+1}(t);u_{n}(t), v_{n}(t))\\ -\overline{f}(t, u_{n+1}(t);u_{n}(t), v_{n}(t)) \end{array} \right] \\ & \quad +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left[ \begin{array} [c]{c} \overline{f_{1}}(\tau, v_{n+1}(\tau);u_{n}(\tau), v_{n}(\tau))\\ -\overline{f}(\tau, u_{n+1}(\tau);u_{n}(\tau), v_{n}(\tau)) \end{array} \right] -\left( t-\tau\right) ^{\alpha-1}d\tau\\ & = \left( 1-\alpha\right) \left[ \begin{array} [c]{c} \frac{f(t, u_{n}(t))-f(t, v_{n}(t))}{u_{n}(t)-v_{n}(t)}\left( y(t)-u_{n} (t)\right) \\ -f_{y}(t, u_{n}(t))\left( y(t)-u_{n}(t)\right) \end{array} \right] \\ & \quad +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left[ \begin{array} [c]{c} \frac{f(\tau, u_{n}(\tau))-f(\tau, v_{n}(\tau))}{u_{n}(\tau)-v_{n}(\tau)}\left( y(\tau)-u_{n}(\tau)\right) \\ -f_{y}(\tau, u_{n}(\tau))\left( y(\tau)-u_{n}(\tau)\right) \end{array} \right] \left( t-\tau\right) ^{\alpha-1}d\tau\\ & \leq\left( 1-\alpha\right) \left[ \begin{array} [c]{c} \frac{f(t, u_{n}(t))-f(t, v_{n}(t))}{u_{n}(t)-v_{n}(t)}\left( v_{n+1} (t)-u_{n}(t)\right) \\ -f_{y}(t, u_{n}(t))\left( u_{n+1}(t)-u_{n}(t)\right) \end{array} \right] \\ & \quad +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left[ \begin{array} [c]{c} \frac{f(\tau, u_{n}(\tau))-f(\tau, v_{n}(\tau))}{u_{n}(\tau)-v_{n}(\tau)}\left( v_{n+1}(\tau)-u_{n}(\tau)\right) \\ -f_{y}(\tau, u_{n}(\tau))\left( u_{n+1}(\tau)-u_{n}(\tau)\right) \end{array} \right] \left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.122)

Using the mean value theorem $\exists\xi$ such that

$\begin{equation} u_{n}(t) < \xi < v_{n}(t), \end{equation}$

(3.123)

then

$\begin{align} v_{n+1}(t)-u_{n+1}(t) & \leq\left( 1-\alpha\right) \left\{ \begin{array} [c]{c} f_{y}(t, \xi)\left[ v_{n+1}(t)-u_{n+1}(t)\right] \\ +\left[ u_{n+1}(t)-u_{n}(t)\right] \left[ f_{y}(t, \xi)-f_{y}(t, u_{n} )\right] \end{array} \right\} \\ & \quad +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left\{ \begin{array} [c]{c} f_{y}(\tau, \xi)\left[ v_{n+1}(\tau)-u_{n+1}(\tau)\right] \\ +\left[ u_{n+1}(\tau)-u_{n}(\tau)\right] \left[ f_{y}(\tau, \xi)-f_{y} (\tau, u_{n})\right] \end{array} \right\} \left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.124)

Also, we have

$f_{y}(t, \xi)-f_{y}(t, u_{n}) = f_{yy}(t, \eta)\left[ \xi-u_{n}(t)\right] ,$

with

$u_{n}(t) < \eta < \xi.$

Then, we will have

$\begin{align} v_{n+1}(t)-u_{n+1}(t) & \leq\left( 1-\alpha\right) \left\{ \begin{array} [c]{c} f_{y}(t, \xi)\left[ v_{n+1}(t)-u_{n+1}(t)\right] \\ +\left[ u_{n+1}(t)-u_{n}(t)\right] f_{yy}(t, \eta)\left[ \xi-u_{n} (t)\right] \end{array} \right\} \\ & \quad +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left\{ \begin{array} [c]{c} f_{y}(\tau, \xi)\left[ v_{n+1}(\tau)-u_{n+1}(\tau)\right] \\ +\left[ u_{n+1}(\tau)-u_{n}(\tau)\right] f_{yy}(\tau, \eta)\left[ \xi -u_{n}(\tau)\right] \end{array} \right\} \left( t-\tau\right) ^{\alpha-1}d\tau. \end{align}$

(3.125)

We have as before that

$\begin{align} &\left\vert \xi-u_{n}(t)\right\vert \leq\left\vert v_{n}(t)-u_{n} (t)\right\vert , \\ & \left\vert u_{n+1}(t)-u_{n}(t)\right\vert \leq\left\vert v_{n} (t)-u_{n}(t)\right\vert . \end{align}$

(3.126)

Therefore, we have

$\begin{align} v_{n+1}(t)-u_{n+1}(t) & \leq\left( 1-\alpha\right) \left\{ \Omega\left[ v_{n+1}(t)-u_{n+1}(t)\right] +\overline{\Omega}\left[ v_{n}(t)-u_{n} (t)\right] ^{2}\right\} \\ & \quad +\frac{\alpha}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}} ^{t}\left\{ \begin{array} [c]{c} \Omega\left[ v_{n+1}(\tau)-u_{n+1}(\tau)\right] \\ +\overline{\Omega}\left[ v_{n}(\tau)-u_{n}(\tau)\right] ^{2} \end{array} \right\} \left( t-\tau\right) ^{\alpha-1}d\tau, \end{align}$

(3.127)

under the condition that

$\begin{equation} 1+\left( \alpha-1\right) \Omega > 0, \end{equation}$

(3.128)

then

$\begin{align} v_{n+1}(t)-u_{n+1}(t) \leq& \frac{\left( 1-\alpha\right) \overline{\Omega }\left[ v_{n}(t)-u_{n}(t)\right] ^{2}}{1+\left( \alpha-1\right) \Omega}\\ & +\frac{\alpha\overline{\Omega}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left( t-\tau\right) ^{\alpha-1}\left[ v_{n}(\tau)-u_{n}(\tau)\right] ^{2} d\tau\\ & +\frac{\alpha\overline{\Omega}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left[ v_{n+1}(\tau)-u_{n+1}(\tau)\right] \left( t-\tau\right) ^{\alpha-1} d\tau\\ & \leq\frac{\left( 1-\alpha\right) \overline{\Omega}}{1+\left( \alpha-1\right) \Omega}\left( \frac{2\lambda}{2^{2n}}\right) ^{2} +\frac{\alpha\overline{\Omega}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) }\left( \frac{2\lambda}{2^{2n} }\right) ^{2}\frac{\beta^{\alpha}}{\alpha}\\ & +\frac{\alpha\overline{\Omega}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left[ v_{n+1}(\tau)-u_{n+1}(\tau)\right] \left( t-\tau\right) ^{\alpha-1} d\tau\\ \leq& \left( \frac{\left( 1-\alpha\right) \overline{\Omega}}{1+\left( \alpha-1\right) \Omega}+\frac{\overline{\Omega}\beta^{\alpha}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) }\right) \left( \frac{2\lambda}{2^{2n}}\right) ^{2}\\ & +\frac{\alpha\overline{\Omega}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t}\left[ v_{n+1}(\tau)-u_{n+1}(\tau)\right] \left( t-\tau\right) ^{\alpha-1} d\tau. \end{align}$

(3.129)

By the Gronwall inequality, we have

$\begin{equation} v_{n+1}(t)-u_{n+1}(t)\leq\left( \begin{array} [c]{c} \frac{\left( 1-\alpha\right) \overline{\Omega}}{1+\left( \alpha-1\right) \Omega}\\ +\frac{\overline{\Omega}\beta^{\alpha}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) } \end{array} \right) \left( \frac{2\lambda}{2^{2n}}\right) ^{2}\exp\left[ \frac {\beta^{\alpha}\overline{\Omega}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) }\right] . \end{equation}$

(3.130)

We will need

$\begin{equation} \lambda.2\exp\left[ \frac{\beta^{\alpha}\overline{\Omega}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) }\right] \left( \frac{\left( 1-\alpha\right) \overline{\Omega}}{1+\left( \alpha-1\right) \Omega}+\frac{\overline{\Omega}\beta^{\alpha}}{\left( 1+\left( \alpha-1\right) \Omega\right) \Gamma\left( \alpha\right) }\right) = 1, \end{equation}$

(3.131)

such that

$\begin{equation} \left\vert v_{n+1}(t)-u_{n+1}(t)\right\vert \leq\frac{2\lambda}{2^{2n+1}}, \end{equation}$

(3.132)

which completes the proof. □

4. Numerical solution

We shall adopt the midpoint approximation to derive a numerical solution to the Caputo fractional differential equations

$\begin{align} _{t_{0}}^{C}D_{t}^{\alpha}y(t) & = f\left( t, y(t)\right) , { \ }0 < \alpha < 1, \\ y(t_{0}) & = y_{0}. \end{align}$

(4.1)

We impose that $f$ satisfies the criteria described in the previous section, such that the existence of a unique solution could be observed. From ^[20], we have that

$\begin{align} y\left( t_{n}\right) & = y\left( t_{0}\right) +\frac{1}{\Gamma\left( \alpha\right) }\int\limits_{t_{0}}^{t_{n}}\left( t_{n}-\tau\right) ^{\alpha-1}f\left( \tau, y(\tau)\right) d\tau \end{align}$

(4.2)

$\begin{align} & = y\left( t_{0}\right) +\frac{h^{\alpha}}{\Gamma\left( \alpha+1\right) }\sum\limits_{j = 0}^{n-1}f\left( t_{j}+\frac{h}{2}, \frac{y_{j}+y_{j+1}}{2}\right) \left\{ \left( n-j\right) ^{\alpha}-\left( n-j-1\right) ^{\alpha }\right\} , \\ y_{n} & = y\left( t_{0}\right) +\frac{h^{\alpha}}{\Gamma\left( \alpha+1\right) }\sum\limits_{j = 0}^{n-2}f\left( t_{j}+\frac{h}{2}, \frac {y_{j+1}+y_{j}}{2}\right) \left\{ \left( n-j\right) ^{\alpha}-\left( n-j-1\right) ^{\alpha}\right\} \\ & \quad +\frac{h^{\alpha}}{\Gamma\left( \alpha+1\right) }f\left( t_{n-1} +\frac{h}{2}, \frac{\overline{y}_{n}+y_{n-1}}{2}\right) , \\ \overline{y}_{n}& = y\left( t_{0}\right) +\frac{h^{\alpha}}{\Gamma\left( \alpha+1\right) }\sum\limits_{j = 0}^{n-1}f\left( t_{j}, y_{j}\right) \left\{ \left( n-j\right) ^{\alpha}-\left( n-j-1\right) ^{\alpha}\right\} , \end{align}$

(4.3)

which is of order $O(h^{\alpha+1})$ . The high order here is when $\alpha = 1$ , and we have $O(h^{2}).$

In the case of the ABC derivative, we have

$\begin{align} y_{n} & = y\left( t_{0}\right) +\left( 1-\alpha\right) f\left( t_{n}, \overline{y}_{n}\right) +\frac{\alpha h^{\alpha}}{\Gamma\left( \alpha+1\right) }\sum\limits_{j = 0}^{n-2}f\left( t_{j}+\frac{h}{2}, \frac {y_{j}+y_{j+1}}{2}\right) \\ & \quad \times\left\{ \left( n-j\right) ^{\alpha}-\left( n-j-1\right) ^{\alpha}\right\} +\frac{\alpha h^{\alpha}}{\Gamma\left( \alpha+1\right) }f\left( t_{n-1}+\frac{h}{2}, \frac{\overline{y}_{n}+y_{n-1}}{2}\right) , \\ \overline{y}_{n} & = y\left( t_{0}\right) +\left( 1-\alpha\right) f\left( t_{n-1}, y_{n-1}\right) +\frac{\alpha h^{\alpha}}{\Gamma\left( \alpha+1\right) }\sum\limits_{j = 0} ^{n-1}f\left( t_{j}, y_{j}\right) \left\{ \left( n-j\right) ^{\alpha }-\left( n-j-1\right) ^{\alpha}\right\} . \end{align}$

(4.4)

The above can be used to solve any nonlinear equation. The stability and convergence analysis of the above is the same with that of the fractional Euler but the order here is $O(h^{\alpha+1})$ if $\alpha = 1$ . We have $O(h^{2}).$

4.1. Application to fractional Bernoulli and Abel nonlinear differential equations

In this section, we shall consider the well-known Abel equation of the first kind and

$\begin{equation} _{t_{0}}^{C}D_{t}^{\alpha}y(t) = f_{3}(t)y^{3}+f_{2}(t)y^{2}+f_{1}(t)y+f_{0}(t), \end{equation}$

(4.5)

and the Bernoulli equation

$\begin{equation} _{t_{0}}^{C}D_{t}^{\alpha}y(t)+P(t)y(t) = Q(t)y^{m}. \end{equation}$

(4.6)

We choose $P(t), Q(t), f_{3}(t), f_{2}(t), f_{1}(t)$ and $f_{0}(t)$ such that if

$\begin{equation} f\left( t, y(t)\right) = f_{3}(t)y^{3}+f_{2}(t)y^{2}+f_{1}(t)y+f_{0}(t), \end{equation}$

(4.7)

and

$\begin{equation} f_{1}\left( t, y(t)\right) = Q(t)y^{m}-P(t)y(t), \end{equation}$

(4.8)

are continuous and obey the criteria described in the theorem, or at least that these functions satisfy the condition under which the midpoint is derived. In the case of the Abel equation, we evaluate the function $f(t, y)$

$\begin{equation} f(t, y) = f_{3}(t)y^{3}+f_{2}(t)y^{2}+f_{1}(t)y+f_{0}(t). \end{equation}$

(4.9)

We chose $f_{3}(t), f_{2}(t), f_{1}(t)$ , and $f_{0}(t)$ to be smooth functions.

$\begin{align} f_{y}(t, y) & = 3f_{3}y^{2}+2f_{2}y+f_{1}, \\ f_{yy}(t, y) & = 6f_{3}y+2f_{2}. \end{align}$

(4.10)

Indeed, $f_{y}(t, y)$ and $f_{yy}(t, y)$ exist and are continuous on $y$ for each fixed $t.$ To satisfy the condition $f_{yy}(t, y) > 0$ , we impose $f_{3}$ and $f_{2}$ to be positive within the chosen interval. Thus, by the fractional Chaplygin uniqueness theorem, the fractional Abel admits a unique solution. In the case of the Bernoulli equation, we have that

$\begin{equation} f_{1}(t, y) = Q(t)y^{m}-P(t)y(t). \end{equation}$

(4.11)

We chose suitable $Q(t)$ and $P(t)$ that will help satisfy the conditions requested.

$\begin{align} f_{1, y}(t, y) & = my^{m-1}Q(t)-P(t), \\ f_{1, yy}(t, y) & = m(n-1)y^{m-2}Q(t), \;\forall m\geq2. \end{align}$

(4.12)

$f_{1, yy}(t, y) > 0$ for each fixed $t$ if $Q(t)$ is positive. Therefore, we have that $f_{1, y}$ and $f_{1, yy}$ exist and, in addition, $f_{1, yy}(t, y) > 0$ . With the Chaplygin for fractional differential equations, the Bernoulli equation admits a unique solution in a suitable chosen interval. For the Abel equation of the first kind, we have

$\begin{align} y\left( t_{n}\right) = & y\left( t_{0}\right) +\frac{h^{\alpha}} {\Gamma\left( \alpha+1\right) }\sum\limits_{j = 0}^{n-1}\left[ \begin{array} [c]{c} f_{3}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) ^{3}\\ +f_{2}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) ^{2}\\ +f_{1}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) +f_{0}\left( t_{j}\right) \end{array} \right] \\ & \times\left\{ \left( n-j\right) ^{\alpha}-\left( n-j-1\right) ^{\alpha}\right\} \\ & +\frac{h^{\alpha}}{\Gamma\left( \alpha+1\right) }\left\{ \begin{array} [c]{c} f_{3}\left( t_{n}\right) \left( \frac{\overline{y}_{n}+y_{n-1}}{2}\right) ^{3}\\ +f_{2}\left( t_{n}\right) \left( \frac{\overline{y}_{n}+y_{n-1}}{2}\right) ^{2}\\ +f_{1}\left( t_{n}\right) \left( \frac{\overline{y}_{n}+y_{n-1}}{2}\right) ^{2}+f_{0}\left( t_{n}\right) \end{array} \right\} , \\ \overline{y}_{n} = & y_{0}+h\sum\limits_{j = 0}^{n-1}\left[ \begin{array} [c]{c} f_{3}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) ^{3}\\ +f_{2}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) ^{2}\\ +f_{1}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) +f_{0}\left( t_{j}\right) \end{array} \right] . \end{align}$

(4.13)

In the case of the ABC derivative, we have

$\begin{align} y_{n} = & y_{0}+\left( 1-\alpha\right) \left\{ \begin{array} [c]{c} f_{3}\left( t_{n}\right) \left( \frac{\overline{y}_{n}+y_{n-1}}{2}\right) ^{3}+f_{2}\left( t_{n}\right) \left( \frac{\overline{y}_{n}+y_{n-1}} {2}\right) ^{2}\\ +f_{1}\left( t_{n}\right) \left( \frac{\overline{y}_{n}+y_{n-1}}{2}\right) ^{2}+f_{0}\left( t_{n}\right) \end{array} \right\} \\ & +\frac{\alpha h^{\alpha}}{\Gamma\left( \alpha+1\right) }\sum\limits_{j = 0} ^{n-2}\left[ \begin{array} [c]{c} f_{3}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) ^{3}\\ +f_{2}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) ^{2} +f_{1}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) +f_{0}\left( t_{j}\right) \end{array} \right] \\ & \times\left\{ \left( n-j\right) ^{\alpha}-\left( n-j-1\right) ^{\alpha}\right\} \\ & +\frac{\alpha h^{\alpha}}{\Gamma\left( \alpha+1\right) }\left\{ \begin{array} [c]{c} f_{3}\left( t_{n}\right) \left( \frac{y_{n}+y_{n-1}}{2}\right) ^{3} +f_{2}\left( t_{n}\right) \left( \frac{y_{n}+y_{n-1}}{2}\right) ^{2}\\ +f_{1}\left( t_{n}\right) \left( \frac{y_{n}+y_{n-1}}{2}\right) ^{2} +f_{0}\left( t_{n}\right) \end{array} \right\} , \end{align}$

(4.14)

where

$\begin{equation} \overline{y}_{n} = y_{0}+h\sum\limits_{j = 0}^{n-1}\left[ \begin{array} [c]{c} f_{3}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) ^{3}\\ +f_{2}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) ^{2} +f_{1}\left( t_{j}\right) \left( \frac{y_{j}+y_{j+1}}{2}\right) +f_{0}\left( t_{j}\right) \end{array} \right] . \end{equation}$

(4.15)

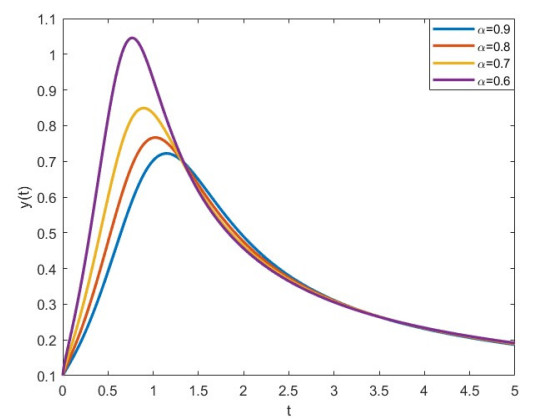
In Figure 1, we present the numerical simulation of the Abel equation with the Caputo derivative for different values of alphas. Here, we chose the following equation:

$\begin{equation} _{0}^{C}D_{t}^{\alpha}y(t) = y^{3}(t)-3ty^{2}(t)+2y(t)+0.1, { \ \ \ \ } y(0) = 0.1. \end{equation}$

(4.16)

Figure 1. Numerical solution of the Caputo fractional Abel equation with different values of fractional orders.

DownLoad: Full-Size Img PowerPoint

5. Conclusions

Fractional ordinary differential equations with singular and nonsingular kernels are powerful mathematical tools used to model real-world problems. They have been applied in many fields of science, technology, and engineering in the last decades. However, due to the complexities associated with these equations, it is sometimes not evident to obtain their exact solutions; thus, many researchers rely on numerical schemes for this purpose. However, it is mathematically important to at least show that they have exact solutions and that those solutions are unique. Some important theories on existence and uniqueness have been developed within the scope of classical differentiation and conditions. In this paper, we have extended some of these conditions within the scope of fractional differentiation with power law and the Mittag-Leffler kernels. In particular, the maximal and minimal techniques with additional conditions for these equations are presented. To establish the existence and uniqueness of solutions for these equations, the Chaplygin approach, which consists of generating two increasing and decreasing sequences surrounding the solution, was presented with additional conditions. For an illustrative example, the Bernoulli and Abel equations were considered.

Acknowledgments

The author would like to thank the anonymous referee for the comments and suggestions, which improved the presentation of the original manuscript.

Conflict of interest

The author declare that there is no conflict of interests regarding the publication of this manuscript. Abdon Atangana is an editorial board member for AIMS Mathematics and was not involved in the editorial review and/or the decision to publish this article.

References

[1]	M. J. Korenberg, I. W. Hunter, The identification of nonlinear biological systems: Volterra kernel approaches, Ann. Biomed. Eng., 24 (1996), 250–268. https://doi.org/10.1007/BF02648117 doi: 10.1007/BF02648117
[2]	D. K. Campbell, Nonlinear physics: Fresh breather, Nature, 432 (2004), 455–456. https://doi.org/10.1038/432455a doi: 10.1038/432455a
[3]	F. Mosconi, T. Julou, N. Desprat, D. K. Sinha, J. F. Allemand, V. Croquette, Some nonlinear challenges in biology, Nonlinearity, 21 (2008), T131. https://doi.org/10.1088/0951-7715/21/8/T03 doi: 10.1088/0951-7715/21/8/T03
[4]	M. Newman, Power laws, Pareto distributions and Zipf's law, Contemp. Phys., 46 (2005), 323–351. https://doi.org/10.1080/00107510500052444 doi: 10.1080/00107510500052444
[5]	D. M. Mackay, Psychophysics of perceived intensity: A theoretical basis for Fechner's and Stevens' laws, Science, 139 (1963), 1213–1216. https://doi.org/10.1126/science.139.3560.1213.b doi: 10.1126/science.139.3560.1213.b
[6]	J. E. Staddon, Theory of behavioral power functions, Psychol. Rev., 85 (1978), 305–320. https://doi.org/10.1037/0033-295X.85.4.305 doi: 10.1037/0033-295X.85.4.305
[7]	A. Corral, A. Osso, J. E. Llebot, Scaling of tropical cyclone dissipation, Nat. Phys., 6 (2010), 693–696. https://doi.org/doi:10.1038/nphys1725 doi: 10.1038/nphys1725
[8]	R. D. Lorenz, Power law of dust devil diameters on mars and earth, Icarus, 203 (2009), 683–684. https://doi.org/10.1016/j.icarus.2009.06.029 doi: 10.1016/j.icarus.2009.06.029
[9]	W. J. Reed, B. D. Hughes, From gene families and genera to incomes and internet file sizes: Why power laws are so common in nature, Phys. Rev. E., 66 (2002), 067103. https://doi.org/10.1103/PhysRevE.66.067103 doi: 10.1103/PhysRevE.66.067103
[10]	Y. Gerchak, Decreasing failure rates and related issues in the social sciences, Oper. Res., 32 (1984), 537–546. https://doi.org/10.1287/opre.32.3.537 doi: 10.1287/opre.32.3.537
[11]	T. Pritz, Five-parameter fractional derivative model for polymeric damping materials, J. Sound Vibration, 265 (2003), 935–952. https://doi.org/10.1016/S0022-460X(02)01530-4 doi: 10.1016/S0022-460X(02)01530-4
[12]	M. Caputo, Linear model of dissipation whose Q is almost frequency independent–Ⅱ, Geophys. J. R. Astron. Soc., 13 (1967), 529–539. https://doi.org/10.1111/j.1365-246X.1967.tb02303.x doi: 10.1111/j.1365-246X.1967.tb02303.x
[13]	A. Atangana, D. Baleanu, New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model, Thermal Sci., 20 (2016), 763–769. https://doi.org/10.2298/TSCI160111018A doi: 10.2298/TSCI160111018A
[14]	W. M. Whyburn, On the fundamental existence theorems for differential systems, Ann. Math., 30 (1929), 31–38. https://doi.org/10.2307/1968263 doi: 10.2307/1968263
[15]	V. Lakshmikantham, S. Leela, Differential and integral inequalities - Theory and applications, Academic Press, 55 (1969), 3–319.
[16]	A. F. Filippov, The existence of solutions of generalized differential equations, Math. Notes Acad. Sci. USSR, 10 (1971), 608–611. https://doi.org/10.1007/BF01464722 doi: 10.1007/BF01464722
[17]	E. E. Viktorovsky, On a general theorem on the existence of solutions of differential equations, connected with the consideration of integral inequalities, Mat. Sb., 31 (1952), 27–33.
[18]	S. A. Chaplygin, A new method of approximate integration of differential equations, Moscow-Leningrad, 1950.
[19]	O. Perron, Über den Integralbegriff, 1914. https://doi.org/10.11588/diglit.37437
[20]	D. V. Griffiths, I. M. Smith, Numerical methods for engineers, 2 Eds., New York: Chapman and Hall/CRC, 2006. https://doi.org/10.1201/9781420010244
[21]	A. A. Tateishi, H. V. Ribeiro, E. K. Lenzi, The role of fractional time-derivative operators on anomalous diffusion, Front. Phys., 5 (2017), 52. https://doi.org/10.3389/fphy.2017.00052 doi: 10.3389/fphy.2017.00052
[22]	F. Mainardi, Why the Mittag-Leffler function can be considered the queen function of the fractional calculus? Entropy, 22 (2020), 1359. https://doi.org/10.3390/e22121359 doi: 10.3390/e22121359
[23]	J. Sabatier, Fractional-order derivatives defined by continuous Kernels: Are they really too restrictive? Fractal Fract., 4 (2020), 40. https://doi.org/10.3390/fractalfract4030040 doi: 10.3390/fractalfract4030040
[24]	W. Al-Sadi, Z. Wei, I. Moroz, A. Alkhazzan, Existence and stability of solution in Banach space for an impulsive system involving Atangana-Baleanu and Caputo-Fabrizio derivatives, Fractals, 31 (2023), 2340085. https://doi.org/10.1142/S0218348X23400856 doi: 10.1142/S0218348X23400856

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(855) PDF downloads(110) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(1)

AIMS Mathematics

Existence and uniqueness of nonlinear fractional differential equations with the Caputo and the Atangana-Baleanu derivatives: Maximal, minimal and Chaplygin approaches

Related Papers:

Abstract

1. Introduction

2. Global existence and uniqueness via Tychonoff's fixed-point and Perron principle

2.1. Global existence and uniqueness for fractional differential equations with Caputo derivative

2.1.1. Global existence

2.1.2. Uniqueness

2.2. Global existence and uniqueness for fractional differential equations with the Atangana-Baleanu fractional derivative

2.2.1. Existence

2.2.2. Uniqueness

3. Existence of maximal and minimal solution

3.1. Extension of the Chaplygin's existence and uniqueness approach to fractional differential equations with singular and nonsingular kernel

4. Numerical solution

4.1. Application to fractional Bernoulli and Abel nonlinear differential equations

5. Conclusions

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Existence and uniqueness of nonlinear fractional differential equations with the Caputo and the Atangana-Baleanu derivatives: Maximal, minimal and Chaplygin approaches

Related Papers:

Abstract

1. Introduction

2. Global existence and uniqueness via Tychonoff's fixed-point and Perron principle

2.1. Global existence and uniqueness for fractional differential equations with Caputo derivative

2.1.1. Global existence

2.1.2. Uniqueness

2.2. Global existence and uniqueness for fractional differential equations with the Atangana-Baleanu fractional derivative

2.2.1. Existence

2.2.2. Uniqueness

3. Existence of maximal and minimal solution

3.1. Extension of the Chaplygin's existence and uniqueness approach to fractional differential equations with singular and nonsingular kernel

4. Numerical solution

4.1. Application to fractional Bernoulli and Abel nonlinear differential equations

5. Conclusions

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog