Simple PKE schemes from the TSPEM problem

1.   Introduction

Graph theory has proven to be extremely advantageous to the study of different mathematical structures. An exciting relationship between number theory and graph theory was suggested by S. Bryant. He used number theory and graph theory to discuss group structures ^[1]. Interesting results about graphs based on congruences were investigated by P. Erdos and L. Somer ^[2,3]. L. Somer constructed the graphs using integers and established the results for the fixed points, isolated fixed points, semi-regular graph, and the number of components, of the proposed graph ^[3]. Khalid et al. introduced and characterized the notion of hyper totient graph and restricted hyper totient graph ^[4] by utilizing the connection between number theory and graph theory. Haris et al. examined a number of intriguing features and talked about power graphs using prime powers in this drive ^[5]. A. D. Christopher investigated graphs based on the set of moduli, termed a congruence graph. He proposed the conditions under which the congruence graph is complete: connected, bipartite, Hamiltonian, regular, path, and tree graph. He extracted the formulas for the degree sequence of vertices of the graph ^[6].

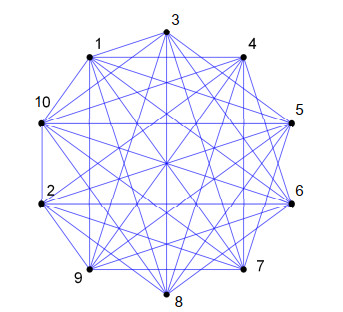
In this paper, we investigate graphs based on prime moduli. The idea is to take all prime numbers that are less than a given integer. We can build a graph by inserting an edge between two vertices if both are congruent with respect to any prime number. This is a new innovation in graphs based on modular arithmetic. Before this idea, the modulus was fixed. In contrast, we are assuming all primes as moduli and residues of given fixed integer as vertices. We characterize these graphs and find results regarding vertex degrees, graph size, chromatic number, domination number, clique number, eccentricity, independence number through the vertex, independence number through edges, covering number through the vertex, and covering number through the edge of the prime congruence simple graphs, together with proofs using number theory. Figure 1 depicts the graph of prime moduli of the integer 10.

2.   Preliminaries

The following results and definitions are important to keep this paper self contained. For proofs of the following results and further details about the idea of a congruence graph, we suggest reading ^[6] and ^[7].

The pair $\mathrm\it{G(V, E)}$ denotes a graph with the vertex set $\mathrm\it{V}$ and edge set $\mathrm\it{E}$. The number of adjacent vertices to any specific vertex $\mathrm\it{t}$ is its $\it{degree}$. If the degree of each vertex of the graph is the same, then the graph is called $\it{regular}$. A vertex $\mathrm\it{u}$ with degree zero is an $\it{isolated\; vertex}$. The total number of edges that are involved in a graph is called the $\it{graph\; size}$. If each pair of distinct vertices is adjacent, then the graph is $\it{complete}$. A graph is said to be $\it{connected}$ if each vertex is reachable from any other vertex. A $\it{path}$ graph is a graph that can be drawn so that all of its vertices and edges lie on a single straight line. A path that starts from a given vertex and ends at the same vertex is called a $\it{cycle}$. A connected graph $\mathrm{G}$ is called a $\it{Hamiltonian\; graph}$ if there is a cycle that includes every vertex of $\it\mathrm{G}$. The distance between any vertex $\mathrm\it{a}$ and the farthest vertex of the graph is called the $\it{eccentricity\; of\; the\; vertex}$ $\mathrm\it{a}$. The minimum eccentricity of the arbitrary vertex of the graph $\mathrm\it{G}$ is called the $\it{radius}$, and the maximum eccentricity of the arbitrary vertex of the graph is termed the $\it{diameter}$ of the graph $\mathrm\it{G}$. A vertex $\it\mathrm{v}$ in a graph $\it\mathrm{G}$ is called a $\it{central\; vertex}$ if the eccentricity of $\it\mathrm{v}$ is identical to the radius of the graph $\it\mathrm{G}$. And if every vertex of $\it\mathrm{G}$ is a central vertex, then $\it\mathrm{G}$ is called $\it{self{-}centered}$. The $\it{complement\; \it\mathrm{\overline{G}}\; of\; a\; graph}$ $\it\mathrm{G}$ is a graph having the same vertices of $\it\mathrm{G}$ such that a pair of vertices is adjacent if and only if they are not adjacent in $\it\mathrm{G}$. The lengths of the longest and shortest cycles in a graph are called the $\it{circumference}$ and $\it{girth}$ of the graph.

In graph theory, the independence of a vertex set is a crucial topic. In any graph $\it\mathrm{G}$, a set of vertices is considered an $\it{independent\; set}$ if no two vertices are adjacent. The cardinality of the largest independent set is called the $\it{vertex\; independence\; number}$ of $\it\mathrm{G}$. $\it{\alpha (\mathrm{G})}$ denotes the vertex independence number of $\it\mathrm{G}$. A subset $\it\mathrm{L}$ of the set of vertices $\it\mathrm{V}$ is called a $\it{cover}$ of the graph if all edges of the graph are covered by $\it\mathrm{L}$. Also, the cardinality of the minimum vertex cover of that graph is known as the $\it{vertex\; covering\; number}$. $\it{\beta (\mathrm{G})}$ denotes the vertex covering number of $\it\mathrm{G}$. A set of edges in a graph is $\it{independent}$ if no two edges in the set are adjacent. The cardinality of the maximum independent set of edges of a graph is called the $\it{edge\; independence\; number}$ of that graph. The edge independence number of a graph $\it\mathrm{G}$ is denoted by $\it{\alpha_{1}(\mathrm{G})}$. A subset $\it\mathrm{F}$ of the set of edges $\it\mathrm{E}$ of the graph $\it\mathrm{G}$, that covers all vertices of $\it\mathrm{G}$ is called an $\it{edge\; cover}$ of the graph. Moreover, the cardinality of the minimum edge cover of a graph $\it\mathrm{G}$ is called the $\it{edge\; covering\; number}$ of the graph $\it\mathrm{G}$. $\it{\beta_{1}(\mathrm{G})}$ represents the edge covering number of the graph.

Theorem 2.1. ^[7] For any graph $\mathrm{G}$ having $\mathrm{n}$ non-isolated vertices.

and,

3.   Congruence graph

In this section, we investigate some new results based on the definition of a congruence graph.

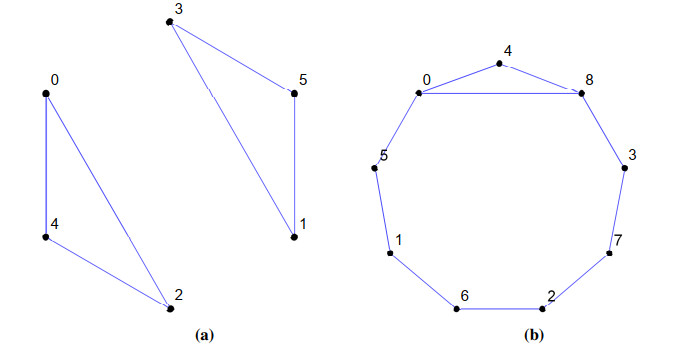
Definition 3.1. ^[6]. Let $\mathrm{n}\geq 3$ be an integer, and the set of moduli $\mathrm{M}\subseteq \mathrm{K}$, where $\mathrm{K} = \{2, 3, \cdots, \mathrm{n}-1\}.$ The congruence graph $\mathrm{G}(\mathrm{n}, \mathrm{\mathrm{M}})$ is the graph in which $\{0, 1, \cdots, \mathrm{n}-1\}$ is the set of vertices and an edge exists between two distinct vertices $\mathrm{s}$ and $\mathrm{t}$ if $\mathrm{s}\equiv \mathrm{t}$ $(mod\; \mathrm{m})$ for some $\mathrm{m}\in \mathrm{M}$.

The graphs in Figure 2 illustrate the idea of a congruence graph.

The congruence graphs are very charming and have many interesting research possibilities. In the following result, we see that the congruence graph is empty if we take a particular singleton set as a moduli set.

Theorem 3.2. If the congruence graph $\mathrm{G}(\mathrm{n}, \mathrm{M})$ has order $\mathrm{n} \geq 5$ and $\mathrm{M} = \{\mathrm{n}-1\}$, then it is an edgeless graph, i.e., $\mathrm{G}(\mathrm{n}, \mathrm{M)}$ is an empty graph.

Proof. For $\mathrm{n} \geq 5$, let $\mathrm{M} = \{\mathrm{n}-1\}.$ Then the vertex set $\mathrm{V}$ is, $\{\mathrm{u_{1}, u_{2}, u_{3}, \cdots, u_{n}}\}$. If the result is false, then not all the vertices of the congruence graph are isolated. So there must exist at least two vertices, $\mathrm{u_{s}}$ and $\mathrm{u_{t}}$, where $\mathrm{s}\neq \mathrm{t}$ such that $\mathrm{u_{s}\equiv u_{t}}(mod\; \mathrm{m})$ for some $\mathrm{u_{s}, u_{t}} \in \mathrm{V}, \mathrm{m}\in \mathrm{M}.$ Since $\mathrm{u_{s}, u_{t}}\leq \mathrm{n}-1$.

contradicting the fact that at least two vertices are adjacent. Hence, no pair of distinct vertices is adjacent. □

Theorem 3.3. Let $\mathrm{n} \geq 6$ be a composite integer and $\mathrm{M} = \{ \mathrm{m}\}$, where $\mathrm{m}$ is the divisor of $\mathrm{n}.$ Then the congruence graph $\mathrm{G}(\mathrm{n}, \mathrm{M})$ is regular, having $\mathrm{m}$ components, and each component will be isomorphic to the complete graph $\mathrm{K}_{\frac{ \mathrm{n}}{\mathrm{m}} -1}$.

Proof. Suppose $\mathrm{n} \geq 6$ is a composite number and $\mathrm{M} = \{\mathrm{m}\}, \mathrm{m|n}$. It is well known that the congruence relation is an equivalence relation on the set of integers, and the vertex set $\mathrm{V} = \{\mathrm{u_{1}, u_{2}, u_{3}, \cdots, u_{n}}\}$ consists of positive integers. Therefore, the congruence relation defines a partition of the vertex set and partitions it into $\mathrm{m}$ classes. Clearly, each class contains $\frac{ \mathrm{n}}{\mathrm{m}}$ elements. Moreover, it is evident that the elements of these equivalent classes are congruent to each other, so vertices in equivalent classes are adjacent to each other. This means that each of the subsets of the vertex set will produce a complete graph. Also, no two vertices of different classes are adjacent to each other, so we will have $\mathrm{m}$ components. Consequently, there must be $\mathrm{m}$ components of complete graphs, and each component will be isomorphic to $\mathrm{K}_{\frac{ \mathrm{n}}{\mathrm{m}}-1}$. □

Corollary 3.4. If $\mathrm{n} = \mathrm{p^{k}}$ and $\mathrm{M} = \{\mathrm{p}\}.$ Then the congruence graph is disconnected and has $\mathrm{p}$ components, and each component is isomorphic to $\mathrm{K_{p^{\{k-1\}}}}-1$.

4.   Prime congruence simple graph

Definition 4.1. Let $\mathrm{n} \geq 5$ be an element of $\mathrm{Z}^{+}$, and let $\mathrm{M_{p}}$ be the set of all primes less than $\mathrm{n}$. A graph $\mathrm{G}(\mathrm{n}, \mathrm{{M_{p}}})$ in which $\mathrm{V} = \{1, 2, 3, \cdots, \mathrm{n}\}$ is the set of vertices and two distinct vertices $\mathrm{c}$ and $\mathrm{d}$ are adjacent if and only if $\mathrm{c}\equiv \mathrm{d}(mod\; \mathrm{m})$ for some $\mathrm{m}$ in $\mathrm{M_{p}}$ is called a prime congruence simple graph (PCSG).

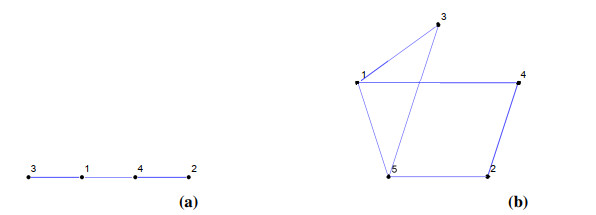
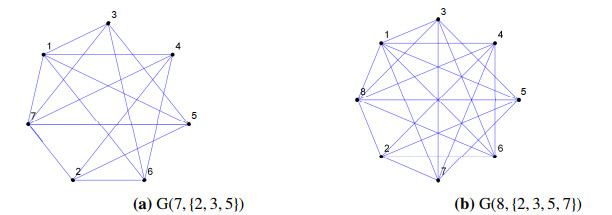
The following graphs in Figure 3 illustrate the idea of prime congruence simple graphs.

Remark. It can be seen that PCSG always produce a complete graph if $\mathrm{M} = \mathrm{M_{p}} \cup \{1\}$. Note that for every two distinct elements $\mathrm{a}$ and $\mathrm{b}$, $\mathrm{a\equiv b}(mod\; 1)$. So each pair of vertices $\mathrm{u_{i}, u_{j}} \in \mathrm{V} = \{\mathrm{u_{1}, u_{2}, u_{3}, \cdots, u_{n}}\}$ are adjacent to each other. Hence, the congruence graph will be complete.

The following theorem 4.2 characterizes the possible path graphs in PCSG.

Theorem 4.2. The PCSG will be a path graph if and only if it has $3$ or $4$ vertices.

Proof. Let PCSG be a path graph for any positive integer $\mathrm{n},$ with $\mathrm{n}\neq 3, 4$. When $\mathrm{n}$ is $1$ or $2$, then by definition, $\mathrm{M}$ must be void, and the graph is not possible. When $\mathrm{n} = 5$, then $\mathrm{u_{1}, u_{2}, u_{3}, u_{4}}$, and $\mathrm{u_{5}}$ are the possible vertices. In this case, $\mathrm{M} = \{2, 3\}$. Clearly, the absolute difference between these vertices is divisible either by $2$ or by $3$. Then vertex $\mathrm{u_{1}}$ will be adjacent to $\mathrm{u_{3}, u_{4}}$, and $\mathrm{u_{5}}$; vertex $\mathrm{u_{2}}$ will be adjacent to $\mathrm{u_{4}}$ and $\mathrm{u_{5}}$, and $\mathrm{u_{3}}$ must be adjacent to $\mathrm{u_{5}}$. If we look into the resultant graph, we note that $\mathrm{u_{1}}\sim \mathrm{u_{4}}\sim \mathrm{u_{2}}\sim \mathrm{u_{5}}\sim \mathrm{u_{3}}\sim \mathrm{u_{1}}$. This means that the graph is a cycle, which is contrary to the fact that PCSG is a path graph. The rest of the cases for $\mathrm{n} = 6, 7, \dots$ can be verified in a similar fashion. Conversely, suppose that PCSG has $3$ or $4$ vertices. When it has $3$ vertices, namely $\mathrm{u_{1}, u_{2}}$, and $\mathrm{u_{3}}$, then the set $\mathrm{M}$ has only one prime, which is $2$. So $\mathrm{u_{1}}$ and $\mathrm{u_{3}}$ are the only adjacent vertices. If $\mathrm{n} = 4$, it has $4$ vertices, namely $\mathrm{u_{1}, u_{2}, u_{3}}$, and $\mathrm{u_{4}}$. In this case, $\mathrm{u_{1}}$ is adjacent to $\mathrm{u_{3}}$ and $\mathrm{u_{4}}$. $\mathrm{u_{2}}$ is adjacent to $\mathrm{u_{4}}$. □

Theorem 4.3. Let $\mathrm{G}(\mathrm{n}, \mathrm{M}_{p})$ be a PCSG of order $\mathrm{n}$ with vertex set $\mathrm{V}.$ Let $\mathrm{u_{i}}\in \mathrm{V}$ be an arbitrary vertex. Then

Proof. Let $\mathrm{G}(\mathrm{n}, \mathrm{M}_{p})$ be a PCSG of order $\mathrm{n}.$ Then, by definition, $\mathrm{V} = \{\mathrm{u_{1}, u_{2}, u_{3}, \cdots, u_{n}} \}$. Note that any two distinct vertices $\mathrm{u_{s}}$, $\mathrm{u_{t}}$ in PCSG are adjacent to each other if and only if $|\mathrm{u}_s-\mathrm{u}_t|\geq 2$, where $1\leq s, t\leq n$. Also, the set $\mathrm{M}$ consists of all primes less than $\mathrm{n}$, so the distinct pair of vertices having an absolute difference greater than or equal to $2$ must be adjacent to each other with respect to some prime modulus $p\in \mathrm{M}$. It is worth mentioning that two consecutive vertices can never be adjacent to each other; hence, the vertex $\mathrm{u_t}$ will not be adjacent to $\mathrm{u_{t-1}}$ and $\mathrm{u_{t+1}}$. While $\mathrm{u_i}$ will be adjacent to all remaining vertices due to having an absolute deviation from $\mathrm{u_i}$ greater than or equal to $2$. This means that the vertex $\mathrm{u_{t}}$ is adjacent to all vertices except $\mathrm{u_{t-1}}$ and $\mathrm{u_{t+1}}$. Moreover, the vertex $\mathrm{u_{t}}$ is not self adjacent since the graph is simple. Consequently, the vertex $\mathrm{u_{1}}$ is not adjacent to $\mathrm{u_{2}}$ only, and hence its degree is $\mathrm{n}-2$. Similarly, the vertex $\mathrm{u_{n}}$ is not connected to $\mathrm{u_{\mathrm{n}-1}}$ only and has degree $\mathrm{n}-2$. Thus, the rest of the vertices have degree $\mathrm{n}-3$. □

The following corollary is a direct consequence of Theorem 4.3.

Corollary 4.4. The PCSG of order $\mathrm{n} \geq 4$ has size $\frac{(\mathrm{n}-1)(\mathrm{n}-2)}{2}$.

Proof. Suppose $\mathrm{u_1, u_2, \cdots, u_n}$ are the $\mathrm{n}$ vertices of a prime congruence simple graph $\mathrm{G}(\mathrm{n}, \mathrm{M_{p}})$. By Theorem 4.3, the degree of the vertices $\mathrm{u_{1}}$, $\mathrm{u_{n}}$ is $\mathrm{n}-2$, and the degree of the remaining $\mathrm{n}-2$ vertices is $\mathrm{n}-3$. Then, by the Handshaking Lemma, the totality of all degrees of the graph having $\mathrm{n}$ vertices is twice the number of edges. That is,

so,

or

□

In graph theory, it is very important to find Hamiltonian paths. We can find the condition for $\mathrm{n}$ such that the PCSG is Hamiltonian. The following corollary characterizes when a PCSG is Hamiltonian by restricting the number of vertices.

Corollary 4.5. For $\mathrm{n} \geq5$ PCSG is Hamiltonian.

Proof. By Theorem 4.3, the vertices $\mathrm{u_{1}}$ and $\mathrm{u_{n}}$ have degrees $\mathrm{n}-2$, and the rest of the vertices have degrees $\mathrm{n}-3$. That is, deg($\mathrm{u_{1}}$) = deg($\mathrm{u_{n}}$) = $\mathrm{n}-2$ and deg($\mathrm{u_{2}}$) = deg($\mathrm{u_{3}}$) = $\cdots$ = deg($\mathrm{u_{\mathrm{n}-1}}) = \mathrm{n}-3$. For $\mathrm{n} \geq6$, it can easily be deduced that deg($\mathrm{u_{i}}$)$\geq$ $\frac{ \mathrm{n}}{2}$. Then, by sufficient condition, Dirac ^[8] compels that PCSG is Hamiltonian. □

A graph that has exactly two odd-degree vertices is called a semi-Eulerian graph. The condition for the prime congruence simple graph to be a semi-Eulerian graph is given in the succeeding corollary.

Corollary 4.6. If $\mathrm{n} \geq 5,$ then PCSG is semi-Eulerian.

Proof. For $\mathrm{n}\geq5$, the vertices $\mathrm{u_1}$ and $\mathrm{u_n}$ have a degree of $\mathrm{n}-2$ and when $\mathrm{n}$ is odd, the degree of $\mathrm{u_1}$ and $\mathrm{u_n}$ will be odd, and the remaining $\mathrm{n}-2$ vertices will have an even degree. So PCSG of odd order is semi-Eulerian. □

Corollary 4.7. The PCSG of order $\mathrm{n} \geq 5$ is a closed walk.

Proof. Suppose a prime congruence simple graph has $\mathrm{n}$ vertices $\mathrm{u_{1}, u_{2}, u_{3}, \cdots, u_{n}}$, where $\mathrm{n} \geq 5$. It is sufficient to show that PCSG has no vertex of degree $1$. By Theorem 4.3, the degree of vertices $\mathrm{u_{1}}$ and $\mathrm{u_{n}}$ is $\mathrm{n}-2$, and the degree of remaining all vertices is $\mathrm{n}-3$. As $\mathrm{n} \geq5$, it is evident that the degree of each vertex is at least $2$. Thus, PCSG will contain no vertex of degree $1$. □

The following Corollary 4.8 can be proven to be similar to Corollary 4.7.

Corollary 4.8. For $\mathrm{n} \geq5$, PCSG has no isolated vertex. That is, PCSG is always connected.

Let $\mathrm{G}$ be any graph, and let $\mathrm{V}$ be the set of vertices. A subset $\mathrm{K}\subseteq \mathrm{V}$ is known as a dominating set if every element of the set $\mathrm{V}\setminus \mathrm{K}$ is adjacent to at least one element of the subset $\mathrm{K}$. If there is no proper subset of $\mathrm{K}$ that is a dominating set for $\mathrm{G}$, then the set $\mathrm{K}$ is called the minimal dominating set. The order of the minimal dominating sets is known as the domination number of the graph $\mathrm{G}$.

Corollary 4.9. For $\mathrm{n} \geq 5$ the domination number of PCSG is $2$.

Proof. In a prime congruence simple graph of $\mathrm{n}$ vertices $\mathrm{u_{1}, u_{2}, \cdots, u_{n}}$, the vertex $\mathrm{u_t}$ is not adjacent to $\mathrm{u_{t-1}}$ and $\mathrm{u_{t+1}}$. And being a simple graph, $\mathrm{u_{t}}$ is also not self adjacent. Thus, the member of every singleton set will not be adjacent to all remaining vertices of the graph. If we choose a set of two consecutive vertices $\{\mathrm{u}_{s}, \mathrm{u}_{t}\}$ then any other vertex must have a prime multiple deviation with one of the vertices in the set. This means that the remaining vertices of the graph are adjacent to either $\mathrm{u}_{s}$ or $\mathrm{u}_{t}$ with respect to that prime modulus. So the set of any two consecutive vertices $\{\mathrm{u}_{s}, \mathrm{u}_{t}\}$ will form the smallest dominating set for the prime congruence simple graph $\mathrm{G}(\mathrm {n}, \mathrm{M_{p}})$. □

Theorem 4.10. For each PCSG of order $\mathrm{n}\geq 5$, ${\mathrm{\overline{G}(n, M_{p})}}\cong \mathrm{P_{n}}$.

Proof. Let $\mathrm{G(n, M_{p})}$ be a prime congruence simple graph of order $\mathrm{n}$. We show that ${\mathrm{\overline{G}(n, M_{p})}}$ is a path graph of order $\mathrm{n}$. In the proof of Theorem $4.3$, we have seen that, for $\mathrm{n}\geq 5$, a pair of consecutive integers is not adjacent in PCSG. This argument leads us to the fact that consecutive integers are adjacent in the complement graph of PCSG. That is, $\mathrm{u_{1}}\sim\mathrm{u_{2}}\sim\mathrm{u_{3}}\sim\cdots\sim\mathrm{u_{n}}$ forms the complement graph of PCSG. This proves the result. □

Theorem 4.11. The circumference and girth of the PCSG of order $\mathrm{n}\geq 5$ are $\mathrm{n}$ and $3$, respectively.

Proof. Consider a prime congruence simple graph of order $\mathrm{n}\geq5$. Let $\{\mathrm{u_{1}}, \mathrm{u_{2}}, \cdots, \mathrm{u_{n}}\}$ be the set of vertices. An arbitrary vertex $\mathrm{u_{i}}$ of the graph is adjacent to the remaining vertices of the graph except $\mathrm{u_{i-1}}$ and $\mathrm{u_{i+1}}$. So the length of the smallest cycle in PCSG is $3$. Now we have the largest cycle in the PCSG. There are two cases, either $\mathrm{n}$ is even or odd.

Case 1. If $\mathrm{n}$ is odd, then $\mathrm{u_{1}}\sim\mathrm{u_{3}}\sim\mathrm{u_{5}}\sim\cdots\sim\mathrm{u_{n}}\sim\mathrm{u_{2}}\sim\mathrm{u_{4}}\sim\cdots\sim\mathrm{u_{n-1}}\sim\mathrm{u_{1}}$ is a required cycle in PCSG that covers all vertices of the graph.

Case 2. If $\mathrm{n}$ is even, then $\mathrm{u_{1}}\sim\mathrm{u_{3}}\sim\mathrm{u_{5}}\sim\cdots\sim\mathrm{u_{n-1}}\sim\mathrm{u_{2}}\sim\mathrm{u_{4}}\sim\cdots\sim\mathrm{u_{n}}\sim\mathrm{u_{1}}$ is a required cycle in PCSG which contains all vertices of the graph. □

Chromatic numbers are among the fundamentals of graph theory. Recall that the chromatic number is the minimum number of colors required to color the graph in such a way that if $\mathrm{uv}\in \mathrm{E}$, then $\mathrm{u}$ and $\mathrm{v}$ are of different colors. In the following theorem, we find the chromatic number of our proposed graph.

Theorem 4.12. For $\mathrm{n} \geq 4$,

where $\gamma (G(\mathrm{n}, M_{p}))$ represents the chromatic number of the prime congruence simple graph.

Proof. Consider a prime congruence simple graph with $\mathrm {n}$ vertices $\mathrm{u_{1}, u_{2}, u_{3}, \cdots, u_{n}}$ where $\mathrm{n} \geq 4$. Suppose that the vertex $\mathrm{u_{1}}$ is assigned the color $C_{1}$. As $\mathrm{u_{1}}$ is not connected to $\mathrm{u_{2}}$ but connected to all other vertices of the graph, $\mathrm{u_{2}}$ can be given the color $C_{1}$, but none of the remaining vertices can be assigned the color $C_{1}$. Also, $\mathrm{u_{3}}$ and $\mathrm{u_{4}}$ are not adjacent, so both can be assigned the color $C_{2}$. Continuing in a similar way reveals that only two vertices, $\mathrm{u_{s}}$ and $\mathrm{u_{t}}$ in the whole graph can have the same color if $|\mathrm{u}_s-\mathrm{u}_t| = 1$. So if PCSG has an even number of vertices, then the graph has $\frac{ \mathrm{n}}{2}$ colors. By a similar argument, if $\mathrm{n}$ is odd, then their must be $\frac{\mathrm {n}-1}{2}$ different colors with one vertex left. We assign this vertex a new color. Thus, we need to have $\frac{\mathrm{n}-1}{2}+1 = \frac{ \mathrm{n}+1}{2}$ different colors. □

For an arbitrary vertex $\mathrm{u}$ in $\mathrm{G}$, the maximum distance of the vertex $\mathrm{u}$ from all other vertices of the graph $\mathrm{G}$ is known as the eccentricity of the $\mathrm{u}$.

Theorem 4.13. For $\mathrm{n} \geq 5$ the eccentricity of every vertex in PCSG is $2$.

Proof. In a prime congruence simple graph of order $\mathrm{n} \geq 5$, each vertex $\mathrm{u_{t}}\in \mathrm{V}$ has an edge with all vertices of the graph except $\mathrm{u_{t-1}}$, $\mathrm{u_{t}}$ and $\mathrm{u_{t+1}}$. Also by Theorem 4.3, $deg(\mathrm{u_{t}})\geq 2$, $\forall n\geq 5$. Thus, there is no vertex of degree $1$ or zero. Now if we denote by $d_{ij}$ the distance of the vertices $i$ and $j$, then we conclude that

Consequently, the largest possible distance between two distinct vertices $\mathrm{u}_{i}$ and $\mathrm{u}_{j}, i\neq j$ is always $2$. □

Corollary 4.14. For $\mathrm{n} \geq 5$, each vertex in PCSG is central.

The diameter of the graph is the maximum possible distance between distinct pairs of vertices. Let $d_i$ be the farthest distances from a vertex $\mathrm{u}$ to all other vertices of a graph, and $d$ be the minimum of all $d_i$'s. Then $d$ is termed the as radius of the graph $\mathrm{G}$ and is denoted by $r(\mathrm{G})$. And the set of all vertices whose eccentricity is a fixed minimum number will form the center of the graph.

The following observation can be proved easily by using the notion of eccentricity.

Remark. (a) In PCSG, diameter = radius = 2.

(b) PCSG is a self-centered graph.

Theorem 4.15. For each PCSG of order $\mathrm{n} \geq 5$, $\alpha(\mathrm{G(\mathrm {n}, \mathrm{M}_{p})}) = 2$ and $\beta(\mathrm{G(\mathrm{n}, \mathrm{M}_{p})}) = \mathrm{n}-2$.

Proof. In PCSG of order $\mathrm{n} \geq 5$, every two consecutive vertices $\mathrm{u}_{s}$ and $\mathrm{u}_{t}$, where $|\mathrm{u}_s-\mathrm{u}_t| = 1$, are not adjacent. We claim that the set of vertices $\{\mathrm{u_{i}, u_{j}}\}$ with $1$ deviation forms the largest independent set for the PCSG. Consider the set with $3$ vertices, $\mathrm{u}_{1}, \mathrm{u}_{2}$ and $\mathrm{u_{3}}$. As $3\equiv1(mod\; 2)$, $\mathrm{u_1}$ and $\mathrm{u_3}$ are adjacent, that is, have an edge. A similar result can be proved for any set with more than three vertices. Thus the set of vertices $\{\mathrm {u}_{s}, \mathrm{u}_{t}\}$ with deviation $1$ is the largest independent set. Therefore, $\alpha(\mathrm{G(\mathrm{n}, \mathrm{M}_{p})}) = 2$. So by Theorem 2.1, $\beta (\mathrm{G(\mathrm{n}, \mathrm{M}_{p})}) = \mathrm{n}-2$. □

Theorem 4.16. For each PCSG of order $\mathrm{n} \geq 5$,

where $\alpha_{1}(\mathrm{G(\mathrm{n}, \mathrm{M}_{p})})$ and $\beta_{1}(\mathrm{G(\mathrm {n}, \mathrm{M}_{p})})$ denote the edge independence number and edge covering number of $\mathrm{G(\mathrm{n}, \mathrm{M}_{p})}$, respectively; each of these two is computed through edges.

Proof. In PCSG of order $\mathrm{n} \geq 5$, $\mathrm{u_{1}}$ is adjacent to all other vertices except $\mathrm{u_{2}}$. And the vertex $\mathrm{u_{2}}$ is adjacent to all other vertices except $\mathrm{u_{1}}$ and $\mathrm{u_{3}}$. Similarly, $\mathrm{u_{3}}$ is connected to all vertices except $\mathrm{u_{2}}$ and $\mathrm{u_{4}}$, and continuing in the same way, all vertices are connected. Now we want to find a set of independent edges. That is, no pair of edges in a set is adjacent. We construct the desired set in this manner.

These are $\frac{ \mathrm{n}}{2}$ in number, if $\mathrm{n}$ is even. The other cases can be proved similarly.

For instance, Figure 4(a) yields that the edges $1-3,$ $5-7,$ and $2-4$ are independent edges, and these are three in number for $\mathrm{n} = 7$. And the edges $1-3$, $5-7$, $2-4$, and $6-8$ are independent, and these are $4$ in number for $\mathrm{n} = 8$, which is revealed from Figure 4(b). □

For any graph $\mathrm{G}$, the complete subgraph $\mathrm{G_{1}}$ of the graph $\mathrm{G}$ is called the clique of $\mathrm{G}$. The clique number $\omega(\mathrm{G})$ is the size of the largest clique in a graph $\mathrm{G}$ ^[7].

Theorem 4.17. For each PCSG having order $\mathrm{n} \geq 5$,

Proof. By definition of PCSG, the vertex $\mathrm{u_{1}}$ is connected to all vertices except the vertices whose absolute deviation from $\mathrm{u_{1}}$ is zero or one. In that case, these vertices cannot define an edge with respect to a prime modulus. Thus, in the vertex set $\mathrm{V} = \{ \mathrm{u_{i}}|\mathrm{u_{i}} = i, i\in N\}$, all even vertices are connected to each other, as absolute differences are divisible by some prime number. Hence, the set of all even vertices forms a clique. In the same way, the set of all odd integer vertices forms a clique. As the set of vertices $\mathrm{V}$ begins with an integer $1$, so the number of odd integers is greater or equal to the number of even integers. Consequently, the set of all odd integer vertices will form the largest clique.

Therefore $\omega (\mathrm{G}(\mathrm{n}, \mathrm{M}_{p})) = \frac{ \mathrm{n}}{2}$ if $\mathrm{n}\equiv 0(mod\; 2)$ and $\frac{ \mathrm{n}+1}{2}$ if $\mathrm{n}$ is $\mathrm{n}\equiv 1(mod\; 2)$. □

5.   Applications via modular arithmetic

Congruence plays a crucial role in geometry and design. Graphs and congruences are highly correlated, as both assist in analyzing objects. The concept of PCSG is instrumental in resolving specific congruence relations.

Theorem 5.1. For $\mathrm{n} \geq4$ and $\mathrm{n}\in Z^{+}$, the linear congruence equation,

is solvable, and deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ in PCSG of order $\mathrm{n}$ is a solution. Here, $\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ represents the greatest integer less than or equal to $\frac{ \mathrm{n}}{2}$.

Proof. In a prime congruence simple graph of order $\mathrm{n}$, the degree of any vertex $\mathrm{u}$ is either $\mathrm{n}-2$ or $\mathrm{n}-3$ by Theorem 4.3. In particular, deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is either $\mathrm{n}-2$ or $\mathrm{n}-3$. But if $\mathrm{n} \geq4$, then deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$, because $\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is neither equal to $1$ nor $\mathrm{n}$. We prove that deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is the solution of the linear congruence

There are two possibilities: either $\mathrm{n}$ is even or odd.

Case 1. When $\mathrm{n}$ is even, then $(\mathrm{n}-1)\equiv 1(mod\; 2)$, $(\mathrm{n}+1)\equiv1(mod\; 2)$, and $(\mathrm{n}-3)\equiv 1(mod\; 2)$. This means that $(\mathrm {n}-1)(\mathrm{n}-3)\equiv 1(mod\; 2)$. It is evident that $(\mathrm{n}-1)(\mathrm{n}-3)\equiv (\mathrm{n}+1)(mod\; 2)$. Thus, deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is the solution of the linear congruence equation.

Case 2. When $\mathrm{n}$ is odd, then $(\mathrm{n}-1)\equiv 0(mod\; 2)$, $(\mathrm{n}+1)\equiv0(mod\; 2)$ and $(\mathrm{n}-3)\equiv 0(mod\; 2)$. Also, $(\mathrm{n}-1)(\mathrm{n}-3)\equiv 0(mod\; 2)$. So, $(\mathrm{n}-1)(\mathrm{n}-3)(\mathrm{n}+1)\equiv0(mod\; 2)$. Thus, deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is the solution to the congruence. □

Theorem 5.2. Let $\mathrm{n} \geq4$, $\mathrm{n}\in \mathrm{Z}^{+}$, and of the form $3m$ or $3m+2.$ Then, the linear congruence equation,

is solvable, and deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ in PCSG of order $\mathrm{n}$ is the solution. Here, $\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ represents the greatest integer less than or equal to $\frac{ \mathrm{n}}{2}$.

Proof. In a prime congruence simple graph of order $\mathrm{n}$, the deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is $\mathrm {n}-3$, as discussed in Theorem 4.3. We prove that deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is the solution of the linear congruence,

As $\mathrm{n}$ is of the form $3m$, or $3m+2$, there are two possibilities.

Case 1. When $\mathrm{n}$ is of the form $3m$, then $(\mathrm {n}+2)\equiv 2(mod\; 3)$, $n\equiv0(mod\; 3)$ and $(\mathrm {n}-3)\equiv 0(mod\; 3)$. Being a product of the form $3m+2$ and $3m$, $(\mathrm{n}+2)(\mathrm{n}-3)$ is of the form $3m$. That is, $(\mathrm{n}+2)(\mathrm{n}-3)\equiv 0(mod\; 3)$. Moreover, $(\mathrm{n}+2)(\mathrm{n}-3)\equiv n(mod\; 2)$. Thus, deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is the solution.

Case 2. When $\mathrm{n}$ is of the form $3m+2$, then $(\mathrm{n}+2)\equiv 1(mod\; 3)$, $n\equiv2(mod\; 3)$, and $(\mathrm{n}-3)\equiv 2(mod\; 3)$. $(\mathrm{n}+2)(\mathrm {n}-3)$ will be of the form $3m+2$, being the product of the forms $3m+1$ and $3m+2$. That is, $(\mathrm {n}+2)(\mathrm {n}-3)\equiv 2(mod\; 3)$. Moreover, $(\mathrm{n}+2)(\mathrm{n}-3)\equiv n(mod\; 3)$. Thus, deg$\lfloor {\frac{ \mathrm {n}}{2}}\rfloor$ is the solution. □

Theorem 5.3. For each positive integer $\mathrm{n} \geq4$ of the form $3m+1$, the linear congruence equation,

is solvable, and deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ in PCSG of order $\mathrm{n}$ is the solution. Here, $\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ represents the greatest integer less than or equal to $\frac{ \mathrm{n}}{2}$.

Proof. As we have discussed in Theorem 4.3, in a prime congruence simple graph of order $\mathrm{n}$, the deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is $\mathrm{n}-3$. We prove that deg$\lfloor {\frac{ \mathrm{n}}{2}}\rfloor$ is a solution to the linear congruence

As $\mathrm{n}$ is of the form $3m+1$, so $(\mathrm{n}-1)\equiv 0(mod\; 3)$, $(\mathrm{n}-3)\equiv1(mod\; 3)$, and $(\mathrm{n}+2)\equiv 0(mod\; 3)$. Also, $(\mathrm{n}-1)(\mathrm{n}-3)$ is of the form $3m$. That is, $(\mathrm{n}-1)(\mathrm{n}-3)\equiv 0(mod\; 3)$. Moreover, $(\mathrm{n}-1)(\mathrm{n}-3)\equiv (\mathrm{n}+2)(mod\; 3)$. Thus, deg$\lfloor {\frac{n}{2}}\rfloor$ is the solution. □

6.   Conclusions

In this article, we introduced the notion of prime congruence simple graphs (PCSG). We characterized the class of prime congruence simple graphs and established conditions under which PCSG is a complete graph, a path graph, a disconnected graph, or a connected graph. We also determined the size, eccentricity, diameter, radius, chromatic number, edge covering number, edge independence number, vertex covering number, vertex independence number, and clique number of the graph. Moreover, we proved that the prime congruence simple graph of order $\mathrm{n} \geq 5$ is always Hamiltonian and also semi-Eulerian if the order of the graph is odd. We have also examined the enumeration of components of the congruence graph. In the future, we will extend this approach to group theory, ring theory, and different algebraic structures.

Author contributions

Sufyan Asif: Formal Analysis, Writing original draft; Muhammad Khalid Mahmood: Supervision; Amal S. Alali: Validation; Abdullah A. Zagaan: Validation.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to Princess Nourah bint Abdulrahman University for funding this research under Researchers Supporting Project number (PNURSP2024R231), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare no conflict of interest.